Abstract
We introduce a new approach to functional causal modeling from observational data, called Causal Generative Neural Networks (CGNN). CGNN leverages the power of neural networks to learn a generative model of the joint distribution of the observed variables, by minimizing the Maximum Mean Discrepancy between generated and observed data. An approximate learning criterion is proposed to scale the computational cost of the approach to linear complexity in the number of observations. The performance of CGNN is studied throughout three experiments. Firstly, CGNN is applied to cause-effect inference, where the task is to identify the best causal hypothesis out of “X → Y ” and “Y → X”. Secondly, CGNN is applied to the problem of identifying v-structures and conditional independences. Thirdly, CGNN is applied to multivariate functional causal modeling: given a skeleton describing the direct dependences in a set of random variables X = [X 1, …, X d], CGNN orients the edges in the skeleton to uncover the directed acyclic causal graph describing the causal structure of the random variables. On all three tasks, CGNN is extensively assessed on both artificial and real-world data, comparing favorably to the state-of-the-art. Finally, CGNN is extended to handle the case of confounders, where latent variables are involved in the overall causal model.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The so-called constraint-based methods base the recovery of graph structure on conditional independence tests. In general, proofs of model identifiability assume the existence of an “oracle” providing perfect knowledge of the CIs, i.e. de facto assuming an infinite amount of training data.
- 2.
After Ramsey (2015), in the linear model with Gaussian variable case the individual BIC score to minimize for a variable X given its parents is up to a constant n ln(s) + c k ln(n), where n ln(s) is the likelihood term, with s the residual variance after regressing X onto its parents, and n the number of data samples. c k ln(n) is a penalty term for the complexity of the graph (here the number of edges). k = 2p + 1, with p the total number of parents of the variable X in the graph. c = 2 by default, chosen empirically. The global score minimized by the algorithm is the sum over all variables of the individual BIC score given the parent variables in the graph.
- 3.
These methods can be extended to the multivariate case and used for causal graph identification by orienting each edge in turn.
- 4.
In some specific cases, such as in the bivariate linear FCM with Gaussian noise and Gaussian input, even by restricting the class of functions considered, the DAG cannot be identified from purely observational data (Mooij et al. 2016).
- 5.
The first four datasets are available at http://dx.doi.org/10.7910/DVN/3757KX. The Tuebingen cause-effect pairs dataset is available at https://webdav.tuebingen.mpg.de/cause-effect/.
- 6.
Using the R program available at https://github.com/ssamot/causality for ANM, IGCI, PNL, GPI and LiNGAM.
- 7.
The data generator is available at https://github.com/GoudetOlivie/CGNN. The datasets considered are available at http://dx.doi.org/10.7910/DVN/UZMB69.
- 8.
The datasets considered are available at http://dx.doi.org/10.7910/DVN/UZMB69.
References
Bühlmann, P., Peters, J., Ernest, J., et al. (2014). Cam: Causal additive models, high-dimensional order search and penalized regression. The Annals of Statistics, 42(6):2526–2556.
Chickering, D. M. (2002). Optimal structure identification with greedy search. Journal of Machine Learning Research, 3(Nov):507–554.
Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., and Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv.
Colombo, D. and Maathuis, M. H. (2014). Order-independent constraint-based causal structure learning. Journal of Machine Learning Research, 15(1):3741–3782.
Colombo, D., Maathuis, M. H., Kalisch, M., and Richardson, T. S. (2012). Learning high-dimensional directed acyclic graphs with latent and selection variables. The Annals of Statistics, pages 294–321.
Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals, and Systems (MCSS), 2(4):303–314.
Daniusis, P., Janzing, D., Mooij, J., Zscheischler, J., Steudel, B., Zhang, K., and Schölkopf, B. (2012). Inferring deterministic causal relations. arXiv preprint arXiv:1203.3475.
Drton, M. and Maathuis, M. H. (2016). Structure learning in graphical modeling. Annual Review of Statistics and Its Application, (0).
Edwards, R. (1964). Fourier analysis on groups.
Fonollosa, J. A. (2016). Conditional distribution variability measures for causality detection. arXiv preprint arXiv:1601.06680.
Goldberger, A. S. (1984). Reverse regression and salary discrimination. Journal of Human Resources.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014). Generative adversarial nets. In Neural Information Processing Systems (NIPS), pages 2672–2680.
Gretton, A., Borgwardt, K. M., Rasch, M., Schölkopf, B., Smola, A. J., et al. (2007). A kernel method for the two-sample-problem. 19:513.
Gretton, A., Herbrich, R., Smola, A., Bousquet, O., and Schölkopf, B. (2005). Kernel methods for measuring independence. Journal of Machine Learning Research, 6(Dec):2075–2129.
Guyon, I. (2013). Chalearn cause effect pairs challenge.
Guyon, I. (2014). Chalearn fast causation coefficient challenge.
Hinton, G., Deng, L., Yu, D., Dahl, G. E., Mohamed, A.-r., Jaitly, N., Senior, A., Vanhoucke, V., Nguyen, P., Sainath, T. N., et al. (2012). Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine.
Hoyer, P. O., Janzing, D., Mooij, J. M., Peters, J., and Schölkopf, B. (2009). Nonlinear causal discovery with additive noise models. In Neural Information Processing Systems (NIPS), pages 689–696.
Kalisch, M., Mächler, M., Colombo, D., Maathuis, M. H., Bühlmann, P., et al. (2012). Causal inference using graphical models with the r package pcalg. Journal of Statistical Software, 47(11):1–26.
Kingma, D. P. and Ba, J. (2014). Adam: A Method for Stochastic Optimization. ArXiv e-prints.
Kingma, D. P. and Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. NIPS.
Lopez-Paz, D. (2016). From dependence to causation. PhD thesis, University of Cambridge.
Lopez-Paz, D., Muandet, K., Schölkopf, B., and Tolstikhin, I. O. (2015). Towards a learning theory of cause-effect inference. In ICML, pages 1452–1461.
Lopez-Paz, D. and Oquab, M. (2016). Revisiting classifier two-sample tests. arXiv preprint arXiv:1610.06545.
Mendes, P., Sha, W., and Ye, K. (2003). Artificial gene networks for objective comparison of analysis algorithms. Bioinformatics, 19(suppl_2):ii122–ii129.
Mooij, J. M., Peters, J., Janzing, D., Zscheischler, J., and Schölkopf, B. (2016). Distinguishing cause from effect using observational data: methods and benchmarks. Journal of Machine Learning Research, 17(32):1–102.
Nandy, P., Hauser, A., and Maathuis, M. H. (2015). High-dimensional consistency in score-based and hybrid structure learning. arXiv preprint arXiv:1507.02608.
Ogarrio, J. M., Spirtes, P., and Ramsey, J. (2016). A hybrid causal search algorithm for latent variable models. In Conference on Probabilistic Graphical Models, pages 368–379.
Pearl, J. (2003). Causality: models, reasoning and inference. Econometric Theory, 19(675-685):46.
Pearl, J. (2009). Causality. Cambridge university press.
Pearl, J. and Verma, T. (1991). A formal theory of inductive causation. University of California (Los Angeles). Computer Science Department.
Peters, J. and Bühlmann, P. (2013). Structural intervention distance (sid) for evaluating causal graphs. arXiv preprint arXiv:1306.1043.
Peters, J., Janzing, D., and Schölkopf, B. (2017). Elements of Causal Inference - Foundations and Learning Algorithms. MIT Press.
Quinn, J. A., Mooij, J. M., Heskes, T., and Biehl, M. (2011). Learning of causal relations. In ESANN.
Ramsey, J. D. (2015). Scaling up greedy causal search for continuous variables. arXiv preprint arXiv:1507.07749.
Richardson, T. and Spirtes, P. (2002). Ancestral graph markov models. The Annals of Statistics, 30(4):962–1030.
Sachs, K., Perez, O., Pe’er, D., Lauffenburger, D. A., and Nolan, G. P. (2005). Causal protein-signaling networks derived from multiparameter single-cell data. Science, 308(5721):523–529.
Scheines, R. (1997). An introduction to causal inference.
Sgouritsa, E., Janzing, D., Hennig, P., and Schölkopf, B. (2015). Inference of cause and effect with unsupervised inverse regression. In AISTATS.
Shen-Orr, S. S., Milo, R., Mangan, S., and Alon, U. (2002). Network motifs in the transcriptional regulation network of escherichia coli. Nature genetics, 31(1):64.
Shimizu, S., Hoyer, P. O., Hyvärinen, A., and Kerminen, A. (2006). A linear non-gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(Oct):2003–2030.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., Schrittwieser, J., Antonoglou, I., Panneershelvam, V., Lanctot, M., et al. (2016). Mastering the game of Go with deep neural networks and tree search. Nature.
Spirtes, P., Glymour, C., and Scheines, R. (1993). Causation, prediction and search. 1993. Lecture Notes in Statistics.
Spirtes, P., Glymour, C. N., and Scheines, R. (2000). Causation, prediction, and search. MIT press.
Spirtes, P., Meek, C., Richardson, T., and Meek, C. (1999). An algorithm for causal inference in the presence of latent variables and selection bias.
Spirtes, P. and Zhang, K. (2016). Causal discovery and inference: concepts and recent methodological advances. In Applied informatics, volume 3, page 3. Springer Berlin Heidelberg.
Statnikov, A., Henaff, M., Lytkin, N. I., and Aliferis, C. F. (2012). New methods for separating causes from effects in genomics data. BMC genomics, 13(8):S22.
Stegle, O., Janzing, D., Zhang, K., Mooij, J. M., and Schölkopf, B. (2010). Probabilistic latent variable models for distinguishing between cause and effect. In Neural Information Processing Systems (NIPS), pages 1687–1695.
Tsamardinos, I., Brown, L. E., and Aliferis, C. F. (2006). The max-min hill-climbing bayesian network structure learning algorithm. Machine learning, 65(1):31–78.
Van den Bulcke, T., Van Leemput, K., Naudts, B., van Remortel, P., Ma, H., Verschoren, A., De Moor, B., and Marchal, K. (2006). Syntren: a generator of synthetic gene expression data for design and analysis of structure learning algorithms. BMC bioinformatics, 7(1):43.
Verma, T. and Pearl, J. (1991). Equivalence and synthesis of causal models. In Proceedings of the Sixth Annual Conference on Uncertainty in Artificial Intelligence, UAI ’90, pages 255–270, New York, NY, USA. Elsevier Science Inc.
Yamada, M., Jitkrittum, W., Sigal, L., Xing, E. P., and Sugiyama, M. (2014). High-dimensional feature selection by feature-wise kernelized lasso. Neural computation, 26(1):185–207.
Zhang, K. and Hyvärinen, A. (2009). On the identifiability of the post-nonlinear causal model. In Proceedings of the twenty-fifth conference on uncertainty in artificial intelligence, pages 647–655. AUAI Press.
Zhang, K., Peters, J., Janzing, D., and Schölkopf, B. (2012). Kernel-based conditional independence test and application in causal discovery. arXiv preprint arXiv:1202.3775.
Zhang, K., Wang, Z., Zhang, J., and Schölkopf, B. (2016). On estimation of functional causal models: general results and application to the post-nonlinear causal model. ACM Transactions on Intelligent Systems and Technology (TIST), 7(2):13.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
1.1 The Maximum Mean Discrepancy (MMD) Statistic
The Maximum Mean Discrepancy (MMD) statistic (Gretton et al. 2007) measures the distance between two probability distributions P and \(\hat {P}\), defined over \(\mathbb {R}^d\), as the real-valued quantity
Here, \(\mu _k = \int k(x, \cdot ) \mathrm {d} P(x)\) is the kernel mean embedding of the distribution P, according to the real-valued symmetric kernel function \(k(x, x') = \langle k(x, \cdot ), k(x', \cdot ) \rangle _{\mathcal {H}_k}\) with associated reproducing kernel Hilbert space \(\mathcal {H}_k\). Therefore, μ k summarizes P as the expected value of the features computed by k over samples drawn from P.
In practical applications, we do not have access to the distributions P and \(\hat {P}\), but to their respective sets of samples \(\mathcal {D}\) and \(\hat {\mathcal {D}}\), defined in Sect. 4.2.1. In this case, we approximate the kernel mean embedding μ k(P) by the empirical kernel mean embedding \(\mu _k(\mathcal {D}) = \frac {1}{|\mathcal {D}|} \sum _{x \in \mathcal {D}} k(x, \cdot )\), and respectively for \(\hat {P}\). Then, the empirical MMD statistic is
Importantly, the empirical MMD tends to zero as n →∞ if and only if \(P = \hat {P}\), as long as k is a characteristic kernel (Gretton et al. 2007). This property makes the MMD an excellent choice to model how close the observational distribution P is to the estimated observational distribution \(\hat {P}\). Throughout this paper, we will employ a particular characteristic kernel: the Gaussian kernel \(k(x, x') = \exp (- \gamma \| x - x' \|{ }_2^2)\), where γ > 0 is a hyperparameter controlling the smoothness of the features.
In terms of computation, the evaluation of \(\text{MMD}_k(\mathcal {D}, \hat {\mathcal {D}})\) takes O(n 2) time, which is prohibitive for large n. When using a shift-invariant kernel, such as the Gaussian kernel, one can invoke Bochner’s theorem (Edwards 1964) to obtain a linear-time approximation to the empirical MMD (Lopez-Paz et al. 2015), with form
and O(mn) evaluation time. Here, the approximate empirical kernel mean embedding has form
where w i is drawn from the normalized Fourier transform of k, and b i ∼ U[0, 2π], for i = 1, …, m. In our experiments, we compare the performance and computation times of both \(\widehat {\text{MMD}}_k\) and \(\widehat {\text{MMD}}_k^m\).
1.2 Proofs
Proposition 1
Let X = [X 1, …, X d] denote a set of continuous random variables with joint distribution P, and further assume that the joint density function h of P is continuous and strictly positive on a compact and convex subset of \(\mathbb {R}^{d}\) , and zero elsewhere. Letting \(\mathcal {G}\) be a DAG such that P can be factorized along \(\mathcal {G}\) ,
there exists f = (f 1, …, f d) with f i a continuous function with compact support in \(\mathbb {R}^{|\mathit{\text{Pa}}({i}; \mathcal {G})|}\times [0,1]\) such that P(X) equals the generative model defined from FCM \(({\mathcal {G}}, f, {\mathcal {E}})\) , with \({\mathcal {E}} = \mathcal {U}[0,1]\) the uniform distribution on [0, 1].
Proof
By induction on the topological order of \(\mathcal {G}\). Let X i be such that \(|\text{Pa}({i}; \mathcal {G})|=0\) and consider the cumulative distribution F i(x i) defined over the domain of X i (F i(x i) = Pr(X i < x i)). F i is strictly monotonous as the joint density function is strictly positive therefore its inverse, the quantile function Q i : [0, 1]↦dom(X i) is defined and continuous. By construction, \(Q_i(e_i) =F_i^{-1}(e_i)\) and setting Q i = f i yields the result.
Assume f i be defined for all variables X i with topological order less than m. Let X j with topological order m and Z the vector of its parent variables. For any noise vector \(e = (e_i, i \in \text{Pa}({j}; \mathcal {G}))\) let \(z = (x_i, i \in \text{Pa}({j}; \mathcal {G}))\) be the value vector of variables in Z defined from e. The conditional cumulative distribution F j(x j|Z = z) = Pr(X j < x j|Z = z) is strictly continuous and monotonous wrt x j, and can be inverted using the same argument as above. Then we can define \(f_j(z,e_j) = F_j^{-1}(z,e_j)\).
Let K j = dom(X j) and \(K_{\text{Pa}({j}; \mathcal {G})} = dom(Z)\). We will show now that the function f j is continuous on \(K_{\text{Pa}({j}; \mathcal {G})} \times [0,1]\), a compact subset of \(\mathbb {R}^{|\text{Pa}({j}; \mathcal {G})|}\times [0,1]\).
By assumption, there exist \(a_j \in \mathcal {R}\) such that, for \((x_j, z) \in K_j \times K_{\text{Pa}({j}; \mathcal {G})}\), \(F(x_j|z) = \int _{a_j}^{x_j} \frac {h_j(u,z)}{h_j(z)} \mathrm {d}u\), with h j a continuous and strictly positive density function. For \((a,b) \in K_j \times K_{\text{Pa}({j}; \mathcal {G})}\), as the function \((u, z) \rightarrow \frac {h_j(u,z)}{h_j(z)}\) is continuous on the compact \(K_j \times K_{\text{Pa}({j}; \mathcal {G})}\), \(\lim \limits _{\substack {x_j \rightarrow a}} F(x_j|z) = \int _{a_j}^{a} \frac {h_j(u,z)}{h_j(z)} \mathrm {d}u\) uniformly on \(K_{\text{Pa}({j}; \mathcal {G})}\) and \(\lim \limits _{\substack {z \rightarrow b}} F(x_j|z) = \int _{a_j}^{x_j} \frac {h_j(u,b)}{h_j(b)}\) on K j, according to exchanging limits theorem, F is continuous on (a, b).
For any sequence z n → z, we have that F(x j|z n) → F(x j|z) uniformly in x j. Let define two sequences u n and x j,n, respectively on [0, 1] and K j, such that u n → u and x j,n → x j. As F(x j|z) = u has unique root x j = f j(z, u), the root of F(x j|z n) = u n, that is, x j,n = f j(z n, u n) converge to x j. Then the function (z, u) → f j(z, u) is continuous on \(K_{\text{Pa}({i}; \mathcal {G})} \times [0,1]\).
Proposition 2
For m ∈ [[1, d]], let Z m denote the set of variables with topological order less than m and let d m be its size. For any d m -dimensional vector of noise values e (m) , let z m(e (m)) (resp. \(\widehat {z_m}(e^{(m)})\) ) be the vector of values computed in topological order from the FCM \(({\mathcal {G}}, f, {\mathcal { E}})\) (resp. the CGNN \(({\mathcal {G}}, \hat {f}, {\mathcal {E}})\) ). For any 𝜖 > 0, there exists a set of networks \(\hat {f}\) with architecture \(\mathcal {G}\) such that
Proof
By induction on the topological order of \(\mathcal {G}\). Let X i be such that \(|\text{Pa}({i}; \mathcal {G})|=0\). Following the universal approximation theorem Cybenko (1989), as f i is a continuous function over a compact of \(\mathbb {R}\), there exists a neural net \(\hat {f_{i}}\) such that \(\|f_i - \hat {f_{i}}\|{ }_\infty < \epsilon /d_1\). Thus Eq. (14) holds for the set of networks \(\hat {f_i}\) for i ranging over variables with topological order 0.
Let us assume that Proposition 2 holds up to m, and let us assume for brevity that there exists a single variable X j with topological order m + 1. Letting \(\hat {f_j}\) be such that \(\|f_j - \hat {f_j}\|{ }_\infty < \epsilon /3\) (based on the universal approximation property), letting δ be such that for all u \(\|\hat f_j(u) - \hat f_j(u+\delta )\|< \epsilon /3\) (by absolute continuity) and letting \(\hat f_i\) satisfying Eq. (14) for i with topological order less than m for min(𝜖∕3, δ)∕d m, it comes: \(\|(z_m,f_j(z_m,e_j)) - (\hat z_m,\hat {f_j}(\hat {z_m}, e_j))\| \le \|z_m - \hat z_m\| + |f_j(z_m,e_j) - \hat {f_j}(z_m, e_j)| + | \hat {f_j}(z_m,e_j) - \hat {f_j}(\hat {z_m}, e_j)| < \epsilon /3 + \epsilon /3 + \epsilon /3\), which ends the proof.
Proposition 3
Let \(\mathcal {D}\) be an infinite observational sample generated from \(({\mathcal {G}}, f, {\mathcal {E}})\) . With same notations as in Proposition 2 , for every sequence 𝜖 t such that 𝜖 t > 0 goes to zero when t →∞, there exists a set \(\widehat {f_t} = (\hat f^{t}_1 \ldots \hat f^{t}_d)\) such that \(\widehat {\mathit{\text{MMD}}_k}\) between \(\mathcal D\) and an infinite size sample \(\widehat {\mathcal {D}}_{t}\) generated from the CGNN \((\mathcal {G},\widehat {f_{t}},\mathcal {E})\) is less than 𝜖 t.
Proof
According to Proposition 2 and with same notations, letting 𝜖 t > 0 go to 0 as t goes to infinity, consider \({\hat f}_t=(\hat f^{t}_1 \ldots \hat f^{t}_d)\) and \(\hat {z_t}\) defined from \({\hat f}_t\) such that for all e ∈ [0, 1]d, \(\|z(e)- \widehat {z}_t(e)\| < \epsilon _t\).
Let \(\{ \hat {\mathcal {D}_t} \}\) denote the infinite sample generated after \(\hat {f_t}\). The score of the CGNN \((\mathcal {G},\hat {f_t},\mathcal {E})\) is \( \widehat {\text{MMD}}_k(\mathcal {D}, \hat {\mathcal {D}_t}) = \mathbb {E}_{e,e'}[k(z(e),z(e')) - 2 k(z(e),\widehat {z}_t(e')) + k(\widehat {z}_t(e), \widehat {z}_t(e'))]\).
As \(\hat {f_t}\) converges towards f on the compact [0, 1]d, using the bounded convergence theorem on a compact subset of \(\mathbb {R}^{d}\), \(\widehat {z_t}(e) \rightarrow z(e)\) uniformly for t →∞, it follows from the Gaussian kernel function being bounded and continuous that \(\widehat {\text{MMD}}_k(\mathcal {D}, \hat {\mathcal {D}_t}) \rightarrow 0\), when t →∞.
Proposition 4
Let X = [X 1, …, X d] denote a set of continuous random variables with joint distribution P, generated by a CGNN \(\mathcal {C}_{\mathcal {G},f} = (\mathcal {G}, f, \mathcal {E})\) with \(\mathcal {G}\) , a directed acyclic graph. And let \(\mathcal {D}\) be an infinite observational sample generated from this CGNN. We assume that P is Markov and faithful to the graph \(\mathcal {G}\) , and that every pair of variables (X i, X j) that are d-connected in the graph are not independent. We note \(\widehat {\mathcal {D}}\) an infinite sample generated by a candidate CGNN, \(\mathcal {C}_{\widehat {\mathcal {G}},\hat {f}} = (\widehat {\mathcal {G}}, \hat {f}, \mathcal {E})\) . Then,
-
(i)
If \(\widehat {\mathcal {G}} = \mathcal {G}\) and \(\hat {f} = f\) , then \(\widehat {\mathit{\text{MMD}}}_k(\mathcal {D}, \widehat {\mathcal {D}}) = 0\).
-
(ii)
For any graph \(\widehat {\mathcal {G}}\) characterized by the same adjacencies but not belonging to the Markov equivalence class of \(\mathcal {G}\) , for all \(\hat {f}\) , \(\widehat {\mathit{\text{MMD}}}_k(\mathcal {D}, \widehat {\mathcal {D}}) \neq 0\).
Proof
The proof of (i) is obvious, as with \(\widehat {\mathcal {G}} = \mathcal {G}\) and \(\hat {f} = f\), the joint distribution \(\hat {P}\) generated by \(\mathcal {C}_{\widehat {\mathcal {G}},\hat {f}} = (\widehat {\mathcal {G}}, \hat {f}, \mathcal {E})\) is equal to P, thus we have \(\widehat {\text{MMD}}_k(\mathcal {D}, \widehat {\mathcal {D}}) = 0\).
(ii) Let consider \(\widehat {\mathcal {G}}\) a DAG characterized by the same adjacencies but that do not belong to the Markov equivalence class of \(\mathcal {G}\). According to Verma and Pearl (1991), as the DAG \(\mathcal {G}\) and \(\widehat {\mathcal {G}}\) have the same adjacencies but are not Markov equivalent, there are not characterized by the same v-structures.
-
a)
First, we consider that a v-structure {X, Y, Z} exists in \(\mathcal {G}\), but not in \(\widehat {\mathcal {G}}\). As the distribution P is faithful to \(\mathcal {G}\) and X and Z are not d-separated by Y in \(\mathcal {G}\), we have that
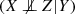 in P. Now we consider the graph \(\widehat {\mathcal {G}}\). Let \(\hat {f}\) be a set of neural networks. We note \(\hat {P}\) the distribution generated by the CGNN \(\mathcal {C}_{\widehat {\mathcal {G}},\hat {f}}\). As \(\widehat {\mathcal {G}}\) is a directed acyclic graph and the variables E
i are mutually independent, \(\hat {P}\) is Markov with respect to \(\widehat {\mathcal {G}}\). As {X, Y, Z} is not a v-structure in \(\widehat {\mathcal {G}}\), X and Z are d-separated by Y . By using the causal Markov assumption, we obtain that (X⊥ ⊥ Z|Y ) in \(\hat {P}\).
in P. Now we consider the graph \(\widehat {\mathcal {G}}\). Let \(\hat {f}\) be a set of neural networks. We note \(\hat {P}\) the distribution generated by the CGNN \(\mathcal {C}_{\widehat {\mathcal {G}},\hat {f}}\). As \(\widehat {\mathcal {G}}\) is a directed acyclic graph and the variables E
i are mutually independent, \(\hat {P}\) is Markov with respect to \(\widehat {\mathcal {G}}\). As {X, Y, Z} is not a v-structure in \(\widehat {\mathcal {G}}\), X and Z are d-separated by Y . By using the causal Markov assumption, we obtain that (X⊥ ⊥ Z|Y ) in \(\hat {P}\). -
b)
Second, we consider that a v-structure {X, Y, Z} exists in \(\widehat {\mathcal {G}}\), but not in \(\mathcal {G}\). As {X, Y, Z} is not a v-structure in \(\mathcal {G}\), there is an “unblocked path” between the variables X and Z, the variables X and Z are d-connected. By assumption, there do not exist a set D not containing Y such that (X⊥ ⊥ Z|D) in P. In \(\widehat {\mathcal {G}}\), as {X, Y, Z} is a v-structure, there exists a set D not containing Y that d-separates X and Z. As for all CGNN \(\mathcal {C}_{\widehat {\mathcal {G}},\hat {f}}\) generating a distribution \(\hat {P}\), \(\hat {P}\) is Markov with respect to \(\widehat {\mathcal {G}}\), we have that X⊥ ⊥ Z|D in \(\hat {P}\).
In the two cases a) and b) considered above, P and \(\hat {P}\) do not encode the same conditional independence relations, thus are not equal. We have then \(\widehat {\text{MMD}}_k(\mathcal {D}, \mathcal {D}') \neq 0\).
1.3 Table of Scores for the Experiments on Cause-Effect Pairs
See Table 3.
1.4 Table of Scores for the Experiments on Graphs
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Goudet, O., Kalainathan, D., Caillou, P., Guyon, I., Lopez-Paz, D., Sebag, M. (2018). Learning Functional Causal Models with Generative Neural Networks. In: Escalante, H., et al. Explainable and Interpretable Models in Computer Vision and Machine Learning. The Springer Series on Challenges in Machine Learning. Springer, Cham. https://doi.org/10.1007/978-3-319-98131-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-98131-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-98130-7
Online ISBN: 978-3-319-98131-4
eBook Packages: Computer ScienceComputer Science (R0)



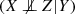 in P. Now we consider the graph
in P. Now we consider the graph