Abstract
We present a very simple yet very powerful idea for turning any passively secure MPC protocol into an actively secure one, at the price of reducing the threshold of tolerated corruptions.
Our compiler leads to a very efficient MPC protocols for the important case of secure evaluation of arithmetic circuits over arbitrary rings (e.g., the natural case of \({\mathbb {Z}}_{2^{\ell }}\!\)) for a small number of parties. We show this by giving a concrete protocol in the preprocessing model for the popular setting with three parties and one corruption. This is the first protocol for secure computation over rings that achieves active security with constant overhead.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Secure Computation. Secure Multiparty Computation (MPC) allows a set of participants \(P_1,\ldots , P_n\) with private inputs respectively \(x_1,\ldots ,x_n\) to learn the output of some public function f evaluated on their private inputs i.e., \(z=f(x_1,\ldots ,x_n)\) without having to reveal any other information about their inputs. Seminal MPC results from the 80s [3, 6, 18, 26] have shown that with MPC it is possible to securely evaluate any boolean or arithmetic circuit with information theoretic security (under the assumption that a strict minority of the participants are corrupt) or with computational security (when no such honest majority can be assumed).
As is well known, the most efficient MPC protocols are only passively secure. What is perhaps less well known is that by settling for passive security, we also get a wider range of domains over which we can do MPC. In addition to the standard approach of evaluating boolean or arithmetic circuits over fields, we can also efficiently perform computations over other rings. This has been demonstrated by the Sharemind suite of protocols [5], which works over the ring \({\mathbb {Z}}_{2^\ell }\). Sharemind’s success in practice is probably, to a large extent, due to the choice of the underlying ring, which closely matches the kind of ring CPUs naturally use. Closely matching an actual CPU architecture allows easier programming of algorithms for MPC, since programmers can reuse some of the tricks that CPUs use to do their work efficiently.
While passive security is a meaningful security notion that is sometimes sufficient, one would of course like to have security against active attacks. However, the known techniques, such as the GMW compiler, for achieving active security incur a significant overhead, and while more efficient approaches exist, they usually need to assume that the computation is done over a field, and they always have an overhead that depends on the security parameter. Typically, such protocols, like the BeDOZa or SPDZ protocols [4, 11, 13], start with a preprocessing phase which generates the necessary correlated randomness [19] in the form of so called multiplication triples. This is followed by an information theoretic and therefore very fast online phase where the triples are consumed to evaluate the arithmetic circuit. To get active security in the on-line phase, protocols employ information-theoretic MACs that allow to detect whether incorrect information is sent. Using such MACs forces the domain of computation to be a field which excludes, of course, the ring \({\mathbb {Z}}_{2^\ell }\). The only exception is recent work subsequent to ours [10]. This is not a compiler but a specific protocol for the preprocessing model which allows MACs for the domain \({\mathbb {Z}}_{2^\ell }\). This is incomparable to our result for this setting: compared to our result, the protocol from [10] tolerates larger number of corruptions, but it introduces an overhead in storage and computational work proportional to the product of the security parameter and the circuit size.
Another alternative is to use garbled circuits. However, they incur a rather large overhead when active security is desired, and cannot be used at all if we want to do arithmetic computation directly over a large ring. Thus, a very natural question is:
Can we go from passive to active security at a small cost and can we do so in a general way which allows us to do computations over general rings?
Our results. In this paper we address the above question by making three main contributions:
-
1.
A generic transformation that compiles a protocol with passive security against at least 2 corruptions into one that is actively secure (but against a smaller number of corruptions). This works both for the preprocessing and the standard model. The transformation preserves perfect and statistical security and its overhead depends only on the number of players, and not on the security parameter. Thus, for a constant number of parties it loses only a constant factor in efficiency.
-
2.
We present a preprocessing protocol for 3 parties. It generates multiplication triples to be used by a particular protocol produced by our compiler. This preprocessing can generate triples over any ring \({\mathbb {Z}}_{m}\) and has constant computational overhead for large enough m; more precisely, if m is exponential in the statistical security parameter. We build this preprocessing from scratch, not by using our compiler. This, together with our compiler, gives a plug-in replacement for the Sharemind protocol as explained below.
-
3.
A generic transformation that works for a large class of protocols including those output by our passive-to-active compiler. It takes as input a protocol that is secure with abort and satisfies certain extra conditions, and produces a new protocol with complete fairness [8]. In security with abort, the adversary gets the output and can then decide if the protocol should abort. In complete fairness the adversary must decide whether to abort without seeing the output. This is relevant in applications where the adversary might “dislike” the result and would prefer that it is not delivered. The transformation has an additive overhead that only depends on the size of the output and not the size of the computation. It works in the honest majority model without broadcast. In this model we cannot guarantee termination in general so security with complete fairness is essentially the best we can hope for.
Discussion of results. Our passive-to-active compiler can, for instance, be applied to the straightforward 3-party protocol that represents secret values using additive secret sharing over \({\mathbb {Z}}_{2^\ell }\) and does secure multiplication using multiplication triples created in a preprocessing phase. This protocol is secure against 2 passive corruptions. Applying our compiler results in a 3-party protocol \({\varPi } \) in the preprocessing model that is information theoretically secure against 1 corruption and obtains active security with abort. \({\varPi } \) can be used as plug-in replacement for the Sharemind protocol. It has better (active) instead of passive security and is essentially as efficient. This, of course, is only interesting if we can implement the required preprocessing efficiently, which is exactly what we do as our second result, discussed in more detail below.
The compiler is based on the idea of turning each party in the passively secure protocol into a “virtual” party, and then each virtual party is independently emulated by 2 or more of the real parties (i.e., each real party will locally run the code of the virtual party). Intuitively, if the number of virtual parties for which a corrupt party is an emulator is not larger than the privacy threshold of the original protocol, then our transform preserves the privacy guarantees of the original protocol. Further, if we can guarantee that each virtual party is emulated by at least one honest party, then this party can detect faulty behaviour by the other emulators and abort if needed, thus guaranteeing correctness. Moreover, if we set the parameters in a way that we are guaranteed an honest majority among the emulators, then we can even decide on the correct behaviour by majority vote and get full active security. While this in hindsight might seem like a simple idea, proving that it actually works in general requires us to take care of some technical issues relating, for instance, to handling the randomness and inputs of the virtual parties.
The approach is closely related to replicated secret sharing which has been used for MPC before [17, 22] (see the related work section for further discussion), but to the best of our knowledge, this is the first general construction that transforms an entire passively secure protocol to active security. From this point of view, it can be seen as a construction that unifies and “explains” several earlier constructions.
While our construction works for any number of parties it unfortunately does not scale well, and the resulting protocol will only tolerate corruptions of roughly \(\sqrt{n}\) of the n parties and has a multiplicative overhead of order n compared to the passively secure protocol. This is far from the constant fraction of corruptions we know can be tolerated with other techniques. We show two ways to improve this. First, while our main compiler preserves adaptive security, we also present an alternative construction that only works for static security but tolerates \(n/\log n\) active corruptions, and has overhead \(\log ^2 n\). Second, we show that using results from [7], we get a protocol for any number n of parties tolerating roughly n / 4 malicious corruptions. We do this by starting from a protocol for 5 parties tolerating 2 passive corruptions, use our result to constructs a 5 party protocol tolerating 1 active corruption, and then use a generic construction from [7] based on monotone formulae. Note that a main motivation for the results from [7] was to introduce a new approach to the design of multiparty protocols. Namely, first design a protocol for a constant number of parties tolerating 1 active corruption, and then apply player emulation and monotone formulae to get actively secure multiparty protocols. From this point of view, adding our result extends their idea in an interesting way: using a generic transformation one can now get active and information theoretic security for a constant fraction of corruptions from a seemingly even simpler object: a protocol for a constant number of parties that is passively secure against 2 corruptions.
Our second result, the preprocessing protocol, is based on the idea that we can quite easily create multiplication triples involving secret shared values \(a,b,c \in {\mathbb {Z}}_{m}\) and where \(ab=c \bmod m\) if parties behave honestly. The problem now is that the standard efficient approach to checking whether \(ab=c \bmod m\) only works if m is prime, or at least has only large prime factors. We solve this by finding a way to embed the problem into a slightly larger field \({\mathbb {Z}}_{p}\) for a prime p. We can then check efficiently if \(ab=c \bmod p\). In addition we make sure that a, b are small enough so that this implies \(ab=c\) over the integers and hence also that \(ab=c \bmod m\).
Our final result, the compiler for complete fairness, works for protocols where the output is only revealed in the last round, as is typically the case for protocols based on secret sharing. Roughly speaking, the idea is to execute the protocol up to its last round just before the outputs are delivered. We then compute verifiable secret sharings of the data that parties would send in the last round – as well as one bit that says whether sending these messages would cause an abort in the original protocol. Of course, this extra computation may abort, but if it does not and we are told that the verifiably shared messages are correct, then it is too late for the adversary to abort; as we assume an honest majority the shared messages can always be reconstructed. While this basic idea might seem simple, the proof is trickier than one might expect – as we need to be careful with the assumptions on the original protocol to avoid selective failure attacks.
1.1 Related Work
Besides what is already mentioned above, there are several other relevant works. Previous compilers, notably the GMW [18] and the IPS compiler [20, 21], allow to transform passively secure protocols into maliciously secure ones. The GMW compiler uses zero-knowledge proofs and, hence, is not blackbox in the underlying construction. It produces protocols which are far from practically efficient. The IPS compiler works, very roughly speaking, by using an inner protocol to simulate the protocol execution of an outer protocol. The outer protocol computes the desired functionality. The inner protocol protocols computes the individual computation steps of the outer protocol. The compiler is blackbox with respect to the inner, but not the outer protocol and it requires the existence of oblivious transfer. It is unclear whether the IPS compiler can be used to produce practically efficient protocols.
In contrast, our compiler does not require any computational assumption and thus preserves any information theoretic guarantees the underlying protocol has. Our transform does not have any large hidden constants and can produce actively secure protocols with efficiency that may be of practical interest.
In a recent work by Furukawa et al. [17], a practically very efficient three-party protocol with one active corruption was proposed. Their protocol uses replicated secret sharing and only works for bits. As the authors state themselves, it is not straightforward to generalize their protocol to more than three parties, while maintaining efficiency. In contrast, our protocol works over any arbitrary ring and can easily be generalized to any number of players. Furthermore our transform produces protocols with constant overhead, whereas their protocol does not have constant overhead.
The idea of using replication to detect active corruptions has been used before. For instance, Mohassel et al. [23] propose a three-party version of Yao’s protocol. In a nutshell, their approach is to let two parties garble a circuit separately and to let the third party check that the circuits are the same. Our results in this work are more general in the sense that we propose a general transform to obtain actively secure protocols from passively secure ones. In [14], Desmedt and Kurosawa use replication to design a mix-net with \(t^2\) servers secure against (roughly) t actively corrupted servers. A simple approach to MPC based on replicated secret sharing was proposed by Maurer in [22]. It has been the basis for practical implementations like [5].
2 Preliminaries
Notation. If \({\mathcal {X}}\) is a set, then \(v \leftarrow {\mathcal {X}}\) means that v is a uniformly random value chosen from \({\mathcal {X}}\). When A is an algorithm, we write \(v \leftarrow A(x)\) to denote a run of A on input x that produces output v. For  , we write \(\left[ n \right] \) to denote the set \(\{1,2,\dots , n \}\). For \(n\) party protocols, we will write \(\mathrm {P}_{i+1}\) and implicitly assume a wrap-around of the party’s index, i.e. \(\mathrm {P}_{n+1} = \mathrm {P}_{1} \) and \(\mathrm {P}_{1-1} = \mathrm {P}_{n} \). All logarithms are assumed to be base 2.
, we write \(\left[ n \right] \) to denote the set \(\{1,2,\dots , n \}\). For \(n\) party protocols, we will write \(\mathrm {P}_{i+1}\) and implicitly assume a wrap-around of the party’s index, i.e. \(\mathrm {P}_{n+1} = \mathrm {P}_{1} \) and \(\mathrm {P}_{1-1} = \mathrm {P}_{n} \). All logarithms are assumed to be base 2.
Security Definitions. We will use the UC model throughout the paper, more precisely the variant described in [9]. We assume the reader has basic knowledge about the UC model and refer to [9] for details. Here we only give a very brief introduction: We consider the following entities: a protocol \({\varPi } _{\mathcal {F}}\) for n players that is meant to implement an ideal functionality \({\mathcal {F}}\). An environment Z that models everything external to the protocol which means that Z chooses inputs for the players and is also the adversarial entity that attacks the protocol. Thus Z may corrupt players passively or actively as specified in more detail below. We have an auxiliary functionality \({\mathcal {G}}\) that the protocol may use to accomplish its goal. Finally we have a simulator S that is used to demonstrate that \({\varPi } _{\mathcal {F}}\) indeed implements \({\mathcal {F}}\) securely.
In the definition of security we compare two processes: First, the real process executes Z, \({\varPi } _{\mathcal {F}}\) and \({\mathcal {G}}\) together, this is denoted \(Z\diamond {\varPi } _{\mathcal {F}}\diamond {\mathcal {G}}\). Second, we consider the ideal process where we execute Z, S and \({\mathcal {F}}\) together, denoted \(Z\diamond S\diamond {\mathcal {F}}\). The role of the simulator S is to emulate Z’s view of the attack on the protocol, this includes the views of the corrupted parties as well as their communication with \({\mathcal {G}}\). To be able to do this, S must send inputs for corrupted players to \({\mathcal {F}}\) and will get back outputs for the corrupted players. A simulator in the UC model is not allowed to rewind the environment.
Both processes are given a security parameter k as input, and the only output is one bit produced by Z. We think of this bit as Z’s guess at whether it has been part of the real or the ideal process. We define \(p_{real}\) respectively \(p_{ideal}\) to be the probabilities that the real, respectively the ideal process outputs 1, and we say that \(Z\diamond {\varPi } _{\mathcal {F}}\diamond {\mathcal {G}}\equiv Z\diamond S\diamond {\mathcal {F}}\) if \(|p_{real} -p_{ideal}|\) is negligible in k.
Definition 1
We say that protocol \({\varPi } _{\mathcal {F}}\) securely implements functionality \({\mathcal {F}}\) with respect to a class of environments Env in the \({\mathcal {G}}\)-hybrid model if there exists a simulator S such that for all \(Z\in Env\) we have \(Z\diamond {\varPi } _{\mathcal {F}}\diamond {\mathcal {G}}\equiv Z\diamond S\diamond {\mathcal {F}}\).
Different types of security can now be captured by considering different classes of environments: For passive t-security, we consider any Z that corrupts at most t players. Initially, it chooses inputs for the players. Corrupt players follow the protocol so Z only gets read access to their views. For biased passive t-security, we consider any Z that corrupts at most t players. Initially, it chooses inputs for the players, as well as random coins for the corrupt players. Then corrupt players follow the protocol so Z only gets read access to their views. This type of security has been considered in [1, 24] and intuitively captures passively secure protocols where privacy only depends on the honest players choosing their randomness properly. This is actually true for almost all known passively secure protocols. Finally, for active t-security, we consider any Z that corrupts at most t players, and Z takes complete control over corrupt players.
One may also distinguish between unconditional or computational security depending on whether the environment class contains all environments of a certain type or only polynomial time ones. We will not be concerned much with this distinction, as our main compiler is the same regardless, and preserves both unconditional and computational security. For simplicity, we will consider unconditional security by default. We also consider by default adaptive security, meaning that Z is allowed to adaptive choose players to corrupt during the protocol.
We will consider synchronous protocols throughout, so protocols proceed in rounds in the standard way, with a rushing adversary. We will always assume that point-to-point secure channels are available. In addition, we will also sometimes make use of other auxiliary functionalities, as specified in the next subsection.
Ideal Functionalities. The broadcast functionality \({\mathcal {F}}_{\mathsf {bcast}}\) (Fig. 1) allows a party to send a value to a set of other parties, such that either all receiving parties receive the same value or all parties jointly abort by outputting \(\bot \). This functionality is known as detectable broadcast [15] and while unconditionally secure broadcast with termination among \(n\) parties requires that strictly less than \(n\)/3 parties are corrupted [25], this bound does not apply to detectable broadcast, which can be instantiated with information-theoretic security tolerating any number of corruptions [16].
Using the coin flip functionality \({\mathcal {F}}_{\mathsf {cflip}}\) (Fig. 2), a set of parties can jointly generate and agree on a uniformly random  -bit string. In the case of an honest majority, this functionality can be implemented with information-theoretic security via verifiable secret sharing (VSS) [9] as follows: Let \({\mathbb {P}}_{} \) be the set of players that want to perform a coin flip. To realize the functionality, every participating party \(\mathrm {P}_{i} \in {\mathbb {P}}_{} \) secret shares a random bit string \(r_i\) among all the other players. Once every player in \({\mathbb {P}}_{} \) shared its bit string \(r_i\), we let all players in \({\mathbb {P}}_{} \) reconstruct all bit strings and output \(\bigoplus _{i} r_i\). This is done by having all players send all their shares to players in \({\mathbb {P}}_{} \). Here we assume that reconstruction is non-interactive, i.e., players send shares to each other and each player locally computes the secret. Such VSS schemes exist, as is well known. It is important to note that a VSS needs broadcast in the sharing phase, and since we only assume detectable broadcast, the adversary may force the VSS to abort. However, since the decision to abort or not must be made without knowing the shared secret (by privacy of the VSS) the adversary cannot use this to bias the output of the coinflip.
-bit string. In the case of an honest majority, this functionality can be implemented with information-theoretic security via verifiable secret sharing (VSS) [9] as follows: Let \({\mathbb {P}}_{} \) be the set of players that want to perform a coin flip. To realize the functionality, every participating party \(\mathrm {P}_{i} \in {\mathbb {P}}_{} \) secret shares a random bit string \(r_i\) among all the other players. Once every player in \({\mathbb {P}}_{} \) shared its bit string \(r_i\), we let all players in \({\mathbb {P}}_{} \) reconstruct all bit strings and output \(\bigoplus _{i} r_i\). This is done by having all players send all their shares to players in \({\mathbb {P}}_{} \). Here we assume that reconstruction is non-interactive, i.e., players send shares to each other and each player locally computes the secret. Such VSS schemes exist, as is well known. It is important to note that a VSS needs broadcast in the sharing phase, and since we only assume detectable broadcast, the adversary may force the VSS to abort. However, since the decision to abort or not must be made without knowing the shared secret (by privacy of the VSS) the adversary cannot use this to bias the output of the coinflip.
The standard functionality \({\mathcal {F}}_{\mathsf {triple}}\) (Fig. 3) allows three parties \(\mathrm {P}_{1}\), \(\mathrm {P}_{2}\), and \(\mathrm {P}_{3}\) to generate a replicated secret sharing of multiplication triples. In this functionality, the adversary can corrupt one party and pick its shares. The remaining shares of the honest parties are chosen uniformly at random. The intuition behind this ideal functionality is that, even though the adversary can pick its own shares, it does not learn anything about the remaining shares, and hence it does not learn anything about the actual value of the multiplication triple that is secret shared. We will present a communication efficient implementation of this functionality in Sect. 5.
Finally, for any function f with n inputs and one output, we will let \({\mathcal {F}}_f\) denote a UC functionality for computing f securely with (individual) abort. That is, once it receives inputs from all n parties it computes f and then sends the output to the environment Z. Z returns for each player a bit indicating if this player gets the output or will abort. \(F_f\) sends the output to the selected players and sends \(\bot \) to the rest. We consider three (stronger) variants of this: \({\mathcal {F}}^{\mathsf {unanimous}} _f\) where Z must give the output to all players or have them all abort; \({\mathcal {F}}^{\mathsf {fair}} _f\) where Z is not given the output when it decides whether to abort; and \({\mathcal {F}}^{\mathsf {fullactive}} _f\) where the adversary cannot abort at all.
3 Our Passive to Active Security Transform
The goal of our transform is to take a passively secure protocol and convert it into a protocol that is secure against a small number of active corruptions.
For simplicity, let us start with a passively secure \(n\)-party protocol (\(n \ge 3\)) that we will convert into an n-party protocol in the \({\mathcal {F}}_{\mathsf {cflip}} \)-hybrid model that is secure against one active corruption.
The main challenge in achieving security against an actively corrupted party, is to prevent it from deviating from the protocol description and sending malformed messages. Our protocol transform is based upon the observation that, assuming one active corruption, every pair of parties contains at least one honest party. Now instead of letting the real parties directly run the passively secure protocol, we will let pairs of real parties simulate virtual parties that will compute, using the passively secure protocol, the desired functionality on behalf of the real parties. More precisely, for \(1 \le i \le n\), the real parties \(\mathrm {P}_{i}\) and \(\mathrm {P}_{i+1}\) will simulate virtual party \({\mathbb {P}}_{i}\). In the first phase of our protocol, \(\mathrm {P}_{i}\) and \(\mathrm {P}_{i+1}\) will agree on some common input and randomness that we will specify in a moment. In the second phase, the virtual parties will run a passively secure protocol on the previously agreed inputs and randomness. Whenever virtual party \({\mathbb {P}}_{i}\) sends a message to \({\mathbb {P}}_{j}\), we will realize this by letting \(\mathrm {P}_{i}\) and \(\mathrm {P}_{i+1}\) both send the same message to \(\mathrm {P}_{j}\) and \(\mathrm {P}_{j+1}\). Note that when both \(\mathrm {P}_{i}\) and \(\mathrm {P}_{i+1}\) are honest, these two messages will be identical since they are constructed according to the same (passively secure) protocol, using the same shared randomness and the previously received messages. The “action” of receiving a message at the virtual party \({\mathbb {P}}_{j}\) is emulated by having the real parties \(\mathrm {P}_{j}\) and \(\mathrm {P}_{j+1}\) both receive two messages each. Both parties now check locally whether the received messages are identical and, if not, broadcast an “abort” message. Otherwise they continue to execute the passively secure protocol. The high-level idea behind this approach is that the adversary controlling one real party cannot send a malformed message and at the same time be consistent with the other honest real party simulating the same virtual party. Hence, either the adversary behaves honestly or the protocol will be aborted.
Remember that we need all real parties emulating the same virtual party to agree on a random tape and a common input. Agreeing on a random tape is trivial in the \({\mathcal {F}}_{\mathsf {cflip}} \)-hybrid model, we can just invoke \({\mathcal {F}}_{\mathsf {cflip}} \) for each virtual \({\mathbb {P}}_{i}\) and have it send the random string to the corresponding real parties \(\mathrm {P}_{i}\) and \(\mathrm {P}_{i+1}\). Moreover, in the process of agreeing on inputs for the virtual parties we need to be careful in not leaking any information about the real parties’ original inputs. Towards this goal, we will let every real party secret share, e.g. XOR, its input among all virtual parties. Now, instead of letting the underlying passively secure protocol compute \(f(x_1, \dots , x_n)\), where real \(\mathrm {P}_{i}\) holds input \(x_i\), we will use it to compute \(f'((x^1_1, \dots , x^1_n), \dots , (x^n _1, \dots , x^n _n)) := f(\bigoplus _i x_1^i, \dots , \bigoplus _i x_n ^i)\), where virtual party \({\mathbb {P}}_{i}\) has input \(\left( x_1^i, \dots , x_n ^i \right) \), i.e. one share of every original input.
As a small example, for the case of three parties, we would get \({\mathbb {P}}_{1} = \{ \mathrm {P}_{1}, \mathrm {P}_{2} \}\) holding input \(\left( x^1_1, x^1_2, x^1_3\right) \), \({\mathbb {P}}_{2} = \{ \mathrm {P}_{2}, \mathrm {P}_{3} \}\) with input \(\left( x^2_1, x^2_2, x^2_3\right) \), and \({\mathbb {P}}_{3} = \{ \mathrm {P}_{3}, \mathrm {P}_{1} \}\) with \(\left( x^3_1, x^3_2, x^3_3\right) \). Since every real party only participates in the simulation of two virtual parties, no real party learns enough shares to reconstruct the other parties’ inputs. More precisely, for arbitrary \(n \ge 3\) and one corruption, each real party will participate in the simulation of two virtual parties, thus the underlying passively secure protocol needs to be at least passively 2-secure. Actually, each real party will learn not only two full views, but also one of the inputs of each other virtual party, since it knows the shares it distributed itself. As we will see in the security proof this is not a problem and passive 2-security is, for one active corruption, a sufficient condition on the underlying passively secure protocol.
The approach described above can be generalized to a larger number of corrupted parties. The main insight for one active corruption was that each set of two parties contains one honest party. For more than one corruption, we need to ensure that each set of parties of some arbitrary size contains at least one honest party that will send the correct message. Given \(n\) parties and \(t\) corruptions, each virtual party needs to be simulated by at least \(t +1\) real parties. We let real parties \(\mathrm {P}_{i}, \dots , \mathrm {P}_{i+t} \) simulate virtual party \({\mathbb {P}}_{i} \)Footnote 1. This means that every real party will participate in the simulation of \(t + 1\) virtual parties. Since we have \(t\) corruptions, the adversary can learn at most \(t \left( t + 1\right) \) views of virtual parties, which means that our underlying passively secure protocol needs to have at least passive \(\left( t ^2 + t \right) \)-security.
In the following formal description, let \({\mathbb {P}}_{i}\) be the virtual party that is simulated by \(\mathrm {P}_{i}, \dots , \mathrm {P}_{i+t} \). By slight abuse of notation, we use the same notation for the virtual party \({\mathbb {P}}_{j} \) and the set of real parties that emulate it. When we say \({\mathbb {P}}_{i}\) sends a message to \({\mathbb {P}}_{j}\), we mean that each real party in \({\mathbb {P}}_{i}\) will send one message to every real party in \({\mathbb {P}}_{j}\). Let \({\mathbb {V}}_{i}\) be the set of virtual parties in whose simulation \(\mathrm {P}_{i}\) participates.
Let f be the \(n\)-party functionality we want to compute, and \({\varPi } _{f'}\) be a passive \(\left( t ^2 + t \right) \)-secure protocol that computes \(f'\), i.e., it computes f on secret shares as described above. We construct \({\tilde{{\varPi }}}_f\) that computes f and is secure against \(t\) active corruption as follows:
The protocol \({\tilde{{\varPi }}}_f\):
-
1.
\(\mathrm {P}_{i}\) splits its input \(x_i\) into \(n\) random shares, s.t. \(x_i = \bigoplus _{1 \le j \le n} x_i^j\), and for all \(j \in \left[ n \right] \) send \((x_i^j, {\mathbb {P}}_{j})\) to \({\mathcal {F}}_{\mathsf {bcast}} \) (which then sends \(x_i^j\) to all parties in \({\mathbb {P}}_{j} \)).
-
2.
For \(i \in \left[ n \right] \) invoke \({\mathcal {F}}_{\mathsf {cflip}} \) on input \({\mathbb {P}}_{i} \). Each \(\mathrm {P}_{i}\) receives \(\{ r_j \vert {\mathbb {P}}_{j} \in {\mathbb {V}}_{i} \}\) from the functionality.
-
3.
\(\mathrm {P}_{i}\) receives \(\left( x_1^j, \dots , x_n ^j\right) \) for every \({\mathbb {P}}_{j} \in {\mathbb {V}}_{i} \) from \({\mathcal {F}}_{\mathsf {bcast}} \). If any \(x_i^j=\bot \), abort the protocol.
-
4.
All virtual parties, simulated by the real parties, jointly execute \({\varPi } _{f'}\), where each real party in \({\mathbb {P}}_{i}\) uses the same randomness \(r_i\) that it obtained through \({\mathcal {F}}_{\mathsf {cflip}}\). Whenever \({\mathbb {P}}_{i}\) receives a message from \({\mathbb {P}}_{j}\), each member of \({\mathbb {P}}_{i}\) checks that it received the same message from all parties in \({\mathbb {P}}_{j}\). If not, it aborts (this includes the case where a message is missing). Once a player makes it to the end of \({\varPi } _{f'}\) without aborting, it outputs whatever is output in \({\varPi } _{f'}\).
Theorem 1
Let \(n \ge 3\). Suppose \({\varPi } _{f'}\) implements \({\mathcal {F}}_{f'}\) with passive \(\left( t ^2 + t \right) \)-security. Then \({\tilde{{\varPi }}}_f\) as described above implements \({\mathcal {F}}_f\) in the (\({\mathcal {F}}_{\mathsf {bcast}}\), \({\mathcal {F}}_{\mathsf {cflip}}\))-hybrid model with active t-security.
Remark 1
We construct a protocol where the adversary can force some honest players to abort while others terminate normally. We can trivially extend this to a protocol implementing \({\mathcal {F}}^{\mathsf {unanimous}} _f\) where all players do the same: we just do a round of detectable broadcast in the end where players say whether they would abort in the original protocol. If a player hears “abort” from anyone, he aborts.
Remark 2
In Step 1 of the protocol the parties perform a XOR based n-out-of-n secret sharing. We remark that any n-out-of-n secret sharing scheme could be used here instead. In particular, when combining the transform with the preprocessing protocol of Sect. 5, it will be more efficient to do the sharing in the ring  .
.
Remark 3
Our compiler is information-theoretically secure. This means that our compiler outputs a protocol that is computationally, statistically, or perfectly secure if the underlying protocol was respectively computationally, statistically, or perfectly secure. This is particularly interesting, since, to the best of our knowledge, our compiler is the first one to preserve statistical and perfect security of the underlying protocol.
Remark 4
The theorem trivially extends to compilation of protocols that use an auxiliary functionality \({\mathcal {G}}\), such as a preprocessing functionality. We would then obtain a protocol in the \(({\mathcal {F}}_{\mathsf {bcast}}, {\mathcal {F}}_{\mathsf {cflip}}, {\mathcal {G}})\)-hybrid model. We leave the details to the reader.
Proof
Before getting into the details of the proof, let us first roughly outline the possibilities of an actively malicious adversary and our approach to simulating his view in the ideal world. The protocol can be split into two separate phases. First all real parties secret share their inputs among the virtual parties through the broadcast functionality. A malicious party \(\mathrm {P}_{i} ^*\) can pick an arbitrary input \(x_i\), but the broadcast functionality ensures that all parties simulating some virtual party \({\mathbb {P}}_{j}\) will receive the same consistent share \(x_i^j\) from the adversary. Since every virtual party is simulated by at least one honest real party, the simulator will obtain all secret shares of all inputs belonging to  . This allows the simulator to reconstruct these inputs and query the ideal functionality to retrieve \(f(x'_1, \dots , x'_n)\) where if \(\mathrm {P}_{j} \) is honest then \(x'_j=x_j\) is the input chosen by the environment and if \(\mathrm {P}_{j} \) is corrupt \(x'_j = \bigoplus _i x_j^i\) is the input extracted by the simulator. Having the inputs of all corrupted parties and the output from the ideal functionality, we can use the simulator of \({\varPi } _{f'}\) to simulate the interaction with the adversary. At this point, there are two things to note.
. This allows the simulator to reconstruct these inputs and query the ideal functionality to retrieve \(f(x'_1, \dots , x'_n)\) where if \(\mathrm {P}_{j} \) is honest then \(x'_j=x_j\) is the input chosen by the environment and if \(\mathrm {P}_{j} \) is corrupt \(x'_j = \bigoplus _i x_j^i\) is the input extracted by the simulator. Having the inputs of all corrupted parties and the output from the ideal functionality, we can use the simulator of \({\varPi } _{f'}\) to simulate the interaction with the adversary. At this point, there are two things to note.
First, we have \(n\) real parties that simulate \(n\) virtual parties. Since the adversary can corrupt at most \(t\) real parties, we simulate each virtual party by \(t + 1\) real parties. As each real party participates in the same amount of simulations of virtual parties, we get that each real party simulates \(t + 1\) virtual parties. This means that the adversary can learn at most \( t ^2 + t \) views of the virtual parties and, hence, since \({\varPi } _{f'}\) is passively \(\left( t ^2 + t \right) \)-secure, the adversary cannot distinguish the simulated transcript from a real execution.
Second, the random tapes are honestly generated by \({\mathcal {F}}_{\mathsf {cflip}} \). The simulator knows the exact messages that the corrupted parties should be sending and how to respond to them. Upon receiving an honest message from a corrupted party, the simulator responds according to underlying simulator. If the adversary tries to cheat, the simulator aborts. Aborting is fine, since, in a real world execution, the adversary would be sending a message, which is inconsistent with at least one honest real party that simulates the same virtual party, and this would make some receiving honest party abort.
Given this intuition, let us now proceed with the formal simulation. Let Z be the environment (that corrupts at most \(t\) parties). Let \({\mathbb {P}}_{} ^*\) be the set of real parties that are corrupted before the protocol execution starts. Let \({\mathbb {V}}^*\) be the set of virtual parties that are simulated by at least one corrupt real party from \({\mathbb {P}}_{} ^*\). We will construct a simulator  using the simulator
using the simulator  for \(f'\). In the specification of the simulator we will often say that it sends some message to a corrupt player. This will actually mean that Z gets the message as Z plays for all the corrupted parties.
for \(f'\). In the specification of the simulator we will often say that it sends some message to a corrupt player. This will actually mean that Z gets the message as Z plays for all the corrupted parties.
 :
:
-
1.
For each \(\mathrm {P}_{i} \in {\mathbb {P}}_{} ^* \) and \(j \in \left[ n \right] \), Z sends \((x_i^j, {\mathbb {P}}_{j})\) to \({\mathcal {F}}_{\mathsf {bcast}} \) (which is emulated by
 ). For each \({\mathbb {P}}_{j} \in {\mathbb {V}}^* \) and each corrupt emulator in \({\mathbb {P}}_{j} \), send to Z the shares this emulator would receive from \({\mathcal {F}}_{\mathsf {bcast}} \), that is, \(\{x_i^j\}_{i=1..n}\) where for a corrupt \(\mathrm {P}_{i} \) we use the share specified by Z before and for honest \(\mathrm {P}_{i} \) we use a random value.
). For each \({\mathbb {P}}_{j} \in {\mathbb {V}}^* \) and each corrupt emulator in \({\mathbb {P}}_{j} \), send to Z the shares this emulator would receive from \({\mathcal {F}}_{\mathsf {bcast}} \), that is, \(\{x_i^j\}_{i=1..n}\) where for a corrupt \(\mathrm {P}_{i} \) we use the share specified by Z before and for honest \(\mathrm {P}_{i} \) we use a random value. -
2.
For each \(\mathrm {P}_{i} \in {\mathbb {P}}_{} ^* \), compute \(x_i = \bigoplus _j x_i^j\) and send it to the ideal functionality \({\mathcal {F}}_f\) to retrieve \(z = f(x_1, \dots , x_n)\), where all \(x_i\) with \(\mathrm {P}_{i} \not \in {\mathbb {P}}_{} ^* \) are the honest parties’ inputs in the ideal execution.
-
3.
To simulate the calls to \({\mathcal {F}}_{\mathsf {cflip}} \), for each corrupt \({\mathbb {P}}_{j} \), choose \(r_j\) at random and send it to each corrupt emulator of \({\mathbb {P}}_{j} \).
Note that, at this point, we know the inputs and random tapes of all currently corrupted parties. With this, we can check in the following whether corrupt players follow the protocol.
-
4.
Start the simulator
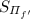 and tell it that the initial set of corrupted players is \({\mathbb {V}}^*\). We will emulate both its interface towards \({\mathcal {F}}_{f'}\) and towards its environment, as described below.
and tell it that the initial set of corrupted players is \({\mathbb {V}}^*\). We will emulate both its interface towards \({\mathcal {F}}_{f'}\) and towards its environment, as described below. -
5.
When
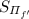 queries \({\mathcal {F}}_{f'}\) for inputs of corrupted players, we return, for each \({\mathbb {P}}_{j} \in {\mathbb {V}}^* \), \(x_1^j,..., x_n^j\). When it queries for the output we return z.
queries \({\mathcal {F}}_{f'}\) for inputs of corrupted players, we return, for each \({\mathbb {P}}_{j} \in {\mathbb {V}}^* \), \(x_1^j,..., x_n^j\). When it queries for the output we return z. -
6.
For each round in \({\varPi } _{f'}\) the following is done until the protocol ends or aborts:
-
(a)
Query
 for the messages sent from honest to corrupt virtual parties in the current round. For each such message to be received by a corrupted \({\mathbb {P}}_{j} \), send this message to all corrupt real parties in \({\mathbb {P}}_{j} \).
for the messages sent from honest to corrupt virtual parties in the current round. For each such message to be received by a corrupted \({\mathbb {P}}_{j} \), send this message to all corrupt real parties in \({\mathbb {P}}_{j} \). -
(b)
Get from Z the messages from corrupt to honest real players in the current round. Compute the set A of honest real players that, given these message, will abort. For all corrupt \({\mathbb {P}}_{j} \) and honest \({\mathbb {P}}_{i} \), compute the correct message \(m_{j,i}\) to be sent in this round from \({\mathbb {P}}_{j} \) to \({\mathbb {P}}_{i} \). Tell
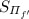 that \({\mathbb {P}}_{j} \) sent \(m_{j,i}\) to \({\mathbb {P}}_{i} \) in this round.
that \({\mathbb {P}}_{j} \) sent \(m_{j,i}\) to \({\mathbb {P}}_{i} \) in this round. -
(c)
If we completed the final round, stop the simulation. Else, if A contains all real honest parties, send “abort” to \({\mathcal {F}}_f\) and stop the simulation. Else, If \(A= \emptyset \) go to step 6a. Else, do as follows in the next round (in which the protocol will abort because \(A\ne \emptyset \)): Query
 for the set of messages M sent from honest to corrupt virtual parties in the current round. For all real parties in A tell Z that they send nothing in this round. For all other real honest players compute, as in step 6a, what messages they would send to corrupt real players given M and send these to Z. Send “abort” to \(F_f\) and stop the simulation.
for the set of messages M sent from honest to corrupt virtual parties in the current round. For all real parties in A tell Z that they send nothing in this round. For all other real honest players compute, as in step 6a, what messages they would send to corrupt real players given M and send these to Z. Send “abort” to \(F_f\) and stop the simulation.
-
(a)
It remains to specify how adaptive corruptions are handled: Whenever the adversary adaptively corrupts a new party \(\mathrm {P}_{i}\), we go through all virtual parties \({\mathbb {P}}_{j}\) in \({\mathbb {V}}_{i}\) (the virtual parties simulated by \(\mathrm {P}_{i}\)) and consider the following two cases. First, if \({\mathbb {P}}_{j}\) already contained a corrupted party, then we already know how to simulate the view for this virtual player. Second, if \(\mathrm {P}_{i}\) is the first corrupted party in \({\mathbb {P}}_{j}\), then we add \({\mathbb {P}}_{i} \) to \({\mathbb {V}}^* \) and tell  that \({\mathbb {P}}_{j}\) is now corrupt and we forward the response of
that \({\mathbb {P}}_{j}\) is now corrupt and we forward the response of  to Z, namely the (simulated) current view of \({\mathbb {P}}_{j}\). Since the view of \({\mathbb {P}}_{j}\) contains this virtual party’s random tape, we can continue our overall simulation as above.
to Z, namely the (simulated) current view of \({\mathbb {P}}_{j}\). Since the view of \({\mathbb {P}}_{j}\) contains this virtual party’s random tape, we can continue our overall simulation as above.
We now need to show that  works as required. For contradiction assume that we have an environment Z for which
works as required. For contradiction assume that we have an environment Z for which  . We will use Z to construct an environment \(Z'\) that breaks the assumed security of \({\varPi } _{f'}\) and so reach a contradiction.
. We will use Z to construct an environment \(Z'\) that breaks the assumed security of \({\varPi } _{f'}\) and so reach a contradiction.
\(Z'\) :
-
1.
Run internally a copy of Z, and get the initial set of corrupted real players from Z, this determines the set \({\mathbb {V}}^* \) of corrupt virtual players as above, so \(Z'\) will corrupt this set (recall that \(Z'\) acts as environment for \({\varPi } _{f'}\)).
-
2.
For each real honest party \(\mathrm {P}_{i} \), get its input \(x_i\) from Z. Choose random shares \(x_i^j\) subject to \(x_i = \bigoplus _j x_i^j\).
-
3.
Execute with Z Step 1 of
 ’s algorithm, but instead of choosing random shares on behalf of honest players, use the shares chosen in the previous step. This will fix the inputs \(\{ x_i^j \}_{i=1..n}\) of every virtual player \({\mathbb {P}}_{j} \). \(Z'\) specifies these inputs for the parties in \({\varPi } _{f'}\).
’s algorithm, but instead of choosing random shares on behalf of honest players, use the shares chosen in the previous step. This will fix the inputs \(\{ x_i^j \}_{i=1..n}\) of every virtual player \({\mathbb {P}}_{j} \). \(Z'\) specifies these inputs for the parties in \({\varPi } _{f'}\). -
4.
Recall that \(Z'\) (being a passive environment) has access to the views of the players in \({\mathbb {V}}^* \). This initially contains the randomness \(r_j\) of corrupt \({\mathbb {P}}_{j} \). \(Z'\) uses this \(r_j\) to execute Step 3 of
 .
. -
5.
Now \(Z'\) can expect to see the views of the corrupt \({\mathbb {P}}_{j} \)’s as they execute the protocol Therefore \(Z'\) can perform Step 6 of
 with one change only: it will get the messages from honest to corrupt players by looking at the views of the corrupt \({\mathbb {P}}_{j} \)’s, but will forward these messages to Z exactly as
with one change only: it will get the messages from honest to corrupt players by looking at the views of the corrupt \({\mathbb {P}}_{j} \)’s, but will forward these messages to Z exactly as  would have done. In the end \(Z'\) outputs the guess produced by Z.
would have done. In the end \(Z'\) outputs the guess produced by Z.
Now, all we need to observe is that if \(Z'\) runs in the ideal process, the view seen by its copy of Z is generated using effectively the same algorithm as in  , since the views of corrupt virtual parties come from
, since the views of corrupt virtual parties come from  . On the other hand, if \(Z'\) runs in the real process, its copy of Z will see a view distributed exactly as what it would see in a normal real process. This is because the first 4 steps of \(Z'\) is a perfect simulation of the real \({\varPi } _f\), and the last step aborts exactly when the real protocol would have aborted and otherwise provides real protocol messages to Z. Therefore \(Z'\) can distinguish real from ideal process with exactly the same advantage as Z. \(\square \)
. On the other hand, if \(Z'\) runs in the real process, its copy of Z will see a view distributed exactly as what it would see in a normal real process. This is because the first 4 steps of \(Z'\) is a perfect simulation of the real \({\varPi } _f\), and the last step aborts exactly when the real protocol would have aborted and otherwise provides real protocol messages to Z. Therefore \(Z'\) can distinguish real from ideal process with exactly the same advantage as Z. \(\square \)
Efficiency of our transform. In our transform every real party emulates \(t+1\) virtual parties which constitutes the only computational overhead of our transform (if we ignore the computational effort in checking that the \(t+1\) received messages are equal).
Since our transform mainly works by sending messages in a redundant fashion, it incurs a multiplicative bandwidth overhead that depends on the number of active corruptions we want to tolerate. Assume the underlying protocol \({\varPi } _{f'}\) sends a total of m messages and further assume that we want to tolerate \(t\) corruptions. This means that every virtual party \({\mathbb {P}}_{i}\) will be simulated by \(t +1\) real parties. Whenever a virtual party \({\mathbb {P}}_{i}\) sends a message to \({\mathbb {P}}_{j}\), we send \(\left( t +1\right) \cdot \left( t +1\right) = t ^2 + 2t + 1\) real messages. Ignoring messages sent for the coin-flips and share distribution, our transform produces a protocol that sends at most \(m \cdot \left( t ^2 + 2t + 1 \right) \) messages.
For the special case, where \(n = 3\), \(t = 1\), and \({\mathbb {P}}_{1} = \{ \mathrm {P}_{1}, \mathrm {P}_{2} \}\), \({\mathbb {P}}_{2} = \{ \mathrm {P}_{2}, \mathrm {P}_{3} \}\), and \({\mathbb {P}}_{3} = \{ \mathrm {P}_{3}, \mathrm {P}_{1} \}\), it holds that for all \(i \ne j\), \(\vert {\mathbb {P}}_{i} \cap {\mathbb {P}}_{j} \vert = 1\). Hence, every message from \({\mathbb {P}}_{i}\) to \({\mathbb {P}}_{j}\) is realized by sending 3 real messages, which results in 3m total messages sent during the second phase of our transform.
Active security without \({\mathcal {F}}_{\mathsf {cflip}}\) and \({\mathcal {F}}_{\mathsf {bcast}}\): By the UC composition theorem, we can replace the functionalities \({\mathcal {F}}_{\mathsf {cflip}}\) and \({\mathcal {F}}_{\mathsf {bcast}}\) in our compiled protocol by secure implementations and still have a secure protocol. It should be noted that for \(t\) corruptions we have \(n \ge \left( t ^2 + t \right) + 1\) and thus we are always in an honest majority setting. This means that both functionalities can be implemented with information theoretic security in the basic point-to-point secure channels model as described in Sect. 2.
The implementation of \({\mathcal {F}}_{\mathsf {cflip}}\) uses verifiable secret sharing (VSS). Note that even though VSS in itself is powerful enough to realize secure multiparty computation, we only use it for the coin flip functionality. Thus, the number of VSSs we need depends only on the amount of randomness used in the passively secure protocol, and this can be reduced using a pseudorandom generator. Besides (and perhaps more importantly) for the large class of protocols with biased passive security we do not need \({\mathcal {F}}_{\mathsf {cflip}}\) at all to compile them. Recall that, in the biased passive security model, we still assume that all parties follow the protocol execution honestly, but corrupted parties have the additional power of choosing their random tapes in a non-adaptive, but arbitrary manner. Adversaries who behave honestly, but tamper with their random tapes have been previously considered in [1, 24].
If our compiler starts with a protocol \({\varPi } _{f'}\) that is secure against biased passive adversaries, then we can avoid the use of a coin-flipping functionality, since any random tape is secure to use. We can modify our compiler in a straightforward fashion. Rather than executing one coin-flip for every \({\mathbb {P}}_{i}\) to agree on a random tape, we simply let one party from each \({\mathbb {P}}_{i}\) broadcast an arbitrarily chosen random tape to the other members of \({\mathbb {P}}_{i}\). Now, since we do not need \({\mathcal {F}}_{\mathsf {cflip}}\), and we do not need to implement VSS for this purpose.
Guaranteed Output Delivery. At the cost of reducing the threshold \(t \) of active corruptions that our transform can tolerate, we can obtain guaranteed output delivery. For this we need to ensure that an adversary cannot abort in neither the first phase, nor the second phase of our protocol. In the first phase, when each real party broadcasts its input shares to the virtual parties, we can ensure termination by simply letting every \({\mathbb {P}}_{i}\) to be simulated by \(3t + 1\) real parties. In this case each \({\mathbb {P}}_{i}\) contains less than 1/3 corruptions and unconditionally secure broadcast (with termination) exists among the members of \({\mathbb {P}}_{i}\). Using this approach, the adversary can learn \(t \left( 3t + 1\right) \) views and thus the underlying protocol needs to have passive \(\left( 3t ^2 + t \right) \)-security.
Another approach that gives slightly better parameters is to only assume an honest majority in each \({\mathbb {P}}_{i}\) and use detectable broadcast. In this case the underlying protocol needs to be passively \(\left( 2t ^2 + t \right) \)-secure and thus, since \(n \ge \left( 2t ^2 + t \right) +1\), unconditionally secure broadcast with termination exists among all parties. If a real party simulating a virtual party aborts during a detectable broadcast (to members of \({\mathbb {P}}_{i}\)), it will broadcast (with guaranteed termination) this abort to all parties. At this point an honest sender, who initiated the broadcast, can broadcast its share for that virtual party among all parties in the protocol. Intuitively, since the broadcast failed, there is at least one corrupted party in the virtual party and thus the adversary already learned the sender’s input share, so we do not need to keep it secret any more. If the sender is corrupt and does not broadcast its share after an abort, then all parties replace the sender’s input by some default value.
In the second phase of our protocol, real parties simulating virtual parties are currently aborting as soon as they receive inconsistent messages, as they cannot distinguish a correct message from a malformed one. If we ensure that every virtual party is simulated by an honest majority, then, whenever a real party receives a set of messages representing a message from a virtual party, it makes a majority decision. That is, it considers the most frequent message as the correct one and continues the protocol based on this message. Let \({\tilde{{\varPi }}}_f\) denote the modified protocol as described above. We then have the following corollary whose proof is a trivial modification of the proof of Theorem 1.
Corollary 1
Let \(n \ge 3\). Suppose \({\varPi } _{f'}\) implements \({\mathcal {F}}_{f'}\) with passive \(\left( 2t ^2 + t \right) \)-security. Then \({\tilde{{\varPi }}}_f\) as described above implements \({\mathcal {F}}_f^{fullactive}\) with active t-security in the (\({\mathcal {F}}_{\mathsf {bcast}}\), \({\mathcal {F}}_{\mathsf {cflip}}\))-hybrid model.
3.1 Tolerating More Corruptions Assuming Static Adversaries
In this section we sketch a technique that allows to improve the number of corruptions tolerated by our compiler if we restrict the adversary to only perform static corruptions, i.e., if the adversary must choose the corrupted parties before the protocol starts, and we assume a sufficiently large number of parties.
In contrast to our compiler from Theorem 1, instead of choosing which real parties will emulate which virtual party in a deterministic way, we will now map real parties to virtual parties in a probabilistic fashion. Intuitively, since the adversary has to choose who to corrupt before the assignment and since the assignment is done in a random way, this can lead to better bounds when transforming protocols with a large number of parties.
Our new transform works as follows: At the start of the protocol, the parties invoke \({\mathcal {F}}_{\mathsf {cflip}} \) and use the obtained randomness to select uniformly at random a set of real parties to emulate each virtual party. Then we execute the transformed protocol \({\varPi } _f\) exactly as we specified above.
Let us define a virtual party in our transform to be controlled by the adversary if it is only emulated by corrupt real parties, and let us define a virtual party to be observed by the adversary if it is emulated by at least one corrupt real party. In the proof of Theorem 1, we need to ensure two conditions for our transform to be secure. (1) No virtual party can be controlled by the adversary and, (2) the number of virtual parties observed by the adversary must be smaller than the privacy threshold of the passively secure protocol \({\varPi } _{f'}\).
We now show that we can set the parameters of the protocol in a way that these two properties are satisfied (except with negligible probability) and in a way that produces better corruption bounds than our original transform.
In the analysis we assume that \(n={\varTheta }(\lambda )\), where n is, as before, the number of virtual and real parties, while \(\lambda \) is the statistical security parameter. We also assume that the security threshold of the underlying passively secure protocol \({\varPi } _{f'}\) is cn for some constant c. Finally, let e be the number of real parties that emulate each virtual party, and let \(e= u \log n\) for a constant u. The number of corrupt real parties that can be tolerated by our transform is then at most \(d \cdot n/\log n\) for some constant d. We choose the constants d and u such that \(c<1-du\).
To show (1), it is easy to see that (by a union bound) the probability that at least one virtual party is fully controlled by the adversary (i.e., it is emulated only by corrupt real parties) is at most:
Since we set \(e= u \log n\), this probability is negligible.
As for (2), the probability that a virtual party is not observed by the adversary (i.e., it is emulated only by honest parties) is \((1- d/\log n)^e\), so that the expected number of such parties is \(n (1- d/\log n)^e\) which for large n (and hence small values of \(d/\log n\)) converges to
As we choose d and u such that \(c < 1-du\), it then follows immediately from a Chernoff bound that the number of virtual parties with only honest emulators is at least cn with overwhelming probability. Let \({\bar{{\varPi }}}_f\) denote the protocol using this probabilistic emulation strategy. We then have:
Corollary 2
Let \(n ={\varTheta }(\lambda )\). Suppose \({\varPi } _{f'}\) realizes the \(n\)-party functionality \({\mathcal {F}}_{f'}\) with passive and static cn-security for a constant c. Then \({\bar{{\varPi }}}_f\) realizes \(F_f\) with active and static \(d \cdot n/\log n\)-security in the \(\left( {\mathcal {F}}_{\mathsf {bcast}}, {\mathcal {F}}_{\mathsf {cflip}} \right) \)-hybrid model, for a constant d.
Moreover, compared to the protocol obtained using our adaptively secure transform, \({\bar{{\varPi }}}_f\) has asymptotically better multiplicative overhead of only \(O((\log n)^2)\).
3.2 Achieving Constant Fraction Corruption Threshold
A different approach for improving the bound of corruptions that we can tolerate is to combine our compiler with the results of Cohen et al. [7].
In [7], the authors show how to construct a multiparty protocol for any number of parties from a protocol for a constant number k of parties and a log-depth threshold formula of a certain form. The formula must contain no constants and consist only of threshold gates with k inputs that output 1 if at least j input bits are 1. The given k-party protocol should be secure against \(j-1\) (active) corruptions. In [7], constructions are given for such formulae, and this results in multiparty protocols tolerating essentially a fraction \((j-1)/(k-1)\) corruptions.
For instance, from a protocol for 5 parties tolerating 2 passive corruptions (in the model without preprocessing), our result constructs a 5 party protocol tolerating 1 active corruption. Applying the results from [7], we get a protocol for any number n of parties tolerating \(n/4 - o(n)\) malicious corruptions. This protocol is maliciously secure with abort, but we can instead start from a protocol for 7 parties tolerating 3 passive corruptions and use Corollary 1 to get a protocol for 7 parties, 1 active corruption and guaranteed output delivery. Applying again the results from [7], we get a protocol for any number n of parties tolerating \(n/6 - o(n)\) malicious corruptions with guaranteed output delivery. These results also imply that if we accept that the protocol construction is not explicit, or we make a computational assumption, then we get threshold exactly n / 4, respectively n / 6.
4 Achieving Security with Complete Fairness
The security notion achieved by our previous results is active security with abort, namely the adversary gets to see the output and then decides whether the protocol should abort – assuming we want to tolerate the maximal number of corruptions the construction can handle. However, security with abort is often not very satisfactory: it is easy to imagine cases where the adversary may for some reason “dislike” the result and hence prefers that it is not delivered.
However, there is a second version that is stronger than active security with abort, yet weaker than full active security, which is called active security with complete fairness [8]. Here the adversary may tell the functionality to abort or ask for the output, but once the output is given, it will also be delivered to the honest parties.
In this section we show how to get general MPC with complete fairness from MPC with abort, with essentially the same efficiency. This will work if we have honest majority and if the given MPC protocol has a compute-then-open structure, a condition that is satisfied by a large class of protocols. The skeptical reader may ask why such a result is interesting, since with honest majority we can get full active security without abort anyway. Note, however, that this is only possible if we assume that unconditionally secure broadcast with termination is given as an ideal functionality. In contrast, we do not need this assumption as our results above can produce compute-then-open protocols that only need detectable broadcast (which can be implemented from scratch) and our construction below that achieves complete fairness does not need broadcast with termination either.
We define the following:
Definition 2
\({\varPi } _f\) is a compute-then-open protocol for computing function f if it satisfies the following:
-
It implements \({\mathcal {F}}_f\) with active t-security, where \(t< n/2\).Footnote 2
-
One can identify a particular round in the protocol, called the output round, that has properties as defined below. The rounds up to but not including the output round are called the computation phase.
-
The adversary’s view of the computation phase is independent of the honest party’s input. More formally, we assume that the simulator always simulates the protocol up to the output round without asking for the output.
-
The total length of the messages sent in the output round depends only on the number of players, the size of the output and (perhaps) on the security parameterFootnote 3. We use \(d_{i,j}\) to denote the message sent from party i to party j in the output round.
-
At the end of the computation phase, the adversary knows whether a given set of messages sent by corrupt parties in the output round will cause an abort. More formally, there is an efficiently computable Boolean function \(f_{abort}\) which takes as input the adversary’s view v of the computation phase and messages \({\varvec{d}} = \{ d_{i,j} | \ 1\le i\le t, 1\le j\le n \}\), where we assume without loss of generality that the first t parties are corrupted. Now, when corrupt parties have state v and send \({\varvec{d}}\) in the output round, then if \(f_{abort}(v,{\varvec{d}})=0\) then all honest players terminate the protocol normally, otherwise at least one aborts, where both properties hold except with negligible probability.
-
One can decide whether the protocol aborts based only on all messages sent in the output roundFootnote 4. More formally, we assume the function \(f_{abort}\) can also take as input messages \({\varvec{d}}_{all} = \{ d_{i,j} | \ 1\le i\le t, 1\le j\le n \}\). Then, if parties \(P_1,..., P_n\) send messages \({\varvec{d}}_{all}\) in the output round and \(f_{abort}({\varvec{d}}_{all})=0\), then all honest players terminate the protocol, otherwise some player aborts (except with negligible probability).
Note that the function \(f_{abort}\) is assumed to be computable in two different ways: from the set of all messages sent in the output round, or from adversary’s view. The former is used by our compiled protocol, while the latter is only used by the simulator of that protocol.
A typical example of a compute-then-open protocol can be obtained by applying our compiler from Sect. 3 to a secret-sharing based and passively secure protocol, such as BGW: In the compiled protocol, the adversary can only make it to the output round by following the protocol. Therefore he knows what he should send in the output round and that the honest players will abort if they don’t see what they expect. From the set of all messages sent in the output round, one can determine if an abort will occur by simple equality checks. More generally, it is straightforward to see that if one applies the compiler to a compute-then-open passively secure protocol, then the resulting protocol also has the same structure.
We can now show the following:
Theorem 2
Assume we are given a compiler that constructs from the circuit for a function f a compute-then-open protocol \({\varPi }_f\) that realizes \({\mathcal {F}}_f\), with active t-security. Then we can construct a new compiler that constructs a compute-then-open protocol \({\varPi }'_f\) that realizes \({\mathcal {F}}^{\mathsf {fair}} _f\) with active t-security. The complexity of \({\varPi }'_f\) is larger than that of \({\varPi }_f\) by an additive term that only depends on the number of players, the size of the outputs and the security parameter.
Proof
Let Deal be a probabilistic algorithm that on input a string s produces shares of s in a verifiable secret sharing scheme with perfect t-privacy and non-interactive reconstruction, we write \(Deal(s)= (Deal_1(s), \dots , Deal_n(s))\) where \(Deal_i(s)\) is the \(i'th\) share produced. For \(t<n/2\) this is easily constructed, e.g., by first doing Shamir sharing with threshold t and then appending to each share unconditionally secure MACs that can be checked by the other parties. Such a scheme will reconstruct the correct secret except with negligible probability (statistical correctness) and has the extra property that given a secret s and an unqualified set of shares, we can efficiently compute a complete set Deal(s) that is consistent with s and the shares we started from.
Now given function f, we construct the protocol \({\varPi }'_f\) from \({\varPi }_f\) as follows:
-
1.
Run the computation phase of \({\varPi }_f\) (where we abort if \({\varPi }_f\) aborts) and let \({\varvec{d}}_{all} = \{ d_{i,j} | \ 1\le i\le t, 1\le j\le n \}\) denote the messages that parties would send in the output round of \({\varPi }_f\). Note that each party \(P_i\) can compute what he would send at this point.
-
2.
Let \(f'\) be the following function: it takes as input a set of strings \({\varvec{d}}_{all} = \{ d_{i,j} | \ 1\le i\le t, 1\le j\le n \}\). It computes \(Deal(d_{i,j})\) for \(1\le i,j\le n\) and outputs to party \(P_l\) \(Deal(d_{i,j})_l\). Finally, it outputs \(f_{abort}({\varvec{d}}_{all})\) to all parties.
Now we run \({\varPi }_{f'}\), where parties input the \(d_{i,j}\)’s they have just computed.
-
3.
Each player uses detectable broadcast to send a bit indicating if he terminated \({\varPi } _{f'}\) or aborted.
-
4.
If any player sent abort, or if \({\varPi } _{f'}\) outputs 1, all honest players abort. Otherwise parties reconstruct each \(d_{i,j}\) from \(Deal(d_{i,j})\) (which we have from the previous step): each party \(P_l\) sends \(Deal(d_{i,j})_l\) to \(P_j\), for \(1\le i\le n\) (recall that \(P_j\) is the receiver of \(d_{i,j}\)), and parties apply the reconstruction algorithm of the VSS.
-
5.
Finally parties complete protocol \({\varPi }_f\), assuming \({\varvec{d}}_{all} = \{ d_{i,j} | \ 1\le i\le t, 1\le j\le n \}\) were sent in the output round.
The claim on the complexity of \({\varPi }'_f\) is clear, since \({\varPi } _f\) is a compute-then-open protocol and steps 2–4 only depend on the size of the messages in the output round and not on the size of the total computation.
As for security, the idea is that just before the output phase of the original protocol, instead of sending the \(d_i\)’s we use a secure computation \({\varPi }_{f'}\) to VSS them instead and also to check if they would cause an abort or not. This new computation may abort or tell everyone that the \(d_i\)’s are bad, but the adversary already knew this by assumption since \({\varPi }_f\) is a compute-then-open protocol. So by privacy of the VSS, nothing is revealed by doing this. On the other hand, if there is no abort and we are told the \(d_i\)’s are good, the adversary can no longer abort, as he cannot stop the reconstruction of the VSSs.
More formally, we construct a simulator T as follows:
-
1.
First run the simulator S for \({\varPi }_f\) up to the output round. Then run the simulator \(S'\) for \({\varPi }_{f'}\) where T also emulates the functionality \({\mathcal {F}}_{f'}\). In particular, T can observe the inputs \(S'\) produced for \(f'\) on behalf of the corrupt parties, that is, messages \({\varvec{d}} = \{ d_{i,j} | \ 1\le i\le t, 1\le j\le n \}\) where we assume without loss of generality that the first t parties are corrupt.
-
2.
Note that T now has the adversary’s view v of the computation phase of \({\varPi }_f\) (from S) and messages \({\varvec{d}}\), so T computes \(f_{abort}(v, {\varvec{d}})\). Since \({\varPi } _f\) is a compute-then-open protocol, this bit equals the output from \(f'\), so we give this bit to \(S'\), who will now, for each honest player, say whether that player aborts or gets the output.
-
3.
T can now trivially simulate the round of detectable broadcasts, as it knows what each honest player will send. If anyone broadcasts “abort”, or the output from \(f'\) was 1, T sends “abort” to \({\mathcal {F}}_f\) and stops. Otherwise, T asks for the output y from f which we pass to S, who will now produce a set of messages \({\varvec{d}}_{honest}\) to be sent by honest players in the output round. In response, we tell S the corrupt parties sent \({\varvec{d}}\). By assumption we know that this will not cause S to abort. So we now have a complete set of messages \({\varvec{d}}_{all}\) (including messages from the honest parties) that is consistent with y.
-
4.
Now T exploits t-privacy of the VSS: during the run of \({\varPi }_{f'}\) t shares of each \(Deal(d_{i,j})\) have been given to the adversary. T now completes each set of shares to be consistent with \(d_{i,j}\), and sends the resulting shares on behalf of the honest parties in \({\varPi }'_f\).
-
5.
Finally, we let S complete its simulation of the execution of \({\varPi }_f\) after the output round (if anything is left).
It is clear that T does not abort after it asks for the output. Further the output of T working with f is statistically close to that of the real protocol. This follows easily from the corresponding properties of S and \(S'\) and statistical correctness of the VSS. \(\square \)
The construction in Theorem 2 is quite natural, and works for a more general class of protocols than those produced by our main result, but we were unable to find it in the literature.
It should also be noted that when applying the construction to protocols produced by our main result, we can get a protocol that is much more efficient than in the general case. This is because the computation done by the function \(f'\) becomes quite simple: we just need a few VSSs and some secure equality checks.
5 Efficient Three-Party Computation Over Rings
To illustrate the potential of our compiler from Sect. 3, we provide a protocol for secure three-party computation over arbitrary rings  that is secure against one active corruption, and has constant online communication overhead for any value of m. That is, during the online phase, the communication overhead does not depend on the security parameter.
that is secure against one active corruption, and has constant online communication overhead for any value of m. That is, during the online phase, the communication overhead does not depend on the security parameter.
The protocol uses the preprocessing/online circuit evaluation approach firstly introduced by Beaver [2]. During the preprocessing phase, independently of the inputs and the function to be computed, the parties jointly generate a sufficient amount of additively secret shared multiplication triples of the form  . During the online phase, the parties then consume these triples to evaluate an arithmetic circuit over their secret inputs.
. During the online phase, the parties then consume these triples to evaluate an arithmetic circuit over their secret inputs.
The online phase of Beaver’s protocol tolerates 2 passive corruptions and thus we can directly apply Theorem 1 to obtain a protocol for the online phase that is secure against one active corruption. What is left is the preprocessing phase, i.e., how to generate the multiplicative triples. Our technical contribution here is a novel protocol for this task. Note that this protocol does not use our compiler. Instead it produces the triples to be used by the compiled online protocol. Furthermore, since Beaver’s online phase is deterministic, our protocol, as opposed to the general compiler, does not require to use any coin flip protocol.
For the sake of concreteness, in this section we give an explicit description of the entire protocol. In the preprocessing protocol we create replicated secret shares of multiplication triplesFootnote 5. Afterwards we briefly describe the online phase we obtain from applying our compiler to Beaver’s online phase. The communication of our preprocessing protocol is only  many bits per generated triple, meaning that the overhead for active security is a constant when m is exponential in the (statistical) security parameter.
many bits per generated triple, meaning that the overhead for active security is a constant when m is exponential in the (statistical) security parameter.
5.1 The Preprocessing Protocol
The goal of our preprocessing protocol is to generate secret shared multiplication triples of the form  , where m is an arbitrary ring modulus. Our approach can be split into roughly three steps. First, we optimistically generate a possibly incorrect multiplication triple over the integers. In the second step, we optimistically generate another possibly incorrect multiplication triple in
, where m is an arbitrary ring modulus. Our approach can be split into roughly three steps. First, we optimistically generate a possibly incorrect multiplication triple over the integers. In the second step, we optimistically generate another possibly incorrect multiplication triple in  , where p is some sufficiently large prime. We interpret our integer multiplication triple from step one as a triple in
, where p is some sufficiently large prime. We interpret our integer multiplication triple from step one as a triple in  and “sacrifice” our second triple from
and “sacrifice” our second triple from  to check its validity. In the third step we exploit the fact that the modulo operation and the product operation are interchangeable. That is, each party reduces its integer share modulo m to obtain a share of a multiplication triple in
to check its validity. In the third step we exploit the fact that the modulo operation and the product operation are interchangeable. That is, each party reduces its integer share modulo m to obtain a share of a multiplication triple in  .
.
The main idea in step one is, that we can securely secret share a value  over the integers by using shares that are \(\log {m}+\lambda \) bits large. The extra \(\lambda \) bits in the share size ensure that for any two values in
over the integers by using shares that are \(\log {m}+\lambda \) bits large. The extra \(\lambda \) bits in the share size ensure that for any two values in  the resulting distributions of shares are statistically close.
the resulting distributions of shares are statistically close.
We now proceed with a more formal description of the different parts of the protocol. We start by introducing some useful notation for replicated secret sharing:
Replicated Secret Sharing – Notation and Invariant: We write  for a replicated integer secret sharing of a and \([a]_p=(a_1,a_2,a_3)\) for a replicated secret sharing modulo p. In both cases it holds that \(a=a_1+a_2+a_3\) (where the additions are over the integer in the first case and modulo p in the latter). As an invariant for both kinds of secret sharing, each party \(\mathrm {P}_{i}\) will know the shares \(a_{i+1}\) and \(a_{i-1}\).
for a replicated integer secret sharing of a and \([a]_p=(a_1,a_2,a_3)\) for a replicated secret sharing modulo p. In both cases it holds that \(a=a_1+a_2+a_3\) (where the additions are over the integer in the first case and modulo p in the latter). As an invariant for both kinds of secret sharing, each party \(\mathrm {P}_{i}\) will know the shares \(a_{i+1}\) and \(a_{i-1}\).
Replicated Secret Sharing – Input: When a party \(\mathrm {P}_{i}\) wants to share a value  , \(\mathrm {P}_{i}\) picks uniformly random
, \(\mathrm {P}_{i}\) picks uniformly random  and defines \(a_3=a-a_1-a_2 \mod p\). Then \(\mathrm {P}_{i}\) sends shares \(a_{j-1}\) and \(a_{j+1}\) to \(\mathrm {P}_{j}\). Finally \(\mathrm {P}_{i+1} \) and \(\mathrm {P}_{i-1} \) echo \(a_i\) to each other and abort if the value they received in this echo phase differs from what they received from \(\mathrm {P}_{i}\). When using integer secret sharing instead, the shares need to be large enough to statistically hide the secret. That is, when a party \(\mathrm {P}_{i}\) wants to share a value \(a\in \{0,\ldots ,m-1\}\), \(\mathrm {P}_{i} \) picks uniformly random
and defines \(a_3=a-a_1-a_2 \mod p\). Then \(\mathrm {P}_{i}\) sends shares \(a_{j-1}\) and \(a_{j+1}\) to \(\mathrm {P}_{j}\). Finally \(\mathrm {P}_{i+1} \) and \(\mathrm {P}_{i-1} \) echo \(a_i\) to each other and abort if the value they received in this echo phase differs from what they received from \(\mathrm {P}_{i}\). When using integer secret sharing instead, the shares need to be large enough to statistically hide the secret. That is, when a party \(\mathrm {P}_{i}\) wants to share a value \(a\in \{0,\ldots ,m-1\}\), \(\mathrm {P}_{i} \) picks uniformly random  and defines \(a_3=a-a_1-a_2\). Then \(\mathrm {P}_{i}\) sends shares \(a_{j-1}\) and \(a_{j+1}\) to \(\mathrm {P}_{j}\). Now, \(\mathrm {P}_{j}\) checks if
and defines \(a_3=a-a_1-a_2\). Then \(\mathrm {P}_{i}\) sends shares \(a_{j-1}\) and \(a_{j+1}\) to \(\mathrm {P}_{j}\). Now, \(\mathrm {P}_{j}\) checks if  and aborts otherwise.Footnote 6 Finally \(\mathrm {P}_{i+1} \) and \(\mathrm {P}_{i-1} \) echo \(a_i\) to each other and abort if the value they received in this echo phase differs from what they received from \(\mathrm {P}_{i}\).
and aborts otherwise.Footnote 6 Finally \(\mathrm {P}_{i+1} \) and \(\mathrm {P}_{i-1} \) echo \(a_i\) to each other and abort if the value they received in this echo phase differs from what they received from \(\mathrm {P}_{i}\).
Replicated Secret Sharing – Reveal: When parties want to open a share [a], \(\mathrm {P}_{i}\) sends its shares \(a_{i+1}\) and \(a_{i-1}\) to \(\mathrm {P}_{i+1}\) and \(\mathrm {P}_{i-1}\) respectively. When \(\mathrm {P}_{i}\) receives share \(a_i\) from \(\mathrm {P}_{i+1}\) and share \(a'_i\) from \(\mathrm {P}_{i-1}\), \(\mathrm {P}_{i}\) aborts if \(a_i\ne a'_i\) or outputs \(a=a_1+a_2+a_3\) otherwise.Footnote 7
Replicated Secret Sharing – Linear Combination: Since the secret sharing we use here is linear, we can compute linear functions without interaction i.e., when executing \([c]=[a]+[b]\) each party will locally add its sharesFootnote 8. We consider three kind of additions:
-
\([c]_p=[a]_p+[b]_p\), where all the shares are added modulo p;
-
 , where the shares are added over the integers (note that the magnitude of the shares will increase when using integer secret sharing);
, where the shares are added over the integers (note that the magnitude of the shares will increase when using integer secret sharing); -
 , where the shares are added modulo p. Note that in the this case, if a is uniform modulo p then c is uniform modulo p.Footnote 9
, where the shares are added modulo p. Note that in the this case, if a is uniform modulo p then c is uniform modulo p.Footnote 9
Replicated Secret Sharing – Multiplication: Given two sharings \([a]_p\), \([b]_p\), we can compute a secret sharing of the product \([c=a\cdot b]\) in the following way:
-
1.
\(\mathrm {P}_{i}\) samples a random
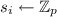 and computes \(u_{i}=a_{i+1}b_{i+1}+a_{i+1}b_{i-1}+a_{i-1}b_{i+1}+s_{i}\);
and computes \(u_{i}=a_{i+1}b_{i+1}+a_{i+1}b_{i-1}+a_{i-1}b_{i+1}+s_{i}\); -
2.
\(\mathrm {P}_{i}\) sends \(u_{i}\) to \(\mathrm {P}_{i+1}\) and \(s_{i}\) to party \(\mathrm {P}_{i-1}\);
-
3.
Finally, party \(\mathrm {P}_{i}\) defines its own two shares of c as \(c_{i+1}=u_{i-1}-s_{i}\) and \(c_{i-1}=u_{i}-s_{i+1}\);
When performing multiplications with integer secret sharings, we need to ensure that the chosen randomness is large enough to hide the underlying secrets. In particular, given two sharings  ,
,  , such that all shares are bounded by B, we can compute a secret sharing of the product
, such that all shares are bounded by B, we can compute a secret sharing of the product  in the following way:
in the following way:
-
1.
\(\mathrm {P}_{i}\) samples a random
 and computes \(u_{i}=a_{i+1}b_{i+1}+a_{i+1}b_{i-1}+a_{i-1}b_{i+1}+s_{i}\);
and computes \(u_{i}=a_{i+1}b_{i+1}+a_{i+1}b_{i-1}+a_{i-1}b_{i+1}+s_{i}\); -
2.
\(\mathrm {P}_{i}\) sends \(u_{i}\) to \(\mathrm {P}_{i+1}\) and \(s_{i}\) to party \(\mathrm {P}_{i-1}\);
-
3.
\(\mathrm {P}_{i}\) checks that the received shares are of the correct size i.e.,
 and
and 
-
4.
Finally, party \(\mathrm {P}_{i}\) defines its own two shares of c as \(c_{i+1}=u_{i-1}-s_{i}\) and \(c_{i-1}=u_{i}-s_{i+1}\);
Armed with these tools we are now ready to describe our preprocessing protocol. The protocol is similar in spirit to previous protocols (e.g., [12, 13]) for generating multiplication triples, and like in previous work we start by generating two possibly incorrect triples, and then “sacrificing” one to check the correctness of the other. The main novelty of this protocol is that the two triples actually live in different domains. One is a an integer secret sharing, while the others is a modular secret sharing. For the sake of exposition we describe the protocol to generate a single multiplicative triple but, as with previous work, it will be more efficient to generate many triples in parallel.
The Preprocessing Protocol – Generate Random Triples:
-
1.
Every \(\mathrm {P}_{i}\) picks random
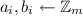 and generates sharings of
and generates sharings of  ;
; -
2.
All parties jointly compute
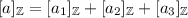 and
and 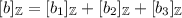 ;Footnote 10
;Footnote 10
-
3.
All parties jointly compute
 (optimistically using the multiplication protocol described above);
(optimistically using the multiplication protocol described above); -
4.
Every \(\mathrm {P}_{i}\) picks random
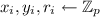 and generates sharings of \([x_i]_p,[y_i]_p,[r_i]_p\);
and generates sharings of \([x_i]_p,[y_i]_p,[r_i]_p\); -
5.
All parties jointly compute \([x]_p=[x_1]_p+[x_2]_p+[x_3]_p\) and \([y]_p=[y_1]_p+[y_2]_p+[y_3]_p\) and \([r]_p=[r_1]_p+[r_2]_p+[r_3]_p\);
-
6.
All parties jointly compute \([z]_p =[x]_p \cdot [y]_p\) (optimistically using the multiplication protocol described above);
-
7.
All parties open r;
-
8.
All parties jointly compute
 ;
; -
9.
All parties jointly compute
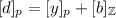 ;
; -
10.
All parties jointly open e, d, then compute and open

and abort if the result is not 0;
-
11.
If the protocol did not abort, all parties output (modular) sharings \([a]_m,[b]_m,[c]_m\) by reducing their integer shares modulo m;
We now argue that:
Theorem 3
The above protocol securely realizes \({\mathcal {F}}_{\mathsf {triple}} \) with statistical security parameter \(\lambda \) in the presence of one active corruption when \(|p|=O(\log {m}+\lambda )\).
Proof
We only give an informal argument for the security of the protocol, since its proof is quite similar to the proof of many previous protocols in the literature (such as [4, 12, 13], etc.).
We first argue for correctness of the protocol, focusing on steps 1,2 and 9: Note that, if there is an output, the output is correct and uniform modulo m. It is correct since, if \(c=ab\) over the integer then \(c=ab\mod m\) as well. And the values a, b, c are distributed uniformly since there is at least one honest party (in fact, two), who will pick \(a_i\) uniformly at random in  , therefore \(a=a_1+a_2+a_3 \mod m\) will be uniform over
, therefore \(a=a_1+a_2+a_3 \mod m\) will be uniform over  as well (the same applies of course also to b and c).
as well (the same applies of course also to b and c).
We now describe the simulator strategy for the individual subroutines, and then we build the overall simulator for the protocol in a bottom-up fashion. To keep the notation simpler we assume that \(\mathrm {P}_{1}\) is corrupt. This is w.l.o.g. due to the symmetry of the protocol. To account for rushing adversaries, we always let the adversary send their message after seeing the message output by the simulator on behalf of the honest parties. As usual, the simulator keeps track of the shares that all parties (honest and corrupt) are supposed to hold at all times.
Simulator – Honest Parties Inputs: To simulate an honest party inputting a value a the simulator follows the share procedure but replacing a with 0. The simulator then sends \(a_2,a_3\) to the adversary \(\mathrm {P}_{1}\) and stores \(a_1,a_2,a_3\). Now the simulator receives \(a'_2\) (or \(a'_3\) depending on whether we are simulating a \(\mathrm {P}_{2}\) input or a \(\mathrm {P}_{3}\) input) back from the adversary and aborts if \(a'_2\ne a_2\) (as an honest party would do).
When performing sharings modulo p, the distribution of the simulated \(a_2,a_3\) are identical as in the real protocol (trivially for \(a_2\), and since \(a_1\) is random and unknown to the adversary, \(a_3\) will be uniformly distributed in both cases). When performing integer sharings, the distribution of the simulated \(a_2\) is trivially identical in the real and simulated execution while \(a_3\) is statistically close. This can be easily seen considering the distribution of \(a_3+a_2\) which is \(a-a_1\) in the real protocol and \(-a_1\) in the simulated execution. Since \(a<m\) and \(a_1\) is uniform between 0 and \(m\cdot 2^\lambda \) the distributions are statistically close with parameter \(\lambda \).
Simulator – Corrupt Party Input: When simulating the input of the corrupt party \(\mathrm {P}_{1}\) the simulator receives \((a_1,a_3)\) (on behalf of \(\mathrm {P}_{2}\)) and \((a'_1,a_2)\) on behalf of \(\mathrm {P}_{3}\). The simulator aborts if \(a_1\ne a'_1\) (like the two honest party would do). When simulating an input in  the simulator reconstructs \(a=\sum _i a_i \mod p\). When simulating an integer input the simulator checks in addition that the shares received are of the right size and then reconstructs \(a=\sum _i a_i\). Note that now
the simulator reconstructs \(a=\sum _i a_i \mod p\). When simulating an integer input the simulator checks in addition that the shares received are of the right size and then reconstructs \(a=\sum _i a_i\). Note that now  which could be larger than m, but not larger than p given our parameters.
which could be larger than m, but not larger than p given our parameters.
Simulator – Multiplication: When simulating multiplications the simulator picks random \((u_3,s_2)\) (see below for the distribution) and sends them to \(\mathrm {P}_{1}\). Then the simulator receives \((u_1,s_1)\) from \(\mathrm {P}_{1}\). This uniquely defines the corrupt party shares of c, namely \(c_2=u_3-s_1\) and \(c_3=u_1-s_2\). Note that the simulator can already now compute the error \(\delta _c = c-ab\) from the stored shares of a, b and the received values \(u_1,s_1\) i.e., \(\delta _c= u_1 - (a_2b_2+a_2b_3+a_3b_2+s_1)\). The simulator sets the final share of c to be \(c_1=ab+\delta _c - c_2 -c_3\) and remembers \((c_1,c_2,c_3)\) and \(\delta _c\).
When simulating multiplications in  the simulator picks \((u_3,s_2)\) uniformly at random, thus the view of the adversary is perfectly indistinguishable in the real and simulated execution: this is trivial for \(s_2\), and for \(u_3\) we can see that it will also be uniformly random as well since in the real protocol \(s_3\) is chosen uniformly at random.
the simulator picks \((u_3,s_2)\) uniformly at random, thus the view of the adversary is perfectly indistinguishable in the real and simulated execution: this is trivial for \(s_2\), and for \(u_3\) we can see that it will also be uniformly random as well since in the real protocol \(s_3\) is chosen uniformly at random.
When simulating integer multiplications the simulator picks \((u_3,s_2)\) uniformly at random in  , thus the view of the adversary is statistically close in the real and simulated execution (trivially for \(s_2\), and since in the protocol \(s_3\) is used to mask a value of magnitude at most \(3B^3\), the distributions are statistically close with parameter \(\lambda \). Note that when simulating integer multiplications the simulator will also abort if the received shares \((u_1,s_1)\) exceed their bounds. This means that at this point the value of \(|c|=|\sum _i c_i|\) is bounded by \(24B^22^\lambda \). As we know from the input phase that all shares are bound by
, thus the view of the adversary is statistically close in the real and simulated execution (trivially for \(s_2\), and since in the protocol \(s_3\) is used to mask a value of magnitude at most \(3B^3\), the distributions are statistically close with parameter \(\lambda \). Note that when simulating integer multiplications the simulator will also abort if the received shares \((u_1,s_1)\) exceed their bounds. This means that at this point the value of \(|c|=|\sum _i c_i|\) is bounded by \(24B^22^\lambda \). As we know from the input phase that all shares are bound by  we get that by setting p to be e.g., larger than \(100m^22^{2\lambda }\) we can ensure that even in the presence of a corrupt party the value of c will not exceed p.
we get that by setting p to be e.g., larger than \(100m^22^{2\lambda }\) we can ensure that even in the presence of a corrupt party the value of c will not exceed p.
Simulator – Fake Reveal: At any point the simulator can open a sharing \((a_1,a_2,a_3)\) to any value \(a+\delta _1\) of its choice. To do so, the simulator sends two identical shares \((a_1+\delta _1)\) to \(\mathrm {P}_{1}\) (simulating that both the honest \(\mathrm {P}_{2}\) and \(\mathrm {P}_{3}\) send the same share to \(\mathrm {P}_{1}\)). Then, \(\mathrm {P}_{1}\) sends its (possibly malicious) shares \(a_2+\delta _2\) and \(a_3+\delta _3\) to the simulator. Now the simulator aborts if \(\delta _2\ne 0\) or if \(\delta _3 \ne 0\). Note the aborting condition is exactly the same as in the real protocol, where e.g., the honest \(\mathrm {P}_{2}\) receives \(a_2\) from \(\mathrm {P}_{1}\) and \(a'_2\) from \(\mathrm {P}_{3}\) and aborts if the two values are different. Finally note that the view of the adversary is exactly the same in the real and simulated execution.
Putting Things Together – Overall Simulator Strategy: We are now ready to describe the overall simulation strategy. Note that all the settings in which the simulator aborts in the previous subroutines are identical to the abort conditions of the honest parties in the protocol and moreover are “predictable” by the adversary (i.e., the adversary knows that sending a certain message will make the protocol abort). The labels of the steps of the simulator refer to the respective steps in the protocol.
- 0.:
-
As already described, the simulator keeps track of the shares that all parties (honest and corrupt) are supposed to hold at all times.
- 1a.:
-
(Send on behalf of \(\mathrm {P}_{2}\) and \(\mathrm {P}_{3}\)) The simulator simulates \(\mathrm {P}_{2}\) and \(\mathrm {P}_{3}\) sharing values \(a_2,a_3,b_2,b_3\) as described above (e.g., the input are set to be 0);
- 1b.:
-
(Receive from \(\mathrm {P}_{1}\)) The simulator receives the (maliciously chosen) shares of \(a_1\) using the procedure described above. In particular, now \(a_1\) is well defined and bounded.
- 2.:
-
The simulator keeps track of the shares of a and b that all parties are supposed to store after the addition; (note that since the shares of the honest parties are simulated to 0 we have \(a=a_1\) and \(b=b_1\) at this point);
- 3.:
-
The simulator uses the simulation strategy for the multiplication protocol as explained above. If the simulation does not abort the value of c and \(\delta _c\) are now well defined and bounded.
- 4.:
-
The simulator runs the sharing subroutine for \(x_2,y_2,r_2,x_3,y_3,r_3\) (e.g., all values are set to 0).
- 5.:
-
The simulator keeps track of the shares of x, y and r that all parties are supposed to store after the addition; (at this point x, y and r are well defined);
- 6.:
-
The simulator uses the simulation strategy for the multiplication protocol as explained above. If the simulation does not abort the value of z and \(\delta _z\) are now well defined.
- 7.:
-
The simulator now runs the fake reveal subroutine and opens r to a uniformly random value;
- 8–9.:
-
The simulator keeps track of the shares of e, d that all parties are supposed to store after the executions of the linear combination;
- 10a.:
-
The simulator runs the fake reveal subroutine and opens e, d to two uniformly random values;
- 10b.:
-
If the simulation did not abort so far the simulator runs the fake reveal subroutine and opens t to \(r\delta _z-\delta _c \mod p\). The simulator aborts if \(t\ne 0\) as an honest party do, but also aborts if \(\delta _c \ne 0\) or \(\delta _z\ne 0\).
- 11.:
-
If the simulator did not abort yet, then the simulator inputs the shares of the multiplicative triple owned by the adversary \((a_2,a_3,b_2,b_3,c_2,c_3)\) to the ideal functionality \({\mathcal {F}}_{\mathsf {triple}}\).
We have already argued for indistinguishability for the various subroutines (thanks to the large masks used in the integer secret sharings). Note that when we combine them in the overall simulator we add an extra aborting condition between a real world execution of the protocol and a simulated execution, namely that the simulation always aborts when the triple is incorrect (during the triple check phase). We conclude that the view of the adversary in these two cases are statistically close in \(\lambda \) thanks to the correctness check at steps 4–10: assume that the multiplication triples are correct i.e., that \(z=xy \mod p\) and \(c=ab\) over the integers. Now, if we make sure that p is large enough such that the shares of a,b, and c are the same over the integers and modulo p, then the resulting t will always be 0. Note that this is guaranteed by the check, during the sharing phase, of the magnitude of the shares chosen by the other parties. Finally, assume that \(c\ne ab\) e.g., \(c=ab+\delta _c\) (with \(\delta _c\ne 0\)) and \(z=xy+\delta _z\).
Now the result of the check will be \(t=r\delta _z-\delta _c \mod p\): Since the value r is picked by the simulator after the values \(\delta _c,\delta _z\) have already been defined, we finally have that t is equal to 0 with probability \(p^{-1}\) which is negligible as desired.
5.2 Online Phase
Here we briefly sketch the online phase of our protocol i.e., the protocol resulting by applying our compiler to Beaver’s passively protocol, which is secure against 1 active corruption. In what follows we describe the protocol explicitly i.e., we describe directly the steps to be performed by the real parties and with no access to helping ideal functionalities: since the online phase of Beaver’s protocol is completely deterministic, we do not need the coin flip functionality and, since we only have 3 parties, the broadcast functionality is easily implemented: when \(\mathrm {P}_{i} \) broadcasts to a set \(\{\mathrm {P}_{i},\mathrm {P}_{j} \}\), this is implemented by sending a message to \(\mathrm {P}_{j} \) and, when \(\mathrm {P}_{i} \) broadcasts to a set \(\{\mathrm {P}_{j},\mathrm {P}_{k} \}\), this is implemented by sending the same message to both parties, who then echo it to each other and abort if the two received messages are different. Finally, note that an additive secret sharing \(a=a_1+a_2+a_3 \bmod {m}\) among the virtual parties \({\mathbb {P}}_{1},{\mathbb {P}}_{2}, {\mathbb {P}}_{3} \) (i.e., where \({\mathbb {P}}_{i} \) knows \(a_i\)) is exactly the same as a replicated secret sharing \([a]_m\) (as described above) between the real parties \(\mathrm {P}_{1},\mathrm {P}_{2},\mathrm {P}_{3} \), and therefore we can continue using the notation introduced for the preprocessing phase.
Online Phase – Setup and Invariant: Let C be the arithmetic circuit that the real parties wish to evaluate, where every input wire is associated to some party \(\mathrm {P}_{i}\). As before, for a value  we write \([x]_m \) to denote the situation where \(\mathrm {P}_{i}\) knows two shares \(x_{i+1},x_{i-1}\) such that \(\sum _i x_i=x\).
we write \([x]_m \) to denote the situation where \(\mathrm {P}_{i}\) knows two shares \(x_{i+1},x_{i-1}\) such that \(\sum _i x_i=x\).
Online Phase – Input Gates: Remember that in our general compiler the secret sharing happened “outside” of the passive MPC protocol and then we modified the circuit to be evaluated by adding a layer of linear operations to reconstruct the secret sharings of the inputs. This is not necessary in the special case of Beaver’s protocol, since after a single sharing we already have the inputs in the desired, replicated secret shared format. Therefore, for every input wire in C associated to \(\mathrm {P}_{i} \) with input  , we let \(\mathrm {P}_{i} \) pick random shares
, we let \(\mathrm {P}_{i} \) pick random shares  s.t., \(\sum _i x_i=x\), and sends \(x_i\) to \(\mathrm {P}_{i-1} \) and \(\mathrm {P}_{i+1} \). Finally \(\mathrm {P}_{i-1} \) and \(\mathrm {P}_{i+1} \) echo \(x_i\) to each other and abort if the value they received in this echo phase differs from what they received from \(\mathrm {P}_{i}\).
s.t., \(\sum _i x_i=x\), and sends \(x_i\) to \(\mathrm {P}_{i-1} \) and \(\mathrm {P}_{i+1} \). Finally \(\mathrm {P}_{i-1} \) and \(\mathrm {P}_{i+1} \) echo \(x_i\) to each other and abort if the value they received in this echo phase differs from what they received from \(\mathrm {P}_{i}\).
Online Phase – Output Gates/Open Subroutine: Whenever the parties need to be able to reveal the content of a shared value \([z]_m\), we let \(\mathrm {P}_{i}\) sends its shares \(z_{i+1}\) and \(z_{i-1}\) to \(\mathrm {P}_{i+1}\) and \(\mathrm {P}_{i-1}\) respectively. When \(\mathrm {P}_{i}\) receives share \(z_i\) from \(\mathrm {P}_{i+1}\) and share \(z'_i\) from \(\mathrm {P}_{i-1}\), \(\mathrm {P}_{i}\) aborts if \(z_i\ne z'_i\) or outputs \(z=z_1+z_2+z_3\) otherwise. During the circuit evaluation we open wires to output the result of the computation and as a subroutine during the evaluation of multiplication gates.
Online Phase – Linear Gates: Linear gates (binary additions, unary additions by constant and multiplication by constant) can be locally implemented by share manipulations in the same way as for the preprocessing phase.
Online Phase – Multiplication Gates: Binary multiplication of two shared values \([x]_m,[y]_m\) is performed by finding an unused preprocessed multiplication triple \([a]_m,[b]_m,[c]_m\) and then running Beaver’s protocol, i.e.:
-
1.
Open \(e = [a]_m + [x]_m \)
-
2.
Open \(d = [b]_m + [y]_m \)
-
3.
Locally compute \([z]_m = [c]_m + e \cdot [y]_m + d \cdot [x]_m - ed\)
Notes
- 1.
Any other distribution of real party among virtual parties that ensures that each real party simulates equally many virtual parties would work as well.
- 2.
We believe that our results also extend to the computational case, but since we are in an honest majority setting, we only focus on statistical and perfect security.
- 3.
In particular, it does not depend on the size of the evaluated function.
- 4.
This restriction is only for simplicity, our results extend to the more general case where termination also depends on some state information that parties keep private, as long as the size of this state only depends on the size of the output.
- 5.
Note that for the three-party case an additively secret shared value among virtual parties, corresponds to a replicated additively secret shared value among the real parties.
- 6.
To keep the protocol symmetric, we use the bound for \(a_3\) for all three shares.
- 7.
There is no need to explicitly check for the size of a share in the reconstruction phase since, by the assumption that at least one among \(\mathrm {P}_{i+1}\) and \(\mathrm {P}_{i-1}\) is honest, one of the received shares will be the correct one.
- 8.
The implementation of \([c]=[a]+k\) and \([c]=k\cdot [a]\) i.e., addition and multiplication by constant, follows trivially.
- 9.
We will use this property twice in the protocol: once, when mixing integer triples and p-modular triples in the multiplication checking phase, and finally, to argue that the resulting triples will be uniform modulo m.
- 10.
Note that if now we convert the sharing of
 to \([a]_m\) by having each party take their shares and locally reduce modulo m, we get that, from the adversary’s point of view, a is uniformly random in
to \([a]_m\) by having each party take their shares and locally reduce modulo m, we get that, from the adversary’s point of view, a is uniformly random in  , since at least one honest party choose \(a_i\) as a uniform value modulo m; the same argument applies symmetrically to
, since at least one honest party choose \(a_i\) as a uniform value modulo m; the same argument applies symmetrically to  .
.
References
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_29
Beaver, D.: Efficient multiparty protocols using circuit randomization. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 420–432. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_34
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: Proceedings of the 20th Annual ACM Symposium on Theory of Computing, 2–4 May 1988, Chicago, Illinois, USA, pp. 1–10 (1988)
Bendlin, R., Damgård, I., Orlandi, C., Zakarias, S.: Semi-homomorphic encryption and multiparty computation. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 169–188. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_11
Bogdanov, D., Laur, S., Willemson, J.: Sharemind: a framework for fast privacy-preserving computations. In: Jajodia, S., Lopez, J. (eds.) ESORICS 2008. LNCS, vol. 5283, pp. 192–206. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-88313-5_13
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: 20th ACM STOC, pp. 11–19. ACM Press, May 1988
Cohen, G., et al.: Efficient multiparty protocols via log-depth threshold formulae. Electronic Colloquium on Computational Complexity (ECCC), 20:107 (2013)
Cohen, R., Lindell, Y.: Fairness versus guaranteed output delivery in secure multiparty computation. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 466–485. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_25
Cramer, R., Damgård, I., Nielsen, J.B.: Secure Multiparty Computation and Secret Sharing. Cambridge University Press, New York (2015)
Cramer, R., Damgrd, I., Escudero, D., Scholl, P., Xing, C.: SPDZ2k: efficient MPC mod \(2^k\) for dishonest majority. CRYPTO (2018). https://eprint.iacr.org/2018/482
Damgård, I., Keller, M., Larraia, E., Pastro, V., Scholl, P., Smart, N.P.: Practical covertly secure MPC for dishonest majority – or: breaking the SPDZ limits. In: Crampton, J., Jajodia, S., Mayes, K. (eds.) ESORICS 2013. LNCS, vol. 8134, pp. 1–18. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40203-6_1
Damgård, I., Orlandi, C.: Multiparty computation for dishonest majority: from passive to active security at low cost. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 558–576. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_30
Damgård, I., Pastro, V., Smart, N.P., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_38
Desmedt, Y., Kurosawa, K.: How to break a practical MIX and design a new one. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 557–572. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_39
Fitzi, M., Gisin, N., Maurer, U.M., von Rotz, O.: Unconditional Byzantine agreement and multi-party computation secure against dishonest minorities from scratch. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 482–501. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_32
Fitzi, M., Gottesman, D., Hirt, M., Holenstein, T., Smith, A.: Detectable Byzantine agreement secure against faulty majorities. In: Ricciardi, A. (ed.) 21st ACM PODC, pp. 118–126. ACM, July 2002
Furukawa, J., Lindell, Y., Nof, A., Weinstein, O.: High-throughput secure three-party computation for malicious adversaries and an honest majority. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part II. LNCS, vol. 10211, pp. 225–255. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_8
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th ACM STOC, pp. 218–229. ACM Press, May 1987
Ishai, Y., Kushilevitz, E., Meldgaard, S., Orlandi, C., Paskin-Cherniavsky, A.: On the power of correlated randomness in secure computation. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 600–620. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_34
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_32
Lindell, Y., Oxman, E., Pinkas, B.: The IPS compiler: optimizations, variants and concrete efficiency. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 259–276. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_15
Maurer, U.M.: Secure multi-party computation made simple. In: Cimato, S., Persiano, G., Galdi, C. (eds.) SCN 2002. LNCS, vol. 2576, pp. 14–28. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36413-7_2
Mohassel, P., Rosulek, M., Zhang, Y.: Fast and secure three-party computation: the garbled circuit approach. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015, pp. 591–602 (2015)
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_26
Pease, M., Shostak, R., Lamport, L.: Reaching agreement in the presence of faults. J. ACM (JACM) 27(2), 228–234 (1980)
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, pp. 162–167. IEEE Computer Society Press, October 1986
Acknowledgements
We thank the anonymous reviewers for their useful feedback. This project has received funding from: the European Research Council (ERC) under the European Unions’s Horizon 2020 research and innovation programme (grant agreement No 669255); the Danish Independent Research Council under Grant-ID DFF-6108-00169 (FoCC); the European Union’s Horizon 2020 research and innovation programme under grant agreement No 731583 (SODA).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Damgård, I., Orlandi, C., Simkin, M. (2018). Yet Another Compiler for Active Security or: Efficient MPC Over Arbitrary Rings. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10992. Springer, Cham. https://doi.org/10.1007/978-3-319-96881-0_27
Download citation
DOI: https://doi.org/10.1007/978-3-319-96881-0_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96880-3
Online ISBN: 978-3-319-96881-0
eBook Packages: Computer ScienceComputer Science (R0)








 ). For each
). For each 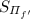 and tell it that the initial set of corrupted players is
and tell it that the initial set of corrupted players is 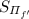 queries
queries  for the messages sent from honest to corrupt virtual parties in the current round. For each such message to be received by a corrupted
for the messages sent from honest to corrupt virtual parties in the current round. For each such message to be received by a corrupted 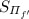 that
that  for the set of messages M sent from honest to corrupt virtual parties in the current round. For all real parties in A tell Z that they send nothing in this round. For all other real honest players compute, as in step
for the set of messages M sent from honest to corrupt virtual parties in the current round. For all real parties in A tell Z that they send nothing in this round. For all other real honest players compute, as in step  ’s algorithm, but instead of choosing random shares on behalf of honest players, use the shares chosen in the previous step. This will fix the inputs
’s algorithm, but instead of choosing random shares on behalf of honest players, use the shares chosen in the previous step. This will fix the inputs  .
. with one change only: it will get the messages from honest to corrupt players by looking at the views of the corrupt
with one change only: it will get the messages from honest to corrupt players by looking at the views of the corrupt  would have done. In the end
would have done. In the end  , where the shares are added over the integers (note that the magnitude of the shares will increase when using integer secret sharing);
, where the shares are added over the integers (note that the magnitude of the shares will increase when using integer secret sharing); , where the shares are added modulo p. Note that in the this case, if a is uniform modulo p then c is uniform modulo p.
, where the shares are added modulo p. Note that in the this case, if a is uniform modulo p then c is uniform modulo p.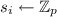 and computes
and computes  and computes
and computes  and
and 
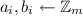 and generates sharings of
and generates sharings of  ;
;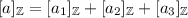 and
and 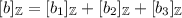 ;
; (optimistically using the multiplication protocol described above);
(optimistically using the multiplication protocol described above);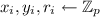 and generates sharings of
and generates sharings of  ;
;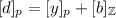 ;
;
 to
to 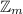 , since at least one honest party choose
, since at least one honest party choose 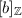 .
.