Abstract
We formulate and study the security of cryptographic hash functions in the backdoored random-oracle (BRO) model, whereby a big brother designs a “good” hash function, but can also see arbitrary functions of its table via backdoor capabilities. This model captures intentional (and unintentional) weaknesses due to the existence of collision-finding or inversion algorithms, but goes well beyond them by allowing, for example, to search for structured preimages. The latter can easily break constructions that are secure under random inversions.
BROs make the task of bootstrapping cryptographic hardness somewhat challenging. Indeed, with only a single arbitrarily backdoored function no hardness can be bootstrapped as any construction can be inverted. However, when two (or more) independent hash functions are available, hardness emerges even with unrestricted and adaptive access to all backdoor oracles. At the core of our results lie new reductions from cryptographic problems to the communication complexities of various two-party tasks. Along the way we establish a communication complexity lower bound for set-intersection for cryptographically relevant ranges of parameters and distributions and where set-disjointness can be easy.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Hash functions are one of the most fundamental building blocks in the design of cryptographic protocols. From a provable security perspective, a particularly successful methodology to use hash functions in protocols has been the introduction of the random-oracle (RO) model [5, 15]. This model formalizes the intuition that the outputs of a well-designed hash function look random by giving all parties, honest or otherwise, oracle access to a uniformly chosen random function. The strong randomness properties inherent in the oracle, in turn, facilitate the security analyses of many protocols.
The cryptanalytic validation of hash functions can strengthen our confidence in this RO-like behavior. On the other hand, as such analyses improve, (unintentional) weaknesses in hash functions are discovered, which can lead to their partial or total break of security. However, cryptanalytic validation might also fail to detect intentional weaknesses that are built into systems. For example such backdoors might be themselves built using cryptographic techniques, which make them hard to detect. Prominent examples show that such backdoors exist and can be exploited in various ways [6, 10, 11].
In this work we revisit a classical question on protecting against failures of hash functions. Numerous works in this area have studied if, and to what level, by combining different hash functions one can offer such protections; see [7, 16, 17, 20] for theoretical treatments and [13, 26, 30] for cryptanalytic work. However, most work has their focus on unintentional failures (to protect against cryptanalytic advances). In this work, we consider a more adversarial view of hash function failures and ask if well-designed, but possibly backdoored hash functions can be used to build backdoor-free hash functions?
Depending on what well-designed means, what adversarial powers the backdoors provide, and what security goals are targeted, different solutions emerge. Hash-function combiners in the works above typically convert two or more hash functions into a new one that is secure as long as any of the underlying hash functions is secure. For example, the concatenation combiner builds a collision-resistant hash function given k hash functions as long as one function is collision resistant. Multi-property combiners for other notions, such as PRG, MAC or PRF security, also exist [17].
Typical combiners, however, do not necessarily offer protection when all hash functions fail. Intuitively, the goal here is more challenging as all “sources of hardness” have been rendered useless. Despite this, a number of works [20, 23, 26, 27, 33] take a more practical approach and introduce an intermediate weakened RO model, where hash functions are vulnerable to strong forms of attack, but are otherwise random.
This is an approach that we also adopt here. Since our goal is to protect against adversarial weaknesses (aka. backdoors), we place no assumptions on hash-function weaknesses—they can go well beyond computing random preimages or collisions.
1.1 Contributions
We introduce a substantially weakened RO model where an adversary, on top of hash values, can also obtain arbitrary functions of the table of the hash function. We formalize this capability via access to a backdoor oracle \(\textsc {Bd}(f)\) that on input a function f returns \(f(\langle \textsf {H} \rangle )\), arbitrary auxiliary information about the function table of the hash function \(\textsf {H}\). We call this the backdoored random-oracle (BRO) model.
Such backdoors are powerful enough to allow for point inversions—simply hardwire the point y that needs to be inverted into a function f[y] that searches for a preimage of y under \(\textsf {H}\)—or finding collisions. But they can go well beyond them. For example, although Liskov [27] proves one-way security of the combiner \(\textsf {H}(0|x_1|x_2)|\textsf {H}(1|x_2|x_1)\) under random inversions, it becomes insecure when inverted points are not assumed to be random: given \(y_1|y_2\) simply look for an inverse \(0|x'_1|x'_2\) for \(y_1\) such that \(1|x'_2|x'_1\) also maps to \(y_2\). BRO can also model arbitrary preprocessing attacks (aka. non-uniform attacks) as any auxiliary information about \(\langle \textsf {H} \rangle \) can be computed via a one-time oracle access at the onset. This means that collisions (without salting) can be easily found. Furthermore, since \(\textsc {Bd}\) calls can be adaptive, salting does not help in our setting at all. Indeed, with a single hash function and arbitrary backdoor capabilities no combiner can exist as any construction  can be easily inverted by a function that sees the entire \(\langle \textsf {H} \rangle \) and searches for inversions.
can be easily inverted by a function that sees the entire \(\langle \textsf {H} \rangle \) and searches for inversions.
In practice it is natural to assume that independent hash functions are available. We can easily model this by an extension to the k-BRO model, whereby k independent ROs and their respective backdoor oracles are made available.Footnote 1 The interpretation in our setting is that different “trusted” authorities have designed and made public hash functions that display good (i.e., RO-like) behaviors, but their respective backdoors enable computing any function of the hash tables. We ask if these hash functions can be combined in way that renders their backdoors useless. We observe that the result of Hoch and Shamir [20] can be seen as one building a collision-resistant hash function in the 2-BRO model assuming backdoor oracles that allow for random inversions only.
From a high-level point of view, our main result shows that in the 2-BRO model cryptographic hardness can be bootstrapped, even with access to both backdoor oracles and even when arbitrary backdoor capabilities are provided. In other words, there are secure constructions in the 2-BRO model that can tolerate arbitrary weaknesses in all underlying hash functions. At the core of our results lies new links with hard problems in the area of communication complexity.
Communication complexity. The communication complexity [24, 38] of a two-party task f(S, T) is the minimum communication cost over two-party protocols that compute f(S, T). Two rich and well-studied problems in this area are the set-disjointness and set-intersection problems (see [9] for a survey). Here two parties hold sets S and T respectively. In set-disjointness, their goal is to decide whether or not \(S \cap T = \emptyset \); in set-intersection they need to compute at least one element in this intersection. Typically, work in communication complexity studies communication cost over all inputs, that is, the worst-case communication complexity of a problem, as the focus is on lower bounds. Cryptographic applications, on the other hand, usually require average-case hardness. Distributional (average-case) communication complexity of a problem averages the communication cost over random choices of (S, T) from some distribution \(\mu \). We will rely on average-case lower bounds in this work.
The basic ideas. In this work, we focus on the parallel (concatenation) and sequential (cascade) composition of hash functions  and
and  and consider the combiners:
and consider the combiners:

Here  and
and  in the first construction, and
in the first construction, and  and
and  in the second.
in the second.
Consider the one-way security of the concatenation combiner in the 2-BRO model. An adversary is given a point  for a random \(x^*\). It has access to the backdoor oracles \(\textsc {Bd}_1\) and \(\textsc {Bd}_2\) for functions
for a random \(x^*\). It has access to the backdoor oracles \(\textsc {Bd}_1\) and \(\textsc {Bd}_2\) for functions  and
and  respectively. Its goal is to compute a preimage x for \(y^*\) under
respectively. Its goal is to compute a preimage x for \(y^*\) under  . This is the case iff
. This is the case iff  and
and  . Now define two sets
. Now define two sets  , the set of preimages of \(y^*_1\) under
, the set of preimages of \(y^*_1\) under  , and
, and  , the set of preimages of \(y^*_2\) under
, the set of preimages of \(y^*_2\) under  . Thus the adversary wins iff \(x \in S \cap T\).
. Thus the adversary wins iff \(x \in S \cap T\).
The two backdoor oracles respectively know S and T as they are part of the descriptions of the two hash functions. This allows us to convert a successful one-way adversary to a two-party protocol that computes an element x of the intersection \(S \cap T\). Put differently, if the communication complexity of set-intersection for sets that are distributed as above has a high lower bound, then the adversary has to place a large number of queries, which, in turn, allows us to conclude that the concatenation combiner is one-way in the 2-BRO model.
The question is: for which sets S and T is set-intersection hard? Suppose the hash functions  are compressing and \(m = n - s\). Then on average the sets S and T would each have \(2^s\) elements. We can of course communicate these sets in \(\mathcal {O}(2^s)\) bits and find a preimage. However, the cost of this attack when s is linear in n (or even super-logarithmic in n) becomes prohibitive. This raises the question if set-intersection is hard for, say, \(s=n/2\) and where the distribution over (S, T) is induced by the two hash functions, where except a single element in common (guaranteed to exist by the rules of the one-way game) all others are sampled uniformly and independently at random and included in the sets.
are compressing and \(m = n - s\). Then on average the sets S and T would each have \(2^s\) elements. We can of course communicate these sets in \(\mathcal {O}(2^s)\) bits and find a preimage. However, the cost of this attack when s is linear in n (or even super-logarithmic in n) becomes prohibitive. This raises the question if set-intersection is hard for, say, \(s=n/2\) and where the distribution over (S, T) is induced by the two hash functions, where except a single element in common (guaranteed to exist by the rules of the one-way game) all others are sampled uniformly and independently at random and included in the sets.
We observe that hardness of the set-disjointness problem implies hardness of set-intersection as the parties can verify that a given element is indeed in both their sets.Footnote 2 Set-disjointness is a better studied problem. To the best of our knowledge two results on set-disjointness with parameters and distributions close to those in our setting have been proven. First, a classical (and technical) result of Babai, Simon and Frankl [1] which shows an \(\mathrm {\Omega }(\sqrt{N})\) lower bound for random and independent sets S and T of size exactly \(\sqrt{N}\) in a universe of size N. Second, a result based on information-theoretic arguments due to Bar-Yossef et al. [2], for dependent sets S and T, which has been adapted to Bernoulli product distributions in lectures by Moshkovitz and Barak [32, Lecture 9] and Guruswami and Cheraghchi [19, Lecture 21]. The distribution is as follows: for each of the N elements in the universe, independent \(\mathrm {Ber}(1/\sqrt{N})\) bits are sampled. (The probability of 1 is \(1/\sqrt{N}\).) The sets then consist of all elements for which the bit is set to 1.Footnote 3 The authors again prove an \(\mathrm {\Omega }(\sqrt{N})\) lower bound (which is tight up to logarithmic factors). We note that both these results only hold for protocols that err with probability at most \(\varepsilon \le 1/100\). However, we only found incomplete proofs of set-disjointness for product Bernoulli distributions, and thus have included a self-contained proof in the full version of this paper [4, Appendix C]. We also prove a distributional communication complexity lower bound for set-intersection for parameters where set-disjointness can be easy.
The second result is better suited for our purposes as the size restriction in the first one would restrict us to regular random oracles. Indeed, the distribution induced on the preimages of \(y^*_1\) (resp. \(y^*_2\)) by the hash function outside the common random point is Bernoulli:  (resp.
(resp.  ) for any x and independently for values of x. We use this fact to show that set-intersection and set-disjointness problems are, respectively, sufficient to prove it is hard to invert random co-domain points (a property that we call random preimage resistance, \(\mathrm {rPre}\)) or even decide if a preimage exists (which we call oblivious PRG, \(\mathrm {oPRG}\)). The main benefit of these games is that they do away with the common point guaranteed to exist by the rules of one-way game (and also similar technicalities associated with the standard \(\mathrm {PRG}\) game). These games can then be related to the one-way and PRG games via cryptographic reductions.
) for any x and independently for values of x. We use this fact to show that set-intersection and set-disjointness problems are, respectively, sufficient to prove it is hard to invert random co-domain points (a property that we call random preimage resistance, \(\mathrm {rPre}\)) or even decide if a preimage exists (which we call oblivious PRG, \(\mathrm {oPRG}\)). The main benefit of these games is that they do away with the common point guaranteed to exist by the rules of one-way game (and also similar technicalities associated with the standard \(\mathrm {PRG}\) game). These games can then be related to the one-way and PRG games via cryptographic reductions.
Our lower bound for set-intersection allows us to prove strong one-way security for some parameters, while the set-disjointness bound only enables proving weak PRG security. Using amplification techniques we can then convert the weak results to strong one-way functions [18] or strong PRGs [29]. Note that the reductions for all these results are fully black-box and thus would relativize [34]. This implies that the same proofs also hold in the presence of backdoor oracles. Construction of other primitives in minicrypt also relativize. This means we also obtain backdoor-free PRFs, MACs, PRPs, and symmetric encryption schemes in our model. The resulting constructions, however, are often too inefficient to be of any practical use. The bottleneck for PRG efficiency here is the proven lower bounds for set-disjointness. New lower bounds that give trade-offs between protocol error and communication complexity will enable more efficient/secure constructions. We discuss in Sect. 4 why the current proof does not permit this.
Recall that collision resistance can not be based on one-way functions [36]. The concatenation combiner, on the other hand, appears to be collision resistant as simultaneous collisions seem hard to find, even with respect to arbitrary backdoors for each hash function. Indeed, an analysis of collision resistance for this combiner reveals a natural multi-instance analogue of the set-intersection problem, which to the best of our knowledge has not been studied yet. Assuming the hardness of this problem (which we leave open) we get collision resistance. We note that fully black-box amplification for collision-resistance also exists [8], and it is sufficient to prove hardness for small values of protocol error \(\varepsilon \) (should this be the case as in the case single-instance set-disjointness).
We carry out similar analyses for the cascade combiner, for which different choices of parameters lead to security. Although the overall approach remains the same, we need to deal with difficulties arising from one of the sets being the image of a hash function. The latter distribution is somewhat different to Bernoulli sets (as elements are not chosen independently). We show, however, that by addition of noise one-way and PRG security can be based on known lower bounds. For collision-resistance we give a reduction to a multi-instance analogue of set-intersection (whose hardness remains open). We analyze the security of the xor combiner in the full version of this paper [4].
We summarize our results in Table 1. Roughly speaking, strong security demands that the advantage of adversaries in the corresponding security game is negligible, while for weak security it suffices that the advantage is not overwhelming. In the table, concatenation is with respect to hash function  and
and  , while cascade is with respect to hash function
, while cascade is with respect to hash function  and
and  . The stretch values \(s_1\) and \(s_2\) can assume negative values (compressing), positive values (expanding), or be zero (length-preserving).
. The stretch values \(s_1\) and \(s_2\) can assume negative values (compressing), positive values (expanding), or be zero (length-preserving).
 have stretch \(s_i\). The parameters for collision resistance are conjectural.
have stretch \(s_i\). The parameters for collision resistance are conjectural.1.2 Discussion
Backdoors as weaknesses. One of the main motivations for the works of Liskov [27] and Hoch and Shamir [20] is the study of design principles for symmetric schemes that can offer protections against weaknesses in their underlying primitives. For example, Hoch and Shamir study the failure-friendly double-pipe hash construction of Lucks [28]. Similarly, Liskov shows that his zipper hash is indifferentiable from a random oracle even with an inversion oracle for its underlying compression function. Proofs of security in the unrestricted BRO model would strengthen these results as they place weaker assumptions on the types of weaknesses that are discovered.
Auxiliary inputs. As mentioned above, a closely related model to BRO is the Auxiliary-Input RO (AI-RO) model, introduced by Unruh [37] and recently refined by Dodis, Guo, and Katz [14] and Coretti et al. [12]. Here the result of a one-time preprocessing attack with access to the full table of the random oracle is made available to an adversary. The BRO and AI-RO models are similar in that they both allow for arbitrary functions of the random oracle to be computed. However, BRO allows for adaptive, instance-dependent auxiliary information, whereas the AI-RO model only permits a one-time access at the onset.Footnote 4 Thus AI-RO is identical to BRO when only a single \(\textsc {Bd}\) query at the onset is allowed. Extension to multiple ROs can also be considered for AI-ROs, where independent preprocessing attacks are performed on the hash functions. A corollary is that any positive result in the k-BRO model would also hold in the k-AI-RO model. Results in k-AI-RO model can be proven more directly using the decomposition of high-entropy densities as the setting is non-interactive.
Feasibility in 1-BRO. As already observed, any combiner in 1-BRO is insecure with respect to arbitrary backdoors. We can, however, consider a model where backdoor capabilities are restricted to inversions only. Security in such models will depend on the exact specification of backdoor functionalities \(\mathcal {F}\). For example, under random inversions positive results can be established using standard lazy sampling techniques. But another natural choice is to consider functions which output possibly adversarial preimages, i.e., functions f[y] whose outputs are restricted to those x for which  . As we have seen, under such generalized inversions provably secure constructions can fail. Moreover, proving security under general inversions seems to require techniques from communication complexity as we do here.
. As we have seen, under such generalized inversions provably secure constructions can fail. Moreover, proving security under general inversions seems to require techniques from communication complexity as we do here.
Other settings. Proofs in the random-oracle model often proceed via direct information-theoretic analyses. Here we give cryptographic reductions (somewhat similarly to the standard model) that isolate the underlying communication complexity problems. These problems have diverse applications in other fields (such as circuit complexity, VLSI design, and combinatorial auctions), which motivate their study outside cryptographic contexts. Any improvement in lower bounds for them would also lead to improvements in the security/efficiency of cryptographic constructions. We discussed the benefits of proofs for arbitrary error above. As other examples, results in multi-party communication complexity would translate to the k-BRO model for \(k>2\) or those in quantum communication complexity can be used to built quantum-secure BRO combiners.
1.3 Future Work
Our work leaves a number of problems open, some of which are closer to work in communication complexity. We discuss these below.
Lower bounds for set-disjointness that do not assume a small error would improve the security and/or efficiency of our PRG constructions. Moreover, we do not currently have a lower bound for the multi-instance analogue of set-intersection that we need for proving collision resistance. Finding the “maximal” backdoor capabilities in the 1-BRO model under which hardness can be bootstrapped remains an interesting open problem. Katz, Lucks, and Thiruvengadam [22] study the construction of collision-resistant hash functions from ideal ciphers that are vulnerable to differential related-key attacks. We leave the study of combiners for other backdoored primitives, such as ideal ciphers, for future work.
2 Preliminaries
We let  denote the set of non-negative integers and
denote the set of non-negative integers and  be the set of all binary strings of length
be the set of all binary strings of length  . For two bit strings x and y, we denote their concatenation by x|y. We let [N] denote the set \(\{1,\ldots ,N\}\). For a finite set S, we denote by
. For two bit strings x and y, we denote their concatenation by x|y. We let [N] denote the set \(\{1,\ldots ,N\}\). For a finite set S, we denote by  the uniform random variable over S. The Bernoulli random variable
the uniform random variable over S. The Bernoulli random variable  takes value 1 with probability p and 0 with probability \(1-p\). The Binomial random variable
takes value 1 with probability p and 0 with probability \(1-p\). The Binomial random variable  constitutes a sequence of n independent Bernoulli samples. We will sometimes use \(e^{-x}:=\lim _{n \rightarrow \infty } (1-x/n)^n\).
constitutes a sequence of n independent Bernoulli samples. We will sometimes use \(e^{-x}:=\lim _{n \rightarrow \infty } (1-x/n)^n\).
2.1 Random Oracles
A hash function  with n-bit inputs and m-bit outputs is simply a function with signature
with n-bit inputs and m-bit outputs is simply a function with signature  . We let \(\mathrm {Fun}[n,m]\) denote the set of all such functions. \(\mathrm {Fun}[n,m]\) is finite and we endow it with the uniform distribution. For a hash function
. We let \(\mathrm {Fun}[n,m]\) denote the set of all such functions. \(\mathrm {Fun}[n,m]\) is finite and we endow it with the uniform distribution. For a hash function  , we let
, we let  denote the function table of
denote the function table of  encoded as a string of length \(m2^n\). We see the x-th m-bit block of
encoded as a string of length \(m2^n\). We see the x-th m-bit block of  as
as  , identifying strings
, identifying strings  with integers in \([1,2^n]\). The random-oracle (RO) model (for a given n and m) is a model of computation where all parties have oracle access to a function
with integers in \([1,2^n]\). The random-oracle (RO) model (for a given n and m) is a model of computation where all parties have oracle access to a function  .
.
Backdoor functions. A backdoor function for  is a function
is a function  . A backdoor capability class \(\mathcal {F}\) is a set of such backdoor functions. The unrestricted class contains all functions. But the class can be also restricted, for example, functions f[y] for
. A backdoor capability class \(\mathcal {F}\) is a set of such backdoor functions. The unrestricted class contains all functions. But the class can be also restricted, for example, functions f[y] for  whose outputs x are restricted to be in
whose outputs x are restricted to be in  , where
, where  is the set preimages of y under
is the set preimages of y under  . Randomness can also be hardwired.
. Randomness can also be hardwired.
The BRO model. In the backdoored random-oracle (BRO) model, a random function  is sampled. All parties are provided with oracle access to
is sampled. All parties are provided with oracle access to  . Adversarial parties are additionally given access to the procedure
. Adversarial parties are additionally given access to the procedure

for \(f \in \mathcal {F}\). Formally, we denote this model by BRO\([n,m,\mathcal {F}]\), but will omit \([n,m,\mathcal {F}]\) when it is clear from the context. When \(\mathcal {F}=\emptyset \), we recover the conventional RO model. As discussed in the introduction, when the adversarial parties call the backdoor oracle only once and before any hash queries, we recover random oracles with auxiliary input, the AI-RO model [12, Definition 2]. Thus, BRO also models oracle-dependent auxiliary input or pre-computation attacks as special cases. In the k-BRO model (with the implicit parameters \([n_i,m_i,\mathcal {F}_i]\) for \(i=1,\ldots ,k\)) access to k independent random oracles  and their respective backdoors \(\textsc {Bd}_i\) with capabilities \(\mathcal {F}_i\) are provided. That is, procedure \(\textsc {Bd}_i(f)\) returns
and their respective backdoors \(\textsc {Bd}_i\) with capabilities \(\mathcal {F}_i\) are provided. That is, procedure \(\textsc {Bd}_i(f)\) returns  . In this work we are primarily interested in the 1-BRO and 2-BRO models with unrestricted \(\mathcal {F}\).
. In this work we are primarily interested in the 1-BRO and 2-BRO models with unrestricted \(\mathcal {F}\).
We observe that the 2-BRO\([n,m,\mathcal {F}_1,n,m,\mathcal {F}_2]\) model is identical to the 1-BRO\([n+1,m,\mathcal {F}]\) model where for  we define
we define  ,
,  and \(\mathcal {F}\) to consist of two types of functions: those in \(\mathcal {F}_1\) and dependent on values
and \(\mathcal {F}\) to consist of two types of functions: those in \(\mathcal {F}_1\) and dependent on values  , that is the function table of
, that is the function table of  , only, and those in \(\mathcal {F}_2\) and dependent on values of
, only, and those in \(\mathcal {F}_2\) and dependent on values of  , that is the function table of
, that is the function table of  , only. Thus the adversary in the unrestricted 2-BRO model has less power than in the unrestricted 1-BRO model.
, only. Thus the adversary in the unrestricted 2-BRO model has less power than in the unrestricted 1-BRO model.
2.2 Cryptographic Notions
We recall the basic notions of one-wayness, pseudorandomness, and collision-resistance for a construction \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model in Fig. 1. We omit the implicit parameters from the subscripts and use \(\mathsf {C}^{\textsf {H}_i}\) in place of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) to ease notation. These notions can also be defined in the 1-BRO model analogously by removing access to \(\textsf {H}_2\) and \(\textsc {Bd}_2\) throughout. The advantage terms are


All probabilities in this model are also taken over random choices of \(\textsf {H}_i\). Informally \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) is OW, PRG, or CR if the advantage of any adversary  querying its oracles, such that the total length of the received responses remains “reasonable”, is “small”. Note that if one only considers backdoor functions with 1-bit output lengths, the total length of the oracle responses directly translates to the number of queries made by
querying its oracles, such that the total length of the received responses remains “reasonable”, is “small”. Note that if one only considers backdoor functions with 1-bit output lengths, the total length of the oracle responses directly translates to the number of queries made by  . We denote by
. We denote by  the number of oracle queries made by an adversary
the number of oracle queries made by an adversary  to \(\textsf {H}_i\) and \(\textsc {Bd}_i\). Weak security in each case means that the corresponding advantage is less than 1 and not overwhelming.
to \(\textsf {H}_i\) and \(\textsc {Bd}_i\). Weak security in each case means that the corresponding advantage is less than 1 and not overwhelming.
We define variants of the above games which will be helpful in our analyses. For a function \(\textsf {H}\in \mathrm {Fun}[n,m]\), define  and
and  . The random preimage-resistance (rPre) game is defined similarly to everywhere preimage-resistance (ePre) [35] except that a random co-domain point (as opposed to any such point) must be inverted. This definition differs from one-way security in two aspects: the distribution of \(\textsf {H}(x)\) for a uniform x might not be uniform. Furthermore, some points in the co-domain might not have any preimages. We also define a decisional variant, called oblivious PRG (oPRG), where the adversary has to decide if a random co-domain point has a preimage. We formalize these games in Fig. 2. The advantage terms are defined as:
. The random preimage-resistance (rPre) game is defined similarly to everywhere preimage-resistance (ePre) [35] except that a random co-domain point (as opposed to any such point) must be inverted. This definition differs from one-way security in two aspects: the distribution of \(\textsf {H}(x)\) for a uniform x might not be uniform. Furthermore, some points in the co-domain might not have any preimages. We also define a decisional variant, called oblivious PRG (oPRG), where the adversary has to decide if a random co-domain point has a preimage. We formalize these games in Fig. 2. The advantage terms are defined as:

Weak analogues of the above security notions (for example weak \(\mathrm {rPre}\) or weak oPRG) are defined by requiring the advantage to be bounded away from 1 (i.e., not to be overwhelming). These definitions can be formalized in the asymptotic language, but we use concrete parameters here.
We state two lemmas that relate OW and rPre, resp. PRG and oPRG: for functions that have uniform images, as defined below, we show that \(\mathrm {OW}\) security is implied by \(\mathrm {rPre}\) security and \(\mathrm {PRG}\) security is implied by \(\mathrm {oPRG}\) security.
Image Uniformity. Let \(\mathsf {C}^{\textsf {H}_i}\in \mathrm {Fun}[n,m]\) be a construction in the 2-BRO model. In the image uniformity game \(\mathrm {IU}\) defined in Fig. 2, an adversary, given access to all backdoor oracles, must decide whether a given value is chosen uniformly at random from the image of \(\mathsf {C}^{\textsf {H}_i}\) or computed as the image of a value x chosen uniformly at random from the domain. The advantage term is

where the probability is taken over random choices of \(\textsf {H}_i\).
The following lemma upper bounds the advantage of adversaries playing the image uniformity game for combiners with different stretch values. We denote by \(\mathcal {U}_S\) the uniform distribution over a set S. We also let \(\mathcal {U}^\mathsf {p}_f\) denote the distribution defined by \(\mathcal {U}^\mathsf {p}_f(x) = |f^{-1}(x)|/2^n\), where \(f\in \mathrm {Fun}[n,m]\) is a uniform function. We refer the readers to [4, Appendix A] for proofs.
Lemma 1
(Combiner image uniformity). Let  be a combiner for \(t\in \{|,\circ \}\). Let
be a combiner for \(t\in \{|,\circ \}\). Let  be a hash function. Then
be a hash function. Then

where \(p_|=0\) and \(p_\circ \le 2^{2n_1-m_1}\) is the probability that  is not injective (i.e., it has at least one collision). Let \(2^n=C\cdot 2^{m\cdot \gamma }\) for constants C and \(\gamma \). Then the above statistical distance is negligible for \(\gamma >1\) and \(0<\gamma <1\) when \(C=1\), while for \(\gamma =1\) and \(C\le 1\) it less than \(e^{-C} \cdot \left( C/(1 - e^{-C}) -1 \right) \) plus negligible terms.
is not injective (i.e., it has at least one collision). Let \(2^n=C\cdot 2^{m\cdot \gamma }\) for constants C and \(\gamma \). Then the above statistical distance is negligible for \(\gamma >1\) and \(0<\gamma <1\) when \(C=1\), while for \(\gamma =1\) and \(C\le 1\) it less than \(e^{-C} \cdot \left( C/(1 - e^{-C}) -1 \right) \) plus negligible terms.
Now we can relate our notions of rPre and oPRG with their classical variants, i.e., one-way and PRG security. Proofs of both lemmas are included in the full version [4, Appendix B].
Lemma 2
(\(\mathrm {rPre}+ \mathrm {IU}\implies \mathrm {OW}\)). Let \(\mathsf {C}^{\textsf {H}_i}\in \mathrm {Fun}[n,m]\) be a construction in the 2-BRO model. Then for any adversary  against the one-way security of \(\mathsf {C}^{\textsf {H}_i}\), there is an adversary
against the one-way security of \(\mathsf {C}^{\textsf {H}_i}\), there is an adversary  against the image uniformity and an adversary
against the image uniformity and an adversary  against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_i}\), all in the 2-BRO model and using identical backdoor functionalities, such that
against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_i}\), all in the 2-BRO model and using identical backdoor functionalities, such that

where \(\alpha :=\Pr [y \in \mathsf {Img}(\mathsf {C}^{\textsf {H}_i})]\) over a random choice of  and \(\textsf {H}_i\).
and \(\textsf {H}_i\).
An analogous result also holds for \(\mathrm {oPRG}\) security.
Lemma 3
(\(\mathrm {oPRG}+ \mathrm {IU}\implies \mathrm {PRG}\)). Let \(\mathsf {C}^{\textsf {H}_i}\in \mathrm {Fun}[n,m]\) be a construction in the 2-BRO model which is expanding with \(m-n \ge 0.53\). Then for any adversary  against the PRG security of \(\mathsf {C}^{\textsf {H}_i}\), there is an adversary
against the PRG security of \(\mathsf {C}^{\textsf {H}_i}\), there is an adversary  against the image uniformity and an adversary
against the image uniformity and an adversary  against the \(\mathrm {oPRG}\) security of \(\mathsf {C}^{\textsf {H}_i}\), both in the 2-BRO model and using identical backdoor functionalities, such that
against the \(\mathrm {oPRG}\) security of \(\mathsf {C}^{\textsf {H}_i}\), both in the 2-BRO model and using identical backdoor functionalities, such that

where \(\alpha :=\Pr [y \in \mathsf {Img}(\mathsf {C}^{\textsf {H}_i})]\) over a random choice of  and \(\textsf {H}_i\).
and \(\textsf {H}_i\).
3 Black-Box Combiners
A standard way to build a good hash function from a number of possibly “faulty” hash functions is to combine them [25]. For instance, given k hash functions \(\textsf {H}_1,\ldots ,\textsf {H}_k\), the classical concatenation combiner is guaranteed to be collision resistant as long as one out of the k hash functions is collision resistant. More formally, a black-box collision-resistance combiner \(\mathsf {C}\) is a pair of oracle circuits  where \(\mathsf {C}^{\textsf {H}_i}\) is the construction and
where \(\mathsf {C}^{\textsf {H}_i}\) is the construction and  is a reduction that given as oracle any procedure
is a reduction that given as oracle any procedure  that finds a collision for \(\mathsf {C}^{\textsf {H}_i}\), returns collisions for all of the underlying \(\textsf {H}_i\)’s. We are interested in a setting where none of the available hash functions is good. Under this assumption, however, a secure hash function must be built from scratch, implying that the source of cryptographic hardness must lie elsewhere. As we discussed above, this question has been studied in the RO model.
that finds a collision for \(\mathsf {C}^{\textsf {H}_i}\), returns collisions for all of the underlying \(\textsf {H}_i\)’s. We are interested in a setting where none of the available hash functions is good. Under this assumption, however, a secure hash function must be built from scratch, implying that the source of cryptographic hardness must lie elsewhere. As we discussed above, this question has been studied in the RO model.
We briefly explore the difficulty in the standard model here. We consider a variant of this problem where the hash functions are weak due to the existence of backdoors. A generation algorithm \(\mathsf {Gen}\) outputs keys (hk, bk), where hk is used for hashing and bk enables an unspecified backdoor capability (such as finding preimages or collisions). Our hardness assumption is that the hash function with key hk is collision resistant without access to bk. However, when bk is available, no security is assumed. In this setting, the definition of a combiner can be simplified: instead of requiring the existence of a reduction  as above, we can proceed in the standard way and require that the advantage of any adversary
as above, we can proceed in the standard way and require that the advantage of any adversary  that gets any subset \(S \subset \{bk_1,\ldots ,bk_k\}\) of the backdoors of size \(|S| \le k-1\) to be small.Footnote 5 Let us call a combiner secure against any set of at most t backdoors a \(k \atopwithdelims ()k-t\)-combiner.
that gets any subset \(S \subset \{bk_1,\ldots ,bk_k\}\) of the backdoors of size \(|S| \le k-1\) to be small.Footnote 5 Let us call a combiner secure against any set of at most t backdoors a \(k \atopwithdelims ()k-t\)-combiner.
It is trivial to see that a \(k \atopwithdelims ()0\)-combiner is also a \(k \atopwithdelims ()1\)-combiner. It is also easy to see that a black-box combiner is also a \(k \atopwithdelims ()1\)-combiner. We are, however, interested in the feasibility of \(k \atopwithdelims ()0\)-combiners. In this setting there is an assumed source of hardness, namely the collision resistance of hash functions without backdoors. But constructions that have to work with a provided set of keys seem hard.Footnote 6 We next give a simple impossibly result that formalizes this intuition under fully black-box constructions.
Theorem 1
For any positive \(k\in \mathbb {N}\), there are no fully black-box constructions of compressing collision-resistant \(k \atopwithdelims ()0\)-combiners.
Proof idea. Let \((\textsf {H},\mathcal {A})\) be a pair of oracles such that \(\textsf {H}(hk,\cdot )\) implements a random function and \(\mathcal {A}(\langle \mathsf {C} \rangle ,hk_1,\ldots ,hk_k,bk_1,\ldots ,bk_k)\) is a break oracle that operates as follows. It interprets \(\langle \mathsf {C} \rangle \) as the description of a combiner. It then checks that each \(bk_i\) indeed enables generating collisions under \(hk_i\). If so, it (inefficiently) finds a random collision for \(\mathsf {C}^{\textsf {H}(hk_1,\cdot ),\ldots ,\textsf {H}(hk_k,\cdot )}\) and returns it. An efficient reduction \(\mathsf {R}\) is given oracle access to \(\mathcal {A}\) and \(\textsf {H}\) as well as a key \(hk^*\) (without its backdoor \(bk^*\)). It should find a collision for \(\textsf {H}(hk^*,\cdot )\) while making a small (below birthday) number of queries to the two oracles \(\mathcal {A}\) and \(\textsf {H}\). We show that any such reduction \(\mathsf {R}\) must have a negligible success probability. \(\square \)
We distinguish between two cases based on whether the reduction \(\mathsf {R}\) uses the provided break oracle \(\mathcal {A}\) or not. Without the use of \(\mathcal {A}\), the reduction would break collision resistance for \(hk^*\) on its own, contradicting the collision resistance of \(hk^*\) beyond the birthday bound. To use \(\mathcal {A}\) the reduction has to provide it with k keys \(hk_i\) and some other keys \(bk_i\) that enable finding collisions (since \(\mathcal {A}\) checks this). However, none of the provided keys \(hk_i\) can be \(hk^*\), since \(\mathsf {R}\) must also provide some \(\tilde{bk}^*\) that enables finding collisions under \(hk^*\), which means that \(\mathsf {R}\) can directly use \(\tilde{bk}^*\) to compute a collision for \(\textsf {H}(hk^*,\cdot )\), once again contradicting the assumed collision resistance of \(hk^*\) beyond the birthday bound. Thus, \(\mathsf {R}\) does not use \(hk^*\). A random oracle \(\textsf {H}(hk^*,\cdot )\), however, is collision resistant even in the presence of random collisions for \(\textsf {H}(hk,\cdot )\) for \(hk \ne hk^*\). This means that \(\mathsf {R}\), which places a small number of oracle queries, will have a negligible success probability.
There is room to circumvent this result by considering non-black-box constructions. Here, we will study hash function combiners in the k-BRO model, where the hash oracles model access to different hk and the backdoor oracles model access to the corresponding bk’s. As mentioned above, this approach has also been adapted in a number of previous works, both from a provable security as well as a cryptanalytic view [20, 21, 23, 26, 31]. In this work we will focus on basic security properties of the concatenation (parallel) and cascade (sequential) combiners in the unrestricted 2-BRO model.
4 Communication Complexity
The communication cost [24, 38] of a two-party deterministic protocol \(\pi \) on inputs (x, y) is the number of bits that are transmitted in a run of the protocol \(\pi (x,y)\). We denote this by  . The worst-case communication complexity of \(\pi \) is
. The worst-case communication complexity of \(\pi \) is  . A protocol \(\pi \) computes a task (function) \(f: X \times Y \rightarrow Z\) if the last message of \(\pi (x,y)\) is f(x, y). The communication complexity of a task f is the minimum communication complexity of any protocol \(\pi \) that computes f. Protocols can also be randomized and thus might err with probability \(\Pr [\pi (x,y) \ne f(x,y)]\). Following cryptographic conventions, we denote protocol correctness by
. A protocol \(\pi \) computes a task (function) \(f: X \times Y \rightarrow Z\) if the last message of \(\pi (x,y)\) is f(x, y). The communication complexity of a task f is the minimum communication complexity of any protocol \(\pi \) that computes f. Protocols can also be randomized and thus might err with probability \(\Pr [\pi (x,y) \ne f(x,y)]\). Following cryptographic conventions, we denote protocol correctness by  , where \(\mathrm {f}\) is a placeholder for the name of the task f.
, where \(\mathrm {f}\) is a placeholder for the name of the task f.
In the cryptographic setting we are interested in distributional (aka. average-case) communication complexity measured by averaging the communication cost over random choices of inputs and coins. A standard coin-fixing argument shows that in the distributional setting any protocol can be derandomized with no change in communication complexity, and thus we can focus on deterministic protocols. For a given distribution \(\mu \) over the inputs (x, y), the protocol error and correctness are computed by taking the probability over the choice of (x, y). We define the distributional communication cost of a deterministic protocol \(\pi \) as

The distributional communication complexity of a task f with error \(\varepsilon \) is
where the minimum is taken over all deterministic protocols \(\pi \) which err with probability at most \(\varepsilon \). In this work, we need to slightly generalize functional tasks to relational tasks \(R(x,y) \subseteq Z\) and define error as \(\Pr [\pi (x,y) \not \in R(x,y)]\).
Two central problems in communication complexity that have received substantial attention are the set-disjointness and the set-intersection problems. In set-disjointness two parties, holding sets S and T respectively, compute the binary function \(\mathrm {DISJ}(S,T) := (S \cap T = \emptyset )\). In set-intersection, their goal is to compute the relation \(\mathrm {INT}(S,T):=S \cap T\); that is, the last message of the protocol should be equal to some element in the intersection. Note that set-disjointness can be seen as a decisional version of set-intersection and is easier. As mentioned, we are interested in average-case lower bounds for these tasks and moreover we focus on product distributions, where the sets are chosen independently.
Two main results to this end have been proven.Footnote 7 A classical result of Babai, Frankl, and Simon [1] establishes an \(\mathrm {\Omega }(\sqrt{N})\) lower bound for set-disjointness where the input sets S and T are independent random subsets of [N] of size exactly \(\sqrt{N}\). This result, however, is restrictive for us as it roughly translates to regular functions in the cryptographic setting. Moreover, its proof uses intricate combinatorial arguments, which are somewhat hard to work with.
A second result considers the following distribution. Each element \(x \in [N]\) is thrown into S independently with probability p. (And similarly for T with probability q.) We can view S as a N-bit string X where its i-th bit \(x_i\) is 1 iff \(i \in S\). Thus the distribution can be viewed as N i.i.d. Bernoulli random variables \(x_i \sim \mathrm {Ber}(p)\) where \(p:=\Pr [x_i=1]\). Thus the elements of the sets form a binomial distribution, and accordingly we write \(S \sim \mathrm {Bin}(N,p)\) and \(T \sim \mathrm {Bin}(N,q)\). We define \(\mu (p,q)\) as the product of these distributions. When \(p=q=1/2\) we get the product uniform distribution over the subsets of \([N] \times [N]\), but typically we will be looking at much smaller values of p and q of order \(1/\sqrt{N}\).
Using information-theoretic techniques [2], the following lower bound can be established.
Theorem 2
(Set-Disjointness Lower Bound). Let \(N\in \mathbb {N}\) and assume \(p,q \in (0,1/2]\) with \(p \le q\) and \(pq=1/(\delta N)\) for some \(\delta > 1\). Let \(\mu (p,q)\) be the product binomial distribution over subsets \(S,T \subseteq [N]\). Assume \(\varepsilon < \frac{(\delta -1) p_0}{(4+\delta )}\) and let \(p_0:= \Pr [\mathrm {DISJ}(S,T)=0]\). Then
We have included a detailed proof of the above theorem in the full version [4, Appendix C], which follows those in [19, 32]. Our proof generalizes the original result, which was only claimed for \(p=q=1/\sqrt{N}\).Footnote 8 Roughly speaking, the proof proceeds along the following lines. We can lower bound the communication complexity of any protocol by the total information leaked by its transcripts about each coordinate \((x_i,y_i)\). The latter can be lower bounded based on the statistical distance in protocol transcripts when \(x_i=1 \wedge y_i=0\) and \(x_i=0 \wedge y_i=1\). This step uses a number of information-theoretic inequalities, which we include with proofs in the full version. Finally, we show that a highly correct protocol can be used as a distinguisher with constant advantage: When \(x_i=0 \wedge y_i=0\), for a constant fraction of the inputs the sets will be disjoint. However, when \(x_i=1 \wedge y_i=1\) they necessarily intersect, but this condition happens for a constant fraction of the inputs. We get a \(\sqrt{N}\) lower bound by averaging over the i’s.
In this section we also prove a communication complexity lower bound for the set-intersection problem over Bernoulli sets for which set-disjointness can be easy. Although the overall proof structure will be similar to that in [19, 32], we will differ in a number of places. First, as above we leave the Bernoulli parameters free so as to be able to compute a feasible region where the lower bound will be non-trivial. We also use the fact that a candidate element can be checked to belong to the intersection (whereas a decision bit for disjointness cannot be checked for correctness). This ensures that the protocol error is one-sided, and allows us to remove the requirement of \(\varepsilon \) being sufficiently small. Finally, we will bound the probability that the protocol outputs a random element in the intersection. This leads to a distinguisher that succeeds with smaller advantage, but overall will lead to a non-trivial bound. We state and prove the formal result next.
Theorem 3
(Set-Intersection Lower Bound). Let \(N\in \mathbb {N}\) and assume \(p,q \in (0,1/2]\) with \(p \le q\). Let \(\mu (p,q)\) be the product binomial distribution over subsets \(S,T \subseteq [N]\). Let \(\varepsilon \) be the protocol error and set \(p_0:= \Pr [\mathrm {DISJ}(S,T)=0]\). If \(\varepsilon \le p_0\) then
For sufficiently large N we have \(p_0 = 1-(1-pq)^N \approx 1-e^{-Npq}\). If \(pq \gg 1/N\) we get that \(p_0 \approx 1\) (the sets intersect with overwhelming probability) and for the theorem we would need that \(\varepsilon \le 1\).
Let us first give some preliminaries and state two lemmas that are used in the proof of Theorem 3. For random variables X and Y, their statistical distance (aka. total variance) is denoted by \(\mathrm {\Delta }_\mathsf {TV}(X,Y)\), their mutual information is denoted by I(X; Y), and their Hellinger distance is denoted by \(\mathrm {\Delta }_\mathsf {Hel}(X,Y)\):
Statistical and Hellinger distance are related (cf. proofs in [4, Appendix C.1]) via:
Below, Lemma 4, proven in the full version [4, Appendix C.1], relates the mutual information of two random variables with their Hellinger distance.
Lemma 4
(Information to Hellinger). Let X and Y be random variables and \(Y_x := Y | X = x\), i.e., Y conditioned on \(X=x\). Then
Next we state the cut-and-paste lemma from communication complexity. A proof is included in [4, Appendix C.2].
Lemma 5
(Cut-and-Paste). Let \(\mathrm {\Pi }(X,Y)\) denote a random variable for the transcripts of a deterministic protocol on input bit strings (X, Y) such that the corresponding sets S and T are drawn from \(\mu \), i.e., \(S,T \sim \mu \). Let  and define \(\mathrm {\Pi }^i_{a,b}(X,Y) := \mathrm {\Pi }(X,Y) ~|~ x_i=a \wedge y_i = b\). Then for each i, it holds that
and define \(\mathrm {\Pi }^i_{a,b}(X,Y) := \mathrm {\Pi }(X,Y) ~|~ x_i=a \wedge y_i = b\). Then for each i, it holds that
Now we can prove the claimed lower bound on the communication complexity of set-intersection.
Proof of Theorem 3. Let \(\pi \) be a deterministic protocol with error at most \(\varepsilon \), i.e.,

where X and Y are bit string representations of S and T as explained above. Let \(\mathrm {\Pi }(X,Y)\) denote a random variable for the transcripts of protocol \(\pi \) on inputs (X, Y) with corresponding sets \((S,T) \sim \mu \). We write \(X=(x_1,\ldots ,x_N)\) and \(Y=(y_1,\ldots ,y_N)\) where  . For random variables A and B, let \(\mathrm {supp}(A)\) denote the support of A (i.e., the set of values that have a non-zero probability of happening), and H(A) denote the Shannon entropy. We have
. For random variables A and B, let \(\mathrm {supp}(A)\) denote the support of A (i.e., the set of values that have a non-zero probability of happening), and H(A) denote the Shannon entropy. We have
where the last inequality holds due to the independence of \(x_1,\ldots ,x_N,y_1,\ldots ,y_N\) (cf. [4, Appendix C.1]). Let \(\mathrm {\Pi }^i_{a,b}\) be \(\mathrm {\Pi }\) conditioned on the i-th coordinates of X and Y being fixed to a and b respectively:
By Lemma 4 we know
where \((a,b) \sim \mathrm {Ber}(p) \times \mathrm {Ber}(q)\) and \(\mathrm {\Delta }_\mathsf {Hel}\) is the Hellinger distance.
Since \(q \ge p\) we have that \(q(1-p) \ge p(1-q)\) and since \(q \le 1/2\), we also have that \(p(1-q) \ge p/2\). Thus
The last inequality is by the triangle inequality for the metric \(\mathrm {\Delta }_\mathsf {Hel}\), and the penultimate inequality uses \(x^2+y^2 \ge (x+y)^2/2\). Hence,
where the third inequality uses the cut-and-paste lemma of communication complexity (Lemma 5) which states that \(\mathrm {\Delta }_\mathsf {Hel}^2(\mathrm {\Pi }^i_{1,0},\mathrm {\Pi }^i_{0,1}) = \mathrm {\Delta }_\mathsf {Hel}^2(\mathrm {\Pi }^i_{0,0},\mathrm {\Pi }^i_{1,1})\) for any deterministic protocol \(\pi \). The penultimate inequality uses \(\mathrm {\Delta }_\mathsf {TV}(A,B) \le \sqrt{2} \mathrm {\Delta }_\mathsf {Hel}(A,B)\), which implies \(\mathrm {\Delta }_\mathsf {Hel}^2(\mathrm {\Pi }^i_{0,0},\mathrm {\Pi }^i_{1,1}) \ge 1/2 \mathrm {\Delta }_\mathsf {TV}^2(\mathrm {\Pi }^i_{0,0},\mathrm {\Pi }^i_{1,1})\), and the last inequality is by Jensen. Thus it remains to lower bound \(\mathrm {\Delta }_\mathsf {TV}(\mathrm {\Pi }^i_{0,0},\mathrm {\Pi }^i_{1,1})\).
For every i we have
This is because we have conditioned on \(x_i=y_i=0\) and the two parties can check whether or not i belongs to their sets.
Now we look at \(x_i=y_i=1\). We show that the protocol over a random choice of i should output i with the expected probability, that is, \(1/|S\cap T|\). Note that the expected size of the intersection is
where we have used the linearity of expectation and independence of \(x_i\) and \(y_i\).
We proceed as follows.
Thus we get that
and overall we obtain
as required. \(\square \)
Letting \(p=1/N^{\alpha }\) and \(q=1/N^{\beta }\) with \(\alpha \ge \beta \) (since we assumed \(p\le q\)), for a non-trivial lower bound—that is an exponentially large right-hand side in the displayed equation above—we would need to have that \(\alpha + 2\beta >1\). We also require that \(1-\alpha -\beta >0\) so that the expected intersection size Npq is exponentially large, in which case \(p_0 \approx 1\) and set-disjointness is easy. These inequalities lead to the feasibility region shown in Fig. 3. We have included the symmetric region for \(\alpha \le \beta \).
In this work, we will rely on set-disjointness and set-intersection problems, as well as the following multi-set extensions of them. These problems are additionally parameterized by the number of sets. Here Alice holds \(M_1\) sets \(S_i \sim \mathrm {Bin}(N,p)\) for \(i \in [M_1]\) and Bob holds \(M_2\) sets \(T_j \sim \mathrm {Bin}(N,q)\) for \(j \in [M_2]\). Their goal is to solve the following problems.
- 1.:
-
Find (i, x) such that \(x \in S_i \cap T_i\), or return \(\perp \) if all the intersections are empty. We call this the
 problem, a natural multi-instance version of \(\mathrm {INT}\). A decisional variant would ask for an index i and a decision bit indicating if \(S_i \cap T_i = \emptyset \). When \(M_1=M_2=1\), these problems are the usual \(\mathrm {INT}\) and \(\mathrm {DISJ}\) problems.
problem, a natural multi-instance version of \(\mathrm {INT}\). A decisional variant would ask for an index i and a decision bit indicating if \(S_i \cap T_i = \emptyset \). When \(M_1=M_2=1\), these problems are the usual \(\mathrm {INT}\) and \(\mathrm {DISJ}\) problems. - 2.:
-
Find \((i,j,x,x')\) with \(x\ne x'\) such that \(x,x' \in S_i \cap T_j\), or return \(\perp \) if no such tuple exists. We call this the
 problem. When \(M_1=M_2=1\) this problem is at least as hard as the \(\mathrm {INT}\) problem since finding two distinct elements in the intersection is harder than finding one.
problem. When \(M_1=M_2=1\) this problem is at least as hard as the \(\mathrm {INT}\) problem since finding two distinct elements in the intersection is harder than finding one.
Remark. Intuitively, the \(\mathrm {INT}\) problem is a harder task than  . One can solve the
. One can solve the  problem using a protocol for \(\mathrm {INT}\) as follows. Alice chooses a random point x in one of its sets \(S_i\) and sends it to Bob. Bob will then search through his sets to find a set \(T_j\) such that \(x \in T_j\). With high probability such a set exists if the number of sets and/or the probability parameters are large enough. Alice and Bob will then run the protocol for \(\mathrm {INT}\) on sets \(S_i\) and \(T_j\) to find an \(x' \in S_i \cap T_j\). This element will be different from x with good probability (again under appropriate choices of parameters). Indeed, this is simply the communication complexity way of saying “collision-resistance implies one-wayness.” However, we are interested in a reduction in the converse direction (as we already have lower bounds for \(\mathrm {INT}\)). This seems hard as from a cryptographic point of view, as a classical impossibility by Simon [36] shows that collision resistance cannot be based on one-way functions (or even permutations) in a black-box way. Despite this, it is conceivable that direct information-theoretic analyses (similar to those for set-disjointness and set-intersection) can lead to non-trivial lower bounds. We leave proving hardness for this “collision resistance” analogue of set-intersection as an interesting open problem for future work.Footnote 9
problem using a protocol for \(\mathrm {INT}\) as follows. Alice chooses a random point x in one of its sets \(S_i\) and sends it to Bob. Bob will then search through his sets to find a set \(T_j\) such that \(x \in T_j\). With high probability such a set exists if the number of sets and/or the probability parameters are large enough. Alice and Bob will then run the protocol for \(\mathrm {INT}\) on sets \(S_i\) and \(T_j\) to find an \(x' \in S_i \cap T_j\). This element will be different from x with good probability (again under appropriate choices of parameters). Indeed, this is simply the communication complexity way of saying “collision-resistance implies one-wayness.” However, we are interested in a reduction in the converse direction (as we already have lower bounds for \(\mathrm {INT}\)). This seems hard as from a cryptographic point of view, as a classical impossibility by Simon [36] shows that collision resistance cannot be based on one-way functions (or even permutations) in a black-box way. Despite this, it is conceivable that direct information-theoretic analyses (similar to those for set-disjointness and set-intersection) can lead to non-trivial lower bounds. We leave proving hardness for this “collision resistance” analogue of set-intersection as an interesting open problem for future work.Footnote 9
5 The Concatenation Combiner
In this section we study the security of the concatenation combiner
in the 2-BRO model, where \(\textsf {H}_1 \in \mathrm {Fun}[n,n+s_1]\) and \(\textsf {H}_2 \in \mathrm {Fun}[n,n+s_2]\). We will prove one-way security, pseudorandomness, and collision resistance for this construction. Our results will rely on the hardness of set-intersection and set-disjointness for the first two properties, and the presumed hardness of finding two elements in the intersection given multiple instances.
5.1 One-Way Security
In the full version of this paper [4, Appendix D] we show that when \(\textsf {H}_1\) or \(\textsf {H}_2\) is (approximately) length preserving or somewhat expanding the concatenation combiner is not (strongly) one-way in the 2-BRO model. In both cases preimage sets will be only polynomially large and can be communicated. Accordingly, only when both hash functions are (somewhat) compressing we can achieve one-way security.
To this end, we first give a direct reduction from random preimage resistance (\(\mathrm {rPre}\), as defined in Fig. 2) to set-intersection. By Lemma 2 we know that any (weak) \(\mathrm {rPre}\)-secure function is also a (weak) \(\mathrm {OW}\)-secure function. In particular, for the highly compressing setting where \(s_1,s_2\le -n/2-4\) we show strong one-way security. For settings where the parameters only enable weak security according to the set-intersection theorem, we can apply hardness amplification [18] to get a strongly one-way function.
In our reductions to communication complexity protocols throughout the paper, we make the following simplifying assumptions. (1) The adversary is deterministic; (2) It does not query \(\textsf {H}_i\) at all and instead computes hash values via the \(\textsc {Bd}_i\) oracles; (3) It queries \(\textsc {Bd}_i\) with functions that have 1-bit outputs; and (4) It starts with a query to \(\textsc {Bd}_1\).
We are now ready to prove our first cryptographic hardness result.
Theorem 4
Let \(\textsf {H}_1\in \mathrm {Fun}[n,n+s_1]\) and \(\textsf {H}_2\in \mathrm {Fun}[n,n+s_2]\) and \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}(x) := \textsf {H}_1(x) | \textsf {H}_2(x)\). Then for any adversary  against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi \) against set-intersection with \(\mu :=\mu (p,q)\) where \(p:=1/2^{n+s_1}\) and \(q:=1/2^{n+s_2}\) and such that
against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi \) against set-intersection with \(\mu :=\mu (p,q)\) where \(p:=1/2^{n+s_1}\) and \(q:=1/2^{n+s_2}\) and such that

Proof
Let  be an adversary against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model for \(\textsf {H}_1\) and \(\textsf {H}_2\). Adversary
be an adversary against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model for \(\textsf {H}_1\) and \(\textsf {H}_2\). Adversary  is given a random point
is given a random point  and needs to either find an x such that \(\textsf {H}_1(x)|\textsf {H}_2(x)=y_1|y_2\) or say that no such x exists. Let
and needs to either find an x such that \(\textsf {H}_1(x)|\textsf {H}_2(x)=y_1|y_2\) or say that no such x exists. Let
Hence  outputs an \(x \in S_1 \cap S_2\) as long as \(S_1\cap S_2\ne \emptyset \). We note that these sets are Bernoulli. Indeed, for each x we have that \(\Pr [x \in S_1] = 1/2^{n+s_1}\) and \(\Pr [x \in S_2] = 1/2^{n+s_2}\), and these events are independent for different values of x.
outputs an \(x \in S_1 \cap S_2\) as long as \(S_1\cap S_2\ne \emptyset \). We note that these sets are Bernoulli. Indeed, for each x we have that \(\Pr [x \in S_1] = 1/2^{n+s_1}\) and \(\Pr [x \in S_2] = 1/2^{n+s_2}\), and these events are independent for different values of x.
We use  to build a 2-party protocol for set-intersection over a product distribution \(\mu :=\mu (p,q)\) with \(p:=1/2^{n+s_1}\) and \(q:=1/2^{n+s_2}\) as follows. Alice holds a set
to build a 2-party protocol for set-intersection over a product distribution \(\mu :=\mu (p,q)\) with \(p:=1/2^{n+s_1}\) and \(q:=1/2^{n+s_2}\) as follows. Alice holds a set  and Bob holds a set
and Bob holds a set  distributed according to \(\mu \). Alice (resp., Bob) samples hash function \(\textsf {H}_1\) (resp., \(\textsf {H}_2\)) as follows. Alice picks a random
distributed according to \(\mu \). Alice (resp., Bob) samples hash function \(\textsf {H}_1\) (resp., \(\textsf {H}_2\)) as follows. Alice picks a random  and Bob picks a random
and Bob picks a random  . Alice defines \(\textsf {H}_1\) to map all points in \(S_1\) to \(y_1\). She maps
. Alice defines \(\textsf {H}_1\) to map all points in \(S_1\) to \(y_1\). She maps  to random points in
to random points in  . Similarly Bob defines \(\textsf {H}_2\) to map all points \(x \in S_2\) to \(y_2\) and
. Similarly Bob defines \(\textsf {H}_2\) to map all points \(x \in S_2\) to \(y_2\) and  to random points in
to random points in  . As a result, Alice knows the full function table of \(\textsf {H}_1\) and similarly Bob knows the full function table of \(\textsf {H}_2\).
. As a result, Alice knows the full function table of \(\textsf {H}_1\) and similarly Bob knows the full function table of \(\textsf {H}_2\).
Alice and Bob now run two copies of  in tandem as follows, where the state values \(st_A\) and \(st_B\) are initially set to \(y_1|y_2\) (with only \(2n+s_1+s_2\) bits of communication).
in tandem as follows, where the state values \(st_A\) and \(st_B\) are initially set to \(y_1|y_2\) (with only \(2n+s_1+s_2\) bits of communication).
- Alice::
-
It resumes/starts
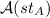 . It terminates if it receives a final guess x from Bob. It answers all pending \(\textsc {Bd}_2\) queries—there are none to start with—using the values just received from Bob. It answers all \(\textsc {Bd}_1\) queries using the function table of \(\textsf {H}_1\) until
. It terminates if it receives a final guess x from Bob. It answers all pending \(\textsc {Bd}_2\) queries—there are none to start with—using the values just received from Bob. It answers all \(\textsc {Bd}_1\) queries using the function table of \(\textsf {H}_1\) until 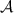 queries \(\textsc {Bd}_2\) or terminates. If
queries \(\textsc {Bd}_2\) or terminates. If  terminates with a final guess x, it forwards x to Bob and terminates. Else it saves the current state \(st_A\) of
terminates with a final guess x, it forwards x to Bob and terminates. Else it saves the current state \(st_A\) of  locally and forwards all \(\textsc {Bd}_1\) answers that it has provided to
locally and forwards all \(\textsc {Bd}_1\) answers that it has provided to  since the last resumption to Bob. It hands the execution over to Bob.
since the last resumption to Bob. It hands the execution over to Bob. - Bob::
-
It resumes
 . It terminates if it receives a final guess x from Alice. It answers all pending \(\textsc {Bd}_1\) queries using the values received from Alice. It answers all \(\textsc {Bd}_2\) queries using the function table of \(\textsf {H}_2\) until
. It terminates if it receives a final guess x from Alice. It answers all pending \(\textsc {Bd}_1\) queries using the values received from Alice. It answers all \(\textsc {Bd}_2\) queries using the function table of \(\textsf {H}_2\) until  queries \(\textsc {Bd}_1\) or terminates. If
queries \(\textsc {Bd}_1\) or terminates. If  terminates with a final guess x, it forwards x to Alice and terminates. Else it saves the current state \(st_B\) of
terminates with a final guess x, it forwards x to Alice and terminates. Else it saves the current state \(st_B\) of  locally and forwards all \(\textsc {Bd}_2\) answers that it has provided to
locally and forwards all \(\textsc {Bd}_2\) answers that it has provided to 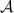 since the last resumption to Alice. It hands the execution over to Alice.
since the last resumption to Alice. It hands the execution over to Alice.
We claim that Alice and Bob run  in an environment that is identical to the \(\mathrm {rPre}\) game in the 2-BRO model. The hash functions \(\textsf {H}_1\) and \(\textsf {H}_2\) sampled by Alice and Bob are uniformly distributed. To see this note that for any (x, y) the probability that
in an environment that is identical to the \(\mathrm {rPre}\) game in the 2-BRO model. The hash functions \(\textsf {H}_1\) and \(\textsf {H}_2\) sampled by Alice and Bob are uniformly distributed. To see this note that for any (x, y) the probability that  is
is  (and similarly for \(\textsf {H}_2\)). Furthermore, this event is independent of the hash values that are set for all other values \(x'\ne x\). Thus, Alice and Bob faithfully run
(and similarly for \(\textsf {H}_2\)). Furthermore, this event is independent of the hash values that are set for all other values \(x'\ne x\). Thus, Alice and Bob faithfully run  in the environment that it expects by answering its backdoor queries using their knowledge of the full tables of the two functions.
in the environment that it expects by answering its backdoor queries using their knowledge of the full tables of the two functions.
Whenever  succeeds in breaking the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\), the protocol above computes an \(x \in S_1 \cap S_2\) or says that no such x exists. In either case, the protocol solves the set-intersection problem. Thus the correctness of this protocol is at least the advantage of the adversary
succeeds in breaking the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\), the protocol above computes an \(x \in S_1 \cap S_2\) or says that no such x exists. In either case, the protocol solves the set-intersection problem. Thus the correctness of this protocol is at least the advantage of the adversary  .
.
This execution of  by Alice and Bob ensures that oracle queries do not affect the communication cost of Alice and Bob. It is only their answers (plus the final x) that affects the communication cost, since the queried functions f are locally computed and only their answers are communicated. If
by Alice and Bob ensures that oracle queries do not affect the communication cost of Alice and Bob. It is only their answers (plus the final x) that affects the communication cost, since the queried functions f are locally computed and only their answers are communicated. If  makes
makes  queries to \(\textsc {Bd}_1\) and \(\textsc {Bd}_2\) in total and each query has a 1-bit output, the total communication complexity of the protocol is
queries to \(\textsc {Bd}_1\) and \(\textsc {Bd}_2\) in total and each query has a 1-bit output, the total communication complexity of the protocol is  plus those bits needed to communicate \(y_1\) and \(y_2\) and the final guess x. \(\square \)
plus those bits needed to communicate \(y_1\) and \(y_2\) and the final guess x. \(\square \)
We now check that the parameters for hash functions can be set such that their concatenation is a one-way function.
Corollary 1
For \(\textsf {H}_1,\textsf {H}_2 \in \mathrm {Fun}[n,(1-\epsilon )n/2]\) with \(0< \epsilon < 1/3\) the concatenation combiner is a strongly one-way compressing function in \(\mathrm {Fun}[n,(1-\epsilon )n]\).
Proof
The feasible region in Fig. 3 for \(\alpha = \beta \) consists of \(1/3<\alpha <1/2\). In our setting \(\alpha =\beta =(1-\epsilon )/2\), which means concatenation is strongly rPre secure when \(0< \epsilon < 1/3\). Since the combined function is compressing (where \(\gamma =1/(1-\epsilon )>1\)), the image-uniformity bound is negligible and also \(\Pr [y \in \mathsf {Img}(\mathsf {C}^{\textsf {H}_i})]\) in Lemma 2 is overwhelming. Using these bounds and Lemma 2 we get that strong rPre security implies strong OW security. \(\square \)
We conjecture that concatenation is strongly one-way even for \(1/3 \le \epsilon <~1\). The intuition is that in the one-way game a point is “planted” in a large intersection, which seems hard to discover without essentially communicating the entire intersection. Tighter lower bounds for set-intersection can be used to establish this.
5.2 PRG Security
We now consider the PRG security of the concatenation combiner. Our reduction in Theorem 4 from \(\mathrm {rPre}\) to set-intersection can be easily adapted to the decisional setting. That is, we can show that a decisional variant of \(\mathrm {rPre}\) can be reduced to the set-disjointness problem. The decisional variant of \(\mathrm {rPre}\) asks the adversary to decide whether or not a random co-domain point \(y_1|y_2\) has a preimage. This is exactly the oblivious PRG (oPRG) notion that we defined in Sect. 2. We get the following result.
Theorem 5
Let \(\textsf {H}_1\in \mathrm {Fun}[n,n+s_1]\) and \(\textsf {H}_2\in \mathrm {Fun}[n,n+s_2]\) and \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}(x) := \textsf {H}_1(x) | \textsf {H}_2(x)\). Then for any adversary  against the oblivious PRG security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi \) against set-disjointness with \(\mu :=\mu (p,q)\) where \(p:=1/2^{n+s_1}\) and \(q:=1/2^{n+s_2}\) and such that
against the oblivious PRG security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi \) against set-disjointness with \(\mu :=\mu (p,q)\) where \(p:=1/2^{n+s_1}\) and \(q:=1/2^{n+s_2}\) and such that

We next check if concrete parameters can be set to obtain an expanding PRG.
Corollary 2
For \(s_1=-n/2+1\) and \(s_2=-n/2\), the concatenation combiner gives a weak \(\mathrm {PRG}\) in \(\mathrm {Fun}[n,n+1]\).
Proof
The theorem gives a reduction to set-disjointness with parameters \(p=1/2^{n/2+1}\) and \(q=1/2^{n/2}\). For large n we get, \(\delta =2\), \(p_0 = 1-e^{-1/2}\) and \((\delta -1) p_0/(4+\delta ) < 0.0656\), which means we can set \(\varepsilon = 0.065\). By set-disjointness lower bound, this means any adversary with advantage at least 0.935 must place at least \(\mathcal {O}(2^{n/2})\) queries in total to its oracles.
By Lemma 1 we have that  In our case \(C=1/2<1\), and the right hand side above is upper bounded by \(\le 0.165\). (We have removed the negligible terms and instead approximated the constants by slightly larger values.)
In our case \(C=1/2<1\), and the right hand side above is upper bounded by \(\le 0.165\). (We have removed the negligible terms and instead approximated the constants by slightly larger values.)
In Lemma 3 in order to meet the bound  , we would need \(0.935 \le (2 - \alpha - 0.165) \cdot \alpha / (1-\alpha )\). After some algebra this gives \(\alpha \ge 0.39343\). With \(m=n+s\), we need to have \(1 - e^{-2^{-s}} \ge 0.39343\), which means \(s\le 1.00018\). Thus we can set \(s=1\) (which also satisfies \(s \ge 0.53\) as required in the lemma). \(\square \)
, we would need \(0.935 \le (2 - \alpha - 0.165) \cdot \alpha / (1-\alpha )\). After some algebra this gives \(\alpha \ge 0.39343\). With \(m=n+s\), we need to have \(1 - e^{-2^{-s}} \ge 0.39343\), which means \(s\le 1.00018\). Thus we can set \(s=1\) (which also satisfies \(s \ge 0.53\) as required in the lemma). \(\square \)
We can obtain a strong PRG by amplification. However, we need an amplifier that woks on PRGs with (very) small stretch. Such a construction is given by Maurer and Tessaro [29]. In their so-called Concatenate-and-Extract (CaE) construction one sets
where \(\mathsf {Ext}\) is a sufficiently good randomness extractor, for instance a two-universal hash function. We refer to the original work for concrete parameters. It is safe to assume the extractor is backdoor-free, since it is an information-theoretic object and relatively easy to implement.
5.3 Collision Resistance
The classical result of Simon [36] shows that collision-resistance relies on qualitatively stronger assumptions than one-way functions. In the theorem below we prove collision resistance based on the hardness of the multi-instance \(2\mathrm {INT}\) problem as defined in Sect. 4. As discussed in the final remark of that section, we do not expect that a reduction to the \(\mathrm {INT}\) problem exists.
Theorem 6
Let \(\textsf {H}_1\in \mathrm {Fun}[n,n+s_1]\) and \(\textsf {H}_2\in \mathrm {Fun}[n,n+s_2]\) and \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}(x) := \textsf {H}_1(x) | \textsf {H}_2(x)\). Then for any adversary  against the collision resistance of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi '\) against multi-instance two-element set-intersection problem over \(\mu ':=\mu (p',q')\) with \(p':=2n \ln 2/2^{n+s_1}\) and \(q':=2n \ln 2/2^{n+s_2}\) and where Alice holds \(M_1 := 2^{n+s_1}\) sets and Bob holds \(M_2 := 2^{n+s_2}\) sets such that
against the collision resistance of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi '\) against multi-instance two-element set-intersection problem over \(\mu ':=\mu (p',q')\) with \(p':=2n \ln 2/2^{n+s_1}\) and \(q':=2n \ln 2/2^{n+s_2}\) and where Alice holds \(M_1 := 2^{n+s_1}\) sets and Bob holds \(M_2 := 2^{n+s_2}\) sets such that

Proof
We follow an overall strategy that is similar to one for the \(\mathrm {rPre}\) reduction. For each  , Alice sets \(\textsf {H}_1^-(i):=S_i\) and for each
, Alice sets \(\textsf {H}_1^-(i):=S_i\) and for each  Bob sets \(\textsf {H}_2^-(j):=T_j\) and they simulate the two hash functions. However, this leads to a problem: \(S_{i}\) are not necessarily disjoint and furthermore their union does not cover the entire domain
Bob sets \(\textsf {H}_2^-(j):=T_j\) and they simulate the two hash functions. However, this leads to a problem: \(S_{i}\) are not necessarily disjoint and furthermore their union does not cover the entire domain  . (The same is true for \(T_j\).) Put differently, the distributions of sets formed by hash preimages of co-domain points do not match independently chosen sets from a Bernoulli distribution.
. (The same is true for \(T_j\).) Put differently, the distributions of sets formed by hash preimages of co-domain points do not match independently chosen sets from a Bernoulli distribution.
We treat this problem in two step. The first step is a direct reduction to a “partitioned” modification of the multi-instance set-intersection. In this partitioned problem Alice gets sets \(S_i:=\textsf {H}_1^-(i)\) for  and a random oracle \(\textsf {H}_1\in \mathrm {Fun}[n,n+s_1]\). Similarly, Bob gets sets \(T_j:=\textsf {H}_2^-(j)\) for
and a random oracle \(\textsf {H}_1\in \mathrm {Fun}[n,n+s_1]\). Similarly, Bob gets sets \(T_j:=\textsf {H}_2^-(j)\) for  and an independent random oracle \(\textsf {H}_2\in \mathrm {Fun}[n,n+s_2]\). Their goal is to find a tuple \((i,j,x,x')\) with \(x\ne x'\) such that \(x,x' \in S_i \cap T_j\). Thus, these sets exactly correspond to hash preimages as needed in the reduction above, and a solution would translate to a collision for the combined hash function.
and an independent random oracle \(\textsf {H}_2\in \mathrm {Fun}[n,n+s_2]\). Their goal is to find a tuple \((i,j,x,x')\) with \(x\ne x'\) such that \(x,x' \in S_i \cap T_j\). Thus, these sets exactly correspond to hash preimages as needed in the reduction above, and a solution would translate to a collision for the combined hash function.
We then show that hardness of the (standard) multi-instance two-element set-intersection problem implies the hardness of the partitioned problem with an increase in the Bernoulli parameter.Footnote 10 \(\square \)
Lemma 6
(Partitioned \(\implies \) Independent). For any two-party protocol \(\pi \) against the partitioned multi-instance set-intersection problem there is a two-party protocol \(\pi '\) against multi-instance set-intersection problem such that

Here \(\mu :=\mu (p,q)\) is the distribution induced by hash preimages and \(\mu ':=\mu '(p',q')\) is a product Bernoulli with \(p':=2n \ln 2 \cdot p\) and \(q':=2n \ln 2 \cdot q\).
Proof
To focus on the core ideas, we simplify and let \(M_1=M_2=M = 2^{n+s}\) and \(p=q=1/2^{n+s}\). Suppose we have sets \(S_i\) and \(T_j\) for \(i=1,\ldots ,M\) and \(j=1,\ldots ,M\) as an instance for the multi-instance intersection. Let \(p'=q'=2n \ln 2 \cdot p\). Then

Thus with these parameters the sets \(S_i\) (and similarly \(T_j\)) will cover the full domain, that is  .
.
Note that with these parameters any two sets \(S_i\) and \(T_j\) will intersect with overwhelming probability. However, finding an element in the intersection may still be hard; see conjecture below.
Our next step it to redistribute the elements among the sets so that they form partitions. We do this via the algorithm \(\mathsf {ReDist}\) shown in Fig. 4. \(\mathsf {ReDist}\) iterates through elements x in the domain and leaves x in exactly one of the sets. (By the above covering property such a set always exits.)
This procedure will be applied to \(S_i\) (resp., \(T_j\)) to produce non-overlapping sets \(\tilde{S}_i\) (resp. \(\tilde{T}_j\)). Furthermore, we always have that \(\tilde{S}_i \subseteq S_i\) and \(\tilde{T}_i \subseteq T_i\), since elements are only deleted from the sets and never added to them. Thus \(\tilde{S}_i \cap \tilde{T}_j \subseteq S_i \cap T_j\) as well, and this means that any solution with respect to the tweaked sets will also be a valid solution for the original (Bernoulli) sets.
We still need to show that the distribution of the tweaked sets is identical to that given by hash preimages under a random oracle. Let \(E_{x,i}\) be the event that \(x \in \widetilde{S}_i\). Since the algorithm does not treat any of the i’s in a special way, we claim that \(\Pr [E_{x,i}]\) is independent of i. Indeed for any i, j we have
This is because \(\Pr [x \in S_i] = \Pr [x \in S_j]\) and \(\Pr [i_x = i | x \in S_i ]= \Pr [i_x = j | x \in S_j ]\). If we call this common probability \(e_x\), since x is guaranteed belongs to one of the M sets, we have that \(\sum _{i \in [M]} e_x =1\). Thus \(e_x = 1/M = \Pr [\textsf {H}_1(x)=i]\). Note that the algorithm assigns different values of x independently of all other values already assigned, we get that the event \(\textsf {H}_1(x)=i\) is independent for different x.
Finally, solutions with respect to the tweaked sets always exist when \(s_1+s_2<0\). This is because the problem is equivalent to finding collisions for a function \(\textsf {H}_1(x)|\textsf {H}_2(x)\) that is compressing, which necessarily exist. \(\square \)
The birthday attack gives a \(2^{\min (n+s_1,n+s_2)/2}\) upper bound on the security of the combined hash function. Balancing the digest lengths with \(s_1=s_2=n/2\), leads to a maximum collision security of at most \(2^{n/4}\). Proving a lower bound, on the other hand, remains an interesting open problem. We formulate a conjecture towards proving this next.
Conjecture 1
The multi-instance 2-element set-intersection problem over Bernoulli sets in a universe of size N with \(p=q=1/\sqrt{N}\) and \(\sqrt{N}\) sets for each party has communication complexity

for a sufficiently small protocol error \(\varepsilon \) and where \(\tilde{\mathrm {\Omega }}\) hides logarithmic factors.
We note that a lower bound for protocols with a sufficiently small error would be sufficient for feasibility results as collision resistance can also be amplified in a black-box way [8].
6 The Cascade Combiner
We now look at the security of the cascade combiner
in the 2-BRO model, where \(\textsf {H}_1 \in \mathrm {Fun}[n,n+s_1]\) and \(\textsf {H}_2 \in \mathrm {Fun}[n+s_1,n+s_1+s_2]\). We will prove one-way security and pseudorandomness based on set-intersection and set-disjointness respectively, and collision resistance based on a variant finding two intersecting points given multiple instances for one party and a single set for the other.
6.1 One-Way Security
Similarly to the concatenation combiner, we can reduce the random preimage resistance (\(\mathrm {rPre}\)) security of the cascade combiner to set-intersection.
Theorem 7
Let \(\textsf {H}_1\in \mathrm {Fun}[n,n+s_1]\) and \(\textsf {H}_2\in \mathrm {Fun}[n+s_1,n+s_1+s_2]\) and \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}(x) := \textsf {H}_2(\textsf {H}_1(x))\). Then for large enough n and any adversary  against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi \) against set-intersection with \(\mu :=\mu (p,q)\) where \(p:=1/2^{s_1}\) and \(q:=1/2^{n+s_1+s_2}\) and such that
against the \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) in the 2-BRO model there is a 2-party protocol \(\pi \) against set-intersection with \(\mu :=\mu (p,q)\) where \(p:=1/2^{s_1}\) and \(q:=1/2^{n+s_1+s_2}\) and such that

Proof
We follow a strategy similar to the reductions in Sect. 5. Given a random  the task of the adversary
the task of the adversary  against \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) is to a find a z such that \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}(z)= y^*\). With such a z, one can then also compute \(x:=\textsf {H}_1(z)\) and conclude that \(x \in I \cap T\) where
against \(\mathrm {rPre}\) security of \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}\) is to a find a z such that \(\mathsf {C}^{\textsf {H}_1,\textsf {H}_2}(z)= y^*\). With such a z, one can then also compute \(x:=\textsf {H}_1(z)\) and conclude that \(x \in I \cap T\) where

with  . The set T is Bernoulli with parameter \(\Pr [y \in T] = 1/2^{n+s_1+s_2}\). Although set I appears to be Bernoulli,
. The set T is Bernoulli with parameter \(\Pr [y \in T] = 1/2^{n+s_1+s_2}\). Although set I appears to be Bernoulli,
it is not, since these probabilities are not independent for different values of x.
Our strategy to deal with this and ultimately construct a protocol \(\pi \) for solving set-intersection is to start with a Bernoulli set S (Alice’s input), and program \(\textsf {H}_1\) on all  to values y that will be taken from S, but are also set to collide with the right probability. This will ensure that the image of \(\textsf {H}_1\) contains most of S and is also distributed as the image of a random oracle.
to values y that will be taken from S, but are also set to collide with the right probability. This will ensure that the image of \(\textsf {H}_1\) contains most of S and is also distributed as the image of a random oracle.
We proceed as follows. Initially the set of assigned domain points X and assigned co-domain points Y are empty. We then iterate through  in a random order. A bit b decides at each iteration decides if the hash value y for x should collide with a previously assigned value or not. If so, we sample y from the set of already assigned values Y. Otherwise, y should be a non-colliding value and we sample it from S if S is non-empty (and remove y from S), or otherwise we sample it outside the already assigned points Y. The pseudo-code for this algorithm, which we call \(\mathsf {HashSam}\), is shown in Fig. 5.
in a random order. A bit b decides at each iteration decides if the hash value y for x should collide with a previously assigned value or not. If so, we sample y from the set of already assigned values Y. Otherwise, y should be a non-colliding value and we sample it from S if S is non-empty (and remove y from S), or otherwise we sample it outside the already assigned points Y. The pseudo-code for this algorithm, which we call \(\mathsf {HashSam}\), is shown in Fig. 5.
Setting \(m:= n+ s_1\), we now need to check that (1) the returned hash function \(\textsf {H}_1\) is distributed as a random oracle  when S is Bernoulli with parameter \(p=1/2^{s_1}\), and (2) if
when S is Bernoulli with parameter \(p=1/2^{s_1}\), and (2) if  , then we also have that \(x \in S \cap T\) with good probability.
, then we also have that \(x \in S \cap T\) with good probability.
We first prove (1). The intuition is that the algorithm treats all inputs and outputs in a uniform way, and hence no particular values are special. Formally, let \(x^*\) and \(y^*\) be any fixed values. We show that \(\Pr [\textsf {H}_1(x^*)=y^*]=1/2^m\), even given the previously assigned values. We use a subscript i to denote the values of various variables in the i-th iteration. Looking at different execution branches of the algorithm we can calculate \(\Pr [y_i = y^* | x_i = x^*, Y_i,X_i]\) as
Letting \(\theta _i:=\Pr [S_i = \emptyset ]\) we can simplify to
Note we have used the fact that \(S_i\) is a Bernoulli set in \(\Pr [y^* \in S_i]=\frac{|S_i|}{2^m}\). Hence

Therefore the probability of sampling any given hash function is \((1/2^m)^{2^n}\), as required.
Let us now consider (2). When \(I \subseteq S\), any solution with respect to I is also one with respect to S (that is, solutions are not lost). Hence we only look at the case \(S \subseteq I\) and bound \(|I \setminus S| = |I| - |S|\). Since \(|I| \le 2^n\) and \({{\mathrm{\mathbb {E}}}}[|S|]= 2^{n+s_1}/2^{s_1}=2^n\), we get that for any t
Applying the Chernoff bounds we obtain
Setting \(t := \sqrt{n/2^n}\), we get with overwhelming probability that \( |I \setminus S| \le \sqrt{n} 2^{n/2}~. \) Hence \(T \cap (I \setminus S)\) will be non-empty with negligible probability \(\sqrt{n}2^{-n/2-s_1-s_2}\), in which case if \(x \in I \cap T \implies x \in S \cap T\). \(\square \)
If \(\textsf {H}_1 \in \mathrm {Fun}[n,(2+\epsilon )n]\) and \(\textsf {H}_2 \in \mathrm {Fun}[(2+\epsilon )n,(1+\epsilon )n]\)), we have a reduction to set-intersection with parameters \(N=2^{(2+\epsilon )n}\), \(p=1/2^{(1+\epsilon )n}\), and \(q=1/2^{(1+\epsilon )n}\). Thus with notation as in the description of the feasible in Fig. 3 we have that \(\alpha = \beta = (1+\epsilon )/(2+\epsilon )\). As in Corollary 1 we would need The point \((\alpha ,\beta )\) lies in the feasible region for \(1/3< (1+\epsilon )/(2+\epsilon ) < 1/2\), which means \(-1/2< \epsilon < 0\). Since the combined function is compressing (with \(\gamma = 1/(1+\epsilon ) > 1\)) and \(p_\circ \approx 1-e^{-2^{-\epsilon \cdot n}}\) is negligible, the image uniformity bound is negligible and hence, similarly to Corollary 1 we get strong OW security.
6.2 PRG and CR Security
We briefly outline how to treat the PRG security and collision resistance of cascade. We omit the proofs as the techniques and proof structures are similar to our other results above.
PRG security. We can prove an analogous result for the oblivious PRG security of the cascade construction. Its reduction is identical to that for \(\mathrm {rPre}\) security given above, except that the underlying assumption is set-disjointness. Setting \(s_1=2n\) (\(\textsf {H}_1\) is length doubling) and \(s_2=-2n+1\) (\(\textsf {H}_2\) compresses by almost a factor of 3) leads to a reduction to an instance of set-intersection with parameters \(N=2^{3n}\), \(p=1/2^{2n}\), and \(q=1/2^{n+1}\). In this case \(\delta = 2\) and \(p_0 = 1- e^{-1/2}\). With these parameters we can carry out an analysis similar to Corollary 2: We set the error \(\varepsilon = 0.065\) which is smaller than \((\delta -1) p_0/(4+\delta ) < 0.0656\) as required in Theorem 2 for an exponential number of queries. The combined hash function maps n bits to \(n+1\) bits and hence \(C=1/2\). Furthermore, \(p_\circ \) is negligible as a function from n bits to 3n bits is injective with overwhelming probability. Thus we can apply Lemma 3 with \(s=1\) as in Corollary 2 to get a weak PRG.
Collision resistance. We can treat the collision resistance of cascade similarly. The difference is that in the reduction Alice will use the \(\mathsf {HashSam}\) algorithm in Fig. 5 to adapt a (single) Bernoulli set S that she holds to a hash image set I. On the other hand, Bob uses the \(\mathsf {ReDist}\) algorithm in Fig. 4 to redistribute elements in multiple Bernoulli sets that he holds so that they form a partition of the entire domain of \(\textsf {H}_2\). The rest of the proof, which is included in the full version [4, Appendix E], proceeds similarly to Lemma 6. For setting parameters, observe that any collision for \(\textsf {H}_1\) is necessarily a collision for \(\textsf {H}_2(\textsf {H}_1(\cdot ))\). Since collisions for \(\textsf {H}_1\) can be easily found using \(\textsc {Bd}_1\), we need \(\textsf {H}_1\) to be injective. For example, \(s_1=2n\) (co-domain points are 3n bits) would lead to an injective \(\textsf {H}_1\) with overwhelming probability.
Notes
- 1.
Note that k-BRO can be viewed as a restricted version of the 1-BRO model where k ROs are built from a single RO acting on k separate domains and backdoor capabilities are restricted to these domains only.
- 2.
On the other hand, for sufficiently large sets that intersect with high probability, set-disjointness is easy whereas set-intersection can remain hard.
- 3.
The expected size of such Bernoulli sets is \(N/\sqrt{N}=\sqrt{N}\), but this size can deviate from the mean and this distribution is not identical to that by Babai et al. [1].
- 4.
Arguably, the AI-RO model is better named the Non-Uniform RO model: auxiliary input is often instance dependent whereas non-uniform input is not.
- 5.
The classical setting can be viewed as one where bk’s are fixed, which leads to a difficulty when the new definition is used: a combiner (formally speaking) can “detect” which hash functions are the good ones and use them. Since this detection procedure is not considered practical, one instead asks for the existence of a reduction \(\mathsf {R}\) as discussed above.
- 6.
Without this restriction, a trivial construction exists: generate a fresh hash key and “forget” its backdoor. In practice, however, hash keys model sampling of a (unkeyed) hash function from a family. Moreover, it is unclear if the designer of the combiner will securely erase the generated backdoor. Thus, we assume that for any generated key its backdoor is also available.
- 7.
We note that most of the work on distributional communication complexity is driven by Yao’s min-max lemma, which lower bounds worst-case communication complexity using distributional communication complexity for some (often non-uniform) distribution.
- 8.
In the full version of this paper [4, Appendix C.3] we give a new refined proof that extends the theorem to \(\delta \ge 0.8\).
- 9.
We note that our setting is different to direct sum/product theorems where the focus is on hardness amplification. One shows, for example, that computing n independent copies of a function requires n times the communication for one copy for product distributions [3].
- 10.
Another strategy would be to change the number of sets involved. But this runs into a problem as this number must match the size of the co-domain of the hash function.
References
Babai, L., Frankl, P., Simon, J.: Complexity classes in communication complexity theory (preliminary version). In: 27th FOCS, pp. 337–347 (1986)
Bar-Yossef, Z., Jayram, T.S., Kumar, R., Sivakumar, D.: An information statistics approach to data stream and communication complexity. In: 43rd FOCS, pp. 209–218 (2002)
Barak, B., Braverman, M., Chen, X., Rao, A.: How to compress interactive communication. In: 42nd ACM STOC, pp. 67–76 (2010)
Bauer, B., Farshim, P., Mazaheri, S.: Combiners for backdoored random oracles. Cryptology ePrint Archive (2018)
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: ACM CCS 1993, pp. 62–73 (1993)
Bernstein, D.J., Lange, T., Niederhagen, R.: Dual EC: a standardized back door. Cryptology ePrint Archive, Report 2015/767 (2015). http://eprint.iacr.org/2015/767
Boneh, D., Boyen, X.: On the impossibility of efficiently combining collision resistant hash functions. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 570–583. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_34
Canetti, R., Rivest, R.L., Sudan, M., Trevisan, L., Vadhan, S.P., Wee, H.: Amplifying collision resistance: a complexity-theoretic treatment. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 264–283. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_15
Chattopadhyay, A., Pitassi, T.: The story of set disjointness. SIGACT News 41(3), 59–85 (2010)
Checkoway, S., Maskiewicz, J., Garman, C., Fried, J., Cohney, S., Green, M., Heninger, N., Weinmann, R.-P., Rescorla, E., Shacham, H.: A systematic analysis of the juniper dual EC incident. In: ACM CCS 2016, pp. 468–479 (2016)
Checkoway, S., et al.: On the practical exploitability of dual EC in TLS implementations. In: 23rd USENIX Security Symposium (USENIX Security 14), pp. 319–335 (2014)
Coretti, S., Dodis, Y., Guo, S., Steinberger, J.: Random oracles and non-uniformity. Cryptology ePrint Archive, Report 2017/937 (2017). http://eprint.iacr.org/2017/937
Dinur, I.: New attacks on the concatenation and XOR hash combiners. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 484–508. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_19
Dodis, Y., Guo, S., Katz, J.: Fixing cracks in the concrete: random oracles with auxiliary input, revisited. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part II. LNCS, vol. 10211, pp. 473–495. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_16
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fischlin, M., Lehmann, A.: Security-amplifying combiners for collision-resistant hash functions. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 224–243. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_13
Fischlin, M., Lehmann, A., Pietrzak, K.: Robust multi-property combiners for hash functions. J. Cryptol. 27(3), 397–428 (2014)
Goldreich, O.: Foundations of Cryptography: Basic Tools, vol. 1. Cambridge University Press, Cambridge (2001)
Guruswami, V., Cheraghchi, M.: Set disjointness lower bound via product distribution. Scribes for Information theory and its applications in theory of computation (2013). http://www.cs.cmu.edu/~venkatg/teaching/ITCS-spr2013/
Hoch, J.J., Shamir, A.: On the strength of the concatenated hash combiner when all the hash functions are weak. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part II. LNCS, vol. 5126, pp. 616–630. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70583-3_50
Joux, A.: Multicollisions in iterated hash functions. Application to cascaded constructions. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 306–316. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_19
Katz, J., Lucks, S., Thiruvengadam, A.: Hash functions from defective ideal ciphers. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 273–290. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16715-2_15
Kawachi, A., Numayama, A., Tanaka, K., Xagawa, K.: Security of encryption schemes in weakened random oracle models. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 403–419. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_24
Kushilevitz, E., Nisan, N.: Communication Complexity. Cambridge University Press, New York (1997)
Lehmann, A.: On the security of hash function combiners. Ph.D. thesis, TU Darmstadt (2010)
Leurent, G., Wang, L.: The sum can be weaker than each part. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part I. LNCS, vol. 9056, pp. 345–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_14
Liskov, M.: Constructing an ideal hash function from weak ideal compression functions. In: Biham, E., Youssef, A.M. (eds.) SAC 2006. LNCS, vol. 4356, pp. 358–375. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74462-7_25
Lucks, S.: A failure-friendly design principle for hash functions. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 474–494. Springer, Heidelberg (2005). https://doi.org/10.1007/11593447_26
Maurer, U.M., Tessaro, S.: A hardcore lemma for computational indistinguishability: security amplification for arbitrarily weak PRGs with optimal stretch. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 237–254. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_15
Mendel, F., Rechberger, C., Schläffer, M.: MD5 is weaker than weak: attacks on concatenated combiners. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 144–161. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_9
Mittelbach, A.: Cryptophia’s short combiner for collision-resistant hash functions. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 136–153. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38980-1_9
Moshkovitz, D., Barak, B.: Communication complexity. Scribes for Advanced Complexity Theory (2012). https://people.csail.mit.edu/dmoshkov/courses/adv-comp/
Numayama, A., Isshiki, T., Tanaka, K.: Security of digital signature schemes in weakened random Oracle models. In: Cramer, R. (ed.) PKC 2008. LNCS, vol. 4939, pp. 268–287. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78440-1_16
Reingold, O., Trevisan, L., Vadhan, S.P.: Notions of reducibility between cryptographic primitives. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 1–20. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_1
Rogaway, P., Shrimpton, T.: Cryptographic hash-function basics: definitions, implications, and separations for preimage resistance, second-preimage resistance, and collision resistance. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 371–388. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-25937-4_24
Simon, D.R.: Finding collisions on a one-way street: can secure hash functions be based on general assumptions? In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 334–345. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054137
Unruh, D.: Random oracles and auxiliary input. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 205–223. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_12
Yao, A.C.-C.: Some complexity questions related to distributive computing (preliminary report). In: Proceedings of the Eleventh Annual ACM Symposium on Theory of Computing, pp. 209–213 (1979)
Acknowledgments
We thank Marc Fischlin for participating in the early stages of this work. We also thank the CRYPTO’18 (sub)reviewers for their valuable comments. Bauer was supported by the French ANR Project ANR-16-CE39-0002 EfTrEC. Farshim was supported by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement no. 339563 - CryptoCloud). Mazaheri was supported by the German Federal Ministry of Education and Research (BMBF) and by the Hessian State Ministry for Higher Education, Research and the Arts, within CRISP.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Bauer, B., Farshim, P., Mazaheri, S. (2018). Combiners for Backdoored Random Oracles. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10992. Springer, Cham. https://doi.org/10.1007/978-3-319-96881-0_10
Download citation
DOI: https://doi.org/10.1007/978-3-319-96881-0_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96880-3
Online ISBN: 978-3-319-96881-0
eBook Packages: Computer ScienceComputer Science (R0)








 problem, a natural multi-instance version of
problem, a natural multi-instance version of  problem. When
problem. When 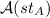 . It terminates if it receives a final guess x from Bob. It answers all pending
. It terminates if it receives a final guess x from Bob. It answers all pending  queries
queries  terminates with a final guess x, it forwards x to Bob and terminates. Else it saves the current state
terminates with a final guess x, it forwards x to Bob and terminates. Else it saves the current state  locally and forwards all
locally and forwards all  since the last resumption to Bob. It hands the execution over to Bob.
since the last resumption to Bob. It hands the execution over to Bob. . It terminates if it receives a final guess x from Alice. It answers all pending
. It terminates if it receives a final guess x from Alice. It answers all pending  queries
queries  terminates with a final guess x, it forwards x to Alice and terminates. Else it saves the current state
terminates with a final guess x, it forwards x to Alice and terminates. Else it saves the current state  locally and forwards all
locally and forwards all  since the last resumption to Alice. It hands the execution over to Alice.
since the last resumption to Alice. It hands the execution over to Alice.

