Abstract
Indistinguishability obfuscation has become one of the most exciting cryptographic primitives due to its far reaching applications in cryptography and other fields. However, to date, obtaining a plausibly secure construction has been an illusive task, thus motivating the study of seemingly weaker primitives that imply it, with the possibility that they will be easier to construct.
In this work, we provide a systematic study of compressing obfuscation, one of the most natural and simple to describe primitives that is known to imply indistinguishability obfuscation when combined with other standard assumptions. A compressing obfuscator is roughly an indistinguishability obfuscator that outputs just a slightly compressed encoding of the truth table. This generalizes notions introduced by Lin et al. (PKC 2016) and Bitansky et al. (TCC 2016) by allowing for a broader regime of parameters.
We view compressing obfuscation as an independent cryptographic primitive and show various positive and negative results concerning its power and plausibility of existence, demonstrating significant differences from full-fledged indistinguishability obfuscation.
First, we show that as a cryptographic building block, compressing obfuscation is weak. In particular, when combined with one-way functions, it cannot be used (in a black-box way) to achieve public-key encryption, even under (sub-)exponential security assumptions. This is in sharp contrast to indistinguishability obfuscation, which together with one-way functions implies almost all cryptographic primitives.
Second, we show that to construct compressing obfuscation with perfect correctness, one only needs to assume its existence with a very weak correctness guarantee and polynomial hardness. Namely, we show a correctness amplification transformation with optimal parameters that relies only on polynomial hardness assumptions. This implies a universal construction assuming only polynomially secure compressing obfuscation with approximate correctness. In the context of indistinguishability obfuscation, we know how to achieve such a result only under sub-exponential security assumptions together with derandomization assumptions.
Lastly, we characterize the existence of compressing obfuscation with statistical security. We show that in some range of parameters and for some classes of circuits such an obfuscator exists, whereas it is unlikely to exist with better parameters or for larger classes of circuits. These positive and negative results reveal a deep connection between compressing obfuscation and various concepts in complexity theory and learning theory.
G. Asharov—Supported by a Junior Fellow award from the Simons Foundation.
N. Ephraim—Supported by an AFOSR grant FA9550-15-1-0262.
I. Komargodski—Supported in part by a Packard Foundation Fellowship and by an AFOSR grant FA9550-15-1-0262.
R. Pass—Supported in part by NSF Award CNS-1561209, NSF Award CNS-1217821, NSF Award CNS-1704788, AFOSR Award FA9550-15-1-0262, a Microsoft Faculty Fellowship, and a Google Faculty Research Award.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Program obfuscation is an intriguing and powerful concept in modern cryptography. A program obfuscator is a compiler that “scrambles” programs into ones that are hard to reverse engineer, while preserving their functionality. The predominant notion that captures the above concept is indistinguishability obfuscation, introduced in the seminal work of Barak et al. [14], which has inspired a vibrant area of research in recent years. Informally, indistinguishability obfuscation (iO) guarantees that the obfuscations of two functionally equivalent circuits of the same size are computationally indistinguishable.
There are two main reasons why iO has become such a central primitive—its potential to exist and its power. As opposed to stronger notions of obfuscation that are known not to exist for all circuits (such as virtual black-box obfuscation [14]), general purpose iO might be realizable, and in fact, since the work of Garg et al. [38] many candidate constructions of iO have emerged [5, 8, 13, 27, 38, 42, 44, 68, 73]. As for its power, iO serves as a hub for an impressive number of cryptographic primitives, ranging from classical concepts such as one-way functions [53], public-key encryption [70], trapdoor permutations [19], ZAPs and non-interactive witness-indistinguishable proofs [18], to ones that are still far beyond the reach of any other assumption, such as deniable encryption [70], fully-secure multi-input functional encryption [45], and many others.
Despite immense efforts to construct iO from concrete assumptions, all currently known candidate constructions have been shown to be vulnerable to attacks [7, 12, 23, 32, 33, 43, 62, 66].Footnote 1 Another line of work shows how to construct iO from some seemingly “simpler” or “weaker” generic cryptographic primitives (together with more standard assumptions). These include primitives such as low-degree multilinear maps [4, 55, 56, 59], compact functional encryption schemes [3, 20], compact randomized encodings [58], and variants of exponentially-efficient indistinguishability obfuscation [17, 57], all of which have no known instantiations from standard assumptions.
The difficulty of constructing iO motivates the study of such seemingly weaker cryptographic primitives, with the hope that such a study could elucidate the foundations of iO. In this paper, we focus on the primitive which is arguably the simplest to define and the closest in its nature to iO: indistinguishability obfuscation with nontrivial compression, or in short, compressing obfuscation.
Compressing obfuscation. For functions t(s, n) and \(\ell (s,n)\), we say that an obfuscator \(\mathcal {O} \) is \((t,\ell )\)-compressing if, when given a circuit C of size s on n inputs, the obfuscator \(\mathcal {O} (C)\) runs in time t(s, n) and has output length \(\ell (s,n)\). In the case of iO, both t and \(\ell \) are polynomial in s and n, but in general, we allow them to be super-polynomial, or even (sub-)exponential. This definition generalizes existing relaxations of iO (such as XiO and SXiO which we discuss below) and allows us to characterize the extent to which efficiency impacts the existence, applications, and limitations of obfuscation. Throughout this work, we mostly focus on the following two settings of parameters, which intuitively, are relaxed versions of iO that only allow obfuscating circuits with logarithmic input size:
-
XiO. The first (and weaker) setting of parameters is that of exponentially-efficient iO (XiO), introduced by Lin et al. [57]. XiO allows the running time of the obfuscator to be as large as the truth table of the circuit to be obfuscated, but requires the size of the obfuscated circuit to be slightly smaller than its truth table. More formally, for a function c (which denotes the compression of XiO), we say that c-XiO is a \((t,\ell )\)-compressing obfuscator with \(t(s,n) = \mathsf {poly}(2^{n},s)\) and \(\ell (s,n) = c(n) \cdot \mathsf {poly}(s)\). When there exists a constant \(\epsilon > 0\) such that \(c(n) = 2^{n(1-\epsilon )}\), we denote c-XiO simply by XiO. Lin et al. [57] showed that XiO for all circuits and Learning With Errors (LWE), both with sub-exponential security, imply iO.
-
SXiO. The second (and stronger) setting of parameters is that of strong XiO (SXiO), introduced by Bitansky et al. [17]. SXiO requires that the time to obfuscate a circuit is slightly smaller than the truth table of the circuit. More formally, for a function c, we say that c-SXiO is a \((t,\ell )\)-compressing obfuscator with \(t(s,n) = \ell (s,n) = c(n) \cdot \mathsf {poly}(s)\). Similar to the above case, when there exists some constant \(\epsilon > 0\) such that \(c(n) = 2^{n(1-\epsilon )}\), we denote this simply by SXiO. Bitansky et al. [17] showed that SXiO and any public-key encryption, both with sub-exponential security, imply iO.
These two settings of parameters have seemingly minor differences, but nevertheless, are not known to be equivalent. Moreover, as mentioned above, their known implications illustrate the richness of the world of compressing obfuscation, and indicate that efficiency is a fundamental property of obfuscation. Since the regime of parameters for compressing obfuscation is somewhat non-standard (especially, the distinction between time and output length in XiO), it has not received adequate attention, and as a result we know very little about it.
In this work, we provide a systematic study of compressing obfuscation as an independent cryptographic primitive, and thus characterize the extent to which efficiency plays a role in obfuscation.
1.1 Our Results
Our results span a wide range of topics concerning compressing obfuscation, including limitations of its power, existence in an information-theoretic setting, constructions for limited classes of functions, and correctness amplification.
XiO vs. PKE. We start by exploring the power of XiO as an independent cryptographic primitive. One the one hand, we know that when combined with LWE it implies full-fledged iO (which in turn implies almost all cryptographic primitives). On the other hand, as opposed to iO [53], we do not even know whether XiO by itselfFootnote 2 implies one-way functions — the most basic cryptographic primitive.
One of the original applications of obfuscation, which was proposed by Diffie and Hellman back in 1976 [36], is to transform private-key encryption into public-key encryption. When combined with one-way functions, iO can be used to perform such a transformation, as shown by [38, 70]. This raises the same question regarding XiO: Can it bridge the gap between the world of private-key cryptography and that of public-key cryptography? We provide evidence that it cannot, and thus show a concrete lower bound on its potential power.
Theorem 1.1
(informal). There is no fully black-box construction of a perfectly correct key-agreement protocol from one-way functions and perfectly correct \(2^{(1-\epsilon ) n}\)-XiO for any constant \(\epsilon >0\), even with sub-exponential security.
The result is obtained by following the black-box framework of [9, 10, 15], where they consider obfuscation for oracle-aided circuits. This captures exactly the flavor of constructions which give public-key encryption from one-way functions and iO [70]. We make various modifications to this framework to capture the notion of XiO for oracle-aided circuits.
Previously, by combining [9, 17], the above result follows for the case of \(2^{(1-\epsilon ) n}\)-XiO where \(0 < \epsilon \le 1/2\) (i.e., the obfuscator has only somewhat weak compression).Footnote 3 In contrast, our separation works even when given access to an obfuscator with very strong compression (i.e. any constant \(\epsilon > 0\)) and even if the obfuscator satisfies perfect correctness.
The frameworks that this result is based on are rooted in the ideas of Impagliazzo and Rudich [51], who show a separation between one-way permutations and key-agreement. Their result holds both for the case of key-agreement with perfect or imperfect completeness. Nevertheless, we note that our separation does not hold for imperfect key-agreement, and we leave the extension to future work.
Statistical security. Our result that it is unlikely that key-agreement can be constructed from XiO and one-way functions can be viewed as “good news”, as it hints that XiO is a somewhat “weak” primitive, and therefore it might be possible to base its existence on well-studied assumptions. In fact, it might even be possible that compressing obfuscation exists unconditionally (even if \(\mathsf {P}\ne \mathsf {NP}\)). Toward this end, we show almost matching upper and lower bounds for the existence of compressing obfuscation with statistical security, both for the case of perfect correctness and that of approximate correctness. Our results show tight connections between compressing obfuscation and various concepts in complexity theory and learning and thus we view this as one of the central takeaways of this work.
For the case of approximate correctness, we show a \(2^{n^\epsilon }\)-SXiO for \(\epsilon >0\) for small classes of circuits (such as \(\mathsf {AC}^{0}\)). On the other hand, we show that such an obfuscator cannot exist for larger classes of circuits that contain a (puncturable) PRF, unless \(\overline{\mathsf {SAT}} \in \mathsf {AM}[2^{n^\epsilon }]\), where \(\overline{\mathsf {SAT}}\) is the problem of deciding whether a formula is unsatisfiable and \(\mathsf {AM}[t(n)]\) is the class of all languages on instances of size n that have an AM protocol in which the running time of the verifier and the message sizes are at most t(n).
Theorem 1.2
(informal). There exists a statistically secure and approximately correct \(2^{n^\epsilon }\)-SXiO for \(\mathsf {AC}^{0}\) and \(\epsilon > 0\). On the contrary, unless \(\overline{\mathsf {SAT}} \in \mathsf {AM}[2^{n^\epsilon }]\), there is no such obfuscator for any class that contains a (puncturable) PRF.
This result naturally leads to the question of whether we can get a similar statement for the case of perfect correctness. We are unable to get such a result for SXiO, but we do get it for XiO, albeit with worse compression.Footnote 4
Theorem 1.3
(informal). There exists a \(2^{n(1-\epsilon )}\)-XiO for \(\epsilon \in 1/\mathsf {poly}\log (n)\) with statistical security and perfect correctness for \(\mathsf {AC}^{0}\).
Ruling out statistically secure XiO with any compression is left as an open problem. We do show that unless \(\overline{\mathsf {SAT}} \in \mathsf {AM}[2^{c(1-\epsilon ) n}]\) for a universal constant \(c\in \mathbb {N} \), there is no statistically secure and perfectly correct \(2^{n(1-\epsilon )}\)-SXiO for \(\mathsf {AC}^{0}\) (see Theorem 5.2). It is known, by the recent result of Williams [72], that \(\overline{\mathsf {SAT}} \in \mathsf {AM}[\tilde{O}(2^{ n/2})]\). However, it might be that for larger values of \(\epsilon \) (such as \(\epsilon = 1-(0.1/c)\) or even \(\epsilon = 1-o(1)\)) it holds that  .
.
The positive results are based on classical (PAC) learning algorithms [60, 71] and the circuit compression algorithm of [31]. Both negative results above rely on and (carefully) extend analogous arguments from the iO literature [24, 47, 53]. Goldwasser and Rothblum [47] showed that statistical iO with perfect correctness cannot exist unless \(\mathsf {NP}\subseteq \mathsf {SZK}\). Brakerski, Brzuska, and Fleischhacker [24] extend the result to handle statistical iO with approximate correctness by showing that (assuming additionally one-way functions) unless \(\mathsf {coNP}\subseteq \mathsf {AM}\), it cannot exist.
Correctness amplification. Our results above suggest that approximate correctness might be easier to achieve than perfect correctness, in an information theoretic setting. Is this the case also in the computational setting? To address this question, we show a transformation from approximately correct XiO to perfectly correct XiO, assuming the original XiO applies to a large enough class of circuits. This transformation achieves optimal parameters and only incurs polynomial security loss, indicating that correctness is not the bottleneck in constructing XiO from standard assumptions.
Theorem 1.4
(informal). If there exists an XiO scheme for all polynomial size circuits which is correct with probability \((1/2 + 1/\mathsf {poly})\) over the the inputs and the obfuscation, then there exists a perfectly correct XiO scheme, assuming polynomially-secure LWE and NIZKs.
Prior to this result, there were no correctness amplification procedures for XiO which required only polynomial security or achieved optimal parameters. Correctness amplifications for related primitives, such as those of [2, 21] for iO, do not apply to XiO, since they involve a random self-reducibility step which inherently requires running the obfuscator on polynomial-size inputs. The transformation of Bitansky et al. [16] shows how to transform an XiO which is correct with probability 0.99 over the inputs and the obfuscation to a weak notion of functional encryption. This notion of functional encryption was known to imply a relaxed notion of XiO, namely, XiO with preprocessing [57]. Our transformation works for a much weaker notion of correctness (as opposed to .99) and results in full-fledged, perfectly correct XiO (as opposed to XiO with preprocessing).
Technically, our regime of parameters introduces many difficulties which require us to tailor a construction that is based on a delicate combination of various types of error-correcting codes together with cryptographic primitives (inspired by [65]).
While we show this transformation for the case of XiO, our result extends naturally to the case of SXiO. In particular, we can obtain perfectly correct XiO from the transformation, or SXiO which is correct on all but a negligible fraction of obfuscations.
Universal construction. Using our correctness amplification procedure, we obtain a universal construction of an XiO (resp. SXiO), assuming only the mere existence of XiO (resp. SXiO) with polynomial security and only (very weak) approximate correctness. For XiO, the resulting universal construction satisfies perfect correctness. Note that in the context of iO, perfect correctness is known to be achievable using only derandomization assumptions [22]. Our result is obtained by adapting the robust combiner of Ananth et al. [1] to the setting of XiO (resp. SXiO) and then using our correctness amplification transformation.
1.2 Related Work
Universal construction and robust combiners. It was shown in [48] that, in general, a robust combiner implies the existence of a universal construction. A robust combiner for a cryptographic primitive takes several candidate constructions of the primitive and outputs one construction that is as good as any of the input constructions (see also [49, 50]). A combiner for encryption appears already in [11], and perhaps the most known universal construction is that of one-way functions, due to [54].
Combiners for obfuscation were given in [1, 2, 37]. The work of [1] shows a robust combiner for indistinguishability obfuscation with sub-exponential security loss, and assuming either LWE or DDH. The work of [2] removes the sub-exponential assumption, but does not go all the way to iO—it shows a transforming combiner from candidates for indistinguishability obfuscation of which one of them is polynomially secure to a secure functional encryption scheme.
Existence of iO. Mahmoody et al. [63] showed that iO cannot be based on random oracles or on constant degree multilinear maps (in a black-box way). Garg et al. [40] showed that iO cannot be constructed from any type of encryption that has an “all-or-nothing” type of security (as in PKE or Witness Encryption). Lastly, Garg et al. [41] studied the minimal compactness needed from a functional encryption scheme to imply iO, and giving matching constructions, following [3, 20].
Limitations on the power of iO were studied by Asharov and Segev [9, 10] and by Bitansky, Degwekar and Vaikuntanathan [15]. So far, we know that iO and one-way functions do not imply collision-resistant hash functions [9], domain-invariant one-way permutations [10], and hardness in \(\mathsf {NP} \cap \mathsf {coNP}\) [15]. Also, iO and one-way permutations do not imply hardness in \(\mathsf {SZK}\) [15].
Relaxations of iO. In addition to (S)XiO, another relaxation of iO is decomposable obfuscation (dO), which was recently introduced by Liu and Zhandry [61]. Decomposable obfuscation relaxes the security requirement of iO by requiring that obfuscations of circuits which satisfy a new notion of functional equivalence are indistinguishable. In particular, it is efficient to verify if two circuits satisfy their notion of functional equivalence, unlike traditional functional equivalence. This is similar to the case of XiO, because it is applied on circuits with only logarithmic input size for polynomial time applications. In [61], they question whether iO with efficiently verifiable functional equivalence implies public-key encryption. In fact, they have to assume the existence of public-key encryption for all the applications of dO that they show which imply public-key encryption. As mentioned above, we show a separation from XiO and OWFs to public key encryption. Therefore, our result serves as further evidence to the hypothesis that (non) efficiently checkable functional equivalence is one of the key factors which distinguishes iO from notions like XiO and dO.
Compressing primitives. Recently, compressing witness encryption (WE) was studied by Brakerski et al. [25]. Witness encryption, introduced by Garg et al. [39], allows encrypting a message relative to a statement \(x\in L\) for a language \(L\in \mathsf {NP}\) such that anyone holding a witness to the statement can decrypt the message, but if \(x\notin L\), then it is computationally hard to decrypt. A compressing WE is such that the encryption time (and thus size) is less than the time it takes to solve the \(\mathsf {NP}\) instance. Brakerski et al. showed that such a WE scheme can be constructed under “standard” assumptions (such as LWE or bilinear maps with sub-exponential security). This is in sharp contrast to SXiO (or even XiO).
Paper organization. We proceed with a technical overview of our results. We refer the reader to the full version of the paper for important preliminaries and definitions. In Sect. 3 we show our correctness amplification transformation, and in Sect. 4 we prove our impossibility result on constructing key-agreement from XiO and OWFs. In Sect. 5 we present our positive and negative results regarding statistically secure compressing obfuscation. Most of the technical material is omitted and appears in the full version.
2 Technical Overview
In this section we provide a high level overview of our results. We start with the correctness amplification (and its application to universal constructions) in Sect. 2.1. We proceed with the limitations on the power of XiO in Sect. 2.2, and conclude with our constructions and impossibilities of statistically secure XiO in Sect. 2.3.
2.1 Correctness Amplification
Our correctness amplification for XiO is a transformation from an approximately correct XiO scheme to an XiO scheme that is perfectly correct. Here, by approximately correct, we mean an XiO scheme which is correct with probability \((1/2 + 1/\mathsf {poly})\) over the inputs and the obfuscation, and by perfectly correct, we mean an XiO scheme which is correct on all inputs and all obfuscations with probability 1. The starting point for our correctness amplification is the transformation of Bitansky et al. [16], which transforms an XiO scheme which is correct with probability .99 over the obfuscation and the inputs to a functional encryption (FE) scheme which is correct on all inputs (with all but negligible probability). At a high level, FE is a type of encryption which enables generating functional keys, such that decryption of a ciphertext corresponding to a message m with a functional key for a circuit C results in C(m). The hope is that if we can adapt the [16] transformation to our case, then we can attempt to transform the correct FE back to XiO.
From approximately correct XiO to correct FE. In [16], they first observe that by averaging and standard BPP-type amplification, their XiO scheme can be amplified to one which is correct with probability .9 only over the inputs. Then, they transform this XiO to a correct FE using an error-correcting code, as follows. To encrypt a message m, they obfuscate a circuit \(G_{m}\) which, on input i, outputs an encryption of (m, i) using a succinct functional encryption scheme \(\mathsf {sFE} \), that exists based on LWE [46]. Call the resulting obfuscated circuit \(\widetilde{G} _{m}\). To generate a secret key for a circuit C, they generate an \(\mathsf {sFE} \) secret key for a circuit \(C'\) that on input (m, i) outputs the ith bit of \(\mathsf {ECC} (C(m))\), where \(\mathsf {ECC} \) is an error-correcting code. To decrypt, they first evaluate the obfuscated circuit \(\widetilde{G} _{m}\) on every input i to obtain a list of encryptions of (m, i) for all i. Then, they use the \(\mathsf {sFE} \) secret key to decrypt each of these encryptions and finally, decode the result.
The reason why this is enough for [16] is that, first, by the BPP amplification, they obtain correct encryptions of (m, i) for a .9 fraction of i’s, with all but negligible probability over the obfuscation. This lets them calculate \((\mathsf {ECC} (C(m))_{i}\) for a large (\(\gg 3/4\)) fraction of the i’s. Second, they rely on the error-correcting code which, given \((\mathsf {ECC} (C(m))_{i}\) for many (\(\gg 3/4\)) i’s, can recover C(m).
In our case, a natural attempt would be to replicate their first step and then use an error-correcting code with better parameters for the second step. However, this approach fails: we are only guaranteed correctness with probability  over the obfuscation and the inputs, which is not enough for averaging and BPP-type amplification. Nevertheless, the framework of [16] is still a convenient starting point for us.
over the obfuscation and the inputs, which is not enough for averaging and BPP-type amplification. Nevertheless, the framework of [16] is still a convenient starting point for us.
Our first challenge is to obtain every bit of the encryption of (m, i) for sufficiently many i’s. One idea is to apply an error-correcting code to the output of \(G_{m}\), so that for any index i for which \(G_{m}\) correctly outputs enough of the bits of the encryption of (m, i), we can decode successfully. While this is not possible for our regime of parameters using classical binary error-correcting codes, this is achievable with binary list-decodable codes, which output a list of possibilities upon decoding a codeword, rather than a unique decoding. Therefore, we modify the circuit \(G_{m}\) to output a list-decodable encoding of the encryption of (m, i), one bit at a time, which will be decoded at decryption time. This introduces the complication that list-decoding gives many possibilities for the encryption of (m, i) for each i. To address this, we employ a combination of NIZK proofs and commitments which enable us to uniquely decode from the decoded list. At a high level, we impose the requirement that in addition to the ciphertext of (m, i), the circuit \(G_{m}\) on input i must output a NIZK proof certifying that the ciphertext is correct. This ensures that we obtain \(\mathsf {sFE} \) encryptions of (m, i) for a noticeable fraction of the inputs i. Thus, we have replaced the BPP-type amplification of [16] with list-decodable codes, NIZK proofs, and commitment schemes.
After this change, we have that for a noticeable (but small, say 1%) fraction of the i’s, we obtain a correct encryption of (m, i). If we decrypt this with the \(\mathsf {sFE} \) secret key of [16], we would hope to obtain \((\mathsf {ECC} (C(m)))_{i}\) for enough i’s such that \(\mathsf {ECC} \) can successfully decode to C(m), but this does not quite work because we only have a very small fraction of correct encryptions. Indeed, no (binary) error-correcting code can recover from more than 50% error! To overcome this, we notice that we have additional information (thanks to the NIZK) – we know exactly for which i’s we obtained correct \(\mathsf {sFE} \) encryptions of (m, i). Therefore, we replace the error-correcting code in the [16] construction with a code that can recover from a high fraction (say 99%) of erasures. To obtain optimal parameters, this requires us to have \(\mathsf {sFE} \) output alphabet symbols rather than bits, but this does not impact the correctness of the scheme. Combining these two steps, we obtain an FE scheme with amplified correctness. As far as we know, this combination of list-decodable codes and erasure-correcting codes is novel to this work.
These techniques nearly work, with the caveat that our first step only gives us the correct encryptions of enough (m, i) when the obfuscator uses “good” random coins. Nevertheless, this can be remedied by using BPP-type amplification and leveraging the fact that our FE scheme always decrypts to \(\bot \) or to the correct output, C(m). Therefore, this results in an FE scheme which is correct for all inputs with all but negligible probability.
From correct FE to correct XiO. The only remaining step is to transform the FE back to XiO. The FE scheme we obtain from the above transformations is weakly sublinear compact, a weak notion of compactness which does not suffice for known transformations to XiO without assuming sub-exponential security. FE with weak sublinear compactness has the property that while the encryption time is proportional to the circuit size of circuits supported by the scheme, the ciphertext lengths are compact. We take advantage of this by having an obfuscation consist of many “short” encryptions, which exactly captures the requirement that the obfuscator has a long running time but a nontrivial output length.
To obfuscate a circuit C, we encrypt a circuit \(C_{x}\) for each  , where
, where  . Then, we generate a functional key
. Then, we generate a functional key  for a circuit T, which, given a circuit on n / 2 bits, outputs its truth table. The ciphertexts and functional key serve as our obfuscation, which gives the desired efficiency for XiO exactly because of the weak compactness of FE. To evaluate the obfuscation on an input
for a circuit T, which, given a circuit on n / 2 bits, outputs its truth table. The ciphertexts and functional key serve as our obfuscation, which gives the desired efficiency for XiO exactly because of the weak compactness of FE. To evaluate the obfuscation on an input  , we use FE to decrypt \(C_{x_{1}}\) with
, we use FE to decrypt \(C_{x_{1}}\) with  , and select the element of the truth table corresponding to \(x_{2}\). This transformation yields a correct and secure XiO scheme, in which for any circuit C and every input x, it holds that the obfuscation of C at the point x agrees with C(x) with all but negligible probability.
, and select the element of the truth table corresponding to \(x_{2}\). This transformation yields a correct and secure XiO scheme, in which for any circuit C and every input x, it holds that the obfuscation of C at the point x agrees with C(x) with all but negligible probability.
In the technical section, we present the full construction in a more streamlined manner. In particular, we compose the XiO to FE transformation with the FE to XiO transformation described above, which yields a transformation from approximately correct XiO to XiO that is correct on any input with all but negligible probability over the randomness of the obfuscator.
Given an XiO which is correct on any input with all but negligible probability, we can then apply another BPP-style transformation (this time we apply parallel repetitions and then take the majority vote) to get an obfuscator that for all but negligible fraction of the obfuscations the obfuscated circuit completely agrees with the input circuit. To conclude our correctness amplification, we observe that the running time for XiO allows the obfuscator to compute the truth table of the circuit it obfuscates. Therefore, we modify the obfuscator to check if an obfuscation \(\widetilde{C} \) of a circuit C is correct by running over all inputs. If \(\widetilde{C} \) agrees with C, then \(\widetilde{C} \) is used as the obfuscation, and if not, we simply output C in the clear. This takes advantage of the running time of XiO, and incurs only a negligible loss in security, thus resulting in a perfectly correct XiO.
A universal construction. An important application of correctness amplification is a universal construction. We show a universal construction for XiO (resp. SXiO) by combining our correctness amplification with the results of [1].
A universal construction for a primitive can be obtained via a robust combiner for that primitive, which is a transformation that takes several candidate constructions of the primitive and outputs one construction that is as good as any of the input constructions. It is robust in the sense that it should work even if some of the candidates have weak correctness guarantees, have bad running times, etc. A universal construction is then acquired by enumerating over all possible candidates while making sure not to be “fooled” by bad faulty candidates so that we end up with a correct candidate. Thus, it is guaranteed that the resulting candidate is correct and secure.
We observe that a combiner (i.e., a secure candidate assuming one exists) for XiO (resp. SXiO) can be obtained by adapting the construction for iO of Ananth et al. [1] which further relied on LWE. In the case of iO, their construction, on input circuit C, obfuscates a variant of C that has the same input domain as C. In the security proof, they go “input-by-input” over this obfuscated circuit which results in a sub-exponential security loss. We notice that, in the case of XiO (resp. SXiO), the number of inputs in the above obfuscated circuit is at most logarithmic, so the very same proof can be carried out, losing only a polynomial term. Then, to make the combiner robust we use our correctness amplification procedure. This results in a universal construction of perfect XiO (resp. imperfect SXiO), assuming the existence of XiO (resp. SXiO) with very weak correctness.
2.2 Impossibility of Key-Agreement
To illustrate the difference between the power of compressing obfuscation and iO, we revisit one of the primary applications of iO—transforming a private-key scheme into a public-key one. In the context of iO, this transformation is performed by obfuscating the encryption circuit of a private-key encryption scheme, while embedding the symmetric secret key into the circuit. The public key is then simply the obfuscated circuit. In order to encrypt a message m, one has to choose randomness r and run the obfuscated circuit on (m, r) to obtain the ciphertext c. An important property of this construction is the ability to obfuscate circuits with “hardwired cryptography”, e.g., the evaluation circuit of a pseudorandom function with a hardwired PRF key.
Since XiO is efficient only when obfuscating circuits with logarithmic size input, one cannot use the above approach with XiO even when the message space is limited to a single bit. Given the public key, the adversary can learn the entire truth table of the obfuscated circuit by enumerating over all inputs, thereby breaking the secrecy of the underlying message. Our proof formalizes this intuition, and shows that other attempts to make such a transformation cannot succeed. We formalize this using a black-box separation, showing that no perfectly complete bit-agreement protocol can be constructed from perfectly correct XiO and one-way functions.
Modeling non-black-box constructions. Constructions that are based on indistinguishability obfuscation are almost always non-black-box in the underlying primitives. In the example above, the circuit being obfuscated is the encryption algorithm of a private-key encryption scheme and thus contains a specific circuit representation of the underlying one-way function as a sub-circuit. We follow the framework of Asharov and Segev [9, 10] that captures such constructions by enabling the obfuscator to run on oracle-aided circuits, i.e., circuits that might contain oracle gates. We refer to [9, 10] for details regarding this model (see also [15]), and for examples of how it capture common techniques such as the punctured programming technique of Sahai and Waters [70] and its variants.
The oracle. Our result is obtained by presenting an oracle \(\varGamma \) relative to which the following properties hold: (1) there exists a one-way function f; (2) there exists a perfectly-correct, exponentially-secure XiO scheme for all oracle-aided circuits \(C^f\); (3) for any perfectly complete bit-agreement protocol between two parties, there exists an eavesdropping adversary that makes polynomially many queries to the oracle \(\varGamma \) and succeeds to recover the bit from the transcript of the interaction. Our oracle consists of three functions, similar to that of [10]: (1) a random function f that will serve as the one-way function; (2) a random length-increasing function \(\mathcal {O} \) that will serve as the obfuscator (an obfuscation of an oracle-aided circuit C is a “handle” \(\widehat{C} =\mathcal {O} (C,r)\) for a random string r), and (3) a function \(\mathcal {E} \) that enables evaluations of obfuscated circuits: given some obfuscated circuit \(\widehat{C} \) and an input x, the function \(\mathcal {E} \) looks for the lexicographically first pair (C, r) for which \(\mathcal {O} (C,r)=\widehat{C} \) and returns \(C^{f}(x)\).
The main difference between our oracle and the oracle of [10] is the expansion factor of the oracle \(\mathcal {O} \). In order to capture compressing obfuscation, the expansion factor that we use is (sub-)exponential in the input size of the circuit C. While this modification is somewhat minor in syntax, it has a major effect – if the expansion factor is “small” then it is possible to construct a polynomial time key-agreement protocol relative to such an oracle (following the construction of Sahai and Waters [70]), whereas for a larger expansion factor this becomes impossible. As for the existence of one-way functions and indistinguishability of obfuscated circuits, we derive these almost for free from [10].
In what follows, we first discuss how to break a perfectly complete key-agreement protocol relative to a random oracle as a warmup. We then discuss the challenges when dealing with our (more structured) oracle, and discuss why our approach does not work for iO.
Separating key-agreement from a random oracle. As a warmup, we first present an overview of the result of Impagliazzo and Rudich [51] and Brakerski et al. [26], who show that for any two polynomial time oracle-aided algorithms \(\mathcal {A} \) and \(\mathcal {B} \), if \(\langle \mathcal {A} ^f,\mathcal {B} ^f\rangle \) implements a perfectly-correct bit-agreement protocol for all functions f, then there exists an oracle-aided algorithm E such that for any function f learns the agreed bit with probability 1 by making only a polynomial number of oracle queries to f. The adversary E is given a transcript T which is a result of an interaction of \(\mathcal {A} \) and \(\mathcal {B} \) relative to some oracle f, and is required to find the key \(k^\star \) that \(\mathcal {A} \) and \(\mathcal {B} \) agreed on. Denote by \(r_\mathcal {A} ^\star \) (resp. \(r_\mathcal {B} ^\star \)) the randomness used by \(\mathcal {A} \) (resp. \(\mathcal {B} \)) in the real interaction that produced T. The adversary E initializes a set of queries/answers Q, which will contain the actual queries made by E to the true oracle f. It also initializes a multiset \(K=\emptyset \), and repeats the following polynomially many times:
-
Simulation: E simulates an oracle \(f'\) that is consistent with Q (i.e., \(f'(w)=f(w)\) for every \(w \in Q)\), and randomness \(r'_\mathcal {A},r_\mathcal {B} '\) such that the interaction \(\langle \mathcal {A} ^{f'}(r'_\mathcal {A}),\mathcal {B} ^{f'}(r'_\mathcal {B})\rangle \) (i.e., running the protocol with respect to the function \(f'\) with randomness \(r'_\mathcal {A} \) for \(\mathcal {A} \) and \(r'_\mathcal {B} \) for \(\mathcal {B} \)) results in the transcript T and key \(k'\). E adds \(k'\) to K.
-
Update: E asks f for all queries in \(f'\) that are not in Q, and updates the set Q.
At the end of the attack, E outputs the majority value in K. The proof then relies on the following observation: In each iteration, either (1) in the update phase, E finds at least one new query that is also made by either \(\mathcal {A} \) or \(\mathcal {B} \) during the real interaction with the function f that produced the transcript T; or (2) E adds the real key \(k^\star \) to K.
Intuitively, if (1) does not hold, then the perfect correctness of the bit-agreement protocol guarantees that (2) holds. In particular, in that case it is possible to construct a “hybrid” oracle \(\widetilde{f} \) that behaves like f in the real execution of \(\mathcal {A} \), i.e., \(\mathcal {A} ^{f}(r_\mathcal {A} ^\star )\), and behaves like \(f'\) in the simulated evaluation of \(\mathcal {B} \), i.e., \(\mathcal {B} ^{f'}(r_\mathcal {B} ')\). According to this hybrid oracle, an execution of \(\mathcal {A} \) with randomness \(r_\mathcal {A} ^\star \) and an execution of \(\mathcal {B} \) with randomness \(r_\mathcal {B} '\) would result in the transcript T, \(\mathcal {A} \) would output \(k^\star \) (as in the real execution) and \(\mathcal {B} \) would output \(k'\) (as in the simulation). Perfect correctness then tells us that \(k^\star =k'\). This hybrid oracle can be constructed since the simulated execution and the real execution have no intersection queries in addition to the queries which are already in Q, and therefore there are no contradicting queries (i.e., queries w that appear in both executions for which \(f(w) \ne f'(w)\)). As the number of oracle queries \(\mathcal {A} \) and \(\mathcal {B} \) make during the execution of the protocol is some polynomial q, the majority value in K is guaranteed to be the correct key after \(2q+1\) iterations.
Attacking key-agreement relative to our oracle. We extend the attack described above relative to our oracle \(\varGamma \), which is a significantly more structured than a random oracle and therefore raises several challenges. Recall that our oracle \(\varGamma \) consists of a three functions f, \(\mathcal {O} \), and \(\mathcal {E} \), that are dependent. Following the above template, we construct an adversary that simulates an execution that produces the transcript T with some simulated oracle \(\varGamma '=(f',\mathcal {O} ',\mathcal {E} ')\). There are two main challenges with this approach. The first is to show that \(\mathcal {A} \) and \(\mathcal {B} \) cannot gain “extra” information from oracle queries that are not in the intersection of their query sets. In particular, in the case of a random oracle, the shared information between \(\mathcal {A} \) and \(\mathcal {B} \) can be recovered completely from their shared oracle queries and the transcript T. In our setting, since the oracles f, \(\mathcal {O} \), and \(\mathcal {E} \) have dependence, this may not be the case.
The second challenge is to show that a hybrid oracle \(\widetilde{\varGamma } =(\widetilde{f},\widetilde{\mathcal {O}},\widetilde{\mathcal {E}})\) can be constructed from the two sets of queries, i.e., from the simulated execution and the real execution.
As an example, suppose there is a query \(\mathcal {E} (\widehat{C},x)\) that is performed in the real execution and a different query \(\mathcal {E} '(\widehat{C},y)\) that appears in the simulated execution. Such two queries raise a challenge for constructing a hybrid oracle \(\widetilde{\mathcal {E}} \) which is consistent with these two queries simultaneously. In order to see this, suppose that in the real execution, the lexicographically first pair (C, r) for which \(\mathcal {O} (C,r)=\widehat{C} \) is some pair \((C_1,r_1)\), and in the simulated execution the lexicographically first pair (C, r) for which \(\mathcal {O} '(C,r)=\widehat{C} \) is some pair \((C_2,r_2)\ne (C_1,r_1)\). As a result, \(\mathcal {E} (\widehat{C},x)\) in the real execution is mapped to \(C_1^{f}(x)\), whereas \(\mathcal {E} '(\widehat{C},y)\) is mapped to \(C_2^{f'}(y)\), but \(C_1 \ne C_2\).
We solve the first challenge by adding additional oracle queries to the set of real queries that the parties make, which makes the dependence between the oracles more explicit. As for the second challenge, interestingly, our proof does not completely solve it, and we do not fully control to which one of the two circuits \(C_1\) or \(C_2\) the hybrid oracle \(\widetilde{\mathcal {E}} \) maps \(\widehat{C} \). Nevertheless, we design the adversary such that, whenever there is such a contradicting scenario between the real execution and the simulated execution, it must hold that \(C_1\) and \(C_2\) are functionally equivalent with respect to the hybrid oracle \(\widetilde{\varGamma } \). Otherwise, i.e., when there is some input for which \(C_1\) and \(C_2\) do not agree, we claim that the adversary learns a new query that is associated with the real execution. As a consequence, E learns the entire truth table of any obfuscated circuit \(\widehat{C} \) that is associated in the real execution, which is possible due to the fact that querying the oracle \(\varGamma \) on all inputs of \(\widehat{C} \) results in polynomially many queries. Notably, for a different expansion factor of the oracle \(\mathcal {O} \) (which results in iO and not XiO), this becomes an exponential number of queries, and the above attack fails.
2.3 Statistically Secure Compressing Obfuscation
This set of results is composed of two main parts. One is positive results showing that for small classes of circuits compressing obfuscation exists unconditionally. The other complements the constructions and shows that improvements in the above obfuscator, either in the compression factor or in the circuit class, will imply some nontrivial speedup for protocols solving SAT or UNSAT. We have positive and negative results both for the case of perfect correctness and for the case of approximate correctness.
Negative results. First, we show that approximately correct and statistically secure \(2^{n^\epsilon }\)-SXiO cannot exist unless \(\mathsf {coNP}\subseteq \mathsf {AM}[2^{n^\epsilon }]\) for \(\epsilon >0\). Here, we follow on the approach of [24] from the world of iO. There, they show how to use iO and puncturable PRFs to create two circuits that differ at a single point but their obfuscations (as random variables) are statistically far. Then, they use an algorithm that can distinguish these two distributions to solve Unique-SAT which then implies that \(\mathsf {coNP}\subseteq \mathsf {AM}\) by a result of Mahmoody and Xiao [64]. We modify the argument to work with compressing obfuscation by making the two circuits receive only short inputs, and observe that the proof still goes through, but then solving Unique-SAT on short inputs (say of poly-logarithmic size). We then apply the result of Mahmoody and Xiao and finally obtain our result by scaling the parameters.
Second, we show that perfectly correct and statistically secure \(2^{n(1-\epsilon )}\)-SXiO cannot exist unless \(\mathsf {coNP}\subseteq \mathsf {AM}[2^{(1-\epsilon )n}]\) (with large enough \(0<\epsilon <1\)). For this, we construct an \(\mathsf {SZK}[2^{(1-\epsilon )n}]\) protocol for all \(\mathsf {NP}\). In this protocol, the verifier, given \(x\in L\) for a language L, chooses a bit b uniformly at random and obfuscates a circuit that gets a witness w as input, checks whether it is a valid witness for x and if so, it outputs b (otherwise it outputs \(\bot \)). This protocol can be shown to be honest-verifier statistical zero-knowledge with a verifier that runs in time \(2^{(1-\epsilon )n}\) for L. This argument is reminiscent to the argument of [47, 53] in the context of iO. We then carefully apply the transformation of Okamoto [67] to translate this protocol into an (honest-verifier) SZK protocol for every language in \(\mathsf {coNP}\). This implies that \(\mathsf {coNP}\subseteq \mathsf {AM}[2^{(1-\epsilon )n}]\).
Positive results. We show that compressing obfuscators exists unconditionally for restricted classes of circuits such as \(\mathsf {AC}^{0}\) (the class of all constant-depth circuits) and \(\textsf {Mon}\) (the class of all monotone functions). We again construct compressing obfuscators with perfect correctness and approximate correctness. The approximately correct obfuscators are obtained by running a classical (PAC) learning algorithm [71] on the given circuit and outputting the hypothesis. Using the most efficient learning algorithms for \(\mathsf {AC}^{0}\) and \(\textsf {Mon}\), we obtain compressing obfuscators for these classes. This construction is aligned with the above impossibility that says that we are unlikely to be able to get such an obfuscator for classes that contain a (puncturable) PRF.
In the perfect correctness case, we use a different tool called a circuit compression algorithm [31]. In circuit compression one is given the truth table of a Boolean function f computable by some unknown circuit from a known class of circuits, and the goal is to find in time \(\mathsf {poly}(2^n)\) a circuit C (not necessarily from the aforementioned family) computing f so that the size of C is less than the trivial circuit size \(\approx \!\!2^n\). We apply such an algorithm on circuits in \(\mathsf {AC}^{0}\) and get an obfuscator with small compression.
3 Correctness Amplification
In this section, we present a correctness amplification procedure for XiO. We show that assuming the existence of an XiO scheme with very weak correctness, there exists an XiO construction with a very strong correctness guarantee.
Theorem 3.1
Let \(p(\cdot )\) be any polynomial. Let \(\mathsf {xi}\mathcal {O} \) be an XiO scheme for \(\mathsf {P}^{\log } \) that is  -approximately correct. Assuming LWE and the existence of NIZKs, there exists a perfectly correct XiO scheme for \(\mathsf {P}^{\log } \).
-approximately correct. Assuming LWE and the existence of NIZKs, there exists a perfectly correct XiO scheme for \(\mathsf {P}^{\log } \).
The correctness amplification proceeds in three phases. First, we transform an approximately-correct XiO scheme to a  -worst-case correct XiO scheme. Then, we transform the resulting scheme to a
-worst-case correct XiO scheme. Then, we transform the resulting scheme to a  -worst-case correct XiO scheme. Then, we transform the resulting scheme to a perfectly correct XiO scheme.
-worst-case correct XiO scheme. Then, we transform the resulting scheme to a perfectly correct XiO scheme.
The main technical contribution of this section is the first step, transforming an approximately-correct XiO scheme to a  -worst-case correct XiO scheme. Therefore, in Sect. 3.1, we present the construction for this step. The full proof of Theorem 3.1 appears in the full version.
-worst-case correct XiO scheme. Therefore, in Sect. 3.1, we present the construction for this step. The full proof of Theorem 3.1 appears in the full version.
3.1 From Approximately-Correct XiO to Worst-Case Correct XiO
Fix any class of circuits \(\mathcal {C} ^{s,n} \in \mathsf {P}^{\log } \). Throughout this section, we let  and
and  . Our transformation relies on the following primitives as building blocks:
. Our transformation relies on the following primitives as building blocks:
-
 is a \((1/2 + \gamma )\)-approximately correct XiO scheme for \(\mathsf {P}^{\log }\), where
is a \((1/2 + \gamma )\)-approximately correct XiO scheme for \(\mathsf {P}^{\log }\), where  for some polynomial p.
for some polynomial p. -
\(\mathsf {ECC} \) is a Reed-Solomon
 erasure correcting code that can correct up to a \((1 - \frac{\gamma }{8})\)-fraction of erasures using the algorithm
erasure correcting code that can correct up to a \((1 - \frac{\gamma }{8})\)-fraction of erasures using the algorithm 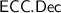 , where
, where  is a polynomial of degree \(d-1\) in its input length. We assume that all inputs to
is a polynomial of degree \(d-1\) in its input length. We assume that all inputs to  are padded to size \(2^{\frac{n}{d}}\) bits. We let
are padded to size \(2^{\frac{n}{d}}\) bits. We let 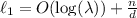 be the length of the output of \(\mathsf {ECC} \).
be the length of the output of \(\mathsf {ECC} \). -
 is a binary error-correcting code that is \((\frac{1}{2}-\frac{\gamma }{4},\mathsf {poly})\)-list decodable using the algorithm
is a binary error-correcting code that is \((\frac{1}{2}-\frac{\gamma }{4},\mathsf {poly})\)-list decodable using the algorithm  . We let
. We let  be the output length of
be the output length of  when run on inputs of size
when run on inputs of size  .
. -
 is a
is a  -output succinct FE scheme for the class \(\mathcal {C} ^{s',n'} \in \mathsf {P} \) where
-output succinct FE scheme for the class \(\mathcal {C} ^{s',n'} \in \mathsf {P} \) where 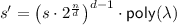 and
and  .
. -
 is a puncturable PRF.
is a puncturable PRF. -
\(\mathsf {C} = (\mathsf {C}.\mathsf {Commit}, \mathsf {C}.\mathsf {Open})\) is a commitment scheme.
-
 is a Multi-NIZK proof system for the NP language L given by
is a Multi-NIZK proof system for the NP language L given by 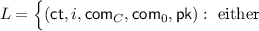
-
1.
\(\exists r_{0}, r_{1},C\) such that
 encrypts (C, i) and \(\mathsf {com} _{C}\) is a commitment to C, that is,
encrypts (C, i) and \(\mathsf {com} _{C}\) is a commitment to C, that is,  , or
, or -
2.
\(\exists r \text { s.t. } \mathsf {com} _{0} = \mathsf {C}.\mathsf {Commit} (1,r) \Big \rbrace \),
We let
 denote the upper bound on the length of statements and witnesses in L when instantiated with security parameter
denote the upper bound on the length of statements and witnesses in L when instantiated with security parameter  (with parameters as used in the following scheme).
(with parameters as used in the following scheme). -
1.
In what follows, we denote by \(C_{x_{1}\cdots x_{k}}\) the circuit C with the first k bits hardwired to \(x_{1} \cdots x_{k}\). We let \(T \) denote a circuit in \(\mathcal {C} ^{s \cdot 2^{\frac{n}{d}}, s}\) that receives as input a circuit and outputs its truth table. The transformation is as follows.
Worst-case correct XiO scheme \(\varvec{\mathsf {xi}\mathcal {O} '}\) :
-
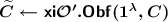 :
:-
1.
Sample
 .
. -
2.
Generate a key
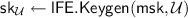 for the circuit
for the circuit  such that
such that 
for any input circuit D, where \(\mathsf {ECC} (T (D))[i]\) denotes the ith block of length
 of \(\mathsf {ECC} (T (D))\).
of \(\mathsf {ECC} (T (D))\). -
3.
For every
 :
:-
(a)
Sample
 , and
, and  .
. -
(b)
Create commitments \(\mathsf {com} _{C_{x}}^{x} = \mathsf {C}.\mathsf {Commit} (C_{x},r_{0}^{x})\) to \(C_{x}\) and \(\mathsf {com} _{0}^{x} = \mathsf {C}.\mathsf {Commit} (0,r_{1}^{x})\) to 0 using randomness
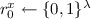 and
and  .
. -
(c)
Generate the circuit
 such that on input (i, j) does the following:
such that on input (i, j) does the following:-
i.
Let
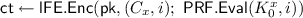 .
. -
ii.
Construct a NIZK proof
 for the statement
for the statement  using the witness
using the witness  .
. -
iii.
Output the jth bit of
 , denoted by
, denoted by  .
.
-
i.
-
(d)
Let
 and let \(\widetilde{C} ^{x} = (\widetilde{G} ^{x}, \sigma ^{x}, \mathsf {com} _{C_{x}}^{x}, \mathsf {com} _{0}^{x})\).
and let \(\widetilde{C} ^{x} = (\widetilde{G} ^{x}, \sigma ^{x}, \mathsf {com} _{C_{x}}^{x}, \mathsf {com} _{0}^{x})\).
-
(a)
-
4.
Output
 .
.
-
1.
-
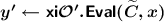 :
:-
1.
Let \(x = x_{1} || x_{2}\) where \(|x_{1} | = n - \frac{n}{d}\).
-
2.
For every \(i \in [2^{\ell _{1}}]\):
-
(a)
For every \(j \in [2^{\ell _{2}}]\), let
 .
. -
(b)
Run
 to obtain a list of possible decodings, where the kth element of the list is
to obtain a list of possible decodings, where the kth element of the list is 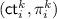 .
. -
(c)
Let \(k^{\star }\) be the first index k such that
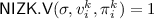 where
where  . Set
. Set  if \(k^{\star }\) exists and otherwise set
if \(k^{\star }\) exists and otherwise set  .
. -
(d)
Run
 .
.
-
(a)
-
3.
If there are at least \(\frac{\gamma }{8} \cdot 2^{\ell _{1}}\) indices i for which
 and run
and run  and output the element corresponding to \(x_{2}\). Otherwise, output \(\bot \).
and output the element corresponding to \(x_{2}\). Otherwise, output \(\bot \).
-
1.
Theorem 3.2
Assume that  is a puncturable PRF, \(\mathsf {lFE} \) is a selectively-secure
is a puncturable PRF, \(\mathsf {lFE} \) is a selectively-secure  -output succinct FE scheme for \(C^{s',n'}\), \(\mathsf {C} \) is a commitment scheme, and
-output succinct FE scheme for \(C^{s',n'}\), \(\mathsf {C} \) is a commitment scheme, and  is a Multi-NIZK for L. Fix any class of circuits \(\mathcal {C} ^{s,n} \in \mathsf {P}^{\log } \). Let \(p(\cdot )\) be any polynomial. Then, if \(\mathsf {xi}\mathcal {O} \) is a
is a Multi-NIZK for L. Fix any class of circuits \(\mathcal {C} ^{s,n} \in \mathsf {P}^{\log } \). Let \(p(\cdot )\) be any polynomial. Then, if \(\mathsf {xi}\mathcal {O} \) is a  -approximately-correct XiO scheme for \(\mathsf {P}^{\log } \), then \(\mathsf {xi}\mathcal {O} '\) is a
-approximately-correct XiO scheme for \(\mathsf {P}^{\log } \), then \(\mathsf {xi}\mathcal {O} '\) is a  -worst-case correct XiO scheme for \(\mathcal {C} ^{s,n}\), for a negligible function
-worst-case correct XiO scheme for \(\mathcal {C} ^{s,n}\), for a negligible function  .
.
The proof of this theorem appears in the full version.
4 On Key-Agreement from XIO and OWFs
In this section, we show a separation from compressing obfuscation and one-way functions to key-agreement. This separation is largely based on [9, 10], and in particular follows the framework of black-box separations presented in [51].
We refer to the full version for important preliminaries, including the class of reductions that our proof captures. Throughout this section, for ease of notation, we denote both the security parameter and the size of circuits by s. While these could be distinguished, it is natural to combine them in this way, as everything can be thought of as a function of the circuit size in question. Hereafter, we say that an oracle-aided algorithm \(M(1^{s})\) with oracle access to \(\varGamma \) is a q-query algorithm if for every \(s \in \mathbb {N} \), the algorithm \(M(1^{s})\) makes at most \(q(s)\) queries, and each of its queries have size at most \(q(s)\).
We show the separation by presenting a distribution over oracles \(\varGamma \) relative to which the following properties hold: (1) there does not exist a perfectly correct key-agreement protocol, (2) there exists an (exponentially) secure one-way function, and (3) there exists an (exponentially) secure XiO.
Let \(\ell \) be a 2-ary function with \(\ell (s,n) > s\). The distribution \(\mathfrak {S} _{\ell }\) over oracles \(\varGamma = (f, \mathcal {O}, \mathcal {E})\) is defined as follows:
-
The function \(\varvec{f = \{f_{s}\}_{s \in \mathbb {N}}}\). For every \(s \in \mathbb {N} \), the function
 is a uniformly chosen function. We will use f to implement a one-way function.
is a uniformly chosen function. We will use f to implement a one-way function. -
The function \(\varvec{\mathcal {O} = \{\mathcal {O} _{s,n}\}_{s,n \in \mathbb {N}}}\). For every \(s,n \in \mathbb {N} \), the function
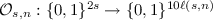 is a uniformly chosen function. Intuitively, \(\mathcal {O} _{s,n}\) will receive a description of a circuit with size s and input length n, as well as a string of length s (which represents the randomness of the obfuscator), and will increase this to a uniformly chosen string of length \(10 \ell (s,n)\). This will be used to implement the obfuscator for \(\mathsf {xi}\mathcal {O} \). Note that \(\ell (s,n) > s\), and therefore the output of \(\mathcal {O} _{s,n}\) is at least 10sn.
is a uniformly chosen function. Intuitively, \(\mathcal {O} _{s,n}\) will receive a description of a circuit with size s and input length n, as well as a string of length s (which represents the randomness of the obfuscator), and will increase this to a uniformly chosen string of length \(10 \ell (s,n)\). This will be used to implement the obfuscator for \(\mathsf {xi}\mathcal {O} \). Note that \(\ell (s,n) > s\), and therefore the output of \(\mathcal {O} _{s,n}\) is at least 10sn. -
The function \(\varvec{\mathcal {E} ^{f,\mathcal {O}} = \{\mathcal {E} _{s,n}^{f,\mathcal {O}}\}_{s \in \mathbb {N}, n \in \mathbb {N}}}\). For every \(s,n \in \mathbb {N} \), the function
 is defined as follows. On input
is defined as follows. On input 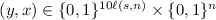 , the function \(\mathcal {E} _{s,n}^{f,\mathcal {O}}\) finds the lexicographically first oracle-aided circuit C of size s and input size n, and a string
, the function \(\mathcal {E} _{s,n}^{f,\mathcal {O}}\) finds the lexicographically first oracle-aided circuit C of size s and input size n, and a string 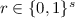 such that \(\mathcal {O} _{s,n}(C,r) = y\), and outputs \(C^f(x)\). If no such (C, r) exists, it outputs \(\bot \). Looking ahead, the oracle \(\mathcal {E} ^{f,\mathcal {O}}\) will be used to implement the evaluator for \(\mathsf {xi}\mathcal {O} \).
such that \(\mathcal {O} _{s,n}(C,r) = y\), and outputs \(C^f(x)\). If no such (C, r) exists, it outputs \(\bot \). Looking ahead, the oracle \(\mathcal {E} ^{f,\mathcal {O}}\) will be used to implement the evaluator for \(\mathsf {xi}\mathcal {O} \).
When \(\ell (s,n) = 2^{n(1-\epsilon )} \cdot \mathsf {poly}(s)\) for a constant \(\epsilon > 0\) and a polynomial \(\mathsf {poly}\), relative to this oracle there exists a one-way function f and perfectly correct XiO scheme. The construction of XiO is natural: Given some circuit C of size s and input length n, the obfuscator chooses a random  and evaluates \(\widehat{C} =\mathcal {O} _{s,n}(C,r)\). Then, it checks that the resulting handle \(\widehat{C} \) agrees with the input circuit C: it runs over all inputs
and evaluates \(\widehat{C} =\mathcal {O} _{s,n}(C,r)\). Then, it checks that the resulting handle \(\widehat{C} \) agrees with the input circuit C: it runs over all inputs  and checks that \(\mathcal {E} _{s,n}(\widehat{C},x)=C^f(x)\). If this holds for every input, it outputs \((0,\widehat{C})\). Otherwise, it outputs (1, C). The evaluator on input circuit \((0,\widehat{C})\) and input x returns \(\mathcal {E} _{s,n}(\widehat{C},x)=C^f(x)\), whereas on input circuit (1, C) and input x evaluates \(C^f(x)\).Footnote 5 The following holds, and is discussed in the full version:
and checks that \(\mathcal {E} _{s,n}(\widehat{C},x)=C^f(x)\). If this holds for every input, it outputs \((0,\widehat{C})\). Otherwise, it outputs (1, C). The evaluator on input circuit \((0,\widehat{C})\) and input x returns \(\mathcal {E} _{s,n}(\widehat{C},x)=C^f(x)\), whereas on input circuit (1, C) and input x evaluates \(C^f(x)\).Footnote 5 The following holds, and is discussed in the full version:
Theorem 4.1
Let \(\ell (s,n) = 2^{n\epsilon } \cdot \mathsf {poly}(s)\) for some constant \(0 \le \epsilon < 1\) and polynomial \(\mathsf {poly}\) and let \(\varGamma \leftarrow \mathfrak {S} _{\ell }\) with \(\varGamma = (f,\mathcal {O},\mathcal {E})\). Then, for any oracle-aided q-query algorithm \(\mathcal {A} \) with \(q(s) < 2^{s/4}\), it holds that

Moreover, for any class of circuits \(\mathcal {C} \) with f-gates, there exists an XiO scheme \(\mathsf {xi}\mathcal {O} \) relative to \(\varGamma \) for the circuit class \(\mathcal {C} \) such that

for any q-query distinguisher \(\mathcal {D} \) that makes at most \(q(s) < 2^{s/4}\) queries.Footnote 6
The main technical difficulty is showing that there is no key-agreement protocol relative to \(\varGamma \).
Theorem 4.2
Let \(\ell (s,n) = 2^{n\epsilon } \cdot \mathsf {poly}(s)\) for a constant \(0 \le \epsilon <1\) and a polynomial \(\mathsf {poly}\). Then, for any perfectly correct oracle-aided bit agreement protocol \(\langle \mathcal {A} (1^{s}), \mathcal {B} (1^{s})\rangle \) in which \(\mathcal {A} \) and \(\mathcal {B} \) run in time at most q(s), there exists an oracle-aided adversary E that makes \(q(s)^{O(1)+1/\epsilon }\) oracle queries such that

where the probability is over \(\varGamma \leftarrow \mathfrak {S} _{\ell }\), and the randomness of \(\mathcal {A} \), \(\mathcal {B} \), and E.Footnote 7 Moreover, the algorithm E can be implemented in polynomial time given access to a PSPACE-complete oracle.
The full proof of this theorem appears in the full version. Here, we give a high level overview. We start by defining some notation.
Notation. Let \(Q_{\mathcal {A}}\), \(Q_{\mathcal {B}}\), and \(Q_{E}\) denote the set of oracle queries made by \(\mathcal {A} \), \(\mathcal {B} \), and E, respectively. Let \([O(x) = y] \in Q_{p}\) denote that a party p queried an oracle O on x and received y. For example, to denote that \(\mathcal {A} \) queried \(\mathcal {O} \) on C and received \(\widetilde{C} \), we write \([\mathcal {O} (C) = \widetilde{C} ] \in Q_{\mathcal {A}}\). Let \(Q_{\mathcal {A} \mathcal {B}} = Q_{\mathcal {A}} \cup Q_{\mathcal {B}}\) be the set of oracle queries in the real protocol.
For a PPT oracle-aided key-agreement protocol \(\langle \mathcal {A} ^{\varGamma }(1^{s}),\mathcal {B} ^{\varGamma }(1^{s})\rangle \), we let \(q=q(s)\) denote an upper bound on the running time of \(\mathcal {A} \) and \(\mathcal {B} \) for any oracle \(\varGamma \). Since \(\mathcal {A} \) and \(\mathcal {B} \) are run in time at most q, this also bounds the space that the algorithms consume and their number of oracle queries. As a result, all \(\mathcal {O} _{s,n}\) and \(\mathcal {E} _{s,n}\) queries satisfy \(s \le q\) and \(2^{\epsilon n} \cdot \mathsf {poly}(s) \le q\). This implies that \(n \le \frac{1}{\epsilon }\log q\). We will use this bound on n to show that \(\mathcal {A} \) and \(\mathcal {B} \) can only query \(\mathcal {O} \) on circuits with logarithmic size input, and thus the adversary can learn the truth table of any circuit queried this way by only making a polynomial number of queries.
We now define an extended set of queries for any query/answer set Q. Intuitively, this captures queries that are “known” to an algorithm that makes the queries in Q. For example, suppose an algorithm M queries \(\mathcal {O} _{s,n}\) on some (C, r) and obtains \(\widetilde{C} \), and queries f on all queries in the evaluation of \(C^{f}(x)\). Then, intuitively M knows that \(\mathcal {E} _{s,n}(\widetilde{C},x) = C^{f}(x)\) (up to the probability of \(\mathcal {O} \) being injective), even without making any \(\mathcal {E} \) query. The following definition captures this dependence between the oracles, and will be helpful in our separation.
Definition 4.3
Given a set of queries Q and an oracle \(\varGamma \), the augmented set of queries \(\mathsf {Aug} (Q)\) with respect to \(\varGamma \) is defined as follows:
-
1.
Every query and answer in Q is also in \(\mathsf {Aug} (Q)\).
-
2.
For every query \([\mathcal {O} _{s,n}(C,r) = \widetilde{C} ] \in \mathsf {Aug} (Q)\), the set \(\mathsf {Aug} (Q)\) contains queries
 for all
for all  .
. -
3.
For every query \([\mathcal {E} _{s,n}(\widetilde{C},x) = y] \in \mathsf {Aug} (Q)\) with \(y \ne \bot \), the set \(\mathsf {Aug} (Q)\) contains the query \(\mathcal {O} _{s,n}(C,r) = \widetilde{C} \), and all f-queries made in the evaluation of \(C^f(x)=y\). where (C, r) is the lexicographically first pre-image of \(\widetilde{C} \) under \(\mathcal {O} _{s,n}\).
For a given set Q with \(|Q| <q\), we bound the size of the set \(|\mathsf {Aug} (Q)|\), and recall that this implies that \(s < q\) and \(n < \frac{1}{\epsilon }\log q\). For every query to \(\mathcal {O} _{s,n}\) in Q, there are at most \(2^{n}\) corresponding \(\mathcal {E} _{s,n}\) queries in \(\mathsf {Aug} (Q)\), each implies at most s queries to f in \(\mathsf {Aug} (Q)\). Likewise for any \(\mathcal {E} _{s,n}\) query in Q might imply at most \(2^n \cdot s\) queries in \(\mathsf {Aug} (Q)\). Therefore, we have
We are now ready to define the adversary E.
The adversary E .
-
Input: A transcript T of an execution \(\langle \mathcal {A} ^{\varGamma }(1^{s}; r_{A}^{\star }), \mathcal {B} ^{\varGamma }(1^{s}; r_{B}^{\star }) \rangle \).
-
Oracle Access: \(\varGamma = (f, \mathcal {O}, \mathcal {E})\).
-
Algorithm:
-
1.
Initialize \(Q_{E} = \emptyset \) and \(K = \emptyset \).
-
2.
Repeat the following \(2q+1\) times:
-
(a)
Simulation phase: Find a valid oracle \(\varGamma ' = (f', \mathcal {O} ', \mathcal {E} ')\) and random strings \(r_{A}',r_{B}'\) such that the following holds:
-
i.
Every query in \(Q_{E}\) is answered the same way in \(\varGamma '\) as in \(Q_{E}\).
-
ii.
\(\mathcal {O} '_{s,n}\) is injective for all \(s,n \in \mathbb {N} \).
-
iii.
The transcript \(T'\) outputted by \(\langle \mathcal {A} ^{\varGamma '}(1^{s}; r_{A}'), \mathcal {B} ^{\varGamma '}(1^{s}, r_{B}') \rangle \) is the same as T.
Abort if no such \(\varGamma ', r_{A}', r_{B}'\) exist. Let \(k_{A}'\) be the key outputted by \(\mathcal {A} \) in this simulation, and add \(k_{A}'\) to K.
-
i.
-
(b)
Update phase: Let \(Q_{\mathsf {Sim}}\) be the queries made by \(\mathcal {A} \) and \(\mathcal {B} \) in the execution \(\langle \mathcal {A} ^{\varGamma '}(1^{s}; r_{A}'), \mathcal {B} ^{\varGamma '}(1^{s}, r_{B}') \rangle \), and consider the set \(\mathsf {Aug} (Q_{\text {Sim}}) \) with respect to \(\varGamma '\). Query \(\varGamma \) with all queries in \(\mathsf {Aug} (Q_{\text {Sim}}) \setminus Q_{E}\) and update \(Q_{E}\) with these queries.
-
(a)
-
1.
-
Output: The majority key k in K.
Observe that in each iteration, \(|Q_\mathsf {Sim} |<q\) and E makes at most \(|\mathsf {Aug} (Q_{\text {Sim}}) |\) queries to \(\varGamma \). Therefore, the total number of queries that E makes is bounded by \((2q+1) \cdot q^2\cdot q^{1/\epsilon } \in q^{O(1)+1/\epsilon }\).
To complete the proof of Theorem 4.2, the main technical difficulty is in showing that the adversary E always succeeds to find the key computed in the real key agreement protocol, assuming that \(\mathcal {O} \) is an injective function. We denote this event by \(\mathsf {injective} ^{\varGamma ,\ell }\) and in the full version, we show that the probability that \(\lnot \mathsf {injective} ^{\varGamma ,\ell }\) occurs is bounded by \(2^{-4}\). We then show the following lemma.
Lemma 4.4
Let \(k^\star \) denote the key computed by \(\mathcal {A}\) and \(\mathcal {B}\) in the real execution of the protocol. If \(\mathsf {injective} ^{\varGamma ,\ell }\) holds, then E does not abort, and in each iteration either (1) E adds a query in \(\mathsf {Aug} (Q_{\mathcal {A} \mathcal {B}}) \) to \(Q_{E}\), or (2) E adds \(k^\star \) to K.
Proof Sketch
At a high level, the proof is as follows. First, assuming \(\mathsf {injective} ^{\varGamma ,\ell }\) holds, we show that E does not abort. This follows from the fact that the real oracle \(\varGamma \) and random strings \(r_{\mathcal {A}}^{\star }\) and \(r_{\mathcal {B}}^{\star }\) satisfy the properties needed to form the simulated oracle \(\varGamma '\) and random strings \(r_{\mathcal {A}}'\) and \(r_{\mathcal {B}}'\). Thus, there exists at least one valid oracle and pair of random strings and therefore E does not abort.
Then, we show that in each iteration, either (1) E adds a query in \(\mathsf {Aug} (Q_{\mathcal {A} \mathcal {B}}) \) to \(Q_{E}\), or (2) E adds \(k^\star \) to K. Consider some iteration in which (1) does not hold. Let \(\varGamma ', r_{A}', r_{B}'\) be the oracle and random strings chosen by E in this iteration. By definition, the transcript of this execution is T. Let \(k'\) be the key outputted by \(\langle \mathcal {A} ^{\varGamma '}(1^{s}; r_{A}'), \mathcal {B} ^{\varGamma '}(1^{s}; r_{B}') \rangle \). Assuming that (1) does not hold, we show that there exists a hybrid oracle \(\widetilde{\varGamma } \) for which \((k',k^\star ,T) \leftarrow \langle \mathcal {A} ^{\widetilde{\varGamma }}(1^s; r_\mathcal {A} '), \mathcal {B} ^{\widetilde{\varGamma }}(1^s;r_\mathcal {B} ^\star )\rangle \). That is, we show an oracle \(\widetilde{\varGamma } \) such that when \(\mathcal {A} \) uses the randomness of the simulation and \(\mathcal {B} \) uses the randomness of the real protocol and both run with respect to \(\widetilde{\varGamma } \), \(\mathcal {A} \) outputs \(k'\) (as in the simulation) while \(\mathcal {B} \) outputs \(k^{\star }\) (as in the real), and the execution produces the transcript T (as in both the real and simulated protocols). We form this oracle by incorporating all queries in \(\mathsf {Aug} (Q_{\mathcal {A} \mathcal {B}})\) and \(\mathsf {Aug} (Q_{\text {Sim}})\) into \(\widetilde{\varGamma } \). Because (1) does not hold, E does not learn any new query in \(\mathsf {Aug} (Q_{\mathcal {A} \mathcal {B}})\), and thus \(\mathsf {Aug} (Q_{\mathcal {A} \mathcal {B}})\) and \(\mathsf {Aug} (Q_{\text {Sim}})\) agree on all queries and answers. In the full version, we show that this implies that \(\widetilde{\varGamma } \) agrees with all queries in \(\mathsf {Aug} (Q_{\mathcal {A} \mathcal {B}}) \cup \mathsf {Aug} (Q_{\text {Sim}}) \), and that this suffices for the result. Given the existence of such an oracle, by the perfect correctness, it must hold that \(k'=k^\star \), and therefore, since E adds \(k' = k^{\star }\) to K, the claim follows. \(\square \)
5 On Statistical Security
In this section we study the possibility for compressing obfuscation with perfect (information-theoretic) security. We will distinguish between approximately correct and perfectly correct compressing obfuscators and show almost tight results.
For approximately correct obfuscators, one the one hand, we show that there exists a statistically secure compressing obfuscator for the class of bounded depth circuits. On the other hand, we show that this is almost tight as any class that contains a (puncturable) PRF cannot be obfuscated with statistical secure (under complexity theoretic conjectures). See Theorems 5.4 and 5.5 for the precise parameters.
For perfectly correct obfuscators, on the one hand, we show that there exists a statistically secure compressing obfuscator for the class of bounded depth circuits, but the compression factor will be very weak (the obfuscation time is \(\mathsf {poly}(2^{n})\)). On the other hand, we show that even for depth two circuits, better compression with better running time is implausible. See Theorems 5.2 and 5.7 for the precise parameters. Due to lack of space, all proofs from this section appear in the full version.
5.1 Negative Results
We show that it is unlikely that there is a statistically secure compressing obfuscator with good enough compression.
Our first result says that if such an obfuscator exists with strong enough compression, namely a \((2^{\epsilon n}, 2^{\epsilon n})\)-compressing obfuscator with statistical security and perfect correctness, then \(\overline{\mathsf {SAT}}\) (the problem of deciding whether a SAT formula is unsatisfiable) has an AM protocol in which the verifier’s running time is bounded by \(2^{\epsilon n}\). This is not believed to be likely for small enough values of \(\epsilon >0\), according to the best of our knowledge. Note that for this result we only need an obfuscator for depth-2 circuits. This argument relies on ideas from [53] and can be seen as an extension of an argument from [47].
Definition 5.1
We denote by \(\mathsf {AM}[t,\ell ]\) the class of all languages on instances of size n that have an \(\mathsf {AM}\) protocol in which the running time of the verifier is at most t(n) and its messages size is at most \(\ell (n)\). The class \(\mathsf {coAM}[t,\ell ]\) is defined, analogously, to be the class that contains all the complement languages. In case that \(t=\ell \), we will write \(\mathsf {AM}[t]\) to denote \(\mathsf {AM}[t,t]\) and \(\mathsf {coAM}[t]\) to denote \(\mathsf {coAM}[t,t]\).
Theorem 5.2
There exists a universal constant \(c>0\) such that the following holds. If there is \(0< \epsilon < 1\) and a statistically secure and perfectly correct \((2^{\epsilon n},2^{\epsilon n})\)-compressing obfuscation for depth-2 circuits, then \(\overline{\mathsf {SAT}} \in \mathsf {AM}[2^{c\epsilon n}]\).
The conclusion in Theorem 5.2 can be stated more generally as a conjecture that is interesting on its own right. This conjecture is parametrized by an \(0< \epsilon < 1\) and it says that \(\overline{\mathsf {SAT}}\) is not in \(\mathsf {AM}[2^{\epsilon n}]\).
Definition 5.3
(Conjecture). There exist \(\epsilon >0\) for which \(\overline{\mathsf {SAT}} \notin \mathsf {AM}[2^{\epsilon n}]\).
It is known that the conjecture is false for \(\epsilon = 1/2\) by the recent result of Williams [72] who showed that \(\overline{\mathsf {SAT}} \in \mathsf {AM}[\tilde{O}(2^{ n/2})]\). However, for smaller values of \(\epsilon \) it is still unknown. The conjecture is particularly appealing in the case that \(\epsilon \) is sub-constant (some o(1)).
Additionally, we give evidence that a compressing obfuscator with statistical security and only approximate correctness cannot exist for classes of functions that contain a (puncturable) PRF. This argument relies on and extends the proof of [24].
Theorem 5.4
[Restatement of Theorem 1.2, part II]. There exists a universal constant \(c>0\) such that the following holds. If there is \(0< \epsilon < 1\) and a statistically secure and approximately correct \((2^{n^\epsilon },2^{n^\epsilon })\)-compressing obfuscation for all circuits, then \(\overline{\mathsf {SAT}} \in \mathsf {AM}[2^{n^{ \epsilon }}]\).
5.2 Positive Results
We show that for small classes of circuits there is a compressing obfuscation with perfect security. We start with the constructions that give approximate correctness.
Theorem 5.5
[Restatement of Theorem 1.2, part I]. There exist constants \(0<\alpha <1\) and \(0< \beta < 1\) such that there exists a \((1-s/2^{n^\beta })\)-approximately correct \((2^{n^\alpha },2^{n^\alpha })\)-compressing obfuscator with perfect security for the class of polynomial-size constant-depth n-input Boolean circuits.
Theorem 5.6
There exists a polynomial \(p(\cdot )\) and a constant \(\alpha >0\) such that there exists a \((1-1/p(n))\)-approximately correct \((2^{(1-\alpha )n},2^{(1-\alpha )n})\)-compressing obfuscator with perfect security for the class of monotone n-input Boolean functions.
We show that the class of bounded-depth circuits above can also be obfuscated with perfect correctness, while still resulting with a compressing obfuscator. However, the resulting compression is very weak (in particular, such compression, even for compressing obfuscation for all circuits is not known to imply full-fledged obfuscation).
Theorem 5.7
[Restatement of Theorem 1.3]. There exists a perfectly correct \((\mathsf {poly}(2^n), 2^{n-n/O(\log s)^{d-1}})\)-obfuscator with perfect security for the class of size s depth d, n-input Boolean circuits.
All of the obfuscators above treat their input circuit as a black box and run a classical learning or compression algorithm on it. We introduce these tasks next.
Preliminaries on PAC learning. We begin by introducing the concept of PAC learning. The Probably Approximately Correct (PAC) learning model, introduced by Valiant [71], is one of the most central definitions in the learning community and in computer science in general. We focus on PAC learning over the uniform distribution with membership queries. In this setting the learner may query the oracle at any point x and get back the value of the oracle at that point.
Definition 5.8
(PAC learning over the uniform distribution with membership queries). Let \(\mathcal {F} \) be a class of Boolean functions over n inputs. The class \(\mathcal {F} \) is \((\epsilon ,\delta )\)-PAC learnable if there exists an algorithm \(\mathcal {A} \) that gets as input two parameters \(\epsilon ,\delta >0\), has membership query access to a function \(f\in \mathcal {F} \), and outputs with probability \(1-\delta \) (over its internal randomness) a circuit C that agrees with f on all but an \(\epsilon \)-fraction of the inputs. That is,
The running time of A is measures as a function of \(n, 1/\epsilon , 1/\delta \), and the circuit size of f.
There has been a tremendous amount of work on obtaining efficient algorithms for PAC learning various classes of functions. It is known that no \(\mathsf {poly}(n)\)-time algorithm can learn arbitrary Boolean functions \(f:\{0,1\}^n\rightarrow \{0,1\}\) to accuracy non-negligibly better than 1 / 2, but many positive results are known for restricted classes of functions. We fix \(\delta =2/3\), and note that this choice is somewhat arbitrary and enough for all of our applications. We thus say that a class is \(\epsilon \)-PAC learnable if it is \((\epsilon ,2/3)\)-PAC learnable.
One well known example is the quasi-polynomial time algorithm of Linial, Mansour, and Nisan [60] for the class of functions computed by \(\mathsf {AC}^{0}\) circuits (constant depth circuits with AND, OR, and NOT gates of unbounded fan-in and fan-out).
Theorem 5.9
(Learning bounded-depth circuits [60]). The class of size-s depth-d circuits is \(\epsilon \)-PAC learnable within \(n^{O(\log ^{d-1} (s/\epsilon ))}\) queries.Footnote 8
Another notable example that is relevant for us is the algorithm of Bshouty and Tamon [28] for learning arbitrary monotone functions.
Theorem 5.10
(Learning monotone functions [28]). The class of monotone functions is \(\epsilon \)-PAC learnable within \(n^{O(\sqrt{n}/\epsilon )}\) queries.
A more recent result of Carmosino et al. [29] showed a (quasi-polynomial-time) learner for \(\mathsf {AC}^{0}[p]\), the class of Boolean constant depth circuits with unbounded fan-in and fan-out with AND, OR, NOT, and MOD-p gates.Footnote 9 Their result follows by a generic implication from natural properties to (randomized) algorithms for learning. More elaborately, [29] showed that any circuit lower bound proved through the very general natural proofs paradigm of Razborov and Rudich [69] yields algorithms for learning and compression. They then apply this result with the natural lower bound of Razborovand Smolenskyfor the class \(\mathsf {AC}^{0}[p]\). Informally, a “natural” lower bound for a circuit class \(\mathcal {C} \) consists of an efficient algorithm that recognized some property that distinguishes between the truth tables functions in \(\mathcal {C} \) and those of random Boolean functions.
Theorem 5.11
(Learning bounded-depth circuits with \(\mathsf {mod}\) gates [29]). For every prime \(p>1\), the class of \(\mathsf {AC}^{0}[p]\) circuits of size s is \(\epsilon \)-PAC learnable within \(2^{\mathsf {poly}\log (ns/\epsilon ) }\) queries.
Tightness of the Approach. The approach of constructing obfuscators via learning algorithms is inherently limited. As observed by Valiant [71], any class that contains a pseudorandom function cannot be learned with nontrivial savings. Moreover, this approach, as shown above, gives the very strong notion of perfect security, which does not exist for all functions (even the computational version, known as virtual black-box, does not exist for circuits that contain a PRF [14]). Thus, to get an obfuscator (that satisfies only indistinguishability obfuscation) for a larger class of functions, one has to use the fact that the obfuscator has access to a circuit rather than treating it as a black-box.
Preliminaries on Circuit Compression. In the problem of circuit compression, studied by Chen et al. [31], one is given the truth table of a Boolean function f computable by some unknown circuit from a known class of circuits, and the goal is to find in time \(\mathsf {poly}(2^n)\) a circuit C (not necessarily from the aforementioned family) computing f so that the size of C is less than the trivial circuit size \(\approx \!\!2^n\). For general functions this is impossible as there are functions that require this size, so the focus is on restricted classes.
Definition 5.12
(\(\mathcal {C} \)-compression). Given the truth table of an n-variate Boolean function \(f\in \mathcal {C} \), find a Boolean circuit of size \(< 2^n / n\) that is functionally equivalent to f.
As mentioned in [31], compression of Boolean functions is related to the setting of exact learning with membership and equivalence queries [6]. In this learning setting, the size of the hypothesis produced by the learning algorithm is upper-bounded by the running time of the algorithm. In the circuit compression setting, the hypothesis (compressed image) size and the running time of the learning (compression) algorithm are decoupled: we allow more running time, but ask for a small-size compression. This may enable improvements in the class of circuits that we can handle. Concretely, exact learning is strictly stronger as any result in exact learning yields a compression algorithm for the corresponding class of functions, but the opposite direction is not known.
We notice that in general good enough compression implies compressing obfuscation where the output size is nontrivial but the running time can be large enough to read the truth table of the function (i.e., as in XiO). However, the other direction is not known since in XO one is given a witness (i.e., a circuit rather than the truth table). The most relevant circuit compression result that is relevant for us is stated next.
Theorem 5.13
([31]). If a Boolean n-variate function is computed by an \(\mathsf {AC}^{0}\) circuit of size s and depth d, then it is compressible to a circuit of size at most \(2^{n-n/O(\log s)^{d-1}}\).
As in the case of learning algorithms, the above compression algorithms directly imply perfectly correct compressing obfuscators satisfying perfect security.
We note that, as in the case of learning, it is impossible to compress a class of circuits that contains a PRF. For this, consider a PRF with key size \(n^{2}\) and input size n which is exponentially secure (namely, secure for adversaries running in time \(2^{\varOmega (n^2)}\)).Footnote 10 In this case, the PRF-or-Random adversary is allowed to query the oracle at all \(2^n\) inputs and yet it still cannot distinguish PRF from random. The impossibility of compression for such a family of circuits now follows from the fact that random functions cannot be compressed.
Notes
- 1.
- 2.
Assuming any average- or worst-case hardness assumption. This is necessary as XiO exists unconditionally if \(\mathsf {P}=\mathsf {NP}\).
- 3.
- 4.
The obfuscator we get is weak due to two reasons. First, the class for which we obtain XiO does not contain (puncturable) PRFs and thus is not sufficient for known transformations to iO. Second, the compression we achieve is not enough for cryptographic applications.
- 5.
We note that the technique of enumerating over all inputs is similar to that used in our correctness amplification, and takes advantage of the ability of XiO to compute the truth table of the obfuscated circuit.
- 6.
The game
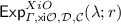 is the indistinguishability experiment for XiO, defined as follows: (1)
is the indistinguishability experiment for XiO, defined as follows: (1)  ; (2)
; (2)  where \(|C_{0} | = |C_{1} | = s\) and \(C_0^{\varGamma } \equiv C_1^{\varGamma }\). (3)
where \(|C_{0} | = |C_{1} | = s\) and \(C_0^{\varGamma } \equiv C_1^{\varGamma }\). (3) 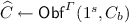 . (4)
. (4)  . (5) If \(b'=b\) then output 1. Otherwise, output 0.
. (5) If \(b'=b\) then output 1. Otherwise, output 0. - 7.
The game
 is defined as follows: (1) \((k_{\mathcal {A}}, k_{\mathcal {B}}, T) \leftarrow \langle \mathcal {A} ^{\varGamma }(1^{s}), \mathcal {B} ^{\varGamma }(1^{s})\rangle \), (2) \(k' \leftarrow E^{\varGamma }(1^{s}, T)\), (3) If \(k' = k_{\mathcal {A}}\) then output 1, otherwise output 0.
is defined as follows: (1) \((k_{\mathcal {A}}, k_{\mathcal {B}}, T) \leftarrow \langle \mathcal {A} ^{\varGamma }(1^{s}), \mathcal {B} ^{\varGamma }(1^{s})\rangle \), (2) \(k' \leftarrow E^{\varGamma }(1^{s}, T)\), (3) If \(k' = k_{\mathcal {A}}\) then output 1, otherwise output 0. - 8.
- 9.
We note that recently Carmosino et al. [30] generalized their result to get an implication from “tolerant” natural proofs to agnostic learning [52]. In agnostic learning, is the same as in PAC learning except that the learner is only guaranteed that f is close to the concept class \(\mathcal {C} \) (rather than assuming it belongs to it).
- 10.
The argument works even with sub-exponential security by increasing the size of the key.
References
Ananth, P., Jain, A., Naor, M., Sahai, A., Yogev, E.: Universal constructions and robust combiners for indistinguishability obfuscation and witness encryption. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 491–520. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_17
Ananth, P., Jain, A., Sahai, A.: Robust transforming combiners from indistinguishability obfuscation to functional encryption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 91–121. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_4
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 152–181. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_6
Ananth, P.V., Gupta, D., Ishai, Y., Sahai, A.: Optimizing obfuscation: avoiding Barrington’s theorem. In: Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, pp. 646–658 (2014)
Angluin, D.: Queries and concept learning. Mach. Learn. 2(4), 319–342 (1987)
Apon, D., Döttling, N., Garg, S., Mukherjee, P.: Cryptanalysis of indistinguishability obfuscations of circuits over GGH13. In: 44th International Colloquium on Automata, Languages, and Programming, ICALP 2017, pp. 38:1–38:16 (2017)
Applebaum, B., Brakerski, Z.: Obfuscating circuits via composite-order graded encoding. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 528–556. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_21
Asharov, G., Segev, G.: Limits on the power of indistinguishability obfuscation and functional encryption. SIAM J. Comput. 45(6), 2117–2176 (2016)
Asharov, G., Segev, G.: On constructing one-way permutations from indistinguishability obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 512–541. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_19
Asmuth, C., Blakley, G.: An efficient algorithm for constructing a cryptosystem which is harder to break than two other cryptosystems. Comput. Math. Appl. 7(6), 447–450 (1981)
Barak, B., Brakerski, Z., Komargodski, I., Kothari, P.K.: Limits on low-degree pseudorandom generators (or: sum-of-squares meets program obfuscation). IACR Cryptology ePrint Archive 2017, 312 (2017)
Barak, B., Garg, S., Kalai, Y.T., Paneth, O., Sahai, A.: Protecting obfuscation against algebraic attacks. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 221–238. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_13
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6:1–6:48 (2012)
Bitansky, N., Degwekar, A., Vaikuntanathan, V.: Structure vs. hardness through the obfuscation lens. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 696–723. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_23
Bitansky, N., Lin, H., Paneth, O.: On removing graded encodings from functional encryption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Proceedings, Part II. LNCS, vol. 10211, pp. 3–29. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_1
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Theory of Cryptography Conference, pp. 391–418 (2016)
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Bitansky, N., Paneth, O., Wichs, D.: Perfect structure on the edge of chaos - trapdoor permutations from indistinguishability obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 474–502. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_20
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, pp. 171–190 (2015)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation: from approximate to exact. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 67–95. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_4
Bitansky, N., Vaikuntanathan, V.: A note on perfect correctness by derandomization. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 592–606. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_20
Boneh, D., Wu, D.J., Zimmerman, J.: Immunizing multilinear maps against zeroizing attacks. IACR Cryptology ePrint Archive 2014, 930 (2014)
Brakerski, Z., Brzuska, C., Fleischhacker, N.: On statistically secure obfuscation with approximate correctness. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 551–578. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_19
Brakerski, Z., Jain, A., Komargodski, I., Passelègue, A., Wichs, D.: Non-trivial witness encryption and null-iO from standard assumptions. IACR Cryptology ePrint Archive 2017, 874 (2017)
Brakerski, Z., Katz, J., Segev, G., Yerukhimovich, A.: Limits on the power of zero-knowledge proofs in cryptographic constructions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 559–578. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_34
Brakerski, Z., Rothblum, G.N.: Virtual black-box obfuscation for all circuits via generic graded encoding. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 1–25. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_1
Bshouty, N.H., Tamon, C.: On the fourier spectrum of monotone functions. J. ACM 43(4), 747–770 (1996)
Carmosino, M.L., Impagliazzo, R., Kabanets, V., Kolokolova, A.: Learning algorithms from natural proofs. In: 31st Conference on Computational Complexity, CCC 2016, vol. 50, pp. 10:1–10:24 (2016)
Carmosino, M.L., Impagliazzo, R., Kabanets, V., Kolokolova, A.: Agnostic learning from tolerant natural proofs. In: Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, APPROX/RANDOM 2017, vol. 81, pp. 35:1–35:19 (2017)
Chen, R., Kabanets, V., Kolokolova, A., Shaltiel, R., Zuckerman, D.: Mining circuit lower bound proofs for meta-algorithms. Comput. Complex. 24(2), 333–392 (2015)
Chen, Y., Gentry, C., Halevi, S.: Cryptanalyses of candidate branching program obfuscators. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 278–307. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_10
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_1
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_26
Coron, J.-S., Lepoint, T., Tibouchi, M.: New multilinear maps over the integers. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 267–286. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_13
Diffie, W., Hellman, M.E.: Multiuser cryptographic techniques. In: American Federation of Information Processing Societies, pp. 109–112 (1976)
Fischlin, M., Herzberg, A., Bin-Noon, H., Shulman, H.: Obfuscation combiners. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 521–550. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_18
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2013, pp. 40–49. IEEE Computer Society (2013)
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: Symposium on Theory of Computing Conference, STOC 2013, pp. 467–476 (2013)
Garg, S., Mahmoody, M., Mohammed, A.: Lower bounds on obfuscation from all-or-nothing encryption primitives. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 661–695. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_22
Garg, S., Mahmoody, M., Mohammed, A.: When does functional encryption imply obfuscation? In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 82–115. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_4
Gentry, C., Gorbunov, S., Halevi, S.: Graph-induced multilinear maps from lattices. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 498–527. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_20
Gentry, C., Halevi, S., Maji, H.K., Sahai, A.: Zeroizing without zeroes: cryptanalyzing multilinear maps without encodings of zero. IACR Cryptology ePrint Archive 2014, 929 (2014)
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, pp. 151–170 (2015)
Goldwasser, S., et al.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_32
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Symposium on Theory of Computing Conference, STOC 2013, pp. 555–564 (2013)
Goldwasser, S., Rothblum, G.N.: On best-possible obfuscation. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 194–213. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_11
Harnik, D., Kilian, J., Naor, M., Reingold, O., Rosen, A.: On robust combiners for oblivious transfer and other primitives. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 96–113. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_6
Herzberg, A.: On tolerant cryptographic constructions. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 172–190. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_13
Herzberg, A.: Folklore, practice and theory of robust combiners. J. Comput. Secur. 17(2), 159–189 (2009)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing, pp. 44–61. ACM (1989)
Kearns, M.J., Schapire, R.E., Sellie, L.: Toward efficient agnostic learning. Mach. Learn. 17(2–3), 115–141 (1994)
Komargodski, I., Moran, T., Naor, M., Pass, R., Rosen, A., Yogev, E.: One-way functions and (im)perfect obfuscation. In: 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014, pp. 374–383 (2014)
Levin, L.A.: One-way functions and pseudorandom generators. Combinatorica 7(4), 357–363 (1987)
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_2
Lin, H.: Indistinguishability obfuscation from SXDH on 5-linear maps and locality-5 PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 599–629. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_20
Lin, H., Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation with non-trivial efficiency. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 447–462. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49387-8_17
Lin, H., Pass, R., Seth, K., Telang, S.: Output-compressing randomized encodings and applications. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016-A. LNCS, vol. 9562, pp. 96–124. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_5
Lin, H., Vaikuntanathan, V.: Indistinguishability obfuscation from DDH-like assumptions on constant-degree graded encodings. In: IEEE 57th Annual Symposium on Foundations of Computer Science, FOCS 2016, pp. 11–20 (2016)
Linial, N., Mansour, Y., Nisan, N.: Constant depth circuits, Fourier transform, and learnability. In: 30th Annual Symposium on Foundations of Computer Science, pp. 574–579 (1989)
Liu, Q., Zhandry, M.: Decomposable obfuscation: a framework for building applications of obfuscation from polynomial hardness. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 138–169. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_6
Lombardi, A., Vaikuntanathan, V.: Limits on the locality of pseudorandom generators and applications to indistinguishability obfuscation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 119–137. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_5
Mahmoody, M., Mohammed, A., Nematihaji, S., Pass, R., Shelat, A.: Lower bounds on assumptions behind indistinguishability obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016-A. LNCS, vol. 9562, pp. 49–66. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_3
Mahmoody, M., Xiao, D.: On the power of randomized reductions and the checkability of SAT. In: CCC 2010, pp. 64–75. IEEE Computer Society (2010)
Micali, S., Peikert, C., Sudan, M., Wilson, D.A.: Optimal error correction against computationally bounded noise. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 1–16. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_1
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_22
Okamoto, T.: On relationships between statistical zero-knowledge proofs. J. Comput. Syst. Sci. 60(1), 47–108 (2000)
Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation from semantically-secure multilinear encodings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 500–517. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_28
Razborov, A.A., Rudich, S.: Natural proofs. J. Comput. Syst. Sci. 55(1), 24–35 (1997)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Symposium on Theory of Computing, STOC 2014, pp. 475–484 (2014)
Valiant, L.G.: A theory of the learnable. Commun. ACM 27(11), 1134–1142 (1984)
Williams, R.R.: Strong ETH breaks with Merlin and Arthur: short non-interactive proofs of batch evaluation. In: CCC, vol. 50, pp. 2:1–2:17 (2016)
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_15
Acknowledgments
We thank Zvika Brakerski for discussions about the possibility of SXiO and XiO with statistical security.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Asharov, G., Ephraim, N., Komargodski, I., Pass, R. (2018). On the Complexity of Compressing Obfuscation. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10993. Springer, Cham. https://doi.org/10.1007/978-3-319-96878-0_26
Download citation
DOI: https://doi.org/10.1007/978-3-319-96878-0_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96877-3
Online ISBN: 978-3-319-96878-0
eBook Packages: Computer ScienceComputer Science (R0)





 is a
is a  for some polynomial p.
for some polynomial p. erasure correcting code that can correct up to a
erasure correcting code that can correct up to a 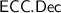 , where
, where  is a polynomial of degree
is a polynomial of degree  are padded to size
are padded to size 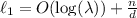 be the length of the output of
be the length of the output of  is a binary error-correcting code that is
is a binary error-correcting code that is  . We let
. We let  be the output length of
be the output length of  when run on inputs of size
when run on inputs of size  .
. is a
is a  -output succinct FE scheme for the class
-output succinct FE scheme for the class 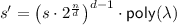 and
and  .
. is a puncturable PRF.
is a puncturable PRF. is a Multi-NIZK proof system for the NP language L given by
is a Multi-NIZK proof system for the NP language L given by 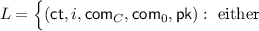
 encrypts (C, i) and
encrypts (C, i) and  , or
, or denote the upper bound on the length of statements and witnesses in L when instantiated with security parameter
denote the upper bound on the length of statements and witnesses in L when instantiated with security parameter  (with parameters as used in the following scheme).
(with parameters as used in the following scheme).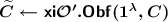 :
: .
.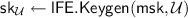 for the circuit
for the circuit  such that
such that 
 of
of  :
: , and
, and  .
.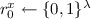 and
and  .
. such that on input (i, j) does the following:
such that on input (i, j) does the following: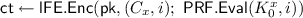 .
. for the statement
for the statement  using the witness
using the witness  .
. , denoted by
, denoted by  .
. and let
and let  .
.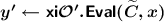 :
: .
. to obtain a list of possible decodings, where the kth element of the list is
to obtain a list of possible decodings, where the kth element of the list is 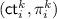 .
.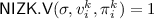 where
where  . Set
. Set  if
if  .
. .
. and run
and run  and output the element corresponding to
and output the element corresponding to  is a uniformly chosen function. We will use f to implement a one-way function.
is a uniformly chosen function. We will use f to implement a one-way function.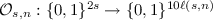 is a uniformly chosen function. Intuitively,
is a uniformly chosen function. Intuitively,  is defined as follows. On input
is defined as follows. On input 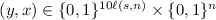 , the function
, the function 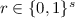 such that
such that  for all
for all  .
.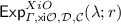 is the indistinguishability experiment for XiO, defined as follows: (1)
is the indistinguishability experiment for XiO, defined as follows: (1)  ; (2)
; (2)  where
where 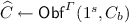 . (4)
. (4)  . (5) If
. (5) If  is defined as follows: (1)
is defined as follows: (1) 