Abstract
Simple stochastic games can be solved by value iteration (VI), which yields a sequence of under-approximations of the value of the game. This sequence is guaranteed to converge to the value only in the limit. Since no stopping criterion is known, this technique does not provide any guarantees on its results. We provide the first stopping criterion for VI on simple stochastic games. It is achieved by additionally computing a convergent sequence of over-approximations of the value, relying on an analysis of the game graph. Consequently, VI becomes an anytime algorithm returning the approximation of the value and the current error bound. As another consequence, we can provide a simulation-based asynchronous VI algorithm, which yields the same guarantees, but without necessarily exploring the whole game graph.
This research was funded in part by the German Excellence Initiative and the European Union Seventh Framework Programme under grant agreement No. 291763 for TUM – IAS, the Studienstiftung des deutschen Volkes project “Formal methods for analysis of attack-defence diagrams”, the Czech Science Foundation grant No. 18-11193S, TUM IGSSE Grant 10.06 (PARSEC), and the German Research Foundation (DFG) project KR 4890/2-1 “Statistical Unbounded Verification”.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Simple Stochastic Game. (SG) [Con92] is a zero-sum two-player game played on a graph by Maximizer and Minimizer, who choose actions in their respective vertices (also called states). Each action is associated with a probability distribution determining the next state to move to. The objective of Maximizer is to maximize the probability of reaching a given target state; the objective of Minimizer is the opposite.
Stochastic games constitute a fundamental problem for several reasons. From the theoretical point of view, the complexity of this problemFootnote 1 is known to be in \(\mathbf {UP}\cap \mathbf {coUP}\) [HK66], but no polynomial-time algorithm is known. Further, several other important problems can be reduced to SG, for instance parity games, mean-payoff games, discounted-payoff games and their stochastic extensions [CF11]. The task of solving SG is also polynomial-time equivalent to solving perfect information Shapley, Everett and Gillette games [AM09]. Besides, the problem is practically relevant in verification and synthesis. SG can model reactive systems, with players corresponding to the controller of the system and to its environment, where quantified uncertainty is explicitly modelled. This is useful in many application domains, ranging from smart energy management [CFK+13a] to autonomous urban driving [CKSW13], robot motion planning [LaV00] to self-adaptive systems [CMG14]; for various recent case studies, see e.g. [SK16]. Finally, since Markov decision processes (MDP) [Put14] are a special case with only one player, SG can serve as abstractions of large MDP [KKNP10].
Solution Techniques. There are several classes of algorithms for solving SG, most importantly strategy iteration (SI) algorithms [HK66] and value iteration (VI) algorithms [Con92]. Since the repetitive evaluation of strategies in SI is often slow in practice, VI is usually preferred, similarly to the special case of MDPs [KM17]. For instance, the most used probabilistic model checker PRISM [KNP11] and its branch PRISM-Games [CFK+13a] use VI for MDP and SG as the default option, respectively. However, while SI is in principle a precise method, VI is an approximative method, which converges only in the limit. Unfortunately, there is no known stopping criterion for VI applied to SG. Consequently, there are no guarantees on the results returned in finite time. Therefore, current tools stop when the difference between the two most recent approximations is low, and thus may return arbitrarily imprecise results [HM17].
Value Iteration with Guarantees. In the special case of MDP, in order to obtain bounds on the imprecision of the result, one can employ a bounded variant of VI [MLG05, BCC+14] (also called interval iteration [HM17]). Here one computes not only an under-approximation, but also an over-approximation of the actual value as follows. On the one hand, iterative computation of the least fixpoint of Bellman equations yields an under-approximating sequence converging to the value. On the other hand, iterative computation of the greatest fixpoint yields an over-approximation, which, however, does not converge to the value. Moreover, it often results in the trivial bound of 1. A solution suggested for MDPs [BCC+14, HM17] is to modify the underlying graph, namely to collapse end components. In the resulting MDP there is only one fixpoint, thus the least and greatest fixpoint coincide and both approximating sequences converge to the actual value. In contrast, for general SG no procedure where the greatest fixpoint converges to the value is known. In this paper we provide one, yielding a stopping criterion. We show that the pre-processing approach of collapsing is not applicable in general and provide a solution on the original graph. We also characterize SG where the fixpoints coincide and no processing is needed. The main technical challenge is that states in an end component in SG can have different values, in contrast to the case of MDP.
Practical Efficiency Using Guarantees. We further utilize the obtained guarantees to practically improve our algorithm. Similar to the MDP case [BCC+14], the quantification of the error allows for ignoring parts of the state space, and thus a speed up without jeopardizing the correctness of the result. Indeed, we provide a technique where some states are not explored and processed at all, but their potential effect is still taken into account The information is further used to decide the states to be explored next and to be analyzed in more detail. To this end, simulations and learning are used as tools. While for MDP this idea has already demonstrated speed ups in orders of magnitude [BCC+14, ACD+17], this paper provides the first technique of this kind for SG. Our contribution is summarized as follows
-
We introduce a VI algorithm yielding both under- and over-approximation sequences, both of which converge to the value of the game. Thus we present the first stopping criterion for VI on SG and the first anytime algorithm with guaranteed precision. We also characterize when a simpler solution is sufficient.
-
We provide a learning-based algorithm, which preserves the guarantees, but is in some cases more efficient since it avoids exploring the whole state space.
-
We evaluate the running times of the algorithms experimentally, concluding that obtaining guarantees requires an overhead that is either negligible or mitigated by the learning-based approach.
Related Work. The works closest to ours are the following. As mentioned above, [BCC+14, HM17] describe the solution to the special case of MDP. While [BCC+14] also provides a learning-based algorithm, [HM17] discusses the convergence rate and the exact solution. The basic algorithm of [HM17] is implemented in PRISM [BKL+17] and the learning approach of [BCC+14] in Storm [DJKV17a]. The extension for SG where the interleaving of players is severely limited (every end component belongs to one player only) is discussed in [Ujm15].
Further, in the area of probabilistic planning, bounded real-time dynamic programming [MLG05] is related to our learning-based approach. However, it is limited to the setting of stopping MDP where the target sink or the non-target sink is reached almost surely under any pair of strategies and thus the fixpoints coincide. Our algorithm works for general SG, not only for stopping ones, without any blowup.
For SG, the tools implementing the standard SI and/or VI algorithms are PRISM-games [CFK+13a], GAVS+ [CKLB11] and GIST [CHJR10]. The latter two are, however, neither maintained nor accessible via the links provided in their publications any more.
Apart from fundamental algorithms to solve SG, there are various practically efficient heuristics that, however, provide none or weak guarantees, often based on some form of learning [BT00, LL08, WT16, TT16, AY17, BBS08]. Finally, the only currently available way to obtain any guarantees through VI is to perform \(\gamma ^2\) iterations and then round to the nearest multiple of \(1/\gamma \), yielding the value of the game with precision \(1/\gamma \) [CH08]; here \(\gamma \) cannot be freely chosen, but it is a fixed number, exponential in the number of states and the used probability denominators. However, since the precision cannot be chosen and the number of iterations is always exponential, this approach is infeasible even for small games.
Organization of the Paper. Section 2 introduces the basic notions and revises value iteration. Section 3 explains the idea of our approach on an example. Section 4 provides a full technical treatment of the method as well as the learning-based variation. Section 5 discusses experimental results and Sect. 6 concludes. The appendix (available in [KKKW18]) gives technical details on the pseudocode as well as the conducted experiments and provides more extensive proofs to the theorems and lemmata; in this paper, there are only proof sketches and ideas.
2 Preliminaries
2.1 Basic Definitions
A probability distribution on a finite set X is a mapping  , such that
, such that  . The set of all probability distributions on X is denoted by \(\mathcal {D}(X)\). Now we define stochastic games, in literature often referred as simple stochastic games or stochastic two-player games with a reachability objective.
. The set of all probability distributions on X is denoted by \(\mathcal {D}(X)\). Now we define stochastic games, in literature often referred as simple stochastic games or stochastic two-player games with a reachability objective.
Definition 1
(SG). A stochastic game (SG) is a tuple  , where
, where  is a finite set of states partitioned into the sets
is a finite set of states partitioned into the sets  and
and  of states of the player Maximizer and Minimizer, respectively,
of states of the player Maximizer and Minimizer, respectively,  is the initial state, target state, and sink state, respectively,
is the initial state, target state, and sink state, respectively,  is a finite set of actions,
is a finite set of actions,  assigns to every state a set of available actions, and
assigns to every state a set of available actions, and  is a transition function that given a state
is a transition function that given a state  and an action
and an action  yields a probability distribution over successor states.
yields a probability distribution over successor states.
A Markov decision process (MDP) is a special case of \(\text {SG}\) where  .
.
We assume that \(\text {SGs}\) are non-blocking, so for all states  we have
we have  . Further,
. Further,  and
and  only have one action and it is a self-loop with probability 1. Additionally, we can assume that the SG is preprocessed so that all states with no path to
only have one action and it is a self-loop with probability 1. Additionally, we can assume that the SG is preprocessed so that all states with no path to  are merged with
are merged with  .
.
For a state  and an available action
and an available action  , we denote the set of successors by
, we denote the set of successors by  . Finally, for any set of states
. Finally, for any set of states  , we use \(T_\Box \) and \(T_\bigcirc \) to denote the states in T that belong to Maximizer and Minimizer, whose states are drawn in the figures as \(\Box \) and \(\bigcirc \), respectively.
, we use \(T_\Box \) and \(T_\bigcirc \) to denote the states in T that belong to Maximizer and Minimizer, whose states are drawn in the figures as \(\Box \) and \(\bigcirc \), respectively.
The semantics of SG is given in the usual way by means of strategies and the induced Markov chain and the respective probability space, as follows. An infinite path  is an infinite sequence
is an infinite sequence  , such that for every \(i \in \mathbb {N}\),
, such that for every \(i \in \mathbb {N}\),  and
and  . Finite paths are defined analogously as elements of
. Finite paths are defined analogously as elements of  . Since this paper deals with the reachability objective, we can restrict our attention to memoryless strategies, which are optimal for this objective. We still allow randomizing strategies, because they are needed for the learning-based algorithm later on. A strategy of Maximizer or Minimizer is a function
. Since this paper deals with the reachability objective, we can restrict our attention to memoryless strategies, which are optimal for this objective. We still allow randomizing strategies, because they are needed for the learning-based algorithm later on. A strategy of Maximizer or Minimizer is a function  or
or  , respectively, such that
, respectively, such that  for all
for all  . We call a strategy deterministic if it maps to Dirac distributions only. Note that there are finitely many deterministic strategies. A pair \((\sigma ,\tau )\) of strategies of Maximizer and Minimizer induces a Markov chain
. We call a strategy deterministic if it maps to Dirac distributions only. Note that there are finitely many deterministic strategies. A pair \((\sigma ,\tau )\) of strategies of Maximizer and Minimizer induces a Markov chain  where the transition probabilities are defined as
where the transition probabilities are defined as  for states of Maximizer and analogously for states of Minimizer, with \(\sigma \) replaced by \(\tau \). The Markov chain induces a unique probability distribution
for states of Maximizer and analogously for states of Minimizer, with \(\sigma \) replaced by \(\tau \). The Markov chain induces a unique probability distribution  over measurable sets of infinite paths [BK08, Chap. 10].
over measurable sets of infinite paths [BK08, Chap. 10].
We write  to denote the (measurable) set of all paths which eventually reach
to denote the (measurable) set of all paths which eventually reach  . For each
. For each  , we define the value in
, we define the value in  as
as

where the equality follows from [Mar75]. We are interested not only in  , but also its \(\varepsilon \)-approximations and the corresponding (\(\varepsilon \)-)optimal strategies for both players.
, but also its \(\varepsilon \)-approximations and the corresponding (\(\varepsilon \)-)optimal strategies for both players.
Now we recall a fundamental tool for analysis of MDP called end components. We introduce the following notation. Given a set of states  , a state
, a state  and an action
and an action  , we say that
, we say that  if
if  . We define an end component of a SG as the end component of the underlying MDP with both players unified.
. We define an end component of a SG as the end component of the underlying MDP with both players unified.
Definition 2
(EC). A non-empty set  of states is an end component (EC) if there is a non-empty set
of states is an end component (EC) if there is a non-empty set  of actions such that
of actions such that
-
1.
for each
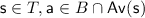 we do not have
we do not have 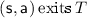 ,
, -
2.
for each
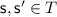 there is a finite path
there is a finite path  , i.e. the path stays inside T and only uses actions in B.
, i.e. the path stays inside T and only uses actions in B.
Intuitively, ECs correspond to bottom strongly connected components of the Markov chains induced by possible strategies, so for some pair of strategies all possible paths starting in the EC remain there. An end component T is a maximal end component (MEC) if there is no other end component \(T'\) such that \(T \subseteq T'\). Given an \(\text {SG}\)  , the set of its MECs is denoted by
, the set of its MECs is denoted by  and can be computed in polynomial time [CY95].
and can be computed in polynomial time [CY95].
2.2 (Bounded) Value Iteration
The value function  satisfies the following system of equations, which is referred to as the Bellman equations:
satisfies the following system of equations, which is referred to as the Bellman equations:

whereFootnote 2

Moreover,  is the least solution to the Bellman equations, see e.g. [CH08]. To compute the value of
is the least solution to the Bellman equations, see e.g. [CH08]. To compute the value of  for all states in an \(\text {SG}\), one can thus utilize the iterative approximation method value iteration (VI) as follows. We start with a lower bound function
for all states in an \(\text {SG}\), one can thus utilize the iterative approximation method value iteration (VI) as follows. We start with a lower bound function  such that
such that  and, for all other
and, for all other  ,
,  . Then we repetitively apply Bellman updates (3) and (4)
. Then we repetitively apply Bellman updates (3) and (4)


until convergence. Note that convergence may happen only in the limit even for such a simple game as in Fig. 1 on the left. The sequence is monotonic, at all times a lower bound on V, i.e.  for all
for all  , and the least fixpoint satisfies
, and the least fixpoint satisfies  .
.
Unfortunately, there is no known stopping criterion, i.e. no guarantees how close the current under-approximation is to the value [HM17]. The current tools stop when the difference between two successive approximations is smaller than a certain threshold, which can lead to arbitrarily wrong results [HM17].
For the special case of MDP, it has been suggested to also compute the greatest fixpoint [MLG05] and thus an upper bound as follows. The function  is initialized for all states
is initialized for all states  as
as  except for
except for  . Then we repetitively apply updates (3) and (4), where
. Then we repetitively apply updates (3) and (4), where  is replaced by
is replaced by  . The resulting sequence
. The resulting sequence  is monotonic, provides an upper bound on
is monotonic, provides an upper bound on  and the greatest fixpoint
and the greatest fixpoint  is the greatest solution to the Bellman equations on \([0,1]^S\).
is the greatest solution to the Bellman equations on \([0,1]^S\).
This approach is called bounded value iteration (BVI) (or bounded real-time dynamic programming (BRTDP) [MLG05, BCC+14] or interval iteration [HM17]). If  then they are both equal to
then they are both equal to  and we say that BVI converges. BVI is guaranteed to converge in MDP if the only ECs are those of
and we say that BVI converges. BVI is guaranteed to converge in MDP if the only ECs are those of  and
and  [BCC+14]. Otherwise, if there are non-trivial ECs they have to be “collapsed”Footnote 3. Computing the greatest fixpoint on the modified MDP results in another sequence
[BCC+14]. Otherwise, if there are non-trivial ECs they have to be “collapsed”Footnote 3. Computing the greatest fixpoint on the modified MDP results in another sequence  of upper bounds on
of upper bounds on  , converging to
, converging to  . Then BVI converges even for general MDPs,
. Then BVI converges even for general MDPs,  [BCC+14], when transformed this way. The next section illustrates this difficulty and the solution through collapsing on an example.
[BCC+14], when transformed this way. The next section illustrates this difficulty and the solution through collapsing on an example.
In summary, all versions of BVI discussed so far and later on in the paper follow the pattern of Algorithm 1. In the naive version, \(\mathsf {UPDATE}\) just performs the Bellman update on  and
and  according to Eqs. (3) and (4).Footnote 4 For a general MDP,
according to Eqs. (3) and (4).Footnote 4 For a general MDP,  does not converge to
does not converge to  , but to
, but to  , and thus the termination criterion may never be met if
, and thus the termination criterion may never be met if  . If the ECs are collapsed in pre-processing then
. If the ECs are collapsed in pre-processing then  converges to
converges to  .
.
For the general case of SG, the collapsing approach fails and this paper provides another version of BVI where  converges to
converges to  , based on a more detailed structural analysis of the game.
, based on a more detailed structural analysis of the game.

3 Example
In this section, we illustrate the issues preventing BVI convergence and our solution on a few examples. Recall that  is the sequence converging to the greatest solution of the Bellman equations, while
is the sequence converging to the greatest solution of the Bellman equations, while  is in general any sequence over-approximating
is in general any sequence over-approximating  that one or another BVI algorithm suggests.
that one or another BVI algorithm suggests.
Firstly, we illustrate the issue that arises already for the special case of MDP. Consider the MPD of Fig. 1 on the left. Although  , we have
, we have  for all i. Indeed, the upper bound for \(\mathsf t\) is always updated as the maximum of
for all i. Indeed, the upper bound for \(\mathsf t\) is always updated as the maximum of  and
and  . Although
. Although  decreases over time,
decreases over time,  remains the same, namely equal to
remains the same, namely equal to  , which in turn remains equal to
, which in turn remains equal to  . This cyclic dependency lets both \(\mathsf s\) and \(\mathsf t\) remain in an “illusion” that the value of the other one is 1.
. This cyclic dependency lets both \(\mathsf s\) and \(\mathsf t\) remain in an “illusion” that the value of the other one is 1.
The solution for MDP is to remove this cyclic dependency by collapsing all MECs into singletons and removing the resulting purely self-looping actions. Figure 1 in the middle shows the MDP after collapsing the EC  . This turns the MDP into a stopping one, where
. This turns the MDP into a stopping one, where  or
or  is under any strategy reached with probability 1. In such MDP, there is a unique solution to the Bellman equations. Therefore, the greatest fixpoint is equal to the least one and thus to
is under any strategy reached with probability 1. In such MDP, there is a unique solution to the Bellman equations. Therefore, the greatest fixpoint is equal to the least one and thus to  .
.
Secondly, we illustrate the issues that additionally arise for general SG. It turns out that the collapsing approach can be extended only to games where all states of each EC belong to one player only [Ujm15]. In this case, both Maximizer’s and Minimizer’s ECs are collapsed the same way as in MDP.
However, when both players are present in an EC, then collapsing may not solve the issue. Consider the SG of Fig. 2. Here \(\alpha \) and \(\beta \) represent the values of the respective actions.Footnote 5 There are three cases:
First, let \(\mathsf {\alpha }<\mathsf {\beta }\). If the bounds converge to these values we eventually observe  and learn the induced inequality. Since \(\mathsf {p}\) is a Minimizer’s state it will never pick the action leading to the greater value of \(\mathsf {\beta }\). Therefore, we can safely merge \(\mathsf {p}\) and \(\mathsf {q}\), and remove the action leading to \(\mathsf {r}\), as shown in the second subfigure.
and learn the induced inequality. Since \(\mathsf {p}\) is a Minimizer’s state it will never pick the action leading to the greater value of \(\mathsf {\beta }\). Therefore, we can safely merge \(\mathsf {p}\) and \(\mathsf {q}\), and remove the action leading to \(\mathsf {r}\), as shown in the second subfigure.
Second, if \(\mathsf {\alpha }>\mathsf {\beta }\), \(\mathsf {p}\) and \(\mathsf {r}\) can be merged in an analogous way, as shown in the third subfigure.
Third, if \(\mathsf {\alpha }=\mathsf {\beta }\), both previous solutions as well as collapsing all three states as in the fourth subfigure is possible. However, since the approximants may only converge to \(\mathsf {\alpha }\) and \(\mathsf {\beta }\) in the limit, we may not know in finite time which of these cases applies and thus cannot decide for any of the collapses.
Consequently, the approach of collapsing is not applicable in general. In order to ensure BVI convergence, we suggest a different method, which we call deflating. It does not involve changing the state space, but rather decreasing the upper bound  to the least value that is currently provable (and thus still correct). To this end, we analyze the exiting actions, i.e. with successors outside of the EC, for the following reason. If the play stays in the EC forever, the target is never reached and Minimizer wins. Therefore, Maximizer needs to pick some exiting action to avoid staying in the EC.
to the least value that is currently provable (and thus still correct). To this end, we analyze the exiting actions, i.e. with successors outside of the EC, for the following reason. If the play stays in the EC forever, the target is never reached and Minimizer wins. Therefore, Maximizer needs to pick some exiting action to avoid staying in the EC.
Left: Collapsing ECs in SG may lead to incorrect results. The Greek letters on the leaving arrows denote the values of the exiting actions. Right three figures: Correct collapsing in different cases, depending on the relationship of \(\alpha \) and \(\beta \). In contrast to MDP, some actions of the EC exiting the collapsed part have to be removed.
For the EC with the states \(\mathsf {s}\) and \(\mathsf {t}\) in Fig. 1, the only exiting action is \(\mathsf {c}\). In this example, since \(\mathsf {c}\) is the only exiting action,  is the highest possible upper bound that the EC can achieve. Thus, by decreasing the upper bound of all states in the EC to that numberFootnote 6, we still have a safe upper bound. Moreover, with this modification BVI converges in this example, intuitively because now the upper bound of \(\mathsf {t}\) depends on action \(\mathsf {c}\) as it should.
is the highest possible upper bound that the EC can achieve. Thus, by decreasing the upper bound of all states in the EC to that numberFootnote 6, we still have a safe upper bound. Moreover, with this modification BVI converges in this example, intuitively because now the upper bound of \(\mathsf {t}\) depends on action \(\mathsf {c}\) as it should.
For the example in Fig. 2, it is correct to decrease the upper bound to the maximal exiting one, i.e. \(\max \{\hat{\alpha },\hat{\beta }\}\), where  are the current approximations of \(\alpha \) and of \(\beta \). However, this itself does not ensure BVI convergence. Indeed, if for instance \(\hat{\alpha } < \hat{\beta }\) then deflating all states to \(\hat{\beta }\) is not tight enough, as values of \(\mathsf {p}\) and \(\mathsf {q}\) can even be bounded by \(\hat{\alpha }\). In fact, we have to find a certain sub-EC that corresponds to \(\hat{\alpha }\), in this case \(\{\mathsf {p,q}\}\) and set all its upper bounds to \(\hat{\alpha }\). We define and compute these sub-ECs in the next section.
are the current approximations of \(\alpha \) and of \(\beta \). However, this itself does not ensure BVI convergence. Indeed, if for instance \(\hat{\alpha } < \hat{\beta }\) then deflating all states to \(\hat{\beta }\) is not tight enough, as values of \(\mathsf {p}\) and \(\mathsf {q}\) can even be bounded by \(\hat{\alpha }\). In fact, we have to find a certain sub-EC that corresponds to \(\hat{\alpha }\), in this case \(\{\mathsf {p,q}\}\) and set all its upper bounds to \(\hat{\alpha }\). We define and compute these sub-ECs in the next section.
In summary, the general structure of our convergent BVI algorithm is to produce the sequence  by application of Bellman updates and occasionally find the relevant sub-ECs and deflate them. The main technical challenge is that states in an EC in SG can have different values, in contrast to the case of MDP.
by application of Bellman updates and occasionally find the relevant sub-ECs and deflate them. The main technical challenge is that states in an EC in SG can have different values, in contrast to the case of MDP.
4 Convergent Over-Approximation
In Sect. 4.1, we characterize SGs where Bellman equations have more solutions. Based on the analysis, subsequent sections show how to alter the procedure computing the sequence  over-approximating
over-approximating  so that the resulting tighter sequence
so that the resulting tighter sequence  still over-approximates
still over-approximates  , but also converges to
, but also converges to  . This ensures that thus modified BVI converges. Section 4.4 presents the learning-based variant of our BVI.
. This ensures that thus modified BVI converges. Section 4.4 presents the learning-based variant of our BVI.
4.1 Bloated End Components Cause Non-convergence
As we have seen in the example of Fig. 2, BVI generally does not converge due to ECs with a particular structure of the exiting actions. The analysis of ECs relies on the extremal values that can be achieved by exiting actions (in the example, \(\alpha \) and \(\beta \)). Given the value function  or just its current over-approximation
or just its current over-approximation  , we define the most profitable exiting action for Maximizer (denoted by \(\Box \)) and Minimizer (denoted by \(\bigcirc \)) as follows.
, we define the most profitable exiting action for Maximizer (denoted by \(\Box \)) and Minimizer (denoted by \(\bigcirc \)) as follows.
Definition 3
(  ). Given a set of states
). Given a set of states  and a function
and a function  (see footnote 2), the f-value of the best T-exiting action of Maximizer and Minimizer, respectively, is defined as
(see footnote 2), the f-value of the best T-exiting action of Maximizer and Minimizer, respectively, is defined as

with the convention that \(\max _\emptyset = 0\) and \(\min _\emptyset = 1\).
Example 1
In the example of Fig. 2 on the left with  and \(\alpha <\beta \), we have
and \(\alpha <\beta \), we have  ,
,  . It is due to \(\beta <1\) that BVI does not converge here. We generalize this in the following lemma. \(\triangle \)
. It is due to \(\beta <1\) that BVI does not converge here. We generalize this in the following lemma. \(\triangle \)
Lemma 1
Let T be an EC. For every m satisfying  , there is a solution
, there is a solution  to the Bellman equations, which on T is constant and equal to m.
to the Bellman equations, which on T is constant and equal to m.
Proof
(Idea). Intuitively, such a constant m is a solution to the Bellman equations on T for the following reasons. As both players prefer getting m to exiting and getting “only” the values of their respective  , they both choose to stay in the EC (and the extrema in the Bellman equations are realized on non-exiting actions). On the one hand, Maximizer (Bellman equations with \(\max \)) is hoping for the promised m, which is however not backed up by any actions actually exiting towards the target. On the other hand, Minimizer (Bellman equations with \(\min \)) does not realize that staying forever results in her optimal value 0 instead of m. \(\square \)
, they both choose to stay in the EC (and the extrema in the Bellman equations are realized on non-exiting actions). On the one hand, Maximizer (Bellman equations with \(\max \)) is hoping for the promised m, which is however not backed up by any actions actually exiting towards the target. On the other hand, Minimizer (Bellman equations with \(\min \)) does not realize that staying forever results in her optimal value 0 instead of m. \(\square \)
Corollary 1
If  for some EC T, then
for some EC T, then  .
.
Proof
Since there are \(m_1,m_2\) such that  , by Lemma 1 there are two different solutions to the Bellman equations. In particular,
, by Lemma 1 there are two different solutions to the Bellman equations. In particular,  , and BVI does not converge. \(\square \)
, and BVI does not converge. \(\square \)
In accordance with our intuition that ECs satisfying the above inequality should be deflated, we call them bloated.
Definition 4
(BEC). An EC T is called a bloated end component (BEC), if  .
.
Example 2
In the example of Fig. 2 on the left with \(\alpha <\beta \), the ECs \(\mathsf {\{p,q\}}\) and \(\mathsf {\{p,q,r\}}\) are  s. \(\triangle \)
s. \(\triangle \)
Example 3
If an EC T has no exiting actions of Minimizer (or no Minimizer’s states at all, as in an MDP), then  (the case with \(\min _\emptyset \)). Hence all numbers between
(the case with \(\min _\emptyset \)). Hence all numbers between  and 1 are a solution to the Bellman equations and
and 1 are a solution to the Bellman equations and  for all states \(s\in T\).
for all states \(s\in T\).
Analogously, if Maximizer does not have any exiting action in T, then it holds that  (the case with \(\max _\emptyset \)), T is a
(the case with \(\max _\emptyset \)), T is a  and all numbers between 0 and
and all numbers between 0 and  are a solution to the Bellman equations.
are a solution to the Bellman equations.
Note that in MDP all ECs belong to one player, namely Maximizer. Consequently, all ECs are  s except for ECs where Maximizer has an exiting action with value 1; all other ECs thus have to be collapsed (or deflated) to ensure BVI convergence in MDPs. Interestingly, all non-trivial ECs in MDPs are a problem, while in SGs through the presence of the other player some ECs can converge, namely if both players want to exit (See e.g. [KKKW18, Appendix A.3]). \(\triangle \)
s except for ECs where Maximizer has an exiting action with value 1; all other ECs thus have to be collapsed (or deflated) to ensure BVI convergence in MDPs. Interestingly, all non-trivial ECs in MDPs are a problem, while in SGs through the presence of the other player some ECs can converge, namely if both players want to exit (See e.g. [KKKW18, Appendix A.3]). \(\triangle \)
We show that  s are indeed the only obstacle for BVI convergence.
s are indeed the only obstacle for BVI convergence.
Theorem 1
If the \(\text {SG}\) contains no  s except for \(\{\mathfrak 0\}\) and \(\{\mathfrak 1\}\), then
s except for \(\{\mathfrak 0\}\) and \(\{\mathfrak 1\}\), then  .
.
Proof
(Sketch). Assume, towards a contradiction, that there is some state  with a positive difference
with a positive difference  . Consider the set D of states with the maximal difference. D can be shown to be an EC. Since it is not a
. Consider the set D of states with the maximal difference. D can be shown to be an EC. Since it is not a  there has to be an action exiting D and realizing the optimum in that state. Consequently, this action also has the maximal difference, and all its successors, too. Since some of the successors are outside of D, we get a contradiction with the maximality of D. \(\square \)
there has to be an action exiting D and realizing the optimum in that state. Consequently, this action also has the maximal difference, and all its successors, too. Since some of the successors are outside of D, we get a contradiction with the maximality of D. \(\square \)
In Sect. 4.2, we show how to eliminate  s by collapsing their “core” parts, called below MSECs (maximal simple end components). Since MSECs can only be identified with enough information about
s by collapsing their “core” parts, called below MSECs (maximal simple end components). Since MSECs can only be identified with enough information about  , Sect. 4.3 shows how to avoid direct a priori collapsing and instead dynamically deflate candidates for MSECs in a conservative way.
, Sect. 4.3 shows how to avoid direct a priori collapsing and instead dynamically deflate candidates for MSECs in a conservative way.
4.2 Static MSEC Decomposition
Now we turn our attention to SG with  s. Intuitively, since in a
s. Intuitively, since in a  all Minimizer’s exiting actions have a higher value than what Maximizer can achieve, Minimizer does not want to use any of his own exiting actions and prefers staying in the EC (or steering Maximizer towards his worse exiting actions). Consequently, only Maximizer wants to take an exiting action. In the MDP case he can pick any desirable one. Indeed, he can wait until he reaches a state where it is available. As a result, in MDP all states of an EC have the same value and can all be collapsed into one state. In the SG case, he may be restricted by Minimizer’s behaviour or even not given any chance to exit the EC at all. As a result, a
all Minimizer’s exiting actions have a higher value than what Maximizer can achieve, Minimizer does not want to use any of his own exiting actions and prefers staying in the EC (or steering Maximizer towards his worse exiting actions). Consequently, only Maximizer wants to take an exiting action. In the MDP case he can pick any desirable one. Indeed, he can wait until he reaches a state where it is available. As a result, in MDP all states of an EC have the same value and can all be collapsed into one state. In the SG case, he may be restricted by Minimizer’s behaviour or even not given any chance to exit the EC at all. As a result, a  may contain several parts (below denoted MSECs), each with different value, intuitively corresponding to different exits. Thus instead of MECs, we have to decompose into finer MSECs and only collapse these.
may contain several parts (below denoted MSECs), each with different value, intuitively corresponding to different exits. Thus instead of MECs, we have to decompose into finer MSECs and only collapse these.
Definition 5
(\(Simple~EC\)). An EC T is called simple (SEC), if for all  we have
we have  .
.
A SEC C is maximal (MSEC) if there is no SEC \(C'\) such that \(C\subsetneq C'\).
Intuitively, an EC is simple, if Minimizer cannot keep Maximizer away from his  . Independently of Minimizer’s decisions, Maximizer can reach the
. Independently of Minimizer’s decisions, Maximizer can reach the  almost surely, unless Minimizer decides to leave, in which case Maximizer could achieve an even higher value.
almost surely, unless Minimizer decides to leave, in which case Maximizer could achieve an even higher value.
Example 4
Assume \(\alpha <\beta \) in the example of Fig. 2. Then  is a SEC and an MSEC. Further observe that action \(\mathsf c\) is sub-optimal for Minimizer and removing it does not affect the value of any state, but simplifies the graph structure. Namely, it destructs the whole EC into several (here only one) SECs and some non-EC states (here \(\mathsf r\)). \(\triangle \)
is a SEC and an MSEC. Further observe that action \(\mathsf c\) is sub-optimal for Minimizer and removing it does not affect the value of any state, but simplifies the graph structure. Namely, it destructs the whole EC into several (here only one) SECs and some non-EC states (here \(\mathsf r\)). \(\triangle \)
Algorithm 2, called \({\textsf {FIND\_MSEC}}\), shows how to compute MSECs. It returns the set of all MSECs if called with parameter  . However, later we also call this function with other parameters
. However, later we also call this function with other parameters  . The idea of the algorithm is the following. The set X consists of Minimizer’s sub-optimal actions, leading to a higher value. As such they cannot be a part of any SEC and thus should be ignored when identifying SECs. (The previous example illustrates that ignoring X is indeed safe as it does not change the value of the game.) We denote the game
. The idea of the algorithm is the following. The set X consists of Minimizer’s sub-optimal actions, leading to a higher value. As such they cannot be a part of any SEC and thus should be ignored when identifying SECs. (The previous example illustrates that ignoring X is indeed safe as it does not change the value of the game.) We denote the game  where the available actions
where the available actions  are changed to the new available actions
are changed to the new available actions  (ignoring the Minimizer’s sub-optimal ones) as
(ignoring the Minimizer’s sub-optimal ones) as  . Once removed, Minimizer has no choices to affect the value and thus each EC is simple.
. Once removed, Minimizer has no choices to affect the value and thus each EC is simple.

Lemma 2
(Correctness of Algorithm 2). \(T \in \) FIND_MSEC  if and only if T is a MSEC.
if and only if T is a MSEC.
Proof
(Sketch). “If”: As T is an MSEC, all states in T have the value  , and hence also all actions that stay inside T have this value. Thus, no action that stays in T is removed by Line 3 and it is still a MEC in the modified game.
, and hence also all actions that stay inside T have this value. Thus, no action that stays in T is removed by Line 3 and it is still a MEC in the modified game.
“Only if”: If  , then T is a MEC of the game where the suboptimal available actions (those in X) of Minimizer have been removed. Hence for all
, then T is a MEC of the game where the suboptimal available actions (those in X) of Minimizer have been removed. Hence for all  , because intuitively Minimizer has no possibility to influence the value any further, since all actions that could do so were in X and have been removed. Since T is a MEC in the modified game, it certainly is an EC in the original game. Hence T is a SEC. The inclusion maximality follows from the fact that we compute MECs in the modified game. Thus T is an MSEC. \(\square \)
, because intuitively Minimizer has no possibility to influence the value any further, since all actions that could do so were in X and have been removed. Since T is a MEC in the modified game, it certainly is an EC in the original game. Hence T is a SEC. The inclusion maximality follows from the fact that we compute MECs in the modified game. Thus T is an MSEC. \(\square \)
Remark 1
(Algorithm with an oracle). In Sect. 3, we have seen that collapsing MECs does not ensure BVI convergence. Collapsing does not preserve the values, since in BECs we would be collapsing states with different values. Hence we want to collapse only MSECs, where the values are the same. If, moreover, we remove X in such a collapsed SG, then there are no (non-sink) ECs and BVI converges on this SG to the original value.
The difficulty with this algorithm is that it requires an oracle to compare values, for instance a sufficiently precise approximation of  . Consequently, we cannot pre-compute the MSECs, but have to find them while running BVI. Moreover, since the approximations converge only in the limit we may never be able to conclude on simplicity of some ECs. For instance, if \(\alpha =\beta \) in Fig. 2, and if the approximations converge at different speeds, then Algorithm 2 always outputs only a part of the EC, although the whole EC on \(\mathsf {\{p,q,r\}}\) is simple.
. Consequently, we cannot pre-compute the MSECs, but have to find them while running BVI. Moreover, since the approximations converge only in the limit we may never be able to conclude on simplicity of some ECs. For instance, if \(\alpha =\beta \) in Fig. 2, and if the approximations converge at different speeds, then Algorithm 2 always outputs only a part of the EC, although the whole EC on \(\mathsf {\{p,q,r\}}\) is simple.
In MDPs, all ECs are simple, because there is no second player to be resolved and all states in an EC have the same value. Thus for MDPs it suffices to collapse all MECs, in contrast to SG.
4.3 Dynamic MSEC Decomposition
Since MSECs cannot be identified from approximants of  for sure, we refrain from collapsingFootnote 7 and instead only decrease the over-approximation in the corresponding way. We call the method deflating, by which we mean decreasing the upper bound of all states in an EC to its
for sure, we refrain from collapsingFootnote 7 and instead only decrease the over-approximation in the corresponding way. We call the method deflating, by which we mean decreasing the upper bound of all states in an EC to its  , see Algorithm 3. The procedure \(\mathsf {DEFLATE}\) (called on the current upper bound
, see Algorithm 3. The procedure \(\mathsf {DEFLATE}\) (called on the current upper bound  ) decreases this upper bound to the minimum possible value according to the current approximation and thus prevents states from only depending on each other, as in SECs. Intuitively, it gradually approximates SECs and performs the corresponding adjustments, but does not commit to any of the approximations.
) decreases this upper bound to the minimum possible value according to the current approximation and thus prevents states from only depending on each other, as in SECs. Intuitively, it gradually approximates SECs and performs the corresponding adjustments, but does not commit to any of the approximations.

Lemma 3
(\(\mathsf {DEFLATE}\) is sound). For any  such that
such that  and any EC T,
and any EC T,  .
.
This allows us to define our BVI algorithm as the naive BVI with only the additional lines 3–4, see Algorithm 4.

Theorem 2
(Soundness and completeness). Algorithm 1 (calling Algorithm 4) produces monotonic sequences  under- and
under- and  over-approximating
over-approximating  , and terminates.
, and terminates.
Proof
(Sketch). The crux is to show that  converges to
converges to  . We assume towards a contradiction, that there exists a state
. We assume towards a contradiction, that there exists a state  with
with  . Then there exists a nonempty set of states X where the difference between
. Then there exists a nonempty set of states X where the difference between  and
and  is maximal. If the upper bound of states in X depends on states outside of X, this yields a contradiction, because then the difference between upper bound and value would decrease in the next Bellman update. So X must be an EC where all states depend on each other. However, if that is the case, calling \(\mathsf {DEFLATE}\) decreases the upper bound to something depending on the states outside of X, thus also yielding a contradiction. \(\square \)
is maximal. If the upper bound of states in X depends on states outside of X, this yields a contradiction, because then the difference between upper bound and value would decrease in the next Bellman update. So X must be an EC where all states depend on each other. However, if that is the case, calling \(\mathsf {DEFLATE}\) decreases the upper bound to something depending on the states outside of X, thus also yielding a contradiction. \(\square \)
Summary of Our Approach:
-
1.
We cannot collapse MECs, because we cannot collapse BECs with non-constant values.
-
2.
If we remove X (the sub-optimal actions of Minimizer) we can collapse MECs (now actually MSECs with constant values).
-
3.
Since we know neither X nor SECs we gradually deflate SEC approximations.
4.4 Learning-Based Algorithm
Asynchronous value iteration selects in each round a subset \(T\subseteq S\) of states and performs the Bellman update in that round only on T. Consequently, it may speed up computation if “important” states are selected. However, using the standard VI it is even more difficult to determine the current error bound. Moreover, if some states are not selected infinitely often the lower bound may not even converge.
In the setting of bounded value iteration, the current error bound is known for each state and thus convergence can easily be enforced. This gave rise to asynchronous VI, such as BRTDP (bounded real time dynamic programing) in the setting of stopping MDPs [MLG05], where the states are selected as those that appear on a simulation run. Very similar is the adaptation for general MDP [BCC+14]. In order to simulate a run, the transition probabilities determine how to resolve the probabilistic choice. In order to resolve the non-deterministic choice of Maximizer, the “most promising action” is taken, i.e., with the highest  . This choice is derived from a reinforcement algorithm called delayed Q-learning and ensures convergence while practically performing well [BCC+14].
. This choice is derived from a reinforcement algorithm called delayed Q-learning and ensures convergence while practically performing well [BCC+14].
In this section, we harvest our convergence results and BVI algorithm for SG, which allow us to trivially extend the asynchronous learning-based approach of BRTDP to SGs. On the one hand, the only difference to the MDP algorithm is how to resolve the choice for Minimizer. Since the situation is dual, we again pick the “most promising action”, in this case with the lowest  . On the other hand, the only difference to Algorithm 1 calling Algorithm 4 is that the Bellman updates of
. On the other hand, the only difference to Algorithm 1 calling Algorithm 4 is that the Bellman updates of  and
and  are performed on the states of the simulation run only, see lines 2–3 of Algorithm 5.
are performed on the states of the simulation run only, see lines 2–3 of Algorithm 5.

If  or
or  is reached in a simulation, we can terminate it. It can happen that the simulation cycles in an EC. To that end, we have a bound k on the maximum number of steps. The choice of k is discussed in detail in [BCC+14] and we use
is reached in a simulation, we can terminate it. It can happen that the simulation cycles in an EC. To that end, we have a bound k on the maximum number of steps. The choice of k is discussed in detail in [BCC+14] and we use  to guarantee the possibility of reaching sinks as well as exploring new states. If the simulation cycles in an EC, the subsequent call of \(\mathsf {DEFLATE}\) ensures that next time there is a positive probability to exit this EC. Further details can be found in [KKKW18, Appendix A.4].
to guarantee the possibility of reaching sinks as well as exploring new states. If the simulation cycles in an EC, the subsequent call of \(\mathsf {DEFLATE}\) ensures that next time there is a positive probability to exit this EC. Further details can be found in [KKKW18, Appendix A.4].
5 Experimental Results
We implemented both our algorithms as an extension of PRISM-games [CFK+13a], a branch of PRISM [KNP11] that allows for modelling \(\text {SGs}\), utilizing previous work of [BCC+14, Ujm15] for MDP and SG with single-player ECs. We tested the implementation on the SGs from the PRISM-games case studies [gam] that have reachability properties and one additional model from [CKJ12] that was also used in [Ujm15]. We compared the results with both the explicit and the hybrid engine of PRISM-games, but since the models are small both of them performed similar and we only display the results of the hybrid engine in Table 1.
Furthermore we ran experiments on MDPs from the PRISM benchmark suite [KNP12]. We compared our results there to the hybrid and explicit engine of PRISM, the interval iteration implemented in PRISM [HM17], the hybrid engine of Storm [DJKV17a] and the BRTDP implementation of [BCC+14].
Recall that the aim of the paper is not to provide a faster VI algorithm, but rather the first guaranteed one. Consequently, the aim of the experiments is not to show any speed ups, but to experimentally estimate the overhead needed for computing the guarantees.
For information on the technical details of the experiments, all the models and the tables for the experiments on MDPs we refer to [KKKW18, Appendix B]. Note that although some of the SG models are parametrized they could only be scaled by manually changing the model file, which complicates extensive benchmarking.
Although our approaches compute the additional upper bound to give the convergence guarantees, for each of the experiments one of our algorithms performed similar to PRISM-games. Table 1 shows this result for three of the four SG models in the benchmarking set. On the fourth model, PRISM’s pre-computations already solve the problem and hence it cannot be used to compare the approaches. For completeness, the results are displayed in [KKKW18, Appendix B.5].
Whenever there are few MSECs, as in mdsm and cdmsn, BVI performs like PRISM-games, because only little time is used for deflating. Apparently the additional upper bound computation takes very little time in comparison to the other tasks (e.g. parsing, generating the model, pre-computation) and does not slow down the verification significantly. For cloud, BVI is slower than PRISM-games, because there are thousands of MSECs and deflating them takes over 80% of the time. This comes from the fact that we need to compute the expensive end component decomposition for each deflating step. BRTDP performs well for cloud, because in this model, as well as generally often if there are many MECs [BCC+14], only a small part of the state space is relevant for convergence. For the other models, BRTDP is slower than the deterministic approaches, because the models are so small that it is faster to first construct them completely than to explore them by simulation.
Our more extensive experiments on MDPs compare the guaranteed approaches based on collapsing (i.e. learning-based from [BCC+14] and deterministic from [HM17]) to our guaranteed approaches based on deflating (so BRTDP and BVI). Since both learning-based approaches as well as both deterministic approaches perform similarly (see Table 2 in [KKKW18, Appendix B]), we conclude that collapsing and deflating are both useful for practical purposes, while the latter is also applicable to SGs. Furthermore we compared the usual unguaranteed value iteration of PRISM’s explicit engine to BVI and saw that our guaranteed approach did not take significantly more time in most cases. This strengthens the point that the overhead for the computation of the guarantees is negligible.
6 Conclusions
We have provided the first stopping criterion for value iteration on simple stochastic games and an anytime algorithm with bounds on the current error (guarantees on the precision of the result). The main technical challenge was that states in end components in SG can have different values, in contrast to the case of MDP. We have shown that collapsing is in general not possible, but we utilized the analysis to obtain the procedure of deflating, a solution on the original graph. Besides, whenever a SEC is identified for sure it can be collapsed and the two techniques of collapsing and deflating can thus be combined.
The experiments indicate that the price to pay for the overhead to compute the error bound is often negligible. For each of the available models, at least one of our two implementations has performed similar to or better than the standard approach that yields no guarantees. Further, the obtained guarantees open the door to (e.g. learning-based) heuristics which treat only a part of the state space and can thus potentially lead to huge improvements. Surprisingly, already our straightforward adaptation of such an algorithm for MDP to SG yields interesting results, palliating the overhead of our non-learning method, despite the most naive implementation of deflating. Future work could reveal whether other heuristics or more efficient implementation can lead to huge savings as in the case of MDP [BCC+14].
Notes
- 1.
Formally, the problem is to decide, for a given \(p\in [0,1]\) whether Maximizer has a strategy ensuring probability at least p to reach the target.
- 2.
Throughout the paper, for any function \(f:S\rightarrow [0,1]\) we overload the notation and also write
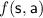 meaning
meaning 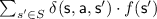 .
. - 3.
All states of an EC are merged into one, all leaving actions are preserved and all other actions are discarded. For more detail see [KKKW18, Appendix A.1].
- 4.
For the straightforward pseudocode, see [KKKW18, Appendix A.2].
- 5.
Precisely, we consider them to stand for a probabilistic branching with probability \(\alpha \) (or \(\beta \)) to
 and with the remaining probability to
and with the remaining probability to 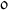 . To avoid clutter in the figure, we omit this branching and depict only the value.
. To avoid clutter in the figure, we omit this branching and depict only the value. - 6.
We choose the name “deflating” to evoke decreasing the overly high “pressure” in the EC until it equalizes with the actual “pressure” outside.
- 7.
Our subsequent method can be combined with local collapsing whenever the lower and upper bounds on
 are conclusive.
are conclusive.
References
Ashok, P., Chatterjee, K., Daca, P., Křetínský, J., Meggendorfer, T.: Value iteration for long-run average reward in Markov decision processes. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10426, pp. 201–221. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63387-9_10
Andersson, D., Miltersen, P.B.: The complexity of solving stochastic games on graphs. In: Dong, Y., Du, D.-Z., Ibarra, O. (eds.) ISAAC 2009. LNCS, vol. 5878, pp. 112–121. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10631-6_13
Arslan, G., Yüksel, S.: Decentralized Q-learning for stochastic teams and games. IEEE Trans. Autom. Control 62(4), 1545–1558 (2017)
Busoniu, L., Babuska, R., De Schutter, B.: A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man Cybern. Part C 38(2), 156–172 (2008)
Brázdil, T., Chatterjee, K., Chmelík, M., Forejt, V., Křetínský, J., Kwiatkowska, M., Parker, D., Ujma, M.: Verification of Markov decision processes using learning algorithms. In: Cassez, F., Raskin, J.-F. (eds.) ATVA 2014. LNCS, vol. 8837, pp. 98–114. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11936-6_8
Baier, C., Katoen, J.-P.: Principles of Model Checking (2008)
Baier, C., Klein, J., Leuschner, L., Parker, D., Wunderlich, S.: Ensuring the reliability of your model checker: interval iteration for Markov decision processes. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10426, pp. 160–180. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63387-9_8
Brafman, R.I., Tennenholtz, M.: A near-optimal polynomial time algorithm for learning in certain classes of stochastic games. Artif. Intell. 121(1–2), 31–47 (2000)
Chatterjee, K., Fijalkow, N.: A reduction from parity games to simple stochastic games. In: GandALF, pp. 74–86 (2011)
Chen, T., Forejt, V., Kwiatkowska, M., Parker, D., Simaitis, A.: PRISM-games: a model checker for stochastic multi-player games. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 185–191. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36742-7_13
Chatterjee, K., Henzinger, T.A.: Value iteration. In: Grumberg, O., Veith, H. (eds.) 25 Years of Model Checking. LNCS, vol. 5000, pp. 107–138. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69850-0_7
Chatterjee, K., Henzinger, T.A., Jobstmann, B., Radhakrishna, A.: Gist: a solver for probabilistic games. In: Touili, T., Cook, B., Jackson, P. (eds.) CAV 2010. LNCS, vol. 6174, pp. 665–669. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14295-6_57
Calinescu, R., Kikuchi, S., Johnson, K.: Compositional reverification of probabilistic safety properties for large-scale complex IT systems. In: Calinescu, R., Garlan, D. (eds.) Monterey Workshop 2012. LNCS, vol. 7539, pp. 303–329. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34059-8_16
Cheng, C.-H., Knoll, A., Luttenberger, M., Buckl, C.: GAVS+: an open platform for the research of algorithmic game solving. In: Abdulla, P.A., Leino, K.R.M. (eds.) TACAS 2011. LNCS, vol. 6605, pp. 258–261. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19835-9_22
Chen, T., Kwiatkowska, M., Simaitis, A., Wiltsche, C.: Synthesis for multi-objective stochastic games: an application to autonomous urban driving. In: Joshi, K., Siegle, M., Stoelinga, M., D’Argenio, P.R. (eds.) QEST 2013. LNCS, vol. 8054, pp. 322–337. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40196-1_28
Cámara, J., Moreno, G.A., Garlan, D.: Stochastic game analysis and latency awareness for proactive self-adaptation. In: 9th International Symposium on Software Engineering for Adaptive and Self-Managing Systems, SEAMS 2014, Proceedings, Hyderabad, India, 2–3 June 2014, pp. 155–164 (2014)
Condon, A.: The complexity of stochastic games. Inf. Comput. 96(2), 203–224 (1992)
Courcoubetis, C., Yannakakis, M.: The complexity of probabilistic verification. J. ACM 42(4), 857–907 (1995)
Dehnert, C., Junges, S., Katoen, J.-P., Volk, M.: A Storm is coming: a modern probabilistic model checker. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 592–600. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_31
PRISM-games Case Studies. prismmodelchecker.org/games/casestudies.php. Accessed 18 Sept 2017
Hoffman, A.J., Karp, R.M.: On nonterminating stochastic games. Manag. Sci. 12(5), 359–370 (1966)
Haddad, S., Monmege, B.: Interval iteration algorithm for MDPs and IMDPs. Theor. Comput. Sci. 735, 111–131 (2018). https://doi.org/10.1016/j.tcs.2016.12.003
Kelmendi, E., Krämer, J., Křetínský, J., Weininger, M.: Value iteration for simple stochastic games: stopping criterion and learning algorithm. Technical report abs/1804.04901, arXiv.org (2018)
Kattenbelt, M., Kwiatkowska, M.Z., Norman, G., Parker, D.: A game-based abstraction-refinement framework for Markov decision processes. Formal Methods Syst. Des. 36(3), 246–280 (2010)
Křetínský, J., Meggendorfer, T.: Efficient strategy iteration for mean payoff in Markov decision processes. In: D’Souza, D., Narayan Kumar, K. (eds.) ATVA 2017. LNCS, vol. 10482, pp. 380–399. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68167-2_25
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_47
Kwiatkowska, M., Norman, G., Parker, D.: The prism benchmark suite. In: 9th International Conference on Quantitative Evaluation of Systems (QEST 2012), pp. 203–204. IEEE (2012)
LaValle, S.M.: Robot motion planning: a game-theoretic foundation. Algorithmica 26(3–4), 430–465 (2000)
Li, J., Liu, W.: A novel heuristic Q-learning algorithm for solving stochastic games. In: IJCNN, pp. 1135–1144 (2008)
Martin, D.A.: Borel determinacy. Ann. Math. 102, 363–371 (1975)
Mcmahan, H.B., Likhachev, M., Gordon, G.J.: Bounded real-time dynamic programming: RTDP with monotone upper bounds and performance guarantees. In: ICML 2005, pp. 569–576 (2005)
Puterman, M.L.: Markov Decision Processes: Discrete Stochastic Dynamic Programming. Wiley, Hoboken (2014)
Svorenová, M., Kwiatkowska, M.: Quantitative verification and strategy synthesis for stochastic games. Eur. J. Control 30, 15–30 (2016)
Tcheukam, A., Tembine, H.: One swarm per queen: a particle swarm learning for stochastic games. In: SASO, pp. 144–145 (2016)
Ujma, M.: On verification and controller synthesis for probabilistic systems at runtime. Ph.D. thesis, Wolfson College, Oxford (2015)
Wen, M., Topcu, U.: Probably approximately correct learning in stochastic games with temporal logic specifications. In: IJCAI, pp. 3630–3636 (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis>This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara><SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Kelmendi, E., Krämer, J., Křetínský, J., Weininger, M. (2018). Value Iteration for Simple Stochastic Games: Stopping Criterion and Learning Algorithm. In: Chockler, H., Weissenbacher, G. (eds) Computer Aided Verification. CAV 2018. Lecture Notes in Computer Science(), vol 10981. Springer, Cham. https://doi.org/10.1007/978-3-319-96145-3_36
Download citation
DOI: https://doi.org/10.1007/978-3-319-96145-3_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96144-6
Online ISBN: 978-3-319-96145-3
eBook Packages: Computer ScienceComputer Science (R0)



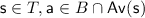 we do not have
we do not have 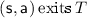 ,
,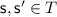 there is a finite path
there is a finite path  , i.e. the path stays inside T and only uses actions in B.
, i.e. the path stays inside T and only uses actions in B.

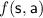 meaning
meaning 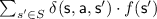 .
. and with the remaining probability to
and with the remaining probability to 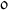 . To avoid clutter in the figure, we omit this branching and depict only the value.
. To avoid clutter in the figure, we omit this branching and depict only the value. are conclusive.
are conclusive.