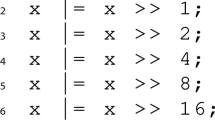Abstract
Program synthesis is the mechanised construction of software. One of the main difficulties is the efficient exploration of the very large solution space, and tools often require a user-provided syntactic restriction of the search space. We propose a new approach to program synthesis that combines the strengths of a counterexample-guided inductive synthesizer with those of a theory solver, exploring the solution space more efficiently without relying on user guidance. We call this approach CEGIS(\(\mathcal {T}\)), where \(\mathcal {T}\) is a first-order theory. In this paper, we focus on one particular challenge for program synthesizers, namely the generation of programs that require non-trivial constants. This is a fundamentally difficult task for state-of-the-art synthesizers. We present two exemplars, one based on Fourier-Motzkin (FM) variable elimination and one based on first-order satisfiability. We demonstrate the practical value of CEGIS(\(\mathcal {T}\)) by automatically synthesizing programs for a set of intricate benchmarks.
Supported by ERC project 280053 (CPROVER) and the H2020 FET OPEN 712689 SC\(^2\). Cristina David is supported by the Royal Society University Research Fellowship UF160079.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Counterexample-guided Inductive Synthesis (CEGIS)
- Theory Solver
- Program Synthesizer
- Fourier Motzkin (FM)
- Efficient Exploration
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction
Program synthesis is the problem of finding a program that meets a correctness specification given as a logical formula. This is an active area of research in which substantial progress has been made in recent years.
In full generality, program synthesis is an exceptionally difficult problem, and thus, the research community has explored pragmatic restrictions. One particularly successful direction is Syntax-Guided Program Synthesis (SyGuS) [2]. The key idea of SyGuS is that the user supplements the logical specification with a syntactic template for the solution. Leveraging the user’s intuition, SyGuS reduces the solution space size substantially, resulting in significant speed-ups.
Unfortunately, it is difficult to provide the syntactic template in many practical applications. A very obvious exemplar of the limits of the syntax-guided approach are programs that require non-trivial constants. In such a scenario, the syntax-guided approach requires that the user provides the exact value of the constants in the solution.
For illustration, let’s consider a user who wants to synthesize a program that rounds up a given 32-bit unsigned number x to the next highest power of two. If we denote the function computed by the program by f(x), then the specification can be written as \( x<2^{31}{\Rightarrow } f(x) \& {(-f(x))}=f(x) \,\wedge \, f(x) \ge x \,\wedge \, 2x \ge f(x)\). The first conjunct forces f(x) to be a power of two, the other requires it to be the next highest. A possible solution for this is given by the following C program:

It is improbable that the user knows that the constants in the solution are exactly 1, 2, 4, 8, 16, and thus, she will be unable to explicitly restrict the solution space. As a result, synthesizers are very likely to enumerate possible combinations of constants, which is highly inefficient.
In this paper we propose a new approach to program synthesis that combines the strengths of a counterexample-guided inductive synthesizer with those of a solver for a first-order theory in order to perform a more efficient exploration of the solution space, without relying on user guidance. Our inspiration for this proposal is DPLL(\(\mathcal {T}\)), which has boosted the performance of solvers for many fragments of quantifier-free first-order logic [16, 23]. DPLL(\(\mathcal {T}\)) combines reasoning about the Boolean structure of a formula with reasoning about theory facts to decide satisfiability of a given formula.
In an attempt to generate similar technological advancements in program synthesis, we propose a new algorithm for program synthesis called CounterExample-Guided Inductive Synthesis(\(\mathcal {T}\)), where \(\mathcal {T}\) is a given first-order theory for which we have a specialised solver. Similar to its counterpart DPLL(\(\mathcal {T}\)), the CEGIS(\(\mathcal {T}\)) architecture features communication between a synthesizer and a theory solver, which results in a much more efficient exploration of the search space.
While standard CEGIS architectures [19, 30] already make use of SMT solvers, the typical role of such a solver is restricted to validating candidate solutions and providing concrete counterexamples that direct subsequent search. By contrast, CEGIS(\(\mathcal {T}\)) allows the theory solver to communicate generalised constraints back to the synthesizer, thus enabling more significant pruning of the search space.
There are instances of more sophisticated collaboration between a program synthesizer and theory solvers. The most obvious such instance is the program synthesizer inside the CVC4 SMT solver [27]. This approach features a very tight coupling between the two components (i.e., the synthesizer and the theory solvers) that takes advantage of the particular strengths of the SMT solver by reformulating the synthesis problem as the problem of refuting a universally quantified formula (SMT solvers are better at refuting universally quantified formulae than at proving them). Conversely, in our approach we maintain a clear separation between the synthesizer and the theory solver while performing comprehensive and well-defined communication between the two components. This enables the flexible combination of CEGIS with a variety of theory solvers, which excel at exploring different solution spaces.
Contributions
-
We propose CEGIS(\(\mathcal {T}\)), a program synthesis architecture that facilitates the communication between an inductive synthesizer and a solver for a first-order theory, resulting in an efficient exploration of the search space.
-
We present two exemplars of this architecture, one based on Fourier-Motzkin (FM) variable elimination [7] and one using an off-the-shelf SMT solver.
-
We have implemented CEGIS(\(\mathcal {T}\)) and compared it against state-of-the-art program synthesizers on benchmarks that require intricate constants in the solution.
2 Preliminaries
2.1 The Program Synthesis Problem
Program synthesis is the task of automatically generating programs that satisfy a given logical specification. A program synthesizer can be viewed as a solver for existential second-order logic. An existential second-order logic formula allows quantification over functions as well as ground terms [28].
The input specification provided to a program synthesizer is of the form \(\exists P .\, \forall {\varvec{x}}.\, \sigma (P, {\varvec{x}})\), where P ranges over functions (where a function is represented by the program computing it), \({\varvec{x}}\) ranges over ground terms, and \(\sigma \) is a quantifier-free formula.
2.2 CounterExample Guided Inductive Synthesis
CounterExample-Guided Inductive Synthesis (CEGIS) is a popular approach to program synthesis, and is an iterative process. Each iteration performs inductive generalisation based on counterexamples provided by a verification oracle. Essentially, the inductive generalisation uses information about a limited number of inputs to make claims about all the possible inputs in the form of candidate solutions.
The CEGIS framework is illustrated in Fig. 1 and consists of two phases: the synthesis phase and the verification phase. Given the specification of the desired program, \(\sigma \), the inductive synthesis procedure generates a candidate program \(P^*\) that satisfies \(\sigma (P^*,{\varvec{x}})\) for a subset \({\varvec{x}}_{ inputs }\) of all possible inputs. The candidate program \(P^*\) is passed to the verification phase, which checks whether it satisfies the specification \(\sigma (P^*, {\varvec{x}})\) for all possible inputs. This is done by checking whether \(\lnot \sigma (P^*, {\varvec{x}})\) is unsatisfiable. If so, \(\forall x.\lnot \sigma (P^*, {\varvec{x}})\) is valid, and we have successfully synthesized a solution and the algorithm terminates. Otherwise, the verifier produces a counterexample \({\varvec{c}}\) from the satisfying assignment, which is then added to the set of inputs passed to the synthesizer, and the loop repeats.
The method used in the synthesis and verification blocks varies in different CEGIS implementations; our CEGIS implementation uses Bounded Model Checking [8].
2.3 DPLL(\(\mathcal {T}\))
DPLL(\(\mathcal {T}\)) is an extension of the DPLL algorithm, used by most propositional SAT solvers, by a theory \(\mathcal {T}\). We give a brief overview of DPLL(\(\mathcal {T}\)) and compare DPLL(\(\mathcal {T}\)) with CEGIS(\(\mathcal {T}\)).
Given a formula F from a theory \(\mathcal {T}\), a propositional formula \(F_p\) is created from F in which the theory atoms are replaced by Boolean variables (the “propositional skeleton”). The standard DPLL algorithm, comprising Decide, Boolean Constraint Propagation (BCP), Analyze-Conflict and BackTrack, generates an assignment to the Boolean variables in \(F_p\), as illustrated in Fig. 2. The theory solver then checks whether this assignment is still consistent when the Boolean variables are replaced by their original atoms. If so, a satisfying assignment for F has been found. Otherwise, a constraint over the Boolean variables in \(F_p\) is passed back to Decide, and the process repeats.
In the very first SMT solvers, a full assignment to the Boolean variables was obtained, and then the theory solver returned only a single counterexample, similar to the implementations of CEGIS that are standard now. Such SMT solvers are prone to enumerating all possible counterexamples, and so the key improvement in DPLL(\(\mathcal {T}\)) was the ability to pass back a more general constraint over the variables in the formula as a counterexample [16]. Furthermore, modern variants of DPLL(\(\mathcal {T}\)) call the theory solver on partial assignments to the variables in \(F_p\). Our proposed, new synthesis algorithm offers equivalents of both of these ideas that have improved DPLL(\(\mathcal {T}\)).
3 Motivating Example
In each iteration of a standard CEGIS loop, the communication from the verification phase back to the synthesis phase is restricted to concrete counterexamples. This is particularly detrimental when synthesizing programs that require non-trivial constants. In such a setting, it is typical that a counterexample provided by the verification phase only eliminates a single candidate solution and, consequently, the synthesizer ends up enumerating possible constants.
For illustration, let’s consider the trivial problem of synthesizing a function f(x) where \(f(x) < 0\) if \(x < 334455\) and \(f(x) = 0\), otherwise. One possible solution is \(f(x)= ite ~ (x<334455) {-1} 0\), where \( ite \) stands for if then else.
In order to make the synthesis task even simpler, we are going to assume that we know a part of this solution, namely we know that it must be of the form \(f(x)= ite ~ (x< \textsf {?})~ {-1}~ 0\), where “\( \textsf {?}\)” is a placeholder for the missing constant that we must synthesize. A plausible scenario for a run of CEGIS is presented next: the synthesis phase guesses \(f(x)= ite ~ (x<0)~ {-1}~ 0\), for which the verification phase returns \(x=0\) as a counterexample. In the next iteration of the CEGIS loop, the synthesis phase guesses \(f(x)= ite (x<1) {-1}~ 0\) (which works for \(x=0\)) and the verifier produces \(x=1\) as a counterexample. Following the same pattern, the synthesis phase will enumerate all the candidates
before finding the solution. This is caused by the fact that each of the concrete counterexamples \(0,\ldots ,334454\) eliminate one candidate only from the solution space. Consequently, we need to propagate more information from the verifier to the synthesis phase in each iteration of the CEGIS loop.
Proving Properties of Programs. Synthesis engines can be used as reasoning engines in program analysers, and constants are important for this application. For illustration, let’s consider the very simple program below, which increments a variable x from 0 to 100000 and asserts that its value is less than 100005 on exit from the loop.

Proving the safety of such a program, i.e., that the assertion at line 3 is not violated in any execution of the program, is a task well-suited for synthesis (the Syntax Guided Synthesis Competition [5] has a track dedicated to synthesizing safety invariants). For this example, a safety invariant is \(x<100002\), which holds on entrance to the loop, is inductive with respect to the loop’s body, and implies the assertion on exit from the loop.
While it is very easy for a human to deduce this invariant, the need for a non-trivial constant makes it surprisingly difficult for state-of-the-art synthesizers: both CVC4 (version 1.5) [27] and EUSolver (version 2017-06-15) [3] fail to find a solution in an hour.
4 CEGIS(\(\mathcal {T}\))
4.1 Overview
In this section, we describe the architecture of CEGIS(\(\mathcal {T}\)), which is obtained by augmenting the standard CEGIS loop with a theory solver. As we are particularly interested in the synthesis of programs with constants, we present CEGIS(\(\mathcal {T}\)) from this particular perspective. In such a setting, CEGIS is responsible for synthesizing program skeletons, whereas the theory solver generates constraints over the literals that denote constants. These constraints are then propagated back to the synthesizer.
In order to explain the main ideas behind CEGIS(\(\mathcal {T}\)) in more detail, we first differentiate between a candidate solution, a candidate solution skeleton, a generalised candidate solution and a final solution.
Definition 1
(Candidate solution). Using the notation in Sect. 2.2, a program P is a candidate solution if \(\forall {\varvec{x}}_{ inputs }.\sigma (P,{\varvec{x}}_{ inputs })\) is true for some subset \({\varvec{x}}_{ inputs }\) of all possible \({\varvec{x}}\).
Definition 2
(Candidate solution skeleton). Given a candidate solution P, the skeleton of P, denoted by \(P[ \textsf {?}]\), is obtained by replacing each constant in P with a hole.
Definition 3
(Generalised candidate solution). Given a candidate solution skeleton \(P[ \textsf {?}]\), we obtain a generalised candidate \(P[{\varvec{v}}]\) by filling each hole in \(P[ \textsf {?}]\) with a distinct symbolic variable, i.e., variable \(v_i\) will correspond to the i-th hole. Then \({\varvec{v}}=[v_1, \ldots , v_n]\), where n denotes the number of holes in \(P[ \textsf {?}]\).
Definition 4
(Final solution). A candidate solution P is a final solution if the formula \(\forall {\varvec{x}}.\sigma (P,{\varvec{x}})\) is valid.
Example 1
(Candidate solution, candidate solution skeleton, generalised candidate solution, final solution). Given the example in Sect. 3, if \({\varvec{x}}_{ inputs }=\{0\}\), then \(f(x)=-2\) is a candidate solution. The corresponding candidate skeleton is \(f[ \textsf {?}](x)= \textsf {?}\) and the generalised candidate is \(f[v_1](x)=v_1\). A final solution for this example is \(f(x)= ite ~(x<334455)~ {-1}~ 0.\)
The communication between the synthesizer and the theory solver in CEGIS(\(\mathcal {T}\)) is illustrated in Fig. 3 and can be described as follows:
-
The CEGIS architecture (enclosed in a red rectangle) deduces the candidate solution \(P^*\), which is provided to the theory solver.
-
The theory solver (enclosed in a blue rectangle) obtains the skeleton \(P^*[ \textsf {?}]\) of \(P^*\) and generalises it to \(P^*[{\varvec{v}}]\) in the box marked constant removal. Subsequently, Deduction attempts to find a constraint over \({\varvec{v}}\) describing those values for which \(P^*[{\varvec{v}}]\) is a final solution. This constraint is propagated back to CEGIS. Whenever there is no valuation of \({\varvec{v}}\) for which \(P^*[{\varvec{v}}]\) becomes a final solution, the constraint needs to block the current skeleton \(P^*[ \textsf {?}]\).
The CEGIS(\(\mathcal {T}\)) algorithm is given as Algorithm 1 and proceeds as follows:
-
CEGIS synthesis phase: checks the satisfiability of \(\forall {\varvec{x}}_{ inputs }.\, \sigma (P, {\varvec{x}}_{ inputs })\) where \({\varvec{x}}_{ inputs }\) is a subset of all possible \({\varvec{x}}\) and obtains a candidate solution \(P^*\). If this formula is unsatisfiable, then the synthesis problem has no solution.
-
CEGIS verification phase: checks whether there exists a concrete counterexample for the current candidate solution by checking the satisfiability of the formula \(\lnot \sigma (P^*, {\varvec{x}})\). If the result is UNSAT, then \(P^*\) is a final solution to the synthesis problem. If the result is SAT, a concrete counterexample \({\varvec{cex}}\) can be extracted from the satisfying assignment.
-
Theory solver: if \(P^*\) contains constants, then they are eliminated, resulting in the \(P^*[ \textsf {?}]\) skeleton, which is afterwards generalised to \(P^*[{\varvec{v}}]\). The goal of the theory solver is to find \(\mathcal {T}\)-implied literals and communicate them back to the CEGIS part in the form of a constraint, \(C(P, P^*, {\varvec{v}})\). In Algorithm 1, this is done by \( Deduction (\sigma , P^*[{\varvec{v}}])\). The result of \( Deduction (\sigma , P^*[{\varvec{v}}])\) is of the following form: whenever there exists a valuation of \({\varvec{v}}\) for which the current skeleton \(P^*[ \textsf {?}]\) is a final solution, \( res = true \) and \(C(P, P^*, {\varvec{v}})=\bigwedge _{i=1{\cdot }n} v_i=c_i\), where \(c_i\) are constants; otherwise, \( res = false \) and \(C(P, P^*, {\varvec{v}})\) needs to block the current skeleton \(P^*[ \textsf {?}]\), i.e., \(C(P, P^*, {\varvec{v}})=P[ \textsf {?}] \ne P^*[ \textsf {?}]\).
-
CEGIS learning phase: adds new information to the problem specification. If we did not use the theory solver (i.e., the candidate \(P^*\) found by the synthesizer did not contain constants or the problem specification was out of the theory solver’s scope), then the learning would be limited to adding the concrete counterexample \({\varvec{cex}}\) obtained from the verification phase to the set \({\varvec{x}}_{ inputs }\). However, if the theory solver is used and returns \( res = true \), then the second element in the tuple contains valuations for \({\varvec{v}}\) such that \(P^*[{\varvec{v}}]\) is a final solution. If \( res = false \), then the second element blocks the current skeleton and needs to be added to \(\sigma \).

4.2 CEGIS(\(\mathcal {T}\)) with a Theory Solver Based on FM Elimination
In this section we describe a theory solver based on FM variable elimination. Other techniques for eliminating existentially quantified variables can be used. For instance, one might use cylindrical algebraic decomposition [9] for specifications with non-linear arithmetic. In our case, whenever the specification \(\sigma \) does not belong to linear arithmetic, the FM theory solver is not called.
As mentioned above, we need to produce a constraint over variables \({\varvec{v}}\) describing the situation when \(P^*[{\varvec{v}}]\) is a final solution. For this purpose, we consider the formula \(\exists {\varvec{x}}.\, \lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}}),\) where \({\varvec{v}}\) is a satisfiability witness if the specification \(\sigma \) admits a counterexample \({\varvec{x}}\) for \(P^*\). Let \(E({\varvec{v}})\) be the formula obtained by eliminating \({\varvec{x}}\) from \(\exists {\varvec{x}}.\, \lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}})\). If \(\lnot E({\varvec{v}})\) is satisfiable, any satisfiability witness gives us the necessary valuation for \({\varvec{v}}\):
If \(\lnot E({\varvec{v}})\) is UNSAT, then the current skeleton \(P^*[ \textsf {?}]\) needs to be blocked. This reasoning is supported by Lemma 1 and Corollary 1.
Lemma 1
Let \(E({\varvec{v}})\) be the formula that is obtained by eliminating \({\varvec{x}}\) from \(\exists {\varvec{x}}.\, \lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}})\). Then, any witness \({\varvec{v}}^{\#}\) to the satisfiability of \(\lnot E({\varvec{v}})\) gives us a final solution \(P^*[{\varvec{v}}^{\#}]\) to the synthesis problem.
Proof
From the fact that \(E({\varvec{v}})\) is obtained by eliminating \({\varvec{x}}\) from \(\exists {\varvec{x}}.\, \lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}})\), we get that \(E({\varvec{v}})\) is equivalent with \(\exists {\varvec{x}}.\, \lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}})\) (we use \(\equiv \) to denote equivalence):
Then:
Consequently, any \({\varvec{v}}^{\#}\) satisfying \(\lnot E({\varvec{v}})\) also satisfies \(\forall {\varvec{x}}.\, \sigma (P^*[{\varvec{v}}], {\varvec{x}})\). From \(\forall {\varvec{x}}.\, \sigma (P^*[{\varvec{v}}^{\#}], {\varvec{x}})\) and Definition 4 we get that \(P^*[{\varvec{v}}^{\#}]\) is a final solution.
Corollary 1
Let E(v) be the formula that is obtained by eliminating \({\varvec{x}}\) from \(\exists {\varvec{x}}.\, \lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}})\). If \(\lnot E({\varvec{v}})\) is unsatisfiable, then the corresponding synthesis problem does not admit a solution for the skeleton \(P^*[ \textsf {?}]\).
Proof
Given that \(\lnot E({\varvec{v}}) \equiv \forall {\varvec{x}}.\, \sigma (P^*[{\varvec{v}}], {\varvec{x}})\), if \(\lnot E({\varvec{v}})\) is unsatisfiable, so is \(\forall {\varvec{x}}.\, \sigma (P^*[{\varvec{v}}], {\varvec{x}})\), meaning that there is no valuation for \({\varvec{v}}\) such that the specification \(\sigma \) is obeyed for all inputs \({\varvec{x}}\).
For the current skeleton \(P^*[ \textsf {?}]\), the constraint \(E({\varvec{v}})\) generalises the concrete counterexample \({\varvec{cex}}\) (found during the CEGIS verification phase) in the sense that the instantiation \({\varvec{v}}^{\#}\) of \({\varvec{v}}\) for which \({\varvec{cex}}\) failed the specification, i.e., \(\lnot \sigma (P^*[{\varvec{v}}^{\#}], {\varvec{cex}})\), is a satisfiability witness for \(E({\varvec{v}})\). This is true as \(E({\varvec{v}}) \equiv \exists {\varvec{x}}.\, \lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}})\), which means that the satisfiability witness \(({\varvec{{\varvec{v}}}}^{\#},{\varvec{cex}})\) for \(\lnot \sigma (P^*[{\varvec{v}}], {\varvec{x}})\) projected on \({\varvec{v}}\) is a satisfiability witness for \(E({\varvec{v}})\).
Disjunction. The specification \(\sigma \) and the candidate solution may contain disjunctions. However, most theory solvers (and in particular the FM variable elimination [7]) work on conjunctive fragments only. A naïve approach could use case-splitting, i.e., transforming the formula into Disjunctive Normal Form (DNF) and then solving each clause separately. This can result in a number of clauses exponential in the size of the original formula. Instead, we handle disjunction using the Boolean Fourier Motzkin procedure [20, 32]. As a result, the constraints we generate may be non-clausal.
Applying CEGIS(\(\varvec{\mathcal {T}}\)) with FM to the Motivational Example. We recall the example in Sect. 3 and apply CEGIS(\(\mathcal {T}\)). The problem is
which gives us the following specification:
The first synthesis phase generates the candidate \(f^*(x)=0\) for which the verification phase returns the concrete counterexample \(x=0\). As this candidate contains the constant 0, we generalise it to \(f^*[v_1](x)=v_1\), for which we get
Next, we use FM to eliminate x from
Note that, given that formula \(\lnot \sigma (f^*[v_1],x)\) is in DNF, for convenience we directly apply FM to each disjunct and obtain \(E(v_1)=v_1 \ge 0 \vee v_1 \ne 0\), which characterises all the values of \(v_1\) for which there exists a counterexample. When negating \(E(v_1)\) we get \(v_1<0 \,\wedge \, v_1=0\), which is UNSAT. As there is no valuation of \(v_1\) for which the current \(f^*\) is a final solution, the result returned by the theory solver is \(( false , f[ \textsf {?}] \ne f^*[ \textsf {?}])\), which is used to augment the specification. Subsequently, a new CEGIS(\(\mathcal {T}\)) iteration starts. The learning phase has changed the specification \(\sigma \) to
This forces the synthesis phase to pick a new candidate solution with a different skeleton. The new candidate solution we get is \(f^*(x)= ite ~(x<100) ~-3 ~1\), which works for the previous counterexample \(x=0\). However, the verification phase returns the counterexample \(x=100\). Again, this candidate contains constants which we replace by symbolic variables, obtaining
Next, we use FM to eliminate x from
As we work with integers, we can rewrite \(x<334455\) to \(x \le 334454\) and \(x<v_1\) to \(x \le v_1-1\). Then, we obtain the following constraint \(E(v_1,v_2,v_3)\) (as aforementioned, we applied FM to each disjunct in \(\lnot \sigma (f^*[v_1,v_2,v_3],x))\)
whose negation is
A satisfiability witness is \(v_1=334455\), \(v_2=-1\) and \(v_3=0\). Thus, the result returned by the theory solver is \(( true ,v_1=334455 \wedge v_2=-1 \wedge v_3=0)\), which is used by CEGIS to obtain the final solution
4.3 CEGIS(\(\mathcal {T}\)) with an SMT-based Theory Solver
For our second variant of a theory solver, we make use of an off-the-shelf SMT solver that supports quantified first-order formulae. This approach is more generic than the one described in Sect. 4.2, as there are solvers for a broad range of theories.
Recall that our goal is to obtain a constraint \(C(P,P^*,{\varvec{v}})\) that either characterises the valuations of \({\varvec{v}}\) for which \(P^*[{\varvec{v}}]\) is a final solution or blocks \(P^*[ \textsf {?}]\) whenever no such valuation exists. Consequently, we use the SMT solver to check the satisfiability of the formula
If \(\varPhi \) is satisfiable, then any satisfiability witness \({\varvec{c}}\) gives us a valuation for \({\varvec{v}}\) such that \(P^*\) is a final solution: \(C(P,P^*, {\varvec{v}}) = \bigwedge _{i=1{\cdot }n} v_i=c_i.\) Conversely, if \(\varPhi \) is unsatisfiable then \(C(P,P^*, {\varvec{v}})\) must block the current skeleton \(P^*[ \textsf {?}]\): \(C(P,P^*, {\varvec{v}}) = P[ \textsf {?}]\ne P^*[ \textsf {?}].\)
Applying SMT-based CEGIS(\(\varvec{\mathcal {T}}\)) to the Motivational Example. Again, we recall the example in Sect. 3. We will solve it by using SMT-based CEGIS(\(\mathcal {T}\)) for the theory of linear arithmetic. For this purpose, we assume that the synthesis phase finds the same sequence of candidate solutions as in Sect. 3. Namely, the first candidate is \(f^*(x)=0\), which gets generalised to \(f^*[v_1](x)=v_1\). Then, the first SMT call is for \(\forall x.\, \sigma (v_1, x)\), where
The SMT solver returns UNSAT, which means that \(C(f,f^*,v_1)=f[ \textsf {?}] \ne \textsf {?}\). The second candidate is \(f^*(x)= ite ~(x<100) ~-3 ~1\), which generalises to \(f^*[v_1,v_2,v_3](x)= ite ~(x<v_1)~ v_2 ~v_3.\) The corresponding call to the SMT solver is for \(\forall x.\, \sigma (( ite ~(x<v_1)~ v_2 ~v_3), x)\), for which we obtain the satisfiability witness \(v_1=334455\), \(v_2=-1\) and \(v_3=0\). Then \(C(f, f^*, v_1,v_2,v_3)=v_1=334455 \wedge v_2=-1 \wedge v_3=0\), which gives us the same final solution we obtained when using FM in Sect. 3.
5 Experimental Evaluation
5.1 Implementation
Incremental Satisfiability Solving. Our implementation of CEGIS may sometimes perform hundreds of loop iterations before finding the correct solution. Recall that the synthesis block of CEGIS is based on Bounded Model Checking (BMC). Ultimately, this BMC module performs calls to a SAT solver. Consequently, we may have hundreds of calls to this SAT solver, which are all very similar (the same base specification with some extra constraints added in each iteration). This makes CEGIS a prime candidate for incremental SAT solving. We implemented incremental solving in the synthesis block of CEGIS.
5.2 Benchmarks
We have selected a set of bitvector benchmarks from the Syntax-Guided Synthesis (SyGuS) competition [4] and a set of benchmarks synthesizing safety invariants and danger invariants for C programs [10]. All benchmarks are written in SyGuS-IF [26], a variant of SMT-LIB2.
Given that the syntactic restrictions (called the grammar or the template) provided in the SyGuS benchmarks contain all the necessary non-trivial constants, we removed them completely from these benchmarks. Removing just the non-trivial constants and keeping the rest of the grammar (with the only constants being 0 and 1) would have made the problem much more difficult, as the constants would have had to be incrementally constructed by applying the operators available to 0 and 1.
We group the benchmarks into three categories: invariant generation, which covers danger invariants, safety invariants and the class of invariant generation benchmarks from the SyGuS competition; hackers/crypto, which includes benchmarks from hackers-delight and cryptographic circuits; and comparisons, composed of benchmarks that require synthesizing longer programs with comparisons, e.g., finding the maximum value of 10 variables.
5.3 Experimental Setup
We conduct the experimental evaluation on a 12-core 2.40 GHz Intel Xeon E5-2440 with 96 GB of RAM and Linux OS. We use the Linux times command to measure CPU time used for each benchmark. The runtime is limited to 600 s per benchmark. We use MiniSat [12] as the SAT solver, and Z3 v4.5.1 [22] as the SMT-solver in CEGIS(\(\mathcal {T}\)) with SMT-based theory solver. The SAT solver could, in principle, be replaced with Z3 to solve benchmarks over a broader range of theories.
We present results for four different configurations of CEGIS:
-
CEGIS(\(\mathcal {T}\))-FM: CEGIS(\(\mathcal {T}\)) with Fourier Motzkin as the theory solver;
-
CEGIS(\(\mathcal {T}\))-SMT: CEGIS(\(\mathcal {T}\)) with Z3 as the theory solver;
-
CEGIS: basic CEGIS as described in Sect. 2.2;
-
CEGIS-Inc: basic CEGIS with incremental SAT solving.
We compare our results against the latest release of CVC4, version 1.5. As we are interested in running our benchmarks without any syntactic template, the first reason for choosing CVC4 [6] as our comparison point is the fact that it performs well when no such templates are provided. This is illustrated by the fact that it won the Conditional Linear Integer Arithmetic track of the SyGuS competition 2017 [4], one of two tracks where a syntactic template was not used. The other track without syntactic templates is the invariant generation track, in which CVC4 was close second to LoopInvGen [24]. A second reason for picking CVC4 is its overall good performance on all benchmarks, whereas LoopInvGen is a solver specialised to invariant generation.
We also give a row of results for a hypothetical 4-core implementation, as would be allowed in the SyGuS Competition, running 4 configurations in parallel: CEGIS(\(\mathcal {T}\))-FM, CEGIS(\(\mathcal {T}\))-SMT, CEGIS, and CEGIS-Inc. A link to the full experimental environment, including scripts to reproduce the results, all benchmarks and the tool, is provided in the footnote as an Open Virtual Appliance (OVA)Footnote 1.
5.4 Results
The results are given in Table 1. In combination, our CEGIS combination (i.e., CEGIS multi-core) solves 27 more benchmarks than CVC4, but the average time per benchmark is significantly higher.
As expected, both CEGIS(\(\mathcal {T}\))-SMT and CEGIS(\(\mathcal {T}\))-FM solve more of the invariant generation benchmarks which require synthesizing arbitrary constants than CVC4. Conversely, CVC4 performs better on benchmarks that require synthesizing long programs with many comparison operations, e.g., finding the maximum value in a series of numbers. CVC4 solves more of the hackers-delight and cryptographic circuit benchmarks, none of which require constants.
Our implementation of basic CEGIS (and consequently of all configurations built on top of this) only increases the length of the synthesized program when no program of a shorter length exists. Thus, it is expensive to synthesize longer programs. However, a benefit of this architecture is that the programs we synthesize are the minimum possible length. Many of the expressions synthesized by CVC4 are very large. This has been noted previously in the Syntax-Guided Synthesis Competition [5], and synthesizing without the syntactic template causes the expressions synthesized to be even longer.
Although CEGIS-Inc is quicker per iteration of the CEGIS loop than basic CEGIS, the average time per benchmark is not significantly better because of the variation in times produced by CEGIS. We hypothesise that the use of incremental solving makes CEGIS-Inc more prone to getting stuck exploring “bad” areas of the solution space than basic CEGIS, and so it requires more iterations than basic CEGIS for some benchmarks. The incremental solving preserves clauses learnt from any conflicts in previous iterations, which means that each SAT solving iteration will begin from exactly the same state as the previous one. The basic implementation doesn’t preserve these clauses and so is free to start exploring a new part of the search space each iteration. These effects could be mitigated by running multiple incremental solving instances in parallel.
In order to validate the assumption that CVC4 works better without a template than with one where the non-trivial constants were removed (see Sect. 5.2), we also ran CVC4 on a subset of the benchmarks with a syntactic template comprising the full instruction set we give to CEGIS, plus the constants 0 and 1. Note for some benchmarks it is not possible to add a grammar because the SYGUS-IF language does not allow syntactic templates for benchmarks that use the loop invariant syntax. With a grammar, CVC4 solves fewer of the benchmarks, and takes longer per benchmark. The syntactic template is helpful only in cases where non-trivial constants are needed and the non-trivial constants are contained within the template.
We ran EUSolver on the benchmarks with the syntactic templates, but the bitvector support is incomplete and missing some key operations. As a result EUSolver was unable to solve any benchmarks in the set, and so we have not included the results in the table.
Benefit of Literal Constants. We have investigated how useful the constants in the problem specification are, and have tried a configuration that seeds all constants in the problem specification as hints into the synthesis engine. This proved helpful for basic CEGIS only but not for the CEGIS(\(\mathcal {T}\)) configurations. Our hypothesis is that the latter do not benefit from this because they already have good support for computing constants. We dropped this option in the results presented in this section.
5.5 Threats to Validity
Benchmark Selection: We report an assessment of our approach on a diverse selection of benchmarks. Nevertheless, the set of benchmarks is limited within the scope of this paper, and the performance may not generalise to other benchmarks.
Comparison with State of the Art: CVC4 has not, as far as we are aware, been used for synthesis of bitvector functions without syntactic templates, and so this unanticipated use case may not have been fully tested. We are unable to compare all results to other solvers from the SyGuS Competition because EUSolver and EUPhony do not support synthesizing bitvector programs without a syntactic template, EUSolver’s support for bitvectors is incomplete even when used with a template, LoopInvGen and DryadSynth do not support bitvectors, and E3Solver tackles only Programming By Example benchmarks [5].
Choice of Theories: We evaluated the benefits of CEGIS(\(\mathcal {T}\)) in the context of two specific theory instances. While the improvements in our experiments are significant, it is uncertain whether this will generalise to other theories.
6 Related Work
The traditional view of program synthesis is that of synthesis from complete specifications [21]. Such specifications are often unavailable, difficult to write, or expensive to check against using automated verification techniques. This has led to the proposal of inductive synthesis and, more recently, of oracle-based inductive synthesis, in which the complete specification is not available and oracles are queried to choose programs [19].
A well-known application of CEGIS is program sketching [29, 31], where the programmer uses a partial program, called a sketch, to describe the desired implementation strategy, and leaves the low-level details of the implementation to an automated synthesis procedure. Inspired by sketching, Syntax-Guided Program Synthesis (SyGuS) [2] requires the user to supplement the logical specification provided to the program synthesizer with a syntactic template that constrains the space of solutions. In contrast to SyGuS, our aim is to improve the efficiency of the exploration to the point that user guidance is no longer required.
Another very active area of program synthesis is denoted by component-based approaches [1, 13,14,15, 17, 18, 25]. Such approaches are concerned with assembling programs from a database of existing components and make use of various techniques, from counterexample-guided synthesis [17] to type-directed search with lightweight SMT-based deduction and partial evaluation [14] and Petri-nets [15]. The techniques developed in the current paper are applicable to any component-based synthesis approach that relies on counterexample-guided inductive synthesis.
Heuristics for constant synthesis are presented in [11], where the solution language is parameterised, inducing a lattice of progressively more expressive languages. One of the parameters is word width, which allows synthesizing programs with constants that satisfy the specification for smaller word widths. Subsequently, heuristics extend the program (including the constants) to the required word width. As opposed to this work, CEGIS(\(\mathcal {T}\)) denotes a systematic approach that does not rely on ad-hoc heuristics.
Regarding the use of SMT solvers in program synthesis, they are frequently employed as oracles. By contrast, Reynolds et al. [27] present an efficient encoding able to solve program synthesis constraints directly within an SMT solver. Their approach relies on rephrasing the synthesis constraint as the problem of refuting a universally quantified formula, which can be solved using first-order quantifier instantiation. Conversely, in our approach we maintain a clear separation between the synthesizer and the theory solver, which communicate in a well-defined manner. In Sect. 5, we provide a comprehensive experimental comparison with the synthesizer described in [27].
7 Conclusion
We proposed CEGIS(\(\mathcal {T}\)), a new approach to program synthesis that combines the strengths of a counterexample-guided inductive synthesizer with those of a theory solver to provide a more efficient exploration of the solution space. We discussed two options for the theory solver, one based on FM variable elimination and one relying on an off-the-shelf SMT solver. Our experiments results showed that, although slower than CVC4, CEGIS(\(\mathcal {T}\)) can solve more benchmarks within a reasonable time that require synthesizing arbitrary constants, where CVC4 fails.
Notes
References
Albarghouthi, A., Gulwani, S., Kincaid, Z.: Recursive program synthesis. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 934–950. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_67
Alur, R., Bodík, R., Juniwal, G., Martin, M.M.K., Raghothaman, M., Seshia, S.A., Singh, R., Solar-Lezama, A., Torlak, E., Udupa, A.: Syntax-guided synthesis. In: FMCAD, pp. 1–8. IEEE (2013)
Alur, R., Černý, P., Radhakrishna, A.: Synthesis through unification. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9207, pp. 163–179. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21668-3_10
Alur, R., Fisman, D., Singh, R., Solar-Lezama, A.: SyGuS-Comp 2017: results and analysis. CoRR abs/1711.11438 (2017)
Alur, R., Fisman, D., Singh, R., Udupa, A.: Syntax guided synthesis competition (2017). http://sygus.seas.upenn.edu/SyGuS-COMP2017.html
Barrett, C., Conway, C.L., Deters, M., Hadarean, L., Jovanović, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_14
Bik, A.J.C., Wijshoff, H.A.G.: Implementation of Fourier-Motzkin elimination. Technical report, Rijksuniversiteit Leiden (1994)
Clarke, E., Kroening, D., Lerda, F.: A tool for checking ANSI-C programs. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 168–176. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24730-2_15
Collins, G.E.: Hauptvortrag: quantifier elimination for real closed fields by cylindrical algebraic decompostion. In: Brakhage, H. (ed.) GI-Fachtagung 1975. LNCS, vol. 33, pp. 134–183. Springer, Heidelberg (1975). https://doi.org/10.1007/3-540-07407-4_17
David, C., Kesseli, P., Kroening, D., Lewis, M.: Danger invariants. In: Fitzgerald, J., Heitmeyer, C., Gnesi, S., Philippou, A. (eds.) FM 2016. LNCS, vol. 9995, pp. 182–198. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48989-6_12
David, C., Kroening, D., Lewis, M.: Using program synthesis for program analysis. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 483–498. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48899-7_34
Eén, N., Sörensson, N.: An extensible SAT-solver. In: Giunchiglia, E., Tacchella, A. (eds.) SAT 2003. LNCS, vol. 2919, pp. 502–518. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24605-3_37
Feng, Y., Bastani, O., Martins, R., Dillig, I., Anand, S.: Automated synthesis of semantic malware signatures using maximum satisfiability. In: NDSS. The Internet Society (2017)
Feng, Y., Martins, R., Geffen, J.V., Dillig, I., Chaudhuri, S.: Component-based synthesis of table consolidation and transformation tasks from examples. In: PLDI, pp. 422–436. ACM (2017)
Feng, Y., Martins, R., Wang, Y., Dillig, I., Reps, T.W.: Component-based synthesis for complex APIs. In: POPL, pp. 599–612. ACM (2017)
Ganzinger, H., Hagen, G., Nieuwenhuis, R., Oliveras, A., Tinelli, C.: DPLL(T): fast decision procedures. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 175–188. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27813-9_14
Gulwani, S., Jha, S., Tiwari, A., Venkatesan, R.: Synthesis of loop-free programs. In: PLDI, pp. 62–73. ACM (2011)
Gulwani, S., Korthikanti, V.A., Tiwari, A.: Synthesizing geometry constructions. In: PLDI, pp. 50–61. ACM (2011)
Jha, S., Gulwani, S., Seshia, S.A., Tiwari, A.: Oracle-guided component-based program synthesis. In: ICSE, no. 1, pp. 215–224. ACM (2010)
Kroening, D., Strichman, O.: Decision Procedures: An Algorithmic Point of View, 1st edn. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-74105-3
Manna, Z., Waldinger, R.: A deductive approach to program synthesis. In: IJCAI. pp. 542–551. William Kaufmann (1979)
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Nieuwenhuis, R., Oliveras, A., Tinelli, C.: Solving SAT and SAT modulo theories: From an abstract Davis-Putnam-Logemann-Loveland procedure to DPLL(T). J. ACM 53(6), 937–977 (2006)
Padhi, S., Millstein, T.D.: Data-driven loop invariant inference with automatic feature synthesis. CoRR abs/1707.02029 (2017)
Perelman, D., Gulwani, S., Grossman, D., Provost, P.: Test-driven synthesis. In: PLDI, pp. 408–418. ACM (2014)
Raghothaman, M., Udupa, A.: Language to specify syntax-guided synthesis problems. CoRR abs/1405.5590 (2014)
Reynolds, A., Deters, M., Kuncak, V., Tinelli, C., Barrett, C.: Counterexample-guided quantifier instantiation for synthesis in SMT. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9207, pp. 198–216. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21668-3_12
Rosen, E.: An existential fragment of second order logic. Arch. Math. Log. 38(4–5), 217–234 (1999)
Solar-Lezama, A.: Program sketching. STTT 15(5–6), 475–495 (2013)
Solar-Lezama, A., Rabbah, R.M., Bodík, R., Ebcioglu, K.: Programming by sketching for bit-streaming programs. In: PLDI, pp. 281–294. ACM (2005)
Solar-Lezama, A., Tancau, L., Bodík, R., Seshia, S.A., Saraswat, V.A.: Combinatorial sketching for finite programs. In: ASPLOS, pp. 404–415. ACM (2006)
Strichman, O.: On solving Presburger and linear arithmetic with SAT. In: Aagaard, M.D., O’Leary, J.W. (eds.) FMCAD 2002. LNCS, vol. 2517, pp. 160–170. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36126-X_10
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis>This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara><SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Abate, A., David, C., Kesseli, P., Kroening, D., Polgreen, E. (2018). Counterexample Guided Inductive Synthesis Modulo Theories. In: Chockler, H., Weissenbacher, G. (eds) Computer Aided Verification. CAV 2018. Lecture Notes in Computer Science(), vol 10981. Springer, Cham. https://doi.org/10.1007/978-3-319-96145-3_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-96145-3_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96144-6
Online ISBN: 978-3-319-96145-3
eBook Packages: Computer ScienceComputer Science (R0)