Abstract
Decision trees are a popular method for a variety of machine learning tasks. A typical application scenario involves a client providing a vector of features and a service provider (server) running a trained decision-tree model on the client’s vector. Both inputs need to be kept private. In this work, we present efficient protocols for privately evaluating decision trees. Our design reduces the complexity of existing solutions with a more interactive setting, which improves the total number of comparisons to evaluate the decision tree. It crucially uses oblivious transfer protocols and leverages their amortized overhead. Furthermore, and of independent interest, we improve by roughly a factor of two the DGK comparison protocol.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Machine learning techniques are currently widely used for many real-world applications. These applications range from spam detection [1], face and pattern recognition [21, 25], to the analysis of genome sequencing and financial markets [17, 22]. Unfortunately, in many cases, data mining and privacy are perceived to be at odds since the data mining algorithm requires access to the user’s information in the clear. Privacy is especially relevant to applications handling sensitive data. As an example, consider the case of a medical study to diagnose a certain disease. In this scenario, medical profiles of patients are considered as highly sensitive data and their usage has to be compliant with regulations [7] such as Health Insurance Portability and Accountability Act (HIPAA).
An important class of machine learning algorithms is known as classification where each datapoint belongs to a certain class. The goal is to generate a model that can predict the class of a new datapoint. These models are useful in applications that provide personalized services, such as recommender systems [29], credit scoring models [35], automatic medical assessments [4], etc.
In this paper, we address the problem of privacy-preserving classification. We focus on commonly used classifiers: decision trees. Decision trees are simple classifiers that consist of a collection of decision nodes in a tree structure. A classical example is the twenty-question game where one player has in mind some object and another player tries to guess the object with no more than 20 yes-or-no questions. Decision trees are non-linear models for classification, yet they are easy to interpret since their evaluation simply corresponds to a tree traversal.
The secure evaluation of decision trees involves two parties. A server possesses a decision-tree model and a client wishes to evaluate the model. This is a typical setting in a cloud-based query system, where the service provider has a model which was trained by integrating the data of thousands of users and the client wants to learn the output of the model for her input data. An evaluation protocol is said to be secure, when at the conclusion of the protocol execution, the server cannot learn anything about the client’s data and the client cannot learn additional information about the server’s model.
The output of a decision-tree model is computed by traversing the tree, level by level. At each level, an entry of the client’s input is compared against a fixed threshold and the result indicates how to traverse to the next level. The comparison at each visited node has to be performed in a secure way, otherwise there would be information leakage about the client’s input and/or the server’s model. At the heart of our privacy-preserving decision-tree evaluation lies an efficient protocol for the secure comparison of private values. It is worth mentioning that comparison is an essential building block for developing many other secure machine learning algorithms. These include clustering [8], support vector machines (SVM) [32], matrix factorization [26], regression [27], and neural networks [23]. Hence, the proposed comparison algorithms can improve the performance of a wide range of applications.
Related work. Privacy-preserving data mining was introduced in [2, 12, 20]. These works present different approaches to securely construct decision trees. Protocols for the private evaluation of decision trees were subsequently developed in [5] and more recently in [7, 31, 34]. In [7], Bost et al. express the decision tree as a polynomial whose output is the result of the classification. Their representation requires a small number of multiplications and is evaluated using a fully homomorphic encryption scheme. Wu et al. [34] reduce the problem of decision-tree evaluation to the oblivious transfer of a leaf node. Assuming a complete decision tree, they hide its structure to the client by applying a random permutation. They so gain an order of magnitude reduction in client computation and bandwidth. Tai et al. [31] replace the evaluation step in [34] via linear functions. This leads to better performance for sparse decision trees. Finally, we note that [34] and [31] also introduce extended protocols that are made secure against malicious adversaries.
In [9,10,11], Damgård, Geisler, and Krøigaard (DGK) present an elegant two-party protocol for comparing private values. It was later modified in [13] and [33], and adapted in [7, 34]. It relies on additively homomorphic encryption. The DGK protocol and its variants are dominated by exponentiations in the group underlying the homomorphic encryption scheme. Those are costly operations. Another drawback in the DGK protocol is the communication cost. The former issue was addressed by Veugen in [33]. The author was able to divide the computational workload by approximately a factor of two, on average. Unfortunately, the resulting implementation is subject to timing attacks [16].
Our contributions. We devise privacy-preserving comparison protocols that reduce by roughly a factor of two both the computational complexity and the necessary bandwidth. Furthermore, unlike [33], provided proper implementation the proposed protocols are made resistant against timing attacks.
Another contribution of this work is a new protocol for evaluating a decision tree model. We borrow from [34] the astute idea of hiding the indexes of the comparison nodes using a random permutation at each level of the tree. However, we reduce the number of comparisons with a more interactive setting. Doing so, we also take advantage of the amortized complexity of efficient OT protocols. The works of [34] and [31] require a comparison for every internal node. In our setting, a single comparison per level is required. For a decision tree of depth d, this amounts to a total of d comparisons. This has to be compared with the m comparisons in [31, 34], where \(m \gg d\) is the number of internal nodes.
Paper outline. The rest of the paper is organized as follows. The next section introduces some cryptographic tools. Sections 3 and 4 are the core of the paper. They present a new design for evaluating decision trees in a privacy-preserving fashion, making use of an enhanced comparison protocol. The security and performance are discussed in Sect. 5. Finally, Sect. 6 concludes the paper.
2 Cryptographic Tools
2.1 Additively Homomorphic Encryption
An additively homomorphic encryption scheme [30] consists of a tuple of four algorithms \((\mathop {\mathsf {KeyGen}}, \mathop {\mathsf {Enc}}\nolimits , \mathop {\mathsf {Dec}}\nolimits , \mathop {\mathsf {AddH}}\nolimits )\). On input a security parameter \(\kappa \), the key generation algorithm \(\mathop {\mathsf {KeyGen}}\) returns a matching pair \(( pk , sk )\) of public key and secret key. Let \(\mathcal {M}\) denote the message space. The encryption algorithm \(\mathop {\mathsf {Enc}}\nolimits \) is a randomized algorithm that takes as input \( pk \) and a plaintext \(m \in \mathcal {M}\), and returns a ciphertext c. Given a valid ciphertext c, the decryption algorithm \(\mathop {\mathsf {Dec}}\nolimits \), using \( sk \), returns the corresponding plaintext m.
For homomorphic encryption, the message space \(\mathcal {M}\) is modeled as a finite ring. Additional public-key algorithm \(\mathop {\mathsf {AddH}}\nolimits \) operates on ciphertexts. It takes as input the encryption of two messages \(m,m' \in \mathcal {M}\) and returns an encryption of \(m + m'\). When the public key is clear from the context, it is customary to write an encryption of m as \([\![{m}]\!]\) in lieu of \(\mathop {\mathsf {Enc}}\nolimits _ pk (m)\). We then use the ‘boxplus’ operator (\(\boxplus \)) to denote the addition of two ciphertexts. Hence, an encryption of \(m + m'\) is obtained as \([\![{m + m'}]\!] = [\![{m}]\!] \boxplus [\![{m'}]\!]\). Likewise, for a known constant d, the encryption of \(d\cdot m\) can be obtained from the encryption of m as \([\![{d\cdot m}]\!] = d\cdot [\![{m}]\!]\); i.e., as \(\sum _{i=1}^d [\![{m}]\!] = [\![{m}]\!]\boxplus [\![{m}]\!]\cdots \boxplus [\![{m}]\!]\) (d times). Finally, we write \([\![{m}]\!] \boxminus [\![{m'}]\!]\) for \([\![{m}]\!] \boxplus [\![{-m'}]\!] = [\![{m-m'}]\!]\).
2.2 Oblivious Transfer
Oblivious transfer (OT) [14, 28] is a two-party protocol between a chooser and a sender. On a 1-out-of-N OT, the sender has a set of N t-bit strings \(\{\sigma _0, \sigma _1, \ldots , \sigma _{N-1}\}\). The chooser selects an index \(j \in \{0, 1,\ldots , N-1\}\) and exactly obtains from the sender the string \(\sigma _j\) in an oblivious way (i.e., the sender does not know the value of j). Oblivious transfer protocols can be constructed from many cryptographic assumptions. Efficient implementations are provided in [24], [3]; see also Appendix A.
3 Private Comparison of Integers
In this section, we introduce our enhanced design for the secure comparison of t-bit values based on additively homomorphic encryption. To make the presentation easier to follow, we describe it in stages. We start with a basic protocol which is not secure when some prior information is known. We then extend it to get full security regardless of the inputs.
3.1 Basic Protocol
The setting is as follows. Each party possesses a private t-bit value: Party A (Alice) has \(x = \sum _{i=0}^{t-1} x_i\,2^i\) while party B (Bob) has \(y = \sum _{i=0}^{t-1} y_i\,2^i\). The goal for parties A and B is to respectively obtain at the conclusion of the protocol bits \(\delta _A\) and \(\delta _B\) such that \(\delta _A \oplus \delta _B = \mathop {\mathbbm {1}}\{x \leqslant y\}\). Neither party can learn anything more about the other party’s input.
We depict in Fig. 1 the protocol by describing the different steps performed by the two parties. Party B is equipped with an additively homomorphic public-key encryption scheme. We let \([\![{m}]\!]\) denote the encryption of a message \(m \in \mathcal {M}\) under B’s public key; see Sect. 2.1. The message space \(\mathcal {M}\) is assumed to be a finite integral domain and to satisfy \(\#\mathcal {M}\geqslant t+1\).
Remark 1
In Step 3 (Fig. 1), note that given \([\![{y_i}]\!]\), A can obtain \([\![{x_i \oplus y_i}]\!]\) as \([\![{y_i}]\!]\) if \(x_i = 0\), and as \([\![{1}]\!] \boxminus [\![{y_i}]\!]\) if \(x_i = 1\).
To show the correctness of the protocol, it is useful to introduce some notation. For a t-bit integer \(a = \sum _{i=0}^{t-1}a_i\,2^i\) with \(a_i \in \{0,1\}\), we let \(\overline{a}\) denote the complement of a; i.e., \(\overline{a} = 2^t - a - 1\). In particular, for \(t=1\), \(a = a_0\) and \(\overline{a} = \overline{a_0} = 1 - a_0\). With this notation, we can reformulate an observation made in [9, Sect. 3].
Proposition 1
Let \(x = \sum _{i=0}^{t-1} x_i\,2^i\) and \(y = \sum _{i=0}^{t-1} y_i\,2^i\), with \(x_i, y_i \in \{0,1\}\), be two t-bit integers. Define

Then \(x < y\) if and only if there exists some unique index i with \(0 \leqslant i \leqslant t-1\) such that \(c_i = 0\). Moreover, \(x = y\) if and only if \(c_{-1} = 0\) and \(c_i = 1\) for \(0 \leqslant i \leqslant t-1\).
Proof
As defined, \(c_i\) is the sum of nonnegative terms. Therefore, for \(0 \leqslant i \leqslant t-1\), \(c_i = 0\) is equivalent to (i) \(x_i = \overline{y_i} = 0\) and (ii) for \(i+1 \leqslant j \leqslant t-1\), \(x_j \oplus y_j = 0\). This in turn is equivalent to (i) \(x_i < y_i\) and (ii) for \(i+1 \leqslant j \leqslant t-1\), \(x_j = y_j\); that is, \(x < y\). To see that index i such that \(c_i = 0\) is unique, suppose that \(c_{i'} = 0\) for some \(i' \ne i\). Without loss of generality, assume that \(i' < i\). This leads to \(c_{i'} = x_{i'} + \overline{y_{i'}} + \sum _{j=i'+1}^{t-1} (x_j \oplus y_j) \geqslant x_i \oplus y_i = 1\), a contradiction.
The second part of the proposition is clear. If \(\sum _{j=0}^{t-1}x_j\,2^j = \sum _{j=0}^{t-1}y_j\,2^j\) then \(c_{-1} = 0\) and \(c_i = 1\) for \(i \geqslant 0\). \(\square \)
By reversing the roles of x and y in Proposition 1, we get as an immediate corollary the following proposition.
Proposition 2
Let \(x = \sum _{i=0}^{t-1} x_i\,2^i\) and \(y = \sum _{i=0}^{t-1} y_i\,2^i\), with \(x_i, y_i \in \{0,1\}\), be two t-bit integers. For \(0 \leqslant i \leqslant t-1\), define
Then \(x \leqslant y\) if and only if there exists no index i with \(0 \leqslant i \leqslant t-1\) such that \(c_i = 0\).
Proof
If there were such an index i, this would imply \(y < x\) by Proposition 1. The absence of such an index therefore implies \(y \geqslant x\). \(\square \)
We are now ready to show that the protocol must terminate with the correct result. Following [33], depending on the value of h (see Step 2 in Fig. 1), we distinguish three cases.
-
1.
Suppose first that the Hamming weight of x is greater than \(\lfloor t/2 \rfloor \) (and thus \(\delta _A = 0\)). This means that x has more ones than zeros in its binary representation. Specifically, among the t bits of x, at most \(\lfloor t/2 \rfloor \) bits are equal to 0. Furthermore, for \(0 \leqslant i \leqslant t-1\), Proposition 1 shows that \(c_i\) needs only to be evaluated when \(x_i = 0\) since when \(x_i = 1\) we already know that the corresponding \(c_i\) cannot be zero. The case \(x = y\) is taken into account using \(c_{-1}\).
-
2.
Now suppose that the Hamming weight of x is less than \(\lceil t/2 \rceil \) (and thus \(\delta _A = 1\)). In this case, among the t bits of x, at most \(\lfloor t/2 \rfloor \) bits are equal to 1. We can then make use of Proposition 2. With at most \(\lfloor t/2\rfloor \) tests for \(c_i = 0\) (i.e., when \(x_i = 1\)), we can decide whether \(x \leqslant y\).
-
3.
The last case is when the Hamming weight of x is t / 2 (and thus \(\delta _A\) is equiprobably equal to 0 or 1). This supposes t even. In this case, among the t bits of x, t / 2 bits are equal to 0 and t / 2 bits are equal to 1. Proposition 1 or Proposition 2 can be used indifferently to decide after at most \(t/2 = \lfloor t/2\rfloor \) tests for \(c_i = 0\) whether \(x \leqslant y\).
The above analysis shows that (i) only the indexes \(i \in \mathscr {L}'\) need to be tested, and (ii) \(\#\mathscr {L}' \leqslant \lfloor t/2 \rfloor \). If \(\#\mathscr {L}' < \lfloor t/2 \rfloor \) then additional indexes are added to \(\mathscr {L}'\) to form \(\mathscr {L}\). This ensures that \(\#\mathscr {L}\) is always equal to \(\lfloor t/2 \rfloor \) and is aimed at preventing timing attacks. Now the correctness follows by noting that the \([\![{c_i^*}]\!]\)’s include the encryptions of \(r_i\cdot c_i\) for all \(i \in \mathscr {L}'\). It is also important to see that \([\![{c_{-1}^*}]\!]\) is the encryption of a non-zero value when \(\delta _B = 1\).
By construction, \(\delta _B = 1\) if one of the \([\![{c_i^*}]\!]\)’s decrypts to 0.
-
When \(\delta _A = 0\), Proposition 1 is used. A decryption to 0 means \(x \leqslant y\). We therefore have \(\mathop {\mathbbm {1}}\{x \leqslant y\} = 1 = \delta _A \oplus \delta _B \), as desired.
-
When \(\delta _A = 1\), Proposition 2 is used and a decryption to 0 means \(x \nleqslant y\). Then, \(\mathop {\mathbbm {1}}\{x \leqslant y\} = 0 = \delta _A \oplus \delta _B\), as desired.
If none of the \([\![{c_i^*}]\!]\)’s decrypts to 0 then \(\delta _B = 0\). When \(\delta _A = 0\), this means \(x \nleqslant y\); when \(\delta _A = 1\), this means \(x \leqslant y\). In both cases, we have \(\mathop {\mathbbm {1}}\{x \leqslant y\} = \delta _A \oplus \delta _B\), as desired.
3.2 Full Protocol
The basic protocol needs special care. In particular, it requires that the Hamming weight of x a priori has the same probability to be greater than \(\lfloor t/2 \rfloor \) or less than \(\lceil t/2\rceil \). This guarantees that \(\delta _A\) is uniformly distributed over \(\{0,1\}\). Indeed, if party B knows for example that the Hamming weight of x is more likely less than \(\lceil t/2 \rceil \) (and thus \(\delta _A\) is more likely equal to 1), a value \(\delta _B = 0\) tells party B that x is more likely less than or equal to y since \(\delta _A \oplus \delta _B = \mathop {\mathbbm {1}}\{x \leqslant y\}\).
We modify our basic protocol so that it remains secure when party B has some prior knowledge on the Hamming weight of x. The resulting distribution of \(\delta _A\) will always be uniform over \(\{0,1\}\), independently of the value of x. The full protocol is detailed in Fig. 2.
It is worth remarking that \(x'\) as defined in Step 1b (Fig. 2) is a random t-bit integer. There is therefore no way for party B to gain more information on its Hamming weight.
The correctness of the protocol is easily verified. By definition, we have \(y^*= y + \eta - 2^tY^*\), \(z^*= y^*+ x' - x - 2^tZ^*\), and \(y' = z^*- \eta - Y'2^t\). This leads to
Reducing the above relation modulo 2 yields \(\delta _A + \delta _B \equiv \delta '_A + \delta '_B + Y^*+ Y' + Z^*\pmod 2\), a solution of which is \(\delta _A = \delta '_A + Z^*\bmod 2\) and \(\delta _B = \delta '_B + Y^*+ Y' \bmod 2\).
3.3 Further Settings
Encrypted comparison bit. Let \(\delta \) denote the comparison bit; i.e., \(\delta = \mathop {\mathbbm {1}}\{x \leqslant y\}\). In certain settings, a party wishes to produce an encryption of \(\delta \) at the end of the protocol, rather than a share \(\delta _A\) of \(\delta \) (the other share, \(\delta _B\), being held by the other party). In this case, we can add the following step to our comparison protocols:
-
5.
Party B encrypts \(\delta _B\) using his public key and sends \([\![{\delta _B}]\!]\) to A. Upon receiving \([\![{\delta _B}]\!]\), party A computes the encryption of \(\delta \) as \([\![{\delta }]\!] = [\![{\delta _B}]\!]\) if \(\delta _A = 0\), and \([\![{\delta }]\!] = [\![{1}]\!] \boxminus [\![{\delta _B}]\!]\) otherwise.
Encrypted inputs. There exists another practical setting for the comparison of private inputs. Suppose that one party possesses \([\![{x}]\!]\) and \([\![{y}]\!]\), the encryption of two t-bit values \(x = \sum _{i=0}^{t-1} x_i\,2^i\) and \(y = \sum _{i=0}^{t-1} y_i\,2^i\). The other party possesses the corresponding decryption key. Our protocols easily generalize to cover this setting as well. An example is given in Sect. 4.2.
Other frameworks. The technique we employed is fairly generic and can be adapted to increase the efficiency of other bit-wise comparison protocols, including the protocol in [18].
4 Application: Private Evaluation of Decision Trees
Secure comparison protocols find numerous practical applications. We apply the results of the previous section to the private evaluation of decision trees. As the values being compared will be random, our basic protocol (Fig. 1) suffices.
4.1 Problem Setup
There are two parties involved: a client and a server. The client has a private feature vector  and the server possesses a decision tree model
and the server possesses a decision tree model  . At the end of protocol, the client obtains the value \(z_r := \mathfrak {T}(\varvec{x})\) and learns nothing else; the server learns nothing.
. At the end of protocol, the client obtains the value \(z_r := \mathfrak {T}(\varvec{x})\) and learns nothing else; the server learns nothing.
In a binary tree, each internal node \(\nu _k^{(\ell )}\) (with \(0 \leqslant k \leqslant \ell \)) at level \(\ell \) in the tree is associated with a Boolean function
where \(i_k^{(\ell )}\) is an index in the feature vector  , and \(T_k^{(\ell )}\) is a threshold.
, and \(T_k^{(\ell )}\) is a threshold.
The depth of the tree (i.e., the longest path from the root to a leaf) is denoted by d. The number of internal nodes is denoted by m. Without loss of generality, we assume that \(\mathfrak {T}\) is a complete binary decision tree; that is, a binary decision tree with exactly \(2^\ell \) nodes at each level \(\ell \). We note that it is easy to derive a complete binary decision tree by introducing dummy internal nodes and assigning an arbitrary value in \(\{0,1\}\) for the corresponding Boolean function \(f_k^{(\ell )}(\varvec{x})\). This is illustrated in the figure below on a decision tree of depth \(d = 2\).
4.2 From Public to Private Evaluation
On input \(\varvec{x}\), the evaluation of a decision tree starts at the root node. At each level \(\ell \), depending on the result of \(f_k^{(\ell )}(\varvec{x})\), either the left branch (for 0) or the right branch (for 1) is taken. The process is repeated until a leaf node is reached. The output of \(\mathfrak {T}(\varvec{x})\) is \(z_r\), the value of the so-obtained leaf node.
Public evaluation. When the feature vector \(\varvec{x}\) and the decision tree \(\mathfrak {T}\) are available in the clear, the decision tree can be evaluated by performing d comparisons. Let \(\beta _{\ell }\in \{0,1\}\) denote the result of the decision (0 or 1) at level \(\ell \), for \(\ell = 0, 1, \ldots , d-1\). It turns out that
Consequently, the index r of the corresponding leaf node can be expressed as \(r = (\beta _0, \beta _1, \ldots , \beta _{d-1})_2 = \sum _{\ell =0}^{d-1}\beta _{\ell }\,2^{d-1-\ell }\), where \((\beta _0, \beta _1, \ldots , \beta _{d-1})_2\) represents the binary expansion of r.
Example 1
Figure 4 depicts an example of a binary decision tree with 4 levels. In this example, the index r of the output, \(z_r\), is given by \(r = (\beta _0, \beta _1, \beta _2, \beta _3)_2 = (0,1,0,1)_2 = 5\).
Private evaluation. In the private setting, the server knows the model \(\mathfrak {T}\) (including \(i_k^{(\ell )}\) and \(T_k^{(\ell )}\), for \(0 \leqslant \ell \leqslant d-1\)) while the client knows \(\varvec{x} = (x_1, \ldots , x_n)\).
-
For \(\ell = 0\), we have \(\beta _0 = \mathop {\mathbbm {1}}\bigl \{x_{i_0^{(0)}} \leqslant T_0^{(0)}\bigr \}\). However, the private comparison protocols of Sect. 3 do not directly apply because the value of \(\smash {i_0^{(0)}}\) is unknown to the client. This issue is resolved by providing the server with
 , for \(1 \leqslant i \leqslant n\). Here,
, for \(1 \leqslant i \leqslant n\). Here,  denotes an encryptionFootnote 1 of \(x_i\) under the public-key of the client. The encryption scheme is supposed being additively homomorphic with message space \(\mathcal {M}\) such that \(\#\mathcal {M}\geqslant 2^{t+\kappa }\) for a certain security parameter \(\kappa \). Using the techniques developed in the previous section, the client and server can now engage in a two-party protocol to secret-share the decision bit \(\beta _0 = b_0 \oplus b'_0\) —where the server holds \(b_0\) and the client holds \(b'_0\). Details are provided in Step 2 of Fig. 6.
denotes an encryptionFootnote 1 of \(x_i\) under the public-key of the client. The encryption scheme is supposed being additively homomorphic with message space \(\mathcal {M}\) such that \(\#\mathcal {M}\geqslant 2^{t+\kappa }\) for a certain security parameter \(\kappa \). Using the techniques developed in the previous section, the client and server can now engage in a two-party protocol to secret-share the decision bit \(\beta _0 = b_0 \oplus b'_0\) —where the server holds \(b_0\) and the client holds \(b'_0\). Details are provided in Step 2 of Fig. 6. -
For \(\ell = 1, \ldots , d-1\), Eqs. (1) and (2) become \(\beta _\ell = \mathop {\mathbbm {1}}\bigl \{x_{i_{k^\star }^{(\ell )}} \leqslant T_{k^\star }^{(\ell )}\bigr \}\) with
 . In particular, for \(\ell = 1\), we obtain $$\begin{aligned} \beta _1 = \mathop {\mathbbm {1}}\bigl \{x_{i_{k^\star }^{(1)}} \leqslant T_{k^\star }^{(1)}\bigr \}\quad \text {with }k^\star = \beta _0 = {\left\{ \begin{array}{ll} b'_0 &{} \text {if }b_0 = 0\\ b'_0 \oplus 1 &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$
. In particular, for \(\ell = 1\), we obtain $$\begin{aligned} \beta _1 = \mathop {\mathbbm {1}}\bigl \{x_{i_{k^\star }^{(1)}} \leqslant T_{k^\star }^{(1)}\bigr \}\quad \text {with }k^\star = \beta _0 = {\left\{ \begin{array}{ll} b'_0 &{} \text {if }b_0 = 0\\ b'_0 \oplus 1 &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$Specifically, if \(b_0 = 0\), the server knows that the client possesses the correct result of the comparison; i.e., \(b'_0 = \beta _0\). If \(b_0 = 1\), the server knows that the client possesses the flipped result. To maintain the consistency, the server uses a copied version \(\mathfrak {T}^*\) of the initial tree. If \(b_0 = 1\), the server updates \(\mathfrak {T}^*\) by switching the left subtree and the right subtree at level \(\ell = 1\). What is important to observe here is that \(k^\star \) coincides with \(b'_0\) in \(\mathfrak {T}^*\). Hence, the client can obtain
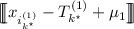 —and in turn \(x_{i_{k^\star }^{(1)}} - T_{k^\star }^{(1)} + \mu _1\) after decryption— from the server, where \(\mu _1\) is a mask chosen by the server to hide the value of \(x_{i_{k^\star }^{(1)}} - T_{k^\star }^{(1)}\). Next, the client and server engage in a two-party protocol to secret-share the decision bit \(\beta _1 = b_1 \oplus b'_1\). To prevent the server to learn the index \(k^\star \),
—and in turn \(x_{i_{k^\star }^{(1)}} - T_{k^\star }^{(1)} + \mu _1\) after decryption— from the server, where \(\mu _1\) is a mask chosen by the server to hide the value of \(x_{i_{k^\star }^{(1)}} - T_{k^\star }^{(1)}\). Next, the client and server engage in a two-party protocol to secret-share the decision bit \(\beta _1 = b_1 \oplus b'_1\). To prevent the server to learn the index \(k^\star \),  is obtained via oblivious transfer. Again, refer to Step 2 in Fig. 6 for details.
is obtained via oblivious transfer. Again, refer to Step 2 in Fig. 6 for details.The same process is iterated for \(\ell = 2, \ldots , d-1\). Each time \(b_\ell = 1\), the server switches all subtrees of \(\mathfrak {T}^*\) at level \(\ell \) and calls \(\mathfrak {T}^*\) the so-obtained tree.
-
At this stage the client knows \((b'_0, \ldots , b'_{d-1})_2\), which is the index of the leaf node containing the result in the permuted tree \(\mathfrak {T}^*\). The client engages in a 1-out-of-\(2^d\) OT with the server and thereby learns \(z_r\).
Example 2
(Example 1 cont’d). Suppose that the server successively obtains \(b_0 = 1\), \(b_1 = 0\), \(b_2 = 1\), and \(b_3 = 1\). For \(\ell = 1, \ldots , 3\): if \(b_\ell = 1\) the subtrees at level \(\ell \) are switched. This is illustrated in Fig. 5. The bottom picture is the final permuted tree \(\mathfrak {T}^*\).
Our decision-tree evaluation protocol is given in Fig. 6. The permuted tree \(\mathfrak {T}^*\) is represented at level \(\ell \geqslant 1\) by the string \(\sigma ^{(\ell )} = (b_0, \ldots , b_{\ell -1})_2\); \(\mathfrak {T}^*= \mathfrak {T}\) for \(\ell = 0\). Step 2d in Fig. 6 outputs shares of the decision at level \(\ell \). It is worth noting that a single execution of the comparison protocol is run per level.
Proposition 3
With the notation of Fig. 6, for \(0 \leqslant \ell \leqslant d-1\), the server and the client secret-share the decision bit at each level; i.e.,
Proof
From \(m'_\ell = M'_\ell - \lfloor M'_\ell /2^t \rfloor 2^t\) and \(m_\ell = \mu _\ell - \lfloor \mu _\ell /2^t\rfloor 2^t\), we can write
Furthermore, defining \(s = \sigma ^{(\ell )} \oplus j\), we have \(M'_\ell = M_j^{(\ell )} = x_{i_s^{(\ell )}} - T_{s}^{(\ell )} + \mu _\ell \). Hence, we get
Putting the two relations together, modulo 2, yields
This concludes the proof by noting that \(s = k^\star \), \(b_\ell = \delta _\ell + \lfloor \mu _\ell /2^t\rfloor \pmod 2\), and \(b'_\ell \equiv \delta '_\ell + \lfloor M'_\ell /2^t \rfloor \pmod 2\). \(\square \)
As a result, the client learns the classification result \(\mathfrak {T}(\varvec{x})\) at the end of the protocol in Fig. 6.
5 Discussion
5.1 Security Considerations
The decision tree evaluation protocol presented in Fig. 6 is secure in the semi-honest model, a.k.a. honest-but-curious model. It assumes two semantically secure additively homomorphic encryption schemes, \([\![{\cdot }]\!]\) and  , and a semi-honest secure 1-out-of-N OT protocol. Informally, if the parties interact according to the protocol specification, the semi-honest model guarantees that (i) the client only learns the classification result and a bound d on the depth of the decision tree, and (ii) the server learns nothing.
, and a semi-honest secure 1-out-of-N OT protocol. Informally, if the parties interact according to the protocol specification, the semi-honest model guarantees that (i) the client only learns the classification result and a bound d on the depth of the decision tree, and (ii) the server learns nothing.
The security is defined via the ideal-world/real-world simulation paradigm; see e.g. the excellent tutorial provided in [19, Chap. 6]. The security proof of our main construction is standard. We refer the reader to [34, Sect. 2.3] for precise security definitions and to [34, Theorem 3.2] for the proof technique.
Selecting parameter \(\kappa \). Step 2a in Fig. 6 requires a random mask \(\mu _\ell \) to blind the value of \(x_{i_{k \oplus \smash {\sigma ^{(\ell )}}}^{(\ell )}} - T_{k \oplus \sigma ^{(\ell )}}^{(\ell )}\) in

for \(k=0,\ldots ,2^\ell -1\). In Step 2c, as the output of the 1-out-\(2^\ell \) OT, the client obtains \(M'_\ell = M_j^{(\ell )}\) for a single value \(j \in [0, \ldots , 2^\ell - 1]\). This justifies that the same mask \(\mu _\ell \) can be re-used at level \(\ell \), for each successive value of k.
Moreover, when the message space \(\mathcal {M}\) for  is much larger than the set \(\{0,1\}^t\), since \(x_{i_{k \oplus \smash {\sigma ^{(\ell )}}}^{(\ell )}}\) and \(T_{k \oplus \sigma ^{(\ell )}}^{(\ell )}\) are t-bit values, there is no need to draw the mask \(\mu _\ell \) in the whole range of \(\mathcal {M}\). Any \((t + \kappa )\)-bit value for a relatively short security length \(\kappa \) will generate a mask that statistically hides \(x_{i_{k \oplus \smash {\sigma ^{(\ell )}}}^{(\ell )}} - T_{k \oplus \sigma ^{(\ell )}}^{(\ell )}\).
is much larger than the set \(\{0,1\}^t\), since \(x_{i_{k \oplus \smash {\sigma ^{(\ell )}}}^{(\ell )}}\) and \(T_{k \oplus \sigma ^{(\ell )}}^{(\ell )}\) are t-bit values, there is no need to draw the mask \(\mu _\ell \) in the whole range of \(\mathcal {M}\). Any \((t + \kappa )\)-bit value for a relatively short security length \(\kappa \) will generate a mask that statistically hides \(x_{i_{k \oplus \smash {\sigma ^{(\ell )}}}^{(\ell )}} - T_{k \oplus \sigma ^{(\ell )}}^{(\ell )}\).
When the message space  (like in [6]), \(\mu _\ell \) and \(M'_\ell \) are defined modulo \(2^t\) as elements in
(like in [6]), \(\mu _\ell \) and \(M'_\ell \) are defined modulo \(2^t\) as elements in  (and thus \(\lfloor \mu _\ell /2^t\rfloor = \lfloor M'_\ell /2^t\rfloor = 0\)). Parameter \(\kappa \) will be in this case set to 0.
(and thus \(\lfloor \mu _\ell /2^t\rfloor = \lfloor M'_\ell /2^t\rfloor = 0\)). Parameter \(\kappa \) will be in this case set to 0.
5.2 Performance Analysis
We compare the proposed evaluation protocol with the two most recent protocols, Wu et al. (PETS 2016) and Tai et al. (ESORICS 2017), in the semi-honest setting.
Let \(\mathfrak {T}\) be a binary decision tree of depth d with m [non-dummy] internal nodes (i.e., decision nodes). Let also n be the number of entries in the feature vector; each entry being represented as a t-bit integer. Both the computation and bandwidth are analyzed. For the computation complexity, we count the number of public-key operations performed by each of the parties. For the bandwidth, we count the number of ciphertexts sent by one party to the other.
In our protocol, the client first encrypts the feature vector. This requires \(\mathop { O }(n)\) public-key operations and produces n ciphertexts. Next, in the main loop, at each level \(\ell \) (for \(0\leqslant \ell \leqslant d -1\)), the client mainly performs two steps with the server: (1) one 1-out-of-\(2^{\ell }\) OT where the client is the chooser and (2) one comparison of two t-bit integers. We assume that the OT is implemented with the Naor-Pinkas protocol (see Appendix A) and that the comparison makes use of our comparison protocol (Fig. 1). So, on the client’s side, the OT requires in total for the main loop \(\mathop { O }(d)\) public-key operations and \(d-1\) ciphertexts; the comparison requires in total \(\mathop { O }(dt)\) public-key operations and \(d(\lfloor t/2 \rfloor +1)\) ciphertexts. The last step is a 1-out-of-\(2^{d}\) OT, which requires \(\mathop { O }(1)\) public-key operation and one ciphertext. Summing up, the total complexity for the client amounts to \(\mathop { O }(n+dt)\) with \(n + d - 1 + d(\lfloor t/2 \rfloor +1) + 1 = d(\lfloor t/2\rfloor + 2) + n\) ciphertexts. On the server’s side, the server processes in addition m encryptions (Step 2a in Fig. 6) to form  for the non-dummy nodes. This corresponds to a complexity of \(\mathop { O }(m)\). The OT in the main loop requires in total \(\mathop { O }(d)\) public-key operations and \(2^d - 1\) ciphertexts. The comparison requires \(\mathop { O }(dt)\) public-key operations and dt ciphertexts (we suppose here that the server plays the role of Party B; cf. Fig. 1). The last step for the final OT incurs for the server \(\mathop { O }(1)\) public-key operation and \(2^d\) ciphertexts. Consequently, the total complexity for the server is of \(\mathop { O }(m + dt)\) and the needed bandwidth is of \(2^d - 1 + dt + 2^d = dt + 2^{d+1} - 1\) ciphertexts.
for the non-dummy nodes. This corresponds to a complexity of \(\mathop { O }(m)\). The OT in the main loop requires in total \(\mathop { O }(d)\) public-key operations and \(2^d - 1\) ciphertexts. The comparison requires \(\mathop { O }(dt)\) public-key operations and dt ciphertexts (we suppose here that the server plays the role of Party B; cf. Fig. 1). The last step for the final OT incurs for the server \(\mathop { O }(1)\) public-key operation and \(2^d\) ciphertexts. Consequently, the total complexity for the server is of \(\mathop { O }(m + dt)\) and the needed bandwidth is of \(2^d - 1 + dt + 2^d = dt + 2^{d+1} - 1\) ciphertexts.
A typical value for the precision is \(t = 64\). As shown in Table 1, since \(d \ll m\), the proposed protocol greatly reduces the workload on both the client’s and server’s sides. The bandwidth usage is also improved on the client’s side with our protocol. On the server’s side, the savings depend on the tree sparsity. Denser decision trees give rise to more savings; for a complete binary tree (i.e., \(m = 2^d - 1\)), our protocol saves \((2^d-d)t\) ciphertexts on the server’s side.
5.3 Random Forests
As in [34], our main construction extend to the evaluation of random forests. Introduced by Ho [15], the random forest improves the quality of the classification task by combining the results of a multitude of decision trees. A random forest \(\mathfrak {F}\) can be defined as an ensemble of decision trees, \(\mathfrak {F} = \{\mathfrak {T}_i\}_{i}\). Its output is computed by taking the majority vote; i.e., \(\mathfrak {F}(\varvec{x}) = {\text {maj}}\{\mathfrak {T}_i(\varvec{x})\}_i\).
6 Conclusion and Future Work
In this work, we introduced an enhanced comparison protocol and several extensions thereof. As an application, combined with a novel design strategy and a number of optimizations, we developed an efficient protocol for the private evaluation of decision trees.
Future work. An interesting direction for future work is to design a privacy-preserving evaluation protocol in the multi-user setting, wherein the feature vector and/or the model are shared among multiple entities. Another interesting direction is to extend the protocol to make it secure against malicious adversaries.
Notes
- 1.
We use triple brackets rather than double brackets to indicate that the encryption scheme may be different from the one used for the comparisons.
References
Abu-Nimeh, S., Nappa, D., Wang, X., Nair, S.: A comparison of machine learning techniques for phishing detection. In: 2nd Annual eCrime Researchers Summit, pp. 60–69. ACM (2007). https://doi.org/10.1145/1299015.1299021
Agrawal, R., Shrikant, R.: Privacy-preserving data mining. ACM SIGMOD Record 29(2), 439–450 (2000). https://doi.org/10.1145/335191.335438
Asharov, G., Lindell, Y., Schneider, T., Zohner, M.: More efficient oblivious transfer extensions. J. Cryptol. 30(3), 805–858 (2017). https://doi.org/10.1007/s00145-016-9236-6
Azar, A.T., El-Metwally, S.M.: Decision tree classifiers for automated medical diagnosis. Neural Comput. Appl. 23(7–8), 2387–2403 (2013). https://doi.org/10.1007/s00521-012-1196-7
Barni, M., et al.: Secure evaluation of private linear branching programs with medical applications. In: Backes, M., Ning, P. (eds.) ESORICS 2009. LNCS, vol. 5789, pp. 424–439. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04444-1_26
Benhamouda, F., Herranz, J., Joye, M., Libert, B.: Efficient cryptosystems from \(2^k\)-th power residue symbols. J. Cryptol. 30(2), 519–549 (2017). https://doi.org/10.1007/s00145-016-9229-5
Bost, R., Popa, R.A., Tu, S., Goldwasser, S.: Machine learning classification over encrypted data. In: 22nd Annual Network and Distributed System Security Symposium (NDSS 2015). The Internet Society (2015). https://doi.org/10.14722/ndss.2015.23241
Bunn, P., Ostrovsky, R.: Secure two-party \(k\)-means clustering. In: 14th ACM Conference on Computer and Communications Security (CCS 2007), pp. 486–497. ACM (2007). https://doi.org/10.1145/1315245.1315306
Damgård, I., Geisler, M., Krøigaard, M.: Efficient and secure comparison for on-line auctions. In: Pieprzyk, J., Ghodosi, H., Dawson, E. (eds.) ACISP 2007. LNCS, vol. 4586, pp. 416–430. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73458-1_30
Damgård, I., Geisler, M., Krøigaard, M.: Homomorphic encryption and secure comparison. Int. J. Appl. Cryptography 1(1), 22–31 (2008). https://doi.org/10.1504/IJACT.2008.017048
Damgård, I., Geisler, M., Krøigaard, M.: A correction to Efficient and secure comparison for on-line auctions. Int. J. Appl. Cryptography 1(4), 323–324 (2009). https://doi.org/10.1504/IJACT.2009.028031
Du, W., Zhan, Z.: Building decision tree classifier on private data. In: IEEE Workshop on Privacy, Security, and Data Mining. Conferences in Research and Practice in Information Technology, vol. 14. Australian Computer Society (2002). http://crpit.com/confpapers/CRPITV14Du.pdf
Erkin, Z., et al.: Privacy-preserving face recognition. In: Goldberg, I., Atallah, M.J. (eds.) PETS 2009. LNCS, vol. 5672, pp. 235–253. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03168-7_14
Even, S., Goldreich, O., Lempel, A.: A randomized protocol for signing contracts. Commun. ACM 28(6), 637–647 (1985). https://doi.org/10.1145/3812.3818
Ho, T.K.: The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 20(8), 832–844 (1998). https://doi.org/10.1109/34.709601
Kocher, P.C.: Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 104–113. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68697-5_9
Libbrecht, M.W., Noble, W.S.: Machine learning applications in genetics and genomics. Nat. Rev. Genet. 16(6), 321–332 (2015). https://doi.org/10.1038/nrg3920
Lin, H.-Y., Tzeng, W.-G.: An efficient solution to the millionaires’ problem based on homomorphic encryption. In: Ioannidis, J., Keromytis, A., Yung, M. (eds.) ACNS 2005. LNCS, vol. 3531, pp. 456–466. Springer, Heidelberg (2005). https://doi.org/10.1007/11496137_31
Lindell, Y. (ed.): Tutorials on the Foundations of Cryptography. Information Security and Cryptography. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57048-8
Lindell, Y., Pinkas, B.: Privacy preserving data mining. J. Cryptol. 15(3), 177–206 (2002). https://doi.org/10.1007/s00145-001-0019-2
Liu, C., Wechsler, H.: Gabor feature based classification using the enhanced Fisher linear discriminant model for face recognition. IEEE Trans. Image Process. 11(4), 467–476 (2002). https://doi.org/10.1109/TIP.2002.999679
Min, J.H., Lee, Y.C.: Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Syst. Appl. 28(4), 603–614 (2005). https://doi.org/10.1016/j.eswa.2004.12.008
Mohassel, P., Zhang, Y.: SecureML: A system for scalable privacy-preserving machine learning. In: 2017 IEEE Symposium on Security and Privacy, pp. 19–38. IEEE (2017). https://doi.org/10.1109/SP.2017.12
Naor, M., Pinkas, B.: Efficient oblivious transfer protocols. In: 12th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2001), pp. 448–457. ACM/SIAM (2001). https://dl.acm.org/citation.cfm?id=365411.365502
Nasrabadi, N.M.: Pattern recognition and machine learning. J. Electronic Imaging 16(4), 049901 (2007). https://doi.org/10.1117/1.2819119
Nikolaenko, V., Ioannidis, S., Weinsberg, U., Joye, M., Taft, N., Boneh, D.: Privacy-preserving matrix factorization. In: 20th ACM Conference on Computer and Communications Security (CCS 2013), pp. 801–812. ACM (2013). https://doi.org/10.1145/2508859.2516751
Nikolaenko, V., Weinsberg, U., Ioannidis, S., Joye, M., Boneh, D., Taft, N.: Privacy-preserving ridge regression on hundreds of millions of records. In: 2013 IEEE Symposium on Security and Privacy, pp. 334–348. IEEE (2013). https://doi.org/10.1109/SP.2013.30
Rabin, M.O.: How to exchange secrets by oblivious transfer. Technical report TR-81. Harvard University (1981). https://ia.cr/2005/187
Resnick, P., Varian, H.R.: Recommender systems. Commun. ACM 40(3), 56–58 (1997). https://doi.org/10.1145/245108.245121
Rivest, R.L., Adleman, L., Dertouzous, M.L.: On data banks and privacy homomorphisms. In: Foundations of Secure Computation, pp. 169–179. Academic Press (1978). https://people.csail.mit.edu/rivest/RivestAdlemanDertouzos-OnDataBanksAndPrivacyHomomorphisms.pdf
Tai, R.K.H., Ma, J.P.K., Zhao, Y., Chow, S.S.M.: Privacy-preserving decision trees evaluation via linear functions. In: Foley, S.N., Gollmann, D., Snekkenes, E. (eds.) ESORICS 2017. LNCS, vol. 10493, pp. 494–512. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66399-9_27
Vaidya, J., Yu, H., Jiang, X.: Privacy-preserving SVM classification. Knowl. Inf. Syst. 14(2), 161–178 (2008). https://doi.org/10.1007/s10115-007-0073-7
Veugen, T.: Improving the DGK comparison protocol. In: 2012 IEEE International Workshop on Information Forensics and Security (WIFS 2012), pp. 49–54. IEEE (2012), https://doi.org/10.1109/WIFS.2012.6412624
Wu, D.J., Feng, T., Naehrig, M., Lauter, K.: Privately evaluating decision trees and random forests. Proc. Priv. Enhancing Technol. 2016(4), 335–355 (2016). https://doi.org/10.1515/popets-2016-0043
Yap, B.W., Ong, S.H., Husain, N.H.M.: Using data mining to improve assessment of credit worthiness via credit scoring models. Expert Syst. Appl. 38(10), 13274–13283 (2011). https://doi.org/10.1016/j.eswa.2011.04.147
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Naor-Pinkas OT Protocol
A Naor-Pinkas OT Protocol
Let \(\mathbb {G}= \langle g \rangle \) be a group of order q, in which the Diffie-Hellman assumption holds. Let also a cryptographic hash function H mapping to \(\{0,1\}^t\), modeled as a random oracle. The sender selects at random \(K_1, \ldots , K_{N-1} \in \mathbb {G}\) and computes \(y = g^x\) for some random integer  . The sender’s public key is \((g, y, K_1, \ldots , K_{N-1})\) and the secret key is x. The sender pre-computes \(S_i = (K_i)^x\) for \(1 \leqslant i \leqslant N-1\).
. The sender’s public key is \((g, y, K_1, \ldots , K_{N-1})\) and the secret key is x. The sender pre-computes \(S_i = (K_i)^x\) for \(1 \leqslant i \leqslant N-1\).
The sender’s input is a set of N bit-strings \(\sigma _0, \ldots , \sigma _{N-1} \in \{0,1\}^t\). Suppose a chooser (Carol) wishes to get string \(\sigma _j\) for some \(j \in \{0, \ldots , N-1\}\). The amortized 1-out-of-N Naor-Pinkas OT protocol [24, § 3.1] proceeds as follows.
-
1.
The chooser draws a random integer
 and computes \( pk _j = g^r\). If \(j\ne 0\), she sets \( pk _0 = K_j/ pk _j\). She sends \( pk _0\) to the sender.
and computes \( pk _j = g^r\). If \(j\ne 0\), she sets \( pk _0 = K_j/ pk _j\). She sends \( pk _0\) to the sender. -
2.
The sender computes \(( pk _0)^x\) and then, for \(1 \leqslant i \leqslant N-1\), sets \(( pk _i)^x\) as \(( pk _i)^x = S_i/( pk _0)^x\). Next, he chooses a nonce R and encrypts each string \(\sigma _i\) as \(c_i = H\bigl (( pk _i)^x, R, i\bigr ) \oplus \sigma _i\), for \(0 \leqslant i \leqslant N-1\). He sends \((c_0, \ldots , c_{N-1}, R)\) to the chooser.
-
3.
The chooser recovers \(\sigma _j\) as \(c_j \oplus H(y^r,R,j)\).
Interestingly, the protocol can be re-used multiple times. After the one-time initialization phase, each transfer only costs a single exponentiation (in \(\mathbb {G}\)) plus \(N-1\) multiplications for the sender. The chooser essentially computes one exponentiation per transfer.
Rights and permissions
Copyright information
© 2018 IFIP International Federation for Information Processing
About this paper
Cite this paper
Joye, M., Salehi, F. (2018). Private yet Efficient Decision Tree Evaluation. In: Kerschbaum, F., Paraboschi, S. (eds) Data and Applications Security and Privacy XXXII. DBSec 2018. Lecture Notes in Computer Science(), vol 10980. Springer, Cham. https://doi.org/10.1007/978-3-319-95729-6_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-95729-6_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-95728-9
Online ISBN: 978-3-319-95729-6
eBook Packages: Computer ScienceComputer Science (R0)






 , for
, for  denotes an encryption
denotes an encryption . In particular, for
. In particular, for 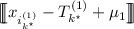 —and in turn
—and in turn  is obtained via oblivious transfer. Again, refer to Step 2 in Fig.
is obtained via oblivious transfer. Again, refer to Step 2 in Fig. 

 and computes
and computes 