Abstract
The LLL basis reduction algorithm was the first polynomial-time algorithm to compute a reduced basis of a given lattice, and hence also a short vector in the lattice. It thereby approximates an NP-hard problem where the approximation quality solely depends on the dimension of the lattice, but not the lattice itself. The algorithm has several applications in number theory, computer algebra and cryptography.
In this paper, we develop the first mechanized soundness proof of the LLL algorithm using Isabelle/HOL. We additionally integrate one application of LLL, namely a verified factorization algorithm for univariate integer polynomials which runs in polynomial time.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The LLL basis reduction algorithm by Lenstra, Lenstra and Lovász [8] is a remarkable algorithm with numerous applications. There even exists a 500-page book solely about the LLL algorithm [10]. It lists applications in number theory and cryptology, and also contains the best known polynomial factorization algorithm that is used in today’s computer algebra systems.
The LLL algorithm plays an important role in finding short vectors in lattices: Given some list of linearly independent integer vectors  , the corresponding lattice L is the set of integer linear combinations of the \(f_i\); and the shortest vector problem is to find some non-zero element in L which has the minimum norm.
, the corresponding lattice L is the set of integer linear combinations of the \(f_i\); and the shortest vector problem is to find some non-zero element in L which has the minimum norm.
Example 1
Consider \(f_1 = (1,1\,894\,885\,908,0)\), \(f_2 = (0,1,1\,894\,885\,908)\), and \(f_3 = (0,0,2\,147\,483\,648)\). The lattice of \(f_1,f_2,f_3\) has a shortest vector \((-3,17,4)\). It is the linear combination \((-3,17,4) = -3f_1 + 5\,684\,657\,741f_2 + 5\,015\,999\,938f_3\).
Whereas finding a shortest vector is NP-hard [9], the LLL algorithm is a polynomial time algorithm for approximating a shortest vector: The algorithm is parametric by some  and computes a short vector, i.e., a vector whose norm is at most \(\alpha ^{\frac{m-1}{2}}\) times as large than the norm of any shortest vector.
and computes a short vector, i.e., a vector whose norm is at most \(\alpha ^{\frac{m-1}{2}}\) times as large than the norm of any shortest vector.
In this paper, we provide the first mechanized soundness proof of the LLL algorithm: the functional correctness is formulated as a theorem in the proof assistant Isabelle/HOL [11]. Regarding the complexity of the LLL algorithm, we did not include a formal statement which would have required an instrumentation of the algorithm by some instruction counter. However, from the termination proof of our Isabelle implementation of the LLL algorithm, one can easily infer a polynomial bound on the number of arithmetic operations.
In addition to the LLL algorithm, we also verify one application, namely a polynomial-timeFootnote 1 algorithm for the factorization of univariate integer polynomials, that is: factorization into the content and a product of irreducible integer polynomials. It reuses most parts of the formalization of the Berlekamp–Zassenhaus factorization algorithm, where the main difference is the replacement of the exponential-time reconstruction phase [1, Sect. 8] by a polynomial-time one based on the LLL algorithm.
The whole formalization is based on definitions and proofs from a textbook on computer algebra [16, Chap. 16]. Thanks to the formalization work, we figured out that the factorization algorithm in the textbook has a serious flaw.
The paper is structured as follows. We present preliminaries in Sect. 2. In Sect. 3 we describe an extended formalization about the Gram–Schmidt orthogonalization procedure. This procedure is a crucial sub-routine of the LLL algorithm whose correctness is verified in Sect. 4. Since our formalization of the LLL algorithm is also executable, in Sect. 5 we compare it against a commercial implementation. We present our verified polynomial-time algorithm to factor integer polynomials in Sect. 6, and describe the flaw in the textbook. Finally, we give a summary in Sect. 7.
Our formalization is available in the archive of formal proofs (AFP) [2, 3].
2 Preliminaries
We assume some basic knowledge of linear algebra, but recall some notions and notations. The inner product of two real vectors \(v=(c_0,\dots ,c_n)\) and \(w=(d_0,\dots ,d_n)\) is  . Two real vectors are orthogonal if their inner product is zero. The Euclidean norm of a real vector v is
. Two real vectors are orthogonal if their inner product is zero. The Euclidean norm of a real vector v is  . A linear combination of vectors \(v_0,\dots ,v_m\) is \(\sum _{i=0}^{m} c_i v_i\) with \(c_0,\dots ,c_m \in \mathbb {R}\), and we say it is an integer linear combination if \(c_0,\dots ,c_m \in \mathbb {Z}\). Vectors are linearly independent if none of them is a linear combination of the others. The span – the set of all linear combinations – of linearly independent vectors \(v_0,\dots ,v_{m-1}\) forms a vector space of dimension m, and \(v_0,\dots ,v_{m-1}\) are its basis. The lattice generated by linearly independent vectors
. A linear combination of vectors \(v_0,\dots ,v_m\) is \(\sum _{i=0}^{m} c_i v_i\) with \(c_0,\dots ,c_m \in \mathbb {R}\), and we say it is an integer linear combination if \(c_0,\dots ,c_m \in \mathbb {Z}\). Vectors are linearly independent if none of them is a linear combination of the others. The span – the set of all linear combinations – of linearly independent vectors \(v_0,\dots ,v_{m-1}\) forms a vector space of dimension m, and \(v_0,\dots ,v_{m-1}\) are its basis. The lattice generated by linearly independent vectors  is the set of integer linear combinations of
is the set of integer linear combinations of  .
.
The degree of a polynomial \(f(x) = \sum _{i=0}^n c_i x^i\) is  , the leading coefficient is
, the leading coefficient is  , the content is the GCD of coefficients \(\{c_0,\dots ,c_n\}\), and the norm
, the content is the GCD of coefficients \(\{c_0,\dots ,c_n\}\), and the norm  is the norm of its corresponding coefficient vector, i.e.,
is the norm of its corresponding coefficient vector, i.e.,  .
.
If \(f = f_0 \cdot \ldots \cdot f_m\), then each \(f_i\) is a factor of f, and is a proper factor if f is not a factor of \(f_i\). Units are the factors of 1, i.e., \(\pm 1\) in integer polynomials and non-zero constants in field polynomials. By a factorization of polynomial f we mean a decomposition \(f = c \cdot f_0 \cdot \ldots \cdot f_m\) into the content c and irreducible factors \(f_0,\dots ,f_m\); here irreducibility means that each \(f_i\) is not a unit and admits only units as proper factors.
Our formalization has been carried out using Isabelle/HOL, and we follow its syntax to state theorems, functions and definitions. Isabelle’s keywords are written in  . Throughout Sects. 3 and 4, we present Isabelle sources in a way where we are inside some context which fixes a parameter
. Throughout Sects. 3 and 4, we present Isabelle sources in a way where we are inside some context which fixes a parameter  , the dimension of the vector space.
, the dimension of the vector space.
3 Gram–Schmidt Orthogonalization
The Gram–Schmidt orthogonalization (GSO) procedure takes a list of linearly independent vectors  from \(\mathbb {R}^n\) or \(\mathbb {Q}^n\) as input, and returns an orthogonal basis
from \(\mathbb {R}^n\) or \(\mathbb {Q}^n\) as input, and returns an orthogonal basis  for the space that is spanned by the input vectors. In this case, we also write that
for the space that is spanned by the input vectors. In this case, we also write that  is the GSO of
is the GSO of  .
.
We already formalized this procedure in Isabelle as a function  when proving the existence of Jordan normal forms [15]. That formalization uses an explicit carrier set to enforce that all vectors are of the same dimension. For the current formalization task, the usage of a carrier-based vector and matrix library is important: Harrison’s encoding of dimensions via types [5] is not expressive enough for our application; for instance for a given square matrix of dimension n we need to multiply the determinants of all submatrices that only consider the first i rows and columns for all \(1 \le i \le n\).
when proving the existence of Jordan normal forms [15]. That formalization uses an explicit carrier set to enforce that all vectors are of the same dimension. For the current formalization task, the usage of a carrier-based vector and matrix library is important: Harrison’s encoding of dimensions via types [5] is not expressive enough for our application; for instance for a given square matrix of dimension n we need to multiply the determinants of all submatrices that only consider the first i rows and columns for all \(1 \le i \le n\).
Below, we summarize the main result that is formally proven about  [15]. To this end, we open a context assuming common conditions for invoking the Gram–Schmidt procedure, namely that
[15]. To this end, we open a context assuming common conditions for invoking the Gram–Schmidt procedure, namely that  is a list of linearly independent vectors, and that
is a list of linearly independent vectors, and that  is the GSO of
is the GSO of  . Here, we also introduce our notion of linear independence for lists of vectors, based on an existing definition of linear independence for sets coming from a formalization of vector spaces [7].
. Here, we also introduce our notion of linear independence for lists of vectors, based on an existing definition of linear independence for sets coming from a formalization of vector spaces [7].

Unfortunately, lemma  does not suffice for verifying the LLL algorithm: We need to know how
does not suffice for verifying the LLL algorithm: We need to know how  is computed, that the connection between
is computed, that the connection between  and
and  can be expressed via a matrix multiplication, and we need recursive equations to compute
can be expressed via a matrix multiplication, and we need recursive equations to compute  and the matrix. In the textbook the Gram–Schmidt orthogonalization on input
and the matrix. In the textbook the Gram–Schmidt orthogonalization on input  is defined via mutual recursion.
is defined via mutual recursion.
where

and the connection between these values is expressed as the equality
by interpreting the \(f_i\)’s and \(g_i\)’s as row vectors.
Whereas there is no conceptual problem in expressing these definitions and proving the equalities in Isabelle/HOL, there still is some overhead because of the conversion of types. For instance in lemma  ,
,  is a list of vectors; in (1), g is a recursively defined function from natural numbers to vectors; and in (3), the list of \(g_i\)’s is seen as a matrix.
is a list of vectors; in (1), g is a recursively defined function from natural numbers to vectors; and in (3), the list of \(g_i\)’s is seen as a matrix.
Consequently, the formalized statement of (3) contains these conversions like  and
and  which convert a function and a list of vectors into matrices, respectively. Note that in the formalization an implicit parameter to \(\mu \) – the input vectors
which convert a function and a list of vectors into matrices, respectively. Note that in the formalization an implicit parameter to \(\mu \) – the input vectors  – is made explicit as
– is made explicit as  .
.

A key ingredient in reasoning about the LLL algorithm are projections. We say \(w \in \mathbb {R}^n\) is a projection of \(v\in \mathbb {R}^n\) into the orthocomplement of \(S \subseteq \mathbb {R}^n\), or just w is an oc-projection of v and S, if \(v - w\) is in the span of S and w is orthogonal to every element of S:

A nice property of oc-projections is that they are unique up to v and the span of S. Back to GSO, since \(g_i\) is the oc-projection of \(f_i\) and \(\{f_0,\dots ,f_{i-1}\}\), we conclude that \(g_i\) is uniquely determined in terms of \(f_i\) and the span of \(\{f_0,\dots ,f_{i-1}\}\). Put differently, we obtain the same \(g_i\) even if we modify some of the first i input vectors of the GSO: only the span of these vectors must be preserved.
The connection between the Gram–Schmidt procedure and short vectors becomes visible in the following lemma: some vector in the orthogonal basis  is shorter than any non-zero vector
is shorter than any non-zero vector  in the lattice generated by
in the lattice generated by  Here,
Here,  denotes the zero-vector of dimension
denotes the zero-vector of dimension  .
.

Whereas this short-vector lemma requires only a half of a page in the textbook, in the formalization we had to expand the condensed paper-proof into 170 lines of more detailed Isabelle source, plus several auxiliary lemmas.
For instance, on papers one easily multiplies two sums ( ) and directly omits quadratically many neutral elements by referring to orthogonality, whereas we first had to prove this auxiliary fact in 34 lines.
) and directly omits quadratically many neutral elements by referring to orthogonality, whereas we first had to prove this auxiliary fact in 34 lines.
The short-vector lemma is the key to obtaining a short vector in the lattice. It tells us that the minimum value of  is a lower bound for the norms of the non-zero vectors in the lattice. If
is a lower bound for the norms of the non-zero vectors in the lattice. If  for some \(\alpha \in \mathbb {R}\), then the basis is weakly reduced w.r.t. \(\alpha \). If moreover \(\alpha \ge 1\), then \(f_0 = g_0\) is a short vector in the lattice generated by
for some \(\alpha \in \mathbb {R}\), then the basis is weakly reduced w.r.t. \(\alpha \). If moreover \(\alpha \ge 1\), then \(f_0 = g_0\) is a short vector in the lattice generated by  :
:  for any non-zero vector h in the lattice.
for any non-zero vector h in the lattice.
In the formalization, we generalize the property of being weakly reduced by adding an argument k, and only demand that the first k vectors satisfy the required inequality. This is important for stating the invariant of the LLL algorithm. Moreover, we also define a partially reduced basis which additionally demands that the first k elements of the basis are nearly orthogonal, i.e., the \(\mu \)-values are small.

The GSO of some basis  will not generally be (weakly) reduced, but this problem can be solved with the LLL algorithm.
will not generally be (weakly) reduced, but this problem can be solved with the LLL algorithm.
4 The LLL Basis Reduction Algorithm
The LLL algorithm modifies the input \(f_0,\dots ,f_{m-1} \in \mathbb {Z}^n\) until the corresponding GSO is reduced, while preserving the generated lattice. It is parametrized by some approximation factorFootnote 2 \(\alpha > \frac{4}{3}\).

A readable, but inefficient, implementation of the LLL algorithm is given by Algorithm 1, which mainly corresponds to the algorithm in the textbook [16, Chap. 16.2–16.3]: the textbook fixes \(\alpha = 2\) and \(m = n\). Here, it is important to know that whenever the algorithm mentions \(\mu _{i,j}\), it is referring to \(\mu \) as defined in (2) for the current values of  and
and  . In the algorithm, \(\lfloor x \rceil \) denotes the integer closest to x, i.e., \(\lfloor x \rceil := \lfloor x + \frac{1}{2}\rfloor \).
. In the algorithm, \(\lfloor x \rceil \) denotes the integer closest to x, i.e., \(\lfloor x \rceil := \lfloor x + \frac{1}{2}\rfloor \).
Let us have a short informal view on the properties of the LLL algorithm. The first required property is maintaining the lattice of the original input  . This is obvious, since the basis is only changed in lines (4) and (6), and since swapping two basis elements, and adding a multiple of one basis element to a different basis element will not change the lattice. Still, the formalization of these facts required 190 lines of Isabelle code.
. This is obvious, since the basis is only changed in lines (4) and (6), and since swapping two basis elements, and adding a multiple of one basis element to a different basis element will not change the lattice. Still, the formalization of these facts required 190 lines of Isabelle code.
The second property is that the resulting GSO should be weakly reduced. This requires a little more argumentation, but is also not too hard: the algorithm maintains the invariant of the while-loop that the first i elements of the GSO are weakly reduced w.r.t. approximation factor \(\alpha \). This invariant is trivially maintained in line (7), since the condition in line (5) precisely checks whether the weakly reduced property holds between elements \(g_{i-1}\) and \(g_i\). Moreover, being weakly reduced up to the first i vectors is not affected by changing the value of \(f_i\), since the first i elements of the GSO only depend on \(f_0,\dots ,f_{i-1}\). So, the modification of \(f_i\) in line (4) can be ignored w.r.t. being weakly reduced.
Hence, formalizing the partial correctness of Algorithm 1 w.r.t. being weakly reduced is not too difficult. What makes it interesting, are the remaining properties we did not yet discuss. The most difficult part is the termination of the algorithm, and it is also nontrivial that the final basis is reduced. Both of these properties require equations which precisely determine how the GSO will change by the modification of  in lines 4 and 6.
in lines 4 and 6.
Once having these equations, we can drop the recomputation of the full GSO within the while-loop and replace it by local updates. Algorithm 2 is a more efficient algorithm to perform basis reduction, incorporating this improvement. Note that the GSO does not change in line 4, which can be shown with the help of oc-projections.

Concerning the complexity, each \(\mu _{i,j}\) can be computed with \(\mathcal{O}(n)\) arithmetic operations using its defining Eq. (2). Also, the updates of the GSO after swapping basis elements require \(\mathcal{O}(n)\) arithmetic operations. Since there are at most m iterations in the for-loop, each iteration of the while-loop in Algorithm 2 requires \(\mathcal{O}(n \cdot m)\) arithmetic operations. As a consequence, if \(n = m\) and I is the number of iterations of the while-loop, then Algorithm 2 requires \(\mathcal{O}(n^3 + n^2 \cdot I)\) many arithmetic operations, where the cubic number stems from the initial computation of the GSO in line 1.
To verify that Algorithm 2 computes a weakly reduced basis, it “only” remains to verify its termination, and the invariant that the updates of \(g_i\)’s indeed correspond to the recomputation of the GSOs. These parts are closely related, because the termination argument depends on the explicit formula for the new value of \(g_{i-1}\) as defined in line 6 as well as on the fact that the GSO remains unchanged in lines 3–4.
Since the termination of the algorithm is not at all obvious, and since it depends on valid inputs (e.g., it does not terminate if \(\alpha \le 0\)) we actually modeled the while-loop as a partial function in Isabelle [6]. Then in the soundness proof we only consider valid inputs and use induction via some measure which in turn gives us an upper bound on the number of loop iterations.
The soundness proof is performed via the following invariant. It is a simplified version of the actual invariant in the formalization, which also includes a property w.r.t. data refinement. It is defined in a context which fixes the lattice  , the number of basis elements
, the number of basis elements  , and an approximation factor \(\alpha \ge \frac{4}{3}\). Here, the function
, and an approximation factor \(\alpha \ge \frac{4}{3}\). Here, the function  converts a list of integer vectors into a list of rational vectors.
converts a list of integer vectors into a list of rational vectors.

Using this invariant, the soundness of lines 3–4 is expressed as follows.

In the lemma,  is a function which implements lines 3–4 of the algorithm. The lemma shows that the invariant is maintained and the GSO is unchanged, and moreover expresses the sole purpose of lines 3–4: they make the values \(\mu _{i,j}\) small.
is a function which implements lines 3–4 of the algorithm. The lemma shows that the invariant is maintained and the GSO is unchanged, and moreover expresses the sole purpose of lines 3–4: they make the values \(\mu _{i,j}\) small.
For the total correctness of the algorithm, we must prove not only that the invariant is preserved in every iteration, but also that some measure decreases for proving termination. This measure is defined below using Gramian determinants, a generalization of determinants which also works for non-square matrices. This is also the point where the condition \(\alpha > \frac{4}{3}\) becomes important: it ensures that the base \(\frac{4\alpha }{4 + \alpha }\) of the logarithm is strictly larger than 1.Footnote 3

In the definition, the matrix  is the
is the  submatrix of
submatrix of  corresponding to the first
corresponding to the first  elements of
elements of  . Note that the measure solely depends on the index
. Note that the measure solely depends on the index  and the basis
and the basis  . However, for lines 3–4 we only proved that
. However, for lines 3–4 we only proved that  and
and  remain unchanged. Hence the following lemma is important: it implies that the measure can also be defined purely from
remain unchanged. Hence the following lemma is important: it implies that the measure can also be defined purely from  and
and  , and that
, and that  will be positive.
will be positive.

With these preparations we are able to prove the most important property of the LLL algorithm, namely that each loop iteration – implemented as function  – preserves the invariant and decreases the measure.
– preserves the invariant and decreases the measure.

Our correctness proofs for  and
and  closely follows the description in the textbook, and we mainly refer to the formalization and the textbook for more details: the presented lemmas are based on a sequence of technical lemmas that we do not expose at this point.
closely follows the description in the textbook, and we mainly refer to the formalization and the textbook for more details: the presented lemmas are based on a sequence of technical lemmas that we do not expose at this point.
Here, we only sketch the termination proof: The value of the Gramian determinant for parameter \(k \ne i\) stays identical when swapping \(f_i\) and \(f_{i-1}\), since it just corresponds to an exchange of two rows which will not modify the absolute value of the determinant. The Gramian determinant for parameter \(k = i\) will decrease by using the first statement of lemma  , the explicit formula for the updated \(g_{i-1}\) in line 6, the condition
, the explicit formula for the updated \(g_{i-1}\) in line 6, the condition  , and the fact that \(|\mu _{i,i-1}| \le \frac{1}{2}\).
, and the fact that \(|\mu _{i,i-1}| \le \frac{1}{2}\).
The termination proof together with the measure function shows that the implemented algorithm requires a polynomial number of arithmetic operations: we prove an upper bound on the number of iterations which in total shows that executing Algorithm 2 for \(n = m\) requires \(\mathcal{O}(n^4 \cdot \log A)\) many arithmetic operations for \(A = \max \, \{|\!|f_i|\!|^2 \mid i < m\}\).

We did not formally prove the polynomial-time complexity in Isabelle. This task would at least require two further steps: since Isabelle/HOL functions are mathematical functions, we would need to instrument them by an instruction counter and hence make its usage more cumbersome; and we would need to formally prove that each arithmetic operation can be performed in polynomial time by giving bounds for the numerators and denominators in \(f_i\), \(g_i\), and \(\mu _{i,j}\).
Note that the reasoning on the number bounds should not be under-estimated. To illustrate this, consider the following modification to the algorithm, which we described in the submitted version of this paper: Since the termination proof only requires that \(|\mu _{i,i-1}|\) must be small, for obtaining a weakly reduced basis one may replace the for-loop in lines 3–4 by a single update \(f_i := f_i - \lfloor \mu _{i,i-1} \rceil \cdot f_{i-1}\). Then the total number of arithmetic operations will reduce to \(\mathcal{O}(n^3 \cdot \log A)\). However, we figured out experimentally that this change is a bad idea, since then the bit-lengths of the norms of \(f_i\) are no longer polynomially bounded: some input lattice of dimension 20 with 20 digit numbers led to the consumption of more than 64 GB of memory so that we had to abort the computation.
This indicates that formally verified bounds would be valuable. And indeed, the textbook contains informal proofs for bounds, provided that each \(\mu _{i,j}\) is small after executing lines 3–4. Here, a weakly reduced basis does not suffice.
With the help of  it is now trivial to formally verify the correctness of the LLL algorithm, which is defined as
it is now trivial to formally verify the correctness of the LLL algorithm, which is defined as  in the sources.
in the sources.
Finally, recall that the first element of a (weakly) reduced basis  is a short vector in the lattice. Hence, it is easy to define a wrapper function
is a short vector in the lattice. Hence, it is easy to define a wrapper function  around
around  , which is a verified algorithm to compute short vectors.
, which is a verified algorithm to compute short vectors.

5 Experimental Evaluation of the Verified LLL Algorithm
We formalized  in a way that permits code generation [4]. Hence, we can evaluate the efficiency of our verified LLL algorithm. Here, we use a fixed approximation factor \(\alpha = 2\), we map Isabelle’s integer operations onto the unbounded integer operations of the target language Haskell, and we compile the code with ghc version 8.2.1 using the -O2 parameter.
in a way that permits code generation [4]. Hence, we can evaluate the efficiency of our verified LLL algorithm. Here, we use a fixed approximation factor \(\alpha = 2\), we map Isabelle’s integer operations onto the unbounded integer operations of the target language Haskell, and we compile the code with ghc version 8.2.1 using the -O2 parameter.
We consider the LatticeReduce procedure of Mathematica version 11.2 as an alternative way to compute short vectors. The documentation does not specify the value of \(\alpha \), but mentions that Storjohann’s variant [12] of the LLL basis reduction algorithm is implemented.
For the input, we use lattices of dimension n where each of the n basis vectors has n-digit random numbers as coefficients. So, the size of the input basis is cubic in n; for instance the bases for \(n = 1\), 10, and 100 are stored in files measured in bytes, kilo-bytes, and mega-bytes, respectively.
Figure 1 displays the execution times in seconds for increasing n. The experiments have all been run on an iMacPro with a 3.2 GHz Intel Xeon W running macOS 10.13.4. The execution times of both algorithms can both be approximated by a polynomial \(c \cdot n^6\) – the gray lines behind the dots – where the ratio between the constant factors c is 306.5, which is also reflected in the diagrams by using different scales for the time-axis.
Note that for \(n \ge 50\), our implementation spends between 28–67 % of its time to compute the initial GSO on rational numbers, and 83–85 % of the total time of each run is used in integer GCD-computations. The GCDs are required for the verified implementation of rational numbers in Isabelle/HOL, which always normalizes rational numbers. Hence, optimizing our verified implementation for random lattices is not at all trivial, since a significant amount of time is spent in the cubic number of rational-number operations required in line 1 of Algorithm 2. Integrating and verifying known optimizations of GSO computations and LLL [10, Chap. 4] also looks challenging, since they depend on floating-point arithmetic. A corresponding implementation outperforms our verified algorithm by far: the tool fplll version 5.2.0 [13] can reduce each of our examples in less than 0.01 s.
Besides efficiency, it is worth mentioning that we did not find bugs in fplll’s or Mathematica’s implementation: the short vectors that are generated by both tools have always been as short as our verified ones, but not much shorter: the average ratio between the norms is 0.74 for fplll and 0.93 for Mathemathica.
Under http://cl-informatik.uibk.ac.at/isafor/LLL_src.tgz one can access the sources and the input lattices for the experiments.
6 Factorization of Polynomials in Polynomial Time
In this section we first describe how the LLL algorithm helps to factor integer polynomials, by following the textbook [16, Chap. 16.4–16.5].
We only summarize how we tried to verify the corresponding factorization Algorithm 16.22 of the textbook. Indeed, we almost finished it: after 1 500 lines of code we had only one remaining goal to prove. However, we were unable to figure out how to discharge this goal and then also started to search for inputs where the algorithm delivers wrong results. After a while we realized that Algorithm 16.22 indeed has a serious flaw, with details provided in Sect. 6.2.
Therefore, we derive another algorithm based on ideas from the textbook, which also runs in polynomial-time, and prove its soundness in Isabelle/HOL.
6.1 Short Vectors for Polynomial Factorization
In order to factor an integer polynomial f, we may assume a modular factorization of f into several monic factors \(u_i\):  modulo m where \(m = p^l\) is some prime power for user-specified l. In Isabelle, we just reuse our verified modular factorization algorithm [1] to obtain the modular factorization of f.
modulo m where \(m = p^l\) is some prime power for user-specified l. In Isabelle, we just reuse our verified modular factorization algorithm [1] to obtain the modular factorization of f.
We briefly explain how to compute non-trivial integer polynomial factors h of f based on Lemma 1, as also informally described in the textbook.
Lemma 1
([16, Lemma 16.20]). Let f, g, u be non-constant integer polynomials. Let u be monic. If u divides f modulo m, u divides g modulo m, and  , then
, then  is non-constant.
is non-constant.
Let f be a polynomial of degree n. Let u be any degree-d factor of f modulo m. Now assume that f is reducible, so \(f = f_1 \cdot f_2\) where w.l.o.g., we assume that u divides \(f_1\) modulo m and that  . Let the lattice \(L_{u,k}\) be the set of all polynomials of degree below \(d+k\) which are divisible by u modulo m. As
. Let the lattice \(L_{u,k}\) be the set of all polynomials of degree below \(d+k\) which are divisible by u modulo m. As  , clearly \(f_1 \in L_{u, n - d}\).
, clearly \(f_1 \in L_{u, n - d}\).
In order to instantiate Lemma 1, it now suffices to take g as the polynomial corresponding to any short vector in \(L_{u,k}\): u will divide g modulo m by definition of \(L_{u,k}\) and moreover  . The short vector requirement will provide an upper bound to satisfy the assumption
. The short vector requirement will provide an upper bound to satisfy the assumption  .
.

Here, the first inequality in (4) is the short vector approximation (\(f_1 \in L_{u,k}\)). The second inequality in (4) is Mignotte’s factor bound (\(f_1\) is a factor of f). Finally, Mignotte’s factor bound and (4) are used as approximations of  and
and  in (5), respectively.
in (5), respectively.
Hence, if l is chosen large enough so that  then all preconditions of Lemma 1 are satisfied, and
then all preconditions of Lemma 1 are satisfied, and  will be a non-constant factor of f. Since \(f_1\) divides f, also
will be a non-constant factor of f. Since \(f_1\) divides f, also  will be a non-constant factor of f. Moreover, the degree of h will be strictly less than n, and so h is a proper factor of f.
will be a non-constant factor of f. Moreover, the degree of h will be strictly less than n, and so h is a proper factor of f.
6.2 Bug in Modern Computer Algebra
In the previous section we have chosen the lattice \(L_{u,k}\) for \(k = n-d\) to find a polynomial h that is a proper factor of f. This has the disadvantage that h is not necessarily irreducible. In contrast, Algorithm 16.22 tries to directly find irreducible factors by iteratively searching for factors w.r.t. the lattices \(L_{u,k}\) for increasing k from 1 up to \(n - d\).
We do not have the space to present Algorithm 16.22 in detail, but just state that the arguments in the textbook and the provided invariants all look reasonable. Luckily, Isabelle was not so convinced: We got stuck with the goal that the content of the polynomial g corresponding to the short vector is not divisible by the chosen prime p, and this is not necessarily true.
The first problem occurs if the content of g is divisible by p. Consider \(f_1 = x^{12}+x^{10}+x^8+x^5+x^4+1\) and \(f_2 = x\). When trying to factor \(f = f_1 \cdot f_2\), then \(p = 2\) is chosen, and at a certain point the short vector computation is invoked for a modular factor u of degree 9 where \(L_{u,4}\) contains \(f_1\). Since \(f_1\) itself is a shortest vector, \(g = p \cdot f_1\) is a short vector: the approximation quality permits any vector of \(L_{u,4}\) of norm at most  . For this valid choice of g, the result of Algorithm 16.22 will be the non-factorization \(f = f_1 \cdot 1\).
. For this valid choice of g, the result of Algorithm 16.22 will be the non-factorization \(f = f_1 \cdot 1\).
We informed the authors of the textbook about this first problem. They admitted the flaw and it is easy to fix.
There is however a second potential problem. If g is even divisible by \(p^l\), then Algorithm 16.22 will again return wrong results. In the formalization we therefore integrate the check  into the factorization algorithmFootnote 4, and then this modified version of Algorithm 16.22 is correct.
into the factorization algorithmFootnote 4, and then this modified version of Algorithm 16.22 is correct.
We could not conclude the question whether the additional check is really required, i.e., whether  can ever happen, and just give some indication that the question is non-trivial. For instance, when factoring \(f_1\) above, then \(p^l\) is a number with 124 digits,
can ever happen, and just give some indication that the question is non-trivial. For instance, when factoring \(f_1\) above, then \(p^l\) is a number with 124 digits,  , so in particular all basis elements of \(L_{u,1}\) will have a norm of at least \(p^l\). Note that \(L_{u,1}\) also does not have quite short vectors: any vector in \(L_{u,1}\) will have norm of at least 111 digits. However, since the approximation factor in this example is only two digits long, the short vector computation must result in a vector whose norm has at most 113 digits, which is not enough for permitting \(p^l\) with its 124 digits as leading coefficient of g.
, so in particular all basis elements of \(L_{u,1}\) will have a norm of at least \(p^l\). Note that \(L_{u,1}\) also does not have quite short vectors: any vector in \(L_{u,1}\) will have norm of at least 111 digits. However, since the approximation factor in this example is only two digits long, the short vector computation must result in a vector whose norm has at most 113 digits, which is not enough for permitting \(p^l\) with its 124 digits as leading coefficient of g.
6.3 A Verified Factorization Algorithm
To verify the factorization algorithm of Sect. 6.1, we formalize the two key facts to relate lattices and factors of polynomials: Lemma 1 and the lattice \(L_{u,k}\).
To prove Lemma 1, we partially follow the textbook, although we do the final reasoning by means of some properties of resultants which were already proved in the previous development of algebraic numbers [14]. We also formalize Hadamard’s inequality, which states that for any square matrix A having rows \(v_i\), then  . Essentially, the proof of Lemma 1 consists of showing that the resultant of f and g is 0, and then deduce
. Essentially, the proof of Lemma 1 consists of showing that the resultant of f and g is 0, and then deduce  . We omit the full-detailed proof, the interested reader can see it in the sources.
. We omit the full-detailed proof, the interested reader can see it in the sources.
To define the lattice \(L_{u,k}\) for a degree d polynomial u and integer k, we define the basis \(v_0,\dots ,v_{k+d-1}\) of the lattice \(L_{u,k}\) such that each \(v_i\) is the \((k+d)\)-dimensional vector corresponding to polynomial \(u(x) \cdot x^i\) if \(i<k\), and to monomial \(m\cdot x^{k+d-i}\) if \(k \le i < k+d\).
We define the basis in Isabelle/HOL as  as follows:
as follows:

Here  is a function that transforms a polynomial p into a vector of dimension n with coefficients in the reverse order and completing with zeroes if necessary. We use it to identify an integer polynomial f of degree \(< n\) with its coefficient vector in \(\mathbb {Z}^{n}\). We also define its inverse operation, which transforms a vector into a polynomial, as
is a function that transforms a polynomial p into a vector of dimension n with coefficients in the reverse order and completing with zeroes if necessary. We use it to identify an integer polynomial f of degree \(< n\) with its coefficient vector in \(\mathbb {Z}^{n}\). We also define its inverse operation, which transforms a vector into a polynomial, as  .
.  denotes the reversed sorted list of natural elements from b to \(a-1\) (with \(b<a\)) and
denotes the reversed sorted list of natural elements from b to \(a-1\) (with \(b<a\)) and  denotes the monomial \(ax^b\). To visualize the definition, for \(u(x) = \sum _{i=0}^d u_i x^i\) we have
denotes the monomial \(ax^b\). To visualize the definition, for \(u(x) = \sum _{i=0}^d u_i x^i\) we have

and  is precisely the basis \((f_1,f_2,f_3)\) of Example 1.
is precisely the basis \((f_1,f_2,f_3)\) of Example 1.
There are some important facts that we must prove about  .
.
-
 is a list of linearly independent vectors as required for applying the LLL algorithm to find a short vector in \(L_{u,k}\).
is a list of linearly independent vectors as required for applying the LLL algorithm to find a short vector in \(L_{u,k}\). -
\(L_{u,k}\) characterizes the polynomials which have u as a factor modulo m:

That is, any polynomial that satisfies the right hand side can be transformed into a vector that can be expressed as integer linear combination of the vectors of
 . Similarly, any vector in the lattice \(L_{u,k}\) can be expressed as integer linear combination of
. Similarly, any vector in the lattice \(L_{u,k}\) can be expressed as integer linear combination of  and corresponds to a polynomial of degree \(<k+d\) which is divisible by u modulo m.
and corresponds to a polynomial of degree \(<k+d\) which is divisible by u modulo m.
The first property is a consequence of obvious facts that the matrix S is upper triangular, and its diagonal entries are non-zero if both u and m are non-zero. Thus, the vectors in  are linearly independent.
are linearly independent.
Now we look at the second property. For one direction, we see the matrix S in (6) as (a generalization of) the Sylvester matrix of polynomial u and constant polynomial m. Then we generalize an existing formalization about Sylvester matrices as follows:

We instantiate  by the constant polynomial m. So for every \(c \in \mathbb {Z}^{k+d}\) we get
by the constant polynomial m. So for every \(c \in \mathbb {Z}^{k+d}\) we get

for some polynomials r and s. As every \(g \in L_{u,k}\) is represented as \(S^{\mathsf T} c\) for some integer coefficient vector \(c \in \mathbb {Z}^{k+d}\), we conclude that every \(g \in L_{u,k}\) is divisible by u modulo m. The other direction requires the use of the division with remainder by the monic polynomial u. Although we closely follow the textbook, the actual formalization of these reasonings requires some more tedious work, namely the connection between the matrix-to-vector multiplication ( ) of Matrix.thy and linear combinations (
) of Matrix.thy and linear combinations ( ) of HOL-Algebra. The former is naturally described as a summation over lists (
) of HOL-Algebra. The former is naturally described as a summation over lists ( which we define via
which we define via  ), while the latter is set-based
), while the latter is set-based  . We follow the existing connection between
. We follow the existing connection between  and
and  of the class-based world to the locale-based world, which demands some generalizations of the standard library.
of the class-based world to the locale-based world, which demands some generalizations of the standard library.
Once those properties are proved, we implement an algorithm for the reconstruction of factors within a context that fixes  and
and  :Footnote 5
:Footnote 5

 is a recursive function which receives two parameters: the polynomial
is a recursive function which receives two parameters: the polynomial  that has to be factored and
that has to be factored and  , which is the list of modular factors of the polynomial
, which is the list of modular factors of the polynomial  .
.  computes a short vector (and transforms it into a polynomial) in the lattice generated by a basis for \(L_{u,k}\) and suitable k, that is,
computes a short vector (and transforms it into a polynomial) in the lattice generated by a basis for \(L_{u,k}\) and suitable k, that is,  .
.  is the list of elements of
is the list of elements of  that divide
that divide  modulo
modulo  , and
, and  contains the rest of elements of
contains the rest of elements of 
 returns the list of irreducible factors of
returns the list of irreducible factors of  Termination follows from the fact that the degree decreases, that is, in each step the degree of both
Termination follows from the fact that the degree decreases, that is, in each step the degree of both  and
and  is strictly less than the degree of
is strictly less than the degree of 
In order to formally verify the correctness of the reconstruction algorithm for a polynomial  we use the following invariants. They consider invocations
we use the following invariants. They consider invocations  for every intermediate factor
for every intermediate factor  of
of 
-
1.
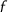 divides
divides 
-
2.

-
3.
 is the unique modular factorization of
is the unique modular factorization of  modulo
modulo 
-
4.
 and
and  are coprime, and
are coprime, and  is square-free in
is square-free in 
-
5.
 is sufficently large:
is sufficently large:  where
where 
Concerning complexity, it is easy to see that if  splits into i factors, then
splits into i factors, then  invokes the short vector computation for exactly \(i + (i-1)\) times: \(i-1\) invocations are used to split
invokes the short vector computation for exactly \(i + (i-1)\) times: \(i-1\) invocations are used to split  into the i irreducible factors, and for each of these factors one invocation is required to finally detect irreducibility.
into the i irreducible factors, and for each of these factors one invocation is required to finally detect irreducibility.
Finally, we combine the new reconstruction algorithm with existing results (the algorithms for computing an appropriate prime p, the corresponding exponent l, the factorization in \(\mathbb {Z}_p[x]\) and its Hensel-lifting to \(\mathbb {Z}_{p^l}[x]\)) presented in the Berlekamp–Zassenhaus development to get a polynomial-time factorization algorithm for square-free and content-free polynomials.

We further combine this algorithm with a pre-processing algorithm of earlier work [1]. This pre-processing splits a polynomial f into \(c \cdot f_1^1 \cdot \ldots \cdot f_k^k\) where c is the content of f which is not further factored. Each \(f_i\) is square-free and content-free, and will then be passed to  . The combined algorithm factors arbitrary univariate integer polynomials into its content and a list of irreducible polynomials.
. The combined algorithm factors arbitrary univariate integer polynomials into its content and a list of irreducible polynomials.
When experimentally comparing our verified LLL-based factorization algorithm with the verified Berlekamp–Zassenhaus factorization algorithm [1] we see no surprises. On the random polynomials from the experiments in [1], Berlekamp–Zassenhaus’s algorithm performs much better: it can factor each polynomial within a minute, whereas the LLL-based algorithm already fails on the smallest example. It is an irreducible polynomial with 100 coefficients where the LLL algorithm was aborted after a day when trying to compute a reduced basis for a lattice of dimension 99 with coefficients having up to 7 763 digits.
7 Summary
We formalized the LLL algorithm for finding a basis with short, nearly orthogonal vectors of an integer lattice, as well as its most famous application to get a verified factorization algorithm for integer polynomials which runs in polynomial time. The work is based on our previous formalization of the Berlekamp–Zassenhaus factorization algorithm, where the exponential reconstruction phase is replaced by the polynomial-time lattice-reduction algorithm. The whole formalization consists of about 10 000 lines of code, including a 2 200-line theory which contains generalizations and theorems that are not exclusive to our development. This theory can extend the Isabelle standard library and up to six different AFP entries. As far as we know, this is the first formalization of the LLL algorithm and its application to factor polynomials in any theorem prover. This formalization led us to find a major flaw in a textbook.
There are some possibilities to extend the current formalization, e.g., by verifying faster variants of the LLL algorithm or by integrating other applications like the more efficient factorization algorithm of van Hoeij [10, Chap. 8]: it uses simpler lattices to factor polynomials, but its verification is much more intricate.
Notes
- 1.
Again, we only mechanized the correctness proof and not the proof of polynomial complexity.
- 2.
The formalization also shows soundness for \(\alpha = \frac{4}{3}\), but then the polynomial runtime is not guaranteed.
- 3.
\(\frac{4\alpha }{4 + \alpha } = 1\) for \(\alpha = \frac{4}{3}\) and in that case one has to drop the logarithm from the measure.
- 4.
When discussing the second problem with the authors, they proposed an even more restrictive check.
- 5.
The corresponding Isabelle/HOL implementation contains some sanity checks which are solely used to ensure termination. We present here a simplified version.
References
Divasón, J., Joosten, S.J.C., Thiemann, R., Yamada, A.: A formalization of the Berlekamp–Zassenhaus factorization algorithm. In: CPP 2017, pp. 17–29. ACM (2017)
Divasón, J., Joosten, S., Thiemann, R., Yamada, A.: A verified factorization algorithm for integer polynomials with polynomial complexity. Archive of Formal Proofs, Formal proof development, February 2018. http://isa-afp.org/entries/LLL_Factorization.html
Divasón, J., Joosten, S., Thiemann, R., Yamada, A.: A verified LLL algorithm. Archive of Formal Proofs, Formal proof development, February 2018. http://isa-afp.org/entries/LLL_Basis_Reduction.html
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) FLOPS 2010. LNCS, vol. 6009, pp. 103–117. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12251-4_9
Harrison, J.: The HOL light theory of Euclidean space. J. Autom. Reason. 50(2), 173–190 (2013)
Krauss, A.: Recursive definitions of monadic functions. In: PAR 2010. EPTCS, vol. 43, pp. 1–13 (2010)
Lee, H.: Vector spaces. Archive of Formal Proofs, Formal proof development, August 2014. http://isa-afp.org/entries/VectorSpace.html
Lenstra, A.K., Lenstra, H.W., Lovász, L.: Factoring polynomials with rational coefficients. Math. Ann. 261, 515–534 (1982)
Micciancio, D.: The shortest vector in a lattice is hard to approximate to within some constant. SIAM J. Comput. 30(6), 2008–2035 (2000)
Nguyen, P.Q., Vallée, B. (eds.): The LLL Algorithm - Survey and Applications. Information Security and Cryptography. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-02295-1
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Storjohann, A.: Faster algorithms for integer lattice basis reduction. Technical report 249, Department of Computer Science, ETH Zurich (1996)
The FPLLL development team. fplll, a lattice reduction library (2016). https://github.com/fplll/fplll
Thiemann, R., Yamada, A.: Algebraic numbers in Isabelle/HOL. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 391–408. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-43144-4_24
Thiemann, R., Yamada, A.: Formalizing Jordan normal forms in Isabelle/HOL. In: CPP 2016, pp. 88–99. ACM (2016)
von zur Gathen, J., Gerhard, J.: Modern Computer Algebra, 3rd edn. Cambridge University Press, New York (2013)
Acknowledgments
This research was supported by the Austrian Science Fund (FWF) project Y757. Jose Divasón is partially funded by the Spanish projects MTM2014-54151-P and MTM2017-88804-P. Akihisa Yamada is supported by ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST. Some of the research was conducted while Sebastiaan Joosten and Akihisa Yamada were working in the University of Innsbruck. We thank Jürgen Gerhard and Joachim von zur Gathen for discussions on the problems described in Sect. 6.2, and Bertram Felgenhauer for discussions on gaps in the paper proofs. The authors are listed in alphabetical order regardless of individual contributions or seniority.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Divasón, J., Joosten, S., Thiemann, R., Yamada, A. (2018). A Formalization of the LLL Basis Reduction Algorithm. In: Avigad, J., Mahboubi, A. (eds) Interactive Theorem Proving. ITP 2018. Lecture Notes in Computer Science(), vol 10895. Springer, Cham. https://doi.org/10.1007/978-3-319-94821-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-319-94821-8_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94820-1
Online ISBN: 978-3-319-94821-8
eBook Packages: Computer ScienceComputer Science (R0)






 is a list of linearly independent vectors as required for applying the LLL algorithm to find a short vector in
is a list of linearly independent vectors as required for applying the LLL algorithm to find a short vector in 
 . Similarly, any vector in the lattice
. Similarly, any vector in the lattice  and corresponds to a polynomial of degree
and corresponds to a polynomial of degree 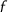 divides
divides 

 is the unique modular factorization of
is the unique modular factorization of  modulo
modulo 
 and
and  are coprime, and
are coprime, and  is square-free in
is square-free in 
 is sufficently large:
is sufficently large:  where
where 