Keywords

1 Introduction

One of the most important tasks in a radar system is to maintain a constant false alarm rate CFAR against all kinds of background heterogeneities. The signals backscattered to the radar can be modeled statistically with various probability density functions pdf [1]. In high-resolution radars with low grazing angles, the sea clutter shows a significant deviation from gaussianity [2] and the conventional detectors are not able to maintain a constant false alarm rate. For this, several distributions were proposed in the literature to model sea clutter.The K distribution, the Generalized Pareto distribution, more recently the Compound Inverse Gaussian distribution were chosen as alternatives to the Gaussian model and are well adapted to impulsive clutter. However, these distributions remain unable to predict the effects related to the presence of heavy echoes. For this reason, these models have been successfully extended to include thermal noise. In high-resolution radars with low grazing angles, a lot of non coherent CFAR detectors have been proposed in the literature. The log-t [3], WH-CFAR [4], the log-t CFARD [5] are robust for the Weibull and log-normal. In [6], Jakubiak proposed a Log-t detector which attains the CFAR property for a shape parameter greater than one. Recently, a detector based on the Max-Mean operations was proposed for the compound Gaussian models and proved to be robust in terms of false alarm regulation [7]. In this paper we propose to generalize the Max-Mean detector to deal with the presence of thermal noise and interfering targets. In Sect. 2, we describe the proposed detector and the clutter models considered. Section 3 discusses the results obtained in different situations. Finally, some conclusions are drawn in Sect. 4.

Fig. 1.
figure 1

Block diagram of the modified detector

Full size image

2 Proposed Modified Robust Detector in the Presence of Thermal Noise and the Interfering Targets

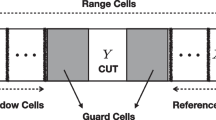
The bloc diagram of the detector under consideration is shown in Fig. 1.

Where the cell under test Z is compared to the adaptive threshold to decide about the presence (Hypothesis \(H_1\)) or the absence (Hypothesis \(H_0\)) of a target. The detector as proposed in [7] uses the maximum value and the mean value of the reference samples to set the adaptive threshold given by

$$\begin{aligned} Z\quad \mathop {\gtrless }_{H_0}^{H_1}\quad T = \frac{1}{N}(Max(x))^\tau (Mean(x))^{1-\tau } \end{aligned}$$
(1)

Where \(\tau \) is a factor set to achieve a desired probability of False Alarm \(P_{fa}\). It was shown in [7] that this detector possesses the CFAR property for a class of compound Gaussian distributions if only four reference cells are considered. However, if one or more interfering targets are present in the reference window, the CFAR property is no longer guaranteed. For this reason, we propose a modified version of the detector proposed in [7] to deal with the presence of interfering targets. We also take into consideration the presence of thermal noise for the three distributions considered in this work, namely; the K distribution, the Generalized Pareto and the Compound Inverse Gaussian distribution. The proposed detector uses six reference cells instead of four. Then, these cells are ranked in an ascending order to obtain \(X_{(1)}\), \(X_{(2)}\),...,\(X_{(6)}\) and the two largest samples are censored. This means that this detector can deal with up to two interfering targets. The threshold is then computed using the remaining samples in the same manner as in [7]. That is

$$\begin{aligned} Z\quad \mathop {\gtrless }_{H_0}^{H_1}\quad T = \frac{1}{N}(X_{(4)})^\tau (Mean(X_{{(1)}:{(4)}}))^{1-\tau } \end{aligned}$$
(2)

2.1 The K-Distribution Plus Thermal Noise

The K distribution is characterized by the shape parameter \(\nu \) and the scale parameter b. First, if the thermal noise is ignored, the probability density function pdf of the speckle and texture are expressed, respectively, by an Exponential distribution and a Gamma distribution [8]

$$\begin{aligned} P(x\vert y)=\frac{1}{y}exp(-\frac{x}{y}) \end{aligned}$$
(3)
$$\begin{aligned} P(y)= \frac{b^\nu }{\varGamma (\nu )}y^{\nu -1}exp(-by) \end{aligned}$$
(4)

The pdf of the K distribution is given by [8]

$$\begin{aligned} P(x)= \int _{0}^{\infty } P(y)P(x\vert y)\,\mathrm {d}y = \frac{2b^{\frac{\nu +1}{2}\frac{\nu -1}{2}}}{\varGamma (\nu )}K_{\nu -1}(2\sqrt{bx}) \end{aligned}$$
(5)

where \(K_{\nu -1}(.)\) is the modified Bessel function of the second kind, and \(\varGamma (.)\) is the Gamma function. In the case of the presence of thermal noise. The probability density function pdf of the speckle component becomes [8].

$$\begin{aligned} P(x\vert y)= \frac{1}{p_n+y}exp(-\frac{x}{p_n+y}) \end{aligned}$$
(6)

Where \(p_n =2\sigma ^2\) is the power of the thermal noise. The resulting pdf of K distribution plus noise becomes

$$\begin{aligned} P(x)= \frac{b^\nu }{\varGamma (\nu )}\int _{0}^{\infty } \frac{y^{\nu -1}}{p_n+y}exp(-\frac{x}{p_n+y}-by)\, \mathrm {d}y \end{aligned}$$
(7)

2.2 The Generalized Pareto Plus Thermal Noise Distribution

The Generalized Pareto (GP) distribution is characterized by the shape parameter \(\alpha \) and the scale parameter b. Its pdf is given by

$$\begin{aligned} P(x) = \frac{\alpha b^\alpha }{(x+b)^{\alpha + 1}} \end{aligned}$$
(8)

When the thermal noise is added to the speckle component, the resulting pdf becomes [9]

$$\begin{aligned} P(x)= \frac{b^\alpha }{\varGamma (\alpha )}\int _{0}^{\infty } \frac{y^{-\alpha -1}}{p_n+y}exp(-\frac{x}{p_n+y})exp(\frac{-b}{y})\, \mathrm {d}y \end{aligned}$$
(9)

2.3 The Compound Inverse Gaussian Plus Thermal Noise Distribution

The Compound Inverse Gaussian (CIG) distribution is characterized by a texture obeying to the inverse Gaussian. It is characterized by the shape parameter \(\lambda \) and the mean \(\mu >0\). If the thermal noise is ignored, the pdf is of the form [10]

$$\begin{aligned} P(x\vert y) = \frac{\varPi x}{2y^2}exp(-\frac{\varPi x^2}{4y^2}) \end{aligned}$$
(10)
$$\begin{aligned} P(y)= \frac{\lambda ^{1/2 }}{\sqrt{2\varPi }y^{{3}/{2}}}exp(-\lambda \frac{(y-\mu )^2}{2\mu ^2y}) \end{aligned}$$
(11)

When the thermal noise is not ignored the speckle can be rewritten as [10]

$$\begin{aligned} P(x\vert y) = \frac{x}{p_n+2y^2/\varPi }exp(-\frac{x^2}{p_n+4y^2/\varPi })) \end{aligned}$$
(12)

And the resulting pdf for \(0 \le x \le \infty \) becomes

$$\begin{aligned} P(x) = \int _{0}^{\infty }\frac{x}{p_n+2y^2/\varPi }exp(-\frac{x^2}{p_n+4y^2/\varPi })\times \frac{\lambda ^{1/2 }}{\sqrt{2\varPi }y^{3/2 }}exp(-\lambda \frac{(y-\mu )^2}{2\mu ^2y})\,dy \end{aligned}$$
(13)

3 Results and Discussions

To illustrate the performance of the proposed detector in terms of the false alarm regulation, we simulated \(P_{fa}\) with respect to the factor \(\tau \) for the three clutter distributions mentioned above and in different situations. We used (N = \(10^6\)) Monte Carlo runs in order to attain a \(P_{fa}\) equal to \(10^{-4}\). The thermal noise power \(p_n\) was set to 0.5, and the target is assumed to be fluctuating according to the Swerling I model. The Interference-to-Clutter Ratio (ICR) is assumed to be equal to 20 dB.

Figures 2 and 3 show the variation of \(P_{fa}\) against the threshold factor \(\tau \) for the K distribution clutter for different values of \(\nu > 1\) and a fixed value of b to 1, in the case of the presence of thermal noise and two interfering targets in the reference cells respectively. It is clear that all the curves almost overlap proves the ability of the proposed detector to maintain the CFAR property independently of \(\nu \) and b. In Figs. 4 and 5, we conducted the same simulations for the Generalized Pareto clutter. The same pattern is observed for a shape parameter greater than 1. In Figs. 6 and 7, we plotted \(P_{fa}\) versus the scale factor \(\tau \) for different values of the shape parameter \(\lambda \) of the CIG distribution of the clutter. Again the different cures overlap even for the case of a very spiky clutter \((\lambda \simeq 0)\). It is also noticed in all the cases studied that the presence of thermal noise or in the presence of interfering targets does not affect the robustness of the proposed detector.

Fig. 2.
figure 2

Variation of \(P_{fa}\) versus the scale factor \(\tau \) for the K-distribution with b = 1 and N = \(10^6\), in the presence of thermal noise

Full size image
Fig. 3.
figure 3

Variation of \(P_{fa}\) versus the scale factor \(\tau \) for the K-distribution with b = 1 and N = \(10^6\), in the presence of thermal noise and two interfering targets

Full size image
Fig. 4.
figure 4

Variation of \(P_{fa}\) versus the scale factor \(\tau \) for the Generalized Pareto with b = 1 and N = \(10^6\), in the presence of thermal noise

Full size image
Fig. 5.
figure 5

Variation of \(P_{fa}\) versus the scale factor \(\tau \) for the Generalized Pareto with b = 1 and N = \(10^6\), in the presence of thermal noise and two interfering targets

Full size image
Fig. 6.
figure 6

Variation of \(P_{fa}\) versus the scale factor \(\tau \) for the Compound Inverse Gaussian with \(\mu = 1\) and N = \(10^6\), in the presence of thermal noise

Full size image
Fig. 7.
figure 7

Variation of \(P_{fa}\) versus the scale factor \(\tau \) for the Compound Inverse Gaussian with \(\mu = 1\) and N = \(10^6\), in the presence of thermal noise and two interfering targets

Full size image

4 Conclusion

In this paper, we have proposed a generalization of a robust detector that deals with the presence of thermal noise and interfering targets in compound Gaussian clutter. The results obtained prove that the proposed detector attains the CFAR property in the presence of thermal noise and two interfering targets in the reference cells, for The K distribution, the Generalized Pareto distribution and the Compound Inverse Gaussian distribution. In all the situations studied, the \(P_{fa}\) curves showed that the latter is almost independent of the clutter parameters except for the K distribution where the robustness is observed for a shape parameter greater than one.