Abstract
Private Set Intersection (PSI) is a popular cryptographic primitive that allows two parties, a client and a server, to compute the intersection of their private sets, so that the client only receives the output of the computation, while the server learns nothing besides the size of the client’s set. A common limitation of PSI is that a dishonest client can progressively learn the server’s set by enumerating it over different executions. Although these “oracle attacks” do not formally violate security according to traditional secure computation definitions, in practice, they often hamper real-life deployment of PSI instantiations, especially if the server’s set does not change much over multiple interactions.
In a first step to address this problem, this paper presents and studies the concept of Reactive PSI (RePSI). We model PSI as a reactive functionality, whereby the output depends on previous instances, and use it to limit the effectiveness of oracle attacks. We introduce a general security model for RePSI in the (augmented) semi-honest model and a construction which enables the server to control how many inputs have been used by the client across several executions. In the process, we also present the first practical construction of a Size-Hiding PSI (SHI-PSI) protocol in the standard model, which may be of independent interest.
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 307937.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Private Set Intersection (PSI) lets two parties compute the intersection of their private sets, drawn from a common universe, without disclosing items outside the intersection. In its most common formulation, only one party, usually referred to as the client, obtains the intersection, while the other, aka server, only learns the size of the client’s set. Over the past few years, PSI has been used in numerous privacy-friendly applications, including ridesharing [HOS17], collaborative threat mitigation [FDCB15], genomic testing [BBD+11], and online advertising [IKN+17].
Nonetheless, there are some challenging issues limiting the adoption of PSI in practice. In particular, if two parties run the protocol several times, the server is vulnerable to oracle attacks. In such an attack, a dishonest client progressively learns the server’s set by enumerating it over different executions. Although this does not formally violate security definitions of two-party computation [Gol04], it may hamper real-life deployment of PSI, especially if the server’s set is mostly static. Moreover, in the Size-Hiding variant of PSI [ADT11], where the server does not learn the size of client’s set, the problem is further compounded as the server cannot limit the size of client’s input.
Aiming to mitigate oracle attacks in PSI protocols, we start reasoning about the security of this cryptographic primitive across multiple runs. To this end, we introduce the notion of Reactive PSI (RePSI), along with a general security model in the augmented semi-honest model [Gol04], and set to propose provably secure instantiations.
Let us first consider a naïve solution. In the non size-hiding setting, using certain PSI protocols, e.g., [DT10], one could in theory let the client re-use the randomness for the elements in its input set that do not change across runs. This way, the server learns how many of the client’s elements are “fresh” in the current run and imposes an upper-bound. However, this approach at the very least makes two protocol executions linkable as it reveals the patterns of the client’s inputs. Moreover, if the distribution of client’s elements is somewhat predictable, this might actually reveal too much information. By contrast, our goal is to provide stronger definitions whereby the client does not reveal its input patterns, but only proves that number of unique elements input from the first run up to the current one is below a given threshold.
1.1 Roadmap
In this paper, we tackle the issue of oracle attacks in Private Set Intersection (PSI) by extending security definitions to account for reactive functionalities, whereby the output of the current execution can depend on previous executions.
First, we introduce the notion of Reactive PSI (RePSI), along with a general security model in the augmented semi-honest model [Gol04]. In this model, the adversary is assumed to follow the specifications of the protocol (as in the standard semi-honest model) but it is allowed to adaptively modify the inputs used by the controlled party at each protocol run. We argue that the augmented semi-honest model can effectively model oracle attacks in PSI, whereas, the standard semi-honest model cannot, since it prevents the adversary to change the input of the corrupted party between protocol executions. That is, the adversary can only leverage honestly generated transcripts. Also, although we do not yet provide security in the fully malicious setting, we believe that ours is an important first step towards the development of efficient protocols. In fact, there exist general transformations [GMW87, Gol04] allowing to compile a semi-honest secure protocol into one secure against malicious adversaries, and efficient PSI-like protocols are also traditionally in semi-honest settings (see Sect. 1.2). Moreover, our definitions are general enough to capture various types of reactive functionalities and they cover the sequential composition of standard (i.e., stateless) PSI protocols.
Then, we provide two constructions, one static and one reactive. We focus on the size-hiding setting since, as mentioned above, the fact that the server cannot even check and limit the number of client’s inputs in a single execution, makes oracle attacks significantly worse. Our static construction, named Bounded-Input PSI limits the size of the client’s input set at every protocol run. We achieve this by adapting the Bounded Size-Hiding PSI recently presented by Bradley et al. [BFT16], which provided security in the Random Oracle Model (ROM). As an additional contribution, we instantiate Bounded Size-Hiding PSI in the standard model, thus also presenting the first practical Size-Hiding PSI protocol not in ROM. Our reactive construction, called Input Controlling RePSI, enables the server to control how many inputs have been used by the other party across several executions. Specifically, it limits the size of the unions set stemming from the union of client’s input sets across all protocol runs. Input Controlling RePSI, therefore, addresses oracle attacks in practical scenarios where a client and a server engage in multiple PSI executions.
By modeling PSI as a reactive functionality, we require that client and server keep state across protocol executions. Nevertheless, the amount of state information kept by the two parties in our constructions is small and independent of the number of runs.
1.2 Related Work
To the best of our knowledge, the problem of Reactive PSI has not been studied in literature. Standard security definitions for semi-honest and malicious two-party and multiparty computation can be extended to model security of generic protocols computing reactive functionalities. The augmented semi-honest model was introduced by Goldreich [Gol04] to bridge the semi-honest model and the malicious model and used it as an intermediate step in the compilation of secure protocols from the semi-honest to the malicious settings. Hazay and Lindell [HL10a] observed that security in the malicious settings sometime does not imply security in the semi-honest settings, while this anomaly does not happen in the augmented semi-honest model.
Overall, prior work on PSI can be grouped in protocols using special-purpose constructions [FNP04, DT10], oblivious transfer and its extensions [PSZ14, PSSZ15], and/or generic garbled circuits [PSSZ15]. Most protocols are secure against semi-honest adversaries [FNP04, DT10, PSZ14, PSSZ15], with fewer, less efficient ones, against malicious ones [DKT10, JL10, RR17]. Also, protocols by Hazay and Lindell [HL08] operate in the covert model (i.e., a malicious adversary may be able to cheat but it can get caught with at least a certain probability).
There are also a few variants to the standard PSI functionality. Besides the size-hiding one discussed above [ADT11, BFT16], Authorized PSI [CZ09, DT10] partially mitigates malicious behavior by introducing a trusted party that authorizes (i.e., signs) the elements that a client can use as input. However, finding a common trusted party may be hard in most practical use cases.
More closely related to our work are the protocols proposed in [BFT16] and [DMV13]. Bradley et al. [BFT16] introduce the concept of Bounded Size-Hiding PSI, which allows the client to hide the size of its input, and the server to impose an upper-bound on the size of the client’s set for the current run. We start from the protocol of [BFT16] and cast it within the framework of RePSI to counter oracle attacks across multiple runs. Furthermore, while [BFT16] works in the random oracle model, we instantiate it in the standard model. Dagdelen et al. [DMV13] introduce the concept of rate-limited Secure Function Evaluation (SFE), whereby protocol participants can monitor and limit the number of distinct inputs (i.e., rate) used by their counterparts in multiple executions of an SFE. They present compilers by which any SFE scheme can be turned into a rate-limited one. In particular, the “rate-hiding” compiler [DMV13] may be applied to a PSI protocol to achieve the same provisions of our Input Controlling RePSI. We take a less general approach and focus on PSI, by incorporating reactiveness in the functionality and achieving a more efficient construction (see Sect. 5.3). A theoretical construction based on fully-homomorphic encryption for size-hiding PSI in the standard model was recently presented in [COV15].
1.3 Paper Organization
Next section introduces some preliminaries, then, Sect. 3 provides security definitions for the Reactive PSI primitive in the augmented semi-honest model. Next, in Sects. 4 and 5, we present our constructions of Bounded Input RePSI and Input Controlling RePSI, respectively. Finally, the paper concludes in Sect. 6.
2 Preliminaries
In this section, we introduce notation, cryptographic assumptions and building blocks used later on in the paper.
We write \(y \leftarrow \mathcal {A}(x)\) for a probabilistic algorithm returning output y given as input x. In case we want to specify the randomness r used, we write \(y=\mathcal {A}(x;r)\). We implicitly assume all the algorithms considered in this paper to receive as input the security parameter \(\lambda \). For functions \(f,g:\mathbb {N}\rightarrow [0,1]\) we write \(f(\lambda )\approx g(\lambda )\) if \(|f(\lambda )-g(\lambda )|=\lambda ^{\omega (1)}\). We say a function f is overwhelming if \(f(\lambda )\approx 1\) and negligible if \(f(\lambda )\approx 0\).
2.1 Bilinear Groups
A bilinear group is a tuple \((p,{\mathbb {G}},{\mathbb {G}}_T,e,g)\) s.t. \({\mathbb {G}}\) and \({\mathbb {G}}_T\) are groups of prime order p and \(g\in {\mathbb {G}}\) generates the group \({\mathbb {G}}\). The function e is an efficiently computable bilinear map \(e:{\mathbb {G}}\times {\mathbb {G}} \rightarrow {\mathbb {G}}_T\) such that e(g, g) is a generator of \({\mathbb {G}}_T\). We assume there are probabilistic polynomial time generators \(\mathcal {G}\) and \(\mathcal {BG}\) that, given as input the security parameter, return the description of a group \((p,{\mathbb {G}},g)\leftarrow \mathcal {G}(\lambda )\) and bilinear group \((p,{\mathbb {G}},{\mathbb {G}}_T,e,g)\leftarrow \mathcal {BG}(\lambda )\), respectively. In the constructions of Sects. 4 and 5, we rely on the exponent Strong Diffie-Hellman (Exponent q-SDH) and the Decisional Bilinear Diffie-Hellmann Inversion problem (q-DBDHI).
2.2 Bilinear Accumulators
A cryptographic accumulator is a primitive that allows to give a compact representation of a set and that enables to efficiently prove membership of an element into the accumulated set. Accumulators were firstly introduced by Benaloh and de Mare [BDM94] and were later extended and provided with additional properties [BP97, CL02, Ngu05, DHS15, GOP+16, CKS09].
A (static) accumulator consists of four algorithms \((\mathsf {KeyGen},\mathsf {Eval},\mathsf {WitGen},\mathsf {Verify})\). The key generation algorithm \(\mathsf {KeyGen}\) takes as input the security parameter and generates a secret and an evaluation key pair (sk, ek) for the accumulator. The evaluation algorithm \(\mathsf {Eval}\) gets as input the evaluation key ek and a set A of values and returns an accumulator \(\mathsf {acc}_A\). The \(\mathsf {WitGen}\) and \(\mathsf {Verify}\) are deterministic algorithms for, respectively, producing and verifying a witness \(\mathsf {wit}\) for the membership of an element \(a\in A\) in a given accumulator \(\mathsf {acc}_A\). We follow [DHS15] on modelling \(\mathsf {Eval}\) and \(\mathsf {WitGen}\) to optionally get as input the secret key sk, since this makes the algorithms more efficient. We denote the optional input by writing  .
.
The main security properties required from accumulators are: correctness, i.e. honestly generated witnesses should verify; collision-freeness, i.e. that it is unfeasible to compute a witness for elements not included in the accumulated set; and indistinguishability, i.e. the accumulator does not reveal any information on the accumulated set.
In our constructions of PSI we will later use the accumulator introduced by Nguyen in [Ngu05] based on bilinear pairings. Since we will not require the possibility of removing elements from an accumulator, we restrict Nguyen’s construction [Ngu05] to a static accumulator, description of which can be found in Fig. 1.
Let \(A=\{a_1,\ldots a_n\}\) be a set of elements \(a_i \in \mathbb {Z}_p\) that we wish to include into an accumulator. We first start by computing the characteristic polynomial representation of set A. This is the monic polynomial \(\mathsf {Ch}_A(X)\in \mathbb {Z}_p[X]\) which has roots in the elements contained in the set A, namely \(\mathsf {Ch}_A(X)=\prod _{i=1}^n(X+a_i)\). In order to efficiently evaluate the accumulator, it will be convenient to express such polynomial using its coefficient representation, i.e. computing \(c_j\) such that \(\mathsf {Ch}_A(X)=\prod _{i=1}^n(X+a_i)=\sum _{j=0}^n c_jX^j\). We stress that given A it is always possible to efficiently compute the coefficient \(c_j\) of \(\mathsf {Ch}_A(X)\).
The evaluation key of [Ngu05] bilinear accumulator consists of \(ek=(g,g^x,g^{x^2},\ldots , g^{x^{q}})\in {\mathbb {G}}^{q+1}\), where g is a generator of the group \({\mathbb {G}}\) and \(x\in \mathbb {Z}_p\) is a secret value.
Given the evaluation key and polynomial \(\mathsf {Ch}_A(X)\) of degree at most q, it is possible to compute \(g^{\mathsf {Ch}_A(x)}\). This is done by first expanding \(\mathsf {Ch}_A(X)\) into its coefficient representation, i.e \(\mathsf {Ch}_A(X)=\sum _{i=0}^q c_i X^i\), and then computing \(g^{\mathsf {Ch}_A(x)}=\prod _{i=0}^{q} (g^{x^i})^{c_i}\). An accumulator \(\mathsf {acc}_A\) to a set A is computed by picking a random \(r\leftarrow \mathbb {Z}_p\) and setting \(\mathsf {acc}_A=(g^{\mathsf {Ch}_A(x)})^r\).
We recall the following result from [Ngu05, DHS15].
Lemma 1
Under the q-SDH assumption, the accumulator described in Fig. 1 is collision-free and indistinguishable.
Subset Queries. The \(\mathsf {WitGen}\) algorithm described in Fig. 1 is used to compute witnesses for the membership of single elements in \(\mathsf {acc}_A\). We now extend it to compute witnesses for multiple elements, namely to show that a set \(B\subseteq A\) is included in \(\mathsf {acc}_A\). We write  for the computation of the witness \(\mathsf {wit}=\mathsf {acc}_A^{\frac{1}{\mathsf {Ch}_B(x)}}=g^{r\mathsf {Ch}_{A\setminus B}(x)}\). Similarly, we let \(\mathsf {Verify}^*(ek,\mathsf {acc}_A,B,\mathsf {wit})\) to return 1 in case \(e(\mathsf {acc}_A,g)=e(\mathsf {wit},g^{\mathsf {Ch}_B(x)})\) holds, and 0 otherwise.
for the computation of the witness \(\mathsf {wit}=\mathsf {acc}_A^{\frac{1}{\mathsf {Ch}_B(x)}}=g^{r\mathsf {Ch}_{A\setminus B}(x)}\). Similarly, we let \(\mathsf {Verify}^*(ek,\mathsf {acc}_A,B,\mathsf {wit})\) to return 1 in case \(e(\mathsf {acc}_A,g)=e(\mathsf {wit},g^{\mathsf {Ch}_B(x)})\) holds, and 0 otherwise.
Furthermore, we can extend \(\mathsf {WitGen}\) to compute witnesses for an accumulator \(\mathsf {acc}_B\) to accumulate a subset of the set accumulated into \(\mathsf {acc}_A\). Let r and \(r'\) be the randomness used to generate \(\mathsf {acc}_A\) and \(\mathsf {acc}_B\), respectively. We define the following
-
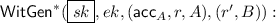 it computes the witness \(\mathsf {wit}^*=\mathsf {acc}_A^{\frac{1}{r'\mathsf {Ch}_B(x)}}=g^{\frac{r}{r'}\mathsf {Ch}_{A\setminus B}(x)}\)
it computes the witness \(\mathsf {wit}^*=\mathsf {acc}_A^{\frac{1}{r'\mathsf {Ch}_B(x)}}=g^{\frac{r}{r'}\mathsf {Ch}_{A\setminus B}(x)}\) -
\(\mathsf {Verify}^*(ek,\mathsf {acc}_A,\mathsf {acc}_B,\mathsf {wit}^*):\) it returns 1 if \(e(\mathsf {acc}_A,g)=e(\mathsf {acc}_B,\mathsf {wit}^*)\) holds, and 0 otherwise.
2.3 Hard Relations
Let p be a polynomial and \(\mathcal {R}_{\mathsf {pp}}\subseteq \{0,1\}^{p(\lambda )} \times \{0,1\}^{p(\lambda )}\) be a binary relation indexed by some public parameters \(\mathsf {pp}\). We call \((u,w)\in \mathcal {R}\) instance and witness, respectively. We assume the public parameters \(\mathsf {pp}\leftarrow \mathcal {G}(\lambda )\) to be efficiently computable given as input the security parameter. Also, let \(L_\mathsf {pp}:=\{u: \exists w \text { s.t. } (u,w) \in \mathcal {R}\}\) to be the NP language corresponding to \(\mathcal {R}_\mathsf {pp}\). We require the language L to be efficiently sampleable and denote with \(u \leftarrow \mathcal {D}(L)\) the process of picking a random element from L. A relation \((\mathcal {G},\mathcal {R}, \mathcal {D})\) is said to be hard if for any probabilistic polynomial time adversary \(\mathcal {A}\) the following probability is negligible
More concretely, we are interested in relations corresponding to hard search problems associated with cryptographic accumulators. For example the relation corresponding to the following language
The above language consists of all accumulators \(\mathsf {acc}_A\) for which there exists a witness for the accumulation of \(a\in \mathbb {Z}_p\). We note that the above language is efficiently sampleable by letting \(\mathsf {acc}_A\leftarrow \mathsf {Eval}(ek,a)\). We now state the following straightforward Lemma and refer to the full version of the paper [CDS18] for the proof.
Lemma 2
Assuming the accumulator is collision-free and indistinguishable, then the above the binary relation corresponding to \(L_{ek}(a)\) is hard for any \(a\in \mathbb {Z}_p\).
2.4 Smooth Projective Hash Function
Smooth Projective Hash Functions (SPHF) were introduced by Cramer and Shoup [CS02] (with the name of hash proof system) as a kind of designated-verifier proof systems for certain classes of algebraic languages. These found great applications towards the development of several primitives such as CCA2 secure public key encryption [CS02] and password authenticated key exchange [GL03, KV09]. Here we define a simpler hash proof system for the language of elements accumulated using the above bilinear accumulator.
An SPHF consists of three algorithms \((\mathsf {HGen},\mathsf {Hash},\mathsf {PHash})\). The key generation algorithm \(\mathsf {HGen}\) takes as input the security parameter and returns a relationFootnote 1, and a pair of secret and public keys (hsk, hpk); we sometimes refer to hpk as the projection key. The keys specify an hash function from the relation \(\mathcal {R}\) to an abelian group \({\mathbb {G}}\). The hash function can be privately evaluated using hsk on any instance in \(L_\mathcal {R}\), namely \(\mathsf {Hash}_{hsk}: L_\mathcal {R}\rightarrow {\mathbb {G}}\). The hash function allows also for public evaluation given hpk but only on instances for which a witness is known, namely \(\mathsf {PHash}_{hpk}: \mathcal {R}\rightarrow {\mathbb {G}}\). An SPHF satisfies two main properties: correctness and smoothness.
-
Correctness: for any \((u,w)\in R\), the private and public evaluation algorithms \(\mathsf {Hash},\mathsf {PHash}\) of the SPHF return the same result, i.e.
$$\mathsf {Hash}_{hsk}(u)=\mathsf {PHash}_{hpk}(u,w)$$ -
(Computational) Smoothness: for any instance for which a witness is not known, the evaluation of the hash function is (computationally) indistinguishable from random. Namely, we say that an SPHF on a relation \((\mathcal {G},\mathcal {R},\mathcal {D})\) is smooth if for any probabilistic polynomial time adversary \(\mathcal {A}\), the following advantage is negligible

We now show the construction for an SPHF defined on the relation specified by \(L_{ek}(a)\), for any \(a\in \mathbb {Z}_p\), to the target group \({\mathbb {G}}_T\) of a bilinear group. The construction of the SPHF is described in Fig. 2 and is a simple combination of the bilinear accumulators of [Ngu05] and the verifiable random function (VRF) constructed by Dodis and Yampolskiy [DY05]. A VRF is a pseudorandom function which admits proofs of correct evaluation that can be publicly verified. In our SPHF we apply the VRF to an accumulator and an element accumulated in it. The proof of evaluation for the function corresponds to the accumulation witness, and the secret key of the SPHF is the secret key of the accumulator. Since the secret key of the accumulator allows to compute witnesses for every element in \(\mathbb {Z}_p\) it also allows to evaluate the SPHF in every pair \((\mathsf {acc},a)\in {\mathbb {G}}\times \mathbb {Z}_p\).
The security of the SPHF constructed in Fig. 2 follows from the security of the verifiable random function of [DY05], based on the q-DHDBI assumption. We refer to the full version of the paper [CDS18] for a proof of the following Lemma.
Lemma 3
Under the q-DBDHI assumption over a bilinear group \((p,{\mathbb {G}},{\mathbb {G}}_T,e,g)\), the construction in Fig. 2 is a smooth projective hash function.
3 Reactive PSI in the Augmented Semi-honest Model
Aiming to prevent oracle attacks in scenarios where two parties engage in several PSI executions, we consider stateful PSI protocols computing reactive functionalities, whereby their outputs can depend on previous instances of the protocol.
We set our security definitions in the augmented semi-honest model of [Gol04]. In this model, the adversary is restricted to follow the specifications of the protocol as in the standard semi-honest settings. In addition, the adversary is allowed to adaptively modify the inputs used by the controlled party before each instance of the protocol. Apart from being more natural [HL10b] to give semi-honest adversaries this capability, we argue that the augmented model is more appropriate than the standard one to study composition of protocols.
Let \(t=t(\lambda )\) be a polynomial. We define the reactive functionality \(\mathsf {ReF}=(\mathsf {F}_1,\mathsf {F}_2, \ldots , \mathsf {F}_{t})\) as a sequence of stateful functionalitiesFootnote 2 \(\mathsf {F}_i\) each taking as input a client set \(\mathsf {C}_i\) and a server set \(\mathsf {S}_i\) and returning a pair \(\mathsf {ReF}_{i}(\mathsf {C}_i,\mathsf {S}_i)=(I_i,b_i)\). These correspond to the outputs of the client and server should have at the at the end of each execution, respectively.
Next, we state our security definitions in terms of a generic reactive functionality and refer to the end of the section for specific instantiations of \(\mathsf {ReF}\) for private set intersection protocols.
Definition 1 (RePSI)
A private set intersection protocol is a tuple \((Setup, \varPi )\)s.t.
-
\(Setup(\lambda )\rightarrow (\mathsf {param}_\mathcal {C};\mathsf {param}_\mathcal {S})\): it takes as input the security parameter and returns a pair of initial parameters for the client and the server. These can include public parameters and secret keys for the client and the server. If a specific protocol does not require a setup algorithm, this can be simply regarded as copying the security parameter into the initial parameters.
-
\(\varPi \langle \mathcal {C}(\mathsf {C};St_\mathcal {C});\mathcal {S}(\mathsf {S};St_\mathcal {S}) \rangle \rightarrow ((\mathsf {out}_\mathcal {C};St_\mathcal {C});(\mathsf {out}_\mathcal {S};St_\mathcal {S}))\): this is a stateful probabilistic polynomial time interactive protocol between a client \( \mathcal {C}\) and a server \(\mathcal {S}\). Each party takes as input a set and a state information (initialised to \(St_\mathcal {C}:=\mathsf {param}_\mathcal {C},St_\mathcal {S}:=\mathsf {param}_\mathcal {S}\) in the first instance of the protocol) and returns an output and an updated the state.
We say that private set intersection protocol \((Setup, \varPi )\) is a RePSI if it securely realizes a reactive functionality \(\mathsf {ReF}\) in the augmented semi-honest model, i.e. if it satisfies correctness, server privacy and client privacy as defined below.
Correctness is defined by the security game \(\mathbf {Exp}_{\mathcal {A}}^{\text {Corr}}(\lambda )\) described in Fig. 3. Informally, a protocol is correct if at the end of each instance both parties return their prescribed outputs.
Definition 2 (Correctness)
Let \(t=t(\lambda )\) a polynomial in the security parameter \(\lambda \), and \(\mathsf {ReF}\) defined as above. A protocol \((Setup, \varPi )\) is correct if for any probabilistic polynomial time adversary \(\mathcal {A}\)
Client privacy is specified by two oracles \(O_\varPi \), \(O_{ Sim }\) described in Fig. 4. The oracle \(O_\varPi \) allows the adversary to run the next interaction between client and server on server’s inputs of her choice. The oracle then returns the server’s view in the protocol \(\mathsf {view}_{i,\mathcal {S}}((\mathsf {C}_i;St_{\mathcal {C}});(\mathsf {S}^*;St_{\mathcal {S}}^*))\), which contains the server’s input, random coins and messages received from the client in the execution of the protocol. Oracle \(O_{ Sim }\) returns instead a simulated view, based only on the input and output of the server. Informally, we say that the protocol achieves client privacy if an adversary is not able to distinguish which oracle she is interacting with.
Definition 3 (Client Privacy)
Let \(t=t(\lambda )\) and \(\mathsf {ReF}\) defined as above. A protocol \((Setup, \varPi )\) has client privacy if for any probabilistic polynomial time adversary \(\mathcal {A}\) there exists a probabilistic polynomial time simulator \( Sim \), such that for every sequence \(\mathsf {S}_1,\ldots ,\mathsf {S}_{t}\) the following advantage is negligible
Server privacy is also specified in terms of two oracles \(O_\varPi \), \(O_{ Sim }\) described in Fig. 5. The oracle \(O_\varPi \) allows the adversary to run the next interaction between client and server on client’s inputs of her choice. The oracle then returns the client’s view \(\mathsf {view}_{_{i,\mathcal {C}}}\) in the protocol. Oracle \(O_{ Sim }\) returns instead a simulated view, based only on the input and output of the client. Informally, we say that the protocol achieves server privacy if an adversary is not able to distinguish which oracle she is interacting with.
Definition 4 (Server Privacy)
Let \(t=t(\lambda )\) and \(\mathsf {ReF}\) defined as above. A protocol \((Setup, \varPi )\) has server privacy if for any probabilistic polynomial time adversary \(\mathcal {A}\) there exists a probabilistic polynomial time simulator \( Sim \), such that for every sequence \(\mathsf {C}_1,\ldots ,\mathsf {C}_{t}\) the following advantage is negligible
Size-Hiding. In the previous definitions of client and server privacy we gave the simulator the size of the honest party’s input set. This captures the security of most protocols in which participants learn information about the size of the other party’s input. However, in certain cases the size of the inputs represents confidential information which should not be leaked in a protocol execution. Protocols achieving this stronger property are usually referred as size-hiding [ADT11]. To formalise size-hiding variants of client and server privacy it is sufficient to remove the size of the honest party’s input from the input of the simulator. Looking ahead to the next sections, our protocols achieve size-hiding only in the case of client privacy.
The above definitions are general enough to capture various types of reactive functionalities \(\mathsf {ReF}\). Moreover, they can also be used to formalise security for the sequential composition of standard PSI stateless protocols. In this case it is sufficient to replace \(\mathsf {ReF}\) with t copies of the same functionality \(\mathsf {F}\) and replace protocol \(\varPi \) with a stateless protocol that does not update the states \((St_\mathcal {C},St_\mathcal {S})\), which are initialised as \((\mathsf {param}_\mathcal {C},\mathsf {param}_\mathcal {S})\).
Next, we specify two functionalities, one static (\(\mathsf {PSI}\)) and one reactive (\(\mathsf {RePSI}\)), which we call Bounded Input PSI and Input Controlling RePSI, respectively.
Bounded Input PSI. A Bounded Input PSI limits the maximum size of the set the client can use in each instance of the protocol. More precisely, let R be a polynomial in the security parameter \(\lambda \), a Bounded Input \(\mathsf {PSI}=(\mathsf {PSI}_1,\mathsf {PSI}_2, \ldots , \mathsf {PSI}_{t})\) is defined as
Input Controlling RePSI. An Input Controlling RePSI limits the number of maximum distinct elements a client can includes in its sets across all the executions. In this case the server’s outputs is a predicate on whether the client has exceeded the allowed bound. More precisely, let R be a polynomial in the security parameter \(\lambda \), an Input Controlling \(\mathsf {RePSI}=(\mathsf {RePSI}_1,\mathsf {RePSI}_2, \ldots , \mathsf {RePSI}_{t})\) is defined as
4 Bounded Input PSI
In this section we introduce our construction for a Bounded Input PSI. Bounded Input PSI allows client and server to compute the intersection of their private sets while imposing a bound R on the size of the client set at each execution of the protocol. Bounded Input PSI is not a reactive RePSI but we will us it as a stepping stone for constructing our Input Controlling RePSI in the next section.
We notice that in several PSI protocols the size of the client set is naturally revealed during the interaction. Hence, a Bounded Input PSI variant can be easily achieved with simple modifications. The server can check the number of inputs used by the client and abort in case it exceeds the bound. This strategy is not viable in size-hiding PSI protocols [ADT11] where the use of cryptographic accumulators hides the size of the client set. We also leverage cryptographic accumulators, thus the server cannot directly check the number of inputs used by the client as just explained. Moreover, we will start from the Bounded Input PSI introduced in this section to construct our Input Controlling RePSI. In the latter, apart from hiding the size of the client set and reducing the communication, the use of accumulators will enable to use compact states for the server whose size does not depend on the number of protocol executions.
Our Bounded Input protocol is a modification of the bounded size-hiding protocol of Bradley et al. [BFT16], whose security is based on the q-SDH assumption in the random oracle model. The idea behind the protocol of Bradley et al. [BFT16] is to have the client to accumulate its input set using a cryptographic accumulator and send it to the server. The server would then use the accumulator secret key to remove her elements from the accumulator. This amounts to compute witnesses for elements in the server set. Then, the server hashes the witnesses using a random oracle and sends back the hash values to the client. The client is able to compute witnesses for each accumulated element and then hash them on the random oracle. The intersection can be then retrieved by checking matches between the two sets of hash values.
The protocol of [BFT16], as well as ours, relies on the boundedness of the underlying accumulator to limit the size of the sets that can be accumulated.
Informally, the protocol of [BFT16] fulfils server privacy because the random oracle hides all the information about the witnesses computed by the server, apart from the ones the client can compute on its own. We modify the protocol and remove the need of random oracles. The idea is to replace it with a function that can be efficiently computed by the client given a witness, but for which the evaluation looks random if a witness is not known. This is exactly the smoothness property of the SPHF we introduced in Sect. 2.4. Thus, we are able to remove the random oracle assumption and reduce the security to the q-DBDHI assumption, on which the SPHF relies on. We note that our Bounded Input PSI is, to the best of our knowledge, the first instantiation of size-hiding PSI in the standard model.
4.1 Bounded Input PSI Without Random Oracles
The setup of the protocol of the bounded-size PSI consists of generating a pair of secret key and evaluation key for a bilinear accumulator, as shown in Fig. 1. The length of the evaluation key ek of the accumulator matches the input bound R allowed to the client input size. The setup algorithm then sets the initial parameters for the client to be the evaluation key of the accumulator, and the initial parameters for the server to include both the secret key and evaluation key. The complete description of the Setup algorithm of our Bounded Input PSI is described in Fig. 6. Note that since we are in semi-honest settings, we can allow the server to run the setup and send the initial parameters to the client in a preliminary interaction with the client.
In the first move of the protocol, the client starts by computing an accumulator \(\mathsf {acc}_\mathsf {C}\) of its input set \(\mathsf {C}\) and send it to the server. The evaluation of the accumulator can be done efficiently by first computing the characteristic polynomial of the set \(\mathsf {C}\), expanding its coefficients, and then performing a multi-exponentiation of the evaluation key ek, using the coefficients of \(\mathsf {Ch}_\mathsf {C}(X)\) as exponents.
In the second move of the protocol, the server then picks a pair of keys (hsk, hpk) for a SPHF associated with the witness relation of the accumulator. The secret key for the SPHF consists of the secret key x of the accumulator and a random element \(z\leftarrow \mathbb {Z}_p^*\). The projective key of the hash function corresponds to the accumulator \(\mathsf {acc}_\mathsf {S}\) of the server set, using randomness z. Then for every \(s_i\) contained in its input set \(\mathsf {S}\), the server evaluates the SPHF on instances \((\mathsf {acc}_\mathsf {C},s_i)\) using the secret key x. The server ends its move by forwarding the projective key \(\mathsf {acc}_\mathsf {S}\) to the client together with the set of SPHF evaluations. Without loss of generality we assume the server to sort the set of evaluations in lexicographic order before sending it to the client. Note that the server is not strictly required to know the secret key of the accumulator. However this can be used to speed up computation. For example, the server can avoid to accumulate its own set and simply set \(\mathsf {acc}_\mathsf {S}=g^z\).
In the last move of the protocol, the client computes a witnesses \(\mathsf {wit}_i\) for the accumulation of his input elements \(c_i \in \mathsf {C}\) in the accumulator \(\mathsf {acc}_\mathsf {C}\). Then, the client evaluates the SPHF using the projective key \(\mathsf {acc}_\mathsf {S}\) on each witness \(\mathsf {wit}_i\) for \((\mathsf {acc}_\mathsf {C},c_i)\). The clients then compares the set of its evaluations of the SPHF with the evaluations received from the server, looking for matches. Finally, the client outputs the subset of elements in \(\mathsf {C}\), for which the evaluation of the SPHF gave a match.
The full description of our Bounded Input PSI protocol is given in Fig. 7. We discuss its security in the following Theorem and refer to the full version of the paper [CDS18] for the proof.
Theorem 1
Under the R-SDH and n-DBDHI assumptions, the protocol \((Setup,\varPi )\) as described in Figs. 6 and 7 is a secure instantiation of a Bounded Input \(PSI \) in the augmented semi-honest model.
5 Input Controlling RePSI
We now introduce our Input Controlling RePSI protocol. The starting point is the Bounded Input protocol introduced in the previous section. The idea is to turn the previous protocol into a stateful one where both parties keep track of previous executions.
5.1 Description of the Protocol
The Setup phase of the protocol is the same as the one described in Fig. 6 for the Bounded Input protocol. We stress that in this case the bound R is not (only) the bound on the size of the client input of a single execution, but also a bound on the maximum number of elements the client can use across multiple executions. Again, since the client initial parameters only include public information we can allow the (semi-honest) server to run the Setup and forward the client the initial parameters \(\mathsf {param}_\mathcal {C}\).
The first instance of Input Controlling RePSI is similar to an execution of a Bounded Input RePSI described in Fig. 7. The only difference here is that at the end of the first instance the client and the server update their output state. The client returns state \(St_\mathcal {C}=(\mathsf {param}_\mathcal {C},\mathsf {C},r)\), which includes the initial parameter \(\mathsf {param}_\mathcal {C}\), its current input set \(\mathsf {C}\) and the randomness used to create the accumulator \(\mathsf {acc}_\mathsf {C}\). The server returns state \(St_\mathcal {S}=(\mathsf {param}_\mathcal {S},\mathsf {acc}_\mathsf {C})\), which includes the initial parameters \(\mathsf {param}_\mathcal {S}\) as well as the accumulator \(\mathsf {acc}_\mathsf {C}\) received from the client. In the rest of the description we implicitly assume that initial parameters \(\mathsf {param}_\mathcal {C}\) and \(\mathsf {param}_\mathcal {S}\) are always part of the states \(St_\mathcal {C}\) and \( St_\mathcal {S}\), respectively, and omit them from the notation to improve readability.
All the instances following the first one proceed as described in Fig. 8. In the first move of the protocol, the client retrieves the set \(\mathsf {C}'\) stored in state \(St_\mathcal {C}\) which contains all the elements used in previous executions of the protocol and computes the union with its current input set, i.e. \(\mathsf {U}=\mathsf {C}\cup \mathsf {C}'\). Then, the client computes fresh accumulators for both the current input set \(\mathsf {C}\) and the union set \(\mathsf {U}\). The client computes also witnesses for the accumulation in \(\mathsf {acc}_\mathsf {U}\) of subsets accumulated into \(\mathsf {acc}_\mathsf {C}\) and \(\mathsf {acc}_{\mathsf {C}'}\). Here \(\mathsf {acc}_{\mathsf {C}'}\) corresponds to the accumulator of the union of all previous client input set, which was generated in the last execution. The client ends its move by sending the accumulators \(\mathsf {acc}_\mathsf {C}, \mathsf {acc}_\mathsf {U}\) and witnesses \(\mathsf {wit}_\mathsf {C},\mathsf {wit}_{\mathsf {C}'}\) to the server.
In the second move of the protocol, the server retrieves the accumulator \(\mathsf {acc}_{\mathsf {C}'}\) from its state, which contains the union of the sets of all previous client sets. Then, the server verifies the witnesses \(\mathsf {wit}_\mathsf {C},\mathsf {wit}_{\mathsf {C}'}\) for the accumulation of \(\mathsf {C}\) and \(\mathsf {C}'\) in \(\mathsf {U}\). If any of these checks fails, then the server terminates the execution of the protocol with output \((0;St_\mathcal {S})\). Note that in this case both client and server do not update their states and might later enter a new instance of the protocol with different inputs. In case both checks pass, the server continues the execution as in the Bounded Input protocol: he sets a public and private key for the SPHF and evaluates it on instances \((\mathsf {acc}_\mathsf {C},s_i)\) for elements \(s_i \in \mathsf {S}\). The server ends its move by sending the public key for the SPHF and the set of evaluations to the client, updates its state with the accumulator \(\mathsf {acc}_\mathsf {U}\) and terminates its execution by outputting \((1,St_\mathcal {S})\).
In the last move of the protocol the client continues the execution as in the case of the Bounded Input RePSI. It computes witnesses for the accumulation of elements in \(\mathsf {C}\) into \(\mathsf {acc}_\mathsf {C}\) and computes evaluations of the SPHF on these. Then it looks for matches between the sets of evaluations and includes the corresponding elements in \(\mathsf {C}\) in the intersection \(\mathsf {out}_\mathcal {C}\). The client updates its state with \((\mathsf {U},s)\), where s is the randomness used in the generation of the accumulator \(\mathsf {acc}_\mathsf {U}\), and terminates the instance execution with output \((\mathsf {out}_\mathcal {C};St_\mathcal {C})\).
5.2 Security of Input Controlling RePSI
Theorem 2
Under the R-SDH and n-DBDHI assumptions, the protocol \((Setup,\varPi )\) as described in Figs. 6 and 8 is a secure instantiation of an Input Controlling RePSI in the augmented semi-honest model.
Proof
Correctness as for the case of the Bounded Input RePSI follows from the correctness of accumulators and of SPHF.
Client privacy follows again from indistinguishability property of the accumulator. In the first instance of the protocol the only message the server receives from the client is the accumulator \(\mathsf {acc}_\mathsf {C}\). In this case the simulator \( Sim \) picks \(r\leftarrow \mathbb {Z}_p\) and sets \(\mathsf {acc}_\mathsf {C}=g^r\). As in the case of Bounded Input RePSI the simulated view is distributed identically to the real view. In the following calls of \(O_{ Sim }\) the simulator picks \(s,t\leftarrow \mathbb {Z}_p\) and sets \(\mathsf {acc}_\mathsf {U}=g^s\) and \(\mathsf {acc}_\mathsf {C}=g^t\) and retrieves \(\mathsf {acc}_{\mathsf {C}'}=g^r\) from the previous instance. The simulator then sets the witnesses to be \(\mathsf {wit}_\mathsf {C}=g^{\frac{s}{t}}\) and \(\mathsf {wit}_{\mathsf {C}'}=g^{\frac{s}{r}}\). The distribution of the simulated \(\mathsf {acc}_{\mathsf {C}},\mathsf {acc}_\mathsf {U},\mathsf {wit}_\mathsf {C},\mathsf {wit}_{\mathsf {C}'}\) is uniformly random, conditioned on satisfying the two witness verification equations, as in a real distribution. Again, the simulator does not need the size of the client’ set and thus client privacy is achieved with respect to the Size-Hiding variant.
The proof of server privacy unfolds as in the case of the Bounded Input RePSI (see [CDS18]) since the messages sent from the server to the client are the same.
5.3 Efficiency
We summarize the efficiency of both our Bounded Input PSI and Input Controlling RePSI in Table 1. The dominant computational cost for the client in the Bounded Input PSI is O(m) pairings and multi-exponentiations of length at most m, where m is the size of the client’s set. With respect to the Bounded Input PSI, the overhead incurred by the client in our Input Controlling RePSI is only of a single multi-exponentiation of length M, the total number of elements used so far in the protocol.
For both the Bounded Input PSI and the Input Controlling RePSI. the computational cost for the server is O(n) pairings and exponentiations, where n is the size of the server set in that run. The overall communication is linear in the size of the server set in that particular instance for both protocols. The communication overhead of the Input Controlling RePSI is of only 3 group elements more than the Bounded Input PSI.
The table also shows that both server and client keep constant state in case of Input Controlling RePSI. When computing the state size for the client, we do not consider the elements input thus far by the client. We argue that any instantiation of Input Controlling RePSI requires the client to include in its state the inputs thus far. This is because the client will have to tell whether the next input is “fresh” or not. This is also true for the instantiation of the protocol via a trusted third party. In this case, the trusted party will have to remember all inputs up to the current run, in order to tell whether the next input violates the bound. If we do not consider the inputs thus far as part of the client’s state, our instantiation of Input Controlling RePSI is optimal from the point of view of storage overhead since it only requires constant state at both the client and the server. In particular the state for each of them is independent of the number of runs.
Comparison with [DMV13]. To the best of our knowledge, the only possible alternative to instantiate an Input Controlling RePSI would be to use the “rate-hiding” compiler of [DMV13] with a PSI protocol such as [HN10]. Since [DMV13] only hints at how to build a rate-hiding PSI,Footnote 3 we cannot compare its communication/computation complexity with the one of our Input Controlling RePSI. However, note that the rate-hiding compiler of [DMV13] requires the client to commit to the inputs of the current run and both parties to keep the commitments to the client’s inputs across all runs. (The client must prove that the number of unique inputs hidden by the commitments does not exceed the rate.). As such, even if we exclude the client’s input from its state, both the client and the server keep a state that is linear in the number of elements used by the client across all executions. Whereas, our protocol features constant state at both parties and communication complexity that is independent on the size of the client’s set.
6 Conclusions
Although a large number of Private Set Intersection (PSI) protocols have been proposed in recent years, their adoption in real-life applications is still hindered by a few challenges. In this paper, we focused on oracle attacks, whereby the client learns the server’s private set by enumerating it across several executions. To address this problem, we set out to model PSI as a reactive functionality, namely, Reactive PSI (RePSI), and provided a construction that allow the server to set an upper bound to the number of elements the client has input up to the current protocol run. Essentially, we made PSI a stateful protocol but provided a construction where the state kept by the two parties is small and independent of the number of runs thus far and, for the server only, independent on the number of elements in either input set.
To the best of our knowledge, our work is the first to formalize and instantiate Reactive PSI. In the process, we also presented the first size-hiding PSI protocol in the standard model, which may be of independent interest.
Notes
- 1.
The original definition of SPHF was introduced for languages related with hard subset membership problems, while here we define SPHF for languages related with a hard search problem.
- 2.
In this paper we restrict our attention to the case of deterministic functionalities.
- 3.
References
Ateniese, G., De Cristofaro, E., Tsudik, G.: (If) Size matters: size-hiding private set intersection. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 156–173. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_10
Baldi, P., Baronio, R., De Cristofaro, E., Gasti, P., Tsudik, G.: Countering GATTACA: efficient and secure testing of fully-sequenced human genomes. In: ACM CCS, pp. 691–702 (2011)
Benaloh, J., de Mare, M.: One-way accumulators: a decentralized alternative to digital signatures. In: Helleseth, T. (ed.) EUROCRYPT 1993. LNCS, vol. 765, pp. 274–285. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48285-7_24
Bradley, T., Faber, S., Tsudik, G.: Bounded size-hiding private set intersection. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 449–467. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_24
Barić, N., Pfitzmann, B.: Collision-free accumulators and fail-stop signature schemes without trees. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 480–494. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_33
Cerulli, A., De Cristofaro, E., Soriente, C.: Nothing Refreshes Like a RePSI: Reactive Private Set Intersection (Full Version). eprint.iacr.org (2018)
Camenisch, J., Kohlweiss, M., Soriente, C.: An accumulator based on bilinear maps and efficient revocation for anonymous credentials. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 481–500. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_27
Camenisch, J., Lysyanskaya, A.: Dynamic accumulators and application to efficient revocation of anonymous credentials. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 61–76. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_5
Chase, M., Ostrovsky, R., Visconti, I.: Executable proofs, input-size hiding secure computation and a new ideal world. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 532–560. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_18
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Camenisch, J., Zaverucha, G.M.: Private intersection of certified sets. In: Dingledine, R., Golle, P. (eds.) FC 2009. LNCS, vol. 5628, pp. 108–127. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03549-4_7
Derler, D., Hanser, C., Slamanig, D.: Revisiting cryptographic accumulators, additional properties and relations to other primitives. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 127–144. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16715-2_7
De Cristofaro, E., Kim, J., Tsudik, G.: Linear-complexity private set intersection protocols secure in malicious model. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 213–231. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_13
Dagdelen, Ö., Mohassel, P., Venturi, D.: Rate-limited secure function evaluation: definitions and constructions. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 461–478. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_28
De Cristofaro, E., Tsudik, G.: Practical private set intersection protocols with linear complexity. In: Sion, R. (ed.) FC 2010. LNCS, vol. 6052, pp. 143–159. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14577-3_13
Dodis, Y., Yampolskiy, A.: A verifiable random function with short proofs and keys. In: Vaudenay, S. (ed.) PKC 2005. LNCS, vol. 3386, pp. 416–431. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30580-4_28
Freudiger, J., De Cristofaro, E., Brito, A.E.: Controlled data sharing for collaborative predictive blacklisting. In: Almgren, M., Gulisano, V., Maggi, F. (eds.) DIMVA 2015. LNCS, vol. 9148, pp. 327–349. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-20550-2_17
Freedman, M.J., Nissim, K., Pinkas, B.: Efficient private matching and set intersection. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 1–19. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_1
Gennaro, R., Lindell, Y.: A framework for password-based authenticated key exchange. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 524–543. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_33
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Proceedings of the 19th Annual ACM Symposium on Theory of Computing, pp. 218–229 (1987)
Goldreich, O.: The Foundations of Cryptography - Volume 2, Basic Applications. Cambridge University Press, Cambridge (2004)
Ghosh, E., Ohrimenko, O., Papadopoulos, D., Tamassia, R., Triandopoulos, N.: Zero-knowledge accumulators and set algebra. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 67–100. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_3
Hazay, C., Lindell, Y.: Efficient protocols for set intersection and pattern matching with security against malicious and covert adversaries. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 155–175. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_10
Hazay, C., Lindell, Y.: Efficient Secure Two-Party Protocols - Techniques and Constructions. Information Security and Cryptography. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14303-8
Hazay, C., Lindell, Y.: A note on the relation between the definitions of security for semi-honest and malicious adversaries. ePrint (2010)
Hazay, C., Nissim, K.: Efficient set operations in the presence of malicious adversaries. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 312–331. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_19
Hallgren, P., Orlandi, C., Sabelfeld, A.: PrivatePool: privacy-preserving ridesharing. In: CSF, pp. 276–291 (2017)
Ion, M., Kreuter, B., Nergiz, E., Patel, S., Saxena, S., Seth, K., Shanahan, D., Yung, M.: Private intersection-sum protocol with applications to attributing aggregate ad conversions. ePrint 2017/738 (2017)
Jarecki, S., Liu, X.: Fast secure computation of set intersection. In: Garay, J.A., De Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 418–435. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15317-4_26
Katz, J., Vaikuntanathan, V.: Smooth projective hashing and password-based authenticated key exchange from lattices. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 636–652. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_37
Nguyen, L.: Accumulators from bilinear pairings and applications. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 275–292. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_19
Pinkas, B., Schneider, T., Segev, G., Zohner, M.: Phasing: private set intersection using permutation-based hashing. In: USENIX Security Symposium (2015)
Pinkas, B., Schneider, T., Zohner, M.: Faster private set intersection based on OT extension. In: USENIX Security Symposium, pp. 797–812 (2014)
Rindal, P., Rosulek, M.: Improved private set intersection against malicious adversaries. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 235–259. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_9
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Cerulli, A., De Cristofaro, E., Soriente, C. (2018). Nothing Refreshes Like a RePSI: Reactive Private Set Intersection. In: Preneel, B., Vercauteren, F. (eds) Applied Cryptography and Network Security. ACNS 2018. Lecture Notes in Computer Science(), vol 10892. Springer, Cham. https://doi.org/10.1007/978-3-319-93387-0_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-93387-0_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93386-3
Online ISBN: 978-3-319-93387-0
eBook Packages: Computer ScienceComputer Science (R0)






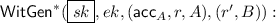 it computes the witness
it computes the witness 





