Abstract
Dynamic partial order reduction (DPOR) algorithms are used in stateless model checking (SMC) to combat the combinatorial explosion in the number of schedulings that need to be explored to guarantee soundness. The most effective of them, the Optimal DPOR algorithm, is optimal in the sense that it explores only one scheduling per Mazurkiewicz trace. In this paper, we enhance DPOR with the notion of observability, which makes dependencies between operations conditional on the existence of future operations, called observers. Observers naturally lead to a lazy construction of dependencies. This requires significant changes in the core of POR algorithms (and Optimal DPOR in particular), but also makes the resulting algorithm, Optimal DPOR with Observers, super-optimal in the sense that it explores exponentially less schedulings than Mazurkiewicz traces in some cases. We argue that observers come naturally in many concurrency models, and demonstrate the performance benefits that Optimal DPOR with Observers achieves in both an SMC tool for shared memory concurrency and a tool for concurrency via message passing, using both synthetic and actual programs as benchmarks.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Testing and verification of concurrent programs is hard, as it requires reasoning about all the ways in which operations executed by different processes (or threads) can interfere. Stateless model checking (SMC) [12] is a technique with low memory requirements that can be effective in finding concurrency errors or proving that a program cannot reach an error state by systematically exploring all the ways in which such operations can be interleaved. The technique requires taking control of the scheduler and subsequently executing the program multiple times, each time imposing a different scheduling of the processes. By considering every process at every execution step, however, the number of possible schedulings grows exponentially w.r.t. the total length of program execution. Partial order reduction (POR) techniques [9, 11, 20, 22] address this problem by prescribing the exploration of only a subset of schedulings, albeit a subset that is sufficient to cover all behaviours. POR techniques take advantage of the fact that most pairs of operations by different processes in typical concurrent programs are not interfering. As a result, a scheduling E that can be obtained from another scheduling \(E'\) by swapping adjacent but non-interfering (independent) execution steps will make the program behave in exactly the same way as \(E'\); such schedulings have the same partial order of interfering operations and belong to the same equivalence class, called a Mazurkiewicz trace [19]. It is sufficient for SMC algorithms to explore only one scheduling in each such equivalence class.
POR algorithms operate by examining pairs of interfering operations. If it is possible to execute such operations in the reverse order, then their partial order will be different, and a scheduling from the relevant equivalence class must also be explored. For soundness, POR techniques need to be conservative, treating operations as interfering even in cases where they are not. Increasing the accuracy of interference detection can therefore significantly improve the effectiveness of any POR technique. In early POR techniques, interference was determined statically, leading to over-approximations and limiting the achievable reduction. The efficiency of POR was later increased using semantic information to decide which operations interfere [13]. Dynamic Partial Order Reduction (DPOR) [10] further improved the effectiveness of POR algorithms by allowing interference to be determined from data obtained during the program’s execution.
In this paper, we introduce the notion of observability of operations, allowing observer operations that appear later in a scheduling to be used when deciding whether earlier operations are interfering. We start by explaining observers with a series of examples (Sect. 2), and continue by presenting key notions of DPOR and explaining why using observers in DPOR algorithms is challenging (Sect. 3). We then present a formal framework (Sect. 4) and describe an extension to the Optimal DPOR algorithm [2] that enables use of observers (Sect. 5). The extension is generic in the sense that it can be applied to several models of concurrency, such as shared memory and message passing. We demonstrate this claim by two implementations: one in an SMC tool for C/C++ programs with pthreads and one in an SMC tool for Erlang programs (Sect. 6). Finally, in Sect. 7 we evaluate our implementations and show that Optimal DPOR with Observers can achieve significantly better reduction in both synthetic and ‘real’ programs.
2 DPOR and Observers by Example
Consider the program shown in Fig. 1 in which a main process spawns two concurrent processes, p and q, which issue write operations on two different shared variables x and y. After p and q finish their execution, the main process reads the values of x and y and checks a correctness property. A DPOR algorithm will begin exploring this program by executing an arbitrary scheduling; see Fig. 1 (middle). Nodes show the values of the shared variables and each transition consists of an execution step. By inspecting the operations in this scheduling, the algorithm sees that if the second step of q is scheduled before the second step of p, the partial order of the writes to the y variable is different. It therefore plans to execute a scheduling in which the second step of p happens after the one from q. The start of this scheduling can be denoted as p.q. Similarly, the order of the writes on x can be reversed, by executing q’s first step before the first step of p. Therefore, a scheduling starting with q should also be explored. In Optimal DPOR [2], future explorations are added as partial schedulings, forming wakeup trees (shown in blue). These trees are quite trivial in this example, each consisting of a single path.
The algorithm continues exploration from the “deepest” point where a new scheduling should be tried; in the example, this is the (1,0) node. A second scheduling is explored with the intention to execute some operation before the second step of p. Without any other constraint, a non-optimal DPOR algorithm could execute p’s second step immediately after the first step of q, ending up in a state identical with the previously explored (2,1) and then again in (2,2). The sleep sets technique [11] can be used to avoid or stop such redundant explorations. Sleep sets retain information from already explored earlier process steps that have not yet been ‘overtaken’ by some step in the current exploration. In our example, information about p’s second step is retained in the sleep set until some other interfering operation (here q’s second step) has been executed. Moreover, sleep sets can be used to infer that swapping (again) the second step of p and the second step of q (based on their interference in the second scheduling) is redundant. Any DPOR algorithm using sleep sets will explore four schedulings for this program (instead of the six ones possible). Each of these four schedulings leads to a different final state. Notice that two writes on the same variable were always deemed as interfering.

Consider now the program shown on the right. The shared variable x (whose initial value is \(\mathtt 0\)) is accessed by processes p, q and r. Here, the correctness property is checked by process r. If interference is decided using the same criteria as a data race (i.e., two operations interfere if they access the same memory location and at least one of them is a write), then all three operations interfere with each other. As a result, each of the \(3! = 6\) possible interleavings has a different partial order and therefore belongs to a different Mazurkiewicz trace that should be explored by a DPOR algorithm. In schedulings starting with r, however, the order of the execution of p and q is irrelevant (if one does not care about the final contents of the memory), as the values written by these operations will never be read. A DPOR algorithm could detect that the written values are not observed and consider the write operations as non-interfering.

Taking this idea further, consider a next example, shown on the right. Here, N processes write on the shared variable x, and as a result there exist N! schedulings. In each such scheduling, however, only the last written value will be read. A DPOR algorithm could consider write operations that are not subsequently observed as independent and therefore explore just N instead of N! schedulings, thereby achieving an exponential reduction.
In the last two examples, better reduction could be obtained if the interference of write operations, which are conservatively considered as “always interfering”, was characterized more accurately by looking at complete executions and taking observability by “future” operations into account. This idea is applicable not only in shared memory but also in other models of concurrency. In the next message passing program, processes p and q each send a different message to the mailbox of process r using the send operator “!”. Process r uses a receive operation to retrieve a message and store it in a (local) variable x.

If we assume that receive operations pick and return the oldest message in the mailbox or return null if no message exists, send operations can interfere (the order of delivery is significant) and so can send and receive operations (an empty mailbox can yield a different value). As a result, six schedulings are possible. However, only three schedulings need to really be explored: the receive operation interferes only with the earliest send operation and cannot be affected by a later send; moreover, if the receive operation is executed first, the order of the send operations is irrelevant.
If we instead assume that receive operations block if no matching message exists, only two schedulings need to be explored, as r can receive either \(\mathtt{M}_{1}\) or \(\mathtt{M}_{2}\). Again, if we generalize the example to N processes instead of just two, the behaviour is similar to the program with N writes: only N schedulings (instead of N!) are relevant, each determined by the first message delivered; the remaining message deliveries are not observable. Note that, in this concurrency model, we are interested in the observability of the first instead of the last operation in an execution sequence.
In some message-passing concurrency models (e.g., in Erlang programs [4]), it is further possible to use selective receive operations instead, which also block when no message can be selected. Using this feature, the previous program can be generalized and rewritten so that r is explicitly picking messages in order, using pattern matching. Such a program is shown on the right. Here r wants to pick up the N messages in order: first \(\mathtt{M}_1\), then \(\mathtt{M}_2\), etc.

Thus, the order of delivery of messages is irrelevant. A DPOR algorithm could take advantage of the additional information provided by the selective receive operations, notice that the messages from \(p_{i+1} \ldots p_N\) cannot be selected before the message from \(p_i\), and therefore determine that the N sends are independent. A single scheduling is enough to explore all behaviours of the program!
Having explained the concept of observability of operations by examples, let us see how it can be combined with the Optimal DPOR algorithm and achieve such reductions.
3 Using Observers in a DPOR Algorithm
Our objective is to construct a DPOR algorithm that lazily considers interferences based on the existence of later operations, called observers. In the simplest case, operations that would be conservatively considered interfering are treated as independent in the absence of an observer. Examples in Sect. 2 included write operations whose values were never read, or cases where the order of message deliveries does not affect the order in which the messages are received.
The intuition behind such an SMC approach comes from the fact that it is only operations that observe a value (e.g., assertions, receive statements, etc.) that can influence the control flow and lead to erroneous or generally unexpected behaviour. Other operations (e.g., writes, sends, etc.) cannot affect program behaviour if no future operation observes their effects. In such cases, interference between those other operations can be ignored.
3.1 POR Concepts and Optimal DPOR
The goal of POR techniques is the exploration of only a (small) subset of the possible schedulings of a concurrent program which is sound; that is, a subset that includes at least one scheduling from each Mazurkiewicz trace. DPOR algorithms perform a depth-first exploration of the tree of all possible schedulings. Reduction is achieved by exploring only a sound subset of all scheduling choices that are possible at each point in the tree. Such subsets are formed on the basis of two complementary techniques.
-
Each point in the tree is associated with a sleep set, which contains a set of processes whose exploration would be redundant. More precisely, a process p is in the sleep set after a sequence of form E.v if p has previously been explored after E, and furthermore p does not interfere with v. Thus, exploring E.v.p is redundant, since it was previously explored after E.p (as E.p.v).
-
From each point in the tree, the set of explored processes must form a source set [2]. (Some DPOR algorithms employ persistent or stubborn sets, which are subsumed by source sets.) Source sets have the property that for any extension which forms a complete (aka maximal) scheduling, there is an equivalent extension in which the next step is taken by a process in the source set. A source set is constructed incrementally during the exploration by inspecting encountered races: whenever a scheduling of form E.p.v is explored, in which the step of p is in a race with some step in v, then the reversal of that race will be explored in some other scheduling, where some process q in v is scheduled immediately after E: this is achieved by adding q to the source set after E.
Most existing DPOR algorithms prescribe that from each point in the tree (i) all processes in a source set should be explored, and (ii) no process in the sleep set should be explored. However, these principles are not sufficient to avoid redundant exploration [2]. The reason is that the reversal of a race in E.p.v may happen only by exploring a particular subsequence of v; since a source set can only contain the first step in such a sequence, it can not prevent continued exploration beyond that first step from being redundant. Optimal DPOR improves on earlier techniques by using wakeup trees [2] in addition to sleep sets. Wakeup trees are composed of partial execution sequences (called wakeup sequences) that (a) reverse the order of the interfering operations, and (b) are provably non-redundant. Optimal DPOR, currently the state-of-the-art DPOR algorithm, always uses wakeup sequences to explore new schedulings. As a result, Optimal DPOR does not even initiate redundant exploration, and can achieve exponential reduction over e.g., the original [10] or the Source DPOR [2] algorithm.
3.2 Observers and Sleep Sets
The use of sleep sets is not trivial when using observers, because interference between events can often not be determined when they occur, but only later in the scheduling. Let us illustrate using an example. In the next program, three processes (p, q and s) send tagged messages (with tags A and B) to a receiver process r, which uses selective receive to read matching messages from its mailbox. Each message also contains the process identifier of the sender.

In standard DPOR, the sends are interfering, since the order of delivery can affect the values assigned to the \(\mathtt{x}\) and \(\mathtt{y}\) variables in r. Using observers, sends are interfering only if justified by an observing receive operation. Assume that the first explored scheduling is p.p.q.s.r.r. Here, the second send by p (sending the message tagged with A) interferes with the send by q, since their order is observed by the first receive of r (if the message from q had been delivered first, it would have been the one picked instead). Furthermore, the first send by p (sending the message tagged with B) interferes with the message send by s, since they have the second receive of r as observer. In order to explore the reversal of the race between the first send of p and that of s, the algorithm needs to explore a scheduling in which p’s first send is executed after s. Such a scheduling must clearly start with s. The rules for sleep sets prescribe that p should be in the sleep set at the start of this exploration, and that p should be removed from the sleep set after executing s if p and s interfere. However, this interference is visible only later, making it unclear what to do. On the one hand, removing p from the sleep set on the grounds that it “might” interfere with s risks to explore redundant schedulings and defeats the purpose of observers. On the other hand, keeping p in the sleep set and “see what happens” prevents exploring the effects of the race reversal, since that requires the second send of p to be explored before q, which is forbidden if p remains in the sleep set. Thus, sleep sets are not a sufficiently precise mechanism for avoiding redundant exploration without missing non-redundant schedulings.
3.3 Introducing Observers to Optimal DPOR
We will now explain how Optimal DPOR can be adapted to work with observers. There are two main challenges: (1) we need to address the fact that, in the presence of observers, interference is conditional, and (2) we also need a suitable replacement for sleep sets, since we can no longer use them to guarantee that there is no redundant exploration.
In Optimal DPOR, it is assumed that operations that are interfering in some execution sequence remain interfering in any prefix of that sequence. This is no longer true when we determine interference by the existence of observing operations. If an observer is not included in a prefix of an execution sequence in which two operations were observably interfering, the same two operations will be independent. To address challenge 1 in Optimal DPOR with observers, we need to extend the wakeup sequences constructed for reversing the order of interfering operations that require an observer, with a suffix that includes the observer. It is allowed for this suffix to include operations happening after the interfering operations (even in program order); any such operations will behave identically in the reversal because in the original scheduling the observer was the first event that could be affected by the ordering of the interfering operations. To address challenge 2, we can build on the intuition behind sleep sets and assert that when our algorithm is done with a particular state, it has explored all schedulings that can start with the step that led to that state. When the algorithm considers a new scheduling (based on a wakeup sequence), information about observers in that scheduling needs to be recalculated from the operations in the sequence. The algorithm can then perform an exhaustive test, that ensures that each step previously explored from any point in the execution is overtaken by some other step in the wakeup sequence under consideration.
4 Framework
We consider a concurrent system composed of a finite set of processes (or threads). Each process executes a deterministic program, in which statements act on the global state of the system. Processes can interact via shared variables, messages, etc. We assume that the state space does not contain cycles, and that executions have bounded length. A step of a process may not disable another process.
Formally, let \(\varSigma \) be the set of states of a concurrent system and \(s_0\in \varSigma \) be the unique initial state. The partial function \(\textit{execute}_{p}:\varSigma \mapsto \varSigma \) describes execution, representing an atomic execution step of process p, which may depend on and affect the state. An execution sequence \({E}\) of the system is a finite sequence of execution steps of its processes that is performed from the initial state. We use \(\langle \rangle \) to denote the empty sequence and . to denote concatenation of sequences of process steps (e.g., p.p.q denotes the execution sequence where first p performs two steps, followed by a step of q). The sequence of process steps in \({E}\) also uniquely determine the state of the system after \({E}\), which is denoted \(s_{[{E}]}\). For a state \(s\), let \({ enabled}(s)\) denote the set of processes p that are enabled in \(s\) (i.e., for which \(\textit{execute}_{p}(s)\) is defined). If \(p \in { enabled}(s_{[{E}]})\), then \({E}.p\) is an execution sequence. A sequence \({E}\) is maximal if \({ enabled}(s_{[{E}]}) = \emptyset \), i.e., no process is enabled after \({E}\). An event \(\langle p,i\rangle \) of \({E}\) is a particular occurrence of a process in \({E}\), representing the i-th occurrence of process p in the execution sequence. We use \(w, w', \ldots \) to range over sequences, \(e, e', \ldots \) to range over events, as well as:
-
\({E} \vdash w\) to denote that \({E}.w\) is an execution sequence.
-
\(w\!\setminus \!p\) to denote the sequence w with its first occurrence of p removed.
-
\({ dom}({E})\) to denote the set of events \(\langle p,i\rangle \) which are in \({E}\).
-
\({ dom}_{[{E}]}(w)\) to denote \({ dom}({E}.w)\setminus { dom}({E})\), i.e., the events in \({E}.w\) which are in w.
-
\({ next}_{[{E}]}(p)\) to denote \({ dom}_{[{E}]}(p)\) as a special case.
-
\(\widehat{e}\) to denote the process p of an event \(e= \langle p,i\rangle \).
-
\(e<_{{E}} e'\) to denote that \(e\) occurs before \(e'\) in \({E}\), i.e., \(<_{{E}}\) is the total order of events.
-
\({E}' \le {E}\) to denote that the sequence \({E}'\) is a prefix of the sequence \({E}\).
We assume a function which assigns a happens-before relation [15] to any execution sequence \({E}\), denoted as \({\rightarrow }_{{E}}\).
We will keep the general approach of Optimal DPOR and require the happens-before relation to satisfy a set of properties, collected in Definition 1. These properties are the first point where we diverge from the underlying model for Optimal DPOR [2, Definition 3.2]. In that definition, Properties (3) and (5) need to be weakened, Property (6) needs to be replaced, whereas Property (7) was only required for Source DPOR and is thus dropped.
Definition 1
(Properties of valid happens-before relations). A happens-before assignment, which assigns a unique happens-before relation \({\rightarrow }_{{E}}\) to any execution sequence \({E}\), is valid if it satisfies the following properties for all execution sequences \({E}\):
-
1.
\({\rightarrow }_{{E}}\) is an irreflexive partial order on \({ dom}({E})\), which is included in \(<_{{E}}\).
-
2.
The execution steps of each process are totally ordered, i.e., \(\langle p,i\rangle {\rightarrow }_{{E}} \langle p,i\! + \!1\rangle \) whenever \(\langle p,i\! + \!1\rangle \in { dom}({E})\).
-
3.
Given an execution sequence \({E}\) and a process p s.t. \({E} \vdash p\), then for all events \(e, e' \in { dom}({E})\), if \(e {\rightarrow }_{{E}} e'\) then \(e {\rightarrow }_{{E}.p} e'\).
-
4.
Any linearization \({E}'\) of \({\rightarrow }_{{E}}\) on \({ dom}({E})\) is an execution sequence which has exactly the same “happens-before” relation \({\rightarrow }_{{E}'}\) as \({\rightarrow }_{{E}}\). This means that the relation \({\rightarrow }_{{E}}\) induces a set of equivalent execution sequences, all containing the same set of events, and with the same “happens-before” relation. We use:
-
\({E}\simeq {E}'\) to denote that \({ dom}({E}) = { dom}({E}')\) and that \({E}\) and \({E}'\) are linearizations of the same “happens-before” relation, and
-
\([{E}]_{\simeq }\) to denote the equivalence class of \({E}\).
-
5.
If \({E}\simeq {E}'\), then \({ enabled}(s_{[{E}]}) = { enabled}(s_{[{E}']})\).
For the last property, we need to introduce a few definitions. Given \({\rightarrow }_{{E}}\), if \(e, e' \in { dom}({E})\) and \(e<_{{E}} e'\), define
-
\(e\lessdot _{{E}} e'\) (read as \(e\) is in a race with \(e'\)) to denote that \(e{\rightarrow }_{{E}} e'\) and \(\widehat{e} \ne \widehat{e'}\) and there is no event \(e'' \in { dom}({E})\), different from \(e'\) and \(e\), such that \(e{\rightarrow }_{{E}} e'' {\rightarrow }_{{E}} e'\).
-
\(e\precsim _{{E}} e'\) (read as \(e\) is in a reversible race with \(e'\)) to denote that \(e\lessdot _{{E}} e'\) and in any equivalent execution sequence \({E}' \simeq {E}\) where \(e\) occurs immediately before \(e'\), \(\widehat{e'}\) is not blocked before the occurrence of \(e\).
Now we continue listing properties of valid happens-before relations.
-
6.
Given an execution sequence \({E}\), then for all events \(e, e' \in { dom}({E})\) where \(e\lessdot _{{E}} e'\), there exists a set \(O= { observers}(e,e',{E}) \subseteq { dom}({E})\) such that:
-
(a)
For all \(o\in O\), it holds that \(e{\rightarrow }_{{E}} o\), \(o\ne e'\), and
 .
. -
(b)
For all \(o, o' \in O\) it holds that
 .
. -
(c)
If \({E}' \simeq {E}\) then \(O' = { observers}(e,e',{E}') = O\).
-
(d)
For every prefix \({E}' < {E}\) of \({E}\) such that \(e, e' \in { dom}({E}')\):
-
If \(O\) is empty, then \(e{\rightarrow }_{{E}'} e'\).
-
If \(O\) is nonempty, then \(e{\rightarrow }_{{E}'} e'\) iff \({ dom}({E}') \cap O\ne \emptyset \).
-
(e)
If \(e\precsim _{{E}} e'\), then for all sequences w such that \({E} \vdash w\) and all events \(e'' \in { dom}({E})\):
-
If
 , then
, then  .
. -
If
 , then
, then 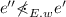 .
.
-
(f)
For all \(e''\in { dom}({E})\) such that \(e' {\rightarrow }_{{E}} e''\) it holds that \(O\cap { observers}(e',e'',{E}) = \emptyset \).
-
(g)
If \(O = \{o\}\) and \(E = E'.\widehat{o}\) for some o and \(E'\), then for any \(E'' \simeq E'\), either \(e{\rightarrow }_{E''.\widehat{o}} e'\) or \(e' {\rightarrow }_{E''.\widehat{o}} e\).
We give some intuition for the changed properties. Property 3 requires the happens-before assignment to maintain edges in extensions, but allows having fewer edges in prefixes. Property 5 allows execution sequences that reach different states (due to unobserved races) to be considered equivalent. Property 6 summarizes properties for races that require observers. Most requirements are intuitive. Property 6.(d) clarifies Property 3: an “observed” race is included in a sequence only if some observers of the race are also included. Property 6.(e) prevents extensions to an execution sequence from adding edges to the events of a reversible race in such a way that the race can not be reversed. Property 6.(f) prohibits an observer from creating “dependency chains”. Finally, Property 6.(g) requires that an observer observes a fixed set of pairs of events in each execution sequence; a consequence of this is that whether or not some particular race is observed never depends on the ordering of some other pair of events observed by the same observer. All these properties are satisfied by “natural” happens-before assignments for events in message passing programs and most shared memory programs. Limitations include e.g., models in which the written memory regions of two write operations may overlap without being equal; such pairs of operations need to be treated as unconditionally racing.
5 Optimal DPOR with Observers
We now present a DPOR algorithm with observers that achieves optimal reduction.
In Sect. 3.2 we explained why sleep sets are not suitable when observers are used. We instead introduce a notion of redundancy based solely on the set of explored steps from each state. We will base this notion on a concept defined in Optimal DPOR.
Definition 2
(Initials and Weak Initials [2]). For an execution sequence \({E}.w\), the set \({ I}_{[{E}]}(w)\) of processes that are initials and the set \({ WI}_{[{E}]}(w)\) of processes that are weak initials are defined as follows:
-
1.
\(p \in { I}_{[{E}]}(w)\) iff there is a sequence \(w'\) such that \({E}.w \simeq {E}.p.w'\)
-
2.
\(p \in { WI}_{[{E}]}(w)\) iff there are sequences \(w'\) and v such that \({E}.w.v \simeq {E}.p.w'\)
Definition 3
(Redundant Sequences). For an execution sequence \({E}\) and a function \({ done} \) from prefixes of \({E}\) to sets of processes, the set of sequences \({ redundant}({E},{ done})\) is defined such that \(v \in { redundant}({E},{ done})\) iff \({E}.v\) is an execution sequence and there is a partitioning \({E}=w.w'\) of \({E}\) such that some process \(p \in { done} (w)\) is also in \(p \in { WI}_{[w]}(w'.v)\).
The intuition is that if \(v \in { redundant}({E},{ done})\), then the execution sequence E.v is equivalent to a previously explored execution sequence. In the special case where races do not need observers (i.e., the set of observers for each race is empty), we can define sleep sets in the classical sense by letting \(p \in { sleep}({E})\) denote that \({E}\) is of form \({E}'.v\) for some v such that \(p \in { done} ({E}')\) and p and v are independent. Then \({ sleep}({E})\) will consists of all single-process sequences in \({ redundant}({E},{ done})\), and \(v \in { redundant}({E},{ done})\) is equivalent to \({ sleep}({E}) \cap { WI}_{[{E}]}(v) \not = \emptyset \).
If \({E}\) is an execution sequence, and v and w are sequences of processes, let:
-
\(v \sqsubseteq _{[{E}]} w\) denote that there is a sequence \(v'\) such that \({E}.v.v'\) and \({E}.w\) are execution sequences with \({E}.v.v' \simeq {E}.w\). Intuitively, \(v \sqsubseteq _{[{E}]} w\) if, after \({E}\), the sequence v is a possible way to start an execution that is equivalent to w.
-
\(v {\sim }_{[{E}]} w\) denote that there are sequences \(v'\) and \(w'\) such that \({E}.v.v'\) and \({E}.w.w'\) are execution sequences with \({E}.v.v' \simeq {E}.w.w'\). Intuitively, \(v {\sim }_{[{E}]} w\) if, after \({E}\), the sequence v is a possible way to start an execution that is equivalent to an execution sequence of form \({E}.w.w'\), and vice versa.
Let us define an ordered tree as a pair \(\langle B,\prec \rangle \), where B (the set of nodes) is a finite prefix-closed set of sequences of processes, with the empty sequence \(\langle \rangle \) being the root. The children of a node w, of form w.p for some set of processes p, are ordered by \(\prec \). In \(\langle B,\prec \rangle \), such an ordering between children has been extended to the total order \(\prec \) on B by letting \(\prec \) be the induced post-order relation between the nodes in B. This means that if the children \(w.p_1\) and \(w.p_2\) are ordered as \(w.p_1 \prec w.p_2\), then \(w.p_1 \prec w.p_2 \prec w\) in the induced post-order.
Definition 4
(Wakeup Tree). Let \({E}\) be an execution sequence, and \({ done} \) be a function from prefixes of \({E}\) to sets of processes. A wakeup tree after \(\langle {E},{ done} \rangle \) is an ordered tree \(\langle B,\prec \rangle \), such that the following properties hold
-
1.
No leaf w of B is redundant after \({E}\), i.e., \(w \not \in { redundant}(E,{ done})\);
-
2.
whenever u.p and u.w are nodes in B with \(u.p \prec u.w\), and u.w is a leaf, then \(p \not \in { WI}_{[{E}.u]}(w)\).
Property (2) is the same as Optimal DPOR; Property (1) has been modified.
Regarding inserting sequences in a wakeup tree, let \(\langle B,\prec \rangle \) be a wakeup tree after \(\langle {E},{ done} \rangle \). For any sequence w such that \(w \not \in { redundant}(E,{ done})\) we need an operation \({ insert}_{[{E}]}(w,\langle B,\prec \rangle )\) that satisfies the following properties:
-
1.
\({ insert}_{[{E}]}(w,\langle B,\prec \rangle )\) is also a wakeup tree after \(\langle {E},{ done} \rangle \),
-
2.
any leaf of \(\langle B,\prec \rangle \) remains a leaf of \({ insert}_{[{E}]}(w,\langle B,\prec \rangle )\), and
-
3.
\({ insert}_{[{E}]}(w,\langle B,\prec \rangle )\) contains a leaf u with \(u {\sim }_{[{E}]} w\).
The \({ insert}_{[{E}]}(w,\langle B,\prec \rangle )\) operation can be implemented as follows. Let v be the smallest (w.r.t. to \(\prec \)) sequence in B such that \(v {\sim }_{[{E}]} w\). If v is a leaf,  can leave the tree unmodified. Otherwise, let \(w'\) be a shortest sequence such that \(w \sqsubseteq _{[{E}]}{v.w'}\), and add \(v.w'\) as a new leaf, ordered after all already existing nodes in B of form \(v.w''\).
can leave the tree unmodified. Otherwise, let \(w'\) be a shortest sequence such that \(w \sqsubseteq _{[{E}]}{v.w'}\), and add \(v.w'\) as a new leaf, ordered after all already existing nodes in B of form \(v.w''\).
5.1 Algorithm
Algorithm 1 is a modified and extended version of the plain Optimal DPOR algorithm [2], so that it supports observers. Since sleep sets is no longer an applicable mechanism for avoiding redundant exploration, the algorithm accepts only two arguments, \({E}\), the prefix to explore, and \({ WuT}\), the initial wakeup tree after \({E}\). It keeps two global variables, \({ wut}\), a mapping from execution sequences to wakeup trees, and \({ done} \), a mapping from execution sequences to sets of processes. For a pair of events \(e, e' \in { dom}({E})\) that are in a reversible race (\(e \precsim _{{E}} e'\)) in \({E}\), the algorithm employs the following notation:
-
\({ pre}({E},e)\) denotes the prefix of \({E}\) up to, but not including, the event \(e\),
-
\({{ notdep}}(e,{E})\) denotes the sub-sequence of \({E}\) consisting of the events that occur after \(e\) but do not “happen after” \(e\) (i.e., the events \(e'\) that occur after \(e\) such that
 ).
). -
\(notobs({e},{e'},{{E}})\) denotes the sub-sequence of \({E}\) containing the events that “happen after” e, but are not observers \(o \in O = { observers}(e,e',{E})\) of the race \(e {\rightarrow }_{{E}} e'\), nor “happen after” any such o: \(notobs({e},{e'},{{E}}) = \langle q\ \Vert \ q \in {E},\, e{\rightarrow }_{{E}}q,\, q\not \in O,\, \not \exists o\in O.o{\rightarrow }_{{E}}q \rangle \).

The first change compared to Optimal DPOR is in lines 6 to 8 which describe how to construct a wakeup sequence for an observed race, including an observer operation. Second, the test \(v \in { redundant}({E},{ done})\) on lines 11 replaces the test  at the corresponding place in Optimal DPOR. The rest of the algorithm is essentially the same, with initialization, update and propagation of sleep sets removed.
at the corresponding place in Optimal DPOR. The rest of the algorithm is essentially the same, with initialization, update and propagation of sleep sets removed.
5.2 Correctness and Optimality
The correctness and optimality of Algorithm 1 are stated in the following theorems.
Theorem 1
(Correctness of Optimal DPOR with Observers). Whenever a call to \({ Explore}({E},{ WuT})\) returns during Algorithm 1, then for all maximal execution sequences \({E}.w\), the algorithm has explored some execution sequence \({E}'\) which is in \([{E}.w]_{\simeq }\).
Since the initial call to the algorithm uses the arguments \({ Explore}(\langle \rangle ,\) \(\langle \{ \langle \rangle \},\emptyset \rangle )\), Theorem 1 implies that for all maximal execution sequences \({E}\) the algorithm explores some execution sequence \({E}'\) which is in \([{E}]_{\simeq }\).
Theorem 2
(Optimality of Optimal DPOR with Observers). Algorithm 1 never explores two maximal execution sequences which are equivalent.
If Algorithm 1 is not at the end of a maximal sequence, it will continue exploring the scheduling either by using information from a wakeup tree (line 15) or by choosing an arbitrary enabled process (line 18). Theorem 2 ensures that all maximal execution sequences reached are non redundant.
6 Implementations
We have implemented Algorithm 1 in two SMC tools: Nidhugg and Concuerror.
Observers in Nidhugg. Nidhugg [1] is a stateless model checking tool for shared-memory pthreads programs written in C or C++ that operates by interpreting LLVM IR. Nidhugg can test programs also under relaxed memory models (TSO, PSO, and Power), but in this paper we will limit ourselves to testing programs under Sequential Consistency.
In the context of shared memory, the observers extension was used to make races between writes to the same memory location conditional on the existence of a read of that memory location that “observes” those writes. In order to add the observers extension to Nidhugg, the tool was first extended to support Optimal DPOR, as it previously only implemented Source DPOR, which is not easily extended with observers, as discussed in Sect. 3.2. The tool now records symbolic representations of program events that contain enough information to reconstruct the happens-before relation induced by a particular execution. For Source DPOR, these symbolic events are unnecessary if the happens-before relation is stored in vector clocks [18], as it is in Nidhugg. For Optimal DPOR, symbolic events are the most reasonable way to implement tests that check whether a given process is a weak initial of some sequence, which is needed for both the redundancy check and wakeup tree insertion.
To extend this implementation with observers, symbolic events for writes were extended with an “observed”-flag, which is unset until a read that reads the value written by that write is executed. At the end of the execution, we compute the vector clocks of the happens-before relation, only considering two write events to the same memory location as interfering if at least one of them has the “observed”-flag set. Then, Optimal DPOR was modified as described in Sect. 5.1. The check whether a wakeup sequence is redundant on line 11 is implemented using sleep sets extended with processes conditionally sleeping unless an address is read, and a set of addresses that must be read, without intervening writes, before the end of the program.
Observers in Concuerror. Concuerror [8] is a stateless model checking tool for Erlang, a functional programming language based on the actor model of concurrency [4]. In Erlang, actors are realized by language-level processes implemented by the runtime system instead of being directly mapped to OS threads. Each Erlang process communicates with other processes via asynchronous message passing. Messages are placed in the mailbox of the receiving process in the order they are delivered. A process can consume messages using selective receive, which is a blocking operation when the mailbox does not contain any matching message, unless a timeout clause is specified. If multiple messages can match, the oldest message is picked from the mailbox.
Concuerror already implemented Optimal DPOR, but treated any two message deliveries to the same mailbox as interfering. With the extension, Concuerror uses receives as observers of sends. When examining a complete scheduling, an extra pass is performed, annotating each message delivery event with the patterns that were used in the receive that picked the message (if present) and the receive order. If the message of a later delivery matches any of the pattern annotations of an earlier delivery, the deliveries interfere. The \({ notobs}\) sequence is constructed from all the events that lead up to the corresponding receive (which is the observer), excluding events in the \({ notdep}\) sequence. Because the resulting wakeup sequence contains fewer events, observer information is recomputed, and then all the earlier done sets are checked for weak initials of the wakeup sequence, exactly as described in Algorithm 1.
7 Experimental Results
We report experimental results that compare the performance of two algorithms: Optimal DPOR (denoted in the tables as “optimal ”) and Optimal DPOR with Observers (denoted as “observers ”). We ran all benchmarks on a desktop with an i7-3770 CPU (3.40 GHz) with 16 GB of RAM running Debian 4.12.0-2-amd64 and LLVM 3.8.1. The machine has four physical cores, but presently both tools use only one of them.
Observers in Nidhugg. Table 1 shows the effect of observers on shared memory C/pthread programs. We used two kinds of programs: (1) synthetic benchmarks similar to those of Sect. 2, and (2) programs from SV-COMP and/or from “similar” papers. We report the number of traces that the two algorithms explore, the time it takes to explore them, and the memory used (although this number is not interesting for an SMC tool).
For lastwrite( n ), we see a reduction in the number of interleavings explored from n! to n, as explained in Sect. 2. For floating_read( n ), optimal shows the predicted \((n+1)!\) interleavings, and for \(n=2\), observers reduce the interleaving count from 6 to 5 as expected. In general, the benchmark has \(n\times 2^{n-1}+1\) interleavings with observers. Notice that any technique that differentiates equivalence classes by the partial order of program steps must explore at least as many interleavings or violate Property 4. The next two programs (apr_1 and fib) are examples of programs for which observers have no effect. We see that the extra overhead is very moderate for both programs.
In the last benchmark (lamport), we see that observers improve performance. As Nidhugg does not implement await statements (which are used by lamport), it emulates these with assumes. In such cases, Nidhugg might explore some traces in which these assumptions are violated. We list those traces separately, so for this benchmark the “Traces Explored” columns show \(a+b\) entries, which means that Nidhugg explored \(a+b\) traces but b of those times an assume statement was violated.
Observers in Concuerror. Table 2 shows the effect of observers in message passing programs; we omit memory used, as both algorithms have similar requirements.
The two benchmarks on the left sub-table confirm the behaviour we expect. When receives are not selective, the number of traces explored by both algorithms is n!. With selective receive (selective benchmark) observers explore only one trace.
The first program on the right sub-table (lock) is originally a shared-memory program that when translated to Erlang simulate locks using message passing. To acquire the lock, a process sends a message with its identifier to the “lock process” and then waits for a reply. Upon receiving the acquire message, the lock process uses the identifier to reply and then waits for a release message. Other acquire messages become queued in the mailbox of the lock process. Upon receiving the release message, the lock process loops back to the start, retrieving the next acquire message and notifying the next process. Notice that, without observers, the delivery of the release message of a process interferes (redundantly) with the delivery of acquire messages of other processes, unlike acquire operations on true locks which cannot be executed before a release operation (such messages were treated exceptionally in the evaluation of Optimal DPOR). Observers remove the need for special handling: the receive statements are enough to precisely determine which pairs of send operations are interfering.
The next two table rows (poolboy and gproc) show results from “real” Erlang programs. We see that observers provide a moderate reduction in both the number of traces that need to be explored as well as in time.
Finally, the last program (corfu-repair) is the one that triggered this work. As can be seen in the table, observers allow Concuerror to complete SMC in a bit more than two days, while without observers the tool needs to explore exactly 24 times as many traces, taking more than 42 days to finish.
8 Related Work
POR techniques have been continuously evolving w.r.t. how they determine interference. Refining the conditions under which higher-level operations interfere has been shown to have significant impact, regardless of whether the states in which such operations are executed is also a parameter or not [13]. In this work, we have extended this idea, parameterizing the interference between operations using distinct observer operations.
DPOR techniques have also been extended to take advantage of special properties of the underlying concurrency model. For the actor model, the transitivity of the dependency relation for send operations has been exploited to defer early planning of interleavings [21]. This improvement is orthogonal with Optimal DPOR (and with our extension), as it reduces the number of wakeup sequences that are added “early” in an exploration. For event-driven systems, it has been shown [17] that two post operations to an event dispatch queue need not be considered dependent: reordering of such operations can be decided later, upon detection of interference between other operations within the respective event handlers. However, this treatment applies only under a specific interpretation of ‘message passing’ that exploits additional semantic structure of an actor’s mailbox. Our technique is applicable to a wider spectrum of programs.
Context-Sensitive DPOR [3] uses an external procedure to decide whether alternative schedulings would lead to identical states and, like optimal DPOR with observer, is also able to achieve exponential reduction in certain cases. However, since it needs to compare states, it is an inherently stateful technique, in contrast to our technique that inspects only one trace at a time to lazily construct reversible races.
Data-Centric DPOR (DC-DPOR) [7] is an SMC technique that explores a related but different notion of observability. It defines two executions to be equivalent if each read reads from (“observes”) the same write in both executions. In contrast, our notion of observability is based on observing interference of operations, not just individual writes. DC-DPOR’s resulting equivalence relation is coarser than ours, which is based on Mazurkiewicz traces. However, DC-DPOR is optimal only for programs with acyclic communication graphs, while being non-optimal otherwise. Also, DC-DPOR models message passing using locks and shared memory, which at best gives as few traces as Optimal DPOR gives without the improvements presented in this paper.
9 Concluding Remarks
In this paper we presented an extension to the Optimal DPOR algorithm for SMC that uses observability to refine which operations are considered as interfering. We described the challenges and motivated the necessary modifications, gave a formal description of the algorithm and the theory behind it and reported on two implementations in SMC tools, demonstrating that Optimal DPOR with Observers can achieve significantly better reduction in both shared memory and message passing programs.
References
Abdulla, P.A., Aronis, S., Atig, M.F., Jonsson, B., Leonardsson, C., Sagonas, K.: Stateless model checking for TSO and PSO. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 353–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_28
Abdulla, P.A., Aronis, S., Jonsson, B., Sagonas, K.: Source sets: a foundation for optimal dynamic partial order reduction. J. ACM 64(4), 251–2549 (2017). http://doi.acm.org/10.1145/3073408
Albert, E., Arenas, P., de la Banda, M.G., Gómez-Zamalloa, M., Stuckey, P.J.: Context-sensitive dynamic partial order reduction. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10426, pp. 526–543. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63387-9_26
Armstrong, J.: Erlang. Commun. ACM 53(9), 68–75 (2010). http://doi.acm.org/10.1145/1810891.1810910
Aronis, S., Fritchie, S.L., Sagonas, K.: Testing and verifying chain repair methods for Corfu using stateless model checking. In: Polikarpova, N., Schneider, S. (eds.) IFM 2017. LNCS, vol. 10510, pp. 227–242. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66845-1_15
Aronis, S., Jonsson, B., Lång, M., Sagonas, K.: Binary artifact for TACAS-2018 paper “Optimal DPOR with Observers”. Figshare, February 2018. https://doi.org/10.6084/m9.figshare.5918701.v1
Chalupa, M., Chatterjee, K., Pavlogiannis, A., Sinha, N., Vaidya, K.: Data-centric dynamic partial order reduction. Proc. ACM Program. Lang. 2(POPL), 31:1–31:30 (2017). http://doi.acm.org/10.1145/3158119
Christakis, M., Gotovos, A., Sagonas, K.: Systematic testing for detecting concurrency errors in Erlang programs. In: Sixth IEEE International Conference on Software Testing, Verification and Validation, ICST 2013, pp. 154–163. IEEE Computer Society, Los Alamitos, CA, USA (2013). https://doi.org/10.1109/ICST.2013.50
Clarke, E.M., Grumberg, O., Minea, M., Peled, D.: State space reduction using partial order techniques. Int. J. Softw. Tools Technol. Transf. 2(3), 279–287 (1999). http://dx.doi.org/10.1007/s100090050035
Flanagan, C., Godefroid, P.: Dynamic partial-order reduction for model checking software. In: Proceedings of the 32nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2005, pp. 110–121. ACM, New York (2005). http://doi.acm.org/10.1145/1040305.1040315
Godefroid, P.: Partial-order methods for the verification of concurrent systems: an approach to the state-explosion problem. Ph.D. thesis, University of Liége (1996). http://www.springer.com/gp/book/9783540607618, also. LNCS, vol. 1032. Springer, Heidelberg
Godefroid, P.: Model checking for programming languages using VeriSoft. In: Proceedings of the 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 1997, pp. 174–186. ACM, New York (1997). http://doi.acm.org/10.1145/263699.263717
Godefroid, P., Pirottin, D.: Refining dependencies improves partial-order verification methods (extended abstract). In: Courcoubetis, C. (ed.) CAV 1993. LNCS, vol. 697, pp. 438–449. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-56922-7_36
Hartmanns, A., Wendler, P.: TACAS 2018 Artifact Evaluation VM. Figshare (2018). https://doi.org/10.6084/m9.figshare.5896615
Lamport, L.: Time, clocks and the ordering of events in a distributed system. Commun. ACM 21(7), 558–565 (1978). http://doi.acm.org/10.1145/359545.359563
Lamport, L.: A fast mutual exclusion algorithm. ACM Trans. Comput. Syst. 5(1), 1–11 (1987). http://doi.acm.org/10.1145/7351.7352
Maiya, P., Gupta, R., Kanade, A., Majumdar, R.: Partial order reduction for event-driven multi-threaded programs. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 680–697. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_44
Mattern, F.: Virtual time and global states of distributed systems. In: Cosnard, M., et al. (eds.) Proceedings of the Workshop on Parallel and Distributed Algorithms, pp. 215–226. North-Holland/Elsevier (1989)
Mazurkiewicz, A.: Trace theory. In: Brauer, W., Reisig, W., Rozenberg, G. (eds.) ACPN 1986. LNCS, vol. 255, pp. 278–324. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-17906-2_30
Peled, D.: All from one, one for all: on model checking using representatives. In: Courcoubetis, C. (ed.) CAV 1993. LNCS, vol. 697, pp. 409–423. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-56922-7_34
Tasharofi, S., Karmani, R.K., Lauterburg, S., Legay, A., Marinov, D., Agha, G.: TransDPOR: a novel dynamic partial-order reduction technique for testing actor programs. In: Giese, H., Rosu, G. (eds.) FMOODS/FORTE -2012. LNCS, vol. 7273, pp. 219–234. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30793-5_14
Valmari, A.: Stubborn sets for reduced state space generation. In: Rozenberg, G. (ed.) ICATPN 1989. LNCS, vol. 483, pp. 491–515. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-53863-1_36
Acknowledgments
This work was carried out within the Linnaeus centre of excellence UPMARC (Uppsala Programming for Multicore Architectures Research Center), and was partly supported by grants from the Swedish Research Council.
Data Availability Statement
The versions of Nidhugg and Concuerror, as well as all the programs we used to obtain the experimental results of Tables 1 and 2 are available in the Figshare repository [6]. Also included in the artifact are instructions on how to use it to reproduce the results reported in this paper. As per the TACAS 2018 submission rules, the artifact is designed for use with the TACAS 2018 Artifact Evaluation Virtual Machine [14], although, as source code is included, it can probably be used on any Linux platform. We refer to the documentation of the respective tool on how to compile them from source code; the tools may of course evolve over time, but the way to build them will not change significantly.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Aronis, S., Jonsson, B., Lång, M., Sagonas, K. (2018). Optimal Dynamic Partial Order Reduction with Observers. In: Beyer, D., Huisman, M. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2018. Lecture Notes in Computer Science(), vol 10806. Springer, Cham. https://doi.org/10.1007/978-3-319-89963-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-89963-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89962-6
Online ISBN: 978-3-319-89963-3
eBook Packages: Computer ScienceComputer Science (R0)






 .
. .
. , then
, then  .
. , then
, then 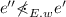 .
. ).
).