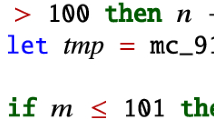Abstract
We propose a method for automatically finding refinement types of higher-order function programs. Our method is an extension of the Ice framework of Garg et al. for finding invariants. In addition to the usual positive and negative samples in machine learning, their Ice framework uses implication constraints, which consist of pairs (x, y) such that if x satisfies an invariant, so does y. From these constraints, Ice infers inductive invariants effectively. We observe that the implication constraints in the original Ice framework are not suitable for finding invariants of recursive functions with multiple function calls. We thus generalize the implication constraints to those of the form \((\{x_1,\dots ,x_k\}, y)\), which means that if all of \(x_1,\dots ,x_k\) satisfy an invariant, so does y. We extend their algorithms for inferring likely invariants from samples, verifying the inferred invariants, and generating new samples. We have implemented our method and confirmed its effectiveness through experiments.

You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Higher-order functional program verification is an interesting but challenging problem. Over the past two decades, several approaches have been proposed: refinement types with manual annotations [10, 31], liquid types [23], and reduction to higher-order recursion schemes [24]. These approaches face the same problem found in imperative and synchronous data-flow program verification: the need for predicates describing how loops and components behave for the verification and/or abstraction method to work in practice [9, 12, 17]. This paper proposes to address this issue by combining refinement types with the recent machine-learning-based, invariant discovery framework Ice from [11, 12].
Consider for instance a function f from integers to integers such that if its input n is less than or equal to 101, then its output is 91, otherwise it is \( \texttt {n} - 10\). (This is the case of the mc_91 function on Fig. 1.) Then our objective is to automatically discover, by using an adaptation of Ice, the refinement type
That is, function f accepts any integer n that satisfies \( true \) as input, and yields an integer r equal to \(n - 10\) when \(n > 101\), and equal to 91 otherwise. The traditional Ice framework is not appropriate for our use-case. We briefly summarize it below, and then discuss how this approach needs to be extended for the purpose of functional program verification.
Brief review of the  framework. Let \(\mathscr {S}\) be a transition system \(\langle \; \vec {s}, \mathcal {I}(\vec {s}), \mathcal {T}(\vec {s},\vec {s}') \;\rangle \), with \(\vec {s}\) its vector of state variables, \(\mathcal {I}(\vec {s})\) its initial predicate, and \(\mathcal {T}(\vec {s},\vec {s}')\) the transition relation between consecutive states. Suppose we wish to prove that \(\mathcal {P}(\vec {s})\) is an invariant, i.e., that a property \(\mathcal {P}(\vec {s})\) holds for any state \(\vec {s}\) reachable from an initial state. Then it suffices to find a predicate \( Inv (\vec {s})\) that satisfies the following conditions.
framework. Let \(\mathscr {S}\) be a transition system \(\langle \; \vec {s}, \mathcal {I}(\vec {s}), \mathcal {T}(\vec {s},\vec {s}') \;\rangle \), with \(\vec {s}\) its vector of state variables, \(\mathcal {I}(\vec {s})\) its initial predicate, and \(\mathcal {T}(\vec {s},\vec {s}')\) the transition relation between consecutive states. Suppose we wish to prove that \(\mathcal {P}(\vec {s})\) is an invariant, i.e., that a property \(\mathcal {P}(\vec {s})\) holds for any state \(\vec {s}\) reachable from an initial state. Then it suffices to find a predicate \( Inv (\vec {s})\) that satisfies the following conditions.
The predicate \( Inv (\vec {s})\) is an invariant that is inductive in that it is preserved by the transition relation, as guaranteed by (3). We call such an \( Inv (\vec {s})\) a  for \(\mathcal {P}(\vec {s})\). It serves as a certificate that \(\mathcal {P}(\vec {s})\) is a (plain) invariant. Given a candidate for \( Inv (\vec {s})\), the conditions (1)–(3) can be checked by an SMT [3] solver. In the rest of this section, “invariant” will always mean “strengthening inductive invariant”.
for \(\mathcal {P}(\vec {s})\). It serves as a certificate that \(\mathcal {P}(\vec {s})\) is a (plain) invariant. Given a candidate for \( Inv (\vec {s})\), the conditions (1)–(3) can be checked by an SMT [3] solver. In the rest of this section, “invariant” will always mean “strengthening inductive invariant”.
The Ice framework is a machine-learning-based method combining a  that incrementally produces candidate invariants, and a
that incrementally produces candidate invariants, and a  that checks whether the candidates are such that (1), (2) and (3) hold. If a given candidate is not an invariant, the teacher produces
that checks whether the candidates are such that (1), (2) and (3) hold. If a given candidate is not an invariant, the teacher produces  as follows, so that the learner can produce a better candidate. Given a candidate \( C _k(\vec {s})\), the teacher checks whether (1) holds — using an SMT solver for instance. If it does not, a concrete state \(\vec {e}\) is extracted and will be given to the learner as an
as follows, so that the learner can produce a better candidate. Given a candidate \( C _k(\vec {s})\), the teacher checks whether (1) holds — using an SMT solver for instance. If it does not, a concrete state \(\vec {e}\) is extracted and will be given to the learner as an  : the next candidate \( C _{k+1}\) should be such that \( C _{k+1}(\vec {e})\) holds. Conversely, if (2) does not hold, a concrete state \(\vec {c}\) is extracted and will be given as a
: the next candidate \( C _{k+1}\) should be such that \( C _{k+1}(\vec {e})\) holds. Conversely, if (2) does not hold, a concrete state \(\vec {c}\) is extracted and will be given as a  : the next candidate should be such that \( C _{k+1}(\vec {c})\) does not hold.
: the next candidate should be such that \( C _{k+1}(\vec {c})\) does not hold.
Unlike traditional machine-learning approaches, in Ice the teacher also extracts learning data from (3) when it does not hold. It takes the form of a pair of (consecutive) concrete states \((\vec {i}, \vec {i}')\), and is called an  : the next candidate should be such that \( C _{k+1}(\vec {i}) \Rightarrow C _{k+1}(\vec {i}')\). Implication constraints are crucial for the learner to discover inductive invariants, as they let it know why its current candidate failed the induction check. The Ice framework does not specify how the learner generates candidates, but this is typically done by building a classifier consistent with the learning data, in the form of a decision tree—discussed further in Sect. 3.
: the next candidate should be such that \( C _{k+1}(\vec {i}) \Rightarrow C _{k+1}(\vec {i}')\). Implication constraints are crucial for the learner to discover inductive invariants, as they let it know why its current candidate failed the induction check. The Ice framework does not specify how the learner generates candidates, but this is typically done by building a classifier consistent with the learning data, in the form of a decision tree—discussed further in Sect. 3.
Refinement Type Inference as a Predicate Synthesis Problem. We now discuss why the original Ice framework is ill-suited for functional program verification. Consider McCarthy’s 91 function from Fig. 1. To prove this program correct in a refinement type setting, it is enough to find some refinement type
for mc_91, where \(\rho _1\) and \(\rho _2\) are such
We can observe some similarities between the Horn clauses above and (1)–(3). The constraints (8) and (9) respectively correspond to the constraints (1) and (2) on initial states and the property to be proved, whereas the constraints (4)–(7) correspond to the induction constraint (3). This observation motivates us to reuse the Ice framework for refinement type inference.
There are, however, two obstacles in adapting the Ice framework to refinement type inference. First, we must infer not one but several mutually-dependent predicates. Second, and more importantly, we need to generalize the notion of implication constraint because of the nested recursive calls found in functional programs. To illustrate, let us assume that we realized that mc_91’s precondition is \(\rho _1(n) = true \). Then the third constraint from the else branch is
Contrary to the ones found in the original Ice framework, this Horn clause is  : it has more than one application of the same predicate (\(\rho _2\), here) in its antecedents. Now, assuming we have a candidate for which this constraint is falsifiable, the implication constraint should have form \((\; \{(n_1, r_1),\; (n_2, r_2)\}, (n, r)\;)\), which means that the next candidate \( C \) should be such that \( C (n_1, r_1) \wedge C (n_2, r_2) \;\Rightarrow \; C (n, r) \). This is because there are two occurrences of \(\rho _2\) on the left-hand side of the implication.
: it has more than one application of the same predicate (\(\rho _2\), here) in its antecedents. Now, assuming we have a candidate for which this constraint is falsifiable, the implication constraint should have form \((\; \{(n_1, r_1),\; (n_2, r_2)\}, (n, r)\;)\), which means that the next candidate \( C \) should be such that \( C (n_1, r_1) \wedge C (n_2, r_2) \;\Rightarrow \; C (n, r) \). This is because there are two occurrences of \(\rho _2\) on the left-hand side of the implication.
The need to infer more than one predicate and support non-linear Horn clauses is not specific to higher-order functional program verification. After all, McCarthy’s 91 function is first-order and is occasionally mentioned in first-order imperative program verification papers [5]. Sv-Comp [4], the main (imperative) software verification competition features 
 (https://github.com/sosy-lab/sv-benchmarks/tree/master/clauses/LIA), 54 of which contain non-linear Horn clauses. In our context of higher-order functional program verification the ratio is much higher, with 63 of our 164 OCaml [20] programs yielding non-linear Horn clauses.
(https://github.com/sosy-lab/sv-benchmarks/tree/master/clauses/LIA), 54 of which contain non-linear Horn clauses. In our context of higher-order functional program verification the ratio is much higher, with 63 of our 164 OCaml [20] programs yielding non-linear Horn clauses.
The main contribution of this paper is to address the two issues aforementioned and propose a modified Ice framework suitable for higher-order program verification in particular. While adapting machine-learning techniques to higher-order program verification has been done before [34, 35], transposing implication constraints to this context is, to the best of our knowledge, new work. We have implemented our approach as a program verifier for a subset of OCaml and report on our experiments.
The rest of the paper is organized as follows. Section 2 introduces our target language and describes verification condition generation and simplification. The modified Ice framework is discussed in Sect. 3. We report on our implementation and experiments of the approach in Sect. 4, and discuss related work in Sect. 5 before concluding in Sect. 6.
2 Target Language and Verification Conditions
In this section, we first introduce the target language of our refinement type inference method. We then introduce a refinement type system and associated verification conditions (i.e., sufficient conditions for the typability of a given program).
2.1 Language
The target of the method is a simply-typed, call-by-value, higher-order functional language with recursion. Its syntax is given by:
We use the meta-variables \(x, y, \dots , f, g, \dots \) for variables. We write \(\,\widetilde{\cdot }\,\) for a sequence; for example, we write \(\widetilde{x}\) for a sequence of variables. For the sake of simplicity, we consider only integers as base values. We represent booleans using integers, and treat 0 as false and non-zero values as true. We sometimes write \( true \) for 1 and \( false \) for 0.
We briefly explain programs and expressions; the formal semantics is given in the longer version [7]. We use let-normal-form-style for simplicity. A program \(D\) is a set of mutually recursive function definitions \(f(\widetilde{z}) = e\). The expression \(\oplus \{a_i \Rightarrow e_i\}_{1 \le i \le n}\) evaluates \(e_i\) non-deterministically if the value of \(a_i\) is non-zero, which can be also used to generate non-deterministic booleans/integers. We also write \((a_1\Rightarrow e_1) \oplus \cdots \oplus (a_n\Rightarrow e_n)\) for \(\oplus \{a_i \Rightarrow e_i\}_{1 \le i \le n}\), and write \( \texttt {if} \; {a} \; \texttt {then} \; {e_1} \; \texttt {else} \; {e_2}\) for \((a \Rightarrow e_1) \oplus (\lnot a \Rightarrow e_2)\). The expression \( \texttt {let} \; {x=*} \; \texttt {in} \; e\) generates an integer, then binds x to it, and evaluates e. The expression \( \texttt {let} \; {x=a} \; \texttt {in} \; e\) (\( \texttt {let} \; {x=yz} \; \texttt {in} \; e\), resp.) binds x to the value of a (yz, resp.), and then evaluates e. The expression \( \texttt {fail} \) aborts the program. An assert expression \( \texttt {assert} (a)\) can be represented as \( \texttt {if} \; {a} \; \texttt {then} \; {0} \; \texttt {else} \; { \texttt {fail} }\). In the definition of values, function application \({f_i}\,{\widetilde{v}}\) must be partial, i.e., the length \(|\widetilde{v}|\) of arguments \(\widetilde{v}\) must be smaller than \(|\widetilde{x_i}|\), where \((f_i(\widetilde{x_i}) = e_i) \in D\).
We assume that a program is well-typed under the standard simple type system. We also assume that every function in \(D\) has a non-zero arity, the body of each function definition has the integer type, and D contains a distinguished function symbol \( \texttt {main} \in \{f_1,\dots ,f_n\}\) whose simple type is \({ \texttt {int} }\rightarrow \texttt {int} \).
The goal of our verification is to find an invariant (represented in the form of refinement types) of the program that is sufficient to verify that, for every integer \(n\), \( \texttt {main} \;n\) does not fail (i.e., is not reduced to \( \texttt {fail} \)).
2.2 Refinement Type System
We present a refinement type system for the target language. The syntax of refinement types is given by:
The refinement type \(\{{x} \mathbin {:}{ \texttt {int} } \mid {a}\}\) denotes the set of integers that satisfy a, i.e., the value of a is non-zero. For example, \(\{{x} \mathbin {:}{ \texttt {int} } \mid {x \ge 0}\}\) represents natural numbers. The type \(({x}\mathbin {:}{T_1})\rightarrow {T_2}\) denotes the set of functions that take an argument x of type \(T_1\) and return a value of type \(T_2\). Here, note that \(x\) may occur in \(T_2\). We write \( \texttt {int} \) for \(\{{x} \mathbin {:}{ \texttt {int} } \mid { true }\}\), and \(T_1\rightarrow T_2\) for \(({x}\mathbin {:}{T_1})\rightarrow {T_2}\) when \(x\) does not occur in \(T_2\). By abuse of notation, we sometimes (as in Sect. 1) write \(\{{x} \mathbin {:}{ \texttt {int} } \mid {a}\}\rightarrow {T}\) for \(({x}\mathbin {:}{\{{x} \mathbin {:}{ \texttt {int} } \mid {a}\}})\rightarrow {T}\).
A judgment \(\Gamma \vdash t \mathbin {:}T\) means that term t has refinement type \(T\) under refinement type environment \(\Gamma \), which is a sequence of refinement type bindings and guard predicates: \( \Gamma \;\,{:}{:=}\; \emptyset \;|\;\Gamma , x \mathbin {:}T\;|\;\Gamma , a. \) Here, \(x\mathbin {:}T\) means that x has refinement type \(T\), and a means that a holds. Figure 2 shows the typing rules, which are the standard ones.
The type system is sound in the sense that if \(\vdash D:\Gamma \) holds for some \(\Gamma \), then \( \texttt {main} \;n\) does not fail for any integer n. We omit to prove this type system sound as it is a rather standard system [23, 28, 29]. The type system is, however, incomplete: there are programs that never fail but are not typable in the refinement type system. Implicit parameters are required to make the type system complete [30].
2.3 Verification Conditions
Our goal has now been reduced to finding \(\Gamma \) such that \(\vdash D: \Gamma \), if such \(\Gamma \) exists. To this end, we first infer simple types for the target program by using the Hindley-Milner type inference algorithm. From the simple types, we construct the refinement type templates by adding predicate variables, and then generate the verification conditions, i.e., constraints on the predicate variables that describe a sufficient condition for \(\vdash D:\Gamma \). The construction of the verification conditions is also rather standard [23, 28, 29], hence we do not discuss it here—see [7]. We note that the verification conditions can be normalized to a set of Horn clauses [5].
Example 1
Consider the following program and its associated simple types:

By assigning a unique predicate variable to each integer type, we can obtain the following refinement type templates.
We then extract the following verification conditions from the body of the program:

2.4 Simplifying Verification Conditions
The number of unknown predicates to infer is critical to the efficiency of our algorithm in Sect. 3, because the algorithm succeeds only when the learner comes up with correct solutions for all the unknown predicates. We discuss here a couple of techniques to reduce the number of unknown predicates.
The first one takes place at the level of Horn clauses and is not limited to refinement type inference over functional programs. Suppose that some predicate \(\rho \) occurs in the clauses \( \varphi \,\models \, \rho \) and \(C[\rho ]\,\models \, \varphi '\), where \(C[\rho ]\) is a formula having only positive occurrences of \(\rho \), and \(\rho \) does not occur in \(\varphi \), \(\varphi '\), nor any other clauses of the verification condition. Then, we can replace the two clauses above with \( C[\varphi ]\,\models \, \varphi ' \) and \( \rho \equiv \varphi \). For example, recall the incr/twice from the example above. The predicate \(\rho _1\) occurs only in the clauses \( \rho '_1(n) \,\models \, \rho _1(n) \) and \( \rho _1(n) \,\models \, \rho _2(n, n + 1) \). Thus, we can replace them with \( \rho '_1(n) \,\models \, \rho _2(n, n + 1) \) and \( \rho _1(n) \equiv \rho '_1(n) \). In this manner we can reduce the number of unknown predicate variables. This optimization itself is not specific to our context of functional program verification; similar (and more sophisticated) techniques are also discussed in [5]. We found this optimization particularly useful in our context, because the standard verification condition generation for higher-order functional programs introduces too many predicate variables.
The other optimization is specific to our context of refinement type inference. Suppose that the simple type of a function \(f\) is \( \texttt {int} \rightarrow \texttt {int} \). Then, in general, we prepare the refinement type template \( {\{{x} \mathbin {:}{ \texttt {int} } \mid {\rho _1(x)}\}}\rightarrow {\{{r} \mathbin {:}{ \texttt {int} } \mid {\rho _2(x,r)}\}} \). If the evaluation of \(f(n)\) does not fail for any integer \(n\), however, then the above refinement type is equivalent to \( {\{{x} \mathbin {:}{ \texttt {int} } \mid { true }\}}\rightarrow { \{{r} \mathbin {:}{ \texttt {int} } \mid {\rho _1(x)\Rightarrow \rho _2(x,r)}\} } \). Thus, the simpler template \( ({x}\mathbin {:}{ \texttt {int} })\rightarrow {\{{r} \mathbin {:}{ \texttt {int} } \mid {\rho _3(x,r)}\}} \) suffices, with \(\rho _3(x,r)\) corresponding to \( \rho _1(x)\Rightarrow \rho _2(x,r) \). For instance, in the mc_91 example from Sect. 1, it is obvious that \( \texttt {mc\_91} (n)\) never fails as its body contains no assertions and contains only calls to itself. Thus, we can actually set \(\rho _1(n)\) to \( true \).
In practice we use effect analysis [22] to check whether a function can fail. To this end, we extend simple types to effect types defined by: \(\sigma \;{:}{:=}\; \texttt {int} \mid {\sigma _1}{\mathop {\rightarrow }\limits ^{\xi }}{\sigma _2}\), where \(\xi \) is either an empty effect \(\epsilon \), or a failure \(\mathtt {f}\). The type \({\sigma _1}{\mathop {\rightarrow }\limits ^{\xi }}{\sigma _2}\) describes functions that take an argument of type \(\sigma _1\) and return a value of type \(\sigma _2\), but with a possible side effect of \(\xi \). We can infer these effect types using a standard effect inference algorithm [22]. A function with effect type \({ \texttt {int} }{\mathop {\rightarrow }\limits ^{\epsilon }}{\sigma }\) takes an integer as input and returns a value of \(\sigma \) without effect, i.e., without failure. For this type, we then use the simpler refinement type template \( \{{x} \mathbin {:}{ \texttt {int} } \mid { true }\}\rightarrow {\cdots } \) instead of \( \{{x} \mathbin {:}{ \texttt {int} } \mid {\rho (x)}\}\rightarrow {\cdots } \). For example, since \( \texttt {mc\_91} \) has effect type \( { \texttt {int} }{\mathop {\rightarrow }\limits ^{\epsilon }}{ \texttt {int} } \), we assign the template \( ({x}\mathbin {:}{ \texttt {int} })\rightarrow {\{{r} \mathbin {:}{ \texttt {int} } \mid {\rho (x,r)}\}} \) for the refinement type of \( \texttt {mc\_91} \).
3 Modified Ice Framework
This section discusses our modified Ice framework tackling the predicate synthesis problem extracted from the input functional program as detailed in Sect. 2. Algorithm 1 details how the teacher supervises the learning process. Following the original Ice approach, teacher and learner only communicate by exchanging guesses for the predicates (from the latter to the former) and positive (\(\mathcal {P}\)), negative (\(\mathcal {N}\)) and implication (\(\mathcal {I}\)) data—from the former to the latter. These three sets of learning data are incrementally populated as long as the verification conditions are falsifiable, as discussed below.

3.1 Teacher
We now describe our modified version of the Ice teacher that, given some candidate predicates for \(\Pi = \{\rho _1, \ldots , \rho _n\}\), returns learning data if the verification conditions instantiated on the candidates are falsifiable. Since there are several predicates to discover, the positive, negative and implication learning data (concrete values) will always be annotated with the predicate(s) concerned.
Now, all the constraints from the verification condition set \( VC \) have one of the following shapes, reminiscent of the original Ice ’s (1)–(3) from Sect. 1:
where each \(\alpha _1, \ldots , \alpha _{m+1}\) is an application of one of the \(\rho _1, \ldots , \rho _n\) to variables of the program, and C is a concrete formula ranging over the variables of the program. In the following, we write \(\rho (\alpha _i)\) for the predicate \(\alpha _i\) is an application of. To illustrate, recall constraint (7) of the example from Fig. 1:
It has the same shape as (10), with \(\rho (\alpha _1) = \rho _1\) and \(\rho (\alpha _2) = \rho (\alpha _3) = \rho (\alpha _4) = \rho _2\).
Given some guesses \(P_1, \ldots , P_n\) for the predicates \(\rho _1, \ldots , \rho _n\), the teacher can check whether \( VC (P_1, \ldots , P_n)\) is falsifiable using an SMT solver. If it is, then function extract_data (Algorithm 1 line 4) extracts new learning data as follows. If a verification condition with shape (10) and \(m = 0\) can be falsified, then we extract some values \(\widetilde{x}\) from the model produced by the solver. This constitutes a  \((\rho (\alpha _1), \widetilde{x})\) since \(\rho (\alpha _1)\) should evaluate to \( true \) for \(\widetilde{x}\). From a counterexample model for a verification condition of the form (11), we extract a
\((\rho (\alpha _1), \widetilde{x})\) since \(\rho (\alpha _1)\) should evaluate to \( true \) for \(\widetilde{x}\). From a counterexample model for a verification condition of the form (11), we extract a  \( \big \{ \; (\rho (\alpha _1), \widetilde{x}_1), \; \ldots , \; (\rho (\alpha _m), \widetilde{x}_m) \;\big \}. \) It means that at least one of the \((\rho (\alpha _i), \widetilde{x}_i)\) should be such that \(\rho (\alpha _i)(\widetilde{x}_i)\) evaluates to \( false \). Last, an
\( \big \{ \; (\rho (\alpha _1), \widetilde{x}_1), \; \ldots , \; (\rho (\alpha _m), \widetilde{x}_m) \;\big \}. \) It means that at least one of the \((\rho (\alpha _i), \widetilde{x}_i)\) should be such that \(\rho (\alpha _i)(\widetilde{x}_i)\) evaluates to \( false \). Last, an  comes from a counterexample model for a verification condition of shape (10) with \(m > 0\) and is a pair
comes from a counterexample model for a verification condition of shape (10) with \(m > 0\) and is a pair
Similarly to the original Ice implication constraints, this constraint means that if \( \rho (\alpha _1)(\widetilde{x}_1) \wedge \ldots \wedge \rho (\alpha _m)(\widetilde{x}_m) \) evaluates to true, then so should \( \rho (\alpha _{m+1})(\widetilde{x}_{m+1}) \).
Remark 1
Note that negative examples and implication constraints in the original Ice framework are special cases of the negative constraints and implication constraints above. A negative example of the original Ice is just a singleton set \( \{(\rho (\alpha _1), \widetilde{x}_1)\} \), and an implication constraint of Ice is a special case of the implication constraint where \(m=1\). Due to the generalization of learning data, negative constraints also contain unclassified data (unless they are singletons).
3.2 Learner
We now describe the learning part of our approach, which is an adaptation of the decision tree construction procedure from the original Ice framework [12]. The main difference is that the unclassified data can also contain values from negative constraints, as explained in Remark 1. This impacts decision tree construction as we now need to make sure the negative constraints are respected, in addition to checking that the implication constraints hold. Also, we adapted the qualifier selection heuristic (discussed in Sect. 3.3) to fit our context.
The learner first prepares a finite set of atomic formulas called qualifiers, and then tries to find solutions for Horn clauses as Boolean combinations of qualifiers, by running Algorithm 2. We first explain Algorithm 2; we discuss how the qualifiers are obtained in Sect. 3.4.
Algorithm 2 first classifies data—pairs of the form \((\rho ,\widetilde{x})\) — to \( true \), \( false \), and \( unknown \). It then calls build_tree (Algorithm 3) for each unknown predicate \(\rho \), to construct a decision tree that encodes a candidate solution for \(\rho \). A  \(T\) is defined by \( T:= Node (q, T_+, T_-) \;|\; Leaf (b) \) where b is a boolean. The formula it corresponds to is given by function f, defined inductively by
\(T\) is defined by \( T:= Node (q, T_+, T_-) \;|\; Leaf (b) \) where b is a boolean. The formula it corresponds to is given by function f, defined inductively by


Algorithm 3 shows the decision tree construction process for a given \(\rho \in \Pi \). It chooses qualifiers splitting the learning data until there is no negative (positive) data left and the unclassified data can be classified as positive (negative). The main difference with the tree construction from the original Ice framework is that the classification checks now take into account the negative constraints introduced earlier. Qualifier selection is discussed separately in Sect. 3.3.
Function \( \texttt {can\_be\_pos} \) checks whether all the unclassified data can be classified as positive. This consists in making sure that negative and implication constraints are verified or contain unclassified data—meaning future choices are able to (and will) verify the constraints. Given unclassified data U, constraint sets \(\mathcal {N}\) and \(\mathcal {I}\), and classifier mapping class, \( \texttt {can\_be\_pos} \) checks that the following conditions hold for every \(u \in U\):

where \( \texttt {class} (n) \simeq b\) means that \( \texttt {class} (n)\) is \( unknown \) or equal to b. Conversely, function \( \texttt {can\_be\_neg} \) checks that all the unclassified data can be classified as negative:

While we did not specify the order in which the trees are constructed (Algorithm 2 line 8), it can impact performance greatly because the classification choices influence later runs of build_tree. Hence, it is better to treat the elements of \(\Pi \) that have the least amount of unclassified data first. Doing so directs the choices of the qualifier q (Algorithm 3 line 8, discussed below) on as much classified data as possible. The data is then split (lines 9 and 10) using q: more classified data thus means more informed splits, leading to more relevant classifications of unclassified data in the terminal cases of the decision tree construction.
3.3 Qualifier Selection in Algorithm 3
We now discuss how to choose qualifier \(q\in Q\) on line 8 in Algorithm 3. The choice of the qualifier q used to split the learning data \(D = (P, N, U)\) in \(D_q = (P_q, N_q, U_q)\) and \(D_{\lnot q} = (P_{\lnot q}, N_{\lnot q}, U_{\lnot q})\) is crucial. In [12], the authors introduce two heuristics based on the notion of  \(\varepsilon \):
\(\varepsilon \):
which yields a value between 0 and 1. This entropy rates the ratio of positive and negative examples: it gets close to 1 when |P| and |N| are close. A small entropy is preferred as it indicates that the data contains significantly more of one than the other. The  \(\gamma \) of a split is
\(\gamma \) of a split is
where \(\lfloor D = (P, N, U) \rceil = |P| + |N|\). A high information gain means q separates the positive examples from the negative ones. Note that the information gain ignores unclassified data, a shortcoming the Ice framework [12] addresses by proposing two qualifier selection heuristics. The first subtracts a penalty to the information gain. It penalizes qualifiers separating data coming from the same implication constraint—called  . The second heuristic changes the definition of entropy by introducing a function approximating the probability that a non-classified example will eventually be classified as positive. We present here our adaptation of this second heuristic, as it is much more natural to transfer to our use-case.
. The second heuristic changes the definition of entropy by introducing a function approximating the probability that a non-classified example will eventually be classified as positive. We present here our adaptation of this second heuristic, as it is much more natural to transfer to our use-case.
The idea is to create a function \( Pr \) that approximates the probability that some values from the projected learning data \(D = (P, N, U)\) end up classified as positive. More precisely, \( Pr (v)\) approximates the ratio between the number of legal (constraint-abiding) classifications in which v is classified positively and the number of all legal classifications. Computing this ratio for the whole data is impractical: it falls in the counting problems class and it is \(\#P\)-complete [2]. The approximation we propose uses the following notion of  :
:
The three terms appearing in function \( Degree \) are based on the following remarks. Let v be some value in the projected learning data. If \((\widetilde{x}, v) \in \mathcal {I}\), there is only one classification for \(\widetilde{x}\) to force v to be true: the classification where all the elements of \(\widetilde{x}\) are classified positively. More elements in \(\widetilde{x}\) generally mean more legal classifications where one of them is false and v need not be true: \( Pr (v)\) should be higher if \(\widetilde{x}\) has few elements. If v appears in the antecedents of a constraint \((\widetilde{x}, y)\), then \( Pr (v)\) should be lower. Still, if \(\widetilde{x}\) has many elements it means v is less constrained. There are statistically more classifications in which v is true without triggering the implication, and thus more legal classifications where v is true. Last, if v appears in a negative constraint \(\widetilde{x}\) then it is less likely to be true. Again, a bigger \(\widetilde{x}\) means v is less constrained, since there are statistically more legal classifications where v is true.
Our \( Pr \) function compresses the degree between 0 and 1, and we define a new multi-predicate-friendly entropy function \(\varepsilon \) to compute the information gain:

Note that it can happen that none of the qualifiers can split the data, i.e. there is no qualifier left or they all have an information gain of 0. In this case we synthesize qualifiers that we know will split the data as described in the next subsection.
3.4 Mining and Synthesizing Qualifiers
We now discuss how to prepare the set \(Q\) of qualifiers used in Algorithm 3. The learner in both the original Ice approach and our modified version spend a lot of time evaluating qualifiers. Having too many of them slows down the learning process considerably, while not considering enough of them reduces the expressiveness of the candidates. The compromise we propose is to (i) mine for (few) qualifiers from the clauses, and (ii) synthesize (possibly many) qualifiers when needed, driven by the data we need to split.
To mine for qualifiers, for every clause C and for every predicate application of the form \(\rho (\widetilde{v})\) in C, we add every boolean atom a in C as a qualifier for \(\rho \) as long as all the free variables of a are in \(\widetilde{v}\). All the other qualifiers are synthesized during the analysis.
Based on our experience, we have chosen the following synthesis strategy. With \(v_1, \dots , v_n\) the formal inputs of \(\rho \), for all \((x_1, \dots , x_n) \in P \cup N \cup U\), we generate the set of new qualifiers
Adding these qualifiers allows to split the data on these (strict, when negated) inequalities, and encode (dis)equalities by combining them in the decision tree. Also, notice that when no qualifier can split the data we have in general small P, N and U sets, and the number of new qualifiers is quite tractable. The learning process is an iterative one where relatively few new samples are added at each step, compared to the set of all samples. Since we could split the samples from the previous iteration, it is very often the case that P, N and U contain mostly new samples. Last, our approach shares the limitation of the original Ice: it will not succeed if a particular relation between the variables is needed to conclude, but no qualifier of the right shape is ever mined for or synthesized.
4 Experimental Evaluation
Let us now briefly present our implementation before reporting on our experimental evaluation. Our implementation consists of two parts. RType is a frontend (written in OCaml) generating Horn clauses from programs written in a subset of OCaml as discussed in Sect. 2. It relies on an external Horn clause solver for actually solving the clauses, and post-processes the solution (if any) to yield refinement types for the original program. HoIceFootnote 1, written in Rust [1], is one such Horn clause solver and implements the modified Ice framework presented in this paper. All experiments in this section use RType v1.0 and HoIce v1.0. Under the hood, HoIce relies on the Z3Footnote 2 SMT solver [21] for satisfiability checks. In the following experiments, RType uses HoIce as the Horn clause solver.
Note that the input OCaml programs are not annotated: the Horn clauses correspond to the verification conditions encoding the fact that the input program cannot falsify its assertion(s). RType supports a subset of OCaml including (mutually) recursive functions and integers, without algebraic data types. Our benchmark suite of 162 programsFootnote 3 includes the programs from [24, 34] in the fragment RType supports, along with programs automatically generated by the termination verification tool from [18], and 10 new benchmarks written by ourselves. We only considered programs that are safe since RType is not refutation-sound. All the experiments presented in this section ran on a machine running Ubuntu (Xeon E5-2680v3, 64 GB of RAM) with a timeout of 100 s. The number between parentheses in the keys of the graphs is the number of benchmarks solved. We begin by evaluating the optimizations discussed in Sect. 2, followed by a comparison against automated verification tools for OCaml programs. Last, we evaluate our predicate synthesis engine against other Horn-clause-level solvers.
4.1 Evaluation of the Optimizations
Figure 3a shows our evaluation of the effect analysis (EA) and clause reduction (Red) simplifications discussed in Sect. 2. It is clear that both effect analysis and Horn reduction speedup the learning process significantly. They work especially well together and can reduce drastically the number of predicates on relatively big synthesis problems, as shown on Fig. 3c.
The 11 programs that we fail to verify show inherent limitations of our approach. Two of them require an invariant of the form \(x + y \ge z\). Our current compromise for qualifier mining and synthesis (in Sect. 3.3) does not consider such qualifiers unless they appear explicitly in the program. We are currently investigating how to alter our qualifier synthesis approach to raise its expressiveness with a reasonable impact on performance. The remaining nine programs are not typable with refinement types, meaning the verification conditions generated by RType are actually unsatisfiable. An extension of the type system is required to prove these programs correct [30].
4.2 Comparison with Other OCaml Program Verifiers
The first tool we compare RType to is the higher-order program verifier MoCHi from [24] (Fig. 3b). MoCHi infers intersection types, which makes it more expressive than RType. The nine programs that MoCHi proves but RType cannot verify are the (refinement-)untypable ones discussed above. While this shows a clear advantage of intersection types over our approach in terms of expressiveness, the rest of the experiments make it clear that, when applicable, RType outperforms MoCHi on a significant part of our benchmarks.
We also evaluated our implementation against DOrder from [34, 35]. This comparison is interesting as DOrder also uses machine-learning to infer refinement types, but does not support implication constraints. DOrder compensates by conducting test runs of the program on random inputs to gather better positive data. It supports a different subset of OCaml than RType though, and after removing the programs it does not support, 124 programs are left. The results are on Fig. 3d, and show that RType overwhelmingly outperforms DOrder. This is consistent with the results reported for the original Ice framework: the benefit gained by considering implication constraints is huge.
These results show that, despite its limitations, our approach is competitive and often outperforms other state-of-the-art automated verification tools for OCaml programs.
4.3 Horn-Clause-Level Evaluation
Last, we compare our Horn clause solver HoIce to other solvers (Fig. 4): Spacer [16], Duality [19], Z3’s PDR [13], and Eldarica [14]. The first three are implemented in Z3 (C++) while Eldarica is implemented in Scala. The benchmarks are the Horn clauses encoding the safety of the 162 programs aforementioned with additional two programs, omitted in the previous evaluation as they are unsafe.
HoIce solves the most benchmarks at 162.Footnote 4 The fastest tool overall is Z3’s Spacer which solves slightly fewer benchmarks. The two timeouts for HoIce come from the programs discussed above for which HoIce does not have the appropriate qualifiers to conclude. Because it mixes IC3 [6] with interpolation, Spacer infers the right predicates quite quickly. Thus, in our use-case, our approach is competitive with state-of-the-art Horn clause solvers in terms of speed, in addition to being more precise. We also include a comparison on the SV-COMP with Spacer on Fig. 4b. HoIce is generally competitive, but timeouts on a significant part of the benchmarks. Quite a few of them are unsatisfiable; the Ice framework is not made to be efficient at proving unstatisfiability. The rest of the timeouts require qualifiers we do not mine for nor synthesizes, showing that some more work is needed on this aspect of the approach.
In our experience, it is often the case that HoIce ’s models are significantly simpler than those of Spacer’s and PDR’s (as illustrated in [7]). Note that simpler models can be interesting if the Horn clause solver is placed inside a CEGAR loop such as the one in MoCHi [24], which is a perspective we want to explore in future work.
5 Related Work
There has been a lot of work on sampling-based approaches to program invariant discoveries during the last decade [11, 12, 25,26,27, 33,34,35]. Among others, most closely related to this paper are Garg et al.’s Ice framework [11, 12] (which this paper extends) and Zhu et al.’s refinement type inference methods [33,34,35]. To the best of our knowledge, Zhu et al. [33,34,35] were the first to apply a sampling-based approach to refinement type inference for higher-order functional programs. They did not, however, consider implication constraints. As discussed in Sect. 4, their tool fails to verify some programs due to the lack of implication constraints.
There are other automated/semi-automated methods for verification of higher-order functional programs [15, 23, 28,29,30, 32, 34, 35], based on some combinations of Horn clause solving, automated theorem proving, counterexample-guided abstraction refinement, (higher-order) model checking, etc. As a representative of such methods, we have chosen MoCHi and compared our tool with it in Sect. 4. As the experimental results indicate, our tool often outperforms MoCHi, although not always. Thus, we think that our learning-based approach is complementary to the aforementioned ones; a good integration of our approach with them is left for future work. Liquid types [23], another representative approach, is semi-automated in that users have to provide qualifiers as hints. By preparing a fixed, default set of qualifiers, Liquid types may also be used as an automated method. From that viewpoint, the main advantage of our approach is that we can infer arbitrary boolean combinations of qualifiers as refinement predicates, whereas Liquid types can infer only conjunctions of qualifiers.
6 Conclusion
In this paper we proposed an adaptation of the machine-learning-based, invariant discovery framework Ice to refinement type inference. The main challenge was that implication constraints and negative examples were ill-suited for solving Horn clauses of the form \( \rho (\widetilde{x_1}) \wedge \dots \wedge \rho (\widetilde{x_n}) \wedge \dots \,\models \, \rho (\widetilde{x}), \) which tend to appear often in our context of functional program verification because of nested recursive calls.
We addressed this issue by generalizing Ice ’s notion of implication constraint. For similar reasons, we also adapted negative examples by turning them into negative constraints. This means that, unlike the original Ice framework, our learner might have to make classification choices to respect the negative learning data. We have introduced a modified version of the Ice framework accounting for these adaptations, and have implemented it, along with optimizations based on effect analysis. Our evaluation on a representative set of programs show that it is competitive with state of the art OCaml model-checkers and Horn clause solvers.
Notes
- 1.
Hosted at https://github.com/hopv/r_type and https://github.com/hopv/hoice.
- 2.
The revision of Z3 in all the experiments is the latest at the time of writing: 5bc4c98.
- 3.
Hosted at https://github.com/hopv/benchmarks.
- 4.
This is consistent with the OCaml results: 151 sat results, 9 unsat from programs RType cannot verify, and 2 unsat from unsafe programs.
References
The Rust language. https://www.rust-lang.org/en-US/
Arora, S., Barak, B.: Computational Complexity - A Modern Approach. Cambridge University Press, Cambridge (2009)
Barrett, C.W., Sebastiani, R., Seshia, S.A., Tinelli, C.: Satisfiability modulo theories. In: Handbook of Satisfiability, Frontiers in Artificial Intelligence and Applications, vol. 185, pp. 825–885. IOS Press (2009)
Beyer, D.: Competition on software verification. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 504–524. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_38
Bjørner, N., Gurfinkel, A., McMillan, K., Rybalchenko, A.: Horn clause solvers for program verification. In: Beklemishev, L.D., Blass, A., Dershowitz, N., Finkbeiner, B., Schulte, W. (eds.) Fields of Logic and Computation II. LNCS, vol. 9300, pp. 24–51. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23534-9_2
Bradley, A.R.: SAT-based model checking without unrolling. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 70–87. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18275-4_7
Champion, A., Chiba, T., Kobayashi, N., Sato, R.: ICE-based refinement type discovery for higher-order functional programs. http://www-kb.is.s.u-tokyo.ac.jp/~koba/papers/tacas18-long.pdf. A longer version
Champion, A., Chiba, T., Kobayashi, N., Sato, R.: ICE-based refinement type discovery for higher-order functional programs. figshare. https://doi.org/10.6084/m9.figshare.5902390.v1
Champion, A., Mebsout, A., Sticksel, C., Tinelli, C.: The kind 2 model checker. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9780, pp. 510–517. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41540-6_29
Freeman, T.S., Pfenning, F.: Refinement types for ML. In: Proceedings of PLDI 1991, pp. 268–277. ACM (1991)
Garg, P., Löding, C., Madhusudan, P., Neider, D.: ICE: A robust framework for learning invariants. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 69–87. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_5
Garg, P., Neider, D., Madhusudan, P., Roth, D.: Learning invariants using decision trees and implication counterexamples. In: Proceedings of POPL 2016, pp. 499–512. ACM (2016)
Hoder, K., Bjørner, N.: Generalized property directed reachability. In: Cimatti, A., Sebastiani, R. (eds.) SAT 2012. LNCS, vol. 7317, pp. 157–171. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31612-8_13
Hojjat, H., Konečný, F., Garnier, F., Iosif, R., Kuncak, V., Rümmer, P.: A verification toolkit for numerical transition systems. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 247–251. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32759-9_21
Jhala, R., Majumdar, R., Rybalchenko, A.: HMC: verifying functional programs using abstract interpreters. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 470–485. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_38
Komuravelli, A., Gurfinkel, A., Chaki, S.: SMT-based model checking for recursive programs. Form. Methods Syst. Des. 48(3), 175–205 (2016)
Kovács, L., Voronkov, A.: Finding loop invariants for programs over arrays using a theorem prover. In: Chechik, M., Wirsing, M. (eds.) FASE 2009. LNCS, vol. 5503, pp. 470–485. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00593-0_33
Kuwahara, T., Terauchi, T., Unno, H., Kobayashi, N.: Automatic termination verification for higher-order functional programs. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 392–411. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54833-8_21
McMillan, K., Rybalchenko, A.: Computing relational fixed points using interpolation. Technical report, January 2013
Minsky, Y.: OCaml for the masses. ACM Queue 9(9), 43 (2011)
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Nielson, F., Nielson, H.R., Hankin, C.: Principles of Program Analysis. Springer, Heiedelberg (1999). https://doi.org/10.1007/978-3-662-03811-6
Rondon, P.M., Kawaguchi, M., Jhala, R.: Liquid types. In: Proceedings of PLDI 2008, pp. 159–169. ACM (2008)
Sato, R., Unno, H., Kobayashi, N.: Towards a scalable software model checker for higher-order programs. In: Proceedings of PEPM 2013, pp. 53–62. ACM (2013)
Sharma, R., Aiken, A.: From invariant checking to invariant inference using randomized search. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 88–105. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_6
Sharma, R., Gupta, S., Hariharan, B., Aiken, A., Liang, P., Nori, A.V.: A data driven approach for algebraic loop invariants. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 574–592. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_31
Sharma, R., Gupta, S., Hariharan, B., Aiken, A., Nori, A.V.: Verification as learning geometric concepts. In: Logozzo, F., Fähndrich, M. (eds.) SAS 2013. LNCS, vol. 7935, pp. 388–411. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38856-9_21
Terauchi, T.: Dependent types from counterexamples. In: Proceedings of POPL, pp. 119–130. ACM (2010)
Unno, H., Kobayashi, N.: Dependent type inference with interpolants. In: Proceedings of PPDP 2009, pp. 277–288. ACM (2009)
Unno, H., Terauchi, T., Kobayashi, N.: Automating relatively complete verification of higher-order functional programs. In: Proceedings of POPL 2013, pp. 75–86. ACM (2013)
Xi, H., Pfenning, F.: Dependent types in practical programming. In: Proceedings of POPL 1999, pp. 214–227. ACM (1999)
Zhu, H., Jagannathan, S.: Compositional and lightweight dependent type inference for ML. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 295–314. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35873-9_19
Zhu, H., Nori, A.V., Jagannathan, S.: Dependent array type inference from tests. In: D’Souza, D., Lal, A., Larsen, K.G. (eds.) VMCAI 2015. LNCS, vol. 8931, pp. 412–430. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46081-8_23
Zhu, H., Nori, A.V., Jagannathan, S.: Learning refinement types. In: Proceedings of ICFP 2015, pp. 400–411. ACM (2015)
Zhu, H., Petri, G., Jagannathan, S.: Automatically learning shape specifications. In: Proceedings of PLDI 2016, pp. 491–507. ACM (2016)
Data Availability Statement and Acknowledgments
We would like to thank He Zhu for his help in benchmarking DOrder, and the reviewers for their constructive feedback. This work was supported by JSPS KAKENHI Grant Number JP15H05706.
The benchmarks analyzed and the datasets generated during the current study are available in the figshare repository:
https://doi.org/10.6084/m9.figshare.5902390.v1
This artifact [8] contains all the benchmarks and tools, as well as scripts allowing to re-generate the data and plots discussed in Sect. 4. The only exception is DOrder, for reasons discussed in the artifact. Consistently with the TACAS 2018 Artifact Evaluation guidelines, all binaries are provided for Ubuntu 64 bits. Please refer to the README in the artifact for more information.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis> This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara> <SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Champion, A., Chiba, T., Kobayashi, N., Sato, R. (2018). ICE-Based Refinement Type Discovery for Higher-Order Functional Programs. In: Beyer, D., Huisman, M. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2018. Lecture Notes in Computer Science(), vol 10805. Springer, Cham. https://doi.org/10.1007/978-3-319-89960-2_20
Download citation
DOI: https://doi.org/10.1007/978-3-319-89960-2_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89959-6
Online ISBN: 978-3-319-89960-2
eBook Packages: Computer ScienceComputer Science (R0)