Abstract
Automated techniques for analysis and optimization of finite-precision computations have recently garnered significant interest. Most of these were, however, developed independently. As a consequence, reuse and combination of the techniques is challenging and much of the underlying building blocks have been re-implemented several times, including in our own tools. This paper presents a new framework, called Daisy, which provides in a single tool the main building blocks for accuracy analysis of floating-point and fixed-point computations which have emerged from recent related work. Together with its modular structure and optimization methods, Daisy allows developers to easily recombine, explore and develop new techniques. Daisy’s input language, a subset of Scala, and its limited dependencies make it furthermore user-friendly and portable.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Finite Precision Computations
- Roundoff Error Analysis
- Affine Arithmetic (AA)
- Fixed-point Arithmetic
- Interval Subdivision
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Floating-point or fixed-point computations are an integral part of many embedded and scientific computing applications, as are the roundoff errors they introduce. They expose an interesting tradeoff between efficiency and accuracy: the more precision we choose, the closer the results will be to the ideal real arithmetic, but the more costly the computation becomes. Unfortunately, the unintuitive and complex nature of finite-precision arithmetic makes manual optimization infeasible such that automated tool support is indispensable.
This has been recognized previously and several tools for the analysis and optimization of finite-precision computations have been developed. For instance, the tools Fluctuat [22], Rosa [14], Gappa [17], FPTaylor [41], Real2Float [31] and PRECiSA [34] automatically provide sound error bounds on floating-point (and some also on fixed-point) roundoff errors. Such a static error analysis is a pre-requisite for any optimization technique providing rigorous results, such as recent ones which choose a mixed-precision assignment [10] or an error-minimizing rewriting of the non-associative finite-precision arithmetic [15, 37].
Many of these techniques are complementary. The static analysis techniques have different strengths, weaknesses, and accuracy/efficiency tradeoffs, and optimization techniques should ideally be combined for best results [16]. However, today’s techniques are mostly developed independently, resulting in re-implementations and making re-combination and re-use challenging and time-consuming.
In this paper, we present the framework Daisy for the analysis and optimization of finite-precision computations. In contrast to previous work, we have developed Daisy from the ground up to be modular, and thus easily extensible. Daisy is being actively developed and currently already provides many of today’s state-of-the-art techniques — all in one tool. In particular, it provides dataflow- as well as optimization-based sound roundoff error analysis, support for mixed-precision and transcendental functions, rewriting optimization, interfaces to several SMT solvers and code generation in Scala and C. Daisy furthermore supports both floating-point and fixed-point arithmetic (whenever the techniques do), making it generally applicable to both scientific computing and embedded applications.
Daisy is aimed at tool developers as well as non-expert users. To make it user-friendly, we adopt the input format of Rosa, which is a real-valued functional domain-specific language in Scala. Unlike other tools today, which have custom input formats [41] or use prefix notation [12], Daisy’s input is easily human readableFootnote 1 and natural to use.
Daisy is itself written in the Scala programming language [35] and has limited and optional dependencies, making it portable and easy to install. Daisy’s main design goals are code readability and extensibility, and not necessarily performance. We demonstrate with our experiments that roundoff errors computed by Daisy are nonetheless competitive with state-of-the-art tools with reasonable running times.
Daisy has replaced Rosa for our own development, and we are happy to report that simple extensions (e.g. adding support for fused multiply-add operations) were integrated quickly by MSc students previously unfamiliar with the tool.
Contributions. We present the new tool Daisy which integrates several techniques for sound analysis and optimization of finite-precision computations:
-
static dataflow analysis for finite-precision roundoff errors [14] with mixed-precision support and additional support for the dReal SMT solver [21],
-
FPTaylor’s optimization-based absolute error analysis [41],
-
transcendental function support, for dataflow analysis following [13],
-
interval subdivision, used by Fluctuat [22] to obtain tighter error bounds,
-
rewriting optimization based on genetic programming [15].
We show in Sect. 5 that results computed by Daisy are competitive. The code is available open-source at https://github.com/malyzajko/daisy.
We focus primarily on sound verification techniques. The goal of this effort is not to develop the next even more accurate technique, rather to consolidate existing ones and to provide a solid basis for further research. Other efforts related to Daisy, which have been described elsewhere and which we do not focus on here are the generation and checking of formal certificates [4], relative error computation [26], and mixed-precision tuning [16].
2 User’s Guide: An Overview of Daisy
We first introduce Daisy’s functionality from a user’s perspective, before reviewing background in roundoff error analysis (Sect. 3) and then describing the developer’s view and the internals of Daisy (Sect. 4).
Installation. Daisy is set up with the simple build tool (sbt) [30], which takes care of installing all Scala-related dependencies fully automatically. This basic setup was successfully tested on Linux, macOS and Windows. Some of Daisy’s functionality requires additional libraries, which are also straight-forward to install: the Z3 and dReal SMT-solvers [19, 21], and the MPFR arbitrary-precision library [20]. Z3 works on all platforms, we have tested MPFR on Linux and Mac, and dReal on Linux.
Input Specification Language. The input to Daisy is a source program written in a real-valued specification language; Fig. 1 shows an example nonlinear embedded controller [15]. The specification language is not executable (as real-valued computation is infeasible), but it is a proper subset of Scala. The  data type is implemented with Scala’s dedicated support for numerical types.
data type is implemented with Scala’s dedicated support for numerical types.
Each input program consists of a number of functions which are handled by Daisy separately. In the function’s precondition (the  clause), the user provides the ranges of all input variablesFootnote 2. In addition, Daisy allows to specify an initial error (beyond only roundoff) on input variables with the notation
clause), the user provides the ranges of all input variablesFootnote 2. In addition, Daisy allows to specify an initial error (beyond only roundoff) on input variables with the notation  as well as additional (non-interval) constraints, e.g.
as well as additional (non-interval) constraints, e.g.  .
.
The function body consists of a numerical expression with possibly local variable declarations. Daisy supports arithmetic (\(+, -, *, /, \sqrt{}\)), the standard transcendental functions (\(\sin , \cos , \tan , \log , \exp \)) as well as fused multiply-add (FMA). Daisy currently does not support conditionals and loops; we discuss the challenges and possible future avenues in Sect. 6. The (optional) postcondition in the  clause specifies the result’s required accuracy in terms of worst-case absolute roundoff error. For our controller, this information may be for instance determined from the specification of the system’s sensors or the analysis of the controller’s stability [32].
clause specifies the result’s required accuracy in terms of worst-case absolute roundoff error. For our controller, this information may be for instance determined from the specification of the system’s sensors or the analysis of the controller’s stability [32].
Main Functionality. The main mode of interaction with Daisy is through a command-line interface. Here we review Daisy’s main features through the most commonly used command-line options. Brackets denote a choice and curly braces optional parameters. For more options and more fine-grained settings, run  .
.
The main feature of Daisy is the analysis of finite-precision roundoff errors. For this, Daisy provides several methods:

Daisy supports forward dataflow analysis (as implemented in Rosa, Fluctuat and Gappa) and an optimization-based analysis (as implemented in FPTaylor and Real2Float). These methods compute absolute error bounds, and whenever a relative error can be computed, it is also reported. Daisy also supports a dedicated relative error computation [26] which is often more accurate, but also more expensive. All methods can be combined with interval subdivision, which can provide tighter error bounds at the expense of larger running times. We explain these analyses in more detail in Sect. 3.
Accuracy and correspondingly cost of both dataflow and optimization-based analysis can be adjusted by choosing the method which is used to bound ranges:

With the  option, the user can select between currently two SMT solvers, which have to be installed separately. For dataflow analysis, one can also select the method for bounding errors:
option, the user can select between currently two SMT solvers, which have to be installed separately. For dataflow analysis, one can also select the method for bounding errors:  .
.
Daisy performs roundoff error analysis by default w.r.t. to uniform double floating-point precision, but it also supports various other floating-point and fixed-point precisions:

Mixed-precision, i.e. choosing different precisions for different variables, is supported by providing a mapping from variables to precisions in a separate file ( ).
).
Finite-precision arithmetic is not associative, i.e. different rewritings, even though they are equivalent under a real-valued semantics, will exhibit different roundoff errors. The  optimization [15] uses genetic search to find a rewriting for which it can show the smallest roundoff error.
optimization [15] uses genetic search to find a rewriting for which it can show the smallest roundoff error.
Daisy prints the analysis result to the terminal. If a postcondition is specified, but the computed error does not satisfy it, Daisy also prints a warning. Optionally, the user can also choose to generate executable code ( ) in Scala or C, which is especially useful for fixed-point arithmetic, as Daisy’s code generator includes all necessary bit shifts.
) in Scala or C, which is especially useful for fixed-point arithmetic, as Daisy’s code generator includes all necessary bit shifts.
Static analysis computes a sound over-approximation of roundoff errors, but an under-approximation can also be useful, e.g. to estimate how big the over-approximation of static analysis is. This is provided by the  analysis in Daisy which runs a program in the finite precision of interest and a higher-precision version side-by-side. For this, the MPFR library is required.
analysis in Daisy which runs a program in the finite precision of interest and a higher-precision version side-by-side. For this, the MPFR library is required.
Online Interface. We also provide an online interface for Daisy, which allows one to quickly try it out, although it does not yet support all the options: daisy.mpi-sws.org, see the screenshot in Fig. 2.
3 Theoretical Foundations
Before describing the inner architecture of Daisy, we review necessary background on finite-precision arithmetic and static analysis of their roundoff errors.
Floating-Point Arithmetic. One of the most commonly used finite-precision representations is floating-point arithmetic, which is standardized by IEEE754 [24]. The standard defines several precisions as well as rounding operators; here we will consider the most commonly used ones, i.e. single and double precision with operations in rounding-to-nearest mode. Then, arithmetic operations satisfy the following abstraction:
where \(\circ \in {+, -, *, /}\) and \(\circ _{fl}\) denotes the respective floating-point version. Square root follows similarly, and unary minus does not introduce roundoff errors. The machine epsilon \(\epsilon _m\) bounds the maximum relative error for so-called normal values. Roundoff errors of subnormal values, which provide gradual underflow, are expressed as an absolute error, bounded by \(\delta _m\). \(\epsilon _m = 2^{-24}, \delta _m = 2^{-150}\) and \(\epsilon _m = 2^{-53}, \delta _m = 2^{-1075}\) for single and double precision, respectively.
Higher precisions are usually implemented in software libraries on top of standard double floating-point precision [2]. Daisy supports quad and quad-double precision, where we assume \(\epsilon _m = 2^{-113}\) and \(\epsilon _m = 2^{-211}\), respectively. Depending on the library, \(\delta _m\) may or may not be defined, and Daisy can be adjusted accordingly.
Static analyses usually use this abstraction of floating-point arithmetic, as bit-precise reasoning does not scale, and furthermore is unsuitable for computing roundoff errors w.r.t. continuous real-valued semantics (note that Eq. 1 is also real-valued). The abstraction furthermore only holds in the absence of not-a-number special values (NaN) and infinities. Daisy’s static analysis detects such cases automatically and reports them as errors.
Fixed-Point Arithmetic. Floating-point arithmetic requires dedicated support, either in hardware or software, and depending on the application this support may be too costly. An alternative is fixed-point arithmetic which can be implemented with integers only, but which in return requires that the radix point alignments are precomputed at compile time. While no standard exists, fixed-point values are usually represented by bit vectors with an integer and a fractional part, separated by an implicit radix point. At runtime, the alignments are then performed by bit-shift operations. These shift operations can also be handled by special language extensions for fixed-point arithmetic [25]. For more details see [1], whose fixed-point semantics we follow. We use truncation as the rounding mode for arithmetic operations. The absolute roundoff error at each operation is determined by the fixed-point format, i.e. the (implicit) number of fractional bits available, which in turn can be computed from the range of possible values at that operation.
Range Arithmetic. The magnitude of floating-point and fixed-point roundoff errors depends on the magnitudes of possible values. Thus, in order to accurately bound roundoff errors, any static analysis first needs to be able to bound the ranges of all (intermediate) expressions accurately, i.e. tightly. Different range arithmetics have been developed and each has a different accuracy/efficiency tradeoff. Daisy supports interval [33] and affine arithmetic [18] as well as a more accurate, but also more expensive, combination of interval arithmetic and SMT [14].
Interval arithmetic (IA) [33] is an efficient choice for range estimation, which computes a bounding interval for each basic operation \(\circ \in \lbrace +, -, *, / \rbrace \) as
and analogously for square root. Interval arithmetic cannot track correlations between variables (e.g. \(x - x \ne [0, 0]\)), and thus can introduce significant over-approximations of the true ranges, especially when the computations are longer.
Affine arithmetic (AA) [18] tracks linear correlations by representing possible values of variables as affine forms:
where \(x_0\) denotes the central value (of the represented interval) and each noise term \(x_i\epsilon _i\) denotes a deviation from this central value. The range represented by an affine form is computed as \([\hat{x}] = [x_0 - rad(\hat{x}), x_0\,+\,rad(\hat{x})]\), \(rad(\hat{x}) = \sum _{i=1}^n |x_i|\). Linear operations are performed term-wise and are computed exactly, whereas nonlinear ones need to be approximated and thus introduce over-approximations. Overall, AA can produce tighter ranges in practice (though not universally). In particular, AA is often beneficial when the individual noise terms (\(x_i\)’s) are small, e.g. when they track roundoff errors.
The over-approximation due to nonlinear arithmetic can be mitigated [14] by refining ranges computed by IA with a binary search in combination with a SMT solver which supports nonlinear arithmetic such as Z3 [19] or dReal [21].
Static Analysis for Roundoff Error Estimation. The worst-case absolute roundoff error that most static analyses approximate is:
where [a, b] is the range for x given in the precondition, and f and x are a mathematical real-valued arithmetic expression and variable, respectively, and \(\tilde{f}\) and \(\tilde{x}\) their finite-precision counterparts. This definition extends to multivariate f component-wise.
An automated and general estimation of relative errors (\(\frac{|f(x) - \tilde{f}(\tilde{x}) |}{|f(x)|}\)), though it may be more desirable, presents a significant challenge today. For instance, when the range of f(x) includes zero, relative errors are not well defined and this is often the case in practice. For a more thorough discussion, we refer the reader to [26]; the technique is also implemented within Daisy.
For bounding absolute errors, two main approaches exist today, which we review in the following.
Dataflow Analysis. One may think that just evaluating a program in interval arithmetic and interpreting the width of the resulting interval as the error bound would be sufficient. While this is certainly a sound approach, it computes too pessimistic error bounds in general. This is especially true if we consider relatively large ranges on inputs; we cannot distinguish which part of the interval width is due to the input interval or due to accumulated roundoff errors.
Thus, dataflow analysis computes roundoff error bounds in two steps, recursively over the abstract syntax tree (AST) of the arithmetic expression:
-
1.
range analysis computes sound range bounds (for real semantics),
-
2.
error analysis propagates errors from subexpressions and computes the new worst-case roundoffs using the previously computed ranges.
In practice, these two steps can be performed in a single pass over the AST. A side effect of this separation is that it provides us with a modular approach: we can choose different range arithmetics with different accuracy/efficiency tradeoffs for ranges and errors (and possibly for different parts of a program).
The main challenge of dataflow analysis is to minimize over-approximations due to nonlinear arithmetic (linear arithmetic can be handled well with AA). Previous tools chose different strategies. For instance, Rosa [14] employs the combination of interval arithmetic with a non-linear SMT-solver, which we described earlier. Fluctuat [22], which uses AA for both bounding the ranges as well as the errors, uses interval subdivision. In Fluctuat, the user can designate up to two variables whose input ranges will be subdivided into intervals of equal width. The analysis is performed separately for each and the overall error is then the maximum error over all subintervals. Interval subdivision increases the runtime of the analysis, especially for multivariate functions, and the choice of which variables to subdivide and by how much is usually not straight-forward.
Optimization-based Analysis. FPTaylor [41], Real2Float [31] and PRECiSA [34], unlike Daisy, Rosa, Gappa and Fluctuat, formulate the roundoff error bounds computation as an optimization problem, where the absolute error expression from Eq. 2 is to be maximized, subject to interval constraints on its parameters. Due to the discrete nature of floating-point arithmetic, FPTaylor optimizes the continuous, real-valued abstraction from Eq. 1. However, this expression is still too complex and features too many variables for optimization procedures in practice.
FPTaylor introduces the Symbolic Taylor approach, where the objective function is simplified using a first order Taylor approximation with respect to e and d (the variables representing roundoff errors at each arithmetic operation). To solve the optimization problem, FPTaylor uses a rigorous branch-and-bound procedure.
4 Developer’s Guide: Daisy’s Internals
This section provides more details on Daisy’s architecture and explains some of our design decisions. Daisy is written in the Scala programming language which provides a strong type system as well as a large collection of (parallel) libraries. While Scala supports both imperative and functional programming styles, we have written Daisy functionally as much as possible, which we found to be beneficial to ensuring correctness and readability of code.
4.1 Input Language and Frontend
Daisy’s input language is implemented as a domain-specific language in Scala, and Daisy’s frontend calls the Scala compiler which performs parsing and type-checking. While designing our own simple input format and parser would be certainly more efficient in terms of Daisy’s running time (and could be done in the future), we have deliberately chosen not to do this. An existing programming language provides clear semantics and feels natural to users. Using the Scala compiler furthermore helps to ensure that Daisy parses the program correctly, for instance that it indeed conforms e.g. to Scala’s typing rules. Furthermore, extending the input language is usually straight-forward.
The other major design decision was to make the input program real-valued. This explicitly specifies the baseline against which roundoff errors should be computed, but it also makes it easy for the user to explore different options. For instance, changing the precision only requires changing a flag, whereas a finite-precision input program (like FPTaylor’s or Fluctuat’s) requires editing the source code.
Mixed-precision is also supported respecting Scala semantics and is thus transparent. The user may annotate variables, including local ones, with different precisions. To specify the precision of every individual operation, the program can be transformed into three-address form (Daisy can do this automatically), and then each arithmetic operation can be annotated via the corresponding variable.
Daisy currently does not support data structures such as arrays or lists in its input language, mainly because the static analysis of these is largely orthogonal to the analysis of the actual computation and we believe that standard strategies like unrolling computations over array elements or abstracting the array as a single variable can be employed.
4.2 Modular Architecture
Daisy is built up in a modular way by implementing its functionality in phases, which can be combined. See the overview in Fig. 3. Each phase takes as input and returns as output a  and a
and a  , and can modify both. For instance, rewriting transforms the program and roundoff error analysis adds the analysis information to the context. This information is then re-used by later phases, for instance the analysis information is used to generate fixed-point arithmetic programs in the code generation phase. This modularity allows, for instance, the rewriting optimization phase to be combined with any other roundoff error analysis.
, and can modify both. For instance, rewriting transforms the program and roundoff error analysis adds the analysis information to the context. This information is then re-used by later phases, for instance the analysis information is used to generate fixed-point arithmetic programs in the code generation phase. This modularity allows, for instance, the rewriting optimization phase to be combined with any other roundoff error analysis.
In addition to the modular architecture, Daisy’s main functionality is provided as a set of library tools, which allows for further reuse across different phases. It could also be used as a separate library in other tools. Here we highlight the main functionality provided:
-
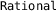 provides an implementation of rational numbers based on Java’s BigInteger library. Rationals are used throughout Daisy for computations in order to avoid internal roundoff errors which could affect soundness.
provides an implementation of rational numbers based on Java’s BigInteger library. Rationals are used throughout Daisy for computations in order to avoid internal roundoff errors which could affect soundness. -
 is an interface to GNU’s MPFR arbitrary precision library [20].
is an interface to GNU’s MPFR arbitrary precision library [20]. -
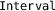 and
and  provide implementations of interval and affine arithmetic. Daisy uses no external libraries for these in order to facilitate extensions and integration.
provide implementations of interval and affine arithmetic. Daisy uses no external libraries for these in order to facilitate extensions and integration. -
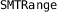 implements Rosa’s combination of interval arithmetic with an SMT solver [14] for improved range bounds. Daisy uses the scala-smtlib libraryFootnote 3 to interface with the Z3 and dReal SMT solvers. Other solvers can be added with little effort, provided they support the SMT-LIB standard [3].
implements Rosa’s combination of interval arithmetic with an SMT solver [14] for improved range bounds. Daisy uses the scala-smtlib libraryFootnote 3 to interface with the Z3 and dReal SMT solvers. Other solvers can be added with little effort, provided they support the SMT-LIB standard [3]. -
 implement dataflow roundoff error analysis. The analysis is parametric in the range method used, and due to its implementation as a library function can be easily used in different contexts.
implement dataflow roundoff error analysis. The analysis is parametric in the range method used, and due to its implementation as a library function can be easily used in different contexts. -
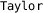 provides methods for computing and simplifying partial derivatives.
provides methods for computing and simplifying partial derivatives. -
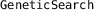 provides a generic implementation of a (simple) genetic search, which is currently used for the rewriting optimization.
provides a generic implementation of a (simple) genetic search, which is currently used for the rewriting optimization.
The fixed-point precision class in Daisy supports any bitlength (i.e. only the frontend has a limited selection) and floating-point types can be straight-forwardly added by specifying the corresponding machine epsilon and representable range.
4.3 Implementation Details
Here we provide details about Daisy’s implementation of previous techniques. The dataflow analysis approach, e.g. in Rosa, only considered arithmetic operations without transcendental functions. Daisy extends this support by implementing these operations in interval and affine arithmetic. The former is straight-forward, whereas for AA Daisy computes sound linear approximations of the functions, following [13] which used this approach in a dynamic analysis. Following most libraries of mathematical functions, we assume that transcendental functions are rounded correctly to one unit in the last place. Since internal computations are performed with rational types, the operations for transcendental functions are approximated with the corresponding outward or upwards rounding to ensure soundness. To support the combination of interval arithmetic and SMT, we integrate the dReal solver in Daisy, which provides support for transcendental functions. Although dReal is only \(\delta \)-complete, this does not affect Daisy’s soundness as the algorithm relies on UNSAT answers, which are always sound in dReal.
Interval subdivision can be an effective tool to reduce overapproximations in static analysis results, which is why Daisy offers it for all its analyses. Daisy subdivides every input variable range into a fixed number of subintervals (the number can be controlled by the user) and takes the cartesian product. The analysis is then performed separately for each set of subintervals. This clearly increases the running time, but is also trivially parallelizable.
Daisy also includes an initial implementation of FPTaylor’s optimization-based static analysis. The major difference is that Daisy does not use a branch-and-bound algorithm for solving the optimization problem, but relies on the already existing range analyses. We would like to include a proper optimization solver in the future; currently custom interfaces have been an obstacle.
5 Experimental Evaluation
We have experimentally evaluated Daisy’s roundoff error analysis on a number of finite-precision verification benchmarks taken from related work [15, 16, 31, 41]. Benchmarks marked with a superscript \(^T\) contain transcendental functions. The goal of this evaluation is twofold. First, Daisy should be able to compute reasonably tight error bounds in a reasonable amount of time to be useful. Secondly, exploiting the fact that Daisy implements several different analysis methods within a single tool allows us to provide a direct comparison of their tradeoffs.
We compare Daisy with FPTaylor, which has been shown previously to provide tight error bounds [41]. It furthermore implements the optimization-based approach, which we re-implement in Daisy (in an albeit preliminary version). We do not compare against tools which employ dataflow static analysis, as Daisy’s analyses essentially subsume those.
Comparison with FPTaylor. We first compare roundoff errors computed by Daisy with different methods against errors computed by FPTaylor (version from 20 Sept 2017) in Table 1. All errors are computed for uniform double floating-point precision, assuming roundoff errors on inputs. We abbreviate the settings used in Daisy by e.g. IA - AA, where IA and AA specify the methods used for computing the ranges and errors, respectively. ‘sub’ means subdivision, ‘rw’ rewriting and ‘opt’ denotes the optimization-based approach. We underline the lowest roundoff errors computed among the different Daisy settings (without rewriting). The column marked ‘%’ denotes the factor by which the lowest error computed by Daisy differs from FPTaylor’s computed error.
FPTaylor supports different backend solvers; we have performed experiments with the internal branch-and-bound and the Gelpia solver, but observed only minor differences. We thus report results for the Gelpia solver. We furthermore chose the lowest verbosity level in both FPTaylor and Daisy to reduce the execution time. Table 1 also shows an underapproximation of roundoff errors computed using Daisy’s dynamic analysis which provides an idea of the tightness of roundoff errors.
Table 2 shows the corresponding execution times of the tools. Execution times are average real time measured by the bash time command. We have performed all experiments on a Linux desktop computer with an Intel Xeon 3.30 GHz processor and 32 GB RAM, with Scala version 2.11.11.
The focus when implementing Daisy was to provide a solid framework with modular and clear code, not to improve roundoff error bounds. Nonetheless, Daisy’s roundoff error bounds are mostly competitive with FPTaylor’s, with the notable exception of the jetEngine benchmark (additionally, interval arithmetic fails to bound the divisor away from zero).
Overall we observe that using an SMT solver for tightening ranges is helpful, but interval subdivision is preferable. Furthermore, using affine arithmetic for bounding errors is preferable over interval arithmetic. Finally, rewriting can often improve roundoff error bounds significantly.
Our optimization-based analysis is not yet quite as good as FPTaylor’s, but acceptable for a first re-implementation. We suspect the difference is mainly due to the fact that Daisy does not use a dedicated optimization procedure, which we hope to include in the future.
Execution times of FPTaylor and Daisy are comparable. It should be noted that the times are end-to-end, and in particular for Daisy this includes the Scala compiler frontend, which takes a constant 1.3 s (irrespective of input). Clearly, with a hand-written parser this could be improved, but we do not consider this as critical. Furthermore, Daisy performs overflow checks at every intermediate subexpression; it is unclear whether FPTaylor does this as well.
Table 1 seems to suggest that one should use FPTaylor’s optimization-based approach for bounding roundoff errors. We include dataflow analysis in Daisy nonetheless for several reasons. First, dataflow analysis computes overflow checks without extra cost. Secondly, the optimization-based approach is only applicable when errors can be specified as relative errors, which is not the case for instance for fixed-point arithmetic, which is important for many embedded applications.
Fixed-Point vs Floating-Point. In Table 3 we use Daisy to compare roundoff errors for 32-bit fixed-point and 32-bit floating-point arithmetic, with and without rewriting. For this comparison, we use the dataflow analysis, as the optimization-based approach is not applicable to fixed-point arithmetic. Not surprisingly, the results confirm that (at least for our examples with limited ranges) fixed-point arithmetic can provide better accuracy for the same bitlength, and furthermore that rewriting can improve the error bounds further.
6 Related Work
We have already mentioned the directly related techniques and tools Gappa, Fluctuat, Rosa, FPTaylor, Real2Float and PRECiSA throughout the paper. Except for Fluctuat and Rosa, these tools also provide either a proof script or a certificate for the correctness (of certain parts) of the analysis, which can be independently checked in a theorem prover. Certificate generation and checking for Daisy has been described in a separate paper [4].
Daisy currently handles straight-line arithmetic expressions, i.e. it does not handle conditionals and loops. Abstract interpretation of floating-point programs handles conditionals by joins, however, for roundoff error analysis this approach is not sufficient. The real-valued and finite-precision computations can diverge and a simple join does not capture this ‘discontinuity error’. Programs with loops are challenging, because roundoff errors in general grow with each loop iteration and thus a nontrivial fixpoint does not exist in general (loop unrolling can however be applied). Widening operators compute non-trivial bounds only for very special cases where roundoff errors decrease with each loop iteration. These challenges have been (partially) addressed [16, 23], and we plan to include those techniques in Daisy in the future. Nonetheless, conditionals and loops remain open problems.
Sound techniques have also been applied for both the range and the error analysis for bitwidth optimization of fixed-point arithmetic, for instance in [28, 29, 36, 38] and Lee et. al. [29] provide a nice overview of static and dynamic techniques.
Dynamic analysis can be used to find inputs which cause large roundoff errors, e.g. running a higher-precision floating-point program alongside the original one [5] or with a guided search to find inputs which maximize errors [11]. In comparison, Daisy’s dynamic analysis is a straight-forward approach, and some more advanced techniques could be integrated as well.
Optimization techniques targeting accuracy of floating-point computations, like rewriting [37] or mixed-precision tuning [10] include some form of roundoff error analysis, and any of the above approaches, including Daisy’s, can be potentially used as a building block.
More broadly related are abstract interpretation-based static analyses, which are sound w.r.t. floating-point arithmetic [6, 9, 27]. These techniques can prove the absence of runtime errors, such as division-by-zero, but cannot quantify roundoff errors. Floating-point arithmetic has also been formalized in theorem provers and entire numerical programs have been proven correct and accurate within these [7, 39]. Most of these formal verification efforts are, however, to a large part manual. Floating-point arithmetic has also been formalized in an SMT-lib [40] theory and SMT solvers exist which include floating-point decision procedures [8, 19]. These are, however, not suitable for roundoff error quantification, as a combination with the theory of reals would be necessary which does not exist today.
7 Conclusion
We have presented the framework Daisy which integrates several state-of-the-art techniques for the analysis and optimization of finite-precision programs. It is actively being developed, improved and extended and we believe that it can serve as a useful building block in future optimization techniques.
Notes
- 1.
We realize a preference for prefix or infix notation is personal.
- 2.
The magnitude of roundoff errors depends on the magnitude of all intermediate expressions; in general, with unbounded ranges, roundoff errors are also unbounded.
- 3.
References
Anta, A., Majumdar, R., Saha, I., Tabuada, P.: Automatic verification of control system implementations. In: EMSOFT (2010)
Bailey, D.H., Hida, Y., Li, X.S., Thompson, B.: C++/Fortran-90 double-double and quad-double package. Technical report (2015)
Barrett, C., Fontaine, P., Tinelli, C.: The SMT-LIB Standard: Version 2.6. Technical report, University of Iowa (2017). www.SMT-LIB.org
Becker, H., Darulova, E., Myreen, M.O.: A verified certificate checker for floating-point error bounds. Technical report (2017). arXiv:1707.02115
Benz, F., Hildebrandt, A., Hack, S.: A dynamic program analysis to find floating-point accuracy problems. In: PLDI (2012)
Blanchet, B., Cousot, P., Cousot, R., Feret, J., Mauborgne, L., Miné, A., Monniaux, D., Rival, X.: A static analyzer for large safety-critical software. In: PLDI (2003)
Boldo, S., Clément, F., Filliâtre, J.-C., Mayero, M., Melquiond, G., Weis, P.: Wave equation numerical resolution: a comprehensive mechanized proof of a C program. J. Autom. Reason. 50(4), 423–456 (2013)
Brain, M., D’Silva, V., Griggio, A., Haller, L., Kroening, D.: Deciding floating-point logic with abstract conflict driven clause learning. Form. Methods Syst. Des. 45(2), 213–245 (2013)
Chen, L., Miné, A., Cousot, P.: A sound floating-point polyhedra abstract domain. In: Ramalingam, G. (ed.) APLAS 2008. LNCS, vol. 5356, pp. 3–18. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89330-1_2
Chiang, W.-F., Gopalakrishnan, G., Rakamaric, Z., Briggs, I., Baranowski, M.S., Solovyev, A.: Rigorous floating-point mixed precision tuning. In: POPL (2017)
Chiang, W.-F., Gopalakrishnan, G., Rakamaric, Z., Solovyev, A.: Efficient search for inputs causing high floating-point errors. In: PPoPP (2014)
Damouche, N., Martel, M., Panchekha, P., Qiu, C., Sanchez-Stern, A., Tatlock, Z.: Toward a standard benchmark format and suite for floating-point analysis. In: Bogomolov, S., Martel, M., Prabhakar, P. (eds.) NSV 2016. LNCS, vol. 10152, pp. 63–77. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-54292-8_6
Darulova, E., Kuncak, V.: Trustworthy numerical computation in scala. In: OOPSLA (2011)
Darulova, E., Kuncak, V.: Sound compilation of reals. In: POPL (2014)
Darulova, E., Kuncak, V., Majumdar, R., Saha, I.: Synthesis of fixed-point programs. In: EMSOFT (2013)
Darulova, E., Sharma, S., Horn, E.: Sound mixed-precision optimization with rewriting. Technical report (2017). arXiv:1707.02118
Daumas, M., Melquiond, G.: Certification of bounds on expressions involving rounded operators. ACM Trans. Math. Softw. 37(1), 2:1–2:20 (2010)
de Figueiredo, L.H., Stolfi, J.: Affine arithmetic: concepts and applications. Numer. Algorithms 37(1), 147–158 (2004)
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Fousse, L., Hanrot, G., Lefèvre, V., Pélissier, P., Zimmermann, P.: MPFR: a multiple-precision binary floating-point library with correct rounding. ACM Trans. Math. Softw. 33(2) (2007)
Gao, S., Kong, S., Clarke, E.M.: dReal: an SMT solver for nonlinear theories over the reals. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 208–214. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_14
Goubault, E., Putot, S.: Static analysis of finite precision computations. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 232–247. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18275-4_17
Goubault, E., Putot, S.: Robustness analysis of finite precision implementations. In: Shan, C. (ed.) APLAS 2013. LNCS, vol. 8301, pp. 50–57. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03542-0_4
Computer Society IEEE. IEEE Standard for Floating-Point Arithmetic. IEEE Std 754–2008 (2008)
ISO/IEC. Programming languages — C — Extensions to support embedded processors. Technical report ISO/IEC TR 18037 (2008)
Izycheva, A., Darulova, E.: On sound relative error bounds for floating-point arithmetic. In: FMCAD (2017)
Jeannet, B., Miné, A.: Apron: a library of numerical abstract domains for static analysis. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 661–667. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02658-4_52
Kinsman, A.B., Nicolici, N.: Finite precision bit-width allocation using SAT-modulo theory. In: DATE (2009)
Lee, D.U., Gaffar, A.A., Cheung, R.C.C., Mencer, O., Luk, W., Constantinides, G.A.: Accuracy-guaranteed bit-width optimization. Trans. Comp.-Aided Des. Integ. Cir. Sys. 25(10), 1990–2000 (2006)
Lightbend. sbt - The interactive build tool (2017). http://www.scala-sbt.org/
Magron, V., Constantinides, G., Donaldson, A.: Certified roundoff error bounds using semidefinite programming. ACM Trans. Math. Softw. 43(4) (2017)
Majumdar, R., Saha, I., Zamani, M.: Synthesis of minimal-error control software. In: EMSOFT (2012)
Moore, R.E.: Interval Analysis. Prentice-Hall, Englewood Cliffs (1966)
Moscato, M., Titolo, L., Dutle, A., Muñoz, C.A.: Automatic estimation of verified floating-point round-off errors via static analysis. In: Tonetta, S., Schoitsch, E., Bitsch, F. (eds.) SAFECOMP 2017. LNCS, vol. 10488, pp. 213–229. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66266-4_14
Odersky, M., Spoon, L., Venners, B.: Programming in Scala: A Comprehensive Step-by-Step Guide. Artima Incorporation (2008)
Osborne, W.G., Cheung, R.C.C., Coutinho, J., Luk, W., Mencer, O.: Automatic accuracy-guaranteed bit-width optimization for fixed and floating-point systems. In: Field Programmable Logic and Applications, pp. 617–620 (2007)
Panchekha, P., Sanchez-Stern, A., Wilcox, J.R., Tatlock, Z.: Automatically improving accuracy for floating point expressions. In: PLDI (2015)
Pang, Y., Radecka, K., Zilic, Z.: An efficient hybrid engine to perform range analysis and allocate integer bit-widths for arithmetic circuits. In: ASPDAC (2011)
Ramananandro, T., Mountcastle, P., Meister, B., Lethin, R.: A unified Coq framework for verifying C programs with floating-point computations. In: CPP (2016)
Rümmer, P., Wahl, T.: An SMT-LIB theory of binary floating-point arithmetic. In: SMT (2010)
Solovyev, A., Jacobsen, C., Rakamarić, Z., Gopalakrishnan, G.: Rigorous estimation of floating-point round-off errors with symbolic Taylor expansions. In: Bjørner, N., de Boer, F. (eds.) FM 2015. LNCS, vol. 9109, pp. 532–550. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19249-9_33
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis> This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara> <SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Darulova, E., Izycheva, A., Nasir, F., Ritter, F., Becker, H., Bastian, R. (2018). Daisy - Framework for Analysis and Optimization of Numerical Programs (Tool Paper). In: Beyer, D., Huisman, M. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2018. Lecture Notes in Computer Science(), vol 10805. Springer, Cham. https://doi.org/10.1007/978-3-319-89960-2_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-89960-2_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89959-6
Online ISBN: 978-3-319-89960-2
eBook Packages: Computer ScienceComputer Science (R0)








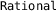 provides an implementation of rational numbers based on Java’s BigInteger library. Rationals are used throughout Daisy for computations in order to avoid internal roundoff errors which could affect soundness.
provides an implementation of rational numbers based on Java’s BigInteger library. Rationals are used throughout Daisy for computations in order to avoid internal roundoff errors which could affect soundness. is an interface to GNU’s MPFR arbitrary precision library [
is an interface to GNU’s MPFR arbitrary precision library [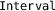 and
and  provide implementations of interval and affine arithmetic. Daisy uses no external libraries for these in order to facilitate extensions and integration.
provide implementations of interval and affine arithmetic. Daisy uses no external libraries for these in order to facilitate extensions and integration.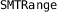 implements Rosa’s combination of interval arithmetic with an SMT solver [
implements Rosa’s combination of interval arithmetic with an SMT solver [ implement dataflow roundoff error analysis. The analysis is parametric in the range method used, and due to its implementation as a library function can be easily used in different contexts.
implement dataflow roundoff error analysis. The analysis is parametric in the range method used, and due to its implementation as a library function can be easily used in different contexts. provides methods for computing and simplifying partial derivatives.
provides methods for computing and simplifying partial derivatives. provides a generic implementation of a (simple) genetic search, which is currently used for the rewriting optimization.
provides a generic implementation of a (simple) genetic search, which is currently used for the rewriting optimization.