Keywords

1 Introduction

1.1 Freshwater Availability in the Netherlands

The Netherlands is rich in water. In the current situation there is hardly any water scarcity, i.e. a situation in which usual consumption rates exceed the average water availability. However, the country has to cope with droughts, the natural phenomena in which there is temporarily decrease in fresh water availability, as occurred during extreme dry historical years 1976 and 2003.

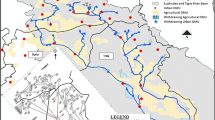
The majority of the water system allows controlled redirection of water where most regions can be supplied from the national water system during dry periods, using the Rhine River and Meuse River as the main sources. After the Rhine and Meuse enters the Netherlands the water is distributed over the branches Waal, Nederrijn, and IJssel by means of a weir by Driel. In general, 2/3 of the inflow goes to the Waal, and 1/3 to the Nederrijn and IJssel. The IJssel supplies the Ijsselmeer and Markermeer lakes with fresh water. From the rivers and lakes, water is distributed to other parts of the country through an extensive network of ditches and canals [1].

Water is used for controlling levels, flushing and actual extractions (e.g. irrigation and drinking water). In the Netherlands there is no absolute shortage of water but a ‘problem’ of the right quality at the right time at the right place. Specific phenomena for the Netherlands as a low-lying country is the risk of salt water intrusion in the western part of the Netherlands; during low flow of rivers sea water enters the main water ways due to the lack of driving forces pressurizing the water supply of the western part of the Netherlands. As described above, in the north water can be stored in the IJsselmeer and Markermeer, a man-made lake (total 2000 ha), that was created in 1932 by building a large dike (the Afsluitdijk) and is fed by the River IJssel. The lake supplies the Northern provinces during summertime. Groundwater is the main water source in the elevated areas in the south and east, since these grounds cannot be reached by re-routed surface water from the rivers. Finally the islands and peninsulas in the south west have to deal with both saltwater intrusion and limited fresh water supply options due to their surrounding by salt water bodies.

Policy arrangements are in place and coordinated by the National Coordination Committee for Drought Conditions (LCW) to deal with reduced water availability conditions. Leading principle is the so-called Verdringingsreeks, a priority lists which puts infrastructure and nature integrity preservation purposes such as water level and water quality control (flushing) above extractions for drinking and industry water above irrigation for agriculture.

1.2 The Adaptation Challenge

Climate change scenarios provided by the Royal Netherlands Meteorological Institute [2] indicate that the Netherlands should expect both an increase in the number and extent of high flow events as well as low flow periods. It is expected that global climate change demands that various measures will be taken to guarantee the control of water levels and a supply of freshwater for the long term (at least until 2100). Socio-economic developments could raise water demands even further, beyond just climate change impacts. A quantitative assessment of both problems and solutions in collaboration with stakeholders should indicate if this expectation could come true and if yes, underpin to what extend one should expect.

In the previous phase of the policy process, the Dutch Deltaprogamme Phase 1, which ended in 2015, an adaptive pathways plan was presented to cope with droughts and water scarcity on the short term (until 2021), midterm (2050) and long term (2100). Funds were allocated for measures and on different levels: for the main water system, regional water system and for water users, that are agreed upon as implementation of the preferred pathway. For the short term it was also agreed upon to make the current system more flexible and robust by ‘smart’ operational water management.

1.3 The Need to Support Screening of Alternative Strategies

In 2008–2009 various Dutch institutes conducting water management research started a collaboration to jointly develop a National Hydrological Model [3]. This National Hydrological Model is a detailed integrated surface-groundwater system of the Netherlands, combining a 250 × 250 m grid model for groundwater (Modflow) and unsaturated zone (Metaswap) with a 8800 network elements based surface water balance and allocation model. This water allocation model uses a heuristic approach to allocate water to various prioritized purposes where the uses with high priority receive water before uses with lower priority. The National Hydrological Model is applied for policy analysis and for operational forecasting.

For the operational forecasting application, the National Hydrological Model is encapsulated in a Delft-FEWS based operational forecasting system call RWsOS-Waterbeheer [4]. Rijkswaterstaat, the Dutch National Authority responsible for the national waterways and water bodies uses RWsOS-Waterbeheer on a daily basis to produce a real-time forecast with a 10 day horizon using the National Hydrological Model. This operational system provides useful information to the National Coordination Committee for Drought Conditions to analyze the current water availability situation in the Netherlands. The Committee has the authority to change the water allocation at a national level if the drought situation is sufficient severe. For this purpose, it wants to be able to conduct what-if analysis runs such that trade-offs between different regions and sectors can be assessed when allocation patterns are changed. Since the runtime of the detailed National Hydrological Model is substantial, a need arose for a so-called Quick Scan Tool to accommodate this screening purpose. This operational tool will be referenced as the LCW-Quick Scan Tool.

In the policy analysis domain the National Hydrological Model is encapsulated in a larger modeling system called the National Water Model. The model is used for detailed policy analysis under future climate scenarios and socio-economic developments. Simulations, conducted for a 30–100 year time series targeted at a mid-term 21st century outlook (2050), take days to weeks. This makes it hard to use the model for an initial screening of interventions to address the issues that arise in terms of water supply and saline intrusion within a dynamic multi-stakeholder policy process. Also for these studies a need arose for a Quick Scan Tool that could be applied to analyze potential interventions for current or future bottlenecks in the water supply system. This policy analysis tool will be referenced as the PA-Quick Scan Tool. Once interesting interventions have been identified, they could be implemented in the National Hydrological Model of the Netherlands to conduct a detailed analysis.

1.4 Quick Scan Tool Requirements

While the two tools have different end users, they have also many similarities. The end users for the LCW-Quick Scan Tool are civil servants, namely the core members of the LCW itself. These people intend to use the tool as a preparation to the Committee meetings to investigate alternative water allocation strategies when hydrological conditions are becoming dry. Their tool needs to be based on the most recent datasets provided by RWsOS-Waterbeheer. The LCW-Quick Scan Tool must be easy and quick to use and provide insight in the current situation as well as the regional trade-off of water balance effects of alternative allocation strategies. The end users for the PA-Quick Scan Tool are Deltares experts conducting the policy analysis for different climate and socio-economic development scenarios. The input datasets for the PA-Quick Scan Tool will be 30 year time series of water demands and river discharge, provided by the National Water Model.

Both applications require a water balance model that can cope with priority based water management rules for extractions and management of lake levels. The challenge for the modeling the national Dutch water system, characterized by a high-density network of waterways, is to design a model schematization that represents the national water system with the main water delivery routes and storages appropriately while regional detail should be neglected when the issues at stake do not ask for those details. This network model has to accommodate regional trade-off analysis as well as analysis of the issues at stake, while potential interventions should transparently be facilitate in the parameterization of the model. Possible interventions can vary from changing requests (water demands for extraction and in-stream uses) to manipulation of the operating rules for the storages and modification of maximum intake capacities. To enable quick turnaround times in the analysis, all above interventions should be facilitated via a Graphical User Interface. Changing the order of water use priorities was left out of scope as reduction of water demands could be applied to accommodate analysis of the same intervention in water shortage conditions.

2 Methods and Techniques

The model underlying the Quick Scan Tool is composed of a coarse network of the Dutch water system including the major water storages, water distribution points and delivery routes to the various uses. Requests for water abstractions (agriculture, industry, drinking water, regional water systems) and instream flows for flushing are prioritized and assigned to the nodes and links in the network.

In the present section we discuss the methods and techniques used to develop a model for solving our water allocation problem.

The central design tenet of our tool is separation of concerns, i.e., implementation of conceptually disjunct functionalities in separate modules. In our case, the physical system model is kept separate from the specification of the water allocation goals. In the subsequent sections, we will discuss the methodologies underpinning the implementation of these two modules.

2.1 Modeling the Water System

The Dutch water system may be viewed as a network composed of elementary objects, such as

  • storage nodes

  • channel reaches

  • weirs and pumping stations.

Objects of the same type share the same parameterized equations governing their dynamics. Storage nodes, for instance, are governed by the mass balance equation:

$$ \frac{dV}{dt} = Q_{I} - Q_{o} $$
(1)

with storage volume V, inflow Q I and outflow Q o . This is a differential equation.

Instantaneous routing in a channel reach is governed by algebraic equations of type

$$ Q_{down} = Q_{up} $$
(2)

with upstream inflow Q up and downstream outflow Q down .

Collecting the equations for all the network elements, results in a system of differential-algebraic equations (DAE). For the Quick Scan Tool a need was identified for a system to describe classes of model elements using DAE, and to combine instances of these classes into a network model. A modeling language that allows this is Modelica [5]. The Modelica objects used for the Quick Scan Tool are reaches with instantaneous routing with an extra term for a lateral flux (discharge/extraction), connection nodes for network confluences and diversions, and storage nodes.

2.2 Optimization with Prioritized Goals

The priority ordering of the control goals of the Dutch water system (the Verdringingsreeks) leads us to consider sequential optimization of the prioritized goals in order. In operations research, this technique is known as lexicographic goal programming (LGP) [6, 7]. The idea of LGP is to optimize the goalFootnote 1 functions ƒi in a given order, prioritizing earlier goals over later goals. The goals are ordered by assigning each a non-negative integer priority value p i . The goals are then solved in their priority order. Following the optimization of a goal ƒi, its attainment level is fixed and added as a constraint to the optimization problem. The optimization of all following goals, in this way, will not worsen the attainment of any preceding goal. At each stage of LGP, optimization takes place within the degrees of freedom left open by the fixation of the attainment levels of the previous goals.

Solving Ordered Goals

Application of LGP to a multi-objective optimization problem results in a series of optimization problems. Let k be the priority level under consideration, and let the overall problem be constrained by the equation g(x) ≤ 0. The k’th optimization problem is then

$$ \begin{array}{*{20}c} {\mathop {\hbox{min} }\limits_{x} f_{k} (x){\text{ subject to}}} \\ {g(x) \le 0} \\ {f_{i} (x) = \varepsilon_{i} \, \forall_{i} < k} \\ \end{array} $$
(3)

with the attainment level of the ith goal

$$ \varepsilon_{i} : = f_{i} (x_{opt,i} ) $$
(4)

and x opt,i being the optimal solution of the ith optimization problem.

LGP has been applied to decision support for the short-term operation of hydropower resources, e.g. [8], to surface water allocation, e.g. [9] and to water quality management.

Inequality Goals

In water systems, one often encounters the need to keep variables within a desired range. A channel reach is a typical case, where one aims to keep the water level within desired lower and upper bounds. It may not always be possible to keep the water level within the desired range, as in case of drought or flooding. Inequality, or range, goals are therefore an important ingredient in a multi-objective optimization framework.

Let h i be a goal function and let [m i , M i ] be its desired range, with \( m_{i} \in {\mathbb{R}} \cup \{ - \infty \} \), \( M_{i} \in {\mathbb{R}} \cup \{ - \infty \} \) and \( m_{i} \le M_{i} \). Let k be the priority order level under consideration, and let the overall problem be constrained by the equation g(x) ≤ 0. The k’th optimization problem is then

$$ \begin{array}{*{20}c} {\mathop {\hbox{min} }\limits_{{x,\delta_{k} }} \parallel \delta_{k} \parallel_{p} {\text{ subject to}}} \\ {\text{h}_{k} (x) \ge m_{k} + \delta_{k} (\underline{h}_{k} - m_{k} )} \\ {\text{h}_{k} (x) \le M_{k} + \delta_{k} (\overline{h}_{k} - M_{k} )} \\ {\delta_{k} \ge 0} \\ {\delta_{k} \le 1} \\ {g(x) \le 0} \\ \end{array} $$
(5)

with violation variable δk and goal function enclosure [11] \( [\overline{h}_{k} ,\overline{h}_{k} ] \) such that \( \underline{h}_{k} \le h_{k} (x) \le \overline{h}_{k} \) for all feasible x. The order p ≥ 1 denotes the norm under consideration. One would select p = 1 for linear penalization, or p = 2 to penalize large violations disproportionately more than small ones. The concept of violation variables is illustrated in Fig. 1 (left). The goal function merely lies within its enclosure when δk = 1, whereas the goal is fully satisfied when δk = 0. Starting from a feasible seed value of δk = 1, the objective is to minimize the value of δk.

Fig. 1.
figure 1

Variable violation concept (left) and Relaxation of state beyond the target range (right)

Full size image

In addition, for every i <  k, the following constraint is added to fix the goal attainment level:

$$ m_{i} + \delta_{i} (\underline{h}_{i} - m_{i} ) \le h_{i} (x) \le M_{i} + \delta_{i} (\overline{h}_{i} - M_{i} ) $$
(6)

When applying an inequality goal for every discretized time instance along the prediction horizon, the effect of an inequality goal is best described as a soft constraint. First, the optimizer will try to find a state trajectory that lies within the desired range. All trajectories that lie within the range incur no penalty cost and are therefore equally preferable. If it is not possible to find a trajectory that fully lies within the desired range, the optimizer will select a trajectory that lies outside of it as little as possible. The desired range, relaxed just enough to accommodate the actual trajectory, is taken as a standard (hard) constraint for subsequent goals. This idea is illustrated in Fig. 1 (right).

LGP with inequality goals has been applied to decision support for the short-term operation of hydropower resources [8].

Multiple Goals per Priority Level

In the Quick Scan Tool, every priority level i may come with multiple goal functions \( \{ f_{i}^{k} \}_{k} \), each covering a different element of the model. These goals are assumed to be equally important, hence allowing the respective goal functions to be summed into a single objective function ƒi:

$$ f_{i} = \sum\limits_{k} {\bar{f}_{i}^{k} } $$
(7)

Optimization Solver

The interior point solver IPOT [11] is used to solve the scalar optimization problems resulting from the lexicographic optimization procedure. IPOPT solves nonlinear problems, which is required for goals with order p > 1.

Software Suite

The techniques covered in the preceding sections are available as standard components in the environmental flow optimization software suite RTC-Tools 2.0 [7], which supports Modelica model formulations. RTC-Tools is available under a dual-licensing scheme. The open source version is available online under the terms of the GNU General Public License version 3 [12]. Precompiled binaries, source code, and documentation are available from the project website at: https://www.deltares.nl/en/software/rtc-tools/.

3 The Quick Scan Tool Application

The Quick Scan Tool application is a combination of two software products. Delft-FEWS provides the Graphical User Interface, the database and general data processing capabilities. The model component uses an internal model based on the RTC-Tools 2 model engine [7].

3.1 The Model Schematization

The Quick Scan Tool holds an internal network model for the water balance. The model, built in Modelica, is composed of model element of type branches, connection nodes, demand nodes, storages as well as boundary nodes (inflow and terminal). Each Modelica element holds its own water balance where flow enters via the ‘in’-port and leaves via the ‘out’-port. Lateral flows (extractions of discharges) can be applied to branches, demand nodes and storages.

The final network model schematization (Fig. 2) is the result of five collaborative design sessions with the end users. The challenge was to design a network which is as simple as possible while providing an appropriate representation of the main water system including the main water delivery routes. The network model should accommodate analysis of the issues at hand while potential interventions should be facilitated transparently in the parameterization. The result is a schematization where areas in the north-east and in the south-east are grossly simplified compared to the actual water system as there are only few relevant water inlets. More network detail has been introduced in the west as many water delivery routes need to be analyzed in relation to saline intrusion of the most westward inlets. Capacities and management rule have been derived from the NHM.

Fig. 2.
figure 2

QST network schematization of the main water delivery system in the Netherlands

Full size image

3.2 The Work and Dataflow of the Application

The dataflow of the Quick Scan Tool is composed of the following steps:

  1. 1.

    acquire the input data sets (requests for extractions and flushing), river discharges and lake levels) from the National Hydrological Model

  2. 2.

    conduct a spatial assignment, using a coupling table, of all requests to a node or branch of the coarse network model

  3. 3.

    transform request by water use function to a request by priority

  4. 4.

    allocate the available water resources using the LGP method

  5. 5.

    The result is a water distribution over the network, with per element the inflow, the outflow and the lateral flux achieved. Since this lateral flux is the total flux for all extracting (and discharging) water uses functions, this flux need to be split

  6. 6.

    split the lateral flux into the portions allocated to each water use

  7. 7.

    aggregate the results by area for presentation purposes

  8. 8.

    compute a delivery rate percentage, broken up by water use, for presentation purposes.

Table 1 illustrates the order of priorities that is adopted in the PA-Quick Scan Tool.

Table 1. Ordering of goals as applied in the PA-Quick scan tool
Full size table

The first three priorities are critical, i.e. similar to ‘hard’ constraints, as they intend to force the solution within the physical bounds of the water system. The remaining goals are water uses with their order prescribed by law and policies. As can be noted, the operating rules for the storages are divided in multiple goals such that lake levels can drop to meet high priority water demands. Target storage levels should be attained if sufficient water is available within the system. The goal with the last priority intends to minimize the outflow in a selected set of branches such that the water remains in the main rivers and only enters the water inlets to meet local water demands. All canal outlets that do not conduct a water delivery function to downstream uses should be included in this selection.

For in-stream flow requests (e.g. flushing and navigation locks), each new goal is identified by taking the maximum of all in-stream water use flow requests up till the priority at stake. For the lateral fluxes the LGP approach intends to squeeze the solution space with each priority such that the end result is at the desired request if the system is not under water shortage. The equations in the Fig. 3 indicate that the requested lateral fluxes for different water uses need to be stacked to obtain a series of goals that squeeze the solution space in the ordering of goals.

Fig. 3.
figure 3

Solution space squeezing and associated goal stacking for lateral fluxes

Full size image

Once the LGP has completed its computation, the resulting flows need to be split according to the different water uses. For any in-stream flow request the request is fulfilled if the realized flow is larger than the request. For lateral flux requests, the delivery per water use needs to be based on the ‘peeling off’ the realized lateral flux by order of priority and allocating the remaining flux to a specific water use up to the request.

4 Validation of Model Results

The QST-model has been validated by comparison of the water allocation against the water allocation result computed in the detailed National Hydrological Model (NHM). Differences may partly be explained by the fact that the NHM uses a heuristic water allocation method. Important items checked are the distribution of the main river inflows, the behavior of the lakes, the flushing on the outlets and the main inlets for the rural area in the west. Figure 4 illustrates the water shortage for the flushing goal at the driest moment in the 30 year historical series, flushing being the goal with the lowest priority. In general the QST model results in fewer shortages. During the driest period, the difference with the NHM model result is 2–6% at this location, while most other network elements show hardly any difference. Also lake levels follow the same pattern between the two models if the QST is to lower the volume in order to meet in-stream flow requests.

Fig. 4.
figure 4

Comparison of shortage at sea outlet between NHM (NieuweWaterWeg) and QST-model (NieuweWaterWeg_uitlaat)

Full size image

5 Discussion and Conclusions

Within the Netherlands, a need arose at the national level to supplement the current high-resolution National Hydrological Model with a water allocation model to enable the screening of national water allocation decisions for their regional trade-offs. This paper illustrates how a so-called Quick Scan Tool has been developed for this purpose. The tool is composed of a water allocation model engine and a software component that offers a front end as well as pre and post-processing capabilities. The water allocation model is built with the RTC-Tools 2 software framework using a lexicographic goal programming approach to priority based water allocation rules. In the pilot version Excel was chosen as the front end offering pre and postprocessing capabilities. Data processing required extensive handling of lookup tables while conducting the necessary aggregations from detailed source data to coarse model input to aggregated output for presentation on areal scale. The prototype application showed that RTC-Tools 2 was meeting the model needs, while Excel was not the appropriate data processing platform. In the final version, the Delft-FEWS software framework was chosen as a data processing and visualization platform. This platform offered much more insight to debug the data flow from aggregating source data to model input data to the aggregation of results.

The resulting Quick Scan Tool has been validated against the detailed National Hydrological Model to confirm that the tool outcomes are sufficiently similar to this accepted model to support the policy process. The visualization capabilities Delft-FEWS, with its map based flow animations and graphs, were very beneficial while discussing model setup and validation results with the water management experts of Rijkswaterstaat, the governmental body who initiated the development of the tool.

At the time of writing, the first actual use of the tool is put in practice with preliminary analysis of a combination of additional flushing and water extraction requests under future conditions for the assessment years 2050 and 2085.

In the near term, functional extensions are foreseen using meta-relations to transform reduced river flows into impacts on salinity rates and navigation depths.

RTC-Tools 2 and Delft-FEWS are software platforms which initially were developed for near real-time water system operations. Based on this Quick Scan Tool, it can be concluded that the flexibility and customization capabilities of these platforms also allow development of decision support tools for strategic planning processes.