Abstract
We present Ellora, a sound and relatively complete assertion-based program logic, and demonstrate its expressivity by verifying several classical examples of randomized algorithms using an implementation in the EasyCrypt proof assistant. Ellora features new proof rules for loops and adversarial code, and supports richer assertions than existing program logics. We also show that Ellora allows convenient reasoning about complex probabilistic concepts by developing a new program logic for probabilistic independence and distribution law, and then smoothly embedding it into Ellora.
This is the conference version of the paper.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The most mature systems for deductive verification of randomized algorithms are expectation-based techniques; seminal examples include PPDL [28] and pGCL [34]. These approaches reason about expectations, functions E from states to real numbers,Footnote 1 propagating them backwards through a program until they are transformed into a mathematical function of the input. Expectation-based systems are both theoretically elegant [16, 23, 24, 35] and practically useful; implementations have verified numerous randomized algorithms [19, 21]. However, properties involving multiple probabilities or expected values can be cumbersome to verify—each expectation must be analyzed separately.
An alternative approach envisioned by Ramshaw [37] is to work with predicates over distributions. A direct comparison with expectation-based techniques is difficult, as the approaches are quite different. In broad strokes, assertion-based systems can verify richer properties in one shot and have specifications that are arguably more intuitive, especially for reasoning about loops, while expectation-based approaches can transform expectations mechanically and can reason about non-determinism. However, the comparison is not very meaningful for an even simpler reason: existing assertion-based systems such as [8, 18, 38] are not as well developed as their expectation-based counterparts.
-
Restrictive Assertions. Existing probabilistic program logics do not support reasoning about expected values, only probabilities. As a result, many properties about average-case behavior are not even expressible.
-
Inconvenient Reasoning for Loops. The Hoare logic rule for deterministic loops does not directly generalize to probabilistic programs. Existing assertion-based systems either forbid loops, or impose complex semantic side conditions to control which assertions can be used as loop invariants. Such side conditions are restrictive and difficult to establish.
-
No Support for External or Adversarial Code. A strength of expectation-based techniques is reasoning about programs combining probabilities and non-determinism. In contrast, Morgan and McIver [30] argue that assertion-based techniques cannot support compositional reasoning for such a combination. For many applications, including cryptography, we would still like to reason about a commonly-encountered special case: programs using external or adversarial code. Many security properties in cryptography boil down to analyzing such programs, but existing program logics do not support adversarial code.
-
Few Concrete Implementations. There are by now several independent implementations of expectation-based techniques, capable of verifying interesting probabilistic programs. In contrast, there are only scattered implementations of probabilistic program logics.
These limitations raise two points. Compared to expectation-based approaches:
-
1.
Can assertion-based approaches achieve similar expressivity?
-
2.
Are there situations where assertion-based approaches are more suitable?
In this paper, we give positive evidence for both of these points.Footnote 2 Towards the first point, we give a new assertion-based logic Ellora for probabilistic programs, overcoming limitations in existing probabilistic program logics. Ellora supports a rich set of assertions that can express concepts like expected values and probabilistic independence, and novel proof rules for verifying loops and adversarial code. We prove that Ellora is sound and relatively complete.
Towards the second point, we evaluate Ellora in two ways. First, we define a new logic for proving probabilistic independence and distribution law properties—which are difficult to capture with expectation-based approaches—and then embed it into Ellora. This sub-logic is more narrowly focused than Ellora, but supports more concise reasoning for the target assertions. Our embedding demonstrates that the assertion-based approach can be flexibly integrated with intuitive, special-purpose reasoning principles. To further support this claim, we also provide an embedding of the Union Bound logic, a program logic for reasoning about accuracy bounds [4]. Then, we develop a full-featured implementation of Ellora in the EasyCrypt theorem prover and exercise the logic by mechanically verifying a series of complex randomized algorithms. Our results suggest that the assertion-based approach can indeed be practically viable.
Abstract Logic. To ease the presentation, we present Ellora in two stages. First, we consider an abstract version of the logic where assertions are general predicates over distributions, with no compact syntax. Our abstract logic makes two contributions: reasoning for loops, and for adversarial code.
Reasoning About Loops. Proving a property of a probabilistic loop typically requires establishing a loop invariant, but the class of loop invariants that can be soundly used depends on the termination behavior—stronger termination assumptions allows richer loop invariants. We identify three classes of assertions that can be used for reasoning about probabilistic loops, and provide a proof rule for each one:
-
arbitrary assertions for certainly terminating loops, i.e. loops that terminate in a finite amount of iterations;
-
topologically closed assertions for almost surely terminating loops, i.e. loops terminating with probability 1;
-
downwards closed assertions for arbitrary loops.
The definition of topologically closed assertion is reminiscent of Ramshaw [37]; the stronger notion of downwards closed assertion appears to be new.
Besides broadening the class of loops that can be analyzed, our rules often enable simpler proofs. For instance, if the loop is certainly terminating, then there is no need to prove semantic side-conditions. Likewise, there is no need to consider the termination behavior of the loop when the invariant is downwards and topologically closed. For example, in many applications in cryptography, the target property is that a “bad” event has low probability: \(\Pr {[E]} \le k\). In our framework this assertion is downwards and topologically closed, so it can be a loop invariant regardless of the termination behavior.
Reasoning About Adversaries. Existing assertion-based logics cannot reason about probabilistic programs with adversarial code. Adversaries are special probabilistic procedures consisting of an interface listing the concrete procedures that an adversary can call (oracles), along with restrictions like how many calls an adversary may make. Adversaries are useful in cryptography, where security notions are described using experiments in which adversaries interact with a challenger, and in game theory and mechanism design, where adversaries can represent strategic agents. Adversaries can also model inputs to online algorithms.
We provide proof rules for reasoning about adversary calls. Our rules are significantly more general than previously considered rules for reasoning about adversaries. For instance, the rule for adversary used by [4] is restricted to adversaries that cannot make oracle calls.
Metatheory. We show soundness and relative completeness of the core abstract logic, with mechanized proofs in the Coq proof assistant.
Concrete Logic. While the abstract logic is conceptually clean, it is inconvenient for practical formal verification—the assertions are too general and the rules involve semantic side-conditions. To address these issues, we flesh out a concrete version of Ellora. Assertions are described by a grammar modeling a two-level assertion language. The first level contains state predicates—deterministic assertions about a single memory—while the second layer contains probabilistic predicates constructed from probabilities and expected values over discrete distributions. While the concrete assertions are theoretically less expressive than their counterparts in the abstract logic, they can already encode common properties and notions from existing proofs, like probabilities, expected values, distribution laws and probabilistic independence. Our assertions can express theorems from probability theory, enabling sophisticated reasoning about probabilistic concepts.
Furthermore, we leverage the concrete syntax to simplify verification.
-
We develop an automated procedure for generating pre-conditions of non-looping commands, inspired by expectation-based systems.
-
We give syntactic conditions for the closedness and termination properties required for soundness of the loop rules.
Implementation and Case Studies. We implement Ellora on top of EasyCrypt, a general-purpose proof assistant for reasoning about probabilistic programs, and we mechanically verify a diverse collection of examples including textbook algorithms and a randomized routing procedure. We develop an EasyCrypt formalization of probability theory from the ground up, including tools like concentration bounds (e.g., the Chernoff bound), Markov’s inequality, and theorems about probabilistic independence.
Embeddings. We propose a simple program logic for proving probabilistic independence. This logic is designed to reason about independence in a lightweight way, as is common in paper proofs. We prove that the logic can be embedded into Ellora, and is therefore sound. Furthermore, we prove an embedding of the Union Bound logic [4].
2 Mathematical Preliminaries
As is standard, we will model randomized computations using sub-distributions.
Definition 1
A sub-distribution over a set A is defined by a mass function \(\mu : A \rightarrow [0,1]\) that gives the probability of the unitary events \(a \in A\). This mass function must be s.t. \(\sum _{a \in A} \mu (a)\) is well-defined and \(|\mu | \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\sum _{a\in A} \mu (a) \le 1\). In particular, the support \(\mathrm{supp}(\mu ) \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\{ a \in A \mid \mu (a) \ne 0 \}\) is discrete.Footnote 3 The name “sub-distribution” emphasizes that the total probability may be strictly less than 1. When the weight \(|\mu |\) is equal to 1, we call \(\mu \) a distribution. We let \(\mathbf {SDist}(A)\) denote the set of sub-distributions over A. The probability of an event E(x) w.r.t. a sub-distribution \(\mu \), written \(\Pr _{x \sim \mu } [E(x)]\), is defined as \(\sum _{x \in A \mid E(x)} \mu (x)\).
Simple examples of sub-distributions include the null sub-distribution \(\mathbf {0}\), which maps each element of the underlying space to 0; and the Dirac distribution centered on x, written \({{\delta }^{}_{x}}\), which maps x to 1 and all other elements to 0. The following standard construction gives a monadic structure to sub-distributions.
Definition 2
Let \(\mu \in \mathbf {SDist}(A)\) and \(f : A \rightarrow \mathbf {SDist}(B)\). Then \(\mathbb {E}_{{a} \sim {\mu }} [{f}] \in \mathbf {SDist}(B)\) is defined by
We use notation reminiscent of expected values, as the definition is quite similar.
We will need two constructions to model branching statements.
Definition 3
Let \(\mu _1,\mu _2\in \mathbf {SDist}(A)\) such that \(|\mu _1|+|\mu _2|\le 1\). Then \(\mu _1+\mu _2\) is the sub-distribution \(\mu \) such that \(\mu (a)=\mu _1(a)+\mu _2(a)\) for every \(a\in A\).
Definition 4
Let \(E \subseteq A\) and \(\mu \in \mathbf {SDist}(A)\). Then the restriction \({\mu }_{| {E}}\) of \(\mu \) to E is the sub-distribution such that \({\mu }_{| {E}} (a)= \mu (a)\) if \(a\in E\) and 0 otherwise.
Sub-distributions are partially ordered under the pointwise order.
Definition 5
Let \(\mu _1,\mu _2\in \mathbf {SDist}(A)\). We say \(\mu _1\le \mu _2\) if \(\mu _1(a) \le \mu _2(a)\) for every \(a\in A\), and we say \(\mu _1 = \mu _2\) if \(\mu _1(a) = \mu _2(a)\) for every \(a\in A\).
We use the following lemma when reasoning about the semantics of loops.
Lemma 1
If \(\mu _1\le \mu _2\) and \(|\mu _1|=1\), then \(\mu _1=\mu _2\) and \(|\mu _2|=1\).
Sub-distributions are stable under pointwise-limits.
Definition 6
A sequence \((\mu _n)_{n\in \mathbb {N}} \in \mathbf {SDist}(A)\) sub-distributions converges if for every \(a \in A\), the sequence \((\mu _n(a))_{n\in \mathbb {N}}\) of real numbers converges. The limit sub-distribution is defined as
for every \(a \in A\). We write \(\lim _{n\rightarrow \infty } \mu _n\) for \(\mu _\infty \).
Lemma 2
Let \((\mu _n)_{n\in \mathbb {N}}\) be a convergent sequence of sub-distributions. Then for any event E(x), we have:
Any bounded increasing real sequence has a limit; the same is true of sub-distributions.
Lemma 3
Let \((\mu _n)_{n\in \mathbb {N}} \in \mathbf {SDist}(A)\) be an increasing sequence of sub-distributions. Then, this sequence converges to \(\mu _\infty \) and \(\mu _n \le \mu _\infty \) for every \(n\in \mathbb {N}\). In particular, for any event E, we have \(\Pr _{x \sim \mu _n} [E]\le \Pr _{x \sim \mu _\infty } [E]\) for every \(n\in \mathbb {N}\).
3 Programs and Assertions
Now, we introduce our core programming language and its denotational semantics.
Programs. We base our development on pWhile, a strongly-typed imperative language with deterministic assignments, probabilistic assignments, conditionals, loops, and an \({\mathbf {abort}}\) statement which halts the computation with no result. Probabilistic assignments  assign a value sampled from a distribution g to a program variable x. The syntax of statements is defined by the grammar:
assign a value sampled from a distribution g to a program variable x. The syntax of statements is defined by the grammar:

where x, e, and g range over typed variables in \(\mathcal {X}\), expressions in \(\mathcal {E}\) and distribution expressions in \(\mathcal {D}\) respectively. The set \(\mathcal {E}\) of well-typed expressions is defined inductively from \(\mathcal {X}\) and a set \(\mathcal {F}\) of function symbols, while the set \(\mathcal {D}\) of well-typed distribution expressions is defined by combining a set of distribution symbols \(\mathcal {S}\) with expressions in \(\mathcal {E}\). Programs may call a set \(\mathcal {I}\) of internal procedures as well as a set \(\mathcal {A}\) of external procedures. We assume that we have code for internal procedures but not for external procedures—we only know indirect information, like which internal procedures they may call. Borrowing a convention from cryptography, we call internal procedures oracles and external procedures adversaries.
Semantics. The denotational semantics of programs is adapted from the seminal work of [27] and interprets programs as sub-distribution transformers. We view states as type-preserving mappings from variables to values; we write \(\mathbf {State}\) for the set of states and \(\mathbf {SDist}(\mathbf {State})\) for the set of probabilistic states. For each procedure name \(f \in \mathcal {I}\cup \mathcal {A}\), we assume a set \(\mathcal {X}^{\mathfrak {L}}_{f} \subseteq \mathcal {X}\) of local variables s.t. \(\mathcal {X}^{\mathfrak {L}}_{f}\) are pairwise disjoint. The other variables \(\mathcal {X}\setminus \bigcup _f \mathcal {X}^{\mathfrak {L}}_{f}\) are global variables.
To define the interpretation of expressions and distribution expressions, we let  denote the interpretation of expression e with respect to state m, and
denote the interpretation of expression e with respect to state m, and  denote the interpretation of expression e with respect to an initial sub-distribution \(\mu \) over states defined by the clause
denote the interpretation of expression e with respect to an initial sub-distribution \(\mu \) over states defined by the clause  . Likewise, we define the semantics of commands in two stages: first interpreted in a single input memory, then interpreted in an input sub-distribution over memories.
. Likewise, we define the semantics of commands in two stages: first interpreted in a single input memory, then interpreted in an input sub-distribution over memories.
Definition 7
The semantics of commands are given in Fig. 1.
-
The semantics
 of a statement s in initial state m is a sub-distribution over states.
of a statement s in initial state m is a sub-distribution over states. -
The (lifted) semantics
 of a statement s in initial sub-distribution \(\mu \) over states is a sub-distribution over states.
of a statement s in initial sub-distribution \(\mu \) over states is a sub-distribution over states.
We briefly comment on loops. The semantics of a loop \({\mathbf {while}}\,\, e \,\, {\mathbf {do}}\,\, c \) is defined as the limit of its lower approximations, where the n-th lower approximation of  is
is  , where \({\mathbf {if}}\,\, e\,\, {\mathbf {then}}\,\, s\) is shorthand for \({\mathbf {if}}\,\, e\,\, {\mathbf {then}}\,\, s\,\, {\mathbf {else}}\,\, {\mathbf {skip}}\) and \(c^n\) is the n-fold composition \(c;\cdots ;c\). Since the sequence is increasing, the limit is well-defined by Lemma 3. In contrast, the n-th approximation of
, where \({\mathbf {if}}\,\, e\,\, {\mathbf {then}}\,\, s\) is shorthand for \({\mathbf {if}}\,\, e\,\, {\mathbf {then}}\,\, s\,\, {\mathbf {else}}\,\, {\mathbf {skip}}\) and \(c^n\) is the n-fold composition \(c;\cdots ;c\). Since the sequence is increasing, the limit is well-defined by Lemma 3. In contrast, the n-th approximation of  defined by
defined by  may not converge, since they are not necessarily increasing. However, in the special case where the output distribution has weight 1, the n-th lower approximations and the n-th approximations have the same limit.
may not converge, since they are not necessarily increasing. However, in the special case where the output distribution has weight 1, the n-th lower approximations and the n-th approximations have the same limit.
Lemma 4
If the sub-distribution  has weight 1, then the limit of
has weight 1, then the limit of  is defined and
is defined and

This follows by Lemma 1, since lower approximations are below approximations so the limit of their weights (and the weight of their limit) is 1. It will be useful to identify programs that terminate with probability 1.
Definition 8
(Lossless). A statement s is lossless if for every sub-distribution \(\mu \),  , where \(|\mu |\) is the total probability of \(\mu \). Programs that are not lossless are called lossy.
, where \(|\mu |\) is the total probability of \(\mu \). Programs that are not lossless are called lossy.
Informally, a program is lossless if all probabilistic assignments sample from full distributions rather than sub-distributions, there are no \({\mathbf {abort}}\) instructions, and the program is almost surely terminating, i.e. infinite traces have probability zero. Note that if we restrict the language to sample from full distributions, then losslessness coincides with almost sure termination.
Another important class of loops are loops with a uniform upper bound on the number of iterations. Formally, we say that a loop \({\mathbf {while}}\,\, e \,\, {\mathbf {do}}\,\, s \) is certainly terminating if there exists k such that for every sub-distribution \(\mu \), we have  . Note that certain termination of a loop does not entail losslessness—the output distribution of the loop may not have weight 1, for instance, if the loop samples from a sub-distribution or if the loop aborts with positive probability.
. Note that certain termination of a loop does not entail losslessness—the output distribution of the loop may not have weight 1, for instance, if the loop samples from a sub-distribution or if the loop aborts with positive probability.
Semantics of Procedure Calls and Adversaries. The semantics of internal procedure calls is straightforward. Associated to each procedure name \(f \in \mathcal {I}\), we assume a designated input variable \({f}_{{\mathbf {arg}}} \in \mathcal {X}^{\mathfrak {L}}_{f}\), a piece of code \({f}_{{\mathbf {body}}}\) that executes the function call, and a result expression \({f}_{{\mathbf {res}}}\). A function call  is then equivalent to
is then equivalent to  . Procedures are subject to well-formedness criteria: procedures should only use local variables in their scope and after initializing them, and should not perform recursive calls.
. Procedures are subject to well-formedness criteria: procedures should only use local variables in their scope and after initializing them, and should not perform recursive calls.
External procedure calls, also known as adversary calls, are a bit more involved. Each name \(a \in \mathcal {A}\) is parametrized by a set \({a}_{{\mathbf {ocl}}} \subseteq \mathcal {I}\) of internal procedures which the adversary may call, a designated input variable \({a}_{{\mathbf {arg}}} \in \mathcal {X}^{\mathfrak {L}}_{a}\), a (unspecified) piece of code \({a}_{{\mathbf {body}}}\) that executes the function call, and a result expression \({a}_{{\mathbf {res}}}\). We assume that adversarial code can only access its local variables in \(\mathcal {X}^{\mathfrak {L}}_{a}\) and can only make calls to procedures in \({a}_{{\mathbf {ocl}}}\). It is possible to impose more restrictions on adversaries—say, that they are lossless—but for simplicity we do not impose additional assumptions on adversaries here.
4 Proof System
In this section we introduce a program logic for proving properties of probabilistic programs. The logic is abstract—assertions are arbitrary predicates on sub-distributions—but the meta-theoretic properties are clearest in this setting. In the following section, we will give a concrete version suitable for practical use.
Assertions and Closedness Conditions. We use predicates on state distribution.
Definition 9
(Assertions). The set \(\mathsf {Assn}\) of assertions is defined as \(\mathcal {P}(\mathbf {SDist}(\mathbf {State}))\). We write \(\eta (\mu )\) for \(\mu \in \eta \).
Usual set operations are lifted to assertions using their logical counterparts, e.g., \(\eta \wedge \eta ' \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\eta \cap \eta '\) and \(\lnot \eta \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\overline{\eta }\). Our program logic uses a few additional constructions. Given a predicate \(\phi \) over states, we define
where \(\mathrm{supp}(\mu )\) is the set of all states with non-zero probability under \(\mu \). Intuitively, \(\phi \) holds deterministically on all states that we may sample from the distribution. To reason about branching commands, given two assertions \(\eta _1\) and \(\eta _2\), we let
This assertion means that the sub-distribution is the sum of two sub-distributions such that \(\eta _1\) holds on the first piece and \(\eta _2\) holds on the second piece.
Given an assertion \(\eta \) and an event \(E \subseteq \mathbf {State}\), we let \( {\eta }_{| {E}}(\mu )\mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\eta ({\mu }_{| {E}}) . \) This assertion holds exactly when \(\eta \) is true on the portion of the sub-distribution satisfying E. Finally, given an assertion \(\eta \) and a function F from \(\mathbf {SDist}(\mathbf {State})\) to \(\mathbf {SDist}(\mathbf {State})\), we define \( \eta [F] \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\lambda \mu .\, \eta (F(\mu )) . \) Intuitively, \(\eta [F]\) is true in a sub-distribution \(\mu \) exactly when \(\eta \) holds on \(F(\mu )\).
Now, we can define the closedness properties of assertions. These properties will be critical to our rules for \({\mathbf {while}}\) loops.
Definition 10
(Closedness properties). A family of assertions \((\eta _n)_{n\in \mathbb {N}^\infty }\) is:
-
u-closed if for every increasing sequence of sub-distributions \((\mu _n)_{n\in \mathbb {N}}\) such that \(\eta _n(\mu _n)\) for all \(n\in \mathbb {N}\) then \(\eta _\infty (\lim _{n\rightarrow \infty }\mu _n)\);
-
t-closed if for every converging sequence of sub-distributions \((\mu _n)_{n\in \mathbb {N}}\) such that \(\eta _n(\mu _n)\) for all \(n\in \mathbb {N}\) then \(\eta _\infty (\lim _{n\rightarrow \infty }\mu _n)\);
-
d-closed if it is t-closed and downward closed, that is for every sub-distributions \(\mu \le \mu '\), \(\eta _\infty (\mu ')\) implies \(\eta _\infty (\mu )\).
When \((\eta _n)_n\) is constant and equal to \(\eta \), we say that \(\eta \) is u-/t-/d-closed.
Note that t-closedness implies u-closedness, but the converse does not hold. Moreover, u-closed, t-closed and d-closed assertions are closed under arbitrary intersections and finite unions, or in logical terms under finite boolean combinations, universal quantification over arbitrary sets and existential quantification over finite sets.
Finally, we introduce the necessary machinery for the frame rule. The set \({\text {mod}}(s)\) of modified variables of a statement s consists of all the variables on the left of a deterministic or probabilistic assignment. In this setting, we say that an assertion \(\eta \) is separated from a set of variables X, written \(\mathsf {separated}({\eta },{X})\), if \(\eta (\mu _1) \iff \eta (\mu _2)\) for any distributions \(\mu _1\), \(\mu _2\) s.t. \(|\mu _1| = |\mu _2|\) and \({\mu _1}_{| \overline{X}} = {\mu _2}_{| \overline{X}}\) where for a set of variables X, the restricted sub-distribution \(\mu _{| X}\) is
where \(\mathbf {State}_{| X}\) and \(m_{| X}\) restrict \(\mathbf {State}\) and m to the variables in X.
Intuitively, an assertion is separated from a set of variables X if every two sub-distributions that agree on the variables outside X either both satisfy the assertion, or both refute the assertion.
Judgments and Proof Rules. Judgments are of the form \(\{\eta \}\,s\,\{\eta '\}\), where the assertions \(\eta \) and \(\eta '\) are drawn from \(\mathsf {Assn}\).
Definition 11
A judgment \(\{\eta \}\,s\,\{\eta '\}\) is valid, written  , if
, if  for every interpretation of adversarial procedures and every probabilistic state \(\mu \) such that \(\eta (\mu )\).
for every interpretation of adversarial procedures and every probabilistic state \(\mu \) such that \(\eta (\mu )\).
Figure 2 describes the structural and basic rules of the proof system. Validity of judgments is preserved under standard structural rules, like the rule of consequence [Conseq]. As usual, the rule of consequence allows to weaken the post-condition and to strengthen the post-condition; in our system, this rule serves as the interface between the program logic and mathematical theorems from probability theory. The [Exists] rule is helpful to deal with existentially quantified pre-conditions.
The rules for \({\mathbf {skip}}\), assignments, random samplings and sequences are all straightforward. The rule for \({\mathbf {abort}}\) requires \(\square {\bot }\) to hold after execution; this assertion uniquely characterizes the resulting null sub-distribution. The rules for assignments and random samplings are semantical.
The rule [Cond] for conditionals requires that the post-condition must be of the form \(\eta _1\,\oplus \,\eta _2\); this reflects the semantics of conditionals, which splits the initial probabilistic state depending on the guard, runs both branches, and recombines the resulting two probabilistic states.
The next two rules ([Split] and [Frame]) are useful for local reasoning. The [Split] rule reflects the additivity of the semantics and combines the pre- and post-conditions using the \(\oplus \) operator. The [Frame] rule asserts that lossless statements preserve assertions that are not influenced by modified variables.
The rule [Call] for internal procedures is as expected, replacing the procedure call f with its definition.
Figure 3 presents the rules for loops. We consider four rules specialized to the termination behavior. The [While] rule is the most general rule, as it deals with arbitrary loops. For simplicity, we explain the rule in the special case where the family of assertions is constant, i.e. we have \(\eta _n=\eta \) and \(\eta '_n=\eta '\). Informally, the \(\eta \) is the loop invariant and \(\eta '\) is an auxiliary assertion used to prove the invariant. We require that \(\eta \) is u-closed, since the semantics of a loop is defined as the limit of its lower approximations. Moreover, the first premise ensures that starting from \(\eta \), one guarded iteration of the loop establishes \(\eta '\); the second premise ensures that restricting to \(\lnot e\) a probabilistic state \(\mu '\) satisfying \(\eta '\) yields a probabilistic state \(\mu \) satisfying \(\eta \). It is possible to give an alternative formulation where the second premise is substituted by the logical constraint \({\eta '}_{| {\lnot e}}\implies \eta \). As usual, the post-condition of the loop is the conjunction of the invariant with the negation of the guard (more precisely in our setting, that the guard has probability 0).
The [While-AST] rule deals with lossless loops. For simplicity, we explain the rule in the special case where the family of assertions is constant, i.e. we have \(\eta _n=\eta \). In this case, we know that lower approximations and approximations have the same limit, so we can directly prove an invariant that holds after one guarded iteration of the loop. On the other hand, we must now require that the \(\eta \) satisfies the stronger property of t-closedness.
The [While-D] rule handles arbitrary loops with a d-closed invariant; intuitively, restricting a sub-distribution that satisfies a downwards closed assertion \(\eta \) yields a sub-distribution which also satisfies \(\eta \).
The [While-CT] rule deals with certainly terminating loops. In this case, there is no requirement on the assertions.
We briefly compare the rules from a verification perspective. If the assertion is d-closed, then the rule [While-D] is easier to use, since there is no need to prove any termination requirement. Alternatively, if we can prove certain termination of the loop, then the rule [While-CT] is the best to use since it does not impose any condition on assertions. When the loop is lossless, there is no need to introduce an auxiliary assertion \(\eta '\), which simplifies the proof goal. Note however that it might still be beneficial to use the [While] rule, even for lossless loops, because of the weaker requirement that the invariant is u-closed rather than t-closed.
Finally, Fig. 4 gives the adversary rule for general adversaries. It is highly similar to the general rule [While-D] for loops since the adversary may make an arbitrary sequence of calls to the oracles in \({a}_{{\mathbf {ocl}}}\) and may not be lossless. Intuitively, \(\eta \) plays the role of the invariant: it must be d-closed and it must be preserved by every oracle call with arbitrary arguments. If this holds, then \(\eta \) is also preserved by the adversary call. Some framing conditions are required, similar to the ones of the [Frame] rule: the invariant must not be influenced by the state writable by the external procedures.
It is possible to give other variants of the adversary rule with more general invariants by restricting the adversary, e.g., requiring losslessness or bounding the number of calls the external procedure can make to oracles, leading to rules akin to the almost surely terminating and certainly terminating loop rules, respectively.
Soundness and Relative Completeness. Our proof system is sound with respect to the semantics.
Theorem 1
(Soundness). Every judgment \(\{\eta \}\,s\,\{\eta '\}\) provable using the rules of our logic is valid.
Completeness of the logic follows from the next lemma, whose proof makes an essential use of the [While] rule. In the sequel, we use \({\mathbf {1}}_{\mu }\) to denote the characteristic function of a probabilistic state \(\mu \), an assertion stating that the current state is equal to \(\mu \).
Lemma 5
For every probabilistic state \(\mu \), the following judgment is provable using the rule of the logic:

Proof
By induction on the structure of s.
-
\(s = {\mathbf {abort}}\), \(s = {\mathbf {skip}}\),
 and
and 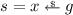 are trivial;
are trivial; -
\(s = s_1;s_2\), we have to prove

We apply the [Seq] rule with
 premises can be directly proved using the induction hypothesis;
premises can be directly proved using the induction hypothesis; -
\(s = {\mathbf {if}}\,\, e\,\, {\mathbf {then}}\,\, s_1\,\, {\mathbf {else}}\,\, s_2\), we have to prove

We apply the [Conseq] rule to be able to apply the [Cond] rule with
 and
and  Both premises can be proved by an application of the [Conseq] rule followed by the application of the induction hypothesis.
Both premises can be proved by an application of the [Conseq] rule followed by the application of the induction hypothesis. -
\(s = {\mathbf {while}}\,\, e \,\, {\mathbf {do}}\,\, s \), we have to prove

We first apply the [While] rule with
 and
and 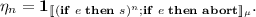
For the first premise we apply the same process as for the conditional case: we apply the [Conseq] and [Cond] rules and we conclude using the induction hypothesis (and the [Skip] rule). For the second premise we follow the same process but we conclude using the [Abort] rule instead of the induction hypothesis. Finally we conclude since \(\mathsf {uclosed}((\eta _n)_{n\in \mathbb {N}^\infty })\). \(\square \)
The abstract logic is also relatively complete. This property will be less important for our purposes, but it serves as a basic sanity check.
Theorem 2
(Relative completeness). Every valid judgment is derivable.
Proof
Consider a valid judgment \(\{\eta \}s\{\eta '\}\). Let \(\mu \) be a probabilistic state such that \(\eta (\mu )\). By the above proposition,  . Using the validity of the judgment and [Conseq], we have \(\{{\mathbf {1}}_{\mu } \wedge \eta (\mu )\}s\{\eta '\}\). Using the [Exists] and [Conseq] rules, we conclude \(\{\eta \}s\{\eta '\}\) as required. \(\square \)
. Using the validity of the judgment and [Conseq], we have \(\{{\mathbf {1}}_{\mu } \wedge \eta (\mu )\}s\{\eta '\}\). Using the [Exists] and [Conseq] rules, we conclude \(\{\eta \}s\{\eta '\}\) as required. \(\square \)
The side-conditions in the loop rules (e.g., \(\mathsf {uclosed}\)/\(\mathsf {tclosed}\)/\(\mathsf {dclosed}\) and the weight conditions) are difficult to prove, since they are semantic properties. Next, we present a concrete version of the logic with give easy-to-check, syntactic sufficient conditions.
5 A Concrete Program Logic
To give a more practical version of the logic, we begin by setting a concrete syntax for assertions
Assertions. We use a two-level assertion language, presented in Fig. 5. A probabilistic assertion \(\eta \) is a formula built from comparison of probabilistic expressions, using first-order quantifiers and connectives, and the special connective \(\oplus \). A probabilistic expression p can be a logical variable v, an operator applied to probabilistic expressions \(o({\varvec{p}})\) (constants are 0-ary operators), or the expectation \(\mathbb {E}_{} [{\tilde{e}}]\) of a state expression \(\tilde{e}\). A state expression \(\tilde{e}\) is either a program variable x, the characteristic function \({\mathbf {1}}_{\phi }\) of a state assertion \(\phi \), an operator applied to state expressions \(o(\tilde{{{\varvec{e}}}})\), or the expectation \(\mathbb {E}_{{v} \sim {g}} [{\tilde{e}}]\) of state expression \(\tilde{e}\) in a given distribution g. Finally, a state assertion \(\phi \) is a first-order formula over program variables. Note that the set of operators is left unspecified but we assume that all the expressions in \(\mathcal {E}\) and \(\mathcal {D}\) can be encoded by operators.
The interpretation of the concrete syntax is as expected. The interpretation of probabilistic assertions is relative to a valuation \(\rho \) which maps logical variables to values, and is an element of \(\mathsf {Assn}\). The definition of the interpretation is straightforward; the only interesting case is  which is defined by
which is defined by  , where
, where  is the interpretation of the state expression \(\tilde{e}\) in the memory m and valuation \(\rho \). The interpretation of state expressions is a mapping from memories to values, which can be lifted to a mapping from distributions over memories to distributions over values. The definition of the interpretation is straightforward; the most interesting case is for expectation
is the interpretation of the state expression \(\tilde{e}\) in the memory m and valuation \(\rho \). The interpretation of state expressions is a mapping from memories to values, which can be lifted to a mapping from distributions over memories to distributions over values. The definition of the interpretation is straightforward; the most interesting case is for expectation  . We present the full interpretations in the supplemental materials.
. We present the full interpretations in the supplemental materials.
Many standard concepts from probability theory have a natural representation in our syntax. For example:
-
the probability that \(\phi \) holds in some probabilistic state is represented by the probabilistic expression \(\Pr [\phi ] \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\mathbb {E}_{} [{{\mathbf {1}}_{\phi }}]\);
-
probabilistic independence of state expressions \(\tilde{e}_1\), ..., \(\tilde{e}_n\) is modeled by the probabilistic assertion
 , defined by the clauseFootnote 4
$$\forall v_1 \ldots v_n,~ \Pr [\top ]^{n - 1} \Pr [\bigwedge _{i=1\ldots n} \tilde{e}_i = v_i] = \prod _{i=1\ldots n}\Pr [\tilde{e}_i = v_i] ; $$
, defined by the clauseFootnote 4
$$\forall v_1 \ldots v_n,~ \Pr [\top ]^{n - 1} \Pr [\bigwedge _{i=1\ldots n} \tilde{e}_i = v_i] = \prod _{i=1\ldots n}\Pr [\tilde{e}_i = v_i] ; $$ -
the fact that a distribution is proper is modeled by the probabilistic assertion \(\mathcal {L}\mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\Pr [\top ] = 1\);
-
a state expression \(\tilde{e}\) distributed according to a law g is modeled by the probabilistic assertion
$$ \tilde{e} \sim g \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\forall w,~ \Pr [\tilde{e}= w] = \mathbb {E}_{} [{\mathbb {E}_{{v} \sim {g}} [{{\mathbf {1}}_{v = w}}]}] .$$The inner expectation computes the probability that v drawn from g is equal to a fixed w; the outer expectation weights the inner probability by the probability of each value of w.
We can easily define \(\square \) operator from the previous section in our new syntax: \(\square {\phi } \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\Pr [\lnot \phi ] = 0\).
Syntactic Proof Rules. Now that we have a concrete syntax for assertions, we can give syntactic versions of many of the existing proof rules. Such proof rules are often easier to use since they avoid reasoning about the semantics of commands and assertions. We tackle the non-looping rules first, beginning with the following syntactic rules for assignment and sampling:

The rule for assignment is the usual rule from Hoare logic, replacing the program variable x by its corresponding expression e in the pre-condition. The replacement \(\eta [x := e]\) is done recursively on the probabilistic assertion \(\eta \); for instance for expectations, it is defined by \( \mathbb {E}_{} [{\tilde{e}}][x := e] \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\mathbb {E}_{} [{\tilde{e}[x := e]}] , \) where \(\tilde{e}[x := e]\) is the syntactic substitution.
The rule for sampling uses probabilistic substitution operator \(\mathcal {P}_{x}^{g}(\eta )\), which replaces all occurrences of x in \(\eta \) by a new integration variable t and records that t is drawn from g; the operator is defined in Fig. 6.
Next, we turn to the loop rule. The side-conditions from Fig. 3 are purely semantic, while in practice it is more convenient to use a sufficient condition in the Hoare logic. We give sufficient conditions for ensuring certain and almost-sure termination in Fig. 7; \(\tilde{e}\) is an integer-valued expression. The first side-condition \(\mathcal {C}_{\mathrm{CTerm}}\) shows certain termination given a strictly decreasing variant \(\tilde{e}\) that is bounded below, similar to how a decreasing variant shows termination for deterministic programs. The second side-condition \(\mathcal {C}_{\mathrm{ASTerm}}\) shows almost-sure termination given a probabilistic variant \(\tilde{e}\), which must be bounded both above and below. While \(\tilde{e}\) may increase with some probability, it must decrease with strictly positive probability. This condition was previously considered by [17] for probabilistic transition systems and also used in expectation-based approaches [20, 33]. Our framework can also support more refined conditions (e.g., based on super-martingales [9, 31]), but the condition \(\mathcal {C}_{\mathrm{ASTerm}}\) already suffices for most randomized algorithms.
While t-closedness is a semantic condition (cf. Definition 10), there are simple syntactic conditions to guarantee it. For instance, assertions that carry a non-strict comparison \(\bowtie \mathbin {\in } \{\le ,\ge ,=\}\) between two bounded probabilistic expressions are t-closed; the assertion stating probabilistic independence of a set of expressions is t-closed.
Precondition Calculus. With a concrete syntax for assertions, we are also able to incorporate syntactic reasoning principles. One classic tool is Morgan and McIver’s greatest pre-expectation, which we take as inspiration for a pre-condition calculus for the loop-free fragment of Ellora. Given an assertion \(\eta \) and a loop-free statement s, we mechanically construct an assertion \(\eta ^*\) that is the pre-condition of s that implies \(\eta \) as a post-condition. The basic idea is to replace each expectation expression p inside \(\eta \) by an expression \(p^*\) that has the same denotation before running s as p after running s. This process yields an assertion \(\eta ^*\) that, interpreted before running s, is logically equivalent to \(\eta \) interpreted after running s.
The computation rules for pre-conditions are defined in Fig. 8. For a probability assertion \(\eta \), its pre-condition \(\text {pc}(s,\eta )\) corresponds to \(\eta \) where the expectation expressions of the form \(\mathbb {E}_{} [{\tilde{e}}]\) are replaced by their corresponding pre-term, \(\text {pe}(s,\mathbb {E}_{} [{\tilde{e}}])\). Pre-terms correspond loosely to Morgan and McIver’s pre-expectations—we will make this correspondence more precise in the next section. The main interesting cases for computing pre-terms are for random sampling and conditionals. For random sampling the result is \(\mathcal {P}_{x}^{g}(\mathbb {E}_{} [{\tilde{e}}])\), which corresponds to the [Sample] rule. For conditionals, the expectation expression is split into a part where e is true and a part where e is not true. We restrict the expectation to a part satisfying e with the operator \( {\mathbb {E}_{} [{\tilde{e}}]}_{| e} \mathrel {{\mathop {=}\limits ^{\scriptscriptstyle \triangle }}}\mathbb {E}_{} [{\tilde{e}\cdot {\mathbf {1}}_{e}}] . \) This corresponds to the expected value of \(\tilde{e}\) on the portion of the distribution where e is true. Then, we can build the pre-condition calculus into Ellora.
Theorem 1
Let s be a non-looping command. Then, the following rule is derivable in the concrete version of Ellora:

6 Case Studies: Embedding Lightweight Logics
While Ellora is suitable for general-purpose reasoning about probabilistic programs, in practice humans typically use more special-purpose proof techniques—often targeting just a single, specific kind of property, like probabilistic independence—when proving probabilistic assertions. When these techniques apply, they can be a convenient and powerful tool.
To capture this intuitive style of reasoning, researchers have considered lightweight program logics where the assertions and proof rules are tailored to a specific proof technique. We demonstrate how to integrate these tools in an assertion-based logic by introducing and embedding a new logic for reasoning about independence and distribution laws, useful properties when analyzing randomized algorithms. We crucially rely on the rich assertions in Ellora—it is not clear how to extend expectation-based approaches to support similar, lightweight reasoning. Then, we show to embed the union bound logic [4] for proving accuracy bounds.
6.1 Law and Independence Logic
We begin by describing the law and independence logic IL, a proof system with intuitive rules that are easy to apply and amenable to automation. For simplicity, we only consider programs which sample from the binomial distribution, and have deterministic control flow—for lack of space, we also omit procedure calls.
Definition 12
(Assertions). IL assertions have the grammar:

where \(e\in \mathcal {E}\), \(E\subseteq \mathcal {E}\), and \(p\in [0,1]\).
The assertion \({\mathsf {det}}(e)\) states that e is deterministic in the current distribution, i.e., there is at most one element in the support of its interpretation. The assertion  states that the expressions in E are independent, as formalized in the previous section. The assertion \(e \sim {\mathrm {B}}(m,p)\) states that e is distributed according to a binomial distribution with parameter m (where m can be an expression) and constant probability p, i.e. the probability that \(e=k\) is equal to the probability that exactly k independent coin flips return heads using a biased coin that returns heads with probability p.
states that the expressions in E are independent, as formalized in the previous section. The assertion \(e \sim {\mathrm {B}}(m,p)\) states that e is distributed according to a binomial distribution with parameter m (where m can be an expression) and constant probability p, i.e. the probability that \(e=k\) is equal to the probability that exactly k independent coin flips return heads using a biased coin that returns heads with probability p.
Assertions can be seen as an instance of a logical abstract domain, where the order between assertions is given by implication based on a small number of axioms. Examples of such axioms include independence of singletons, irreflexivity of independence, anti-monotonicity of independence, an axiom for the sum of binomial distributions, and rules for deterministic expressions:

Definition 13
Judgments of the logic are of the form \(\left\{ \xi \right\} \;\,s\,\;\left\{ \xi '\right\} \), where \(\xi \) and \(\xi '\) are IL-assertions. A judgment is valid if it is derivable from the rules of Fig. 9; structural rules and rule for sequential composition are similar to those from Sect. 4 and omitted.
The rule [IL-Assgn] for deterministic assignments is as in Sect. 4. The rule [IL-Sample] for random assignments yields as post-condition that the variable x and a set of expressions E are independent assuming that E is independent before the sampling, and moreover that x follows the law of the distribution that it is sampled from. The rule [IL-Cond] for conditionals requires that the guard is deterministic, and that each of the branches satisfies the specification; if the guard is not deterministic, there are simple examples where the rule is not sound. The rule [IL-While] for loops requires that the loop is certainly terminating with a deterministic guard. Note that the requirement of certain termination could be avoided by restricting the structural rules such that a statement s has deterministic control flow whenever \(\left\{ \xi \right\} \;s\;\left\{ \xi '\right\} \) is derivable.
We now turn to the embedding. The embedding of IL assertions into general assertions is immediate, except for \({\mathsf {det}}(e)\) which is translated as \(\square {e}\vee \square {\lnot e}\). We let \(\overline{\xi }\) denote the translation of \(\xi \).
Theorem 2
(Embedding and soundness of IL logic). If \(\left\{ \xi \right\} \;\,s\,\;\left\{ \xi '\right\} \) is derivable in the IL logic, then \(\{\overline{\xi }\}\,s\,\{\overline{\xi '}\}\) is derivable in (the syntactic variant of) Ellora. As a consequence, every derivable judgment \(\left\{ \xi \right\} \;s\;\left\{ \xi '\right\} \) is valid.
Proof sketch
By induction on the derivation. The interesting cases are conditionals and loops. For conditionals, the soundness follows from the soundness of the rule:

To prove the soundness of this rule, we proceed by case analysis on \(\square {e} \vee \square {\lnot e}\). We treat the case \(\square {e}\); the other case is similar. In this case, \(\eta \) is equivalent to \(\eta _1\wedge \square {e} \oplus \eta _2\wedge \square {\lnot e}\), where \(\eta _1=\eta \) and \(\eta _2=\bot \). Let \(\eta _1'=\eta '\) and \(\eta _2=\square {\bot }\); again, \(\eta _1'\oplus \eta _2'\) is logically equivalent to \(\eta '\). The soundness of the rule thus follows from the soundness of the [Cond] and [Conseq] rules. For loops, there exists a natural number n such that \({\mathbf {while}}\,\, b \,\, {\mathbf {do}}\,\, s \) is semantically equivalent to \(({\mathbf {if}}\,\, b\,\, {\mathbf {then}}\,\, s)^n\). By assumption \(\left\{ \xi \right\} \;s\;\left\{ \xi \right\} \) holds, and thus by induction hypothesis \(\{\overline{\xi }\}\,s\,\{\overline{\xi }\}\). We also have \(\xi \implies {\mathsf {det}}(b)\), and hence \(\{\overline{\xi }\}\,{\mathbf {if}}\,\, b\,\, {\mathbf {then}}\,\, s\,\{\overline{\xi }\}\). We conclude by [Seq]. \(\square \)
To illustrate our system IL, consider the statement s in Fig. 10 which flips a fair coin N times and counts the number of heads. Using the logic, we prove that  is a post-condition for s. We take the invariant:
is a post-condition for s. We take the invariant:

The invariant holds initially, as \(0 \sim B(0,{1}/{2})\). For the inductive case, we show:

where \(s_0\) represents the loop body, i.e.  . First, we apply the rule for sequence taking as intermediate assertion
. First, we apply the rule for sequence taking as intermediate assertion

The first premise follows from the rule for random assignment and structural rules. The second premise follows from the rule for deterministic assignment and the rule of consequence, applying axioms about sums of binomial distributions.
We briefly comment on several limitations of IL. First, IL is restricted to programs with deterministic control flow, but this restriction could be partially relaxed by enriching IL with assertions for conditional independence. Such assertions are already expressible in the logic of Ellora; adding conditional independence would significantly broaden the scope of the IL proof system and open the possibility to rely on axiomatizations of conditional independence (e.g., based on graphoids [36]). Second, the logic only supports sampling from binomial distributions. It is possible to enrich the language of assertions with clauses \(c \sim g\) where g can model other distributions, like the uniform distribution or the Laplace distribution. The main design challenge is finding a core set of useful facts about these distributions. Enriching the logic and automating the analysis are interesting avenues for further work.
6.2 Embedding the Union Bound Logic
The program logic aHL [4] was recently introduced for estimating accuracy of randomized computations. One main application of aHL is proving accuracy of randomized algorithms, both in the offline and online settings—i.e. with adversary calls. aHL is based on the union bound, a basic tool from probability theory, and has judgments of the form  where s is a statement, \(\varPhi \) and \(\varPsi \) are first-order formulae over program variables, and \(\beta \) is a probability, i.e. \(\beta \in {[0,1]}\). A judgment
where s is a statement, \(\varPhi \) and \(\varPsi \) are first-order formulae over program variables, and \(\beta \) is a probability, i.e. \(\beta \in {[0,1]}\). A judgment  is valid if for every memory m such that \(\varPhi (m)\), the probability of \(\lnot \varPsi \) in
is valid if for every memory m such that \(\varPhi (m)\), the probability of \(\lnot \varPsi \) in  is upper bounded by \(\beta \), i.e.
is upper bounded by \(\beta \), i.e.  .
.
Figure 11 presents some key rules of aHL, including a rule for sampling from the Laplace distribution \(\mathcal {L}_\epsilon \) centered around e. The predicate \(\mathcal {C}_{\mathrm{CTerm}}(k)\) indicates that the loop terminates in at most k steps on any memory that satisfies the pre-condition. Moreover, \(\beta \) is a function of \(\epsilon \).
aHL has a simple embedding into Ellora.
Theorem 3
(Embedding of aHL). If  is derivable in aHL, then \(\{\square {\varPhi }\}\,s\,\{\mathbb {E}_{} [{{\mathbf {1}}_{\lnot \varPsi }}] \le \beta \}\) is derivable in Ellora.
is derivable in aHL, then \(\{\square {\varPhi }\}\,s\,\{\mathbb {E}_{} [{{\mathbf {1}}_{\lnot \varPsi }}] \le \beta \}\) is derivable in Ellora.
7 Case Studies: Verifying Randomized Algorithms
In this section, we will demonstrate Ellora on a selection of examples; we present further examples in the supplemental material. Together, they exhibit a wide variety of different proof techniques and reasoning principles which are available in the Ellora ’s implementation.
Hypercube Routing. will begin with the hypercube routing algorithm [41, 42]. Consider a network topology (the hypercube) where each node is labeled by a bitstring of length D and two nodes are connected by an edge if and only if the two corresponding labels differ in exactly one bit position.
In the network, there is initially one packet at each node, and each packet has a unique destination. The algorithm implements a routing strategy based on bit fixing: if the current position has bitstring i, and the target node has bitstring j, we compare the bits in i and j from left to right, moving along the edge that corrects the first differing bit. Valiant’s algorithm uses randomization to guarantee that the total number of steps grows logarithmically in the number of packets. In the first phase, each packet i select an intermediate destination \(\rho (i)\) uniformly at random, and use bit fixing to reach \(\rho (i)\). In the second phase, each packet use bit fixing to go from \(\rho (i)\) to the destination j. We will focus on the first phase since the reasoning for the second phase is nearly identical. We can model the strategy with the code in Fig. 12, using some syntactic sugar for the \({\mathbf {for}}\) loops.Footnote 5
We assume that initially, the position of the packet i is at node i (see  ). Then, we initialize the random intermediate destinations \(\rho \). The remaining loop encodes the evaluation of the routing strategy iterated T time. The variable
). Then, we initialize the random intermediate destinations \(\rho \). The remaining loop encodes the evaluation of the routing strategy iterated T time. The variable  is a map that logs if an edge is already used by a packet, it is empty at the beginning of each iteration. For each packet, we try to move it across one edge along the path to its intermediate destination. The function
is a map that logs if an edge is already used by a packet, it is empty at the beginning of each iteration. For each packet, we try to move it across one edge along the path to its intermediate destination. The function  returns the next edge to follow, following the bit-fixing scheme. If the packet can progress (its edge is not used), then its current position is updated and the edge is marked as used.
returns the next edge to follow, following the bit-fixing scheme. If the packet can progress (its edge is not used), then its current position is updated and the edge is marked as used.
We show that if the number of timesteps T is \(4 D + 1\), then all packets reach their intermediate destination in at most T steps, except with a small probability \(2^{-2D}\) of failure. That is, the number of timesteps grows linearly in D, logarithmic in the number of packets. This is formalized in our system as:

Modeling Infinite Processes. Our second example is the coupon collector process. The algorithm draws a uniformly random coupon (we have N coupon) on each day, terminating when it has drawn at least one of each kind of coupon. The code of the algorithm is displayed in Fig. 13; the array  records of the coupons seen so far,
records of the coupons seen so far,  holds the number of steps taken before seeing a new coupon, and X tracks of the total number of steps. Our goal is to bound the average number of iterations. This is formalized in our logic as:
holds the number of steps taken before seeing a new coupon, and X tracks of the total number of steps. Our goal is to bound the average number of iterations. This is formalized in our logic as:

Limited Randomness. Pairwise independence says that if we see the result of \(X_i\), we do not gain information about all other variables \(X_k\). However, if we see the result of two variables \(X_i, X_j\), we may gain information about \(X_k\). There are many constructions in the algorithms literature that grow a small number of independent bits into more pairwise independent bits. Figure 14 gives one procedure, where \(\oplus \) is exclusive-or, and  is the set of positions set to 1 in the binary expansion of
is the set of positions set to 1 in the binary expansion of  . The proof uses the following fact, which we fully verify: for a uniformly distributed Boolean random variable Y, and a random variable Z of any type,
. The proof uses the following fact, which we fully verify: for a uniformly distributed Boolean random variable Y, and a random variable Z of any type,

for any two Boolean functions f, g. Then, note that  where the big XOR operator ranges over the indices j where the bit representation of i has bit j set. For any two
where the big XOR operator ranges over the indices j where the bit representation of i has bit j set. For any two  distinct, there is a bit position in
distinct, there is a bit position in  where i and k differ; call this position r and suppose it is set in i but not in k. By rewriting,
where i and k differ; call this position r and suppose it is set in i but not in k. By rewriting,

Since  are all independent,
are all independent,  follows from Eq. (1) taking Z to be the distribution on tuples
follows from Eq. (1) taking Z to be the distribution on tuples  excluding
excluding  . This verifies pairwise independence:
. This verifies pairwise independence:

Adversarial Programs. Pseudorandom functions (PRF) and pseudorandom permutations (PRP) are two idealized primitives that play a central role in the design of symmetric-key systems. Although the most natural assumption to make about a blockcipher is that it behaves as a pseudorandom permutation, most commonly the security of such a system is analyzed by replacing the blockcipher with a perfectly random function. The PRP/PRF Switching Lemma [6, 22] fills the gap: given a bound for the security of a blockcipher as a pseudorandom function, it gives a bound for its security as a pseudorandom permutation.
Lemma 4
(PRP/PRF switching lemma). Let A be an adversary with blackbox access to an oracle O implementing either a random permutation on \(\{0,1\}^{l}\) or a random function from \(\{0,1\}^{l}\) to \(\{0,1\}^{l}\). Then the probability that the adversary A distinguishes between the two oracles in at most q calls is bounded by
where H is a map storing each adversary call and |H| is its size.
Proving this lemma can be done using the Fundamental Lemma of Game-Playing, and bounding the probability of bad in the program from Fig. 15. We focus on the latter. Here we apply the [Adv] rule of Ellora with the invariant  where |H| is the size of the map H, i.e. the number of adversary call. Intuitively, the invariant says that at each call to the oracle the probability that
where |H| is the size of the map H, i.e. the number of adversary call. Intuitively, the invariant says that at each call to the oracle the probability that  has been set before and that the number of adversary call is less than k is bounded by a polynomial in k.
has been set before and that the number of adversary call is less than k is bounded by a polynomial in k.
The invariant is d-closed and true before the adversary call, since at that point  . Then we need to prove that the oracle preserves the invariant, which can be done easily using the precondition calculus ([PC] rule).
. Then we need to prove that the oracle preserves the invariant, which can be done easily using the precondition calculus ([PC] rule).
8 Implementation and Mechanization
We have built a prototype implementation of Ellora within EasyCrypt [2, 5], a theorem prover originally designed for verifying cryptographic protocols. EasyCrypt provides a convenient environment for constructing proofs in various Hoare logics, supporting interactive, tactic-based proofs for manipulating assertions and allowing users to invoke external tools, like SMT-solvers, to discharge proof obligations. EasyCrypt provides a mature set of libraries for both data structures (sets, maps, lists, arrays, etc.) and mathematical theorems (algebra, real analysis, etc.), which we extended with theorems from probability theory.
We used the implementation for verifying many examples from the literature, including all the programs presented in Sect. 7 as well as some additional examples in Table 1 (such as polynomial identity test, private running sums, properties about random walks, etc.). The verified proofs bear a strong resemblance to the existing, paper proofs. Independently of this work, Ellora has been used to formalize the main theorem about a randomized gossip-based protocol for distributed systems [26, Theorem 2.1]. Some libraries developed in the scope of Ellora have been incorporated into the main branch of EasyCrypt, including a general library on probabilistic independence.
A New Library for Probabilistic Independence. In order to support assertions of the concrete program logic, we enhanced the standard libraries of EasyCrypt, notably the ones dealing with big operators and sub-distributions. Like all EasyCrypt libraries, they are written in a foundational style, i.e. they are defined instead of axiomatized. A large part of our libraries are proved formally from first principles. However, some results, such as concentration bounds, are currently declared as axioms.
Our formalization of probabilistic independence deserves special mention. We formalized two different (but logically equivalent) notions of independence. The first is in terms of products of probabilities, and is based on heterogenous lists. Since Ellora (like EasyCrypt) has no support for heterogeneous lists, we use a smart encoding based on second-order predicates. The second definition is more abstract, in terms of product and marginal distributions. While the first definition is easier to use when reasoning about randomized algorithms, the second definition is more suited for proving mathematical facts. We prove the two definitions equivalent, and formalize a collection of related theorems.
Mechanized Meta-Theory. The proofs of soundness and relative completeness of the abstract logic, without adversary calls, and the syntactical termination arguments have been mechanized in the Coq proof assistant. The development is available in supplemental material.
9 Related Work
More on Assertion-Based Techniques. The earliest assertion-based system is due to Ramshaw [37], who proposes a program logic where assertions can be formulas involving frequencies, essentially probabilities on sub-distributions. Ramshaw’s logic allows assertions to be combined with operators like \(\oplus \), similar to our approach. [18] presents a Hoare-style logic with general assertions on the distribution, allowing expected values and probabilities. However, his while rule is based on a semantic condition on the guarded loop body, which is less desirable for verification because it requires reasoning about the semantics of programs. [8] give decidability results for a probabilistic Hoare logic without while loops. We are not aware of any existing system that supports assertions about general expected values; existing works also restrict to Boolean distributions. [38] formalize a Hoare logic for probabilistic programs but unlike our work, their assertions are interpreted on distributions rather than sub-distributions. For conditionals, their semantics rescales the distribution of states that enter each branch. However, their assertion language is limited and they impose strong restrictions on loops.
Other Approaches. Researchers have proposed many other approaches to verify probabilistic program. For instance, verification of Markov transition systems goes back to at least [17, 40]; our condition for ensuring almost-sure termination in loops is directly inspired by their work. Automated methods include model checking (see e.g., [1, 25, 29]) and abstract interpretation (see e.g., [12, 32]). Techniques for reasoning about higher-order (functional) probabilistic languages are an active subject of research (see e.g., [7, 13, 14]). For analyzing probabilistic loops, in particular, there are tools for reasoning about running time. There are also automated systems for synthesizing invariants [3, 11]. [9, 10] use a martingale method to compute the expected time of the coupon collector process for \(N=5\)—fixing N lets them focus on a program where the outer while loop is fully unrolled. Martingales are also used by [15] for analyzing probabilistic termination. Finally, there are approaches involving symbolic execution; [39] use a mix of static and dynamic analysis to check probabilistic programs from the approximate computing literature.
10 Conclusion and Perspectives
We introduced an expressive program logic for probabilistic programs, and showed that assertion-based systems are suited for practical verification of probabilistic programs. Owing to their richer assertions, program logics are a more suitable foundation for specialized reasoning principles than expectation-based systems. As evidence, our program logic can be smoothly extended with custom reasoning for probabilistic independence and union bounds. Future work includes proving better accuracy bounds for differentially private algorithms, and exploring further integration of Ellora into EasyCrypt.
Notes
- 1.
Treating a program as a function from input states s to output distributions \(\mu (s)\), the expected value of E on \(\mu (s)\) is an expectation.
- 2.
Note that we do not give mathematically precise formulations of these points; as we are interested in the practical verification of probabilistic programs, a purely theoretical answer would not address our concerns.
- 3.
We work with discrete distributions to keep measure-theoretic technicalities to a minimum, though we do not see obstacles to generalizing to the continuous setting.
- 4.
The term \(\Pr [\top ]^{n - 1}\) is necessary since we work with sub-distributions.
- 5.
Recall that the number of node in a hypercube of dimension D is \(2^D\) so each node can be identified by a number in \([1,2^D]\).
References
Baier, C.: Probabilistic model checking. In: Dependable Software Systems Engineering, NATO Science for Peace and Security Series - D: Information and Communication Security, vol. 45, pp. 1–23. IOS Press (2016), https://doi.org/10.3233/978-1-61499-627-9-1
Barthe, G., Dupressoir, F., Grégoire, B., Kunz, C., Schmidt, B., Strub, P.-Y.: EasyCrypt: A tutorial. In: Aldini, A., Lopez, J., Martinelli, F. (eds.) FOSAD 2012-2013. LNCS, vol. 8604, pp. 146–166. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10082-1_6
Barthe, G., Espitau, T., Ferrer Fioriti, L.M., Hsu, J.: Synthesizing probabilistic invariants via Doob’s decomposition. In: International Conference on Computer Aided Verification (CAV), Toronto, Ontario (2016). https://arxiv.org/abs/1605.02765
Barthe, G., Gaboardi, M., Grégoire, B., Hsu, J., Strub, P.Y.: A program logic for union bounds. In: International Colloquium on Automata, Languages and Programming (ICALP), Rome, Italy (2016). http://arxiv.org/abs/1602.05681
Barthe, G., Grégoire, B., Heraud, S., Béguelin, S.Z.: Computer-aided security proofs for the working cryptographer. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 71–90. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_5
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: IACR International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT), Saint Petersburg, Russia, pp. 409–426 (2006). https://doi.org/10.1007/11761679_25
Bizjak, A., Birkedal, L.: Step-indexed logical relations for probability. In: Pitts, A. (ed.) FoSSaCS 2015. LNCS, vol. 9034, pp. 279–294. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46678-0_18
Chadha, R., Cruz-Filipe, L., Mateus, P., Sernadas, A.: Reasoning about probabilistic sequential programs. Theoretical Computer Science 379(1–2), 142–165 (2007)
Chakarov, A., Sankaranarayanan, S.: Probabilistic program analysis with martingales. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 511–526. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_34
Chakarov, A., Sankaranarayanan, S.: Expectation invariants for probabilistic program loops as fixed points. In: Müller-Olm, M., Seidl, H. (eds.) SAS 2014. LNCS, vol. 8723, pp. 85–100. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10936-7_6
Chatterjee, K., Fu, H., Novotný, P., Hasheminezhad, R.: Algorithmic analysis of qualitative and quantitative termination problems for affine probabilistic programs. In: ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL), Saint Petersburg, Florida, pp. 327–342 (2016). https://doi.org/10.1145/2837614.2837639
Cousot, P., Monerau, M.: Probabilistic abstract interpretation. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 169–193. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_9
Crubillé, R., Dal Lago, U.: On probabilistic applicative bisimulation and call-by-value \(\lambda \)-calculi. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 209–228. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54833-8_12
Dal Lago, U., Sangiorgi, D., Alberti, M.: On coinductive equivalences for higher-order probabilistic functional programs. In: ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL), San Diego, California, pp. 297–308 (2014). https://arxiv.org/abs/1311.1722
Fioriti, L.M.F., Hermanns, H.: Probabilistic termination: Soundness, completeness, and compositionality. In: ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL), Mumbai, India, pp. 489–501 (2015)
Gretz, F., Katoen, J.P., McIver, A.: Operational versus weakest pre-expectation semantics for the probabilistic guarded command language. Perform. Eval. 73, 110–132 (2014)
Hart, S., Sharir, M., Pnueli, A.: Termination of probabilistic concurrent programs. ACM Trans. Program. Lang. Syst. 5(3), 356–380 (1983)
den Hartog, J.: Probabilistic extensions of semantical models. Ph.D. thesis, Vrije Universiteit Amsterdam (2002)
Hurd, J.: Formal verification of probabilistic algorithms. Technical report, UCAM-CL-TR-566, University of Cambridge, Computer Laboratory (2003)
Hurd, J.: Verification of the Miller-Rabin probabilistic primality test. J. Log. Algebr. Program. 56(1–2), 3–21 (2003). https://doi.org/10.1016/S1567-8326(02)00065–6
Hurd, J., McIver, A., Morgan, C.: Probabilistic guarded commands mechanized in HOL. Theor. Comput. Sci. 346(1), 96–112 (2005)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: ACM SIGACT Symposium on Theory of Computing (STOC), Seattle, Washington, pp. 44–61 (1989). https://doi.org/10.1145/73007.73012
Kaminski, B.L., Katoen, J.-P., Matheja, C.: Inferring covariances for probabilistic programs. In: Agha, G., Van Houdt, B. (eds.) QEST 2016. LNCS, vol. 9826, pp. 191–206. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-43425-4_14
Kaminski, B., Katoen, J.P., Matheja, C., Olmedo, F.: Weakest precondition reasoning for expected run-times of probabilistic programs. In: European Symposium on Programming (ESOP), Eindhoven, The Netherlands, January 2016
Katoen, J.P.: The probabilistic model-checking landscape. In: IEEE Symposium on Logic in Computer Science (LICS), New York (2016)
Kempe, D., Dobra, A., Gehrke, J.: Gossip-based computation of aggregate information. In: Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, pp. 482–491 (2003). https://doi.org/10.1109/SFCS.2003.1238221
Kozen, D.: Semantics of probabilistic programs. J. Comput. Syst. Sci. 22, 328–350 (1981). https://www.sciencedirect.com/science/article/pii/0022000081900362
Kozen, D.: A probabilistic PDL. J. Comput. Syst. Sci. 30(2), 162–178 (1985)
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: Verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_47
McIver, A., Morgan, C.: Abstraction, refinement, and proof for probabilistic systems. Monographs in Computer Science. Springer, New York (2005)
McIver, A., Morgan, C., Kaminski, B.L., Katoen, J.P.: A new rule for almost-certain termination. In: Proceedings of the ACM on Programming Languages 1(POPL) (2018). https://arxiv.org/abs/1612.01091, appeared at ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL), Los Angeles, California
Monniaux, D.: Abstract interpretation of probabilistic semantics. In: Palsberg, J. (ed.) SAS 2000. LNCS, vol. 1824, pp. 322–339. Springer, Heidelberg (2000). https://doi.org/10.1007/978-3-540-45099-3_17
Morgan, C.: Proof rules for probabilistic loops. In: BCS-FACS Conference on Refinement, Bath, England (1996)
Morgan, C., McIver, A., Seidel, K.: Probabilistic predicate transformers. ACM Trans. Program. Lang. Syst. 18(3), 325–353 (1996)
Olmedo, F., Kaminski, B.L., Katoen, J.P., Matheja, C.: Reasoning about recursive probabilistic programs. In: IEEE Symposium on Logic in Computer Science (LICS), New York, pp. 672–681 (2016)
Pearl, J., Paz, A.: Graphoids: graph-based logic for reasoning about relevance relations. In: ECAI, pp. 357–363 (1986)
Ramshaw, L.H.: Formalizing the Analysis of Algorithms. Ph.D. thesis, Computer Science (1979)
Rand, R., Zdancewic, S.: VPHL: a verified partial-correctness logic for probabilistic programs. In: Conference on the Mathematical Foundations of Programming Semantics (MFPS), Nijmegen, The Netherlands (2015)
Sampson, A., Panchekha, P., Mytkowicz, T., McKinley, K.S., Grossman, D., Ceze, L.: Expressing and verifying probabilistic assertions. In: ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), Edinburgh, Scotland, p. 14 (2014)
Sharir, M., Pnueli, A., Hart, S.: Verification of probabilistic programs. SIAM J. Comput. 13(2), 292–314 (1984)
Valiant, L.G.: A scheme for fast parallel communication. SIAM J. Comput. 11(2), 350–361 (1982)
Valiant, L.G., Brebner, G.J.: Universal schemes for parallel communication. In: ACM SIGACT Symposium on Theory of Computing (STOC), Milwaukee, Wisconsin, pp. 263–277 (1981). https://doi.org/10.1145/800076.802479
Acknowledgments
We thank the reviewers for their helpful comments. This work benefited from discussions with Dexter Kozen, Annabelle McIver, and Carroll Morgan. This work was partially supported by ERC Grant #679127, and NSF grant 1718220.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
1 Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Barthe, G., Espitau, T., Gaboardi, M., Grégoire, B., Hsu, J., Strub, PY. (2018). An Assertion-Based Program Logic for Probabilistic Programs. In: Ahmed, A. (eds) Programming Languages and Systems. ESOP 2018. Lecture Notes in Computer Science(), vol 10801. Springer, Cham. https://doi.org/10.1007/978-3-319-89884-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-89884-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89883-4
Online ISBN: 978-3-319-89884-1
eBook Packages: Computer ScienceComputer Science (R0)






 of a statement s in initial state m is a sub-distribution over states.
of a statement s in initial state m is a sub-distribution over states. of a statement s in initial sub-distribution
of a statement s in initial sub-distribution 


 and
and 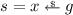 are trivial;
are trivial;
 premises can be directly proved using the induction hypothesis;
premises can be directly proved using the induction hypothesis;
 and
and  Both premises can be proved by an application of the [
Both premises can be proved by an application of the [
 and
and 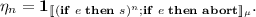

 , defined by the clause
, defined by the clause








