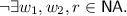Abstract
A valid compiler optimisation transforms a block in a program without introducing new observable behaviours to the program as a whole. Deciding which optimisations are valid can be difficult, and depends closely on the semantic model of the programming language. Axiomatic relaxed models, such as C++11, present particular challenges for determining validity, because such models allow subtle effects of a block transformation to be observed by the rest of the program. In this paper we present a denotational theory that captures optimisation validity on an axiomatic model corresponding to a fragment of C++11. Our theory allows verifying an optimisation compositionally, by considering only the block it transforms instead of the whole program. Using this property, we realise the theory in the first push-button tool that can verify real-world optimisations under an axiomatic memory model.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Context and Objectives. Any program defines a collection of observable behaviours: a sorting algorithm maps unsorted to sorted sequences, and a paint program responds to mouse clicks by updating a rendering. It is often desirable to transform a program without introducing new observable behaviours – for example, in a compiler optimisation or programmer refactoring. Such transformations are called observational refinements, and they ensure that properties of the original program will carry over to the transformed version. It is also desirable for transformations to be compositional, meaning that they can be applied to a block of code irrespective of the surrounding program context. Compositional transformations are particularly useful for automated systems such as compilers, where they are known as peephole optimisations.
The semantics of the language is highly significant in determining which transformations are valid, because it determines the ways that a block of code being transformed can interact with its context and thereby affect the observable behaviour of the whole program. Our work applies to a relaxed memory concurrent setting. Thus, the context of a code-block includes both code sequentially before and after the block, and code that runs in parallel. Relaxed memory means that different threads can observe different, apparently contradictory orders of events – such behaviour is permitted by programming languages to reflect CPU-level relaxations and to allow compiler optimisations.
We focus on axiomatic memory models of the type used in C/C++ and Java. In axiomatic models, program executions are represented by structures of memory actions and relations on them, and program semantics is defined by a set of axioms constraining these structures. Reasoning about the correctness of program transformations on such memory models is very challenging, and indeed, compiler optimisations have been repeatedly shown unsound with respect to models they were intended to support [23, 25]. The fundamental difficulty is that axiomatic models are defined in a global, non-compositional way, making it very challenging to reason compositionally about the single code-block being transformed.
Approach. Suppose we have a code-block B, embedded into an unknown program context. We define a denotation for the code-block which summarises its behaviour in a restricted representative context. The denotation consists of a set of histories which track interactions across the boundary between the code-block and its context, but abstract from internal structure of the code-block. We can then validate a transformation from code-block B to \(B'\) by comparing their denotations. This approach is compositional: it requires reasoning only about the code-blocks and representative contexts; the validity of the transformation in an arbitrary context will follow. It is also fully abstract, meaning that it can verify any valid transformation: considering only representative contexts and histories does not lose generality.
We also define a variant of our denotation that is finite at the cost of losing full abstraction. We achieve this by further restricting the form of contexts one needs to consider in exchange for tracking more information in histories. For example, it is unnecessary to consider executions where two context operations read from the same write.
Using this finite denotation, we implement a prototype verification tool, Stellite. Our tool converts an input transformation into a model in the Alloy language [12], and then checks that the transformation is valid using the Alloy* solver [18]. Our tool can prove or disprove a range of introduction, elimination, and exchange compiler optimisations. Many of these were verified by hand in previous work; our tool verifies them automatically.
Contributions. Our contribution is twofold. First, we define the first fully abstract denotational semantics for an axiomatic relaxed model. Previous proposals in this space targeted either non-relaxed sequential consistency [6] or much more restrictive operational relaxed models [7, 13, 21]. Second, we show it is feasible to automatically verify relaxed-memory program transformations. Previous techniques required laborious proofs by hand or in a proof assistant [23,24,25,26,27]. Our target model is derived from the C/C++ 2011 standard [22]. However, our aim is not to handle C/C++ per se (especially as the model is in flux in several respects; see Sect. 3.7). Rather we target the simplest axiomatic model rich enough to demonstrate our approach.
2 Observation and Transformation
Observational Refinement. The notion of observation is crucial when determining how different programs are related. For example, observations might be I/O behaviour or writes to special variables. Given program executions \(X_1\) and \(X_2\), we write \(X_1 \preccurlyeq _\mathsf{ex}X_2\) if the observations in \(X_1\) are replicated in \(X_2\) (defined formally in the following). Lifting this notion, a program \(P_1\) observationally refines another \(P_2\) if every observable behaviour of one could also occur with the other – we write this \(P_1 \preccurlyeq _\mathsf{pr}P_2\). More formally, let \(\llbracket - \rrbracket \) be the map from programs to sets of executions. Then we define \(\preccurlyeq _\mathsf{pr}\) as:

Compositional Transformation. Many common program transformations are compositional: they modify a sequential fragment of the program without examining the rest of the program. We call the former the code-block and the latter its context. Contexts can include sequential code before and after the block, and concurrent code that runs in parallel with it. Code-blocks are sequential, i.e. they do not feature internal concurrency. A context C and code-block B can be composed to give a whole program C(B).
A transformation \(B_2 \leadsto B_1\) replaces some instance of the code-block \(B_2\) with \(B_1\). To validate such a transformation, we must establish whether every whole program containing \(B_1\) observationally refines the same program with \(B_2\) substituted. If this holds, we say that \(B_1\) observationally refines \(B_2\), written \(B_1 \preccurlyeq _\mathsf{bl}B_2\), defined by lifting \(\preccurlyeq _\mathsf{pr}\) as follows:

If \(B_1 \preccurlyeq _\mathsf{bl}B_2\) holds, then the compiler can replace block \(B_2\) with block \(B_1\) irrespective of the whole program, i.e. \(B_2 \leadsto B_1\) is a valid transformation. Thus, deciding \(B_1 \preccurlyeq _\mathsf{bl}B_2\) is the core problem in validating compositional transformations.
The language semantics is highly significant in determining observational refinement. For example, the code blocks \(B_1 :\texttt {store(x,5)}\) and \(B_2 :\texttt {store(x,2); store(x,5)}\) are observationally equivalent in a sequential setting. However, in a concurrent setting the intermediate state, \(\mathtt{x} = 2\), can be observed in \(B_2\) but not \(B_1\), meaning the code-blocks are no longer observationally equivalent. In a relaxed-memory setting there is no global state seen by all threads, which further complicates the notion of observation.
Compositional Verification. To establish \(B_1 \preccurlyeq _\mathsf{bl}B_2\), it is difficult to examine all possible syntactic contexts. Our approach is to construct a denotation for each code-block – a simplified, ideally finite, summary of possible interactions between the block and its context. We then define a refinement relation on denotations and use it to establish observational refinement. We write \(B_1 \sqsubseteq B_2\) when the denotation of \(B_1\) refines \(B_2\).
Refinement on denotations should be adequate, i.e., it should validly approximate observational refinement: \( B_1 \sqsubseteq B_2 \implies B_1 \preccurlyeq _\mathsf{bl}B_2 \). Hence, if \(B_1 \sqsubseteq B_2\), then \(B_2 \leadsto B_1\) is a valid transformation. It is also desirable for the denotation to be fully abstract: \( B_1 \preccurlyeq _\mathsf{bl}B_2 \implies B_1 \sqsubseteq B_2 \). This means any valid transformation can be verified by comparing denotations. Below we define several versions of \(\sqsubseteq \) with different properties.
3 Target Language and Core Memory Model
Our language’s memory model is derived from the C/C++ 2011 standard (henceforth ‘C11’), as formalised by [5, 22]. However, we simplify our model in several ways; see the end of section for details. In C11 terms, our model covers release-acquire and non-atomic operations, and sequentially consistent fences. To simplify the presentation, at first we omit non-atomics, and extend our approach to cover them in Sect. 7. Thus, all operations in this section correspond to C11’s release-acquire.
3.1 Relaxed Memory Primer
In a sequentially consistent concurrent system, there is a total temporal order on loads and stores, and loads take the value of the most recent store; in particular, they cannot read overwritten values, or values written in the future. A relaxed (or weak) memory model weakens this total order, allowing behaviours forbidden under sequential consistency. Two standard examples of relaxed behaviour are store buffering (SB) and message passing (MP), shown in Fig. 1.
In most relaxed models \(\mathtt{v1}=\mathtt{v2}=0\) is a possible post-state for SB. This cannot occur on a sequentially consistent system: if \(\mathtt{v1}=0\), then store(y,1) must be ordered after the load of y, which would order store(x,1) before the load of x, forcing it to assign \(\mathtt{v2} =1\). In some relaxed models, \(\mathtt{b} = 1 \wedge \mathtt{r} = 0\) is a possible post-state for MP. This is undesirable if, for example, x is a complex data-structure and f is a flag indicating it has been safely created.
3.2 Language Syntax
Programs in the language we consider manipulate thread-local variables \(l, l_1, l_2 \ldots \in \mathsf{LVar}\) and global variables \(x,y,\ldots \in \mathsf{GVar}\), coming from disjoint sets \(\mathsf{LVar}\) and \(\mathsf{GVar}\). Each variable stores a value from a finite set Val and is initialised to \(0 \in \mathsf{Val}\). Constants are encoded by special read-only thread-local variables. We assume that each thread uses the same set of thread-local variable names LVar. The syntax of the programming language is as follows:

Many of the constructs are standard. \(\mathtt{LL}(x)\) and \(\mathtt{SC}(x,l)\) are load-link and store-conditional, which are basic concurrency operations available on many platforms (e.g., Power and ARM). A load-link \(\mathtt{LL}(x)\) behaves as a standard load of global variable x. However, if it is followed by a store-conditional \(\mathtt{SC}(x,l)\), the store fails and returns false if there are intervening writes to the same location. Otherwise the store-conditional writes l and returns true. The fence command is a sequentially consistent fence: interleaving such fences between all statements in a program guarantees sequentially consistent behaviour. We do not include compare-and-swap (CAS) command in our language because LL-SC is more general [2]. Hardware-level LL-SC is used to implement C11 CAS on Power and ARM. Our language does not include loops because our model in this paper does not include infinite computations (see Sect. 3.7 for discussion). As a result, loops can be represented by their finite unrollings. Our load commands write into a local variable. In examples, we sometimes use ‘bare’ loads without a variable write.
The construct \(\{ - \}\) represents a block-shaped hole in the program. To simplify our presentation, we assume that at most one hole appears in the program. Transformations that apply to multiple blocks at once can be simulated by using the fact our approach is compositional: transformations can be applied in sequence using different divisions of the program into code-block and context.
The set Prog of whole programs consists of programs without holes, while the set Contx of contexts consists of programs with a hole. The set Block of code-blocks are whole programs without parallel composition. We often write \(P \in \mathsf{Prog}\) for a whole program, \(B \in \mathsf{Block}\) for a code-block, and \(C \in \mathsf{Contx} \) for a context. Given a context C and a code-block B, the composition C(B) is C with its hole syntactically replaced by B. For example:

We restrict Prog, Contx and Block to ensure LL-SC pairs are matched correctly. Each SC must be preceded in program order by a LL to the same location. Other types of operations may occur between the LL and SC, but intervening SC operations are forbidden. For example, the program LL(x); SC(x,v1); SC(x,v2); is forbidden. We also forbid LL-SC pairs from spanning parallel compositions, and from spanning the block/context boundary.
3.3 Memory Model Structure
The semantics of a whole program P is given by a set \(\llbracket P \rrbracket \) of executions, which consist of actions, representing memory events on global variables, and several relations on these. Actions are tuples in the set \(\mathsf{Action}\, {\mathop {=}\limits ^{\varDelta }}\, \mathsf{ActID} \times \mathsf{Kind} \times \mathsf{Option}(\mathsf{GVar}) \times \mathsf{Val}^{*} \). In an action \((a,k,z,b) \in \mathsf{Action}\): \(a \in \mathsf{ActID}\) is the unique action identifier; \(k \in \mathsf{Kind}\) is the kind of action – we use load, store, LL, SC, and the failed variant \({\mathsf{SC}_f}\) in the semantics, and will introduce further kinds as needed; \(z \in \mathsf{Option}(\mathsf{GVar})\) is an option type consisting of either a single global variable \(\mathsf{Just}(x)\) or None; and \(b \in \mathsf{Val}^{*}\) is the vector of values (actions with multiple values are used in Sect. 4).
Given an action v, we use \(\mathsf{gvar}(v)\) and \(\mathsf{val}(v)\) as selectors for the different fields. We often write actions so as to elide action identifiers and the option type. For example, \(\mathsf{load}(x,3)\) stands for  . We also sometimes elide values. We call \(\mathsf{load}\) and \(\mathsf{LL}\) actions reads, and \(\mathsf{store}\) and successful \(\mathsf{SC}\) actions writes. Given a set of actions \({\mathcal {A}}\), we write, e.g., \(\mathsf{reads}({\mathcal {A}})\) to identify read actions in \({\mathcal {A}}\). Below, we range over all actions by u, v; read actions by r; write actions by w; and LL, SC actions by \(\textit{ll}\) and \(\textit{sc}\) respectively.
. We also sometimes elide values. We call \(\mathsf{load}\) and \(\mathsf{LL}\) actions reads, and \(\mathsf{store}\) and successful \(\mathsf{SC}\) actions writes. Given a set of actions \({\mathcal {A}}\), we write, e.g., \(\mathsf{reads}({\mathcal {A}})\) to identify read actions in \({\mathcal {A}}\). Below, we range over all actions by u, v; read actions by r; write actions by w; and LL, SC actions by \(\textit{ll}\) and \(\textit{sc}\) respectively.
Selected clauses of the thread-local semantics. The full semantics is given in [10, Sect. A]. We write  for a union that is defined only when actions in \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) use disjoint sets of identifiers. We omit identifiers from actions to avoid clutter.
for a union that is defined only when actions in \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) use disjoint sets of identifiers. We omit identifiers from actions to avoid clutter.
The semantics of a program \(P \in \mathsf{Prog}\) is defined in two stages. First, a thread-local semantics of P produces a set \(\langle P \rangle \) of pre-executions \(({\mathcal {A}}, \mathsf{sb}) \in \mathsf{PreExec}\). A pre-execution contains a finite set of memory actions \({\mathcal {A}}\subseteq \mathsf{Action}\) that could be produced by the program. It has a transitive and irreflexive sequence-before relation \(\mathsf{sb}\subseteq {\mathcal {A}}\times {\mathcal {A}}\), which defines the sequential order imposed by the program syntax.
For example two sequential statements in the same thread produce actions ordered in sb. The thread-local semantics takes into account control flow in P’s threads and operations on local variables. However, it does not constrain the behaviour of global variables: the values threads read from them are chosen arbitrarily. This is addressed by extending pre-executions with extra relations, and filtering the resulting executions using validity axioms.
3.4 Thread-Local Semantics
The thread-local semantics is defined formally in Fig. 2. The semantics of a program \(P \in \mathsf{Prog}\) is defined using function \( \langle -, - \rangle :\mathsf{Prog} \times \mathsf{VMap} \rightarrow \mathcal {P}(\mathsf{PreExec} \times \mathsf{VMap}) \). The values of local variables are tracked by a map \(\sigma \in \mathsf{VMap} {\mathop {=}\limits ^{\varDelta }}\mathsf{LVar} \rightarrow \mathsf{Val}\). Given a program and an input local variable map, the function produces a set of pre-executions paired with an output variable map, representing the values of local variables at the end of the execution. Let \(\sigma _0\) map every local variable to 0. Then \(\langle P \rangle \), the thread-local semantics of a program P, is defined as
The significant property of the thread-local semantics is that it does not restrict the behaviour of global variables. For this reason, note that the clause for load in Fig. 2 leaves the value a unrestricted. We follow [16] in encoding the fence command by a successful \(\mathsf{LL}\)-\(\mathsf{SC}\) pair to a distinguished variable \(\textit{fen} \in \mathsf{GVar}\) that is not otherwise read or written.
3.5 Execution Structure and Validity Axioms
The semantics of a program P is a set \(\llbracket P \rrbracket \) of executions \(X = ({\mathcal {A}}, \mathsf{sb}, \mathsf{at}, \mathsf{rf}, \mathsf{mo}, \mathsf{hb}) \in \mathsf{Exec}\), where \(({\mathcal {A}}, \mathsf{sb})\) is a pre-execution and \(\mathsf{at}, \mathsf{rf}, \mathsf{mo}, \mathsf{hb}\subseteq {\mathcal {A}}\times {\mathcal {A}}\). Given an execution X we sometimes write \({\mathcal {A}}(X), \mathsf{sb}(X), \ldots \) as selectors for the appropriate set or relation. The relations have the following purposes.
-
Reads-from (rf) is an injective map from reads to writes at the same location of the same value. A read and a write actions are related
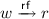 if r takes its value from w.
if r takes its value from w. -
Modification order (mo) is an irreflexive, total order on write actions to each distinct variable. This is a per-variable order in which all threads observe writes to the variable; two threads cannot observe these writes in different orders.
-
Happens-before (hb) is analogous to global temporal order – but unlike the sequentially consistent notion of time, it is partial. Happens-before is defined as \((\mathsf{sb}\cup \mathsf{rf})^+\): therefore statements ordered in the program syntax are ordered in time, as are reads with the writes they observe.
-
Atomicity (\(\mathsf{at}\subseteq \mathsf{sb}\)) is an extension to standard C11 which we use to support LL-SC (see below). It is an injective function from a successful load-link action to a successful store-conditional, giving a LL-SC pair.
The semantics \(\llbracket P \rrbracket \) of a program P is the set of executions \(X \in \mathsf{Exec}\) compatible with the thread-local semantics and the validity axioms, denoted \(\mathsf{valid}(X)\):

The validity axioms on an execution  are:
are:
-
HBdef:
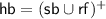 and
and 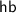 is acyclic.
is acyclic.This axiom defines hb and enforces the intuitive property that there are no cycles in the temporal order. It also prevents an action reading from its hb-future: as rf is included in hb, this would result in a cycle.
-
HBvsMO: \(\lnot \exists w_1, w_2.\)
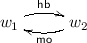 This axiom requires that the order in which writes to a location become visible to threads cannot contradict the temporal order. But take note that writes may be ordered in mo but not hb.
This axiom requires that the order in which writes to a location become visible to threads cannot contradict the temporal order. But take note that writes may be ordered in mo but not hb. -
Coherence: \(\lnot \exists w_1, w_2, r.\)
 This axiom generalises the sequentially consistent prohibition on reading overwritten values. If two writes are ordered in mo, then intuitively the second overwrites the first. A read that follows some write in hb or mo cannot read from writes earlier in mo – these earlier writes have been overwritten. However, unlike in sequential consistency, hb is partial, so there may be multiple writes that an action can legally read.
This axiom generalises the sequentially consistent prohibition on reading overwritten values. If two writes are ordered in mo, then intuitively the second overwrites the first. A read that follows some write in hb or mo cannot read from writes earlier in mo – these earlier writes have been overwritten. However, unlike in sequential consistency, hb is partial, so there may be multiple writes that an action can legally read. -
RFval:
 Most reads must take their value from a write, represented by an rf edge. However, the RFval axiom allows the rf edge to be omitted if the read takes the initial value 0 and there is no hb-earlier write to the same location. Intuitively, an hb-earlier write would supersede the initial value in a similar way to Coherence.
Most reads must take their value from a write, represented by an rf edge. However, the RFval axiom allows the rf edge to be omitted if the read takes the initial value 0 and there is no hb-earlier write to the same location. Intuitively, an hb-earlier write would supersede the initial value in a similar way to Coherence. -
Atom:
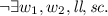
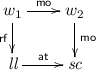 This axiom is adapted from [16]. For an LL-SC pair \(\textit{ll}\) and \(\textit{sc}\), it ensures that there is no mo-intervening write \(w_2\) that would invalidate the store.
This axiom is adapted from [16]. For an LL-SC pair \(\textit{ll}\) and \(\textit{sc}\), it ensures that there is no mo-intervening write \(w_2\) that would invalidate the store.
Our model forbids the problematic relaxed behaviour of the message-passing (MP) program in Fig. 1 that yields \(\mathtt{b} = 1 \wedge \mathtt{r} = 0\). Figure 3 shows an (invalid) execution that would exhibit this behaviour. To avoid clutter, here and in the following we omit hb edges obtained by transitivity and local variable values. This execution is allowed by the thread-local semantics of the MP program, but it is ruled out by the Coherence validity axiom. As hb is transitively closed, there is a derived hb edge  , which forms a Coherence violation. Thus, this is not an execution of the MP program. Indeed, any execution ending in \(\mathsf{load}(\mathtt{x}, 0)\) is forbidden for the same reason, meaning that the MP relaxed behaviour cannot occur.
, which forms a Coherence violation. Thus, this is not an execution of the MP program. Indeed, any execution ending in \(\mathsf{load}(\mathtt{x}, 0)\) is forbidden for the same reason, meaning that the MP relaxed behaviour cannot occur.
3.6 Relaxed Observations
Finally, we define a notion of observational refinement suitable for our relaxed model. We assume a subset of observable global variables, \(\textsf {OVar} \subseteq \mathsf{GVar}\), which can only be accessed by the context and not by the code-block. We consider the actions and the hb relation on these variables to be the observations. We write \(X|_{\textsf {OVar}}\) for the projection of X’s action set and relations to \(\textsf {OVar}\), and use this to define \(\preccurlyeq _\mathsf{ex}\) for our model:

This is lifted to programs and blocks as in Sect. 2, def. (1) and (2). Note that in the more abstract execution, actions on observable variables must be the same, but hb can be weaker. This is because we interpret hb as a constraint on time order: two actions that are unordered in hb could have occurred in either order, or in parallel. Thus, weakening hb allows more observable behaviours (see Sect. 2).
3.7 Differences from C11
Our language’s memory model is derived from the C11 formalisation in [5], with a number of simplifications. We chose C11 because it demonstrates most of the important features of axiomatic language models. However, we do not target the precise C11 model: rather we target an abstracted model that is rich enough to demonstrate our approach. Relaxed language semantics is still a very active topic of research, and several C11 features are known to be significantly flawed, with multiple competing fixes proposed. Some of our differences from [5] are intended to avoid such problematic features so that we can cleanly demonstrate our approach.
In C11 terms, our model covers release-acquire and non-atomic operations (the latter addressed in Sect. 7), and sequentially consistent fences. We deviate from C11 in the following ways:
-
We omit sequentially consistent accesses because their semantics is known to be flawed in C11 [17]. We do handle sequentially consistent fences, but these are stronger than those of C11: we use the semantics proposed in [16]. It has been proved sound under existing compilation strategies to common multiprocessors.
-
We omit relaxed (RLX) accesses to avoid well-known problems with thin-air values [4]. There are multiple recent competing proposals for fixing these problems, e.g. [14, 15, 20].
-
Our model does not include infinite computations, because their semantics in C11-style axiomatic models remains undecided in the literature [4]. However, our proofs do not depend on the assumption that execution contexts are finite.
-
Our language is based on shared variables, not dynamically allocated addressable memory, so for example we cannot write y:=*x; z:=*y. This simplifies our theory by allowing us to fix the variables accessed by a code-block up-front. We believe our results can be extended to support addressable memory, because C11-style models grant no special status to pointers; we elaborate on this in Sect. 4.
-
We add LL-SC atomic instructions to our language in addition to C11’s standard CAS. To do this, we adapt the approach of [16]. This increases the observational power of a context and is necessary for full abstraction in the presence of non-atomics; see Sect. 8. LL-SC is available as a hardware instruction on many platforms supporting C11, such as Power and ARM. However, we do not propose adding LL-SC to C11: rather, it supports an interesting result in relaxed memory model theory. Our adequacy results do not depend on LL-SC.
4 Denotations of Code-Blocks
We construct the denotation for a code-block in two steps: (1) generate the block-local executions under a set of special cut-down contexts; (2) from each execution, extract a summary of interactions between the code-block and the context called a history.
4.1 Block-Local Executions
The block-local executions of a block \(B \in \mathsf{Block}\) omit context structure such as syntax and actions on variables not accessed in the block. Instead the context is represented by special actions call and ret, a set \({\mathcal {A}}_B\), and relations \(R_B\) and \(S_B\), each covering an aspect of the interaction of the block and an arbitrary unrestricted context. Together, each choice of \(\mathsf{call} \), \(\mathsf{ret} \), \({\mathcal {A}}_B\), \(R_B\), and \(S_B\) abstractly represents a set of possible syntactic contexts. By quantifying over the possible values of these parameters, we cover the behaviour of all syntactic contexts. The parameters are defined as follows:
-
Local variables. A context can include code that precedes and follows the block on the same thread, with interaction through local variables, but – due to syntactic restriction – not through \(\mathsf{LL}\)/\(\mathsf{SC}\) atomic regions. We capture this with special action \(\mathsf{call} (\sigma )\) at the start of the block, and \(\mathsf{ret} (\sigma ')\) at the end, where \(\sigma , \sigma ' :\mathsf{LVar} \rightarrow \mathsf{Val}\) record the values of local variables at these points. Assume that variables in LVar are ordered: \(l_1, l_2, \ldots , l_n\). Then \(\mathsf{call} (\sigma )\) is encoded by the action \( (i, \mathsf{call}, \mathsf{None}, [\sigma (l_1),\, \ldots \, \sigma (l_n)] ) \), with fresh identifier i. We encode \(\mathsf{ret} \) in the same way.
-
Global variable actions. The context can also interact with the block through concurrent reads and writes to global variables. These interactions are represented by set \({\mathcal {A}}_B\) of context actions added to the ones generated by the thread-local semantics of the block. This set only contains actions on the variables \(\mathsf{VS}_B\) that B can access (\(\mathsf{VS}_B\) can be constructed syntactically). Given an execution X constructed using \({\mathcal {A}}_B\) (see below) we write \(\mathsf{contx}(X)\) to recover the set \({\mathcal {A}}_B\).
-
Context happens-before. The context can generate \(\mathsf{hb}\) edges between its actions, which affect the behaviour of the block. We track these effects with a relation \(R_B\) over actions in \({\mathcal {A}}_B\), call and ret :
 (4)
(4)The context can generate hb edges between actions directly if they are on the same thread, or indirectly through inter-thread reads. Likewise call /ret may be related to context actions on the same or different threads.
-
Context atomicity. The context can generate \(\mathsf{at}\) edges between its actions that we capture in the relation \(S_B \subseteq {\mathcal {A}}_B \times {\mathcal {A}}_B\). We require this relation to be an injective function from \(\mathsf{LL}\) to \(\mathsf{SC}\) actions. We consider only cases where LL/SC pairs do not cross block boundaries, so we need not consider boundary-crossing \(\mathsf{at}\) edges.
Together, \(\mathsf{call} \), \(\mathsf{ret} \), \({\mathcal {A}}_B\), \(R_B\), and \(S_B\) represent a limited context, stripped of syntax, relations sb, mo, and rf, and actions on global variables other than \(\mathsf{VS}_B\). When constructing block-local executions, we represent all possible interactions by quantifying over all possible choices of \(\sigma \), \(\sigma '\), \({\mathcal {A}}_B\), \(R_B\) and \(S_B\). The set \(\llbracket B, {\mathcal {A}}_B, R_B, S_B \rrbracket \) contains all executions of B under this special limited context. Formally, an execution \(X = ({\mathcal {A}}, \mathsf{sb}, \mathsf{at}, \mathsf{rf}, \mathsf{mo}, \mathsf{hb})\) is in this set if:
-
1.
\({\mathcal {A}}_B \subseteq {\mathcal {A}}\) and there exist variable maps \(\sigma , \sigma '\) such that \(\{ \mathsf{call} (\sigma ), \mathsf{ret} (\sigma ')\} \subseteq {\mathcal {A}}\). That is, the call, return, and extra context actions are included in the execution.
-
2.
There exists a set \({\mathcal {A}}_l\) and relation \(\mathsf{sb}_l\) such that (i) \(({\mathcal {A}}_l, \mathsf{sb}_l, \sigma ') \in \langle B, \sigma \rangle \); (ii) \({\mathcal {A}}_l = {\mathcal {A}}\setminus ({\mathcal {A}}_B \cup \{\mathsf{call}, \mathsf{ret} \})\); (iii) \(\mathsf{sb}_l = \mathsf{sb}\setminus \{ (\mathsf{call}, u), (u, \mathsf{ret}) \mid u \in {\mathcal {A}}_l \}\). That is, actions from the code-block satisfy the thread-local semantics, beginning with map \(\sigma \) and deriving map \(\sigma '\). All actions arising from the block are between \(\mathsf{call} \) and \(\mathsf{ret} \) in sb.
-
3.
X satisfies the validity axioms, but with modified axioms HBdef\('\) and Atom\('\). We define HBdef\('\) as: \(\mathsf{hb}= (\mathsf{sb}\cup \mathsf{rf}\cup R_B)^{+}\) and hb is acyclic. That is, context relation \(R_B\) is added to \(\mathsf{hb}\).
 is defined analogously with \(S_B\) added to \(\mathsf{at}\).
is defined analogously with \(S_B\) added to \(\mathsf{at}\).
We say that \({\mathcal {A}}_B\), \(R_B\) and \(S_B\) are consistent with B if they act over variables in the set \(\mathsf{VS}_B\). In the rest of the paper we only consider consistent choices of \({\mathcal {A}}_B\), \(R_B\), \(S_B\). The block-local executions of B are then all executions \(X \in \llbracket B, {\mathcal {A}}_B, R_B, S_B \rrbracket \).Footnote 1
Example Block-Local Execution. The left of Fig. 4 shows a block-local execution for the code-block
Here the set \(\mathsf{VS}_B\) of accessed global variables is \(\{ \mathtt{f}, \mathtt{x} \}\), As before, we omit local variables to avoid clutter. The context action set \({\mathcal {A}}_B\) consists of the three stores, and \(R_B\) is denoted by dotted edges.
In this execution, both \({\mathcal {A}}_B\) and \(R_B\) affect the behaviour of the code-block. The following path is generated by \(R_B\) and the load of \(\mathtt{f}=1\):

Because hb includes sb, rf, and \(R_B\), there is a transitive edge  . The edge
. The edge  is forced because the HBvsMO axiom prohibits mo from contradicting hb. Consequently, the Coherence axiom forces the code-block to read \(\mathtt{x}=1\).
is forced because the HBvsMO axiom prohibits mo from contradicting hb. Consequently, the Coherence axiom forces the code-block to read \(\mathtt{x}=1\).
4.2 Histories
From any block-local execution X, its history summarises the interactions between the code-block and the context. Informally, the history records \(\mathsf{hb}\) over context actions, call, and ret. More formally the history, written \(\mathsf{hist}(X)\), is a pair \(({\mathcal {A}}, G)\) consisting of an action set \({\mathcal {A}}\) and guarantee relation \(G \subseteq {\mathcal {A}}\times {\mathcal {A}}\). Recall that we use \(\mathsf{contx}(X)\) to denote the set of context actions in X. Using this, we define the history as follows:
-
The action set \({\mathcal {A}}\) is the projection of X’s action set to call, ret, and \(\mathsf{contx}(X)\).
-
The guarantee relation G is the projection of \(\mathsf{hb}(X)\) to
 (6)
(6)
The guarantee summarises the code-block’s effect on its context: it suffices to only track hb and ignore other relations. Note the guarantee definition is similar to the context relation \(R_B\), definition (4). The difference is that call and ret are switched: this is because the guarantee represents hb edges generated by the code-block, while \(R_B\) represents the edges generated by the context. The right of Fig. 4 shows the history corresponding to the block-local execution on the left.
To see the interactions captured by the guarantee, compare the block given in def. (5) with the block l2:=load(x). These blocks have differing effects on the following syntactic context:

For the two-load block embedded into this context, \(\mathtt{l1} = 1 \wedge \mathtt{l3} = 1\) is not a possible post-state. For the single-load block, this post-state is permitted.Footnote 2
In Fig. 5, we give executions for both blocks embedded into this context. We draw the context actions that are not included into the history in grey. In these executions, the code block determines whether the load of y can read value 1 (represented by the edge labelled ‘rf?’). In the first execution, the context load of y cannot read 1 because there is the path  which would contradict the Coherence axiom. In the second execution there is no such path and the load may read 1.
which would contradict the Coherence axiom. In the second execution there is no such path and the load may read 1.
It is desirable for our denotation to hide the precise operations inside the block – this lets it relate syntactically distinct blocks. Nonetheless, the history must record hb effects such as those above that are visible to the context. In Execution 1, the Coherence violation is still visible if we only consider context operations, call, ret, and the guarantee G – i.e. the history. In Execution 2, the fact that the read is permitted is likewise visible from examining the history. Thus the guarantee, combined with the local variable post-states, capture the effect of the block on the context without recording the actions inside the block.
4.3 Comparing Denotations
The denotation of a code-block B is the set of histories of block-local executions of B under each possible context, i.e. the set

To compare the denotations of two code-blocks, we first define a refinement relation on histories: \( ({\mathcal {A}}_1, G_1) \sqsubseteq _\mathsf{h}({\mathcal {A}}_2,G_2) \) holds iff \( {\mathcal {A}}_1 = {\mathcal {A}}_2 \wedge G_2 \subseteq G_1 \). The history \(({\mathcal {A}}_2, G_2)\) places fewer restrictions on the context than \(({\mathcal {A}}_1, G_1)\) – a weaker guarantee corresponds to more observable behaviours. For example in Fig. 5, History 1 \(\sqsubseteq _\mathsf{h}\) History 2 but not vice versa, which reflects the fact that History 1 rules out the read pattern discussed above.
We write \(B_1 \sqsubseteq _\mathsf{q}B_2\) to state that the denotation of \(B_1\) refines that of \(B_2\). The subscript ‘q’ stands for the fact we quantify over both \({\mathcal {A}}\) and \(R_B\). We define \(\sqsubseteq _\mathsf{q}\) by lifting \(\sqsubseteq _\mathsf{h}\):

In other words, two code-blocks are related \(B_1 \sqsubseteq _\mathsf{q}B_2\) if for every block-local execution of \(B_1\), there is a corresponding execution of \(B_2\) with a related history. Note that the corresponding history must be constructed under the same cut-down context \({\mathcal {A}}, R, S\).
Theorem 1
(Adequacy of \(\sqsubseteq _\mathsf{q}\)). \(B_1 \sqsubseteq _\mathsf{q}B_2 \implies B_1 \preccurlyeq _\mathsf{bl}B_2\).
Theorem 2
(Full abstraction of \(\sqsubseteq _\mathsf{q}\)). \(B_1 \preccurlyeq _\mathsf{bl}B_2 \implies B_1 \sqsubseteq _\mathsf{q}B_2\).
As a corollary of the above theorems, a program transformation \(B_2 \leadsto B_1\) is valid if and only if \(B_1 \sqsubseteq _\mathsf{q}B_2\) holds. We prove Theorem 1 in [10, Sect. B]. We give a proof sketch of Theorem 2 in Sect. 8 and a full proof in [10, Sect. F].
4.4 Example Transformation
We now consider how our approach applies to a simple program transformation:

To verify this transformation, we must show that \(B_1 \sqsubseteq _\mathsf{q}B_2\). To do this, we must consider the unboundedly many block-local executions. Here we just illustrate the reasoning for a single block-local execution; in Sect. 5 below we define a context reduction which lets us consider a finite set of such executions.
In Fig. 6, we illustrate the necessary reasoning for an execution \(X_1 \in \llbracket B_1, {\mathcal {A}}, R, S \rrbracket \), with a context action set \({\mathcal {A}}\) consisting of a single load \(\mathtt{x} = 1\), a context relation R relating ret to the load, and an empty S relation. This choice of R forces the context load to read from the store in the block. We can exhibit an execution \(X_2 \in \llbracket B_2, {\mathcal {A}}, R, S \rrbracket \) with a matching history by making the context load read from the final store in the block.
5 A Finite Denotation
The approach above simplifies contexts by removing syntax and non-hb structure, but there are still infinitely many \({\mathcal {A}}/ R / S\) contexts for any code-block. To solve this, we introduce a type of context reduction which allows us to consider only finitely many block-local executions. This means that we can automatically check transformations by examining all such executions. However this ‘cut down’ approach is no longer fully abstract. We modify our denotation as follows:
-
We remove the quantification over context relation R from definition (7) by fixing it as \(\emptyset \). In exchange, we extend the history with an extra component called a deny.
-
We eliminate redundant block-local executions from the denotation, and only consider a reduced set of executions X that satisfy a predicate \(\mathsf{cut}(X)\).
These two steps are both necessary to achieve finiteness. Removing the R relation reduces the amount of structure in the context. This makes it possible to then remove redundant patterns – for example, duplicate reads from the same write.
Before defining the two steps in detail, we give the structure of our modified refinement \(\sqsubseteq _\mathsf{c}\). In the definition, \({\mathsf{hist}_\mathsf{E}}(X)\) stands for the extended history of an execution X, and \(\sqsubseteq _\mathsf{E}\) for refinement on extended histories.

As with \(\sqsubseteq _\mathsf{q}\) above, the refinement \(\sqsubseteq _\mathsf{c}\) is adequate. However, it is not fully abstract (we provide a counterexample in [10, Sect. D]). We prove the following theorem in [10, Sect. E].
Theorem 3
(Adequacy of \(\sqsubseteq _\mathsf{c}\)). \(B_1 \sqsubseteq _\mathsf{c}B_2 \implies B_1 \preccurlyeq _\mathsf{bl}B_2\).
5.1 Cutting Predicate
Removing the context relation R in definition (8) removes a large amount of structure from the context. However, there are still unboundedly many block-local executions with an empty R – for example, we can have an unbounded number of reads and writes that do not interact with the block. The cutting predicate identifies these redundant executions.
We first identify the actions in a block-local execution that are visible, meaning they directly interact with the block. We write \(\mathsf{code}(X)\) for the set of actions in X generated by the code-block. Visible actions belong to \(\mathsf{code}(X)\), read from \(\mathsf{code}(X)\), or are read by \(\mathsf{code}(X)\). In other words,

Informally, cutting eliminates three redundant patterns: (i) non-visible context reads, i.e. reads from context writes; (ii) duplicate context reads from the same write; and (iii) duplicate non-visible writes that are not separated in mo by a visible write. Formally we define \(\mathsf{cut}'(X)\), the conjunction of \(\mathsf{cutR}{}\) for read, and \(\mathsf{cutW}\) for write.

The final predicate \(\mathsf{cut}(X)\) extends this in order to keep LL-SC pairs together: it requires that, if \(\mathsf{cut}'()\) permits one half of an LL-SC, the other is also permitted implicitly (for brevity we omit the formal definition of \(\mathsf{cut}()\) in terms of \(\mathsf{cut}'\)).
It should be intuitively clear why the first two of the above patterns are redundant. The main surprise is the third pattern, which preserves some non-visible writes. This is required by Theorem 3 for technical reasons connected to per-location coherence. We illustrate the application of \(\mathsf{cut}()\) to a block-local execution in Fig. 7.
5.2 Extended History ( )
)
In our approach, each block-local execution represents a pattern of interaction between block and context. In our previous definition of \(\sqsubseteq _\mathsf{q}\), constraints imposed by the block are captured by the guarantee, while constraints imposed by the context are captured by the R relation. The definition (8) of \(\sqsubseteq _\mathsf{c}\) removes the context relation R, but these constraints must still be represented. Instead, we replace R with a history component called a deny. This simplifies the block-local executions, but compensates by recording more in the denotation.
The deny records the hb edges that cannot be enforced due to the execution structure. For example, consider the block-local executionFootnote 3 of Fig. 8.
This pattern could not occur in a context that generates the dashed edge D as a hb – to do so would violate the HBvsMO axiom. In our previous definition of \(\sqsubseteq _\mathsf{q}\), we explicitly represented the presence or absence of this edge through the R relation. In our new formulation, we represent such ‘forbidden’ edges in the history by a deny edge.
The extended history of an execution X, written \({\mathsf{hist}_\mathsf{E}}(X)\) is a triple \(({\mathcal {A}}, G, D)\), consisting of the familiar notions of action set \({\mathcal {A}}\) and guarantee \(G \subseteq {\mathcal {A}}\times {\mathcal {A}}\), together with deny \(D \subseteq {\mathcal {A}}\times {\mathcal {A}}\) as defined below:

Each of the predicates HBvsMO-d, Cohere-d, and RFval-d generates the deny for one validity axiom. In the diagrammatic definitions below, dashed edges represent the deny edge, and \(\mathsf{hb}^{*}\) is the reflexive-transitive closure of hb:



One can think of a deny edge as an ‘almost’ violation of an axiom. For example, if \(\textsf {HBvsMO-d}(u,v)\) holds, then the context cannot generate an extra hb-edge  – to do so would violate HBvsMO.
– to do so would violate HBvsMO.
Because deny edges represent constraints on the context, weakening the deny places fewer constraints, allowing more behaviours, so we compare them with relational inclusion:

This refinement on extended histories is used to define our refinement relation on blocks, \(\sqsubseteq _\mathsf{c}\), def. (8).
5.3 Finiteness
Theorem 4
(Finiteness). If for a block B and state \(\sigma \) the set of thread-local executions \(\langle B, \sigma \rangle \) is finite, then so is the set of resulting block-local executions,  .
.
Proof
(sketch). It is easy to see for a given thread-local execution there are finitely many possible visible reads and writes. Any two non-visible writes must be distinguished by at least one visible write, limiting their number. \(\square \)
Theorem 4 means that any transformation can be checked automatically if the two blocks have finite sets of thread-local executions. We assume a finite data domain, meaning action can only take finitely many distinct values in Val. Recall also that our language does not include loops. Given these facts, any transformations written in our language will satisfy finiteness, and can therefore by automatically checked.
6 Prototype Verification Tool
Stellite is our prototype tool that verifies transformations using the Alloy* model checker [12, 18]. Our tool takes an input transformation \(B_2 \leadsto B_1\) written in a C-like syntax. It automatically converts the transformation into an Alloy* model encoding \(B_1 \sqsubseteq _\mathsf{c}B_2\). If the tool reports success, then the transformation is verified for unboundedly large syntactic contexts and executions.
An Alloy model consists of a collection of predicates on relations, and an instance of the model is a set of relations that satisfy the predicates. As previously noted in [28], there is therefore a natural fit between Alloy models and axiomatic memory models.
At a high level, our tool works as follows:
-
1.
The two sides of an input transformation \(B_1\) and \(B_2\) are automatically converted into Alloy predicates expressing their syntactic structure. Intuitively, these block predicates are built by following the thread-local semantics from Sect. 3.
-
2.
The block predicates are linked with a pre-defined Alloy model expressing the memory model and \(\sqsubseteq _\mathsf{c}\).
-
3.
The Alloy* solver searches (using SAT) for a history of \(B_1\) that has no matching history of \(B_2\). We use the higher-order Alloy* solver of [18] because the standard Alloy solver cannot support the existential quantification on histories in \(\sqsubseteq _\mathsf{c}\).
The Alloy* solver is parameterised by the maximum size of the model it will examine. However, our finiteness theorem for \(\sqsubseteq _\mathsf{c}\) (Theorem 4) means there is a bound on the size of cut-down context that needs to be considered to verify any given transformation. If our tool reports that a transformation is correct, it is verified in all syntactic contexts of unbounded size.
Given a query \(B_1 \sqsubseteq _\mathsf{c}B_2\), the required context bound grows in proportion to the number of internal actions on distinct locations in \(B_1\). This is because our cutting predicate permits context actions if they interact with internal actions, either directly, or by interleaving between internal actions. In our experiments we run the tool with a model bound of 10, sufficient to give soundness for all the transformations we consider. Note that most of our example transformations do not require such a large bound, and execution times improve if it is reduced.
If a counter-example is discovered, the problematic execution and history can be viewed using the Alloy model visualiser, which has a similar appearance to the execution diagrams in this paper. The output model generated by our tool encodes the history of \(B_1\) for which no history of \(B_2\) could be found. As \(\sqsubseteq _\mathsf{c}\) is not fully abstract, this counter-example could, of course, be spurious.
Stellite currently supports transformations on code-blocks with atomic reads, writes, and fences. It does not yet support code-blocks with non-atomic accesses (see Sect. 7), LL-SC, or branching control-flow. We believe supporting the above features would not present fundamental difficulties, since the structure of the Alloy encoding would be similar. Despite the above limitations, our prototype demonstrates that our cut-down denotation can be used for automatic verification of important program transformations.
Results from executing Stellite on a 32 core 2.3 GHz AMD Opteron, with 128 GB RAM, over Linux 3.13.0-88 and Java 1.8.0_91. \(\mathtt{load}\)/\(\mathtt{store}\)/\(\mathtt{fence}\) are abbreviated to \(\mathtt{ld}\)/\(\mathtt{st}\)/\(\mathtt{fc}\). \(\checkmark \) and \({\textsf {x}}\) denote whether the transformation satisfies \(\sqsubseteq _\mathsf{c}\). \(\infty \) denotes a timeout after 8 h.
Experimental Results. We have tested our tool on a range of different transformations. A table of experimental results is given in Fig. 9. Many of our examples are derived from [23] – we cover all their examples that fit into our tool’s input language. Transformations of the sort that we check have led to real-world bugs in GCC [19] and LLVM [8]. Note that some transformations are invalid because of their effect on local variables, e.g. \(\mathtt{skip}\leadsto l\ {:}{=}\ \mathtt{load}(x)\). The closely related transformation \(\mathtt{skip}\leadsto \mathtt{load}(x)\) throws away the result of the read, and is consequently valid.
Our tool takes significant time to verify some of the above examples, and two of the transformations cause the tool to time out. This is due to the complexity and non-determinism of the C11 model. In particular, our execution times are comparable to existing C++ model simulators such as Cppmem when they run on a few lines of code [3]. However, our tool is a sound transformation verifier, rather than a simulator, and thus solves a more difficult problem: transformations are verified for unboundedly large syntactic contexts and executions, rather than for a single execution.
7 Transformations with Non-atomics
We now extend our approach to non-atomic (i.e. unsynchronised) accesses. C11 non-atomics are intended to enable sequential compiler optimisations that would otherwise be unsound in a concurrent context. To achieve this, any concurrent read-write or write-write pair of non-atomic actions on the same location is declared a data race, which causes the whole program to have undefined behaviour. Therefore, adding non-atomics impacts not just the model, but also our denotation.
7.1 Memory Model with Non-atomics
Non-atomic loads and stores are added to the model by introducing new commands \({\mathtt{store}}_\mathsf{NA}(x,l)\) and \(l := {\mathtt{load}}_\mathsf{NA}(x)\) and the corresponding kinds of actions: \(\mathsf{\mathsf{store}_\mathsf{NA}}, \mathsf{\mathsf{load}_\mathsf{NA}} \in \mathsf{Kind}\). We let \(\mathsf{NA}\) be the set of all actions of these kinds. We partition global variables so that they are either only accessed by non-atomics, or by atomics. We do not permit non-atomic LL-SC operations. Two new validity axioms ensure that non-atomics read from writes that happen before them, but not from stale writes:
-
RFHBNA:

-
CoherNA:
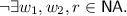

Modification order (mo) does not cover non-atomic accesses, and we change the definition of happens-before (hb), so that non-atomic loads do not add edges to it:
-
HBdef: \(\mathsf{hb}= (\mathsf{sb}\cup (\mathsf{rf}\cap \{(w,r) \mid w,r \notin \mathsf{NA}\}))^{+}\)
Consider the code on the left in Fig. 10: it is similar to MP from Fig. 1, but we have removed the if-statement, made all accesses to x non-atomic, and we have added an additional load of x at the start of the right-hand thread. The valid execution of this code on the left-hand side demonstrates the additions to the model for non-atomics:
-
modification order (mo) relates writes to atomic y, but not non-atomic x;
-
the first load of x is forced to read from the initialisation by RFHBNA; and
-
the second read of x is forced to read 1 because the \(\mathsf{hb}\) created by the load of y obscures the now-stale initialisation write, in accordance with CoherNA.
The most significant change to the model is the introduction of a safety axiom, data-race freedom (DRF). This forbids non-atomic read-write and write-write pairs that are unordered in hb:

We write \(\mathsf{safe}(X)\) if an execution satisfies this axiom. Returning to the left of Fig. 10, we see that there is a violation of DRF – a race on non-atomics – between the first load of x and the store of x on the left-hand thread.
Let \(\llbracket P \rrbracket _v^\mathsf{NA}\) be defined same way as \(\llbracket P \rrbracket \) is in Sect. 3, def. (3), but with adding the axioms RFHBNA and CoherNA and substituting the changed axiom HBdef. Then the semantics \(\llbracket P \rrbracket \) of a program with non-atomics is:

The undefined behaviour \(\top \) subsumes all others, so any program observationally refines a racy program. Hence we modify our notion of observational refinement on whole programs:
This always holds when \(P_2\) is unsafe; otherwise, it requires \(P_1\) to preserve safety and observations to match. We define observational refinement on blocks, \(\preccurlyeq _\mathsf{bl}^\mathsf{NA}\), by lifting \(\preccurlyeq _\mathsf{pr}^\mathsf{NA}\) as per Sect. 2, def. (2).
7.2 Denotation with Non-atomics
We now define our denotation for non-atomics, \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\), building on the ‘quantified’ denotation \(\sqsubseteq _\mathsf{q}\) defined in Sect. 4. (We have also defined a finite variant of this denotation using the cutting strategy described in Sect. 5 – we leave this to [10, Sect. C].)
Non-atomic actions do not participate in happens-before (hb) or coherence order (mo). For this reason, we need not change the structure of the history. However, non-atomics introduce undefined behaviour \(\top \), which is a special kind of observable behaviour. If a block races with its context in some execution, the whole program becomes unsafe, for all executions. Therefore, our denotation must identify how a block may race with its context. In particular, for the denotation to be adequate, for any context C and two blocks \(B_1 \mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}B_2\), we must have that if \(C(B_1)\) is racy, then \(C(B_2)\) is also racy.
To motivate the precise definition of \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\), we consider the following (sound) ‘anti-roach-motel’ transformationFootnote 4, noting that it might be applied to the right-hand thread of the code in the left of Fig. 10:

In a standard roach-motel transformation [25], operations are moved into a synchronised block. This is sound because it only introduces new happens-before ordering between events, thereby restricting the execution of the program and preserving data-race freedom. In the above transformation, the second NA load of x is moved past the atomic load of y, effectively out of the synchronised block, reducing happens-before ordering, and possibly introducing new races. However, this is sound, because any data-race generated by \(B_1\) must have already occurred with the first NA load of x, matching a racy execution of \(B_2\). Verifying this transformation requires that we reason about races, so \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\) must account for both racy and non-racy behaviour.
The code on the left of Fig. 10 represents a context, composed with \(B_2\), and the execution of Fig. 10 demonstrates that together they are racy. If we were to apply our transformation to the fragment \(B_2\) of the right-hand thread, then we would produce the code on the right in Fig. 10. On the right in Fig. 10, we present a similar execution to the one given on the left. The reordering on the right-hand thread has led to the second load of x taking the value 0 rather than 1, in accordance with RFHBNA. Note that the execution still has a race on the first load of x, albeit with different following events. As this example illustrates, when considering racy executions in the definition of \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\), we may need to match executions of the two code-blocks that behave differently after a race. This is the key subtlety in our definition of \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\).
In more detail, for two related blocks \(B_1 \mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}B_2\), if \(B_2\) generates a race in a block-local execution under a given (reduced) context, then we require \(B_1\) and \(B_2\) to have corresponding histories only up to the point the race occurs. Once the race has occurred, the following behaviours of \(B_1\) and \(B_2\) may differ. This still ensures adequacy: when the blocks \(B_1\) and \(B_2\) are embedded into a syntactic context C, this ensures that a race can be reproduced in \(C(B_2)\), and hence, \(C(B_1) \preccurlyeq _\mathsf{pr}^\mathsf{NA}C(B_2)\).
By default, C11 executions represent a program’s complete behaviour to termination. To allow us to compare executions up to the point a race occurs, we use prefixes of executions. We therefore introduce the downclosure \(X^\downarrow \), the set of \((\mathsf{hb}\cup \mathsf{rf})^+\)-prefixes of an execution X:

Here \(X|_{\mathcal {A}}\) is the projection of the execution X to actions in \({\mathcal {A}}\). We lift the downclosure to sets of executions in the standard way.
Now we define our refinement relation \(B_1 \mathrel {\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}} B_2\) as follows:

In this definition, for each execution \(X_1\) of block \(B_1\), we witness an execution \(X_2\) of block \(B_2\) that is related. The relationship depends on whether \(X_2\) is safe or unsafe.
-
If \(X_2\) is safe, then the situation corresponds to \(\sqsubseteq _\mathsf{q}\) – see Sect. 4, def. (7). In fact, if \(B_2\) is certain to be safe, for example because it has no non-atomic accesses, then the above definition is equivalent to \(\sqsubseteq _\mathsf{q}\).
-
If \(X_2\) is unsafe then it has a race, and we do not have to relate the whole executions \(X_1\) and \(X_2\). We need only show that the race in \(X_2\) is feasible by finding a prefix in \(X_1\) that refines the prefix leading to the race in \(X_2\). In other words, \(X_2\) will behave consistently with \(X_1\) until it becomes unsafe. This ensures that the race in \(X_2\) will in fact occur, and its undefined behaviour will subsume the behaviour of \(B_1\). After \(X_2\) becomes unsafe, the two blocks can behave entirely differently, so we need not show that the complete histories of \(X_1\) and \(X_2\) are related.
Recall the transformation \(B_2 \leadsto B_1\) given above. To verify it, we must establish that \(B_1 \mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}B_2\). As before, we illustrate the reasoning for a single block-local execution – verifying the transformation would require a proof for all block-local executions.
In Fig. 11 we give an execution \(X_1 \in \llbracket B_1, {\mathcal {A}}, R, S \rrbracket \), with a context action set \({\mathcal {A}}\) consisting of a non-atomic store of \(\mathtt{x} = 1\) and an atomic store of \(\mathtt{y} = 1\), and a context relation R relating the store of \(\mathtt{x}\) to the store of \(\mathtt{y}\). Note that this choice of context actions matches the left-hand thread in the code listings of Fig. 10, and there are data races between the loads and the store on x.
To prove the refinement for this execution, we exhibit a corresponding unsafe execution \(X_2 \in \llbracket B_2, {\mathcal {A}}, R, S \rrbracket _v\). The histories of the complete executions \(X_1\) and \(X_2\) differ in their return action. In \(X_2\) the load of \(\mathtt{y}\) takes the value of the context store, so CoherNA forces the second load of \(\mathtt{x}\) to read from the context store of \(\mathtt{x}\). This changes the values of local variables recorded in \(\mathsf{ret} '\). However, because \(X_2\) is unsafe, we can select a prefix \(X'_2\) which includes the race (we denote in grey the parts that we do not include). Similarly, we can select a prefix \(X'_1\) of \(X_1\). We have that \(\mathsf{hist}(X'_1) = \mathsf{hist}(X'_2)\) (shown in the figure), even though the histories \(\mathsf{hist}(X_1)\) and \(\mathsf{hist}(X_2)\) do not correspond.
Theorem 5
(Adequacy of \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\)). \(B_1 \mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}B_2 \implies B_1 \preccurlyeq _\mathsf{bl}^\mathsf{NA}B_2 \).
Theorem 6
(Full abstraction of \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\)). \(B_1 \preccurlyeq _\mathsf{bl}^\mathsf{NA}B_2 \Rightarrow B_1 \mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}B_2 \).
We prove Theorem 5 in [10, Sect. B] and Theorem 6 in [10, Sect. F]. Note that the prefixing in our definition of \(\mathrel {\sqsubseteq _\mathsf{q}^\mathsf{NA}}\) is required for full abstraction—but it would be adequate to always require complete executions with related histories.
8 Full Abstraction
The key idea of our proofs of full abstraction (Theorems 2 and 6, given in full in [10, Sect. F]) is to construct a special syntactic context that is sensitive to one particular history. Namely, given an execution X produced from a block B with context happens-before R, this context \(C_X\) guarantees: (1) that X is the block portion of an execution of \(C_X(B)\); and (2) for any block \(B'\), if \(C_X(B')\) has a different block history from X, then this is visible in different observable behaviour. Therefore for any blocks that are distinguished by different histories, \(C_X\) can produce a program with different observable behaviour, establishing full abstraction.
Special Context Construction. The precise definition of the special context construction \(C_X\) is given in [10, Sect. F] – here we sketch its behaviour. \(C_X\) executes the context operations from X in parallel with the block. It wraps these operations in auxiliary wrapper code to enforce context happens-before, R, and to check the history. If wrapper code fails, it writes to an error variable, which thereby alters the observable behaviour.
The context must generate edges in R. This is enforced by wrappers that use watchdog variables to create hb-edges: each edge \((u, v) \in R\) is replicated by a write and read on variable \(h_{(u,v)}\). If the read on \(h_{(u,v)}\) does not read the write, then the error variable is written. The shape of a successful read is given on the left in Fig. 12.
The context must also prohibit history edges beyond those in the original guarantee G, and again it uses watchdog variables. For each (u, v) not in G, the special context writes to watchdog variable \(g_{(u,v)}\) before u and a reads \(g_{(u,v)}\) after v. If the read of \(g_{(u,v)}\) does read the value written before u, then there is an errant history edge, and the error location is written. An erroneous execution has the shape given on the right in Fig. 12 (omitting the write to the error location).
Full Abstraction and LL-SC. Our proof of full abstraction for the language with C11 non-atomics requires the language to also include LL-SC, not just C11’s standard CAS: the former operation increases the observational power of the context. However, without non-atomics (Sect. 4) CAS would be sufficient to prove full abstraction.
9 Related Work
Our approach builds on our prior work [3], which generalises linearizability [11] to the C11 memory model. This work represented interactions between a library and its clients by sets of histories consisting of a guarantee and a deny; we do the same for code-block and context. However, our previous work assumed information hiding, i.e., that the variables used by the library cannot be directly accessed by clients; we lift this assumption here. We also establish both adequacy and full abstraction, propose a finite denotation, and build an automated verification tool.
Our approach is similar in structure to the seminal concurrency semantics of Brookes [6]: i.e. a code block is represented by a denotation capturing possible interactions with an abstracted context. In [6], denotations are sets of traces, consisting of sequences of global program states; context actions are represented by changes in these states. To handle the more complex axiomatic memory model, our denotation consists of sets of context actions and relations on them, with context actions explicitly represented as such. Also, in order to achieve full abstraction, Brookes assumes a powerful atomic await() instruction which blocks until the global state satisfies a predicate. Our result does not require this: all our instructions operate on single locations, and our strongest instruction is LL-SC, which is commonly available on hardware.
Brookes-like approaches have been applied to several relaxed models: operational hardware models [7], TSO [13], and SC-DRF [21]. Also, [7, 21] define tools for verifying program transformations. All three approaches are based on traces rather than partial orders, and are therefore not directly portable to C11-style axiomatic memory models. All three also target substantially stronger (i.e. more restrictive) models.
Methods for verifying code transformations, either manually or using proof assistants, have been proposed for several relaxed models: TSO [24, 26, 27], Java [25] and C/C++ [23]. These methods are non-compositional in the sense that verifying a transformation requires considering the trace set of the entire program—there is no abstraction of the context. We abstract both the sequential and concurrent context and thereby support automated verification. The above methods also model transformations as rewrites on program executions, whereas we treat them directly as modifications of program syntax; the latter corresponds more closely to actual compilers. Finally, these methods all require considerable proof effort; we build an automated verification tool.
Our tool is a sound verification tool – that is, transformations are verified for all context and all executions of unbounded size. Several tools exist for testing (not verifying) program transformations on axiomatic memory models by searching for counter-examples to correctness, e.g., [16] for GCC and [8] for LLVM. Alloy was used by [28] in a testing tool for comparing memory models – this includes comparing language-level constructs with their compiled forms.
10 Conclusions
We have proposed the first fully abstract denotational semantics for an axiomatic relaxed memory model, and using this, we have built the first tool capable of automatically verifying program transformation on such a model. Our theory lays the groundwork for further research into the properties of axiomatic models. In particular, our definition of the denotation as a set of histories and our context reduction should be portable to other axiomatic models based on happens-before, such as those for hardware [1].
Notes
- 1.
This definition relies on the fact that our language supports a fixed set of global variables, not dynamically allocated addressable memory (see Sect. 3.7). We believe that in the future our results can be extended to support dynamic memory. For this, the block-local construction would need to quantify over actions on all possible memory locations, not just the static variable set \(\mathsf{VS}_B\). The rest of our theory would remain the same, because C11-style models grant no special status to pointer values. Cutting down to a finite denotation, as in Sect. 5 below, would require some extra abstraction over memory – for example, a separation logic domain such as [9].
- 2.
We choose these post-states for exposition purposes – in fact these blocks are also distinguishable through local variable l1 alone.
- 3.
We use this execution for illustration, but in fact the \(\mathsf{cut}()\) predicate would forbid the load.
- 4.
This example was provided to us by Lahav, Giannarakis and Vafeiadis in personal communication.
References
Alglave, J., Maranget, L., Tautschnig, M.: Herding cats: modelling, simulation, testing, and data mining for weak memory. ACM Trans. Program. Lang. Syst. 36(2), 7:1–7:74 (2014)
Anderson, J.H., Moir, M.: Universal constructions for multi-object operations. In: Symposium on Principles of Distributed Computing (PODC), pp. 184–193 (1995)
Batty, M., Dodds, M., Gotsman, A.: Library abstraction for C/C++ concurrency. In: Symposium on Principles of Programming Languages (POPL), pp. 235–248 (2013)
Batty, M., Memarian, K., Nienhuis, K., Pichon-Pharabod, J., Sewell, P.: The problem of programming language concurrency semantics. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 283–307. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46669-8_12
Batty, M., Owens, S., Sarkar, S., Sewell, P., Weber, T.: Mathematizing C++ concurrency. In: Symposium on Principles of Programming Languages (POPL), pp. 55–66 (2011)
Brookes, S.: Full abstraction for a shared-variable parallel language. Inf. Comput. 127(2), 145–163 (1996)
Burckhardt, S., Musuvathi, M., Singh, V.: Verifying local transformations on relaxed memory models. In: International Conference on Compiler Construction (CC), pp. 104–123 (2010)
Chakraborty, S., Vafeiadis, V.: Validating optimizations of concurrent C/C++ programs. In: International Symposium on Code Generation and Optimization (CGO), pp. 216–226 (2016)
Distefano, D., O’Hearn, P.W., Yang, H.: A local shape analysis based on separation logic. In: Hermanns, H., Palsberg, J. (eds.) TACAS 2006. LNCS, vol. 3920, pp. 287–302. Springer, Heidelberg (2006). https://doi.org/10.1007/11691372_19
Dodds, M., Batty, M., Gotsman, A.: Compositional verification of compiler optimisations on relaxed memory (extended version). CoRR, arXiv:1802.05918 (2018)
Herlihy, M.P., Wing, J.M.: Linearizability: a correctness condition for concurrent objects. ACM Trans. Program. Lang. Syst. 12(3), 463–492 (1990)
Jackson, D.: Software Abstractions - Logic Language and Analysis, Revised edn. MIT Press, Cambridge (2012)
Jagadeesan, R., Petri, G., Riely, J.: Brookes is relaxed, almost! In: International Conference on Foundations of Software Science and Computational Structures (FOSSACS), pp. 180–194 (2012)
Jeffrey, A., Riely, J.: On thin air reads towards an event structures model of relaxed memory. In: Symposium on Logic in Computer Science (LICS), pp. 759–767 (2016)
Kang, J., Hur, C.-K., Lahav, O., Vafeiadis, V., Dreyer, D.: A promising semantics for relaxed-memory concurrency. In: Symposium on Principles of Programming Languages (POPL), pp. 175–189 (2017)
Lahav, O., Giannarakis, N., Vafeiadis, V.: Taming release-acquire consistency. In: Symposium on Principles of Programming Languages (POPL), pp. 649–662 (2016)
Lahav, O., Vafeiadis, V., Kang, J., Hur, C.-K., Dreyer, D.: Repairing sequential consistency in C/C++11. In: Conference on Programming Language Design and Implementation (PLDI), pp. 618–632 (2017)
Milicevic, A., Near, J.P., Kang, E., Jackson, D.: Alloy*: a general-purpose higher-order relational constraint solver. In: International Conference on Software Engineering (ICSE), pp. 609–619 (2015)
Morisset, R., Pawan, P., Zappa Nardelli, F.: Compiler testing via a theory of sound optimisations in the C11/C++11 memory model. In: Conference on Programming Language Design and Implementation (PLDI), pp. 187–196 (2013)
Pichon-Pharabod, J., Sewell, P.: A concurrency semantics for relaxed atomics that permits optimisation and avoids thin-air executions. In: Symposium on Principles of Programming Languages (POPL), pp. 622–633 (2016)
Poetzl, D., Kroening, D.: Formalizing and checking thread refinement for data-race-free execution models. In: International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS), pp. 515–530 (2016)
The C++ Standards Committee: Programming Languages – C++ (2011). ISO/IEC JTC1 SC22 WG21
Vafeiadis, V., Balabonski, T., Chakraborty, S., Morisset, R., Zappa Nardelli, F.: Common compiler optimisations are invalid in the C11 memory model and what we can do about it. In: Symposium on Principles of Programming Languages (POPL), pp. 209–220 (2015)
Vafeiadis, V., Zappa Nardelli, F.: Verifying fence elimination optimisations. In: International Conference on Static Analysis (SAS), pp. 146–162 (2011)
Ševčík, J., Aspinall, D.: On validity of program transformations in the Java memory model. In: Vitek, J. (ed.) ECOOP 2008. LNCS, vol. 5142, pp. 27–51. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70592-5_3
Ševčík, J., Vafeiadis, V., Zappa Nardelli, F., Jagannathan, S.: Sewell, P.: Relaxed-memory concurrency and verified compilation. In: Symposium on Principles of Programming Languages (POPL), pp. 43–54 (2011)
Ševčík, J., Vafeiadis, V., Zappa Nardelli, F., Jagannathan, S., Sewell, P.: CompCertTSO: a verified compiler for relaxed-memory concurrency. J. ACM 60(3), 22:1–22:50 (2013)
Wickerson, J., Batty, M., Sorensen, T., Constantinides, G.A.: Automatically comparing memory consistency models. In: Symposium on Principles of Programming Languages (POPL), pp. 190–204 (2017)
Acknowledgements
Thanks to Jeremy Jacob, Viktor Vafeiadis, and John Wickerson for comments and suggestions. Dodds was supported by a Royal Society Industrial Fellowship, and undertook this work while faculty at the University of York. Batty is supported by a Lloyds Register Foundation and Royal Academy of Engineering Research Fellowship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Dodds, M., Batty, M., Gotsman, A. (2018). Compositional Verification of Compiler Optimisations on Relaxed Memory. In: Ahmed, A. (eds) Programming Languages and Systems. ESOP 2018. Lecture Notes in Computer Science(), vol 10801. Springer, Cham. https://doi.org/10.1007/978-3-319-89884-1_36
Download citation
DOI: https://doi.org/10.1007/978-3-319-89884-1_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89883-4
Online ISBN: 978-3-319-89884-1
eBook Packages: Computer ScienceComputer Science (R0)







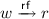 if r takes its value from w.
if r takes its value from w.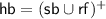 and
and  is acyclic.
is acyclic.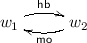 This axiom requires that the order in which writes to a location become visible to threads cannot contradict the temporal order. But take note that writes may be ordered in
This axiom requires that the order in which writes to a location become visible to threads cannot contradict the temporal order. But take note that writes may be ordered in  This axiom generalises the sequentially consistent prohibition on reading overwritten values. If two writes are ordered in
This axiom generalises the sequentially consistent prohibition on reading overwritten values. If two writes are ordered in  Most reads must take their value from a write, represented by an
Most reads must take their value from a write, represented by an 
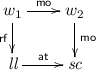 This axiom is adapted from [
This axiom is adapted from [

 is defined analogously with
is defined analogously with 




 )
)