Abstract
We address the problem of validity in eventually consistent (EC) systems: In what sense does an EC data structure satisfy the sequential specification of that data structure? Because EC is a very weak criterion, our definition does not describe every EC system; however it is expressive enough to describe any Convergent or Commutative Replicated Data Type (CRDT).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In a replicated implementation of a data structure, there are two impediments to requiring that all replicas achieve consensus on a global total order of the operations performed on the data structure (Lamport 1978): (a) the associated serialization bottleneck negatively affects performance and scalability (e.g. see (Ellis and Gibbs 1989)), and (b) the cap theorem imposes a tradeoff between consistency and partition-tolerance (Gilbert and Lynch 2002).
In systems based on optimistic replication (Vogels 2009; Saito and Shapiro 2005), a replica may execute an operation without synchronizing with other replicas. If the operation is a mutator, the other replicas are updated asynchronously. Due to the vagaries of the network, the replicas could receive and apply the updates in possibly different orders.
For sequential systems, the correctness problem is typically divided into two tasks: proving termination and proving partial correctness. Termination requires that the program eventually halt on all inputs, whereas partial correctness requires that the program only returns results that are allowed by the specification.
For replicated systems, the analogous goals are convergence and validity. Convergence requires that all replicas eventually agree. Validity requires that they agree on something sensible. In a replicated list, for example, if the only value put into the list is 1, then convergence ensures that all replicas eventually see the same value for the head of the list; validity requires that the value be 1.
Convergence has been well-understood since the earliest work on replicated systems. Convergence is typically defined as eventual consistency, which requires that once all messages are delivered, all replicas have the same state. Strong eventual consistency (sec) additionally requires convergence for all subsets of messages: replicas that have seen the same messages must have the same state.
Perhaps surprisingly, finding an appropriate definition of validity for replicated systems remains an open problem. There are solutions which use concurrent specifications, discussed below. But, as Shavit (2011) noted:
“It is infinitely easier and more intuitive for us humans to specify how abstract data structures behave in a sequential setting, where there are no interleavings. Thus, the standard approach to arguing the safety properties of a concurrent data structure is to specify the structure’s properties sequentially, and find a way to map its concurrent executions to these ‘correct’ sequential ones.”
In this paper we give the first definition of validity that is both (1) derived from standard sequential specifications and (2) validates the examples of interest.
We take the “examples of interest” to be Convergent/Commutative Replicated Data Types (crdts). These are replicated structures that obey certain monotonicity or commutativity properties. As an example of a crdt, consider the add-wins set, also called an “observed remove” set in Shapiro et al. (2011a). The add-wins set behaves like a sequential set if add and remove operations on the same element are ordered. The concurrent execution of an add and remove result in the element being added to the set; thus the remove is ignored and the “add wins.” This concurrent specification is very simple, but as we will see in the next section, it is quite difficult to pin down the relationship between the crdt and the sequential specification used in the crdt’s definition. This paper is the first to successfully capture this relationship.
Many replicated data types are crdts, but not all (Shapiro et al. 2011a). Notably, Amazon’s Dynamo (DeCandia et al. 2007) is not a crdt. Indeed, interest in crdts is motivated by a desire to avoid the well-know concurrency anomalies suffered by Dynamo and other ad hoc systems (Bieniusa et al. 2012).
Shapiro et al. (2011b) introduced the notion of crdt and proved that every crdt has an sec implementation. Their definition of sec includes convergence, but not validity.
The validity requirement can be broken into two components. We describe these below using the example of a list data type that supports only two operations: the mutator put, which adds an element to the end of the list, and the query q, which returns the state of the list. This structure can be specified as a set of strings such as  and
and  .
.
-
Linearization requires that a response be consistent with some specification string. A state that received put(1) and put(3), may report q=[1,3] or q=[3,1], but not q=[2,1,3], since 2 has not been put into the list.
-
Monotonicity requires that states evolve in a sensible way. We might permit the state q=[1,3] to evolve into q=[1,2,3], due to the arrival of action put(2). But we would not expect that q=[1,3] could evolve into q=[3,1], since the data type does not support deletion or reordering.
Burckhardt et al. (2012) provide a formal definition of validity using partial orders over events: linearizations respect the partial order on events; monotonicity is ensured by requiring that evolution extends the partial order. Similar definitions can be found in Jagadeesan and Riely (2015) and Perrin et al. (2015). Replicated data structures that are sound with respect to this definition enjoy many good properties, which we discuss throughout this paper. However, this notion of correctness is not general enough to capture common crdts, such as the add-wins set.
This lack of expressivity lead Burckhardt et al. (2014) to abandon notions of validity that appeal directly to a sequential specification. Instead they work directly with concurrent specifications, formalizing the style of specification found informally in Shapiro et al. (2011b). This has been a fruitful line of work, leading to proof rules (Gotsman et al. 2016) and extensions (Bouajjani et al. 2014). See (Burckhardt 2014; Viotti and Vukolic 2016) for a detailed treatment.
Positively, concurrent specifications can be used to validate any replicated structure, including crdts as well as anomalous structures such as Dynamo. Negatively, concurrent specifications have no the clear connection to their sequential counterparts. In this paper, we restore this connection. We arrive at a definition of sec that admits crdts, but rejects Dynamo.
The following “corner cases” are a useful sanity-check for any proposed notion of validity.
-
The principle of single threaded semantics (psts) (Haas et al. 2015) states that if an execution uses only a single replica, it should behave according to the sequential semantics.
-
The principle of single master (psm) (Budhiraja et al. 1993) states that if all mutators in an execution are initiated at a single replica, then the execution should be linearizable (Herlihy and Wing 1990).
-
The principle of permutation equivalence (ppe) (Bieniusa et al. 2012) states that “if all sequential permutations of updates lead to equivalent states, then it should also hold that concurrent executions of the updates lead to equivalent states.”
psts and psm say that a replicated structure should behave sequentially when replication is not used. ppe says that the order of independent operations should not matter. Our definition implies all three conditions. Dynamo fails ppe (Bieniusa et al. 2012), and thus fails to pass our definition of sec.
In the next section, we describe the validity problem and our solution in detail, using the example of a binary set. The formal definitions follow in Sect. 3. We state some consequences of the definition and prove that the add-wins set satisfies our definition. In Sect. 4, we describe a collaborative text editor and prove that it is sec. In Sect. 5 we characterize the programmer’s view of a crdt by defining the most general crdt that satisfies a given sequential specification. We show that any program that is correct using the most general crdt will be correct using a more restricted crdt. We also show that our validity criterion for sec is local in the sense of Herlihy and Wing (1990): independent structures can be verified independently. In Sect. 6, we apply these results to prove the correctness of a graph that is implemented using two sec sets.
Our work is inspired by the study of relaxed memory, such as (Alglave 2012). In particular, we have drawn insight from the rmo model of Higham and Kawash (2000).
2 Understanding Replicated Sets
In this section, we motivate the definition of sec using replicated sets as an example. The final definition is quite simple, but requires a fresh view of both executions and specifications. We develop the definition in stages, each of which requires a subtle shift in perspective. Each subsection begins with an example and ends with a summary.
2.1 Mutators and Non-mutators
An implementation is a set of executions. We model executions abstractly as labelled partial orders (lpos). The ordering of the lpo captures the history that precedes an event, which we refer to as visibility.

Here the events are \(a\) through \(j\), with labels  ,
,  , etc., and order represented by arrows. The lpo describes an execution with two replicas, shown horizontally, with time passing from left to right. Initially, the top replica receives a request to add 0 to the set (
, etc., and order represented by arrows. The lpo describes an execution with two replicas, shown horizontally, with time passing from left to right. Initially, the top replica receives a request to add 0 to the set ( ). Concurrently, the bottom replica receives a request to add 1 (
). Concurrently, the bottom replica receives a request to add 1 ( ). Then each replica is twice asked to report on the items contained in the set. At first, the top replica replies that 0 is present and 1 is absent (
). Then each replica is twice asked to report on the items contained in the set. At first, the top replica replies that 0 is present and 1 is absent ( ), whereas the bottom replica answers with the reverse (
), whereas the bottom replica answers with the reverse ( ). Once the add operations are visible at all replicas, however, the replicas give the same responses (
). Once the add operations are visible at all replicas, however, the replicas give the same responses ( and
and  ).
).
lpos with non-interacting replicas can be denoted compactly using sequential and parallel composition. For example, the prefix of (1) that only includes the first three events at each replica can be written  .
.
A specification is a set of strings. Let \({\textsc {set}}\) be the specification of a sequential set with elements 0 and 1. Then we expect that set includes the string “ ”, but not “
”, but not “ ”. Indeed, each specification string can uniquely be extended with either
”. Indeed, each specification string can uniquely be extended with either  or
or  and either
and either  or
or  .
.
There is an isomorphism between strings and labelled total orders. Thus, specification strings correspond to the restricted class of lpos where the visibility relation provides a total order.
Linearizability (Herlihy and Wing 1990) is the gold standard for concurrent correctness in tightly coupled systems. Under linearizability, an execution is valid if there exists a linearization \(\tau \) of the events in the execution such that for every event e, the prefix of e in \(\tau \) is a valid specification string.
Execution (1) is not linearizable. The failure can already be seen in the sub-lpo  . Any linearization must have either
. Any linearization must have either  before
before  or
or  before
before  . In either case, the linearization is invalid for set.
. In either case, the linearization is invalid for set.
Although it is not linearizable, execution (1) is admitted by every crdt set in Shapiro et al.
(2011a). To validate such examples, Burckhardt et al.
(2012) develop a weaker notion of validity by dividing labels into mutators and accessors (also known as non-mutators). Similar definitions appear in Jagadeesan and Riely
(2015) and Perrin et al.
(2015). Mutators change the state of a replica, and accessors report on the state without changing it. For \({\textsc {set}}\), the mutators \(\mathbf {M}\) and non-mutators  are as follows.
are as follows.

Define the mutator prefix of an event e to include e and the mutators visible to e. An execution is valid if there exists a linearization of the execution, \(\tau \), such that for every event e, the mutator prefix of e in \(\tau \) is a valid specification string.
It is straightforward to see that execution (1) satisfies this weaker criterion. For both  and
and  , the mutator prefix is
, the mutator prefix is  . This includes
. This includes  but not
but not  , and thus their answers are validated. Symmetrically, the mutator prefixes of
, and thus their answers are validated. Symmetrically, the mutator prefixes of  and
and  only include
only include  . The mutator prefixes for the final four events include both
. The mutator prefixes for the final four events include both  and
and  , but none of the prior accessors.
, but none of the prior accessors.
Summary: Convergent states must agree on the final order of mutators, but intermediate states may see incompatible subsequences of this order. By restricting attention to mutator prefixes, the later states need not linearize these incompatible views of the partial past.
This relaxation is analogous to the treatment of non-mutators in update serializability (Hansdah and Patnaik 1986; Garcia-Molina and Wiederhold 1982), which requires a global serialization order for mutators, ignoring non-mutators.
2.2 Dependency
The following lpo is admitted by the add-wins set discussed in the introduction.

In any crdt implementation, the effect of  is negated by the subsequent
is negated by the subsequent  The same reasoning holds for
The same reasoning holds for  and
and  . In an add-wins set, however, the concurrent adds,
. In an add-wins set, however, the concurrent adds,  and
and  , win over the deletions. Thus, in the final state both 0 and 1 are present.
, win over the deletions. Thus, in the final state both 0 and 1 are present.
This lpo is not valid under the definition of the previous subsection: Since  and
and  see the same mutators, they must agree on a linearization of
see the same mutators, they must agree on a linearization of  . Any linearization must end in either
. Any linearization must end in either  or
or  ; thus it is not possible for both
; thus it is not possible for both  and
and  to be valid.
to be valid.
Similar issues arise in relaxed memory models, where program order is often relaxed between uses of independent variables (Alglave et al. 2014). Generalizing, we write  to indicate that labels \(m\) and \(n\) are dependent. Dependency is a property of a specification, not an implementation. Our results only apply to specifications that support a suitable notion of dependency, as detailed in Sect. 3. For set,
to indicate that labels \(m\) and \(n\) are dependent. Dependency is a property of a specification, not an implementation. Our results only apply to specifications that support a suitable notion of dependency, as detailed in Sect. 3. For set,  is an equivalence relation with two equivalence classes, corresponding to actions on the independent values 0 and 1.
is an equivalence relation with two equivalence classes, corresponding to actions on the independent values 0 and 1.

While the dependency relation for set is an equivalence, this is not required: In Sect. 4 we establish the correctness of collaborative text editing protocol with an intransitive dependency relation.
The dependent restriction of (2) is as follows.

In the previous subsection, we defined validity using the mutator prefix of an event. We arrive at a weaker definition by restricting attention to the mutator prefix of the dependent restriction.
Under this definition, execution (2) is validated: Any interleaving of the strings  and
and  linearizes the dependent restriction of (2) given in (3).
linearizes the dependent restriction of (2) given in (3).
Summary: crdts allow independent mutators to commute. We formalize this intuition by restricting attention to mutator prefixes of the dependent restriction. The crdt must respect program order between dependent operations, but is free to reorder independent operations.
This relaxation is analogous to the distinction between program order and preserved program order (ppo) in relaxed memory models (Higham and Kawash 2000; Alglave 2012). Informally, ppo is the suborder of program order that removes order between independent memory actions, such as successive reads on different locations without an intervening memory barrier.
2.3 Puns
The following lpo is admitted by the add-wins set.

As in execution (2), the add  is undone by the following remove
is undone by the following remove  , but the concurrent add
, but the concurrent add  wins over
wins over  , allowing
, allowing  . In effect,
. In effect,  sees the order of the mutators as
sees the order of the mutators as  . Symmetrically,
. Symmetrically,  sees the order as
sees the order as  . While this is very natural from the viewpoint of a crdt, there is no linearization of the events that includes both
. While this is very natural from the viewpoint of a crdt, there is no linearization of the events that includes both  and
and  since
since  and
and  must appear in different orders.
must appear in different orders.
Indeed, this lpo is not valid under the definition of the previous subsection. First note that all events are mutually dependent. To prove validity we must find a linearization that satisfies the given requirements. Any linearization of the mutators must end in either  or
or  . Suppose we choose
. Suppose we choose  and look for a mutator prefix to satisfy
and look for a mutator prefix to satisfy  . (All other choices lead to similar problems.) Since
. (All other choices lead to similar problems.) Since  precedes
precedes  and is the last mutator in our chosen linearization, every possible witness for
and is the last mutator in our chosen linearization, every possible witness for  must end with mutator
must end with mutator  . Indeed the only possible witness is
. Indeed the only possible witness is  . However, this is not a valid specification string.
. However, this is not a valid specification string.
The problem is that we are linearizing events, rather than labels. If we shift to linearizing labels, then execution (4) is allowed. Fix the final order for the mutators to be  . The execution is allowed if we can find a subsequence that linearizes the labels visible at each event. It suffices to choose the witnesses as follows. In the table, we group events with a common linearization together.
. The execution is allowed if we can find a subsequence that linearizes the labels visible at each event. It suffices to choose the witnesses as follows. In the table, we group events with a common linearization together.

Each of these is a valid specification string. In addition, looking only at mutators, each is a subsequence of  .
.
In execution (4), each of the witnesses is actually a prefix of the final mutator order, but, in general, it is necessary to allow subsequences.

Execution (5) is admitted by the add-wins set. It is validated by the final mutator sequence  . The mutator prefix
. The mutator prefix  of \(b\) is a subsequence of
of \(b\) is a subsequence of  , but not a prefix.
, but not a prefix.
Summary: While dependent events at a single replica must be linearized in order, concurrent events may slip anywhere into the linearization. A crdt may pun on concurrent events with same label, using them in different positions at different replicas. Thus a crdt may establish a final total over the labels of an execution even when there is no linearization of the events.
2.4 Frontiers
In the introduction, we mentioned that the validity problem can be decomposed into the separate concerns of linearizability and monotonicity. The discussion thus far has centered on the appropriate meaning of linearizability for crdts. In this subsection and the next, we look at the constraints imposed by monotonicity.
Consider the prefix  of execution (4), extended with action
of execution (4), extended with action  , with visibility order as follows.
, with visibility order as follows.

This execution is not strong ec, since  and
and  see exactly the same mutators, yet provide incompatible answers.
see exactly the same mutators, yet provide incompatible answers.
Unfortunately, execution (6) is valid by the definition given in the previous section: The witnesses for \(a\)–\(f\) are as before. In particular, the witness for  is “
is “ ”. The witness for
”. The witness for  is “
is “ ”. In each case, the mutator prefix is a subsequence of the global mutator order “
”. In each case, the mutator prefix is a subsequence of the global mutator order “ ”.
”.
It is well known that punning can lead to bad jokes. In this case, the problem is that  is punning on a concurrent
is punning on a concurrent  that cannot be matched by a visible
that cannot be matched by a visible  in its history: the execution
in its history: the execution  that is visible to
that is visible to  must appear between the two
must appear between the two  operations; the specification
operations; the specification  that is used by
that is used by  must appear after. The final states of execution (4) have seen both remove operations, therefore the pun is harmless there. But
must appear after. The final states of execution (4) have seen both remove operations, therefore the pun is harmless there. But  and
and  have seen only one remove. They must agree on how it is used.
have seen only one remove. They must agree on how it is used.
Up to now, we have discussed the linearization of each event in isolation. We must also consider the relationship between these linearizations. When working with linearizations of events, it is sufficient to require that the linearization chosen for each event be a subsequence for the linearization chosen for each visible predecessor; since events are unique, there can be no confusion in the linearization about which event is which. Execution (6) shows that when working with linearizations of labels, it is insufficient to consider the relationship between individual events. The linearization “ ” chosen for
” chosen for  is a supersequence of those chosen for its predecessors: “
is a supersequence of those chosen for its predecessors: “ ” for
” for  and “
and “ ” for
” for  . The linearization “
. The linearization “ ” chosen for
” chosen for  is also a supersequence for the same predecessors. And yet,
is also a supersequence for the same predecessors. And yet,  and
and  are incompatible states.
are incompatible states.
Sequential systems have a single state, which evolves over time. In distributed systems, each replica has its own state, and it is this set of states that evolves. Such a set of states is called a (consistent) cut (Chandy and Lamport 1985).
A cut of an lpo is a sub-lpo that is down-closed with respect to visibility. The frontier of cut is the set of maximal elements. For example, there are 14 frontiers of execution (6): the singletons  ,
,  ,
,  ,
,  ,
,  ,
,  , the pairs
, the pairs  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and the triple
, and the triple  . As we explain below, we consider non-mutators in isolation. Thus we do not consider the last four cuts, which include a non-mutator with other events. That leaves 10 frontiers. The definition of the previous section only considered the 6 singletons. Singleton frontiers are generated by pointed cuts, with a single maximal element.
. As we explain below, we consider non-mutators in isolation. Thus we do not consider the last four cuts, which include a non-mutator with other events. That leaves 10 frontiers. The definition of the previous section only considered the 6 singletons. Singleton frontiers are generated by pointed cuts, with a single maximal element.
When applied to frontiers, the monotonicity requirement invalidates execution (6). Monotonicity requires that the linearization chosen for a frontier be a subsequence of the linearization chosen for any extension of that frontier. If we are to satisfy state  in execution (6), the frontier
in execution (6), the frontier  must linearize to “
must linearize to “ ”. If we are to satisfy state
”. If we are to satisfy state  , the frontier
, the frontier  must linearize to “
must linearize to “ ”. Since we require a unique linearization for each frontier, the execution is disallowed.
”. Since we require a unique linearization for each frontier, the execution is disallowed.
Since crdts execute non-mutators locally, it is important that we ignore frontiers with multiple non-mutators. Recall execution (4):

There is no specification string that linearizes the cut with frontier  , since we cannot have
, since we cannot have  immediately after
immediately after  . If we consider only pointed cuts for non-mutators, then the execution is sec, with witnesses as follows.
. If we consider only pointed cuts for non-mutators, then the execution is sec, with witnesses as follows.

In order to validate non-mutators, we must consider singleton non-mutator frontiers. The example shows that we must not consider frontiers with multiple non-mutators. There is some freedom in the choices otherwise. For set, we can “saturate” an execution with accessors by augmenting the execution with accessors that witness each cut of the mutators. In a saturated execution, it is sufficient to consider only the pointed accessor cuts, which end in a maximal accessor. For non-saturated executions, we are forced to examine each mutator cut: it is possible that a future accessor extension may witness that cut. The status of “mixed” frontiers, which include mutators with a single maximal non-mutator, is open for debate. We choose to ignore them, but the definition does not change if they are included.
Summary: A crdt must have a strategy for linearizing all mutator labels, even in the face of partitions. In order to ensure strong ec, the definition must consider sets of events across multiple replicas. Because non-mutators are resolved locally, sec must ignore frontiers with multiple non-mutators.
Cuts and frontiers are well-known concepts in the literature of distributed systems (Chandy and Lamport 1985). It is natural to consider frontiers when discussing the evolving correctness of a crdt.
2.5 Stuttering
Consider the following execution.

This lpo represents a partitioned system with events \(a\)–\(e\) in one partition and \(x\)–\(z\) in the other. As the partition heals, we must be able to account for the intermediate states. Because of the large number of events in this example, we have elided all accessors. We will present the example using the semantics of the add-wins set. Recall that the add-wins set validates  if and only if there is a maximal
if and only if there is a maximal  beforehand. Thus, a replica that has seen the cut with frontier
beforehand. Thus, a replica that has seen the cut with frontier  must answer
must answer  , whereas a replica that has seen
, whereas a replica that has seen  must answer
must answer  .
.
Any linearization of  must end in
must end in  , since the add-win set must reply
, since the add-win set must reply  : the only possibility is “
: the only possibility is “ ”. The linearization of
”. The linearization of  must end in
must end in  . If it must be a supersequence, the only possibility is “
. If it must be a supersequence, the only possibility is “ ”. Taking one more step on the left,
”. Taking one more step on the left,  must linearize to “
must linearize to “ ”. Thus the final state
”. Thus the final state  must linearize to “
must linearize to “ ”. Reasoning symmetrically, the linearization of
”. Reasoning symmetrically, the linearization of  must be “
must be “ ”, and thus the final
”, and thus the final  must linearize to “
must linearize to “ ”. The constraints on the final state are incompatible. Each of these states can be verified in isolation; it is the relation between them that is not satisfiable.
”. The constraints on the final state are incompatible. Each of these states can be verified in isolation; it is the relation between them that is not satisfiable.
Recall that monotonicity requires that the linearization chosen for a frontier be a subsequence of the linearization chosen for any extension of that frontier. The difficulty here is that subsequence relation ignores the similarity between “ ” and “
” and “ ”. Neither of these is a subsequence of the other, yet they capture exactly the same sequence of states, each with six alternations between
”. Neither of these is a subsequence of the other, yet they capture exactly the same sequence of states, each with six alternations between  and
and  . The canonical state-based representative for these sequences is “
. The canonical state-based representative for these sequences is “ ”.
”.
crdts are defined in terms of states. In order to relate crdts to sequential specifications, it is necessary to extract information about states from the specification itself. Adapting Brookes
(1996), we define strings as stuttering equivalent (notation  ) if they pass through the same states. So
) if they pass through the same states. So  but
but  If we consider subsequences up to stuttering, then execution (7) is sec, with witnesses as follow:
If we consider subsequences up to stuttering, then execution (7) is sec, with witnesses as follow:

Recall that without stuttering, we deduced that  must linearize to “
must linearize to “ ” and
” and  must linearize to “
must linearize to “ ”. Under stuttering equivalence, these are the same, with canonical representative “
”. Under stuttering equivalence, these are the same, with canonical representative “ ”. Thus, monotonicity under stuttering allows both linearizations to be extended to satisfy the final state
”. Thus, monotonicity under stuttering allows both linearizations to be extended to satisfy the final state  , which has canonical representative “
, which has canonical representative “ ”.
”.
Summary: crdts are described in terms of convergent states, whereas specifications are described as strings of actions. Actions correspond to labels in the lpo of an execution. Many strings of actions may lead to equivalent states. For example, idempotent actions can be applied repeatedly without modifying the state.
The stuttering equivalence of Brookes (1996) addresses this mismatch. In order to capture the validity of crdts, the definition of subsequence must change from a definition over individual specification strings to a definition over equivalence classes of strings up to stuttering.
3 Eventual Consistency for CRDTs
This section formalizes the intuitions developed in Sect. 2. We define executions, specifications and strong eventual consistency (sec). We discuss properties of eventual consistency and prove that the add-wins set is sec.
3.1 Executions
An execution realizes causal delivery if, whenever an event is received at a replica, all predecessors of the event are also received. Most of the crdts in Shapiro et al. (2011a) assume causal delivery, and we assumed it throughout the introductory section. There are costs to maintaining causality, however, and not all crdts assume that executions incur these costs. In the formal development, we allow non-causal executions.
Shapiro et al. (2011a) draw executions as timelines, explicitly showing the delivery of remote mutators. Below left, we give an example of such a timeline.

This is a non-causal execution: at the bottom replica,  is received before
is received before  , even though
, even though  precedes
precedes  at the top replica.
at the top replica.
Causal executions are naturally described as Labelled Partial Orders (lpos), which are transitive and antisymmetric. Section 2 presented several examples of lpos. To capture non-causal systems, we move to Labelled Visibility Orders (lvos), which are merely acyclic. Acyclicity ensures that the transitive closure of an lvo is an lpo. The right picture above shows the lvo corresponding to the timeline on the left. The zigzag arrow represents an intransitive communication. When drawing executions, we use straight lines for “transitive” edges, with the intuitive reading that “this and all preceding actions are delivered”.
lvos arise directly due to non-causal implementations. As we will see in Sect. 4, they also arise via projection from an lpo.
lvos are unusual in the literature. To make this paper self-contained, we define the obvious generalizations of concepts familiar from lpos, including isomorphism, suborder, restriction, maximality, downclosure and cut.
Fix a set \(\mathbf {L}\) of labels. A Labelled Visibility Order (lvo, also known as an execution) is a triple  where
where  is a finite set of events,
is a finite set of events,  and
and  is reflexive and acyclic.
is reflexive and acyclic.
Let \({u}\), \(v\) range over lvos. Many concepts extend smoothly from lpos to lvos.
-
Isomorphism: Write
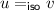 when \({u}\) and \(v\) differ only in the carrier set. We are often interested in the isomorphism class of an lvo.
when \({u}\) and \(v\) differ only in the carrier set. We are often interested in the isomorphism class of an lvo. -
Pomset: We refer to the isomorphism class of an lvo as a pomset. Pomset abbreviates Partially Ordered Multiset (Plotkin and Pratt 1997). We stick with the name “pomset” here, since “vomset” is not particularly catchy.
-
Suborder: Write
 when
when 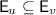 ,
, 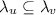 ,
,  , and
, and  .
. -
Restriction:Footnote 1 When
 , define
, define  . Restriction lifts subsets to suborders:
. Restriction lifts subsets to suborders: 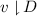 denotes the sub-lvo derived from a subset
denotes the sub-lvo derived from a subset  of events. See Sect. 2.2 for an example of restriction.
of events. See Sect. 2.2 for an example of restriction. -
Maximal elements:
 .
.We say that \(d\) is maximal for \(v\) when if
 .
. -
Non-maximal suborder:
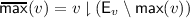 .
. is the suborder with the maximal elements removed.
is the suborder with the maximal elements removed. -
Downclosure: \(D\) is downclosed for \(v\) if
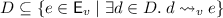 .
. -
Cut: \({u}\) is a cut of \(v\) if \({u}\subseteq v\) and
 is downclosed for \(v\).
is downclosed for \(v\).Let
 be the set of all cuts of \(v\). A cut is the sub-lvo corresponding to a downclosed set. Cuts are also known as prefixes. See Sect. 2.4 for an example. A cut is determined by its maximal elements: if
be the set of all cuts of \(v\). A cut is the sub-lvo corresponding to a downclosed set. Cuts are also known as prefixes. See Sect. 2.4 for an example. A cut is determined by its maximal elements: if  then
then  .
. -
Linearization: For
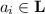 , we say that
, we say that  is a linearization of
is a linearization of 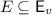 if there exists a bijection
if there exists a bijection  such that
such that  and
and 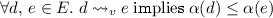 .
.
Replica-Specific Properties. In the literature on replicated data types, some properties of interest (such as “read your writes” (Tanenbaum and Steen 2007)) require the concept of “session” or a distinction between local and remote events. These can be accommodated by augmenting lvos with a replica labelling  which maps events to a set \(\mathbf {R}\) of replica identifiers.
which maps events to a set \(\mathbf {R}\) of replica identifiers.
Executions can be generated operationally as follows: Replicas receive mutator and accessor events from the local client; they also receive mutator events that are forwarded from other replicas. Each replica maintains a set of seen events: an event that is received is added to this set. When an event is received from the local client, the event is additionally added to the execution, with the predecessors in the visibility relation corresponding to the current seen set. If we wish to restrict attention to causal executions, then we require that replicas forward all the mutators in their seen sets, rather than individual events, and, thus, the visibility relation is transitive over mutators.
All executions that are operationally generated satisfy the additional property that  is per-replica total:
is per-replica total:  . We do not demand per-replica totality because our results do not rely on replica-specific information.
. We do not demand per-replica totality because our results do not rely on replica-specific information.
3.2 Specifications and Stuttering Equivalence
Specifications are sets of strings, equipped with a distinguished set of mutators and a dependency relation between labels. Specifications are subject to some constraints to ensure that the mutator set and dependency relations are sensible; these are inspired by the conditions on Mazurkiewicz executions (Diekert and Rozenberg 1995). Every specification set yields a derived notion of stuttering equivalence. This leads to the definition of observational subsequence ( ).
).
We use standard notation for strings: Let \(\sigma \) and \(\tau \) range over strings. Then  denotes concatenation, \(\sigma ^*\) denotes Kleene star, \(\sigma |||\tau \) denotes the set of interleavings, \(\varepsilon \) denotes the empty string and \(\sigma ^{i}\) denotes the \(i^{\text {th}}\) element of \(\sigma \). These notations lift to sets of strings via set union.
denotes concatenation, \(\sigma ^*\) denotes Kleene star, \(\sigma |||\tau \) denotes the set of interleavings, \(\varepsilon \) denotes the empty string and \(\sigma ^{i}\) denotes the \(i^{\text {th}}\) element of \(\sigma \). These notations lift to sets of strings via set union.
A specification is a quadruple  where
where
-
\(\mathbf {L}\) is a set of actions (also known as labels),
-
\(\mathbf {M}\subseteq \mathbf {L}\) is a distinguished set of mutator actions,
-
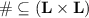 is a symmetric and reflexive dependency relation, and
is a symmetric and reflexive dependency relation, and -
\({\varSigma }\subseteq \mathbf {L}^*\) is a set of valid strings.
Let  be the sets of non-mutators.
be the sets of non-mutators.
A specification must satisfy the following properties:
-
(a)
prefix closed:
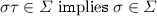
-
(b)
non-mutators are closed under stuttering, and commutation:
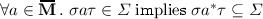

-
(c)
independent actions commute:

Property (b) ensures that non-mutators do not affect the state of the data structure. Property (c) ensures that commuting of independent actions does not affect the state of the data structure.
Recall that the set specification takes  , representing addition and removal of bits 0 and 1, and
, representing addition and removal of bits 0 and 1, and  , representing membership tests returning false or true. The dependency relation is
, representing membership tests returning false or true. The dependency relation is  , where \(D^2=D\times D\).
, where \(D^2=D\times D\).
The dependency relation for set is an equivalence, but this need not hold generally. We will see an example in Sect. 4.
The definitions in the rest of the paper assume that we have fixed a specification  . In the examples of this section, we use set.
. In the examples of this section, we use set.
State and Stuttering Equivalence. Specification strings \(\sigma \) and \(\tau \) are state equivalence (notation  ) if every valid extension of \(\sigma \) is also a valid extension of \(\tau \), and vice versa. For example,
) if every valid extension of \(\sigma \) is also a valid extension of \(\tau \), and vice versa. For example,  and
and  but
but  . In particular, state equivalent strings agree on the valid accessors that can immediately follow them: either
. In particular, state equivalent strings agree on the valid accessors that can immediately follow them: either  or
or  and either
and either  or
or  . Formally, we define state equivalence,
. Formally, we define state equivalence,  , as followsFootnote 2.
, as followsFootnote 2.

From specification property (b), we know that non-mutators do not affect the state. Thus we have that  whenever
whenever  and
and  . From specification property (c), we know that independent actions commute. Thus we have that
. From specification property (c), we know that independent actions commute. Thus we have that  whenever
whenever  and
and  .
.
Two strings are stuttering equivalentFootnote 3 if they only differ in operations that have no effect on the state of the data structure, as given by \({\varSigma }\). Adapting Brookes
(1996) to our notion of state equivalence, we define stuttering equivalence,  , to be the least equivalence relation generated by the following rules, where
, to be the least equivalence relation generated by the following rules, where  ranges over
ranges over  .
.

The first rule above handles the empty string. The second rule allows stuttering in any context. The third rule motivates the name stuttering equivalence, for example, allowing  . The last case captures the equivalence generated by independent labels, for example, allowing
. The last case captures the equivalence generated by independent labels, for example, allowing  but not
but not  Using the properties of
Using the properties of  discussed above, we can conclude, for example, that
discussed above, we can conclude, for example, that 
Consider specification strings for a unary set over value 0. Since stuttering equivalence allows us to remove both accessors and adjacent mutators with the same label we deduce that the canonical representatives of the equivalence classes induced by \(\sim \) are generated by the regular expression  .
.
Observational Subsequence. Recall that  is a subsequence of
is a subsequence of  , although it is not a prefix. We write
, although it is not a prefix. We write  for subsequence and
for subsequence and  for observational subsequence, defined as follows.
for observational subsequence, defined as follows.

Note that observational subsequence includes both subsequence and stuttering equivalence  .
.
 can be understood in isolation, whereas
can be understood in isolation, whereas  can only be understood with respect to a given specification. In the remainder of the paper, the implied specification will be clear from context.
can only be understood with respect to a given specification. In the remainder of the paper, the implied specification will be clear from context.  is a partial order, whereas
is a partial order, whereas  is only a preorder, since it is not antisymmetric.
is only a preorder, since it is not antisymmetric.
Let \(\sigma \) and \(\tau \) be strings over the unary set with canonical representatives  and
and  . Then we have that
. Then we have that  exactly when either
exactly when either  and
and  or
or  and
and  . Thus, observational subsequence order is determined by the number of alternations between the mutators.
. Thus, observational subsequence order is determined by the number of alternations between the mutators.
Specification strings for the binary set, then, are stuttering equivalent exactly when they yield the same canonical representatives when restricted to 0 and to 1. Thus, observational subsequence order is determined by the number of alternations between the mutators, when restricted to each dependent subsequence. (The final rule in the definition of stuttering, which allows stuttering across independent labels, is crucial to establishing this canonical form.)
3.3 Eventual Consistency
Eventual consistency is defined using the cuts of an execution and the observational subsequence order of the specification. As noted in Sects. 2.2 and 2.4, it is important that we not consider all cuts. Thus, before we define sec, we must define dependent cuts.
The dependent restriction of an execution is defined:  where
where  when
when  . See Sect. 2.2 for an example of dependent restriction.
. See Sect. 2.2 for an example of dependent restriction.
The dependent cuts of \(v\) are cuts of the dependent restriction. As discussed in Sect. 2.4, we only consider pointed cuts (with a single maximal element) for non-mutators. See Sect. 2.4 for an example.

An execution \(v\) is Eventually Consistent (sec) for specification  iff there exists a function
iff there exists a function  that satisfies the following.
that satisfies the following.
- Linearization::
-
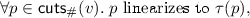 and
and - Monotonicity::
-
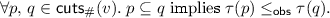
A data structure implementation is \(\textsc {sec}{}\) if all of its executions are \(\textsc {sec}{}\).
In Sect. 2, we gave several examples that are sec. See Sects. 2.4 and 2.5 for examples where  is given explicitly. Section 2.4 also includes an example that is not sec.
is given explicitly. Section 2.4 also includes an example that is not sec.
The concerns raised in Sect. 2 are reflected in the definition.
-
Non-mutators are ignored by the dependent restriction of other non-mutators. As discussed in Sect. 2.1, this relaxation is similar that of update-serializability (Hansdah and Patnaik 1986; Garcia-Molina and Wiederhold 1982).
-
Independent events are ignored by the dependent restriction of an event. As discussed in Sect. 2.2, this relaxation is similar to preserved program order in relaxed memory models (Higham and Kawash 2000; Alglave 2012).
-
As discussed in Sect. 2.3, punning is allowed: each cut \(p\) is linearized separately to a specification string
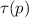 .
. -
As discussed in Sect. 2.4, we constrain the power puns by considering cuts of the distributed system (Chandy and Lamport 1985).
-
Monotonicity ensures that the system evolves in a sensible way: new order may be introduced, but old order cannot be forgotten. As discussed in Sect. 2.5, the preserved order is captured in the observational subsequence relation, which allows stuttering (Brookes 1996).
3.4 Properties of Eventual Consistency
We discuss some basic properties of sec. For further analysis, see Sect. 5.
An important property of crdts is prefix closure: If an execution is valid, then every prefix of the execution should also be valid. Prefix closure follows immediately from the definition, since whenever \({u}\) is a prefix of \(v\) we have that  .
.
Prefix closure looks back in time. It is also possible to look forward: A system satisfies eventual delivery if every valid execution can be extended to a valid execution with a maximal element that sees every mutator. If one assumes that every specification string can be extended to a longer specification string by adding non-mutators, then eventual delivery is immediate.
The properties psts, psm and ppe are discussed in the introduction. An sec implementation must satisfies ppe since every dependent set of mutators is linearized: sec enforces the stronger property that there are no new intermediate states, even when executing all mutators in parallel. For causal systems, where  is transitive, psts and psm follow by observing that if there is a total order on the mutators of \({u}\) then any linearization of \({u}\) is a specification string.
is transitive, psts and psm follow by observing that if there is a total order on the mutators of \({u}\) then any linearization of \({u}\) is a specification string.
Burckhardt (2014, Sect. 5) provides a taxonomy of correctness criteria for replicated data types. Our definition implies NoCircularCausality and CausalArbitration, but does not imply either ConsistentPrefix or CausalVisibility. For lpos, which model causal systems, our definition implies CausalVisibility. ReadMyWrites and MonotonicReads require a distinction between local and remote events. If one assumes the replica-specific constraints given in Sect. 3.1, then our definition satisfies these properties; without them, our definition is too abstract.
3.5 Correctness of the Add-Wins Set
The add-wins set is defined to answer  for a cut \({u}\) exactly when
for a cut \({u}\) exactly when

It answers  otherwise. The add-wins set is called the “observed-remove” set.
otherwise. The add-wins set is called the “observed-remove” set.
We show that any lpo that meets this specification is sec with respect to set. We restrict attention to lpos since causal delivery is assumed for the add-wins set in (Shapiro et al. 2011a).
For set, the dependency relation is an equivalence. For an equivalence relation R, let  denote the set of (disjoint) equivalence classes for R. For set,
denote the set of (disjoint) equivalence classes for R. For set,  . When dependency is an equivalence, then every interleaving of independent actions is valid if any interleaving is valid. Formally, we have the following, where \(|||\) denotes interleaving.
. When dependency is an equivalence, then every interleaving of independent actions is valid if any interleaving is valid. Formally, we have the following, where \(|||\) denotes interleaving.

Using the forthcoming composition result (Theorem 2), it suffices for us to address the case when \({u}\) only involves operations on a single element, say 0. For any such lvo \({u}\), we choose a linearization  that has a maximum number of alternations between
that has a maximum number of alternations between  and
and  . If there is a linearization that begins with
. If there is a linearization that begins with  , then we choose one of these. Below, we summarize some of the key properties of such a linearization.
, then we choose one of these. Below, we summarize some of the key properties of such a linearization.
-
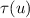 ends with
ends with  iff there is an
iff there is an  that is not followed by any
that is not followed by any  in \({u}\).
in \({u}\). -
For any lpo \(v\subseteq {u}\),
 has at most as many alternations as
has at most as many alternations as  .
.
The first property above ensures that the accessors are validated correctly, i.e., 0 is deemed to be present iff there is an  that is not followed by any
that is not followed by any  .
.
We are left with proving monotonicity, i.e., if \({u}\subseteq v\), then  . Consider
. Consider  and
and  .
.
-
If
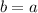 , the second property above ensures that
, the second property above ensures that  .
. -
In the case that
 , we deduce by construction that
, we deduce by construction that 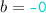 and
and  . In this case, \(\rho \) starts with
. In this case, \(\rho \) starts with 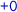 and has at least as many alternations as
and has at least as many alternations as  . So, we deduce that
. So, we deduce that 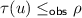 . The required result follows since
. The required result follows since  .
.
4 A Collaborative Text Editing Protocol
In this section we consider a variant of the collaborative text editing protocol defined by Attiya et al. (2016). After stating the sequential specification, text, we sketch a correctness proof with respect to our definition of eventual consistency. This example is interesting formally: the dependency relation is not an equivalence, and therefore the dependent projection does not preserve transitivity. The generality of intransitive lvos is necessary to understand text, even assuming a causal implementation.
Specification. Let \(a\), \(b\) range over nodes, which contain some text, a unique identifier, and perhaps other information. Labels have the following forms:
-
Mutator
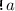 initializes the text to node \(a\).
initializes the text to node \(a\). -
Mutator
 adds node \(a\) immediately before node \(b\).
adds node \(a\) immediately before node \(b\). -
Mutator
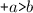 adds node \(a\) immediately after node \(b\).
adds node \(a\) immediately after node \(b\). -
Mutator
 removes node \(b\).
removes node \(b\). -
Non-mutator query
 returns the current state of the document.
returns the current state of the document.
We demonstrate the correct answers to queries by example. Initially, the document is empty, whereas after initialization, the document contains a single node; thus the specification contains strings such as  , where \(\varepsilon \) represents the empty document. Nodes can be added either before or after other nodes; thus
, where \(\varepsilon \) represents the empty document. Nodes can be added either before or after other nodes; thus  results in the document
results in the document  . Nodes are always added adjacent to the target; thus, order matters in
. Nodes are always added adjacent to the target; thus, order matters in  which results in
which results in  rather than
rather than  . Removal does what one expects; thus
. Removal does what one expects; thus  results in
results in  .
.
Attiya et al. (2016) define the interface for text using integer indices as targets, rather than nodes. Using the unique correspondence between the nodes and it indices (since node are unique), one can easily adapt an implementation that satisfies our specification to their interface.
We say that node \(a\) is a added in the actions  ,
,  and
and  . Node
. Node  is a target in
is a target in  and
and  . In addition to correctly answering queries, specifications must satisfy the following constraints:
. In addition to correctly answering queries, specifications must satisfy the following constraints:
-
Initialization may occur at most once,
-
each node may be added at most once,
-
a node may be removed only after it is added, and
-
a node may be used as a target only if it has been added and not removed.
These constraints forbid adding to a target that has been removed; thus  is a valid string, but
is a valid string, but  is not. It also follows that initialization must precede any other mutators.
is not. It also follows that initialization must precede any other mutators.
Because add operations use unique identifiers, punning and stuttering play little role in this example. In order to show the implementation correct, we need only choose an appropriate notion of dependency. As we will see, it is necessary that removes be independent of adds with disjoint label sets, but otherwise all actions may be dependent. Let  be the set of add and query labels, and let
be the set of add and query labels, and let  return the set of nodes that appear in a label. Then we define dependency as follows.
return the set of nodes that appear in a label. Then we define dependency as follows.

Implementation. We consider executions that satisfy the same four conditions above imposed on specifications. We refer the reader to the algorithm of Attiya et al. (2016) that provides timestamps for insertions that are monotone with respect to causality.
As an example, Attiya et al.
(2016) allow the execution given on the left below. In this case, the dependent restriction is an intransitive lvo, even though the underlying execution is an lpo: in particular,  does not precede
does not precede  in the dependent restriction. We give the order considered by dependent cuts on the right—this is a restriction of the dependent restriction: since we only consider pointed accessor cuts, we can safely ignore order out of non-mutators.
in the dependent restriction. We give the order considered by dependent cuts on the right—this is a restriction of the dependent restriction: since we only consider pointed accessor cuts, we can safely ignore order out of non-mutators.

This execution is not linearizable, but it is sec, choosing witnesses to be subsequences of the mutator string  . Here, the document is initialized to \(b\), then \(c\) and \(d\) are added after \(b\), resulting in
. Here, the document is initialized to \(b\), then \(c\) and \(d\) are added after \(b\), resulting in  . The order of \(c\) and \(d\) is determined by their timestamps. Afterwards, the top replica removes \(d\) and adds \(a\); the bottom replica removes \(b\) and adds \(e\), resulting in the final state
. The order of \(c\) and \(d\) is determined by their timestamps. Afterwards, the top replica removes \(d\) and adds \(a\); the bottom replica removes \(b\) and adds \(e\), resulting in the final state  . In the right execution, the removal of order out of the non-mutators shows the “update serializability” effect; the removal of order between
. In the right execution, the removal of order out of the non-mutators shows the “update serializability” effect; the removal of order between  and
and  (and between
(and between  and
and  ) shows the “preserved program order” effect.
) shows the “preserved program order” effect.
Correctness. Given an execution, we can find a specification string \(s_1 s_2\) that linearizes the mutators in the dependent restriction of the execution such that \(s_1\) contains only adds and \(s_2\) contains only removes. Such a specification string exists because by the conditions on executions, deletes do not have any outgoing edges to other mutators in the dependent restriction; so, they can be moved to the end in the matching specification string. In order to find \(s_1\) that linearizes the add events, any linearization that respects causality and timestamps (yielded by the algorithm of Attiya et al. (2016)) suffices for our purposes. The conditions required by sec follow immediately.
5 Compositional Reasoning
The aim of this section is to establish compositional methods to reason about replicated data structures. We do so using Labelled Transition Systems (ltss), where the transitions are labelled by dependent cuts. We show how to derive an lts from an execution,  . We also define an lts for the most general crdt that validates a specification,
. We also define an lts for the most general crdt that validates a specification,  . We show that \({u}\) is sec for \({\varSigma }\) exactly when
. We show that \({u}\) is sec for \({\varSigma }\) exactly when  is a refinement of
is a refinement of  . We use this alternative characterization to establish composition and abstraction results.
. We use this alternative characterization to establish composition and abstraction results.
LTSs. An lts is a triple consisting of a set a states, an initial state and a labelled transition function between states. We first define the ltss for executions and specifications, then provide examples and discussion.
For both executions and specifications, the labels of the lts are dependent cuts: for executions, these are dependent cuts of the execution itself; for specifications, they are drawn from the set  of all possible dependent cuts. We compare lts labels up to isomorphism, rather than identity. Thus it is safe to think of lts labels as (potentially intransitive) pomsets (Plotkin and Pratt 1997).
of all possible dependent cuts. We compare lts labels up to isomorphism, rather than identity. Thus it is safe to think of lts labels as (potentially intransitive) pomsets (Plotkin and Pratt 1997).
The states of the lts are different for the execution and specification. For executions, the states are cuts of the execution \({u}\) itself,  ; these are general cuts, not just dependent cuts. For specifications, the states are the stuttering equivalence classes of strings allowed by the specification,
; these are general cuts, not just dependent cuts. For specifications, the states are the stuttering equivalence classes of strings allowed by the specification,  .
.
There is an isomorphism between strings and total orders. We make use of this in the definition, treating strings as totally-ordered lvos.
Define  where
where  if
if  and
and

Define  where
where  if
if  and
and

We explain the definitions using examples from set, first for executions, then for specifications. Consider the execution on the left below. The derived lts is given on the right.

The states of the lts are cuts of the execution. The labels on transitions are dependent cuts. The requirements for execution transitions relate the source \(p\), target \(q\) and label \(v\). The leftmost requirements state that the target state must extend both the source and the label; thus the target state must be a combination of events and order from source and label. The middle requirements state that the maximal elements of the label must be new in the target; only the maximal elements of the label are added when moving from source to target. The upper right requirement states that the non-maximal order of the label must be respected by the source; thus the causal history reported by the label cannot contradict the causal history of the source. The lower right requirement ensures that maximal elements of the label are also maximal in the target. The restriction to dependent cuts explains the labels on transitions  and
and  . By definition, there is a self-transition labelled with the empty lvo at every state; we elide these transitions in drawings.
. By definition, there is a self-transition labelled with the empty lvo at every state; we elide these transitions in drawings.
The specification lts for set is infinite, of course. To illustrate, below we give two sub-ltss with limitations on mutators. On the left, we only allow  and
and  . On the right, we only allow
. On the right, we only allow  and
and  and only consider the case in which there is at most one alternation between them. The states are shown using their canonical representatives. Because of the number of transitions, we show all dependent accessors as a single transition, with labels separated by commas.
and only consider the case in which there is at most one alternation between them. The states are shown using their canonical representatives. Because of the number of transitions, we show all dependent accessors as a single transition, with labels separated by commas.

The requirements for specification transitions are similar to those for implementations, but the states are equivalence classes over specification strings: with source \({[}\sigma {]}\) and target \({[}\tau {]}\). There is a transition between the states if there are members of the equivalence classes, \(\sigma \) and \(\tau \), that satisfy the requirements. Since these are total orders, the leftmost requirements state that there must be linearizations of the source and label that are subsequences of the target. Similarly, the upper right requirement states that the non-maximal order of the label must be respected by the source; thus we have  but not
but not  for any \(\sigma \). The use of sub-order rather than subsequence allows
for any \(\sigma \). The use of sub-order rather than subsequence allows  but prevents nonsense transitions such as
but prevents nonsense transitions such as  . Because the states are total orders, we drop the implementation lts requirement that maximal events of the label must be maximal in the target. If we were to impose this restriction, we would disallow
. Because the states are total orders, we drop the implementation lts requirement that maximal events of the label must be maximal in the target. If we were to impose this restriction, we would disallow  .
.
It is worth noting that the specification of the add-wins set removes exactly three edges from the right lts: 
 and
and  .
.
Refinement. Refinement is a functional form of simulation (Hoare 1972; Lamport 1983; Lynch and Vaandrager 1995). Let  and
and  be ltss. A function
be ltss. A function  is a (strong) refinement if
is a (strong) refinement if  imply that there exist
imply that there exist  and
and  such that
such that  . Then \({P}\) refines \({Q}\) (notation
. Then \({P}\) refines \({Q}\) (notation  ) if there exists a refinement
) if there exists a refinement  such that the initial states are related, i.e., \(f(p_{0}) =q_{0}\).
such that the initial states are related, i.e., \(f(p_{0}) =q_{0}\).
We now prove that sec can be characterized as a refinement. We write  when \(p_n\) is reachable from \(p_0\) via a finite sequence of steps
when \(p_n\) is reachable from \(p_0\) via a finite sequence of steps  .
.
Theorem 1
 is EC for the specification \({\varSigma }\) iff
is EC for the specification \({\varSigma }\) iff  .
.
Proof
For the forward direction, assume \({u}\) is EC and therefore there exists a function  such that
such that  . For each cut
. For each cut  , we start with the dependent restriction,
, we start with the dependent restriction,  . We further restriction attention to mutators,
. We further restriction attention to mutators,  . The required refinement maps \(p\) to the equivalence class of the linearization of
. The required refinement maps \(p\) to the equivalence class of the linearization of  chosen by
chosen by  :
:  . We abuse notation below by identifying each equivalence class with a canonical element of the class.
. We abuse notation below by identifying each equivalence class with a canonical element of the class.
We show that  implies
implies  . Since \(p\subseteq q\), we deduce that
. Since \(p\subseteq q\), we deduce that  and by monotonicity,
and by monotonicity,  .
.
We show that  implies
implies  . Suppose \(v\) only contains mutators. Since \(v\subseteq q\), we deduce that
. Suppose \(v\) only contains mutators. Since \(v\subseteq q\), we deduce that  and by monotonicity,
and by monotonicity,  . On the other hand, suppose \(v\) contains the non-mutator \(a\). Let \(A= \mathbf {M}\cup \{a\}\). Since \(v\subseteq q\), we deduce that
. On the other hand, suppose \(v\) contains the non-mutator \(a\). Let \(A= \mathbf {M}\cup \{a\}\). Since \(v\subseteq q\), we deduce that  . By monotonicity,
. By monotonicity,  . Since
. Since  we have
we have  as required.
as required.
Thus  , completing this direction of the proof.
, completing this direction of the proof.
For the reverse direction, we are given a refinement  . For any
. For any  , define
, define  to be a string in the equivalence class
to be a string in the equivalence class  that includes any non-mutator found in \(p\).
that includes any non-mutator found in \(p\).
We first prove that  is a linearization of \(p\). A simple inductive proof demonstrates that for any
is a linearization of \(p\). A simple inductive proof demonstrates that for any  , there is a transition sequence of the form
, there is a transition sequence of the form  . Thus, we deduce from the label on the final transition into \(p\) that the
. Thus, we deduce from the label on the final transition into \(p\) that the  related to \(p\) is a linearization of \(p\).
related to \(p\) is a linearization of \(p\).
We now establish monotonicity. A simple inductive proof shows that for any  ,
,  . Thus
. Thus  , by the properties of
, by the properties of  and the definition of
and the definition of  .
.
Composition. Given two non-interacting data structures whose replicated implementations satisfy their sequential specifications, the implementation that combines them satisfies the interleaving of their specifications. We formalize this as a composition theorem in the style of Herlihy and Wing (1990).
Given an execution \({u}\) and \(L\subseteq \mathbf {L}\), write  for the execution that results by restricting \({u}\) to events with labels in L:
for the execution that results by restricting \({u}\) to events with labels in L:  . This notation lifts to sets in the standard way:
. This notation lifts to sets in the standard way:  . Write
. Write  to indicate that \({u}\) is sec for \({\varSigma }\).
to indicate that \({u}\) is sec for \({\varSigma }\).
Theorem 2 (Composition)
Let \(L_1\) and \(L_2\) be mutually independent subsets of \(\mathbf {L}\). For \(i\in \{1,2\}\), let \({\varSigma }_i\) be a specification with labels chosen from \(L_i\), such that \({\varSigma }_1|||{\varSigma }_2\) is also a specification. If  and
and  then
then  (equivalently
(equivalently  ).
).
The proof is immediate. Since \(L_1\) and \(L_2\) are mutually independent, any interleaving of the labels will satisfy the definition.
Abstraction. We describe a process algebra with parallel composition and restriction and establish congruence results. We ignore syntactic details and work directly with ltss. Replica identities do not play a role in the definition; thus, we permit implicit mobility of the client amongst replicas with the only constraint being that the replica has at least as much history on the current item of interaction as the client. This constraint is enforced by the synchronization of the labels, defined below. While the definition includes the case where the client itself is replicated, it does not provide for out-of-band interaction between the clients at different replicas: All interaction is assumed to happen through the data structure.
The relation  is defined between ltss so that
is defined between ltss so that  describes the system that results when client \({P}\) interacts with data structure \({Q}\). For ltss \({P}\) and \({Q}\), define
describes the system that results when client \({P}\) interacts with data structure \({Q}\). For ltss \({P}\) and \({Q}\), define  inductively, as follows, where
inductively, as follows, where  represents the empty lvo.
represents the empty lvo.

Let

The  operator is asymmetric between the client and data structure in two ways. First, note that every action of the client must be matched by the data structure. The condition of client quiescence in the definition of \(S_{\times }\), that all of the actions of the client \({P}\) must be matched by \({Q}\); otherwise
operator is asymmetric between the client and data structure in two ways. First, note that every action of the client must be matched by the data structure. The condition of client quiescence in the definition of \(S_{\times }\), that all of the actions of the client \({P}\) must be matched by \({Q}\); otherwise  . However, the first rule for
. However, the first rule for  explicitly permits actions of the data structure that may not be matched by the client. This asymmetry permits the composition of the data structure with multiple clients to be described incrementally, one client at a time. Thus, we expect that
explicitly permits actions of the data structure that may not be matched by the client. This asymmetry permits the composition of the data structure with multiple clients to be described incrementally, one client at a time. Thus, we expect that  .
.
Second, note that right rule for  interaction permits the data structure \({Q}\) to introduce order not found in the clients. This is clearly necessary to ensure that that the composition of client
interaction permits the data structure \({Q}\) to introduce order not found in the clients. This is clearly necessary to ensure that that the composition of client  with the set data structure is nonempty. In this case, the client has no order between
with the set data structure is nonempty. In this case, the client has no order between  and
and  whereas the data structure orders
whereas the data structure orders  after
after  . In this paper, we do not permit the client to introduce order that is not seen in the data structure. For a discussion of this issue, see (Jagadeesan and Riely 2015).
. In this paper, we do not permit the client to introduce order that is not seen in the data structure. For a discussion of this issue, see (Jagadeesan and Riely 2015).
We can also define restriction for some set  of labels, a lá CCS.
of labels, a lá CCS.  . The definitions lift to sets:
. The definitions lift to sets:  and
and  .
.
Lemma 3
If  and
and  then
then  and
and  . \(\square \)
. \(\square \)
It suffices to show that:  . The proof proceeds in the traditional style of such proofs in process algebra. We illustrate by sketching the case for client parallel composition. Let \(f\) be the witness for
. The proof proceeds in the traditional style of such proofs in process algebra. We illustrate by sketching the case for client parallel composition. Let \(f\) be the witness for  . The proof proceeds by constructing a “product” refinement \(\mathrel {\mathcal {S}}\) relation of the identity on the states of \({P}\) with \(f\), i.e.:
. The proof proceeds by constructing a “product” refinement \(\mathrel {\mathcal {S}}\) relation of the identity on the states of \({P}\) with \(f\), i.e.:  .
.
Thus, an sec implementation can be replaced by the specification.
Theorem 4 (Abstraction)
If \({u}\) is sec for \({\varSigma }\), then  .
.
6 A Replicated Graph Algorithm
We describe a graph implemented with sets for vertices and edges, as specified by Shapiro et al. (2011a). The graph maintains the invariant that the vertices of an edge are also part of the graph. Thus, an edge may be added only if the corresponding vertices exist; conversely, a vertex may be removed only if it supports no edge. In the case of a concurrent addition of an edge with the deletion of either of its vertices, the deletion takes precedence.
The vertices \(v,w, \ldots \) are drawn from some universe \({\mathcal U}\). An edge \(e, e', \ldots \) is a pair of vertices. Let \(\mathsf{vert}(e) = \{ v,w\}\) be the vertices of edge \(e=(v,w)\). The vocabulary of the set specification includes mutators for the addition and removal of vertices and edges and non-mutators for membership tests.

Valid graph specification strings answer queries like sets. In addition, we require the following.
-
Vertices and edges added at most once: Each add label is unique.
-
Removal of a vertex or edge is preceded by a corresponding add.
-
Vertices are added before they are mentioned in any edges: If
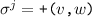 , or
, or 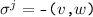 there exists \(i,i' <j\) such that:
there exists \(i,i' <j\) such that:  ,
, 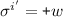 .
. -
Vertices are removed only after they are mentioned in edges: If
 , or
, or 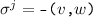 , then for all \(i<j\):
, then for all \(i<j\):  and
and  .
.
Graph Implementation. We rewrite the graph program of Shapiro et al. (2011a) in a more abstract form. Our distributed graph implementation is written as a client of two replicate set: for vertices (V) and for edges (E). The implementation uses usets, which require that an element be added at most once and that each remove causally follow the corresponding add. Here we show the graph implementation for various methods as client code that runs at each replica. At each replica, the code accesses its local copy of the usets. All the message passing needed to propagate the updates is handled by the uset implementations of the sets V, E. For several methods, we list preconditions, which prescribe the natural assumptions that need to satisfied when these client methods are invoked. For example, an edge operation requires the presence of the vertices at the current replica.

We assume a causal transition system (as needed in Shapiro et al. (2011a)).
Correctness Using the Set Specification. We first show the correctness of the graph algorithm, using the set specification for the vertex and edge sets. We then apply the abstraction and composition theorems to show the correctness of the algorithm using a set implementation.
Let \({u}\) be a lvo generated in an execution of the graph implementation. The preconditions ensure that \({u}\) has the following properties:
-
(a)
For any \(v\),
 is never ordered after
is never ordered after  , and likewise for \(e\).
, and likewise for \(e\). -
(b)
 or
or  is never ordered after
is never ordered after  or -w.
or -w. -
(c)
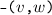 or
or  is always ordered after some
is always ordered after some  and
and  .
.
Define \(\sigma _1\), \(\sigma _2\) and \(\sigma _3\) as follows.
-
All elements of \(\sigma _1\) are of the form
 . \(\sigma _1\) exists by (c) above.
. \(\sigma _1\) exists by (c) above. -
All elements of \(\sigma _3\) are of the form
 . \(\sigma _3\) exists by (b) above.
. \(\sigma _3\) exists by (b) above. -
For each edge
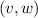 that is accessed in \({u}\), let
that is accessed in \({u}\), let  be any interleaving of the events involving
be any interleaving of the events involving  in \({u}\) such that no
in \({u}\) such that no  occurs after any
occurs after any 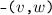 in
in 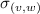 .
.  exists by (a) above. \(\sigma _2\) is any interleaving of all the
exists by (a) above. \(\sigma _2\) is any interleaving of all the  .
.
Then \({u}\) is sec with witness  .
.
Full Correctness of the Implementation. We now turn to proving the correctness of the algorithm when the two sets are replaced by their implementations.
Consider two (distributed implementations of) separate and independent sets for vertices and edges, i.e.  . Suppose we have two implementations, each of which is correct individually:
. Suppose we have two implementations, each of which is correct individually:  . By composition, we have that they are correct when composed together:
. By composition, we have that they are correct when composed together:  . Let \(\mathcal {P}\) be the graph implementation, which is a client of the two sets. By abstraction, we know that
. Let \(\mathcal {P}\) be the graph implementation, which is a client of the two sets. By abstraction, we know that  implies
implies  . By congruence, we deduce:
. By congruence, we deduce:

Thus, in order to validate the full graph implementation, it is sufficient to establish the correctness of the graph client when interacting with the specification of the two independent sets for edges and vertices, which we have already done in the previous treatment of abstract correctness.
7 Conclusions
We have provided a definition of strong eventual consistency that captures validity with respect to a sequential specification. Our definition reflects an attempt to resolve the tension between expressivity (cover the extant examples in the literature) and facilitating reasoning (by retaining a direct relationship with the sequential specification). The notion of concurrent specification developed by Burckhardt et al. (2014) has been used to prove the validity of several replicated data structure implementations. In future work, we would like to discover sufficient conditions relating concurrent and sequential specifications such that any implementation that is correct under the concurrent specification (as defined by Burckhardt et al. (2014)) will also be correct under the sequential counterpart (as defined here).
Notes
- 1.
We use the standard definitions for restriction on functions and relations. Given a function
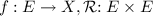 and \(D\subseteq E\), define
and \(D\subseteq E\), define 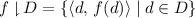 and
and  .
. - 2.
To extend the definition to non-specification strings, we allow
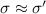 when
when  .
. - 3.
Readers of Brookes (1996) should note that mumbling is not relevant here, since all mutators are visible.
References
Alglave, J.: A formal hierarchy of weak memory models. Formal Methods Syst. Des. 41(2), 178–210 (2012)
Alglave, J., Maranget, L., Tautschnig, M.: Herding cats: modelling, simulation, testing, and data mining for weak memory. ACM Trans. Program. Lang. Syst. 36(2), 7:1–7:74 (2014)
Attiya, H., Burckhardt, S., Gotsman, A., Morrison, A., Yang, H., Zawirski, M.: Specification and complexity of collaborative text editing. In: Proceedings of the 2016 ACM Symposium on Principles of Distributed Computing, PODC 2016, Chicago, IL, USA, pp. 259–268, 25–28 July 2016
Bieniusa, A., Zawirski, M., Preguiça, N., Shapiro, M., Baquero, C., Balegas, V., Duarte, S.: Brief announcement: semantics of eventually consistent replicated sets. In: Aguilera, M.K. (ed.) DISC 2012. LNCS, vol. 7611, pp. 441–442. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33651-5_48
Bouajjani, A., Enea, C., Hamza, J.: Verifying eventual consistency of optimistic replication systems. In: POPL 2014, pp. 285–296 (2014)
Brookes, S.D.: Full abstraction for a shared-variable parallel language. Inf. Comput. 127(2), 145–163 (1996)
Budhiraja, N., Marzullo, K., Schneider, F.B., Toueg, S.: The primary-backup approach. In: Mullender, S. (ed.) Distributed Systems, 2nd edn., pp. 199–216 (1993)
Burckhardt, S.: Principles of eventual consistency. Found. Trends Program. Lang. 1(1–2), 1–150 (2014). ISSN 2325-1107
Burckhardt, S., Leijen, D., Fähndrich, M., Sagiv, M.: Eventually consistent transactions. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 67–86. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_4
Burckhardt, S., Gotsman, A., Yang, H., Zawirski, M.: Replicated data types: specification, verification, optimality. In: POPL 2014, pp. 271–284 (2014)
Chandy, K.M., Lamport, L.: Distributed snapshots: determining global states of distributed systems. ACM Trans. Comput. Syst. 3(1), 63–75 (1985)
DeCandia, G., Hastorun, D., Jampani, M., Kakulapati, G., Lakshman, A., Pilchin, A., Sivasubramanian, S., Vosshall, P., Vogels, W.: Dynamo: Amazon’s highly available key-value store. SIGOPS Oper. Syst. Rev. 41(6), 205–220 (2007)
Diekert, V., Rozenberg, G. (eds.): The Book of Traces. World Scientific Publishing Co., Inc., River Edge (1995). ISBN 9810220588
Ellis, C.A., Gibbs, S.J.: Concurrency control in groupware systems. ACM SIGMOD Rec. 18(2), 399–407 (1989)
Garcia-Molina, H., Wiederhold, G.: Read-only transactions in a distributed database. ACM Trans. Database Syst. 7(2), 209–234 (1982)
Gilbert, S., Lynch, N.: Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services. SIGACT News 33(2), 51–59 (2002)
Gotsman, A., Yang, H., Ferreira, C., Najafzadeh, M., Shapiro, M.: ‘Cause i’m strong enough: reasoning about consistency choices in distributed systems. In: Proceedings of the 43rd Annual ACM SIGPLAN-SIGACT POPL, pp. 371–384 (2016)
Haas, A., Henzinger, T.A., Holzer, A., Kirsch, C.M., Lippautz, M., Payer, H., Sezgin, A., Sokolova, A., Veith, H.: Local linearizability. CoRR, abs/1502.07118 (2015)
Hansdah, R.C., Patnaik, L.M.: Update serializability in locking. In: Ausiello, G., Atzeni, P. (eds.) ICDT 1986. LNCS, vol. 243, pp. 171–185. Springer, Heidelberg (1986). https://doi.org/10.1007/3-540-17187-8_36
Herlihy, M., Wing, J.M.: Linearizability: a correctness condition for concurrent objects. ACM TOPLAS 12(3), 463–492 (1990)
Higham, L., Kawash, J.: Memory consistency and process coordination for SPARC multiprocessors. In: Valero, M., Prasanna, V.K., Vajapeyam, S. (eds.) HiPC 2000. LNCS, vol. 1970, pp. 355–366. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44467-X_32
Hoare, C.A.R.: Proof of correctness of data representations. Acta Informatica 1(4), 271–281 (1972)
Jagadeesan, R., Riely, J.: From sequential specifications to eventual consistency. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015, Part II. LNCS, vol. 9135, pp. 247–259. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_20
Lamport, L.: Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21(7), 558–565 (1978)
Lamport, L.: Specifying concurrent program modules. ACM Trans. Program. Lang. Syst. 5(2), 190–222 (1983)
Lynch, N., Vaandrager, F.: Forward and backward simulations. Inf. Comput. 121(2), 214–233 (1995)
Perrin, M., Mostéfaoui, A., Jard, C.: Update consistency for wait-free concurrent objects. In: 2015 IEEE International Parallel and Distributed Processing Symposium, IPDPS 2015, Hyderabad, India, pp. 219–228, 25–29 May 2015
Plotkin, G., Pratt, V.: Teams can see pomsets. In: Workshop on Partial Order Methods in Verification. DIMACS Series, vol. 29, pp. 117–128. AMS (1997)
Saito, Y., Shapiro, M.: Optimistic replication. ACM Comput. Surv. 37(1), 42–81 (2005)
Shapiro, M., Preguiça, N., Baquero, C., Zawirski, M.: A comprehensive study of Convergent and Commutative Replicated Data Types. TR 7506, Inria (2011a)
Shapiro, M. , Preguiça, N.M., Baquero, C., Zawirski, M.: Conflict-free replicated data types. In: Proceedings of the 13th International Symposium on Stabilization, Safety, and Security of Distributed Systems, pp. 386–400 (2011b)
Shavit, N.: Data structures in the multicore age. Commun. ACM 54(3), 76–84 (2011)
Tanenbaum, A., Steen, M.V.: Distributed systems. Pearson Prentice Hall, Upper Saddle River, NJ (2007)
Viotti, P., Vukolic, M.: Consistency in non-transactional distributed storage systems. ACM Comput. Surv. 49(1), 19 (2016)
Vogels, W.: Eventually consistent. Commun. ACM 52(1), 40–44 (2009)
Acknowledgements
This paper has been greatly improved by the comments of the anonymous reviewers.
This material is based upon work supported by the National Science Foundation under Grant No. 1617175. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Jagadeesan, R., Riely, J. (2018). Eventual Consistency for CRDTs. In: Ahmed, A. (eds) Programming Languages and Systems. ESOP 2018. Lecture Notes in Computer Science(), vol 10801. Springer, Cham. https://doi.org/10.1007/978-3-319-89884-1_34
Download citation
DOI: https://doi.org/10.1007/978-3-319-89884-1_34
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89883-4
Online ISBN: 978-3-319-89884-1
eBook Packages: Computer ScienceComputer Science (R0)





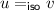 when
when  when
when 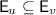 ,
, 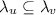 ,
,  , and
, and  .
. , define
, define  . Restriction lifts subsets to suborders:
. Restriction lifts subsets to suborders: 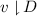 denotes the sub-
denotes the sub- of events. See Sect.
of events. See Sect.  .
. .
.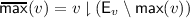 .
. is the suborder with the maximal elements removed.
is the suborder with the maximal elements removed.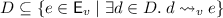 .
. is downclosed for
is downclosed for  be the set of all cuts of
be the set of all cuts of  then
then  .
. , we say that
, we say that  is a linearization of
is a linearization of 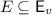 if there exists a bijection
if there exists a bijection  such that
such that  and
and 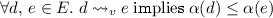 .
.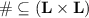 is a symmetric and reflexive dependency relation, and
is a symmetric and reflexive dependency relation, and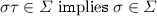
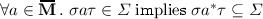


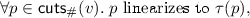 and
and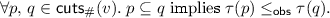
 .
.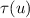 ends with
ends with  iff there is an
iff there is an  that is not followed by any
that is not followed by any  in
in  has at most as many alternations as
has at most as many alternations as  .
.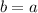 , the second property above ensures that
, the second property above ensures that  .
. , we deduce by construction that
, we deduce by construction that 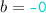 and
and  . In this case,
. In this case, 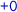 and has at least as many alternations as
and has at least as many alternations as  . So, we deduce that
. So, we deduce that 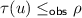 . The required result follows since
. The required result follows since  .
.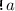 initializes the text to node
initializes the text to node  adds node
adds node 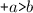 adds node
adds node  removes node
removes node  returns the current state of the document.
returns the current state of the document.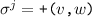 , or
, or 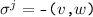 there exists
there exists  ,
, 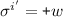 .
. , or
, or 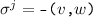 , then for all
, then for all  and
and  .
. is never ordered after
is never ordered after  , and likewise for
, and likewise for  or
or  is never ordered after
is never ordered after  or -w.
or -w.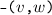 or
or  is always ordered after some
is always ordered after some  and
and  .
. .
.  .
. 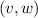 that is accessed in
that is accessed in  be any interleaving of the events involving
be any interleaving of the events involving  in
in  occurs after any
occurs after any 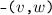 in
in 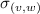 .
.  exists by (a) above.
exists by (a) above.  .
.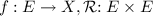 and
and 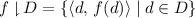 and
and  .
. when
when  .
.