Abstract
Formal verification of systems-level software such as hypervisors and operating systems can enhance system trustworthiness. However, without taking low level features like caches into account the verification may become unsound. While this is a well-known fact w.r.t. timing leaks, few works have addressed latent cache storage side-channels, whose effects are not limited to information leakage. We present a verification methodology to analyse soundness of countermeasures used to neutralise these channels. We apply the proposed methodology to existing countermeasures, showing that they allow to restore integrity of the system. We decompose the proof effort into verification conditions that allow for an easy adaption of our strategy to various software and hardware platforms. As case study, we extend the verification of an existing hypervisor whose integrity can be tampered using cache storage channels. We used the HOL4 theorem prover to validate our security analysis, applying the verification methodology to a generic hardware model.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Formal verification of low-level software such as microkernels, hypervisors, and drivers has made big strides in recent years [3, 4, 17, 21, 22, 33, 37, 38]. We appear to be approaching the point where the promise of provably secure, practical system software is becoming a reality. However, system verification is usually based on models that are far simpler than contemporary state-of-the-art hardware. Many features pose significant challenges: Memory models, pipelines, speculation, out-of-order execution, peripherals, and various coprocessors, for instance for system management. In a security context, caches are notorious. They have been known for years to give rise to timing side channels that are difficult to fully counteract [13, 16, 26, 28, 32, 36]. Also, cache management is closely tied to memory management, which—since it governs memory mapping, access control, and cache configuration through page-tables residing in memory—is one of the most complex and security-critical components in the computer architecture flora.
Computer architects strive to hide this complexity from application programmers, but system software and device drivers need explicit control over features like cacheability attributes. In virtualization scenarios, for instance, it is critical for performance to be able to delegate cache management authority for pages belonging to a guest OS to the guest itself. With such a delegated authority a guest is free to configure its share of the memory system as it wishes, including configurations that may break conventions normally expected for a well-behaved OS. For instance, a guest OS will usually be able to create memory aliases and to set cacheability attributes as it wishes. Put together, these capabilities can, however, give rise to memory incoherence, since the same physical location can now be pointed to by two virtual addresses, one to cache and one to memory. This opens up for cache storage attacks on both confidentiality and integrity, as was shown in [20]. Analogous problems arise due to the presence of instruction-caches, that can contain binary code that differs from the one stored in memory. Differently from timing channels, which are external to models used for formal analysis and do not invalidate verification of integrity properties, storage channels make the cacheless models unsound: Using them for security analysis can lead to conclusions that are false.
This shows the need to develop verification frameworks for low-level system software that are able to adequately reflect the presence of caches. It is particularly desirable if this can be done in a manner that allows to reuse existing verification tools on simpler models that do not consider caches. This is the goal we set ourselves in this paper.
Our Contributions. We undertake the first rigorous analysis of integrity-preserving countermeasures against cache storage channel attacks. We propose a practical verification framework, which is independent of a specific hardware and the software executing on the platform, and can be used to analyse security of low-level software on models with enabled caches. Our framework accommodates both data and instruction caches and we have proved its soundness in the HOL4 theorem prover. Our strategy consists in introducing hardware and software proof obligations and demonstrating that they prevent attacks on integrity. The framework is used to verify soundness of two countermeasures for data-caches and two countermeasures for instruction-caches. This results in code verification conditions that can be analysed on cacheless models, so that existing tools [6, 11, 31] (mostly not available on cache-enabled models) can automate this task to a large extent. To demonstrate that our methodology can be applied to commodity hardware, we formally model a generic cache and demonstrate that extensions of existing cacheless architectural models with the generic cache model satisfy all requirements imposed by our methodology. The practicability of our approach is shown by applying it to repair the verification of an existing and vulnerable hypervisor [21], demonstrating that the modified design prevents cache-attacks.
2 Related Work
Cache Storage Channels. The existence of cache storage channels due to mismatched cacheability attributes was first pointed out in [20]. That paper also sketches how prior integrity and confidentiality proofs for a sequential memory model could be repaired, identifying that coherency of data-cache is a key requirement. However, the verification methodology is only sketched and provides merely an intuition about the proof strategy. The present paper develops these ideas in detail, providing several new contributions, including (i) a formal cache-aware hardware model, (ii) a revised and detailed proof strategy that allows to decompose verification into hardware-, software-, and countermeasure-dependent proof obligations, (iii) introduction and verification of instruction cache coherency, (iv) formal definitions of all proof obligations and invariants, (v) a detailed explanation of the proof and how the proof obligations can be discharged for given applications and countermeasures, and (vi) a complete mechanization in HOL4.
Formal Verification. Recent works on kernel and hypervisor verification [8, 10, 17,18,19, 21, 24, 25, 33, 34] all assume a sequential memory model and leave cache issues to be managed by model external means, while the CVM framework [4] treats caches only in the context of device management [23]. In [21], a cacheless model was used to prove security of the hypervisor used here as a case study. Due to absence of caches in the underlying hardware model, the verification result is unsound in presence of uncacheable aliases, as demonstrated in [20].
Timing Channels. Timing attacks and countermeasures have been formally verified to varying degrees of detail in the literature. Since their analysis generally ignores caches, verified kernels are susceptible to timing attacks. For instance, Cock et al. [13] examined the bandwidth of timing channels in seL4 and possible countermeasures including cache coloring. Other related work includes those adopting formal analysis to either check the rigour of countermeasures [5, 7, 9, 15, 20, 35] or to examine bandwidth of side-channels [14, 27].
There is no comparable formal treatment for cache storage channels. These channels carry information through memory and, additionally to permitting illicit information flows, can be used to compromise integrity. To the best of our knowledge we are the first to present a detailed security proof for countermeasures against cache storage channel attacks.
3 Threats, Countermeasures, and Verification Goal
Data-Caches and Aliases. Modern CPU architectures such as ARM, Power, and x64 permit to configure if a given virtual page is cacheable or not. This capability can result in a class of attacks called “alias-driven attacks”. Suppose a victim reference monitor that (1) validates an input stored in a memory location against a security policy and (2) uses such input for implementing a critical functionality. Assume an incoherent state for this memory location: the data-cache contains a value for this location that differs from the content of the memory but the cache is not dirty. If the cache line is evicted between (1) and (2), its content is not written into the memory, since it is not dirty. In this case, the victim can potentially evaluate the policy using the value fetched from the cache and later use the content stored in memory to implement the critical functionality, allowing untrusted inputs to bypass the policy. This behavior has been demonstrated for ARMv7 and ARMv8 CPUs [20] as well as for MIPS, where uncacheable aliases have been used to establish incoherency. This behavior clearly departs from the behavior of a system that has no cache. However, x64 processors that implement “self-snooping” appear to be immune to this phenomenon.
A system that (1) permits an attacker to configure cacheability of its virtual memory, (2) acquires ownership of that location from the attacker, and (3) uses the location to read security critical information can be target of this attack. An example is the hypervisor presented in Sect. 5.5. The runtime monitor presented in [12], which forbids the execution of unsigned code, can also be attacked using caches. The attacker can load a signed process in cache and a malware in memory. Similarly, remote attestation checks the integrity of a device by a trusted measuring function. If this function accesses stale data from the caches then the measurements can be inaccurate.
In this paper we analyse two countermeasures against alias-driven attacks: “always cacheability” consists in defining a fixed region of memory that is made always cacheable and ensuring that the trusted software rejects any input pointing outside this region; “selective eviction” consists in flushing from the cache every location that is accessed by the trusted software and that has been previously accessed by the attacker. A description and evaluation of other possible countermeasures against cache storage channels was provided in [20].
Instruction-Caches. In a similar vein, instruction-caches may be dangerous if the content of executable pages is changed without using cache management instructions to maintain memory coherency. Suppose that a software (1) executes instructions from a region of memory, thus filling the instruction-cache with the instructions of a program, (2) it updates the memory with the code of a new program without flushing the cache, and (3) it executes the new program. Since between (1) and (3) some lines of the instruction-cache are evicted and other not, the CPU can execute a mix of the code of the two programs, resulting in a behavior that is hard to predict.
The presence of instruction-caches affect systems whose security depends on dynamically loaded code. This includes the aforementioned runtime monitor, boot-loaders that load or relocate programs, systems that implement dynamic code randomization, and Software Fault Isolation [29] (SFI) sandboxes that inspect binary code to isolate loadable third party modules.
We analyse two countermeasures against attacks that use instruction-caches: “Constant program memory” ensures the trusted executable code is never modified; “Selective eviction” consists in selectively evicting lines of the instruction-cache and flushing lines of the data-cache for locations that are modified.
3.1 Verification Goals
In this work we consider a trusted system software (the “kernel”) that shares the system with an untrusted user level software (the “application”): the application requests services from the kernel. The hardware execution mode used by the application is less privileged than the mode used by the kernel. The application is potentially malicious and takes the role of the attacker. The kernel dynamically manages memory ownership and can provide various services, for instance for secure ownership transfer. This enables the application to pass data to the kernel services, while avoiding expensive copy operations: The application prepares the input inside its own memory, the ownership of this memory is transferred to the kernel, and the corresponding kernel routine operates on the input in-place.
Intuitively for guaranteeing integrity we mean that it is not possible for the application to influence the kernel using cache features (except possibly for timing channels, which are not considered in this work). That is, if there is a possibility for the application to affect the kernel behavior (e.g. by providing parameters to a system call) in a system with caches, there must be the same possibility in an idealized system that has no caches. This goal is usually formalized by requiring that the cacheless system can simulate all possible executions of the system with caches (i.e. all executions of the real system are admitted by the specification, that in this case is represented by the cacheless system).
Unfortunately, ensuring this property for complete executions is not possible: since the application is untrusted we need to assume that its code is unknown and that it can exploit behaviors of caches that are not available in the cacheless system, making impossible to guarantee that the behavior of the application is the same in both systems. For this reason, we analyse executions of the application and of the kernel separately.
We first identify a set of memory resources called “critical”. These are the resources for which integrity must be preserved and that affect the kernel behavior. For example, in an operating system the memory allocator uses a data structure to keep track of the ownership of allocated memory pages. Thus all pages not belonging to the untrusted process (the application) are considered critical. Since this classification depends on the content of the allocator data structure, this is also a critical resource. Similarly in [21] the page type data structure identifies critical resources.
Then we phrase integrity as two complementary properties: (1) direct or indirect modification of the critical resources is impossible while the application is executing on the system with caches; and (2) the kernel has the same behavior in the cacheless and the cache-aware system.
An alternative approach to phrase integrity might be to show the absence of information flow from application to kernel. There are a number of issues with such an approach in this context, however: First, attacks that do not involve information flow would not be covered; Second, it is not clear how an information flow oriented account would handle kernel invocations; these generally correspond to endorsement actions in a multi-level security lattice setting and are challenging to map to the present setting. On the other hand, our account of integrity permits any safety property that only depends on the critical resources and holds for the cacheless system to be transferred to the system with caches.
4 Formalisation
As basis for our study we define two models, a cacheless and a cache-aware model. The cacheless model represents a memory-coherent single-core system where all caches are disabled. The cache-aware model is the same system augmented by a single-level separated data- and instruction-cache.
4.1 Cacheless Model
The cacheless model is ARM-flavoured but general enough to apply to other architectures. A (cacheless) state \(s = \langle reg , psreg , coreg , mem \rangle \in \mathbb {S}\) is a tuple of general-purpose registers \( reg \) (including program counter \( pc \)), program-status registers \( psreg \), coprocessor registers \( coreg \), and memory \( mem \). The core executes either in non-privileged mode \( U \) or privileged mode \( P \), \({ Mode (s) \in \{ U , P \}}\). Executions in privileged mode are necessarily trusted, since they are able to modify the system configuration, e.g., coprocessor registers, in arbitrary ways. The program-status registers \( psreg \) encode the execution mode and other execution parameters such as the arithmetic flags. The coprocessor registers \( coreg \) determine a range of system configuration parameters, including virtual memory mapping and memory protection. The word addressable memory is represented by \(mem:\mathbb {PA}\rightarrow \mathbb {B}^{ w }\), where \(\mathbb {B}= \{0,1\}\), \(\mathbb {PA}\) is the set of physical addresses, and \( w \) is the word size.
Executions in non-privileged mode are unable to directly modify coprocessor registers as well as certain critical program-status registers. For instance, the execution mode can be switched to \( P \) only by raising an exception. Memory accesses are controlled by a Memory Management Unit (MMU), which also determines memory region attributes such as cacheability. Let \(A = \{ wt , rd , ex \}\) be the set of access permissions (for write, read, and execute respectively) and \(M = \{ U , P \}\) be the set of execution modes. The MMU model is the function \({ MMU (s,va) \in (2^{M \times A} \times \mathbb {PA}\times \mathbb {B})}\) which yields for a virtual address \(va \in \mathbb {VA}\) the set of granted access rights, the translation, and the cacheability attribute. Note that the same physical addresses can be accessed with different access rights and different cacheability settings using different virtual aliases. Hereafter, when it is clear from the context, we use \( MMU (s, va )\) to represent the translation of \( va \).
The behaviour of the system is defined as a labeled transition system using relation \({\rightarrow _{ m } \subseteq \mathbb {S}\times \mathbb {S}}\), where \( m \in M\) and if \(s \rightarrow _{ m } s'\) then \( Mode (s) = m \). Each transition represents the execution of a single instruction. When needed, we let \(s \rightarrow _{ m } s' \ [{{ ops }}]\) denote that the operations \({ ops }\) are performed on the memory subsystem, where \({ ops }\) is a list whose elements are either \( wt (pa, c)\) (pa was written with cacheability attribute c), \( rd (pa, c)\) (pa was read with cacheability attribute c), \( fl_D (pa)\), or \( fl_I (pa)\) (the data- or instruction-cache flush operation for pa, which have no effects in the cacheless model). We use  to represent the weak transition relation that holds if there is an execution \({s_0\xrightarrow {}\cdots \xrightarrow {}s_n}\) such that \( Mode (s_n) = U \) and \( Mode (s_j)\ne U \) for \(0< j < n\), i.e. the weak transition hides states while the kernel is running.
to represent the weak transition relation that holds if there is an execution \({s_0\xrightarrow {}\cdots \xrightarrow {}s_n}\) such that \( Mode (s_n) = U \) and \( Mode (s_j)\ne U \) for \(0< j < n\), i.e. the weak transition hides states while the kernel is running.
4.2 Cache-Aware Model
We model a single-core processor with single-level separated instruction and data-caches, i.e., a modified Harvard architecture. In Sect. 7 we discuss variations and generalizations of this model.
A state \(\bar{s}\in \mathbb {\bar{S}}\) in the cache-aware model has the components of the cacheless model together with a data-cache \(\textit{d-cache}\) and an instruction-cache \(\textit{i-cache}\), \(\bar{s}= \langle reg , psreg , coreg , mem , \textit{d-cache}, \textit{i-cache} \rangle \). The function \( MMU \) and the transition relation \({\rightarrow _{ m } \subseteq \mathbb {\bar{S}}\times \mathbb {\bar{S}}}\) are extended to take into account caches.
Other definitions of the previous subsection are extended trivially. We use  to denote a data-cache hit for address pa,
to denote a data-cache hit for address pa,  to identify dirtiness of the address pa (i.e. if the value of pa has been modified in cache and differs from the memory content), and
to identify dirtiness of the address pa (i.e. if the value of pa has been modified in cache and differs from the memory content), and  to obtain the value for pa stored in the data-cache (respectively
to obtain the value for pa stored in the data-cache (respectively  ,
,  , and
, and  for the instruction-cache).
for the instruction-cache).
Due to the use of the modified Harvard architecture and the presence of caches, there are three views of the memory subsystem: the data-view \(\textit{Dv}\), the instruction-view \(\textit{Iv}\), and the memory-view \( Mv \):

We require that the kernel always uses cacheable virtual aliases. Therefore, kernel reads access the data-view and kernel instruction fetches access the instruction-view. Moreover, the MMU always consults first the data-cache when it fetches a page-table descriptor, as is the case for instance in ARM Cortex-A53 and ARM Cortex-A8. Therefore, the MMU model uses the data-view. Finally, the memory-view represents what can be observed from the data-view after non-dirty cache lines have been evicted.
4.3 Security Properties
As is common in designs of low-level software, we assume that the kernel uses a static region of virtual memory \(\mathbf {K_{vm}}\subseteq \mathbb {VA}\) for its memory accesses and that the static region \(\mathbf {K_{ex}}\subseteq \mathbf {K_{vm}}\) maps the kernel code.
We first identify the critical resources, i.e., those resources for which integrity must be preserved and on which kernel behavior depends. This set always includes the coprocessor registers, which the architecture protects from non-privileged modifications. The security type of memory locations, however, can dynamically change due to transfer of memory ownership, i.e., the criticality of resources depends on the state of the system. The function \( CR : \mathbb {\bar{S}}\rightarrow 2^\mathbb {PA}\) retrieves the subset of memory resources that are critical. Function \( CR \) itself depends on a subset of resources, namely the internal kernel data-structures that determine the security type of memory resources (for the kernel being an operating system and the application being one of its user processes, imagine the internal state of the page allocator and the process descriptors). Similarly, the function \( EX : \mathbb {\bar{S}}\rightarrow 2^\mathbb {PA}\) retrieves the subset of critical memory resources that contain trusted executable code. These definitions are naturally lifted to the cacheless model, by extending a cacheless state with empty caches. Two states \(\bar{s}\) and \(\bar{s}'\) have the same data-view (respectively instruction-view) of the critical memory, written \(\bar{s}\equiv _{D}\bar{s}'\) (respectively \(\bar{s}\equiv _{I}\bar{s}'\)), if
(respectively \(\textit{Iv}\) and \( EX \)). Finally, two states \(\bar{s}\) and \(\bar{s}'\) have the same critical resources, and we write \(\bar{s}\equiv _{CR}\bar{s}'\), iff \(\bar{s}\equiv _{D}\bar{s}'\), \(\bar{s}\equiv _{I}\bar{s}'\), and \(\bar{s}. coreg = \bar{s}'. coreg \).
Our verification approach requires to introduce a system invariant \( \bar{I} \) that is software dependent and defined per kernel. This invariant ensures that the kernel can work properly (e.g. stack pointer and its data structures are correctly configured) and its properties are detailed in Sect. 5. A corresponding invariant \( I \) for the cacheless model is derived from \( \bar{I} \) by excluding properties that constrain caches. Our goal is to establish two theorems: an application integrity theorem showing that \( \bar{I} \) correctly constrains application behaviour in the cache-aware model, and a kernel integrity theorem showing that kernel routines in the cache-aware model correctly refine the cacheless model.
As the application is able to break its memory coherency at will, the application integrity theorem is a statement about the processor hardware and its correct configuration. In particular, Theorem 1 shows that non-privileged execution in the cache-aware model preserves the required invariant, that the invariant is adequate to preserve the critical resources, and that entries into privileged level correctly follow the hardware mode switching convention. For the latter, we use predicate \(\textit{ex-entry}(\bar{s})\) to identify states of the system immediately after switching to the kernel, i.e., when an exception is triggered, the mode becomes privileged and the program counter points to an entry in the exception vector table.
Theorem 1
(Application Integrity). For all \(\bar{s}\), if \( \bar{I} (\bar{s})\) and \(\bar{s}\rightarrow _{ U } \bar{s}'\) then \( \bar{I} (\bar{s}')\), \(\bar{s}\equiv _{CR}\bar{s}'\), and if \( Mode (\bar{s}') \ne U \) then \(\textit{ex-entry}(\bar{s}')\).
For the kernel we prove that the two models behave equivalently. We prove this using forward simulation, by defining a simulation relation \(\mathrel {\mathcal {R}_{ sim }}\) guaranteeing equality of all registers and critical memory resources, and then showing that both the invariant and the relation are preserved by privileged transitions:
Theorem 2
(Kernel Integrity). For all \(\bar{s}_1\) and \(s_1\) such that \( \bar{I} (\bar{s}_1)\), \(\bar{s}_1 \mathrel {\mathcal {R}_{ sim }}s_1\), and \(\textit{ex-entry}(\bar{s}_1)\), if  then
then  , \(\bar{s}_2 \mathrel {\mathcal {R}_{ sim }}s_2\) and \( \bar{I} (\bar{s}_2)\).
, \(\bar{s}_2 \mathrel {\mathcal {R}_{ sim }}s_2\) and \( \bar{I} (\bar{s}_2)\).
5 Proof Strategy
Theorems 1 and 2 are proved in five steps:
-
1.
First we introduce crucial properties of the hardware, abstracting from the details of a specific hardware architecture. We obtain a set of proof obligations (i.e. HW Obligation) that must be discharged for any given hardware.
-
2.
Next, we reduce application integrity, Theorem 1, to proof obligations (i.e. SW-I Obligation) on software-specific invariants of the cache-aware model.
-
3.
The same approach applies for kernel integrity, Theorem 2, where we also derive proof obligations (i.e. SW-C Obligation) on the kernel code.
-
4.
We then demonstrate correctness of the selected countermeasures of Sect. 3 by discharging the corresponding proof obligations.
-
5.
The last step is kernel-specific: we sketch how our results allow standard cache-oblivious binary analysis tools to show that a kernel implements the countermeasures, establishing Theorems 1 and 2.
A fundamental notion for our proof is coherency, which captures memory resources whose content cannot be indirectly effected through cache eviction.
Definition 1
(Data-Coherency). We say that a memory resource \(pa\in \mathbb {PA}\) is data-coherent in \(\bar{s}\), \(\textit{D-Coh}(\bar{s}, pa)\), iff  and
and  implies
implies  . A set \(R \subseteq \mathbb {PA}\) is data-coherent iff all \(pa \in R\) are.
. A set \(R \subseteq \mathbb {PA}\) is data-coherent iff all \(pa \in R\) are.
In other words, a physical location pa is data-coherent if a non-dirty cache hit of pa in \(\bar{s}\) implies that the cached value is equal to the value stored in memory. The general intuition is that, for an incoherent resource, the view can be changed indirectly without an explicit memory write by evicting a clean cache-line with different values in the cache and memory. For instance, consider an MMU that looks first into the caches when it fetches a descriptor. Then if the page-tables are coherent, a cache eviction cannot indirectly affect the behaviour of the MMU. This intuition also underpins the definition of instruction-coherency.
Definition 2
(Instruction-Coherency). We say that a memory resource \(pa\in \mathbb {PA}\) is instruction-coherent in \(\bar{s}\), \(\textit{I-Coh}(\bar{s}, pa)\), iff the following statements hold:
-
1.
pa is data-coherent,
-
2.
if
 then
then  , and
, and -
3.
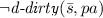
Instruction-coherency requires the data-cache to be not dirty to ensure that eviction from the data-cache does not break part (2) of the definition.
The role of coherency is highlighted by the following Lemma. The memory-view differs from the data-view only in memory resources that are cached, clean, and have different values stored in the cache and memory, and data-view differs from instruction-view only for resources that are not instruction-coherent.
Lemma 1
Let \(pa\in \mathbb {PA}\) and \(\bar{s}\in \mathbb {\bar{S}}\). Then:
-
1.
\(\textit{D-Coh}(\bar{s},\{pa\}) \Leftrightarrow (\textit{Dv}(\bar{s},pa)= Mv (\bar{s},pa))\).
-
2.
\(\textit{I-Coh}(\bar{s},\{pa\}) \Rightarrow (\textit{Dv}(\bar{s},pa)=\textit{Iv}(\bar{s},pa))\).
5.1 Hardware Abstraction Layer
ISA models are complex because they describe the behavior of hundreds of possible instructions. For this reason we introduce three key notions in order to isolate verification tasks that are architecture-dependent and that can be verified once and reused for multiple countermeasures and kernels. These notions are:
-
1.
MMU Domain: This identifies the memory resources that affect the virtual memory translation.
-
2.
Derivability: This provides an overapproximation of the effects over the memory and cache for instructions executed in non-privileged mode.
-
3.
Instruction Dependency: This identifies the memory resources that affect the behavior of the current instruction.
Here we provide an intuitive definition of these notions and formalize the properties that must be verified for the specific hardware model to ensure that these abstractions are sound. Section 6 comments on the verification of these properties for a generic hardware model in HOL4.
MMU domain is the function \( MD (\bar{s}, V) \subseteq \mathbb {PA}\) that determines the memory resources (i.e., the current master page-table and the linked page-tables) that affect the translation of virtual addresses in \(V \subseteq \mathbb {VA}\).
HW Obligation 1
-
1.
\( MD \) is monotone, i.e., \(V' \subseteq V\) implies \( MD (\bar{s}, V') \subseteq MD (\bar{s}, V)\).
-
2.
For all \(\bar{s}, \bar{s}'\) and \(V \subseteq \mathbb {VA}\) if \(\textit{Dv}(\bar{s}, pa) = \textit{Dv}(\bar{s}', pa)\) for all \(pa\in MD (\bar{s}, V)\) and \(\bar{s}. coreg = \bar{s}'. coreg \) then \( MD (\bar{s}, V) = MD (\bar{s}', V)\) and for all \(va \in V\), \( MMU (\bar{s},va) = MMU (\bar{s}',va)\).
Definition 3
(Derivability). We say \(\bar{s}'\) is derivable from \(\bar{s}\) in non-privileged mode (denoted as \(\bar{s}\rhd \bar{s}'\)) if \(\bar{s}. coreg = \bar{s}'. coreg \) and for every \(pa \in \mathbb {PA}\) at least one of \(D_{acc}\) properties and at least one of \(I_{acc}\) hold:
-
\(D_{\emptyset }(\bar{s}, \bar{s}', pa)\): Independently of the access rights for the address pa, a data-cache line can always change due to an eviction. An eviction of a dirty cache entry causes a write back; eviction of clean entries does not affect the memory.
-
\(D_{ rd }(\bar{s}, \bar{s}', pa)\): If non-privileged mode can read the address pa, the value of pa in the memory can be filled into its data-cache line, making it clean.
-
\(D_{ wt }(\bar{s}, \bar{s}', pa)\): If non-privileged mode can write the address pa, it can either write directly into the data-cache, potentially making it dirty, or bypass it, by using an uncacheable alias. Only writes can make a location in data-cache dirty.
-
\(I_{\emptyset }(\bar{s}, \bar{s}', pa)\): Independently of the access rights for the address pa, the corresponding line can always be evicted, leaving memory unchanged.
-
\(I_{ ex }(\bar{s}, \bar{s}', pa)\): If non-privileged mode can execute the address pa, the instruction-cache state can change through a fill operation which updates the cache with the value of pa in the memory. Instruction-cache lines never become dirty.
Figure 1 reports the formal definition of these predicates for a cache operating in write-back mode, assuming cache line granularity is finer than page granularity, i.e., the same memory permissions hold for all entries of a given line.
Note that in a cache, one cache line contains several locations and that writing one such location marks the whole line of the data-cache dirty. However, due to our definition of  the locations in the written line are not considered dirty, if they have the same value in cache as in memory.
the locations in the written line are not considered dirty, if they have the same value in cache as in memory.
In practice, if \(\bar{s}\rhd \bar{s}'\) then for a given location \(\textit{D-Coh}\) can be invalidated only if there exists a non-cacheable writable alias and \(\textit{I-Coh}\) can be invalidated only if there exists a writable alias. The following obligation shows that derivability correctly overapproximates the hardware behavior:
HW Obligation 2
For all \(\bar{s}\) such that \(\textit{D-Coh}(\bar{s}, MD (\bar{s}, \mathbb {VA}))\) and \( MD (\bar{s}, \mathbb {VA}) \cap \{ pa \mid \exists va . \ MMU (\bar{s}, va) = (acc, pa, c) \text{ and } ( U , wt ) \in acc \} = \emptyset \), if \(\bar{s}'\) is reachable by a non-privileged transition, i.e. \(\bar{s}\rightarrow _{ U } \bar{s}'\), then
-
1.
\(\bar{s}\rhd \bar{s}'\), i.e., \(\bar{s}'\) is derivable from \(\bar{s}\), and
-
2.
if \( Mode (\bar{s}')\!\ne \! U \) then \(\textit{ex-entry}(\bar{s}')\), i.e., the mode can only change by entering an exception handler
The precondition of the obligation requires the MMU domain to be data-coherent and to not overlap with the memory writable in non-privileged mode. This ensures that the MMU configuration is constant during the execution of instructions that update multiple memory locations. This requirement also ensures transitivity of derivability.
To complete the hardware abstraction we need sufficient conditions to ensure that the cache-aware model behaves like the cacheless one. We use the functions \(\textit{p-deps}(\bar{s}) \subseteq \mathbb {PA}\) and \(\textit{v-deps}(\bar{s}) \subseteq \mathbb {VA}\) to extract an overapproximation of the physical and virtual addresses that affect the next transition of \(\bar{s}\). For instance, \(\textit{v-deps}\) includes the program counter, the locations loaded and stored, while \(\textit{p-deps}(s)\) includes the translation of the program counter, the translation of the virtual addresses read, and the addresses that affect the translation of \(\textit{v-deps}\) (i.e. \( MD (\bar{s}, \textit{v-deps}(\bar{s}))\)). As usual, these definitions are lifted to the cacheless model using empty caches. We say that \(\bar{s}\) and s are similar, if \((\bar{s}. reg , \bar{s}. psreg , \bar{s}. coreg ) = (s. reg , s. psreg , s. coreg )\), \(\textit{Dv}(\bar{s}, pa) = s. mem (pa)\) for all pa in \(\textit{p-deps}(s) \cap \textit{p-deps}(\bar{s})\), and \(\textit{Iv}(\bar{s}, MMU (\bar{s},\bar{s}. reg . pc ) = s. mem ( MMU (s,s. reg . pc )) \).
HW Obligation 3
For all similar \(\bar{s}\) and s
-
1.
\(\textit{p-deps}(\bar{s}) = \textit{p-deps}(s)\) and \(\textit{v-deps}(\bar{s}) = \textit{v-deps}(s)\)
-
2.
if \(s \rightarrow _{ m } s' \ [{{ ops }_1}]\), \(\bar{s}\rightarrow _{ m } \bar{s}' \ [{{ ops }_2}]\) and all accesses in \({ ops }_1\) are cacheable (i.e. \( wt (pa, c) \in { ops }_1\) or \( rd (pa, c) \in { ops }_1\) implies c) then
-
(a)
\({ ops }_2 = { ops }_1\)
-
(b)
\((\bar{s}'. reg , \bar{s}'. psreg , \bar{s}'. coreg ) = (s'. reg ,s'. psreg , s'. coreg )\)
-
(c)
for every pa if \( wt (pa, c) \in { ops }_1\) then \(\textit{Dv}(\bar{s}', pa) = s'. mem (pa)\), otherwise \( Mv (\bar{s}, pa) = Mv (\bar{s}', pa)\) and \(s. mem (pa) = s'. mem (pa)\)
-
(a)
The obligation, thus, is to show that if \(\bar{s}\) and s are similar, then their instructions have the same dependencies; the same physical addresses are read, written, and flushed; registers are updated in the same way; addresses written have the same values; addresses that are not written preserve their memory view.
The last obligation describes cache effects of operations:
HW Obligation 4
For every \(\bar{s}\) if \(\bar{s}\rightarrow _{ m } \bar{s}' \ [{{ ops }}]\) and all accesses in \({ ops }\) are cacheable then
-
1.
for every pa if \( wt (pa, c) \in { ops }\) then \(\textit{D-Coh}(\bar{s}',\{pa\})\), otherwise \(\textit{D-Coh}\), \(\textit{I-Coh}\) and
 of pa are preserved
of pa are preserved -
2.
if \( fl_D (pa) \in { ops }\) then \(\textit{D-Coh}(\bar{s}',\{pa\})\) and
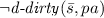
-
3.
if \( fl_I (pa) \in { ops }\), \(\textit{D-Coh}(\bar{s},\{pa\})\), and
 then \(\textit{I-Coh}(\bar{s}',\{pa\})\)
then \(\textit{I-Coh}(\bar{s}',\{pa\})\)
If the kernel only uses cacheable aliases then memory writes establish data-coherency; data- and instruction-coherency, as well as non-dirtyness are preserved for non-updated locations; data-cache flushes establish data-coherency and make locations non-dirty; instruction-cache flushes make data-coherent, non-dirty locations instruction-coherent.
5.2 Application Level: Theorem 1
To decompose the proof of Theorem 1, the invariant \( \bar{I} \) is split in three parts: a functional part \( \bar{I} _{ fun }\) which only depends on the data-view of the critical resources, an invariant \( \bar{I} _{ coh }\) which only depends on data-coherency of the critical resources and instruction-coherency of executable resources, and an optional countermeasure-specific invariant \( \bar{I} _{ cm }\) which depends on coherency of non-critical memory resources such as resources in an always-cacheable region:
SW-I Obligation 1
For all \(\bar{s}\), \( \bar{I} (\bar{s})\!=\! \bar{I} _{ fun }(\bar{s})\!\wedge \! \bar{I} _{ coh }(\bar{s})\!\wedge \! \bar{I} _{ cm }(\bar{s})\) and:
-
1.
for all \(\bar{s}'\) if \(\bar{s}\equiv _{CR}\bar{s}'\) then \( \bar{I} _{ fun }(\bar{s})\!=\! \bar{I} _{ fun }(\bar{s}')\);
-
2.
for all \(\bar{s}'\) if \(\bar{s}\equiv _{CR}\bar{s}'\), \(\textit{D-Coh}(\bar{s}, CR (\bar{s}))\), \(\textit{D-Coh}(\bar{s}', CR (\bar{s}'))\), \(\textit{I-Coh}(\bar{s}, EX (\bar{s}))\), and \(\textit{I-Coh}(\bar{s}', EX (\bar{s}'))\), then \( \bar{I} _{ coh }(\bar{s})\!=\! \bar{I} _{ coh }(\bar{s}')\);
-
3.
for all \(\bar{s}'\) if \( \bar{I} (\bar{s})\) and \(\bar{s}\rhd \bar{s}' \) then \( \bar{I} _{ cm }(\bar{s}')\).
The invariants must prevent direct modification of the critical resources by the application, i.e., there is no address writable in non-privileged mode that points to a critical resource. Similarly, indirect modification, e.g., by line eviction, must be impossible. This is guaranteed if critical resources are data-coherent and executable resources are instruction-coherent.
SW-I Obligation 2
For all \(\bar{s}\):
-
1.
If \( \bar{I} _{ fun }(\bar{s})\) and \(pa \in CR (\bar{s})\) then there is no va such that \( MMU (\bar{s}, va) = (acc, pa, c)\) and \(( U , wt ) \in acc\)
-
2.
If \( \bar{I} _{ fun }(\bar{s})\) and \( \bar{I} _{ coh }(\bar{s})\) then \(\textit{D-Coh}(\bar{s}, CR (\bar{s}))\) and \(\textit{I-Coh}(\bar{s}, EX (\bar{s}))\)
Also, the functions \( CR \) and \( EX \) must be correctly defined: resources needed to identify the set of critical kernel resources are critical themselves, as are resources affecting the MMU configuration (i.e., the page-tables).
SW-I Obligation 3
For all \(\bar{s}, \bar{s}'\):
-
1.
If \( \bar{I} _{ fun }(\bar{s})\), \(\bar{s}\equiv _{D}\bar{s}'\) and \(\bar{s}. coreg = \bar{s}'. coreg \) then \( CR (\bar{s}) = CR (\bar{s}')\), \( EX (\bar{s}) = EX (\bar{s}')\), and \( EX (\bar{s}) \subseteq CR (\bar{s})\)
-
2.
If \( \bar{I} _{ fun }(\bar{s})\) then \( MD (\bar{s}, \mathbb {VA}) \subseteq CR (\bar{s})\)
The following lemmas assume HW Obligation 2 and SW-I Obligations 1–3. First, we show that the application cannot modify critical resources.
Lemma 2
For all \(\bar{s}, \bar{s}'\) such that \( \bar{I} (\bar{s})\) if \(\bar{s}\rhd \bar{s}'\) then \(\bar{s}\equiv _{CR}\bar{s}'\).
Proof
Since \( \bar{I} (\bar{s})\) holds, the MMU prohibits writable accesses of the application to critical resources (SW-I Obligation 2.1). Also, derivability shows that the application can directly change only resources that are writable according to the MMU. Thus, the application cannot directly update \( CR (\bar{s})\). Besides, the invariant guarantees data-coherency of critical resources and instruction-coherency of executable resources in \(\bar{s}\) (SW-I Obligation 2.2). This prevents indirect modifications of these resources. Finally, SW-I Obligation 3.1 ensures that the kernel data-structures that identify what is critical cannot be altered. \(\blacksquare \)
To complete the proof of Theorem 1 we additionally need to show that coherency of critical resources (Lemma 3) and the functional invariant (Lemma 4) are preserved by non-privileged transitions.
Lemma 3
For all \(\bar{s}\) if \( \bar{I} (\bar{s})\) and \(\bar{s}\rhd \bar{s}'\) then \(\textit{D-Coh}(\bar{s}', CR (\bar{s}'))\), \(\textit{I-Coh}(\bar{s}', EX (\bar{s}'))\).
Proof
From the previous lemma we get \( CR (\bar{s}')= CR (\bar{s})\) and \( EX (\bar{s}')= EX (\bar{s})\). Coherency of these resources in \(\bar{s}\) is given by SW-I Obligation 2.2. From derivability we know that data-coherency can be invalidated only through non-cacheable writes; instruction-coherency can be invalidated only through writes to executable resources. SW-I Obligation 2.1 yields that there is no alias writable in non-privileged mode pointing to a critical resource, using SW-I Obligation 3.1 then also executable resources cannot be written. \(\blacksquare \)
Lemma 4
For all \(\bar{s}\) and \(\bar{s}'\) if \( \bar{I} (\bar{s})\) and \(\bar{s}\rightarrow _{ U } \bar{s}'\) then \( \bar{I} _{ fun }(\bar{s}')\).
Proof
To show that non-privileged transitions preserve the invariant we use HW Obligation 2.1, Lemma 2, and SW-I Obligation 1.1. \(\blacksquare \)
We are now able to complete the proof of application integrity. The following Lemma directly proves Theorem 1 if the proof obligations are met.
Lemma 5
(Application Integrity). For all \(\bar{s}\), if \( \bar{I} (\bar{s})\) and \(\bar{s}\rightarrow _{ U } \bar{s}'\) then \( \bar{I} (\bar{s}')\), \(\bar{s}\equiv _{CR}\bar{s}'\), and if \( Mode (\bar{s}') \ne U \) then \(\textit{ex-entry}(\bar{s}')\).
Proof
By HW Obligation 2, \(\bar{s}\rhd \bar{s}'\) and if \( Mode (\bar{s}')\!\ne \! U \) then \(\textit{ex-entry}(\bar{s}')\). By Lemma 2, \(\bar{s}\equiv _{CR}\bar{s}'\). By Lemma 4, \( \bar{I} _{ fun }(\bar{s}')\). By Lemma 3, \(\textit{D-Coh}(\bar{s}',\! CR (\bar{s}'))\) and \(\textit{I-Coh}(\bar{s}',\! EX (\bar{s}'))\). By SW-I Obligation 2.2, \(\textit{D-Coh}(\bar{s},\! CR (\bar{s}))\) and \(\textit{I-Coh}(\bar{s},\! EX (\bar{s}))\). By SW-I Obligation 1.2 and \( \bar{I} (\bar{s})\), \( \bar{I} _{ coh }(\bar{s}')\). Then by SW-I Obligation 1.3, \( \bar{I} _{ cm }(\bar{s}')\), thus \( \bar{I} (\bar{s}')= \bar{I} _{ fun }(\bar{s}')\wedge \bar{I} _{ coh }(\bar{s}')\wedge \bar{I} _{ cm }(\bar{s}')\) holds. \(\blacksquare \)
5.3 Kernel Level: Theorem 2
Our goal is to constrain kernel execution in such a way that it behaves identically in the cache-aware and the cacheless model. The challenge is to find suitable proof obligations for the kernel code that are stated on the cacheless model, so they can be verified using existing tools for binary analysis.
The first code verification obligation requires to show that the kernel preserves the invariant when there is no cache:
SW-C Obligation 1
For all s,\(s'\) if \( I (s)\), \(\textit{ex-entry}(s)\), and  , then \( I (s')\).
, then \( I (s')\).
We impose two requirements on the kernel virtual memory: the addresses in \(\mathbf {K_{vm}}\) must be cacheable (so that the kernel uses the data-view of memory resources) and \(\mathbf {K_{ex}}\) must be mapped to a subset of the executable resources.
SW-I Obligation 4
For all s such that \( I (s)\):
-
1.
For every \(va \in \mathbf {K_{vm}}\) if \( MMU (s,va) = (acc, pa, c)\) then c holds.
-
2.
For every \(va \in \mathbf {K_{ex}}\) if \( MMU (s,va) = (acc, pa, c)\) then \(pa \in EX (s )\).
A common problem of verifying low-level software is to couple the invariant with every possible internal state of the kernel. This is a major concern here, since the set of critical resources changes dynamically and can be stale while the kernel is executing. We solve this problem by defining an internal invariant \( II (s, s')\), which allows us to define properties of the state \(s'\) in relation with the initial state s of the kernel handler.
Definition 4
The intermediate invariants \( II (s,s')\) for the cacheless model and \(\overline{ II }(\bar{s},\bar{s}')\) for the cache-aware model hold if:
-
1.
\(s'. reg . pc \in \mathbf {K_{ex}}\) and \(\bar{s}'. reg . pc \in \mathbf {K_{ex}}\), respectively,
-
2.
for all \(pa\in \mathbb {PA}\): if \(pa\in MD (s, \mathbf {K_{vm}})\) then \(s. mem (pa) = s'. mem (pa)\) and if \(pa \in MD (\bar{s}, \mathbf {K_{vm}})\) then \(\textit{Dv}(\bar{s}, pa) = \textit{Dv}(\bar{s}', pa)\), respectively,
-
3.
\(\textit{v-deps}(s') \subseteq \mathbf {K_{vm}}\) and \(\textit{v-deps}(\bar{s}') \subseteq \mathbf {K_{vm}}\), respectively,
-
4.
\( II _{ cm }(s, s')\) and \(\overline{ II }_{ cm }(\bar{s}, \bar{s}')\), respectively: additional countermeasure-specific requirements that will be instantiated in Sect. 5.4, and
-
5.
only for the cache-aware model: \(\textit{D-Coh}(\bar{s}', CR (\bar{s}))\).
Now we demand a proof that the intermediate invariant is preserved in the cacheless model during kernel execution, i.e., that (1) the kernel does not execute instructions outside its code region, (2) the kernel does not change page-table entries that map its virtual memory, (3) the kernel does not leave its virtual address space, and (4) the kernel implements the countermeasure correctly.
SW-C Obligation 2
For all s,\(s'\) if \( I (s)\), \(\textit{ex-entry}(s)\), and \(s \rightarrow ^{*}_{ P } s'\), then \( II (s, s')\).
We require to demonstrate correctness of the countermeasure, by showing that it guarantees coherency of dependencies during kernel execution.
SW-I Obligation 5
For all \(\bar{s}, \bar{s}'\), if \( \bar{I} (\bar{s})\), \(\overline{ II }_{ cm }(\bar{s}, \bar{s}')\), and \(\bar{s}'. reg . pc \in \mathbf {K_{ex}}\) then \(\textit{D-Coh}(\bar{s}', \textit{p-deps}(\bar{s}'))\) and \(\textit{I-Coh}(\bar{s}', MMU (\bar{s}',\bar{s}'. reg . pc ))\).
We introduce the simulation relation between the two models: \(\bar{s}\mathrel {\mathcal {R}_{ sim }}s\) iff \((\bar{s}. reg , \bar{s}. psreg , \bar{s}. coreg ) = (s. reg , s. psreg , s. coreg )\) and for all pa, \( Mv (\bar{s},pa) = s. mem (pa)\). The intuition in using the memory-view is that it is equal to the data-view for coherent locations and is unchanged (as demonstrated by HW Obligation 3) for incoherent locations that are not directly accessed by the kernel.
The following proof obligation connects the simulation relation, the invariants and the intermediate invariants: (1) the invariant of the cache-aware model can be transferred to the cacheless model via the simulation; (2) after the execution of a handler (i.e. \( Mode (s') = U \)) if the two intermediate invariants hold then the simulation allows to transfer the functional invariant of the cacheless model to the cache-aware model and guarantees coherency of critical resources; and (3) the cache-aware intermediate invariant ensures the countermeasure requirements.
SW-I Obligation 6
For all \(\bar{s}, s\) such that \(\bar{s}\mathrel {\mathcal {R}_{ sim }}s\) and \( \bar{I} (\bar{s})\)
-
1.
\( I (s)\) holds and \( II _{ cm }(s,s)\) implies \(\overline{ II }_{ cm }(\bar{s},\bar{s})\),
-
2.
for all \(\bar{s}', s'\) such that \(\bar{s}' \mathrel {\mathcal {R}_{ sim }}s'\) if \(\overline{ II }(\bar{s}, \bar{s}')\), \( II (s, s')\), \( I (s')\), and \( Mode (s') = U \) then \( \bar{I} _{ fun }(\bar{s}')\) and \( \bar{I} _{ coh }(\bar{s}')\), and
-
3.
for all \(\bar{s}'\) if \( \bar{I} _{ fun }(\bar{s}')\), \( \bar{I} _{ coh }(\bar{s}')\), and \(\overline{ II }(\bar{s}, \bar{s}')\) then \( \bar{I} _{ cm }(\bar{s}')\).
The following lemmas assume that the proof obligations hold. First we show that the intermediate invariant can be transferred from the cacheless to the cache-aware model.
Lemma 6
Suppose that \(\bar{s}_0 \mathrel {\mathcal {R}_{ sim }}s_0\), \(\bar{s}\mathrel {\mathcal {R}_{ sim }}s\), \(\bar{s}\rightarrow _{ P } \bar{s}' [{ ops }]\), \(s \rightarrow _{ P } s' [{ ops }]\), and \(\bar{s}' \mathrel {\mathcal {R}_{ sim }}s'\). If \( \bar{I} (\bar{s}_0)\), \( II (s_0,s)\), \( II (s_0,s')\), and \(\overline{ II }(\bar{s}_0, \bar{s})\) then \(\overline{ II }(\bar{s}_0, \bar{s}')\).
Proof
Transferring the property of Definition 4.1 from \(s'\) to \(\bar{s}'\) is trivial, since \(\mathrel {\mathcal {R}_{ sim }}\) guarantees equivalence of registers.
For Definition 4.5 we show that the kernel only performs cacheable accesses in \({ ops }\) from s (due to SW-I Obligation 4 and HW Obligation 1.2); these are the same accesses performed in \(\bar{s}\); \( CR (\bar{s}_0)\) is data-coherent in \(\bar{s}\) due to \(\overline{ II }(\bar{s}_0,\bar{s})\); coherency is preserved from \(\bar{s}\) to \(\bar{s}'\) due to HW Obligation 4.
For Definition 4.2: Let \(D = MD (s_0, \mathbf {K_{vm}})\); \( II (s_0,s')\) ensures that the memory in D is the same in \(s_0\), s, and \(s'\); \(\mathrel {\mathcal {R}_{ sim }}\) guarantees that the memory-view of D in \(\bar{s}_0\) is the equal to the content of the memory in \(s_0\); D is data-coherent in \(\bar{s}_0\) by HW Obligation 1.1, SW-I Obligations 3.2 and 2.2, hence by Lemma 1 the data-view of D in \(\bar{s}_0\) is equal to its memory content in \(s_0\) and \(s'\); also \(D= MD (\bar{s}_0, \mathbf {K_{vm}})\) due to HW Obligation 1.2; similarly, \(\mathrel {\mathcal {R}_{ sim }}\) guarantees that the memory-view of D in \(\bar{s}'\) is equal to the memory content of D in \(s'\); then locations D have the same data-view in \(\bar{s}_0\) and \(\bar{s}'\) via Lemma 1, if D is coherent in \(\bar{s}'\). This follows from \(\textit{D-Coh}(\bar{s}', CR (\bar{s}_0))\) (shown above), HW Obligation 1.1, and SW-I Obligation 3.2.
For Definition 4.4 we rely on a further proof obligation that demonstrates correctness of the countermeasure: if the software implements the countermeasure in the cacheless model, then the additional coherency requirements on the cache-aware model are satisfied.
SW-I Obligation 7
Assume \(\bar{s}_0 \mathrel {\mathcal {R}_{ sim }}s_0\), \(\bar{s}\mathrel {\mathcal {R}_{ sim }}s\), \(\bar{s}\rightarrow _{ P } \bar{s}' [{ ops }]\), \(s \rightarrow _{ P } s' [{ ops }]\), and \(\bar{s}' \mathrel {\mathcal {R}_{ sim }}s'\). If \( \bar{I} (\bar{s}_0)\), \( II (s_0,s)\), \( II (s_0,s')\), and \(\overline{ II }(\bar{s}_0, \bar{s})\) then \(\overline{ II }_{ cm }(\bar{s}_0, \bar{s}')\).
From this we also establish coherency of the dependencies of \(\bar{s}'\) (due to SW-I Obligation 5), thus the data-view and the memory-view of the dependencies of \(\bar{s}'\) are the same (Lemma 1). The dependencies of \(s'\) and \(\bar{s}'\) have the same memory content via the simulation relation. Therefore \(s'\) and \(\bar{s}'\) are similar; by HW Obligation 3.1, we transfer the property of Definition 4.3 from \(s'\) to \(\bar{s}'\). \(\blacksquare \)
The following lemma shows that the simulation relation and the intermediate invariant is preserved while the kernel is executing.
Lemma 7
Suppose that \( \bar{I} (\bar{s})\), \(\textit{ex-entry}(\bar{s})\), and \(\bar{s}\mathrel {\mathcal {R}_{ sim }}s\). If \(\bar{s}\rightarrow ^{n}_{ P } \bar{s}'\) then \(s \rightarrow ^{n}_{ P } s'\) for some \(s'\) such that \(\bar{s}' \mathrel {\mathcal {R}_{ sim }}s'\), \(\overline{ II }(\bar{s}, \bar{s}')\), and \( II (s, s')\).
Proof
Internal invariant \( II (s,s')\) is directly obtained from SW-C Obligation 2. We prove the remaining goals by induction on the execution length. Simulation in the base case is trivial, as no step is taken, and \(\overline{ II }(\bar{s}, \bar{s})\) follows from \( II (\bar{s}, \bar{s})\), the coherency of critical resources in \(\bar{s}\), SW-I Obligations 6.1 and 5, the simulation relation and Lemma 1, as well as HW Obligation 3.1.
For the inductive case we first show that the simulation relation is preserved. \(\mathrel {\mathcal {R}_{ sim }}\) guarantees that \(s'\) and \(\bar{s}'\) have the same registers, SW-I Obligation 5 ensures that the memory pointed by the program counter is instruction-coherent and the instruction dependencies are data-coherent. Therefore, by Lemma 1 and \(\mathrel {\mathcal {R}_{ sim }}\) we can ensure all preconditions of HW Obligation 3, which shows that the simulation is preserved. We use Lemma 6 to transfer the intermediate invariant. \(\blacksquare \)
Figure 2 indicates how the various proof obligations and lemmas of the section tie together. We are now able to complete the proof of kernel integrity. The following lemma directly proves Theorem 2 if the proof obligations are met.
Lemma 8
(Kernel Integrity). For all \(\bar{s}_1\) and \(s_1\) such that \( \bar{I} (\bar{s}_1)\), \(\bar{s}_1 \mathrel {\mathcal {R}_{ sim }}s_1\), and \(\textit{ex-entry}(\bar{s}_1)\), if  then
then  , \(\bar{s}_2 \mathrel {\mathcal {R}_{ sim }}s_2\) and \( \bar{I} (\bar{s}_2)\).
, \(\bar{s}_2 \mathrel {\mathcal {R}_{ sim }}s_2\) and \( \bar{I} (\bar{s}_2)\).
Proof
From  . we have \(\bar{s}_1 \rightarrow ^{n}_{ P } \bar{s}_2\) for some n; by Lemma 7 we find \(s_2\) such that \(s_1 \rightarrow ^{n}_{ P } s_2\), \(\bar{s}_2 \mathrel {\mathcal {R}_{ sim }}s_2\), \(\overline{ II }(\bar{s}_1, \bar{s}_2)\), and \( II (s_1, s_2)\). Then
. we have \(\bar{s}_1 \rightarrow ^{n}_{ P } \bar{s}_2\) for some n; by Lemma 7 we find \(s_2\) such that \(s_1 \rightarrow ^{n}_{ P } s_2\), \(\bar{s}_2 \mathrel {\mathcal {R}_{ sim }}s_2\), \(\overline{ II }(\bar{s}_1, \bar{s}_2)\), and \( II (s_1, s_2)\). Then  as \(s_2\) and \(\bar{s}_2\) are in the same mode. By SW-I Obligation 6.1 we obtain \( I (s_1)\). Then by SW-C Obligation 1, \( I (s_2)\). SW-I Obligation 6.2 yields \( \bar{I} _{ fun }(\bar{s}_2)\) and \( \bar{I} _{ coh }(\bar{s}_2)\), and by SW-I Obligation 6.3, \( \bar{I} _{ cm }(\bar{s}_2)\). It follows that \( \bar{I} (\bar{s}_2)\) holds, as desired. \(\blacksquare \)
as \(s_2\) and \(\bar{s}_2\) are in the same mode. By SW-I Obligation 6.1 we obtain \( I (s_1)\). Then by SW-C Obligation 1, \( I (s_2)\). SW-I Obligation 6.2 yields \( \bar{I} _{ fun }(\bar{s}_2)\) and \( \bar{I} _{ coh }(\bar{s}_2)\), and by SW-I Obligation 6.3, \( \bar{I} _{ cm }(\bar{s}_2)\). It follows that \( \bar{I} (\bar{s}_2)\) holds, as desired. \(\blacksquare \)
5.4 Correctness of Countermeasures
Verification of a countermeasure amounts to instantiating all invariants that are not software-specific and discharging the corresponding proof obligations. We verify combinations of always cacheablility or selective eviction of the data-cache, and constant program memory or selective eviction of the instruction-cache.
Always Cacheablility and Constant Program Memory. Let \( M_{ac} \subseteq \mathbb {PA}\) be the region of physical memory that must always be accessed using cacheable aliases. The software needs to preserve two properties: (8.1) there are no uncacheable aliases to \( M_{ac} \), (8.2) the kernel never allocates critical resources outside \( M_{ac} \):
SW-I Obligation 8
If \( I (s)\) holds, then:
-
1.
For every va, if \( MMU (s,va)\!=\!(acc, pa, c)\) and \(pa \in M_{ac} \) then c.
-
2.
\( CR (s) \subseteq M_{ac} \).
For this countermeasure, the non-functional invariants are defined as follows
-
\( \bar{I} _{ coh }(\bar{s})\) states that critical resources are data-coherent and executable resources are instruction-coherent (from which SW-I Obligation 1.2 and SW-I Obligation 2.2 follow directly).
-
\( \bar{I} _{ cm }(\bar{s})\) states that addresses in \( M_{ac} \) that are not critical are data-coherent (SW-I Obligation 1.3 holds as there are no uncacheble aliases to \( M_{ac} \)).
-
\( II _{cm}(s, s')\) states that dependencies of instructions in \(s'\) are in \( M_{ac} \), no kernel write targets \( EX (\bar{s})\) (i.e. there is no self-modifying code), and when the kernel handler completes \( EX (\bar{s}') \subseteq EX (\bar{s})\).
-
\(\overline{ II }_{cm}(\bar{s}, \bar{s}')\) states that dependencies of instruction in \(\bar{s}'\) are in \( M_{ac} \), \( M_{ac} \) is data-coherent, and \( EX (\bar{s})\) is instruction-coherent (SW-I Obligation 5 holds due to SW-I Obligation 4, i.e., the kernel fetches instructions from \( EX (\bar{s})\) only).
The cache-aware functional invariant \( \bar{I} _{ fun }\) is defined equivalently to \( I \) using \(\textit{Dv}(\bar{s}, pa)\) in place of \(s. mem (pa)\). This and the two intermediate invariants enable to transfer properties between the two models, establishing SW-I Obligation 6.
The proof of SW-I Obligation 7 (i.e. the cache-aware intermediate invariant \(\overline{ II }_{cm}\) is preserved) consists of three tasks: (1) data-coherency of \( M_{ac} \) is preserved, since SW-I Obligation 4 and \( II \) imply that the kernel only performs cacheble accesses, therefore, data-coherency cannot be invalidated; (2) instruction-coherency is guaranteed by the fact that there is no self-modifying code and HW Obligation 4; (3) the hypothesis of HW Obligation 3.1 (which shows that cacheless and cache-aware model have the same dependencies) is ensured by the fact that cacheless dependencies are in \( M_{ac} \) which is data-coherent.
Selective Eviction of Data-Cache and Constant Program Memory. Differently from always cacheability, selective eviction does not require to establish a functional property (i.e. SW-I Obligation 8). Instead, it is necessary to verify that resources acquired from the application are accessed by the kernel only after they are made coherent via cache flushing. For this purpose, we extend the two models with a history variable h that keeps track of all effects of instruction executed by the kernel (i.e. \(s \rightarrow _{ m } s' \ [{{ ops }}]\) then \((s,h) \rightarrow _{ m } (s',h') \ [{{ ops }}]\) and \(h'=h; { ops }\)). Let \(C(s, s')\) be the set of resources that were critical in s or that have been data-flushed in the history of \(s'\). Hereafter we only describe the parts of the non-functional invariants that deal with the data-cache, since for the instruction-cache we use the same countermeasure as in the previous case.
-
\( \bar{I} _{ coh }(\bar{s})\) is the same as always cacheability, while \( \bar{I} _{ cm }(\bar{s}) = true\), since the countermeasure is not a state-based property.
-
\( II _{cm}(s, s')\) (and \(\overline{ II }_{cm}(\bar{s}, \bar{s}')\)) states that dependencies in \(s'\) are in \(C(s, s')\) (\(C(\bar{s},\bar{s}')\), respectively) and that \( CR (s')\subseteq CR (s) \cup C(s, s')\) if \( Mode (s') = U \).
Again, the cache-aware functional invariant \( \bar{I} _{ fun }\) is defined equivalently to \( I \) using the data-view of memory resources.
The proofs of SW-I Obligation 6 and SW-I Obligation 7 are similar to the ones above. Instead of \( M_{ac} \) they rely on the data-coherency of \(C(\bar{s},\bar{s}')\) and the fact that data-cache flushes always establish coherency (HW Obligation 4).
Selective Eviction of Instruction-Cache. The two previous countermeasures for data-cache can be combined with selective eviction of instruction-cache to support dynamic code. The requirements that the kernel does not write into executable resources and that these are not extended are changed with the following property. Let \(C'(s, s')\) be the set of executable resources in s that have not been written in the history of \(s'\), joined with the resources that have been data-flushed, instruction-flushed, and have not been overwritten after the flushes. The intermediate invariant \( II _{cm}(s, s')\) (and analogously \(\overline{ II }_{cm}(\bar{s}, \bar{s}')\) for the cache-aware model) states that the translation of the program counter is in \(C'(s, s')\), and when the kernel handler completes, \( EX (s') \subseteq C'(s, s')\). Additionally, \(\overline{ II }_{cm}(\bar{s}, \bar{s}')\) states that \(C'(\bar{s}, \bar{s}')\) is instruction-coherent. SW-I Obligation 5 holds because the kernel only fetches instructions from \(C'(\bar{s}, \bar{s}')\).
The main change to the proof of SW-I Obligation 7 consists in showing instruction-coherency of \(C'(\bar{s}, \bar{s}')\), which is ensured by the fact that data- and instruction-flushing a location makes it instruction-coherent (HW Obligation 4).
5.5 Verification of a Specific Software
Table 1 summarizes the proof obligations we identified. As the countermeasures are verified, three groups of proof obligations remain for a specific software: (1) SW-I Obligation 2.1, SW-I Obligation 3, and SW-C Obligation 1: these are requirements for a secure kernel independently of caches; (2) SW-I Obligation 4 (and SW-I Obligation 8 for always-cacheability): these only constrain the configuration of the MMU; (3) SW-C Obligation 2: during the execution the kernel (i) stays in its code region, (ii) does not change or leave its virtual memory, (iii) preserves the countermeasure specific intermediate invariant. These must be verified for intermediate states of the kernel, e.g., by inlining assertions that guarantee (i–iii). Notice that the two code verification tasks (SW-C Obligation 1 and SW-C Obligation 2) do not require the usage of the cache-aware model, enabling the usage of existing binary analysis tools.
Case Study. As a case study, we use a hypervisor capable of hosting a Linux guest that has been formally verified previously on a cacheless model [21] and its vulnerability to cache storage channel attacks is shown in [20]. The memory subsystem is virtualized through direct paging. To create a page-table, a guest prepares it in guest memory and requests its validation. If the validation succeeds the hypervisor can use the page-table to configure the MMU, without requiring memory copy operations. The validation ensures that the page-table does not allow writable accesses of the guest outside the guest’s memory or to the page-tables. Other hypercalls allow to free and modify validated page-tables.
Using mismatched cacheability attributes, a guest can potentially violate memory isolation: it prepares a valid page-table in cache and a malicious page-table in memory; if the hypervisor validates stale data from the cache, after eviction, the MMU can be made to use the malicious page-table, enabling the guest to violate memory isolation. We fix this vulnerability by using always cacheability: The guest is forced to create page-tables only inside an always cacheable region of memory.
The general concepts of Sect. 4.1 are easily instantiated for the hypervisor. Since it uses a static region of physical memory \( HM \), the critical resources consist of \( HM \) and every memory page that is allocated to store a page-table. Additionally to the properties described in [21], the invariant requires that all page-tables are allocated in \( M_{ac} \) and all aliases to \( M_{ac} \) are cacheable. To guarantee these properties the hypervisor code has been updated: validation of a page-table checks that the page resides in \( M_{ac} \) and that all new mapping to \( M_{ac} \) are cacheable; modification of a page-table forbids uncacheable aliases to \( M_{ac} \).
6 Implementation
The complete proof strategy has been implemented [2] and machine-checked using the HOL4 interactive theorem prover [1]. The resulting application and kernel integrity theorems are parametric in the countermeasure-dependent proof obligations. These obligations have been discharged for the selected countermeasures yielding theorems that depend only on code verification conditions and properties of the functional kernel invariant. Hardware obligations have been verified on a single-core model consisting of a generic processor and memory interface. While the processor interface has not been instantiated yet, all assumptions on the memory system have been validated for an instantiation with single-level data- and instruction-caches using a rudimentary cache implementation. Instantiation with more realistic models is ongoing. The formal analysis took three person months and consists of roughly 10000 LoC for the hardware model specification and verification of its instantiation, 2500 LoC for the integrity proof, and 2000 LoC for the countermeasure verification.
For the case study we augmented the existing hypervisor with the always cacheability countermeasure. This entailed some engineering effort to adapt the memory allocator of the Linux kernel to allocate page-tables inside \( M_{ac} \). The adaptation required changes to 45 LoC in the hypervisor and an addition of 35 LoC in the paravirtualized Linux kernel and imposes a negligible performance overhead (\(\le 1\%\) in micro- and macro-benchmarks [20]). The HOL4 model of the hypervisor design has been modified to include the additional checks performed by the hypervisor. Similarly, we extended the invariant with the new properties guaranteed by the adopted countermeasure. The model has been used to show that the new design preserves the invariant and that all proof obligations on the invariant hold, which required 2000 HOL4 LoC. Verification of the augmented hypervisor binary is left for future work. Even if binary verification can be automated to a large extent using binary analysis tools (e.g. [11, 30]), it still requires a substantial engineering effort.
7 Conclusion
Modern hardware architectures are complex and can exhibit unforeseen vulnerabilities if low level details are not properly taken into account. The cache storage channels of [20], as well as the recent Meltdown [26] and Spectre [28] attacks are examples of this problem. They shows the importance of low-level system details and the need of sound and tractable strategies to reason about them in the verification of security-critical software.
Here we presented an approach to verify integrity-preserving countermeasures in the presence of cache storage side-channels. In particular, we identified conditions that must be met by a security mechanism to neutralise the attack vector and we verified correctness of some of the existing techniques to counter both (instruction- and data-cache) integrity attacks.
The countermeasures are formally modelled as new proof obligations that can be imposed on the cacheless model to ensure the absence of vulnerability due to cache storage channels. The result of this analysis are theorems in Sect. 4.3. They demonstrate that a software satisfying a set of proof obligations (i.e., correctly implementing the countermeasure) is not vulnerable because of cache storage channels.
Our analysis is based on an abstract hardware model that should fit a number of architectures. While here we only expose two execution modes, we can support multiple modes of executions, where the most privileged is used by the kernel and all other modes are considered to be used by the application. Also our MMU model is general enough to cover other hardware-based protection mechanisms, like Memory Protection Units or TrustZone memory controllers.
While this paper exemplifies the approach for first-level caches, our methodology can be extended to accommodate more complex scenarios and other hardware features too. For instance our approach can be used to counter storage channels due to TLBs, multi-level caches, and multi-core processing.
Translation Look-aside Buffers (TLBs) can be handled similarly to instruction-caches. Non-privileged instructions are unable to directly modify the TLB and incoherent behaviours can arise only by the assistance of kernel modifying the page-tables. Incoherent behavior can be prevented using TLB cleans or demonstrating that the page-tables are not changed.
Multi-level caches can be handled iteratively in a straightforward fashion, starting from the cacheless model and adding CPU-closer levels of cache at each iteration. Iterative refinement has three benefits: Enabling the use of existing (cache unaware) analysis tools for verification, enabling transfer of results from Sects. 5.3 and 5.4 to the more complex models, and allowing to focus on each hardware feature independently, so at least partially counteracting the pressure towards ever larger and more complex global models.
In the same way the integrity proof can be repeated for the local caches in a multi-core system. For shared caches the proof strategy needs to be adapted to take into account interleaved privileged and non-privileged steps of different cores, depending on the chosen verification methodology for concurrent code.
It is also worth noting that our verification approach works for both preemptive and non-preemptive kernels, due to the use of the intermediate invariants \( II \) and \(\overline{ II }\) that do not depend on intermediate states of kernel data structures.
For non-privileged transitions the key tool is the derivability relation, which is abstract enough to fit a variety of memory systems. However, derivability has the underlying assumption that only uncacheable writes can bypass the cache and break coherency. If a given hardware allows the application to break coherency through other means, e.g., non-temporal store instructions or invalidate-only cache flushes, these cases need to be added to the derivability definition.
The security analysis requires trustworthy models of hardware, which are needed to verify platform-dependent proof obligations. Some of these properties require extensive tests to demonstrate that corner cases are correctly handled by models. For example, while the conventional wisdom is that flushing caches can close side-channels, a new study [16] showed flushing does not sanitize caches thoroughly and leaves some channels active, e.g. instruction-cache attack vectors.
There are several open questions concerning side-channels due to similar shared low-level hardware features such as branch prediction units, which undermine the soundness of formal verification. This is an unsatisfactory situation since formal proofs are costly and should pay off by giving reliable guarantees. Moreover, the complexity of contemporary hardware is such that a verification approach allowing reuse of models and proofs as new hardware features are added is essential for formal verification in this space to be economically sustainable. Our results represent a first step towards giving reliable guarantees and reusable proofs in the presence of low level storage channels.
References
HOL4. http://hol.sourceforge.net/. Accessed 13 Feb 2018
HOL4 implementation of proofs of this paper. https://github.com/rauhbein/cacheproofs. Accessed 13 Feb 2018
seL4 Project. http://sel4.systems/. Accessed 13 Feb 2018
Alkassar, E., Hillebrand, M.A., Leinenbach, D., Schirmer, N., Starostin, A., Tsyban, A.: Balancing the load. J. Autom. Reason. 42(2–4), 389–454 (2009)
Almeida, J.B., Barbosa, M., Barthe, G., Dupressoir, F.: Verifiable side-channel security of cryptographic implementations: constant-time MEE-CBC. In: Peyrin, T. (ed.) FSE 2016. LNCS, vol. 9783, pp. 163–184. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52993-5_9
Balliu, M., Dam, M., Guanciale, R.: Automating information flow analysis of low level code. In: Proceedings of CCS, pp. 1080–1091 (2014)
Barthe, G., Betarte, G., Campo, J.D., Chimento, J.M., Luna, C.: Formally verified implementation of an idealized model of virtualization. In: Proceedings of TYPES, pp. 45–63 (2013)
Barthe, G., Betarte, G., Campo, J.D., Luna, C.: Formally verifying isolation and availability in an idealized model of virtualization. In: Butler, M., Schulte, W. (eds.) FM 2011. LNCS, vol. 6664, pp. 231–245. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21437-0_19
Barthe, G. Betarte, G., Campo, J.D., Luna, C.: Cache-leakage resilient OS isolation in an idealized model of virtualization. In: Proceedings of CSF, pp. 186–197 (2012)
Becker, H., Crespo, J.M., Galowicz, J., Hensel, U., Hirai, Y., Kunz, C., Nakata, K., Sacchini, J.L., Tews, H., Tuerk, T.: Combining mechanized proofs and model-based testing in the formal analysis of a hypervisor. In: Fitzgerald, J., Heitmeyer, C., Gnesi, S., Philippou, A. (eds.) FM 2016. LNCS, vol. 9995, pp. 69–84. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48989-6_5
Brumley, D., Jager, I., Avgerinos, T., Schwartz, E.J.: BAP: a binary analysis platform. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 463–469. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_37
Chfouka, H., Nemati, H., Guanciale, R., Dam, M., Ekdahl, P.: Trustworthy prevention of code injection in linux on embedded devices. In: Pernul, G., Ryan, P.Y.A., Weippl, E. (eds.) ESORICS 2015. LNCS, vol. 9326, pp. 90–107. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24174-6_5
Cock, D., Ge, Q., Murray, T., Heiser, G.: The last mile: an empirical study of some timing channels on seL4. In: Proceedings of CCS, pp. 570–581 (2014)
Doychev, G., Feld, D., Köpf, B., Mauborgne, L., Reineke, J.: Cacheaudit: a tool for the static analysis of cache side channels. In: Proceedings SEC, pp. 431–446 (2013)
Doychev, G., Köpf, B.: Rigorous analysis of software countermeasures against cache attacks. CoRR, abs/1603.02187 (2016)
Ge, Q., Yarom, Y., Heiser, G.: Do Hardware Cache Flushing Operations Actually Meet Our Expectations? ArXiv e-prints, December 2016
Gu, L., Vaynberg, A., Ford, B., Shao, Z., Costanzo, D.: CertiKOS: a certified kernel for secure cloud computing. In: Proceedings of APSys, p. 3 (2011)
Gu, R., Koenig, J., Ramananandro, T., Shao, Z., Wu, X.N., Weng, S.-C., Zhang, H., Guo, Y.: Deep specifications and certified abstraction layers. In: SIGPLAN Notices, vol. 50, pp. 595–608. ACM (2015)
Gu, R., Shao, Z., Chen, H., Wu, X., Kim, J., Sjöberg, V., Costanzo, D.: Certikos: an extensible architecture for building certified concurrent OS kernels. In: Proceedings of OSDI, pp. 653–669 (2016)
Guanciale, R., Nemati, H., Baumann, C., Dam, M.: Cache storage channels: alias-driven attacks and verified countermeasures. In: SP, pp. 38–55 (2016)
Guanciale, R., Nemati, H., Dam, M., Baumann, C.: Provably secure memory isolation for Linux on ARM. J. Comput. Secur. 24(6), 793–837 (2016)
Heitmeyer, C.L., Archer, M., Leonard, E.I., McLean, J.: Formal specification and verification of data separation in a separation kernel for an embedded system. In: CCS, pp. 346–355 (2006)
Hillebrand, M.A., der Rieden, T.I., Paul, W.J.: Dealing with I/O devices in the context of pervasive system verification. In: Proceedings of ICCD, pp. 309–316 (2005)
Klein, G., Andronick, J., Elphinstone, K., Murray, T.C., Sewell, T., Kolanski, R., Heiser, G.: Comprehensive formal verification of an OS microkernel. ACM Trans. Comput. Syst. 32(1), 2 (2014)
Klein, G., Elphinstone, K., Heiser, G., Andronick, J., Cock, D., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolanski, R., Norrish, M., Sewell, T., Tuch, H., Winwood, S.: seL4: formal verification of an OS kernel. In: Proceedings of SOSP, pp. 207–220 (2009)
Kocher, P., Genkin, D., Gruss, D., Haas, W., Hamburg, M., Lipp, M., Mangard, S., Prescher, T., Schwarz, M., Yarom, Y.: Spectre attacks: exploiting speculative execution. ArXiv e-prints, January 2018
Köpf, B., Mauborgne, L., Ochoa, M.: Automatic quantification of cache side-channels. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 564–580. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31424-7_40
Lipp, M., Schwarz, M., Gruss, D., Prescher, T., Haas, W., Mangard, S., Kocher, P., Genkin, D., Yarom, Y., Hamburg, M.: Meltdown. ArXiv e-prints, January 2018
Morrisett, G., Tan, G., Tassarotti, J., Tristan, J.-B., Gan, E.: RockSalt: better, faster, stronger SFI for the x86. In: ACM SIGPLAN Notices, vol. 47, pp. 395–404 (2012)
Sewell, T.A.L., Myreen, M.O., Klein, G.: Translation validation for a verified OS kernel. In: Proceedings of PLDI, pp. 471–482 (2013)
Song, D., Brumley, D., Yin, H., Caballero, J., Jager, I., Kang, M.G., Liang, Z., Newsome, J., Poosankam, P., Saxena, P.: BitBlaze: a new approach to computer security via binary analysis. In: Sekar, R., Pujari, A.K. (eds.) ICISS 2008. LNCS, vol. 5352, pp. 1–25. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89862-7_1
Stefan, D., Buiras, P., Yang, E.Z., Levy, A., Terei, D., Russo, A., Mazières, D.: Eliminating cache-based timing attacks with instruction-based scheduling. In: Crampton, J., Jajodia, S., Mayes, K. (eds.) ESORICS 2013. LNCS, vol. 8134, pp. 718–735. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40203-6_40
Steinberg, U., Kauer, B.: NOVA: a microhypervisor-based secure virtualization architecture. In: Proceedings of EuroSys, pp. 209–222 (2010)
Tews, H., Völp, M., Weber, T.: Formal memory models for the verification of low-level operating-system code. J. Autom. Reason. 42(2–4), 189–227 (2009)
Tiwari, M., Oberg, J.K., Li, X., Valamehr, J., Levin, T., Hardekopf, B., Kastner, R., Chong, F.T., Sherwood, T.: Crafting a usable microkernel, processor, and I/O system with strict and provable information flow security. In: Proceedings of ISCA, pp. 189–200 (2011)
Weiß, M., Heinz, B., Stumpf, F.: A cache timing attack on AES in virtualization environments. In: Keromytis, A.D. (ed.) FC 2012. LNCS, vol. 7397, pp. 314–328. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32946-3_23
Wilding, M.M., Greve, D.A., Richards, R.J., Hardin, D.S.: Formal verification of partition management for the AAMP7G microprocessor. In: Hardin, D. (ed.) Design and Verification of Microprocessor Systems for High-Assurance Applications, pp. 175–191. Springer, Boston (2010). https://doi.org/10.1007/978-1-4419-1539-9_6
Zhao, L., Li, G., De Sutter, B., Regehr, J.: ARMor: fully verified software fault isolation. In: EMSOFT, pp. 289–298 (2011)
Acknowledgments
This work was supported by the PROSPER project funded by the Swedish Foundation for Strategic Research, the KTH CERCES Center for Resilient Critical Infrastructures funded by the Swedish Civil Contingencies Agency, as well as the German Federal Ministry of Education and Research (BMBF) through funding for the CISPA-Stanford Center for Cybersecurity (FKZ: 13N1S0762).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Nemati, H., Baumann, C., Guanciale, R., Dam, M. (2018). Formal Verification of Integrity-Preserving Countermeasures Against Cache Storage Side-Channels. In: Bauer, L., Küsters, R. (eds) Principles of Security and Trust. POST 2018. Lecture Notes in Computer Science(), vol 10804. Springer, Cham. https://doi.org/10.1007/978-3-319-89722-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-89722-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89721-9
Online ISBN: 978-3-319-89722-6
eBook Packages: Computer ScienceComputer Science (R0)





 then
then  , and
, and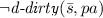

 and
and  denote the cache-line contents corresponding to pa in
denote the cache-line contents corresponding to pa in  of pa are preserved
of pa are preserved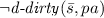
 then
then 