Abstract
Quantitative information flow (QIF) is concerned with measuring how much of a secret is leaked to an adversary who observes the result of a computation that uses it. Prior work has shown that QIF techniques based on abstract interpretation with probabilistic polyhedra can be used to analyze the worst-case leakage of a query, on-line, to determine whether that query can be safely answered. While this approach can provide precise estimates, it does not scale well. This paper shows how to solve the scalability problem by augmenting the baseline technique with sampling and symbolic execution. We prove that our approach never underestimates a query’s leakage (it is sound), and detailed experimental results show that we can match the precision of the baseline technique but with orders of magnitude better performance.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
As more sensitive data is created, collected, and analyzed, we face the problem of how to productively use this data while preserving privacy. One approach to this problem is to analyze a query f in order to quantify how much information about secret input s is leaked by the output f(s). More precisely, we can consider a querier to have some prior belief of the secret’s possible values. The belief can be modeled as a probability distribution [10], i.e., a function \(\delta \) from each possible value of s to its probability. When a querier observes output \(o = f(s)\), he revises his belief, using Bayesian inference, to produce a posterior distribution \(\delta '\). If the posterior could reveal too much about the secret, then the query should be rejected. One common definition of “too much” is Bayes Vulnerability, which is the probability of the adversary guessing the secret in one try [41]. Formally,
Various works [6, 19, 24, 25] propose rejecting f if there exists an output that makes the vulnerability of the posterior exceed a fixed threshold K. In particular, for all possible values i of s (i.e., \(\delta (i) > 0\)), if the output \(o = f(i)\) could induce a posterior \(\delta '\) with \(V(\delta ') > K\), then the query is rejected.
One way to implement this approach is to estimate \(f(\delta )\)—the distribution of f’s outputs when the inputs are distributed according to \(\delta \)—by viewing f as a program in a probabilistic programming language (PPL) [18]. Unfortunately, as discussed in Sect. 9, most PPLs are approximate in a manner that could easily result in underestimating the vulnerability, leading to an unsafe security decision. Techniques designed specifically to quantify information leakage often assume only uniform priors, cannot compute vulnerability (favoring, for example, Shannon entropy), and/or cannot maintain assumed knowledge between queries.
Mardziel et al. [25] propose a sound analysis technique based on abstract interpretation [12]. In particular, they estimate a program’s probability distribution using an abstract domain called a probabilistic polyhedron (PP), which pairs a standard numeric abstract domain, such as convex polyhedra [13], with some additional ornaments, which include lower and upper bounds on the size of the support of the distribution, and bounds on the probability of each possible secret value. Using PP can yield a precise, yet safe, estimate of the vulnerability, and allows the posterior PP (which is not necessarily uniform) to be used as a prior for the next query. Unfortunately, PPs can be very inefficient. Defining intervals [11] as the PP’s numeric domain can dramatically improve performance, but only with an unacceptable loss of precision.
In this paper we present a new approach that ensures a better balance of both precision and performance in vulnerability computation, augmenting PP with two new techniques. In both cases we begin by analyzing a query using the fast interval-based analysis. Our first technique is then to use sampling to augment the result. In particular, we execute the query using possible secret values i sampled from the posterior \(\delta '\) derived from a particular output \(o_i\). If the analysis were perfectly accurate, executing f(i) would produce \(o_i\). But since intervals are overapproximate, sometimes it will not. With many sampled outcomes, we can construct a Beta distribution to estimate the size of the support of the posterior, up to some level of confidence. We can use this estimate to boost the lower bound of the abstraction, and thus improve the precision of the estimated vulnerability.
Our second technique is of a similar flavor, but uses symbolic reasoning to magnify the impact of a successful sample. In particular, we execute a query result-consistent sample concolically [39], thus maintaining a symbolic formula (called the path condition) that characterizes the set of variable valuations that would cause execution to follow the observed path. We then count the number of possible solutions and use the count to boost the lower bound of the support (with 100% confidence).
Sampling and concolic execution can be combined for even greater precision.
We have formalized and proved our techniques are sound (Sects. 3–6) and implemented and evaluated them (Sects. 7 and 8). Using a privacy-sensitive ship planning scenario (Sect. 2) we find that our techniques provide similar precision to convex polyhedra while providing orders-of-magnitude better performance. More experiments are needed to see if the approach provides such benefits more generally. Our implementation freely available at https://github.com/GaloisInc/TAMBA.
2 Overview
To provide an overview of our approach, we will describe the application of our techniques to a scenario that involves a coalition of ships from various nations operating in a shared region. Suppose a natural disaster has impacted some islands in the region. Some number of individuals need to be evacuated from the islands, and it falls to a regional disaster response coordinator to determine how to accomplish this. While the coalition wants to collaborate to achieve these humanitarian aims, we assume that each nation also wants to protect their sensitive data—namely ship locations and capacity.
More formally, we assume the use of the data model shown in Fig. 1, which considers a set of ships, their coalition affiliation, the evacuation capacity of the ship, and its position, given in terms of latitude and longitude.Footnote 1 We sometimes refer to the latter two as a location L, with L.x as the longitude and L.y as the latitude. We will often index properties by ship ID, writing \(\text {Capacity}(z)\) for the capacity associated with ship ID z, or \(\text {Location}(z)\) for the location.
The evacuation problem is defined as follows
Given a target location L and number of people to evacuate N, compute a set of nearby ships S such that \(\sum _{z \in S} \text {Capacity}(z) \ge N\).
Our goal is to solve this problem in a way that minimizes the vulnerability to the coordinator of private information, i.e., the ship locations and their exact capacity. We assume that this coordinator initially has no knowledge of the positions or capabilities of the ships other than that they fall within certain expected ranges.
If all members of the coalition share all of their data with the coordinator, then a solution is easy to compute, but it affords no privacy. Figure 2 gives an algorithm the response coordinator can follow that does not require each member to share all of their data. Instead, it iteratively performs queries AtLeast and Nearby. These queries do not reveal precise values about ship locations or capacity, but rather admit ranges of possibilities. The algorithm works by maintaining upper and lower bounds on the capacity of each ship  in the array
in the array  . Each ship’s bounds are updated based on the results of queries about its capacity and location. These queries aim to be privacy preserving, doing a sort of binary search to narrow in on the capacity of each ship in the operating area. The procedure completes once
. Each ship’s bounds are updated based on the results of queries about its capacity and location. These queries aim to be privacy preserving, doing a sort of binary search to narrow in on the capacity of each ship in the operating area. The procedure completes once  determines the minimum required capacity is reached.
determines the minimum required capacity is reached.
2.1 Computing Vulnerability with Abstract Interpretation
Using this procedure, what is revealed about the private variables (location and capacity)? Consider a single \( Nearby (z,l,d)\) query. At the start, the coordinator is assumed to know only that z is somewhere within the operating region. If the query returns  , the coordinator now knows that s is within d units of l (using Manhattan distance). This makes \(\textit{Location}(z)\) more vulnerable because the adversary has less uncertainty about it.
, the coordinator now knows that s is within d units of l (using Manhattan distance). This makes \(\textit{Location}(z)\) more vulnerable because the adversary has less uncertainty about it.
Mardziel et al. [25] proposed a static analysis for analyzing queries such as \( Nearby (z,l,d)\) to estimate the worst-case vulnerability of private data. If the worst-case vulnerability is too great, the query can be rejected. A key element of their approach is to perform abstract interpretation over the query using an abstract domain called a probabilistic polyhedron. An element P of this domain represents the set of possible distributions over the query’s state. This state includes both the hidden secrets and the visible query results. The abstract interpretation is sound in the sense that the true distribution \(\delta \) is contained in the set of distributions represented by the computed probabilistic polyhedron P.
A probabilistic polyhedron P is a tuple comprising a shape and three ornaments. The shape C is an element of a standard numeric domain—e.g., intervals [11], octagons [29], or convex polyhedra [13]—which overapproximates the set of possible values in the support of the distribution. The ornaments \(p \in [0, 1]\), \(m \in \mathbb {R}\), and \(s \in \mathbb {Z}\) are pairs which store upper and lower bounds on the probability per point, the total mass, and number of support points in the distribution, respectively. (Distributions represented by P are not necessarily normalized, so the mass m is not always 1.)
Figure 3(a) gives an example probabilistic polyhedron that represents the posterior of a Nearby query that returns true. In particular, if Nearby(z,\(L_1\),D) is true then Location(z) is somewhere within the depicted diamond around \(L_1\). Using convex polyhedra or octagons for the shape domain would permit representing this diamond exactly; using intervals would overapproximate it as the depicted 9\(\,\times \,\)9 bounding box. The ornaments would be the same in any case: the size s of the support is 41 possible (x,y) points, the probability p per point is 0.01, and the total mass is 0.41, i.e., \(p \cdot s\). In general, each ornament is a pair of a lower and upper bound (e.g., \(s_\text {min}\) and \(s_\text {max}\)), and m might be a more accurate estimate than \(p \cdot s\). In this case shown in the figure, the bounds are tight.
Mardziel et al’s procedure works by computing the posterior P for each possible query output o, and from that posterior determining the vulnerability. This is easy to do. The upper bound \(p_\text {max}\) of p maximizes the probability of any given point. Dividing this by the lower bound \(m_\text {min}\) of the probability mass m normalizes this probability for the worst case. For P shown in Fig. 3(a), the bounds of p and m are tight, so the vulnerability is simply \(0.01 / 0.41 = 0.024\).
2.2 Improving Precision with Sampling and Concolic Execution
In Fig. 3(a), the parameters s, p, and m are precise. However, as additional operations are performed, these quantities can accumulate imprecision. For example, suppose we are using intervals for the shape domain, and we wish to analyze the query \(\textit{Nearby}(z,L_1,4) \vee \textit{Nearby}(z,L_2,4)\) (for some nearby point \(L_2\)). The result is produced by analyzing the two queries separately and then combining them with an abstract join; this is shown in the top row of Fig. 3(b). Unfortunately, the result is very imprecise. The bottom row of Fig. 3(b) illustrates the result we would get by using convex polyhedra as our shape domain. When using intervals (top row), the vulnerability is estimated as 0.036, whereas the precise answer (bottom row) is actually 0.026. Unfortunately, obtaining this precise answer is far more expensive than obtaining the imprecise one.
This paper presents two techniques that can allow us to use the less precise interval domain but then recover lost precision in a relatively cheap post-processing step. The effect of our techniques is shown in the middle-right of Fig. 3(b). Both techniques aim to obtain better lower bounds for s. This allows us to update lower bounds on the probability mass m since \(m_\text {min}\) is at least \(s_\text {min} \cdot p_\text {min}\) (each point has at least probability \(p_\text {min}\) and there are at least \(s_\text {min}\) of them). A larger m means a smaller vulnerability.
The first technique we explore is sampling, depicted to the right of the arrow in Fig. 3(b). Sampling chooses random points and evaluates the query on them to determine whether they are in the support of the posterior distribution for a particular query result. By tracking the ratio of points that produce the expected output, we can produce an estimate of s, whose confidence increases as we include more samples. This approach is depicted in the figure, where we conclude that \(s \in [72,81]\) and \(m \in [0.72,1.62]\) with 90% confidence after taking 1000 samples, improving our vulnerability estimate to \(V \le \frac{0.02}{0.72} = 0.028\).
The second technique we explore is the use of concolic execution to derive a path condition, which is a formula over secret values that is consistent with a query result. By performing model counting to estimate the number of solutions to this formula, which are an underapproximation of the true size of the distribution, we can safely boost the lower bound of s. This approach is depicted to the left of the arrow in Fig. 3(b). The depicted shapes represent discovered path condition’s disjuncts, whose size sums to 63. This is a better lower bound on s and improves the vulnerability estimate to 0.032.
These techniques can be used together to further increase precision. In particular, we can first perform concolic execution, and then sample from the area not covered by this underapproximation. Importantly, Sect. 8 shows that using our techniques with the interval-based analysis yields an orders of magnitude performance improvement over using polyhedra-based analysis alone, while achieving similar levels of precision, with high confidence.
3 Preliminaries: Syntax and Semantics
This section presents the core language—syntax and semantics—in which we formalize our approach to computing vulnerability. We also review probabilistic polyhedra [25], which is the baseline analysis technique that we augment.
3.1 Core Language and Semantics
The programming language we use for queries is given in Fig. 4. The language is essentially standard, apart from \(\mathsf {pif}\;{q}\;\mathsf {then}\;{ S _1}\;\mathsf {else}\;{ S _2}\), which implements probabilistic choice: \( S _1\) is executed with probability q, and \( S _2\) with probability \(1-q\). We limit the form of expressions E so that they can be approximated by standard numeric abstract domains such as convex polyhedra [13]. Such domains require linear forms; e.g., there is no division operator and multiplication of two variables is disallowed.Footnote 2
We define the semantics of a program in terms of its effect on (discrete) distributions of states. States \(\sigma \) are partial maps from variables to integers; we write \( \textit{domain}(\sigma ) \) for the set of variables over which \(\sigma \) is defined. Distributions \(\delta \) are maps from states to nonnegative real numbers, interpreted as probabilities (in range [0, 1]). The denotational semantics considers a program as a relation between distributions. In particular, the semantics of statement \( S \), written \([\![{ S }]\!]{}\), is a function of the form Dist \(\rightarrow \) Dist; we write \([\![{ S }]\!]{\delta } = \delta '\) to say that the semantics of \( S \) maps input distribution \(\delta \) to output distribution \(\delta '\). Distributions are not necessarily normalized; we write \(\mathord {\parallel }\delta \mathord {\parallel }\) as the probability mass of \(\delta \) (which is between 0 and 1). We write \(\dot{\sigma }\) to denote the point distribution that gives \(\sigma \) probability 1, and all other states 0.
The semantics is standard and not crucial in order to understand our techniques. In Appendix B we provide the semantics in full. See Clarkson et al. [10] or Mardziel et al. [25] for detailed explanations.
3.2 Probabilistic Polyhedra
To compute vulnerability for a program \( S \) we must compute (an approximation of) its output distribution. One way to do that would be to use sampling: Choose states \(\sigma \) at random from the input distribution \(\delta \), “run” the program using that input state, and collect the frequencies of output states \(\sigma '\) into a distribution \(\delta '\). While using sampling in this manner is simple and appealing, it could be both expensive and imprecise. In particular, depending on the size of the input and output space, it may take many samples to arrive at a proper approximation of the output distribution.
Probabilistic polyhedra [25] can address both problems. This abstract domain combines a standard domain \(C_{}\) for representing numeric program states with additional ornaments that all together can safely represent \( S \)’s output distribution.
Probabilistic polyhedra work for any numeric domain; in this paper we use both convex polyhedra [13] and intervals [11]. For concreteness, we present the definition using convex polyhedra. We use the meta-variables \(\beta , \beta _1, \beta _2\), etc. to denote linear inequalities.
Definition 1
A convex polyhedron \(C= (B, V)\) is a set of linear inequalities \(B= \{\beta _1,\ldots ,\beta _m\}\), interpreted conjunctively, over variables V. We write \(\mathbb {C}\) for the set of all convex polyhedra. A polyhedron \(C\) represents a set of states, denoted \(\gamma _{\mathbb {C}}(C)\), as follows, where \(\sigma \,\models \, \beta \) indicates that the state \(\sigma \) satisfies the inequality \(\beta \).
Naturally we require that \(\textit{domain}(\{\beta _1,\ldots ,\beta _n\}) \subseteq V \); i.e., V mentions all variables in the inequalities. Let \( \textit{domain}(\left( B, V \right) ) = V \).
Probabilistic polyhedra extend this standard representation of sets of program states to sets of distributions over program states.
Definition 2
A probabilistic polyhedron \(P_{}\) is a tuple \((C_{},\mathrm {s}^\mathrm {min}_{},\) \(\mathrm {s}^\mathrm {max}_{}, \mathrm {p}^\mathrm {min}_{},\) \(\mathrm {p}^\mathrm {max}_{}, \mathrm {m}^\mathrm {min}_{},\) \(\mathrm {m}^\mathrm {max}_{})\). We write \(\mathbb {P}\) for the set of probabilistic polyhedra. The quantities \(\mathrm {s}^\mathrm {min}_{}\) and \( \mathrm {s}^\mathrm {max}_{}\) are lower and upper bounds on the number of support points in the concrete distribution(s) \(P_{}\) represents. A support point of a distribution is one which has non-zero probability. The quantities \(\mathrm {p}^\mathrm {min}_{} \) and \( \mathrm {p}^\mathrm {max}_{} \) are lower and upper bounds on the probability mass per support point. The \( \mathrm {m}^\mathrm {min}_{} \) and \( \mathrm {m}^\mathrm {max}_{} \) components give bounds on the total probability mass (i.e., the sum of the probabilities of all support points). Thus \(P_{}\) represents the set of distributions \(\gamma _{\mathbb {P}}(P_{})\) defined below.

We will write \( \textit{domain}(P_{}) \,\,{\mathop {=}\limits ^{\smash {\scriptscriptstyle \mathrm {def}}}}\,\, \textit{domain}(C) \) to denote the set of variables used in the probabilistic polyhedron.
Note the set \(\gamma _{\mathbb {P}}(P_{})\) is a singleton exactly when \(\mathrm {s}^\mathrm {min}_{} = \mathrm {s}^\mathrm {max}_{} = \#(C_{})\) and \(\mathrm {p}^\mathrm {min}_{} = \mathrm {p}^\mathrm {max}_{}\), and \(\mathrm {m}^\mathrm {min}_{} = \mathrm {m}^\mathrm {max}_{}\), where \(\#(C_{})\) denotes the number of discrete points in convex polyhedron \(C_{}\). In such a case \(\gamma _{\mathbb {P}}(P_{})\) contains only the uniform distribution where each state in \(\gamma _{\mathbb {C}}(C_{})\) has probability \(\mathrm {p}^\mathrm {min}_{}\). In general, however, the concretization of a probabilistic polyhedron will have an infinite number of distributions, with per-point probabilities varied somewhere in the range \( \mathrm {p}^\mathrm {min}_{} \) and \( \mathrm {p}^\mathrm {max}_{} \). Distributions represented by a probabilistic polyhedron are not necessarily normalized. In general, there is a relationship between \(\mathrm {p}^\mathrm {min}_{}, \mathrm {s}^\mathrm {min}_{}, \) and \(\mathrm {m}^\mathrm {min}_{}\), in that \(\mathrm {m}^\mathrm {min}_{} \ge \mathrm {p}^\mathrm {min}_{} \cdot \mathrm {s}^\mathrm {min}_{}\) (and \(\mathrm {m}^\mathrm {max}_{} \le \mathrm {p}^\mathrm {max}_{} \cdot \mathrm {s}^\mathrm {max}_{}\)), and the combination of the three can yield more information than any two in isolation.
The abstract semantics of \( S \) is written \(\langle \!\langle { S }\rangle \!\rangle \,{P} = P'\), and indicates that abstractly interpreting \( S \) where the distribution of input states are approximated by \(P\) will produce \(P'\), which approximates the distribution of output states. Following standard abstract interpretation terminology,  (sets of distributions) is the concrete domain, \(\mathbb {P}\) is the abstract domain, and
(sets of distributions) is the concrete domain, \(\mathbb {P}\) is the abstract domain, and  is the concretization function for \(\mathbb {P}\). We do not present the abstract semantics here; details can be found in Mardziel et al. [25]. Importantly, this abstract semantics is sound:
is the concretization function for \(\mathbb {P}\). We do not present the abstract semantics here; details can be found in Mardziel et al. [25]. Importantly, this abstract semantics is sound:
Theorem 1
(Soundness). For all \( S , P_1, P_2, \delta _1, \delta _2\), if \(\delta _1 \in \gamma _{\mathbb {P}}(P_1)\) and \(\langle \!\langle { S }\rangle \!\rangle \,{P_1} = P_2\), then \([\![{ S }]\!]{\delta _1} = \delta _2\) with \(\delta _2 \in \gamma _{\mathbb {P}}(P_2)\).
Proof
See Theorem 6 in Mardziel et al. [25].
Consider the example from Sect. 2.2. We assume the adversary has no prior information about the location of ship s. So, \(\delta _1\) above is simply the uniform distribution over all possible locations. The statement \( S \) is the query issued by the adversary, \(\textit{Nearby}(z,L_1,4) \vee \textit{Nearby}(z,L_2,4)\).Footnote 3 If we assume that the result of the query is  then the adversary learns that the location of s is within (Manhattan) distance 4 of \(L_1\) or \(L_2\). This posterior belief (\(\delta _2\)) is represented by the overlapping diamonds on the bottom-right of Fig. 3(b). The abstract interpretation produces a sound (interval) overapproximation (\(P_2\)) of the posterior belief. This is modeled by the rectangle which surrounds the overlapping diamonds. This rectangle is the “join” of two overlapping boxes, which each correspond to one of the \(\textit{Nearby}\) calls in the disjuncts of \( S \).
then the adversary learns that the location of s is within (Manhattan) distance 4 of \(L_1\) or \(L_2\). This posterior belief (\(\delta _2\)) is represented by the overlapping diamonds on the bottom-right of Fig. 3(b). The abstract interpretation produces a sound (interval) overapproximation (\(P_2\)) of the posterior belief. This is modeled by the rectangle which surrounds the overlapping diamonds. This rectangle is the “join” of two overlapping boxes, which each correspond to one of the \(\textit{Nearby}\) calls in the disjuncts of \( S \).
4 Computing Vulnerability: Basic Procedure
The key goal of this paper is to quantify the risk to secret information of running a query over that information. This section explains the basic approach by which we can use probabilistic polyhedra to compute vulnerability, i.e., the probability of the most probable point of the posterior distribution. Improvements on this basic approach are given in the next two sections.
Our convention will be to use \(C_{1}\), \(\mathrm {s}^\mathrm {min}_{1}\), \(\mathrm {s}^\mathrm {max}_{1}\), etc. for the components associated with probabilistic polyhedron \(P_{1}\). In the program \( S \) of interest, we assume that secret variables are in the set T, so input states are written \(\sigma _T\), and we assume there is a single output variable r. We assume that the adversary’s initial uncertainty about the possible values of the secrets T is captured by the probabilistic polyhedron \(P_0\) (such that \(\textit{domain}(P_0) \supseteq T\)).
Computing vulnerability occurs according to the following procedure.
-
1.
Perform abstract interpretation: \(\langle \!\langle { S }\rangle \!\rangle \,{P_0} = P\)
-
2.
Given a concrete output value of interest, o, perform abstract conditioning to define \(P_{r=o} \,\,{\mathop {=}\limits ^{\smash {\scriptscriptstyle \mathrm {def}}}}\,\, (P\wedge r\!=\!o)\).Footnote 4
The vulnerability V is the probability of the most likely state(s). When a probabilistic polyhedron represents one or more true distributions (i.e., the probabilities all sum to 1), the most probable state’s probability is bounded by \(\mathrm {p}^\mathrm {max}_{}\). However, the abstract semantics does not always normalize the probabilistic polyhedron as it computes, so we need to scale \(\mathrm {p}^\mathrm {max}_{}\) according to the total probability mass. To ensure that our estimate is on the safe side, we scale \(\mathrm {p}^\mathrm {max}_{}\) using the minimum probability mass: \(V = \frac{\mathrm {p}^\mathrm {max}_{}}{\mathrm {m}^\mathrm {min}_{}}\). In Fig. 3(b), the sound approximation in the top-right has \(V \le \frac{0.02}{0.55} = 0.036\) and the most precise approximation in the bottom-right has \(V \le \frac{0.02}{0.77} = 0.026\).
5 Improving Precision with Sampling
We can improve the precision of the basic procedure using sampling. First we introduce some notational convenience:
\(P_{T}\) is equivalent to step 2, above, but projected onto the set of secret variables T. \(P_{T+}\) is the improved (via sampling) polyhedron.
After computing \(P_T\) with the basic procedure from the previous section we take the following additional steps:
-
1.
Set counters \(\alpha \) and \(\beta \) to zero.
-
2.
Do the following N times (for some N, see below):
-
(a)
Randomly select an input state \(\sigma _T \in \gamma _{\mathbb {C}}(C_{T})\).
-
(b)
“Run” the program by computing \([\![{ S }]\!]{\dot{\sigma _T}} = \delta \). If there exists \(\sigma \in \textit{support}(\delta )\) with \(\sigma (r) = o\) then increment \(\alpha \), else increment \(\beta \).
-
(a)
-
3.
We can interpret \(\alpha \) and \(\beta \) as the parameters of a Beta distribution of the likelihood that an arbitrary state in \(\gamma _{\mathbb {C}}(C_{T})\) is in the support of the true distribution. From these parameters we can compute the credible interval \([p_L,p_U]\) within which is contained the true likelihood, with confidence \(\omega \) (where \(0 \le \omega \le 1\)). A credible interval is essentially a Bayesian analogue of a confidence interval and can be computed from the cumulative distribution function (CDF) of the Beta distribution (the 99% credible interval is the interval [a, b] such that the CDF at a has value 0.005 and the CDF at b has value 0.995). In general, obtaining a higher confidence or a narrower interval will require a higher N. Let result \(P_{T+} = P_T\) except that \(\mathrm {s}^\mathrm {min}_{T+} = p_L \cdot \#(C_{T})\) and \(\mathrm {s}^\mathrm {max}_{T+} = p_U \cdot \#(C_{T})\) (assuming these improve on \(\mathrm {s}^\mathrm {min}_{T}\) and \(\mathrm {s}^\mathrm {max}_{T}\)). We can then propagate these improvements to \(\mathrm {m}^\mathrm {min}_{}\) and \(\mathrm {m}^\mathrm {max}_{}\) by defining \(\mathrm {m}^\mathrm {min}_{T+} = \mathrm {p}^\mathrm {min}_{T} \cdot \mathrm {s}^\mathrm {min}_{T+}\) and \(\mathrm {m}^\mathrm {max}_{T+} = \mathrm {p}^\mathrm {max}_{T} \cdot \mathrm {s}^\mathrm {max}_{T+}\). Note that if \(\mathrm {m}^\mathrm {min}_{T} > \mathrm {m}^\mathrm {min}_{T+}\) we leave it unchanged, and do likewise if \(\mathrm {m}^\mathrm {max}_{T} < \mathrm {m}^\mathrm {max}_{T+}\).
At this point we can compute the vulnerability as in the basic procedure, but using \(P_{T+}\) instead of \(P_T\).
Consider the example of Sect. 2.2. In Fig. 3(b), we draw samples from the rectangle in the top-right. This rectangle overapproximates the set of locations where s might be, given that the query returned  . We sample locations from this rectangle and run the query on each sample. The green (red) dots indicate
. We sample locations from this rectangle and run the query on each sample. The green (red) dots indicate  (
( ) results, which are added to \(\alpha \) (\(\beta \)). After sampling \(N = 1000\) locations, we have \(\alpha = 570\) and \(\beta = 430\). Choosing \(\omega = .9\) (90%), we compute the credible interval [0.53, 0.60]. With \(\#(C_{T}) = 135\), we compute \([\mathrm {s}^\mathrm {min}_{T+},\mathrm {s}^\mathrm {max}_{T+}]\) as \([0.53 \cdot 135, 0.60 \cdot 135] = [72,81]\).
) results, which are added to \(\alpha \) (\(\beta \)). After sampling \(N = 1000\) locations, we have \(\alpha = 570\) and \(\beta = 430\). Choosing \(\omega = .9\) (90%), we compute the credible interval [0.53, 0.60]. With \(\#(C_{T}) = 135\), we compute \([\mathrm {s}^\mathrm {min}_{T+},\mathrm {s}^\mathrm {max}_{T+}]\) as \([0.53 \cdot 135, 0.60 \cdot 135] = [72,81]\).
There are several things to notice about this procedure. First, observe that in step 2b we “run” the program using the point distribution \(\dot{\sigma }\) as an input; in the case that \( S \) is deterministic (has no \(\mathsf {pif}\) statements) the output distribution will also be a point distribution. However, for programs with \(\mathsf {pif}\) statements there are multiple possible outputs depending on which branch is taken by a \(\mathsf {pif}\). We consider all of these outputs so that we can confidently determine whether the input state \(\sigma \) could ever cause \( S \) to produce result o. If so, then \(\sigma \) should be considered part of \(P_{T+}\). If not, then we can safely rule it out (i.e., it is part of the overapproximation).
Second, we only update the size parameters of \(P_{T+}\); we make no changes to \(\mathrm {p}^\mathrm {min}_{T+}\) and \(\mathrm {p}^\mathrm {max}_{T+}\). This is because our sampling procedure only determines whether it is possible for an input state to produce the expected output. The probability that an input state produces an output state is already captured (soundly) by \(p_T\) so we do not change that. This is useful because the approximation of \(p_T\) does not degrade with the use of the interval domain in the way the approximation of the size degrades (as illustrated in Fig. 3(b)). Using sampling is an attempt to regain the precision lost on the size component (only).
Finally, the confidence we have that sampling has accurately assessed which input states are in the support is orthogonal to the probability of any given state. In particular, \(P_T\) is an abstraction of a distribution \(\delta _T\), which is a mathematical object. Confidence \(\omega \) is a measure of how likely it is that our abstraction (or, at least, the size part of it) is accurate.
We prove (in our extended report [43]) that our sampling procedure is sound:
Theorem 2
(Sampling is Sound). If \(\delta _0 \in \gamma _{\mathbb {P}}(P_0)\), \(\langle \!\langle { S }\rangle \!\rangle \,{P_0} = P\), and \([\![{ S }]\!]{\delta _0} = \delta \) then \(\delta _{T} \in \gamma _{\mathbb {P}}(P_{T+}) \text { with confidence } \omega \) where
6 Improving Precision with Concolic Execution
Another approach to improving the precision of a probabilistic polyhedron \(P\) is to use concolic execution. The idea here is to “magnify” the impact of a single sample to soundly increase \(\mathrm {s}^\mathrm {min}_{}\) by considering its execution symbolically. More precisely, we concretely execute a program using a particular secret value, but maintain symbolic constraints about how that value is used. This is referred to as concolic execution [39]. We use the collected constraints to identify all points that would induce the same execution path, which we can include as part of \(\mathrm {s}^\mathrm {min}_{}\).
We begin by defining the semantics of concolic execution, and then show how it can be used to increase \(\mathrm {s}^\mathrm {min}_{}\) soundly.
6.1 (Probabilistic) Concolic Execution
Concolic execution is expressed as rewrite rules defining a judgment \(\langle {\varPi }, { S } \rangle \longrightarrow ^{p}_\pi \langle {\varPi '}, { S '} \rangle \). Here, \(\varPi \) is pair consisting of a concrete state \(\sigma \) and symbolic state \(\zeta \). The latter maps variables \(x \in \) Var to symbolic expressions \(\mathcal {E}\) which extend expressions E with symbolic variables \(\alpha \). This judgment indicates that under input state \(\varPi \) the statement \( S \) reduces to statement \( S '\) and output state \(\varPi '\) with probability p, with path condition \(\pi \). The path condition is a conjunction of boolean symbolic expressions \(\mathcal {B}\) (which are just boolean expressions \( B \) but altered to use symbolic expressions \(\mathcal {E}\) instead of expressions E) that record which branch is taken during execution. For brevity, we omit \(\pi \) in a rule when it is \(\mathsf {true}\).
The rules for the concolic semantics are given in Fig. 5. Most of these are standard, and deterministic (the probability annotation p is 1). Path conditions are recorded for \(\mathsf {if}\) and \(\mathsf {while}\), depending on the branch taken. The semantics of \(\mathsf {pif}\;{q}\;\mathsf {then}\;{ S _1}\;\mathsf {else}\;{ S _2}\) is non-deterministic: the result is that of \( S _1\) with probability q, and \( S _2\) with probability \(1 - q\). We write \(\zeta (B)\) to substitute free variables \(x \in B\) with their mapped-to values \(\zeta (x)\) and then simplify the result as much as possible. For example, if \(\zeta (x) = \alpha \) and \(\zeta (y) = 2\), then \(\zeta (x> y + 3) = \alpha > 5\). The same goes for \(\zeta (E)\).
We define a complete run of the concolic semantics with the judgment \(\langle {\varPi }, { S } \rangle \Downarrow ^p_{\pi } \varPi '\), which has two rules:
A complete run’s probability is thus the product of the probability of each individual step taken. The run’s path condition is the conjunction of the conditions of each step.
The path condition \(\pi \) for a complete run is a conjunction of the (symbolic) boolean guards evaluated during an execution. \(\pi \) can be converted to disjunctive normal form (DNF), and given the restrictions of the language the result is essentially a set of convex polyhedra over symbolic variables \(\alpha \).
6.2 Improving Precision
Using concolic execution, we can improve our estimate of the size of a probabilistic polyhedron as follows:
-
1.
Randomly select an input state \(\sigma _T \in \gamma _{\mathbb {C}}(C_{T})\) (recall that \(C_{T}\) is the polyhedron describing the possible valuations of secrets T).
-
2.
Set \(\varPi = (\sigma _T,\zeta _T)\) where \(\zeta _T\) maps each variable \(x \in T\) to a fresh symbolic variable \(\alpha _x\). Perform a complete concolic run \(\langle {\varPi }, { S } \rangle \Downarrow ^p_\pi (\sigma ',\zeta ')\). Make sure that \(\sigma '(r) = o\), i.e., the expected output. If not, select a new \(\sigma _T\) and retry. Give up after some number of failures N. For our example shown in Fig. 3(b), we might obtain a path condition \(|Loc(z).x - L_1.x| + |Loc(z).y - L_1.y| \le 4\) that captures the left diamond of the disjunctive query.
-
3.
After a successful concolic run, convert path condition \(\pi \) to DNF, where each conjunctive clause is a polyhedron \(C_{i}\). Also convert uses of disequality (\(\le \) and \(\ge \)) to be strict (< and >).
-
4.
Let \(C_{} = C_{T} \sqcap (\bigsqcup _i C_{i}\)); that is, it is the join of each of the polyhedra in \(DNF(\pi )\) “intersected” with the original constraints. This captures all of the points that could possibly lead to the observed outcome along the concolically executed path. Compute \(n = \#(C_{})\). Let \(P_{T+} = P_T\) except define \(\mathrm {s}^\mathrm {min}_{T+} = n\) if \(\mathrm {s}^\mathrm {min}_{T} < n\) and \(\mathrm {m}^\mathrm {min}_{T+} = \mathrm {p}^\mathrm {min}_{T} \cdot n\) if \(\mathrm {m}^\mathrm {min}_{T} < \mathrm {p}^\mathrm {min}_{T} \cdot n\). (Leave them as is, otherwise.) For our example, \(n = 41\), the size of the left diamond. We do not update \(\mathrm {s}^\mathrm {min}_{T}\) since \(41 < 55\), the probabilistic polyhedron’s lower bound (but see below).
Theorem 3
(Concolic Execution is Sound). If \(\delta _0 \in \gamma _{\mathbb {P}}(P_0)\), \(\langle \!\langle { S }\rangle \!\rangle \,{P_0} = P\), and \([\![{ S }]\!]{\delta _0} = \delta \) then \(\delta _{T} \in \gamma _{\mathbb {P}}(P_{T+}) \) where
The proof is in the extended technical report [43].
6.3 Combining Sampling with Concolic Execution
Sampling can be used to further augment the results of concolic execution. The key insight is that the presence of a sound under-approximation generated by the concolic execution means that it is unnecessary to sample from the under-approximating region. Here is the algorithm:
-
1.
Let \(C_{} = C_{0} \sqcap (\bigsqcup _i C_{i})\) be the under-approximating region.
-
2.
Perform sampling per the algorithm in Sect. 5, but with two changes:
-
if a sampled state
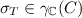 , ignore it
, ignore it -
When done sampling, compute \(\mathrm {s}^\mathrm {min}_{T+} = p_L \cdot (\#(C_{T}) - \#(C_{})) + \#(C_{})\) and \(\mathrm {s}^\mathrm {max}_{T+} = p_U \cdot (\#(C_{T}) - \#(C_{})) + \#(C_{})\). This differs from Sect. 5 in not including the count from concolic region \(C_{}\) in the computation. This is because, since we ignored samples \(\sigma _T \in \gamma _{\mathbb {C}}(C_{})\), the credible interval \([p_L,p_U]\) bounds the likelihood that any given point in \(C_{T} \setminus C_{}\) is in the support of the true distribution.
-
For our example, concolic execution indicated there are at least 41 points that satisfy the query. With this in hand, and using the same samples as shown in Sect. 5, we can refine \(s \in [74,80]\) and \(m \in [0.74,0.160]\) (the credible interval is formed over only those samples which satisfy the query but fall outside the under-approximation returned by concolic execution). We improve the vulnerability estimate to \(V \le \frac{0.02}{0.0.74} = 0.027\). These bounds (and vulnerability estimate) are better than those of sampling alone (\(s \in [72,81]\) with \(V \le 0.028\)).
The statement of soundness and its proof can be found in the extended technical report [43].
7 Implementation
We have implemented our approach as an extension of Mardziel et al. [25], which is written in OCaml. This baseline implements numeric domains \(C_{}\) via an OCaml interface to the Parma Polyhedra Library [4]. The counting procedure \(\#(C_{})\) is implemented by LattE [15]. Support for arbitrary precision and exact arithmetic (e.g., for manipulating \(\mathrm {m}^\mathrm {min}_{}\), \(\mathrm {p}^\mathrm {min}_{}\), etc.) is provided by the mlgmp OCaml interface to the GNU Multi Precision Arithmetic library. Rather than maintaining a single probabilistic polyhedron \(P\), the implementation maintains a powerset of polyhedra [3], i.e., a finite disjunction. Doing so results in a more precise handling of join points in the control flow, at a somewhat higher performance cost.
We have implemented our extensions to this baseline for the case that domain \(C_{}\) is the interval numeric domain [11]. Of course, the theory fully applies to any numeric abstract domain. We use Gibbs sampling, which we implemented ourselves. We delegate the calculation of the beta distribution and its corresponding credible interval to the ocephes OCaml library, which in turn uses the GNU Scientific Library. It is straightforward to lift the various operations we have described to the powerset domain. All of our code is available at https://github.com/GaloisInc/TAMBA.
8 Experiments
To evaluate the benefits of our techniques, we applied them to queries based on the evacuation problem outlined in Sect. 2. We found that while the baseline technique can yield precise answers when computing vulnerability, our new techniques can achieve close to the same level of precision far more efficiently.
8.1 Experimental Setup
For our experiments we analyzed queries similar to \( Nearby (s,l,d)\) from Fig. 2. We generalize the Nearby query to accept a set of locations L—the query returns true if s is within d units of any one of the islands having location \(l \in L\). In our experiments we fix \(d = 100\). We consider the secrecy of the location of s, \( Location (s)\). We also analyze the execution of the resource allocation algorithm of Fig. 2 directly; we discuss this in Sect. 8.3.
We measure the time it takes to compute the vulnerability (i.e., the probability of the most probable point) following each query. In our experiments, we consider a single ship s and set its coordinates so that it is always in range of some island in L, so that the concrete query result returns  (i.e. \( Nearby (s, L, 100) = true\)). We measure the vulnerability following this query result starting from a prior belief that the coordinates of s are uniformly distributed with \(0 \le \mathrm {Location}(s).x \le 1000\) and \(0 \le \mathrm {Location}(s).y \le 1000\).
(i.e. \( Nearby (s, L, 100) = true\)). We measure the vulnerability following this query result starting from a prior belief that the coordinates of s are uniformly distributed with \(0 \le \mathrm {Location}(s).x \le 1000\) and \(0 \le \mathrm {Location}(s).y \le 1000\).
In our experiments, we varied several experimental parameters: analysis method (either P, I, CE, S, or CE+S), query complexity c; AI precision level p; and number of samples n. We describe each in turn.
Analysis Method. We compared five techniques for computing vulnerability:
- P::
-
Abstract interpretation (AI) with convex polyhedra for domain \(C_{}\) (Sect. 4),
- I::
-
AI with intervals for \(C_{}\) (Sect. 4),
- S::
-
AI with intervals augmented with sampling (Sect. 5),
- CE::
-
AI with intervals augmented with concolic execution (Sect. 6), and
- CE+S::
-
AI with intervals augmented with both techniques (Sect. 6.3)
The first two techniques are due to Mardziel et al. [25], where the former uses convex polyhedra and the latter uses intervals (aka boxes) for the underlying polygons. In our experiments we tend to focus on P since I’s precision is unacceptably poor (e.g., often vulnerability = 1).
Query Complexity. We consider queries with different L; we say we are increasing the complexity of the query as L gets larger. Let \(c = |L|\); we consider \(1 \le c \le 5\), where larger L include the same locations as smaller ones. We set each location to be at least \(2 \cdot d\) Manhattan distance units away from any other island (so diamonds like those in Fig. 3(a) never overlap).
Precision. The precision parameter p bounds the size of the powerset abstract domain at all points during abstract interpretation. This has the effect of forcing joins when the powerset grows larger than the specified precision. As p grows larger, the results of abstract interpretation are likely to become more precise (i.e. vulnerability gets closer to the true value). We considered p values of 1, 2, 4, 8, 16, 32, and 64.
Samples Taken. For the latter three analysis methods, we varied the number of samples taken n. For analysis CE, n is interpreted as the number of samples to try per polyhedron before giving up trying to find a “valid sample.”Footnote 5 For analysis S, n is the number of samples, distributed proportionally across all the polyhedra in the powerset. For analysis CE+S, n is the combination of the two. We considered sample size values of \(1,000 - 50,000\) in increments of 1, 000. We always compute an interval with \(\omega \) = 99.9% confidence (which will be wider when fewer samples are used).
System Description. We ran experiments varying all possible parameters. For each run, we measured the total execution time (wall clock) in seconds to analyze the query and compute vulnerability. All experiments were carried out on a MacBook Air with OSX version 10.11.6, a 1.7 GHz Intel Core i7, and 8 GB of RAM. We ran a single trial for each configuration of parameters. Only wall-clock time varies across trials; informally, we observed time variations to be small.
8.2 Results
Figure 6(a)–(c) measure vulnerability (y-axis) as a function of time (x-axis) for each analysis.Footnote 6 These three figures characterize three interesting “zones” in the space of complexity and precision. The results for method I are not shown in any of the figures. This is because I always produces a vulnerability of 1. The refinement methods (CE, S, and CE+S) are all over the interval domain, and should be considered as “improving” the vulnerability of I.
In Fig. 6(a) we fix \(c = 1\) and \(p = 1\). In this configuration, baseline analysis P can compute the true vulnerability in \(\sim \!0.95\) s. Analysis CE is also able to compute the true vulnerability, but in \(\sim \!0.19\) s. Analysis S is able to compute a vulnerability to within \(\sim \!5 \cdot e^{-6}\) of optimal in \(\sim \!0.15\) s. These data points support two key observations. First, even a very modest number of samples improves vulnerability significantly over just analyzing with intervals. Second, concolic execution is only slightly slower and can achieve the optimal vulnerability. Of course, concolic execution is not a panacea. As we will see, a feature of this configuration is that no joins take place during abstract interpretation. This is critical to the precision of the concolic execution.
In Fig. 6(b) we fix \(c = 2\) and \(p = 4\). In contrast to the configuration of Fig. 6(a), the values for c and p in this configuration are not sufficient to prevent all joins during abstract interpretation. This has the effect of taking polygons that represent individual paths through the program and joining them into a single polygon representing many paths. We can see that this is the case because baseline analysis P is now achieving a better vulnerability than CE. However, one pattern from the previous configuration persists: all three refinement methods (CE, S, CE+S) can achieve vulnerability within \(\sim \!1 \cdot e^{-5}\) of P, but in \(\frac{1}{4}\) the time. In contrast to the previous configuration, analysis CE+S is now able to make a modest improvement over CE (since it does not achieve the optimal).
In Fig. 6(c) we fix \(c = 5\) and \(p = 32\). This configuration magnifies the effects we saw in Fig. 6(b). Similarly, in this configuration there are joins happening, but the query is much more complex and the analysis is much more precise. In this figure, we label the X axis as a log scale over time. This is because analysis P took over two minutes to complete, in contrast to the longest-running refinement method, which took less than 6 seconds. The relationship between the refinement analyses is similar to the previous configuration. The key observation here is that, again, all three refinement analyses achieve within \(\sim \!3 \cdot e^{-5}\) of P, but this time in \(4\%\) of the time (as opposed to \(\frac{1}{4}\) in the previous configuration).
Figure 6(d) makes more explicit the relationship between refinements (CE, S, CE+S) and P. We fix \(n = 50,000\) (the maximum) here, and \(p = 64\) (the maximum). We can see that as query complexity goes up, P gets exponentially slower, while CE, S, and CE+S slow at a much lower rate, while retaining (per the previous graphs) similar precision.
8.3 Evacuation Problem
We conclude this section by briefly discussing an analysis of an execution of the resource allocation algorithm of Fig. 2. In our experiment, we set the number of ships to be three, where two were in range \(d=300\) of the evacuation site, and their sum-total berths (500) were sufficient to satisfy demand at the site (also 500). For our analysis refinements we set \(n=1000\). Running the algorithm, a total of seven pairs of Nearby and Capacity queries were issued. In the end, the algorithm selects two ships to handle the evacuation.
Table 1 shows the time to execute the algorithm using the different analysis methods, along with the computed vulnerability—this latter number represents the coordinator’s view of the most likely nine-tuple of the private data of the three ships involved (x coordinate, y coordinate, and capacity for each). We can see that, as expected, our refinement analyses are far more efficient than baseline P, and far more precise than baseline I. The CE methods are precise but slower than S. This is because of the need to count the number of points in the DNF of the concolic path conditions, which is expensive.
Discussion. The queries considered in Fig. 6 have two features that contribute to the effectiveness of our refinement methods. First, they are defined over large domains, but return  for only a small subset of those values. For larger subsets of values, the benefits of sampling may degrade, though concolic execution should still provide an improvement. Further experiments are needed to explore such scenarios. Second, the example in Fig. 6 contains short but complex queries. A result of this query structure is that abstract interpretation with polyhedra is expensive but sampling can be performed efficiently. The evacuation problem results in Table 1 provide some evidence that the benefits of our techniques also apply to longer queries. However it may still be possible to construct queries where the gap in runtime between polyhedral analysis and sampling is smaller, in which case sampling would provide less improvement.
for only a small subset of those values. For larger subsets of values, the benefits of sampling may degrade, though concolic execution should still provide an improvement. Further experiments are needed to explore such scenarios. Second, the example in Fig. 6 contains short but complex queries. A result of this query structure is that abstract interpretation with polyhedra is expensive but sampling can be performed efficiently. The evacuation problem results in Table 1 provide some evidence that the benefits of our techniques also apply to longer queries. However it may still be possible to construct queries where the gap in runtime between polyhedral analysis and sampling is smaller, in which case sampling would provide less improvement.
9 Related Work
Quantifying Information Flow. There is a rich research literature on techniques that aim to quantify information that a program may release, or has released, and then use that quantification as a basis for policy. One question is what measure of information release should be used. Past work largely considers information theoretic measures, including Bayes vulnerability [41] and Bayes risk [8], Shannon entropy [40], and guessing entropy [26]. The g-vulnerability framework [1] was recently introduced to express measures having richer operational interpretations, and subsumes other measures.
Our work focuses on Bayes Vulnerability, which is related to min-entropy. Vulnerability is appealing operationally: As Smith [41] explains, it estimates the risk of the secret being guessed in one try. While challenging to compute, this approach provides meaningful results for non-uniform priors. Work that has focused on other, easier-to-compute metrics, such as Shannon entropy and channel capacity, require deterministic programs and priors that conform to uniform distributions [2, 22, 23, 27, 32]. The work of Klebanov [20] supports computation of both Shannon entropy and min-entropy over deterministic programs with non-uniform priors. The work takes a symbolic execution and program specification approach to QIF. Our use of concolic execution for counting polyhedral constraints is similar to that of Klebanov. However, our language supports probabilistic choice and in addition to concolic execution we also provide a sampling technique and a sound composition. Like Mardziel et al. [25], we are able to compute the worst-case vulnerability, i.e., due to a particular output, rather than a static estimate, i.e., as an expectation over all possible outputs. Köpf and Basin [21] originally proposed this idea, and Mardziel et al. were the first to implement it, followed by several others [6, 19, 24].
Köpf and Rybalchenko [22] (KR) also use sampling and concolic execution to statically quantify information leakage. But their approach is quite different from ours. KR uses sampling of a query’s inputs in lieu of considering (as we do) all possible outputs, and uses concolic execution with each sample to ultimately compute Shannon entropy, by underapproximation, within a confidence interval. This approach benefits from not having to enumerate outputs, but also requires expensive model counting for each sample. By contrast, we use sampling and concolic execution from the posterior computed by abstract interpretation, using the results to boost the lower bound on the size/probability mass of the abstraction. Our use of sampling is especially efficient, and the use of concolic execution is completely sound (i.e., it retains 100% confidence in the result). As with the above work, KR requires deterministic programs and uniform priors.
Probabilistic Programming Langauges. A probabilistic program is essentially a lifting of a normal program operating on single values to a program operating on distributions of values. As a result, the program represents a joint distribution over its variables [18]. As discussed in this paper, quantifying the information released by a query can be done by writing the query in a probabilistic programming language (PPL) and representing the uncertain secret inputs as distributions. Quantifying release generally corresponds to either the maximum likelihood estimation (MLE) problem or the maximum a-posteriori probability (MAP) problem. Not all PPLs support computation of MLE and MAP, but several do.
PPLs based on partial sampling [17, 34] or full enumeration [37] of the state space are unsuitable in our setting: they are either too inefficient or too imprecise. PPLs based on algebraic decision diagrams [9], graphical models [28], and factor graphs [7, 30, 36] translate programs into convenient structures and take advantage of efficient algorithms for their manipulation or inference, in some cases supporting MAP or MLE queries (e.g. [33, 35]). PSI [16] supports exact inference via computation of precise symbolic representations of posterior distributions, and has been used for dynamic policy enforcement [24]. Guarnieri et al. [19] use probabilistic logic programming as the basis for inference; it scales well but only for a class of queries with certain structural limits, and which do not involve numeric relationships.
Our implementation for probabilistic computation and inference differs from the above work in two main ways. Firstly, we are capable of sound approximation and hence can trade off precision for performance, while maintaining soundness in terms of a strong security policy. Even when using sampling, we are able to provide precise confidence measures. The second difference is our compositional representation of probability distributions, which is based on numerical abstractions: intervals [11], octagons [29], and polyhedra [13]. The posterior can be easily used as the prior for the next query, whereas prior work would have to repeatedly analyze the composition of past queries.
A few other works have also focused on abstract interpretation, or related techniques, for reasoning about probabilistic programs. Monniaux [31] defines an abstract domain for distributions. Smith [42] describes probabilistic abstract interpretation for verification of quantitative program properties. Cousot [14] unifies these and other probabilistic program analysis tools. However, these do not deal with sound distribution conditioning, which is crucial for belief-based information flow analysis. Work by Sankaranarayanan et al. [38] uses a combination of techniques from program analysis to reason about distributions (including abstract interpretation), but the representation does not support efficient retrieval of the maximal probability, needed to compute vulnerability.
10 Conclusions
Quantitative information flow is concerned with measuring the knowledge about secret data that is gained by observing the answer to a query. This paper has presented a combination of static analysis using probabilistic abstract interpretation, sampling, and underapproximation via concolic execution to compute high-confidence upper bounds on information flow. Preliminary experimental results are promising and suggest that this approach can operate more precisely and efficiently than abstract interpretation alone. As next steps, we plan to evaluate the technique more rigorously – including on programs with probabilistic choice. We also plan to integrate static analysis and sampling more closely so as to avoid precision loss at decision points in programs. We also look to extend programs to be able to store random choices in variables, to thereby implement more advanced probabilistic structures.
Notes
- 1.
We give latitude and longitude values as integer representations of decimal degrees fixed to four decimal places; e.g., 14.3579 decimal degrees is encoded as 143579.
- 2.
Relaxing such limitations is possible—e.g., polynominal inequalities can be approximated using convex polyhedra [5]—but doing so precisely and scalably is a challenge.
- 3.
Appendix A shows the code, which computes Manhattan distance between s and \(L_1\) and \(L_2\) and then sets an output variable if either distance is within four units.
- 4.
We write \(P\wedge B\) and not \(P\mid B\) because \(P\) need not be normalized.
- 5.
This is the N parameter from Sect. 6.
- 6.
These are best viewed on a color display.
References
Alvim, M.S., Chatzikokolakis, K., Palamidessi, C., Smith, G.: Measuring information leakage using generalized gain functions. In: Proceedings of the IEEE Computer Security Foundations Symposium (CSF) (2012)
Backes, M., Köpf, B., Rybalchenko, A.: Automatic discovery and quantification of information leaks. In: Proceedings of the IEEE Symposium on Security and Privacy (S&P) (2009)
Bagnara, R., Hill, P.M., Zaffanella, E.: Widening operators for powerset domains. Int. J. Softw. Tools Tech. Transf. 8(4), 449–466 (2006)
Bagnara, R., Hill, P.M., Zaffanella, E.: The Parma polyhedra library: toward a complete set of numerical abstractions for the analysis and verification of hardware and software systems. Sci. Comput. Program. 72, 3–21 (2008)
Bagnara, R., Rodríguez-Carbonell, E., Zaffanella, E.: Generation of basic semi-algebraic invariants using convex polyhedra. In: Hankin, C., Siveroni, I. (eds.) SAS 2005. LNCS, vol. 3672, pp. 19–34. Springer, Heidelberg (2005). https://doi.org/10.1007/11547662_4
Besson, F., Bielova, N., Jensen, T.: Browser randomisation against fingerprinting: a quantitative information flow approach. In: Bernsmed, K., Fischer-Hübner, S. (eds.) NordSec 2014. LNCS, vol. 8788, pp. 181–196. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11599-3_11
Borgström, J., Gordon, A.D., Greenberg, M., Margetson, J., Van Gael, J.: Measure transformer semantics for Bayesian machine learning. In: Barthe, G. (ed.) ESOP 2011. LNCS, vol. 6602, pp. 77–96. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19718-5_5
Chatzikokolakis, K., Palamidessi, C., Panangaden, P.: On the Bayes risk in information-hiding protocols. J. Comput. Secur. 16(5), 531–571 (2008)
Claret, G., Rajamani, S.K., Nori, A.V., Gordon, A.D., Borgstroem, J.: Bayesian inference for probabilistic programs via symbolic execution. Technical report MSR-TR-2012-86. Microsoft Research (2012)
Clarkson, M.R., Myers, A.C., Schneider, F.B.: Quantifying information flow with beliefs. J. Comput. Secur. 17(5), 655–701 (2009)
Cousot, P., Cousot, R.: Static determination of dynamic properties of programs. In: Proceedings of the Second International Symposium on Programming (1976)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Proceedings of the ACM SIGPLAN Conference on Principles of Programming Languages (POPL) (1977)
Cousot, P., Halbwachs, N.: Automatic discovery of linear restraints among variables of a program. In: POPL (1978)
Cousot, P., Monerau, M.: Probabilistic abstract interpretation. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 169–193. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_9
De Loera, J.A., Haws, D., Hemmecke, R., Huggins, P., Tauzer, J., Yoshida, R.: LattE (2008). https://www.math.ucdavis.edu/~latte/
Gehr, T., Misailovic, S., Vechev, M.: PSI: exact symbolic inference for probabilistic programs. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 62–83. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_4
Goodman, N.D., Mansinghka, V.K., Roy, D.M., Bonawitz, K., Tenenbaum, J.B.: Church: a language for generative models. In: Proceedings of the Conference on Uncertainty in Artificial Intelligence (UAI) (2008)
Gordon, A.D., Henzinger, T.A., Nori, A.V., Rajamani, S.K.: Probabilistic programming. In: Conference on the Future of Software Engineering, FOSE 2014, pp. 167–181. ACM, New York (2014)
Guarnieri, M., Marinovic, S., Basin, D.: Securing databases from probabilistic inference. In: Proceedings of IEEE Computer Security Foundations Symposium (CSF) (2017)
Klebanov, V.: Precise quantitative information flow analysis—a symbolic approach. Theor. Comput. Sci. 538, 124–139 (2014)
Köpf, B., Basin, D.: An information-theoretic model for adaptive side-channel attacks. In: Proceedings of the ACM Conference on Computer and Communications Security (CCS) (2007)
Köpf, B., Rybalchenko, A.: Approximation and randomization for quantitative information-flow analysis. In: Proceedings of the IEEE Computer Security Foundations Symposium (CSF) (2010)
Köpf, B., Rybalchenko, A.: Automation of quantitative information-flow analysis. In: Bernardo, M., de Vink, E., Di Pierro, A., Wiklicky, H. (eds.) SFM 2013. LNCS, vol. 7938, pp. 1–28. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38874-3_1
Kučera, M., Tsankov, P., Gehr, T., Guarnieri, M., Vechev, M.: Synthesis of probabilistic privacy enforcement. In: Proceedings of the ACM Conference on Computer and Communications Security (CCS) (2017)
Mardziel, P., Magill, S., Hicks, M., Srivatsa, M.: Dynamic enforcement of knowledge-based security policies using probabilistic abstract interpretation. J. Comput. Secur. 21, 463–532 (2013)
Massey, J.L.: Guessing and entropy. In: Proceedings of IEEE International Symposium on Information Theory (ISIT) (1994)
McCamant, S., Ernst, M.D.: Quantitative information flow as network flow capacity. In: Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI) (2008)
Milch, B., Marthi, B., Russell, S., Sontag, D., Ong, D.L., Kolobov, A.: Blog: probabilistic models with unknown objects. In: Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI) (2005)
Miné, A.: The octagon abstract domain. In: Proceedings of the Working Conference on Reverse Engineering (WCRE) (2001)
Minka, T., Winn, J., Guiver, J., Webster, S., Zaykov, Y., Yangel, B., Spengler, A., Bronskill, J.: Infer.NET 2.6. Microsoft Research, Cambridge (2014). http://research.microsoft.com/infernet
Monniaux, D.: Analyse de programmes probabilistes par interprétation abstraite. Thése de doctorat, Université Paris IX Dauphine (2001)
Mu, C., Clark, D.: An interval-based abstraction for quantifying information flow. Electron. Notes Theor. Comput. Sci. 253(3), 119–141 (2009)
Narayanan, P., Carette, J., Romano, W., Shan, C., Zinkov, R.: Probabilistic inference by program transformation in Hakaru (system description). In: Kiselyov, O., King, A. (eds.) FLOPS 2016. LNCS, vol. 9613, pp. 62–79. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29604-3_5
Park, S., Pfenning, F., Thrun, S.: A probabilistic language based on sampling functions. ACM Trans. Program. Lang. Syst. (TOPLAS) 31(1), 4:1–4:46 (2008)
Pfeffer, A.: Figaro: an object-oriented probabilistic programming language. Technical report. Charles River Analytics (2000)
Pfeffer, A.: The design and implementation of IBAL: a general-purpose probabilistic language. In: Getoor, L., Taskar, B. (eds.) Statistical Relational Learning. MIT Press, Cambridge (2007)
Radul, A.: Report on the probabilistic language scheme. In: Proceedings of the Dynamic Languages Symposium (DLS) (2007)
Sankaranarayanan, S., Chakarov, A., Gulwani, S.: Static analysis for probabilistic programs: inferring whole program properties from finitely many paths. In: Conference on Programming Language Design and Implementation, PLDI (2013)
Sen, K., Marinov, D., Agha, G.: CUTE: a concolic unit testing engine for C. In: ESEC/FSE (2005)
Shannon, C.: A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948)
Smith, G.: On the foundations of quantitative information flow. In: de Alfaro, L. (ed.) FoSSaCS 2009. LNCS, vol. 5504, pp. 288–302. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00596-1_21
Smith, M.J.A.: Probabilistic abstract interpretation of imperative programs using truncated normal distributions. Electron. Notes Theor. Comput. Sci. 220, 43–59 (2008)
Sweet, I., Trilla, J.M.C., Scherrer, C., Hicks, M., Magill, S.: What’s the over/under? probabilistic bounds on information leakage. CoRR abs/1802.08234, February 2018. https://arxiv.org/abs/1802.08234
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Query Code
The following is the query code of the example developed in Sect. 2.2. Here,  and
and  represent a ship’s secret location. The variables
represent a ship’s secret location. The variables  and
and  are inputs to the query. The first pair represents position \(L_1\), the second pair represents the position \(L_2\), and the last is the distance threshold, set to 4. We assume for the example that \(L_1\) and \(L_2\) have the same y coordinate, and their x coordinates differ by 6 units.
are inputs to the query. The first pair represents position \(L_1\), the second pair represents the position \(L_2\), and the last is the distance threshold, set to 4. We assume for the example that \(L_1\) and \(L_2\) have the same y coordinate, and their x coordinates differ by 6 units.
We express the query in the language of Fig. 4 basically as follows:

The variable  is the result of the query. We simplify the code by assuming the absolute value function is built-in; we can implement this with a simple conditional. We run this query probabilistically under the assumption that
is the result of the query. We simplify the code by assuming the absolute value function is built-in; we can implement this with a simple conditional. We run this query probabilistically under the assumption that  and
and  are uniformly distributed within the range given in Fig. 1. We then condition the output on the assumption that
are uniformly distributed within the range given in Fig. 1. We then condition the output on the assumption that  . When using intervals as the baseline of probabilistic polyhedra, this produces the result given in the upper right of Fig. 3(b); when using convex polyhedra, the result is shown in the lower right of the figure. The use of sampling and concolic execution to augment the former is shown via arrows between the two.
. When using intervals as the baseline of probabilistic polyhedra, this produces the result given in the upper right of Fig. 3(b); when using convex polyhedra, the result is shown in the lower right of the figure. The use of sampling and concolic execution to augment the former is shown via arrows between the two.
B Formal Semantics
Here we defined the probabilistic semantics for the programming language given in Fig. 4. The semantics of statement \( S \), written \([\![{ S }]\!]{}\), is a function of the form Dist \(\rightarrow \) Dist, i.e., it is a function from distributions of states to distributions of states. We write \([\![{ S }]\!]{\delta } = \delta '\) to say that the semantics of \( S \) maps input distribution \(\delta \) to output distribution \(\delta '\).
Figure 7 gives this denotational semantics along with definitions of relevant auxiliary operations. We write \([\![{E}]\!]{\sigma }\) to denote the (integer) result of evaluating expression E in \(\sigma \), and \([\![{B}]\!]{\sigma }\) to denote the truth or falsehood of B in \(\sigma \). The variables of a state \(\sigma \), written \(\textit{domain}(\sigma )\), is defined by \(\textit{domain}(\sigma )\); sometimes we will refer to this set as just the domain of \(\sigma \). We will also use the this notation for distributions; \(\textit{domain}(\delta )\,\,{\mathop {=}\limits ^{\smash {\scriptscriptstyle \mathrm {def}}}}\,\,\textit{domain}(\textit{domain}(\delta ))\). We write \(\mathrm {lfp}\) as the least fixed-point operator. The notation \(\sum _{x \;:\;\phi } \rho \) can be read \(\rho \) is the sum over all x such that formula \(\phi \) is satisfied (where x is bound in \(\rho \) and \(\phi \)).
This semantics is standard. See Clarkson et al. [10] or Mardziel et al. [25] for detailed explanations.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Sweet, I., Trilla, J.M.C., Scherrer, C., Hicks, M., Magill, S. (2018). What’s the Over/Under? Probabilistic Bounds on Information Leakage. In: Bauer, L., Küsters, R. (eds) Principles of Security and Trust. POST 2018. Lecture Notes in Computer Science(), vol 10804. Springer, Cham. https://doi.org/10.1007/978-3-319-89722-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-89722-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89721-9
Online ISBN: 978-3-319-89722-6
eBook Packages: Computer ScienceComputer Science (R0)










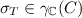 , ignore it
, ignore it
