Wealth, Savings and Children Among Swiss, German and Australian Families

Abstract

Although sociologists pay increasing attention to wealth, we know very little about the relationship between children and wealth accumulation. Using the information on wealth from panel surveys (the Swiss Household Panel, the Household of Income and Labour Dynamics in Australia and the German Socio-Economic Panel), we study families’ wealth accumulation in different social and political settings. This contribution tests how children affect the propensity to save and net worth. It also addresses anticipation effects when individuals plan to have a child. The results from fixed effects models show that dependent children reduce the probability to save, whereas planning for a child increases the probability to save. To test whether lower or higher expenditure is responsible for lower saving probability, we estimate models with earned income and labour supply as mediator variables. Small children are found to reduce saving mostly through income losses, and older children reduce saving through higher expenditures. In the long run, children have moderate negative consequences on wealth accumulation in all countries (6714 CHF per grown-up child in Switzerland, 15,462 AU$ in Australia, and 619 EUR in Germany).

Keywords

Introduction

The accumulation of wealth is an important aspect when evaluating the economic situation of families. For many years, the lack of wealth information in survey data in general, particularly longitudinal data, has restrained the research on this topic. Recent demographic changes such as delays in fertility and population ageing, rising female labour force participation and insecure future retirement pensions make the relationship between children and wealth accumulation a particularly relevant topic.

The overall effect of children on net worth is ambiguous because children may influence parents’ wealth accumulation through different paths. On the one hand, parents might save more for their financial protection, in anticipation of future income losses, or out of a bequest motive. On the other hand, children might bring higher expenses and lower income (e.g., through reduced labour force participation) and, therefore, reduce the capacity to save. To the best of our knowledge, the link between children and wealth has never been specifically investigated in a comparative perspective. A comparative study using panel data will therefore provide useful insights about the ability of families to save in different settings.

In this contribution, we analyse data from the Swiss Household Panel (SHP), the German Socio-Economic Panel (SOEP) and the Australian Household, Income and Labour Dynamics (HILDA) Survey. We chose these databases because of their panel structure. Germany has been selected as another continental European country, and both Germany and Australia act as references because of previous literature on the link between children and wealth in these countries.

Our empirical strategy has the following three aims: first, we establish the effect of children on net worth and saving behaviour. Second, we disentangle the effects of income changes from consumption changes by controlling for earned income and labour supply. Third, we use a comparative perspective to indicate whether results are general or country specific.

This chapter is organised as follows. We first provide a brief literature review on the theoretical and the empirical relationships between children and wealth. We then continue with the description of the data, the sample and the methodology. The results are presented separately for short-term effects and long-term effects. The conclusion summarises our findings and points to possible further research.

The Role of Children in Wealth Accumulation

There are different potential effects of children on wealth. Among the motives for wealth accumulation (Keynes 1936; Browning and Lusardi 1996), several might be reinforced through the presence of children. First, parents might save more to protect themselves and their children from financial risks. Second, future parents might save more before the arrival of a child in anticipation of future income losses (e.g., due to reduced labour force participation) or higher expenses. Third, the accumulation of capital necessary to buy houses, cars or other durable goods and finally the bequest motive might be more important for fathers and mothers than for childless individuals.

The increased incentives for wealth accumulation are paired with income losses and higher expenses for children (e.g., for food, accommodation, child-care, education or insurances) (Bradbury 2014). This aspect is also considered in the life-cycle model of Modigliani and Brumberg (1954), which assumes that people choose to maintain stable lifestyles. In its simplest form, people are expected to save during their mature active life and to dissave when young and during retirement. An addition to this theory highlights that the presence of children reduces current savings and the future level of accumulated net worth (Modigliani 1986).¹ Dockery and Bawa (2015) question the expenditure part of this framework and claim that expenditures for children might substitute other expenditures. For example, instead of long distance travels to exotic destinations or visits to fancy restaurants, parents engage in inexpensive activities such as walks in the park, nights at home or visits to close relatives. In addition to this, home production might also increase if activities such as cooking, gardening and do-it-yourself become more frequent. Lower expenses in other areas might therefore compensate the additional expenses resulting from having children. Furthermore, the impact of children on wealth accumulation also depends on institutional characteristics, such as child allowances, availability and costs of child-care, the tax system, special programmes targeting children and other programmes of this type (Grinstein-Weiss et al. 2006).

A final point to mention is the potential endogeneity of the relationship between fertility and wealth. Debt and financial instability have been shown to delay marriage (Addo 2014) and are therefore likely to delay or cancel the decision to have children. We know from Dockery and Bawa (2015) that fertility in Australia is inversely related to income, but we do not know its relationship with wealth.

Previous Findings on the Effect of Children on Wealth and Savings

The few studies on the subject focused mainly on Anglo-Saxon countries and show a weak negative effect of children on wealth. Scholz and Seshadri (2009) found that each additional child reduces the average net wealth of US-American families by $6384. In Australia, a recent study estimated that each dependent child reduces couples’ wealth by approximately $2000 per year (Dockery and Bawa 2015). Contrary to this, the presence of children benefits savings in the long-run. A simulation study by Love (2010) using the Panel Study of Income Dynamics in the USA indicates that households with children accumulate substantially less wealth during the working years, but, probably out of a bequest motive, save more during retirement and end with more savings than households that have never had children. The effects might be different for some family types, particularly for single parents (Austen et al. 2014). Controlling for other factors, the results from Switzerland indicate that single mothers have 17,890 CHF less in non-housing wealth than childless single women (Ravazzini and Chesters 2018). This difference is large, but single mothers are not representative of the overall population and constitute a particularly disadvantaged and vulnerable group (Grinstein-Weiss et al. 2008). In Germany, having children under five years old was found to have a negative, but insignificant, impact on net worth (Sierminska et al. 2010). A recent study found that parenthood is associated with lower wealth accumulation for women but not for men. This effect can be explained by discontinuous employment experiences (Lersch et al. 2017). Additionally, for Germany, Rottke and Klos (2016) found that overall household consumption drops after a child moves out of the household, but at the same time, adult-equivalent consumption significantly increases. After all children are gone, parents are found to upgrade their personal lifestyle to a level approximately equal to childless peers and save only a small proportion of their resources. Therefore, the saving behaviour in Germany seems quite different from that in America, where savings increase when children leave the households.

Data and Sample

Our analysis is based on three Household Panels of the Cross National Equivalent File (CNEF), namely, the Swiss Household Panel (SHP), the German Socio-Economic Panel (SOEP) and the Household, Income and Labour Dynamics Survey in Australia (HILDA). The main advantage of these databases is that they provide a longitudinal perspective following the same households over time. A disadvantage for an analysis on wealth with survey data is that people at the top – and in some cases at the bottom – of the distribution are underrepresented. To at least partially correct for this problem, the SOEP oversamples high-income households by including a high-income sample since 2002. In the HILDA, wealth variables are top-coded using an average value for all the cases that exceed a given threshold. We decide not to top-code wealth in the SHP and in the SOEP because this would present a loss of information.

There are some important differences between surveys regarding the main variables of interest. The HILDA and the SHP collect wealth at the household level, whereas household wealth in the SOEP is aggregated from information at the individual level. In contrast to the HILDA and the SOEP, which contain detailed information on different assets,² the SHP provides only basic information about wealth and does not include negative wealth. More specifically, the SHP distinguishes only between family home wealth and other wealth. In terms of frequency of data collection, the Australian panel offers wealth information for four time points (2002, 2006, 2010 and 2014) and the German panel for three (2002, 2007 and 2012). Currently, a longitudinal analysis on wealth is not possible with the SHP because information about wealth has been collected only in 2012. More information about the quality of the wealth variables in the Swiss panel can be found in Kuhn and Crettaz (2015).

Our analytic sample consists of single adult and couple households with and without children. Other household types have been excluded because, with the exception of the SOEP, we do not know how income and wealth are pooled inside the household.

In addition to wealth variables, the three panel surveys collect information on saving behaviour. The SHP contains a yearly categorical variable at the household level (household can save, household spends what it earns, households eats into wealth, household goes into debt). A similar variable is present in the HILDA in 9 waves of 14, but the question is asked at the individual level. We therefore consider the information given by the main earner of each couple but also comment on findings including the partner’s saving behaviours. In two waves, the HILDA additionally provides the reasons why people save. Among these reasons,³ there are two specific answers on descendants (Education for children or grandchildren, To help children or other relatives) and three possible answers about home-related expenditures (Pay off mortgage on home, To buy a home (other than present one), Home improvements / extensions / repairs), which might still be related to children’s needs. The SOEP contains a yearly variable with the amount that households can save for wealth creation and for precautionary savings.

Methodology

Our empirical analysis focuses on the following two dependent variables: the probability to save and net worth. For the first model, we compare households that are saving with those that are not saving. Because a binary variable has been observed in (almost) all panel waves, we can exploit the variance within households over time with a fixed effects (FE) regression. The main advantage of this method is that it excludes any unobserved heterogeneity bias. Even though we have a dichotomous dependent variable, we estimate a linear probability model.⁴ As main independent variables, we include the number of dependent children living in the household by age groups (0–4 years, 5–9 years, 10–14 years or 15–24 years). Children older than 15 years are considered as dependent if they are in education and do not work full-time. In addition, we include a binary variable for planning/wanting a child to test whether anticipating a child increases motivation for saving. This variable has not been collected in the German SOEP, however. To test the mediating effect of income on savings, we include household income (yearly earnings adjusted to household size)⁵ and working hours (mean working hours for couples). We control for the following variables that have been revealed to be important in previous studies (Finke and Pierce 2006; Pericoli and Ventura 2011; Vespa and Painter II 2011): age and its squared term (of the household head), civil status, years of cohabitation of the couples and home ownership. Despite its possible endogeneity, we also include an indicator about home ownership because repayment of a mortgage might not be considered as savings and because home ownership might increase the money available for non-housing consumption.

The main advantage of the FE models is that they capture the causal effect of dependent children on the probability to save. As these models have two important limitations, we complement the analysis with an OLS regression on net worth. First, FE models can only analyse changes that occur within the duration of the panel (e.g., maximal until children are 25 in the SOEP). Accordingly, FE models measure the impact of having dependent children in the household compared to the situation of no dependent children in the household. Second, the dependent variable indicates the presence of savings but not the amount saved (this information is available only for Germany). The OLS regression can capture long-term effects of children (once children left the household) on wealth accumulation and will reveal the size of the effect. Net worth is defined as the sum of all assets minus the level of accumulated debts. For couples, we split the amount of household wealth in half. As each country is analysed separately, we use national currencies and adjust for inflation. As a method of analysis, we use (pooled) linear regressions.⁶ To address individuals without wealth or debts and to limit the influence of extremely high values, we apply an inverse hyperbolic sine transformation (hereafter IHS) on total net worth (see Friedline et al. 2015 for details). Because we are interested in the effect of children on wealth accumulation in the long term, we need to consider children irrespective of their age and of whether they live in the household. Following Dockery and Bawa (2015), we compute a variable that we call child-years. This variable multiplies the number of children by their age with a maximum of 18 years per child. Lacking more precise information, the maximum of 18 is set as the average age for independency. This maximum considers that children pursuing professional training might become independent before and that children enrolled in university might finish their education later. As in the FE model, we estimate a separate model controlling for income and labour supply. Income refers here to permanent household income, which we define as the average of all available previous earnings and pensions. In addition to the variables included in the FE model (age, civil status, years of cohabitation and home ownership), we control for variables’ stable characteristics. The educational level (three levels with the highest educational level of the couple) is included as a proxy for wiser choices in saving and investing behaviours. Living in a city centre is included because it might imply not only higher living costs but also higher property values. We also take into account the number of siblings (in Switzerland the presence of siblings) and a measure for parental socio-economic status to capture possible effects of inheritances on the accumulation of wealth over the life-course. Other control variables are country specific. In Australia, we include a binary variable for the English mother tongue because non-native speakers find difficulties in terms of integration, whereas we identify foreign-born individuals in Switzerland and in Germany. In Switzerland, we include a variable for the linguistic region, and in Germany we distinguish the Western from the Eastern part. For age, nationality, siblings and parental socio-economic status of couple households, we consider the information provided by the main earner.

When comparing models of different countries and different surveys, we have to pay attention to different sample sizes and differences in the definition of the variables. We commented on these differences whenever necessary.

The Short-Term Effect of Children on Savings

Using FE models, we first address the probability to save. The first model in Table 11.1 (M1 for Switzerland, M3 for Australia and M5 for Germany) shows that households are less likely to save when they have children in the household. A first general finding is that children older than ten years have a weaker effect on saving propensity than younger children. In Switzerland and Germany, pre-school children (between 0 and 4 years) have, with 5.7% and 2.2%, the strongest negative effect on savings, whereas in Australia, children from 5 to 9 years of age reduce the probability to save most strongly (by 1.8 percent). To test whether lower income or higher consumption are responsible for the lower saving propensity, models M2, M4 and M6 in Table 11.1 control for the mediating effects of income and working hours. In Switzerland, the coefficients for children in the household become only slightly weaker (M2 compared to M1), which means that income and labour supply explain only a small part of the negative effect of small children. Rather, high expenses for children, and most likely high childcare costs, are responsible for the lower saving probability.⁷ The same holds for 5- to 9-year-old children in Australia. In Germany, the entire negative effect of pre-school children disappears once we control for income and working hours (M6). This means that households with small children can save less because labour and income drops after childbirth.⁸ A second general finding is that expenditures reduce saving propensity considerably for children between 15 and 24 years old. After controlling for income and labour supply, older children reduce the probability to save by 3.5% in Switzerland, by 1.2% in Germany and by 1.9% in Australia.⁹ This result is in line with previous findings on consumption for children in other countries (Bonke and Browning 2011). As a cautionary note, we must say that we might underestimate the negative effect of children on savings because we consider only the effect of children living in the household and neglect the effects on parents who do not live with their children.

Table 11.1 FE regression on the probability to save

The models in Table 11.1 test also whether planning to have a child increases the probability to save. This hypothesis is supported in Australia, where planning to have a child increases the probability to save by 4.9%. An additional analysis on Australians who save in 2002 and in 2006 (the only waves with information about the reasons for saving) shows that 13% of them declare to save for their children and 28% for home-related expenditures. In Switzerland, planning to have a child has no significant impact on the saving propensity. The coefficient is close to statistical significance, but the effect, even when significant, would be very small.

More generally, the FE analysis on saving behaviour confirms the life-cycle hypothesis. Children slow wealth accumulation because of both lower income and higher expenditures. We are confident that we measured a causal effect because these models analysed only the variation within households over time and not the variation between different household types.¹⁰

The Long-Term Effect of Children on Net Worth

So far, the analysis was based on children living in the household and was not aimed at establishing the long-term effects that children have on wealth. We now look at net worth to estimate the magnitude of the coefficients in real economic terms and use the variable child-years to capture long-term effects.

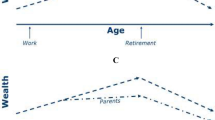
Figure 11.1 gives an overview of wealth accumulation over the life course in the three countries and shows average net worth by the age of the household head. Note that absolute wealth levels cannot be compared directly because wealth is measured in national currency. In Australia, the accumulation of wealth is almost linear before 65 years of age, and dissaving starts after retirement.¹¹ In Germany, dissaving after retirement is much less pronounced. The analysis with Swiss data shows no dissaving directly after retirement, but only later in life. This finding is in line with Moser (2006), who analysed wealth levels by age groups using tax records from the canton of Zurich.

Fig. 11.1

Wealth over the life-cycle in Australia, Germany and Switzerland (Sources: SHP 2012, HILDA 2006, 2010, 2014, SOEP 2002, 2007, 2012. Note: Local currencies represent 2011 AUS$000 s, 2012 CHF000s and 2011 EUR000s. Wealth of couple households has been divided by 2. Weighted data)

Because this descriptive figure does not distinguish the accumulation of wealth for parents and households without children, we now move to the results of the regression models shown in Table 11.2. In all countries, parents are less wealthy than childless individuals, although the effect is weak.¹² In Switzerland, one child-year reduces net worth by 377 CHF, which amounts to 6714 CHF per child in the long term. This estimation increases slightly (374 per child year) when permanent income and years in paid work are included. Higher expenditures rather than durable income losses explain therefore why parents in Switzerland have lower wealth than childless households. In Australia, children have a slightly stronger negative impact on net worth (859 AU$ per child-year, 15,462 AU$ for children up to 18 years old). Lost years in paid employment or permanent income losses explain a small part of this effect (118 AU$ per child-year explain 14% of the total negative impact of children on net worth). In Germany, children have an almost negligible impact on the total amount of accumulated wealth (34 EUR per child-year and 619 EUR for children up to 18 years old). This effect is not affected by permanent income or years in paid work. These differences between countries might be generated by institutional contexts or by saving behaviours.

Table 11.2 OLS regression with IHS transformation on net worth

We briefly comment on an additional test that we do not report in tables because of limits of space. When we constrain the analysis of Table 11.2 to retirees, wealth differences between parents and childless households disappear in Switzerland and decrease in Germany and in Australia (−0.005**). A possible explanation for this interesting finding would be that individuals in retirement spend less than childless individuals probably out of a bequest motive.

We also tested whether wealthier individuals are more likely to have children. In Switzerland and in Australia, neither home-ownership nor wealth is significant in simple fertility models. This leads us to conclude that a selection bias is very unlikely in these two countries. In Germany, however, richer parents seem to have more children. This endogeneity constitutes a bias that might underestimate the importance of children on wealth in the OLS regression, but not in the FE model, which takes into account only the variation within households over time.

Conclusions

This study has illustrated how children affect the probability to save and accumulate wealth. The analysis has been run on Swiss, Australian and German panel data using the longest possible time span. Although the selected countries differ in several aspects, this analysis has brought to light some similarities. Dependent children older than 15 are the most expensive and make savings more difficult in all contexts. Pre-school children in Switzerland, who are even more costly than older children, present an exception that is most likely due to high costs for child care. Moreover, small children considerably reduce the propensity to save in Germany and in Switzerland because women tend to drastically reduce their labour supply and, therefore, their income after the arrival of children. The effect of young children on saving is rather small in Australia.

Over the entire life course, the effects of children on wealth and savings show a brighter picture. The accumulated level of net worth is hardly compromised by child rearing. Each child reduces wealth by 6714 CHF in Switzerland, 15,462 AU$ in Australia and 619 EUR in Germany. When we look at the wealth of retirees, the effect wanes or even disappears. This suggests the importance of the bequest motive for wealth accumulation. Therefore, in the long term, children do not seem to be a major financial risk.

The analysis has also highlighted some interesting differences between countries, which merit further investigation. Parents in Germany do not seem to have considerably lower wealth than childless individuals. This could be due to either endogeneity (wealthy individuals tend to have more children), to small costs associated with children (subsidised childcare and public schools) or to particularly thrifty lifestyles. Higher costs of children in terms of wealth accumulation in Switzerland and in Australia could be explained with a more contained family policy. Frequent private schooling and high costs for university in Australia might be an element that hinders positive savings of parents in this country. More generally, the role of institutions and legislations deserves a closer look. Other interesting aspects for future studies are the distinction between the ability to save and the willingness to save and the longitudinal dynamics of net worth. This last analysis will be possible when more waves of data of the SHP become available.