Abstract
Instead of a monolithic programming language trying to cover all features of interest, some programming systems are designed by combining together simpler languages that cooperate to cover the same feature space. This can improve usability by making each part simpler than the whole, but there is a risk of abstraction leaks from one language to another that would break expectations of the users familiar with only one or some of the involved languages.
We propose a formal specification for what it means for a given language in a multi-language system to be usable without leaks: it should embed into the multi-language in a fully abstract way, that is, its contextual equivalence should be unchanged in the larger system.
To demonstrate our proposed design principle and formal specification criterion, we design a multi-language programming system that combines an ML-like statically typed functional language and another language with linear types and linear state. Our goal is to cover a good part of the expressiveness of languages that mix functional programming and linear state (ownership), at only a fraction of the complexity. We prove that the embedding of ML into the multi-language system is fully abstract: functional programmers should not fear abstraction leaks. We show examples of combined programs demonstrating in-place memory updates and safe resource handling, and an implementation extending OCaml with our linear language.
Note: Due to severe space restrictions, many details have been omitted from this presentation of our work. We strongly encourage the reader to consult the complete version at https://arxiv.org/pdf/1707.04984.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Linear Languages
- Multi-language System
- Full Abstraction
- Intuitionistic Linear Propositional Logic
- Fine-grained Composition
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Feature accretion is a common trend among mature but actively evolving programming languages, including C++, Haskell, Java, OCaml, Python, and Scala. Each new feature strives for generality and expressiveness, and may provide a large usability improvement to users of the particular problem domain or programming style it was designed to empower (e.g., XML documents, asynchronous communication, staged evaluation). But feature creep in general-purpose languages may also make it harder for programmers to master the language as a whole, degrade the user experience (e.g., leading to more cryptic error messages), require additional work on the part of tooling providers, and lead to fragility in language implementations.
A natural response to increased language complexity is to define subsets of the language designed for a better programming experience. For instance, a subset can be easier to teach (e.g., “Core” MLFootnote 1, Haskell 98 as opposed to GHC Haskell, Scala mastery levelsFootnote 2); it can facilitate static analysis or decrease the risk of programming errors, while remaining sufficiently expressive for the target users’ needs (e.g., MISRA C, Spark/Ada); it can enforce a common style within a company; or it can be designed to encourage a transition to deprecate some ill-behaved language features (e.g., strict Javascript).
Once a subset has been selected, it may be the case that users write whole programs purely in the subset (possibly using tooling to enforce that property), but programs will commonly rely on other libraries that are not themselves implemented in the same subset of the language. If users stay in the subset while using these libraries, they will only interact with the part of the library whose interface is expressible in the subset. But does the behavior of the library respect the expectations of users who only know the subset? When calling a function from within the subset breaks subset expectations, it is a sign of leaky abstraction.
How should we design languages with useful subsets that manage complexity and avoid abstraction leaks?
We propose to look at this question from a different, but equivalent, angle: instead of designing a single big monolithic language with some nicer subsets, we propose to consider multi-language programming systems where several smaller programming languages interact together to cover the same feature space. Each language or sub-combination of languages is a subset, in the above sense, of the multi-language, and there is a clear definition of abstraction leaks in terms of user experience: a user who only knows some of the languages of the system should be able to use the multi-language system, interacting with code written in the other languages, without have their expectations violated. If we write a program in Java and call a function that, internally, is implemented in Scala, there should be no surprises—our experience should be the same as when calling a pure Java function. Similarly, consider the subset of Haskell that does not contain IO (input-output as a type-tracked effect): the expectations of a user of this language, for instance in terms of valid equational reasoning, should not be violated by adding IO back to the language—in the absence of the abstraction-leaking unsafePerformIO.
We propose a formal specification for a “no abstraction leaks” guarantee that can be used as a design criterion to design new multi-language systems, with graceful interoperation properties. It is based on the formal notion of full abstraction which has previously been used to study the denotational semantics of programming languages (Meyer and Sieber 1988; Milner 1977; Cartwright and Felleisen 1992; Jeffrey and Rathke 2005; Abramsky, Jagadeesan, and Malacaria 2000), and the formal property of compilers (Ahmed and Blume 2008, 2011; Devriese et al. 2016; New et al. 2016; Patrignani et al. 2015), but not for user-facing languages. A compiler C from a source language S to a target language T is fully abstract if, whenever two source terms \(s_1\) and \(s_2\) are indistinguishable in S, their translations \(C(s_1)\) and \(C(s_2)\) are indistinguishable in T. In a multi-language \(G + E\) formed of a general-purpose, user-friendly language G and a more advanced language E—one that provides an escape hatch for experts to write code that can’t be implemented in G—we say that E does not leak into G if the embedding of G into the multi-language \(G + E\) is fully abstract.
To demonstrate that our formal specification is reasonable, we design a novel multi-language programming system that satisfies it. Our multi-language  combines a general-purpose functional programming language
combines a general-purpose functional programming language  (unrestricted) of the ML family with an advanced language
(unrestricted) of the ML family with an advanced language  (linear) with linear types and linear state. It is less convient to program in
(linear) with linear types and linear state. It is less convient to program in  ’s restrictive type system, but users can write programs in
’s restrictive type system, but users can write programs in  that could not be written in
that could not be written in  : they can use linear types, locally, to enforce resource usage protocols (typestate), and they can use linear state and the linear ownership discipline to write programs that do in-place update to allocate less memory, yet remain observationally pure.
: they can use linear types, locally, to enforce resource usage protocols (typestate), and they can use linear state and the linear ownership discipline to write programs that do in-place update to allocate less memory, yet remain observationally pure.
Consider for example the following mixed-language program. The blue fragments are written in the general-purpose, user-friendly functional language, while the red fragments are written in the linear language. The boundaries  and
and  allow switching between languages. The program reads all lines from a file, accumulating them in a list, and concatenating it into a single string when the end-of-file (EOF) is reached.
allow switching between languages. The program reads all lines from a file, accumulating them in a list, and concatenating it into a single string when the end-of-file (EOF) is reached.

The linear type system ensures that the file handle is properly closed: removing the  call would give a type error. On the other hand, only the parts concerned with the resource-handling logic need to be written in the red linear language; the user can keep all general-purpose logic (here, how to accumulate lines and what to do with them at the end) in the more convenient general-purpose blue language—and call this function from a blue-language program. Fine-grained boundaries allow users to rely on each language’s strength and to use the advanced features only when necessary.
call would give a type error. On the other hand, only the parts concerned with the resource-handling logic need to be written in the red linear language; the user can keep all general-purpose logic (here, how to accumulate lines and what to do with them at the end) in the more convenient general-purpose blue language—and call this function from a blue-language program. Fine-grained boundaries allow users to rely on each language’s strength and to use the advanced features only when necessary.
In this example, the file-handle API specifies that the call to  , which reads a line, returns the data at type
, which reads a line, returns the data at type  . The latter represents how
. The latter represents how  values of type
values of type  can be put into a lump type to be passed to the linear world where they are treated as opaque blackboxes that must be passed back to the ML world for consumption. For other examples, such as in-place list manipulation or transient operations on an persistent data structure, we will need a deeper form of interoperability where the linear world creates, dissects or manipulates
can be put into a lump type to be passed to the linear world where they are treated as opaque blackboxes that must be passed back to the ML world for consumption. For other examples, such as in-place list manipulation or transient operations on an persistent data structure, we will need a deeper form of interoperability where the linear world creates, dissects or manipulates  values. To enable this, our multi-language supports translation of types from one language to the other, using a type compatibility relation
values. To enable this, our multi-language supports translation of types from one language to the other, using a type compatibility relation  between
between  types
types  and
and  types
types  .
.
We claim the following contributions:
-
1.
We propose a formal specification of what it means for advanced language features to be introduced in a (multi-)language system without introducing a class of abstraction leaks that break equational reasoning. This specification captures a useful usability property, and we hope it will help us and others design more usable programming languages, much like the formal notion of principal types served to better understand and design type inference systems.
-
2.
We design a simple linear language,
 , that supports linear state (Sect. 2). This simple design for linear state is a contribution of its own. A nice property of the language (shared by some other linear languages) is that the code has both an imperative interpretation—with in-place memory update, which provides resource guarantees—and a functional interpretation—which aids program reasoning. The imperative and functional interpretations have different resource usage, but the same input/output behavior.
, that supports linear state (Sect. 2). This simple design for linear state is a contribution of its own. A nice property of the language (shared by some other linear languages) is that the code has both an imperative interpretation—with in-place memory update, which provides resource guarantees—and a functional interpretation—which aids program reasoning. The imperative and functional interpretations have different resource usage, but the same input/output behavior. -
3.
We present a multi-language programming system
 combining a core ML language,
combining a core ML language, 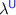 (
( for Unrestricted, as opposed to Linear) with
for Unrestricted, as opposed to Linear) with 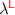 and prove that the embedding of the ML language
and prove that the embedding of the ML language  in
in  is fully abstract (Sect. 3). Moreover, the multi-language is designed to ensure that our full abstraction result is stable under extension of the embedded ML language
is fully abstract (Sect. 3). Moreover, the multi-language is designed to ensure that our full abstraction result is stable under extension of the embedded ML language 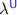 .
.
2 The 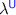 and
and 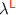 Languages
Languages
The unrestricted language  is a run-of-the-mill idealized ML language with functions, pairs, sums, iso-recursive types and polymorphism. It is presented in its explicitly typed form—we will not discuss type inference in this work. The full syntax is described in Fig. 1, and the typing rules in Fig. 2. The dynamic semantics is completely standard. Having binary sums, binary products and iso-recursive types lets us express algebraic datatypes in the usual way.
is a run-of-the-mill idealized ML language with functions, pairs, sums, iso-recursive types and polymorphism. It is presented in its explicitly typed form—we will not discuss type inference in this work. The full syntax is described in Fig. 1, and the typing rules in Fig. 2. The dynamic semantics is completely standard. Having binary sums, binary products and iso-recursive types lets us express algebraic datatypes in the usual way.
The novelty lies in the linear language  , which we present in several steps. As is common in \(\lambda \)-calculi with references, the small-step operational semantics is given for a language that is not exactly the surface language in which programs are written, because memory allocation returns locations
, which we present in several steps. As is common in \(\lambda \)-calculi with references, the small-step operational semantics is given for a language that is not exactly the surface language in which programs are written, because memory allocation returns locations  that are not in the grammar of surface terms. Reductions are defined on configurations, a local store paired with a term in a slightly larger internal language. We have two type systems, a type system on surface terms, that does not mention locations and stores—which is the one a programmer needs to know—and a type system on configurations, which contains enough static information to reason about the dynamics of our language and prove subject reduction. Again, this follows the standard structure of syntactic soundness proofs for languages with a mutable store.
that are not in the grammar of surface terms. Reductions are defined on configurations, a local store paired with a term in a slightly larger internal language. We have two type systems, a type system on surface terms, that does not mention locations and stores—which is the one a programmer needs to know—and a type system on configurations, which contains enough static information to reason about the dynamics of our language and prove subject reduction. Again, this follows the standard structure of syntactic soundness proofs for languages with a mutable store.
2.1 The Core of 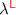
Figure 3 presents the surface syntax of our linear language  . For the syntactic categories of types
. For the syntactic categories of types  , and expressions
, and expressions  , the last line contains the constructions related to the linear store that we only discuss in Sect. 2.2.
, the last line contains the constructions related to the linear store that we only discuss in Sect. 2.2.
In technical terms, our linear type system is exactly propositional intuitionistic linear logic, extended with iso-recursive types. For simplicity and because we did not need them, our current system also does not have polymorphism or additive/lazy pairs  . Additive pairs would be a trivial addition, but polymorphism would require more work when we define the multi-language semantics in Sect. 3.
. Additive pairs would be a trivial addition, but polymorphism would require more work when we define the multi-language semantics in Sect. 3.
In less technical terms, our type system can enforce that values be used linearly, meaning that they cannot be duplicated or erased, they have to be deconstructed exactly once. Only some types have this linearity restriction; others allow duplication and sharing of values at will. We can think of linear values as resources to be spent wisely; for any linear value somewhere in a term, there can be only one way to access this value, so we can interpret the language as enforcing an ownership discipline where whoever points to a linear value owns it.
In particular, linear functions of type  must be called exactly once, and their results must in turn be consumed – they can safely capture linear resources. On the other hand, the non-linear, duplicable values are those at types of the form
must be called exactly once, and their results must in turn be consumed – they can safely capture linear resources. On the other hand, the non-linear, duplicable values are those at types of the form  — the exponential modality of linear logic. If the term
— the exponential modality of linear logic. If the term  has duplicable type
has duplicable type  , then the term
, then the term  has type
has type  : this creates a local copy of the value that is uniquely-owned by its receiver and must be consumed linearily.
: this creates a local copy of the value that is uniquely-owned by its receiver and must be consumed linearily.
This resource-usage discipline is enforced by the surface typing rules of  , presented in Fig. 4. They are exactly the standard (two-sided) logical rules of intuitionistic linear logic, annotated with program terms. The non-duplicability of linear values is enforced by the way contexts are merged by the inference rules: if
, presented in Fig. 4. They are exactly the standard (two-sided) logical rules of intuitionistic linear logic, annotated with program terms. The non-duplicability of linear values is enforced by the way contexts are merged by the inference rules: if  is type-checked in the context
is type-checked in the context  and
and  in
in  , then the linear pair
, then the linear pair  is only valid in the combined context
is only valid in the combined context  . The
. The  operation is partial; this combined context is defined only if the variables shared by
operation is partial; this combined context is defined only if the variables shared by  and
and  are duplicable—their type is of the form
are duplicable—their type is of the form  . In other words, a variable at a non-duplicable type in
. In other words, a variable at a non-duplicable type in  cannot possibly appear in both
cannot possibly appear in both  and
and  : it must appear exactly onceFootnote 3.
: it must appear exactly onceFootnote 3.
The expression  takes a term at some type
takes a term at some type  and creates a “shared” term, whose value will be duplicable. Its typing rule uses a context of the form
and creates a “shared” term, whose value will be duplicable. Its typing rule uses a context of the form  , which is defined as the pointwise application of the
, which is defined as the pointwise application of the  connectives to all the types in
connectives to all the types in  . In other words, the context of this rule must only have duplicable types: a term can only be made duplicable if it does not depend on linear resources from the context. Otherwise, duplicating the shared value could break the unique-ownership discipline on these linear resources.
. In other words, the context of this rule must only have duplicable types: a term can only be made duplicable if it does not depend on linear resources from the context. Otherwise, duplicating the shared value could break the unique-ownership discipline on these linear resources.
Finally, the linear isomorphism notation for  and
and  in Fig. 4 defines them as primitive functions, at the given linear function type, in the empty context – using them does not consume resources. This notation also means that, operationally, these two operations shall be inverses of each other. The rules for the linear store type
in Fig. 4 defines them as primitive functions, at the given linear function type, in the empty context – using them does not consume resources. This notation also means that, operationally, these two operations shall be inverses of each other. The rules for the linear store type  and
and  are described in Sect. 2.2.
are described in Sect. 2.2.
2.2 Linear Memory in 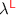
The surface typing rules for the linear store are given at the end of Fig. 4. The linear type  represents a memory location that holds a value of type
represents a memory location that holds a value of type  . The type
. The type  represents a location that has been allocated, but does not currently hold a value. The primitive operations to act on this type are given as linear isomorphisms:
represents a location that has been allocated, but does not currently hold a value. The primitive operations to act on this type are given as linear isomorphisms:  allocates, turning a unit value into an empty location; conversely,
allocates, turning a unit value into an empty location; conversely,  reclaims an empty location. Putting a value into the location and taking it out are expressed by
reclaims an empty location. Putting a value into the location and taking it out are expressed by  and
and  , which convert between a pair of an empty location and a value, of type
, which convert between a pair of an empty location and a value, of type  , and a full location, of type
, and a full location, of type  .
.
For example, the following program takes a full reference and a value, and swaps the value with the content of the reference:

The programming style following from this presentation of linear memory is functional, or applicative, rather than imperative. Rather than insisting on the mutability of references—which is allowed by the linear discipline—we may think of the type  as representing the indirection through the heap that is implicit in functional programs. In a sense, we are not writing imperative programs with a mutable store, but rather making explicit the allocations and dereferences happening in higher-level purely functional language. In this view, empty cells allow memory reuse.
as representing the indirection through the heap that is implicit in functional programs. In a sense, we are not writing imperative programs with a mutable store, but rather making explicit the allocations and dereferences happening in higher-level purely functional language. In this view, empty cells allow memory reuse.
This view that  represents indirection through the memory suggests we can encode lists of values of type
represents indirection through the memory suggests we can encode lists of values of type  by the type
by the type  . The placement of the box inside the sum mirrors the fact that empty list is represented as an immediate value in functional languages. From this type definition, one can write an in-place reverse function on lists of
. The placement of the box inside the sum mirrors the fact that empty list is represented as an immediate value in functional languages. From this type definition, one can write an in-place reverse function on lists of  as follows:
as follows:

Our linear language  is a formal language that is not terribly convenient to program directly. We will not present a full surface language in this work, but one could easily define syntactic sugar to write the exact same function as follows:
is a formal language that is not terribly convenient to program directly. We will not present a full surface language in this work, but one could easily define syntactic sugar to write the exact same function as follows:

One can read this function as the usual functional rev_append function on lists, annotated with memory reuse information: if we assume we are the unique owner of the input list and won’t need it anymore, we can reuse the memory of its cons cells (given in this example the name  ) to store the reversed list. On the other hand, if you read the
) to store the reversed list. On the other hand, if you read the  and
and  as imperative operations, this code expresses the usual imperative pointer-reversal algorithm.
as imperative operations, this code expresses the usual imperative pointer-reversal algorithm.
This double view of linear state occurs in other programming systems with linear state. It was recently emphasized in O’Connor et al. (2016), where the functional point of view is seen as easing formal verification, while the imperative view is used as a compilation technique to produce efficient C code from linear programs.
2.3 Internal 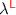 Syntax and Typing
Syntax and Typing
To give a dynamic semantics for  and prove it sound, we need to extend the language with explicit stores and store locations. Indeed, the allocating term
and prove it sound, we need to extend the language with explicit stores and store locations. Indeed, the allocating term  should reduce to a “fresh location”
should reduce to a “fresh location”  allocated in some store
allocated in some store  , and neither are part of the surface-language syntax. The corresponding internal typing judgment is more complex, but note that users do not need to know about it to reason about correctness of surface programs. The internal typing is essential for the soundness proof, but also useful for defining the multi-language semantics in Sect. 3.
, and neither are part of the surface-language syntax. The corresponding internal typing judgment is more complex, but note that users do not need to know about it to reason about correctness of surface programs. The internal typing is essential for the soundness proof, but also useful for defining the multi-language semantics in Sect. 3.
We work with configurations  , which are pairs of a store
, which are pairs of a store  and a term
and a term  . Our internal typing judgment
. Our internal typing judgment  checks configurations, not just terms, and relies not only on a typing context for variables
checks configurations, not just terms, and relies not only on a typing context for variables  but also on a store typing
but also on a store typing  , which maps the locations of the configuration to typing assumptions.
, which maps the locations of the configuration to typing assumptions.
Unfortunately, due to space limits, we will not present this part of the type system – which is not directly exposed to users of the language. See some examples of reduction rules in Fig. 5, and the long version of this work.
2.4 Reduction of Internal Terms
In the long version of this work we give a reduction relation between linear configurations  and prove a subject reduction result.
and prove a subject reduction result.
Theorem 1
(Subject reduction for  ). If
). If  and
and  , then there exists a (unique)
, then there exists a (unique)  such that
such that  .
.
3 Multi-language Semantics
To formally define our multi-language semantics we create a combined language  which lets us compose term fragments from both
which lets us compose term fragments from both  and
and  together, and we give an operational semantics to this combined language. Interoperability is enabled by specifying how to transport values across the language boundaries.
together, and we give an operational semantics to this combined language. Interoperability is enabled by specifying how to transport values across the language boundaries.
Multi-language systems in the wild are not defined in this way: both languages are given a semantics, by interpretation or compilation, in terms of a shared lower-level language (C, assembly, the JVM or CLR bytecode, or Racket’s core forms), and the two languages are combined at that level. Our formal multi-language description can be seen as a model of such combinations, that gives a specification of the expected observable behavior of this language combination.
Another difference from multi-languages in the wild is our use of very fine-grained language boundaries: a term written in one language can have its subterms written in the other, provided the type-checking rules allow it. Most multi-language systems, typically using Foreign Function Interfaces, offer coarser-grained composition at the level of compilation units. Fine-grained composition of existing languages, as done in the Eco project (Barrett et al. 2016), is difficult because of semantic mismatches. In the full version of this work we demonstrate that fine-grained composition is a rewarding language design, enabling new programming patterns.
3.1 Lump Type and Language Boundaries
The core components the multi-language semantics are shown Fig. 6—the communication of values from one language to the other will be described in the next section. The multi-language  has two distinct syntactic categories of types, values, and expressions: those that come from
has two distinct syntactic categories of types, values, and expressions: those that come from  and those that come from
and those that come from  . Contexts, on the other hand, are mixed, and can have variables of both sorts. For a mixed context
. Contexts, on the other hand, are mixed, and can have variables of both sorts. For a mixed context  , the notation
, the notation  only applies
only applies  to its linear variables.
to its linear variables.
The typing rules of  and
and  are imported into our multi-language system, working on those two separate categories of program. They need to be extended to handle mixed contexts
are imported into our multi-language system, working on those two separate categories of program. They need to be extended to handle mixed contexts  instead of their original contexts
instead of their original contexts  and
and  . In the linear case, the rules look exactly the same. In the ML case, the typing rules implicitly duplicate all the variables in the context. It would be unsound to extend them to arbitrary linear variables, so they use a duplicable context
. In the linear case, the rules look exactly the same. In the ML case, the typing rules implicitly duplicate all the variables in the context. It would be unsound to extend them to arbitrary linear variables, so they use a duplicable context  .
.
To build interesting multi-language programs, we need a way to insert a fragment coming from a language into a term written in another. This is done using language boundaries, two new term formers  and
and  that inject an ML term into the syntactic category of linear terms, and a linear configuration into the syntactic category of ML terms.
that inject an ML term into the syntactic category of linear terms, and a linear configuration into the syntactic category of ML terms.
Of course, we need new typing rules for these term-level constructions, clarifying when it is valid to send a value from  into
into  and vice versa. It would be incorrect to allow sending any type from one language into the other—for instance, by adding the counterpart of our language boundaries in the syntax of types—since values of linear types must be uniquely owned so they cannot possibly be sent to the ML side as the ML type system cannot enforce unique ownership.
and vice versa. It would be incorrect to allow sending any type from one language into the other—for instance, by adding the counterpart of our language boundaries in the syntax of types—since values of linear types must be uniquely owned so they cannot possibly be sent to the ML side as the ML type system cannot enforce unique ownership.
On the other hand, any ML value could safely be sent to the linear world. For closed types, we could provide a corresponding linear type ( maps to
maps to  , etc.), but an ML value may also be typed by an abstract type variable
, etc.), but an ML value may also be typed by an abstract type variable  , in which case we can’t know what the linear counterpart should be. Instead of trying to provide translations, we will send any ML type
, in which case we can’t know what the linear counterpart should be. Instead of trying to provide translations, we will send any ML type  to the lump type
to the lump type  , which embeds ML types into linear types. A lump is a blackbox, not a type translation: the linear language does not assume anything about the behavior of its values—the values of
, which embeds ML types into linear types. A lump is a blackbox, not a type translation: the linear language does not assume anything about the behavior of its values—the values of  are of the form
are of the form  , where
, where  is an ML value that the linear world cannot use. More precisely, we only propagate the information that ML values are all duplicable by sending
is an ML value that the linear world cannot use. More precisely, we only propagate the information that ML values are all duplicable by sending  to
to  .
.
The typing rules for language boundaries insert lumps when going from  to
to  , and remove them when going back from
, and remove them when going back from  to
to  . In particular, arbitrary linear types cannot occur at the boundary, they must be of the form
. In particular, arbitrary linear types cannot occur at the boundary, they must be of the form  .
.
Finally, boundaries have reduction rules: a term or configuration inside a boundary in reduction position is reduced until it becomes a value, and then a lump is added or removed depending on the boundary direction. Note that because the  in
in  is at a duplicable type
is at a duplicable type  , we know by inversion that the store is empty.
, we know by inversion that the store is empty.
3.2 Interoperability: Static Semantics
If the linear language could not interact with lumped values at all, our multi-language programs would be rather boring, as the only way for the linear extension to provide a value back to ML would be to have received it from  and pass it back unchanged (as in the lump embedding of Matthews and Findler
(2009)). To provide a real interaction, we provide a way to extract values out of a lump
and pass it back unchanged (as in the lump embedding of Matthews and Findler
(2009)). To provide a real interaction, we provide a way to extract values out of a lump  , use it at some linear type
, use it at some linear type  , and put it back in before sending the result to
, and put it back in before sending the result to  .
.
The correspondence between intuitionistic types  and linear types
and linear types  is specified by a heterogeneous compatibility relation
is specified by a heterogeneous compatibility relation  – defined in full in Fig. 7. The specification of this relation is that if
– defined in full in Fig. 7. The specification of this relation is that if  holds, then the space of values of
holds, then the space of values of  and
and  are isomorphic: we can convert back and forth between them. When this relation holds, the term-formers
are isomorphic: we can convert back and forth between them. When this relation holds, the term-formers  and
and  perform the conversion.
perform the conversion.
The term  turns a
turns a  into a lumped type
into a lumped type  , and we need to unlump it with some
, and we need to unlump it with some  for a compatible
for a compatible  to interact with it on the linear side. It is common to combine both operations and we provide syntactic sugar for it:
to interact with it on the linear side. It is common to combine both operations and we provide syntactic sugar for it:  . Similarly
. Similarly  first lumps a linear term then sends the result to the ML world.
first lumps a linear term then sends the result to the ML world.
3.3 Interoperability: Dynamic Semantics
When the relation  holds, we can define a relation
holds, we can define a relation  between the values of
between the values of  and the values of
and the values of  – see the long version of this work. It is functional in both direction: with our definition
– see the long version of this work. It is functional in both direction: with our definition  is uniquely determined from
is uniquely determined from  and conversely. We then define the reduction rule for (un)lumping: if
and conversely. We then define the reduction rule for (un)lumping: if  , then
, then

3.4 Full Abstraction from 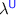 into
into 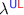
We can now state the major meta-theoretical result of this work, which is the proposed multi-language design extends the simple language  in a way that provably has, in a certain sense, “no abstraction leaks”.
in a way that provably has, in a certain sense, “no abstraction leaks”.
Definition 1
(Contextual equivalence in  ). We say that
). We say that  such that
such that  are contextually equivalent, written
are contextually equivalent, written  , if, for any expression context
, if, for any expression context  such that
such that  , the closed terms
, the closed terms  and
and  are equi-terminating.
are equi-terminating.
Definition 2
(Contextual equivalence in  ). We say that
). We say that  such that
such that  are contextually equivalent, written
are contextually equivalent, written  , if, for any expression context
, if, for any expression context  such that
such that  , the closed terms
, the closed terms  and
and  are equi-terminating.
are equi-terminating.
Theorem 2
(Full Abstraction). The embedding of  into
into  is fully-abstract:
is fully-abstract:

4 Conclusion and Related Work
Having a stack of usable, interoperable languages, extensions or dialects is at the forefront of the Racket approach to programming environments, in particular for teaching (Felleisen et al. 2004).
Our multi-language semantics builds on the seminal work by Matthews and Findler (2009), who gave a formal semantics of interoperability between a dynamically and a statically typed language. Others have followed the Matthews-Findler approach of designing multi-language systems with fine-grained boundaries—for instance, formalizing interoperability between a simply and dependently typed language (Osera et al. 2012); between a functional and typed assembly language (Patterson et al. 2017); between an ML-like and an affinely typed language, where linearity is enforced at runtime on the ML side using stateful contracts (Tov and Pucella 2010); and between the source and target languages of compilation to specify compiler correctness (Perconti and Ahmed 2014). However, all these papers address only the question of soundness of the multi-language; we propose a formal treatment of usability and absence of abstraction leaks.
The only work to establish that a language embeds into a multi-language in a fully abstract way is the work on fully abstract compilation by Ahmed and Blume (2011) and New et al. (2016) who show that their compiler’s source language embeds into their source-target multi-language in a fully abstract way. But the focus of this work was on fully abstract compilation, not on usability of user-facing languages.
The Eco project (Barrett et al. 2016) is studying multi-language systems where user-exposed languages are combined in a very fine-grained way; it is closely related in that it studies the user experience in a multi-language system. The choice of an existing dynamic language creates delicate interoperability issues (conflicting variable scoping rules, etc.) as well as performance challenges. We propose a different approach, to design new multi-languages from scratch with interoperability in mind to avoid legacy obstacles.
We are not aware of existing systems exploiting the simple idea of using promotion to capture uniquely-owned state and dereliction to copy it—common formulations would rather perform copies on the contraction rule.
The general idea that linear types can permit reuse of unused allocated cells is not new. In Wadler (1990), a system is proposed with both linear and non-linear types to attack precisely this problem. It is however more distant from standard linear logic and somewhat ad-hoc; for example, there is no way to permanently turn a uniquely-owned value into a shared value, it provides instead a local borrowing construction that comes with ad-hoc restrictions necessary for safety. (The inability to give up unique ownership, which is essential in our list-programming examples, seems to also be missing from Rust, where one would need to perform a costly operation of traversing the graph of the value to turn all pointers into Arc nodes.)
The RAML project (Hoffmann et al. 2012) also combines linear logic and memory reuse: its destructive match operator will implicitly reuse consumed cells in new allocations occurring within the match body. Multi-languages give us the option to explore more explicit, flexible representations of those low-level concern, without imposing the complexity to all programmers.
A recent related work is the Cogent language (O’Connor et al. 2016), in which linear state is also viewed as both functional and imperative – the latter view enabling memory reuse. The language design is interestingly reversed: in Cogent, the linear layer is the simple language that everyone uses, and the non-linear language is a complex but powerful language that is used when one really has to, named C.
Our linear language  is sensibly simpler, and in several ways less expressive, than advanced programming languages based on linear logic (Tov and Pucella 2011), separation logic (Balabonski et al. 2016), fine-grained permissions (Garcia et al. 2014): it is not designed to stand on its own, but to serve as a useful side-kick to a functional language, allowing safer resource handling.
is sensibly simpler, and in several ways less expressive, than advanced programming languages based on linear logic (Tov and Pucella 2011), separation logic (Balabonski et al. 2016), fine-grained permissions (Garcia et al. 2014): it is not designed to stand on its own, but to serve as a useful side-kick to a functional language, allowing safer resource handling.
One major simplification of our design compared to more advanced linear or separation-logic-based languages is that we do not separate physical locations from the logical capability/permission to access them (e.g., as in Ahmed et al. (2007)). This restricts expressiveness in well-understood ways (Fahndrich and DeLine 2002): shared values cannot point to linear values.
Alms (Tov and Pucella 2011), Quill (Morris 2016) and Linear Haskell (Bernardy et al. 2018) add linear types to a functional language, trying hard not to lose desirable usability property, such as type inference or the genericity of polymorphic higher-order functions. This is very challenging; for example, Linear Haskell gives up on principality of inferenceFootnote 4. Our multi-language design side-steps this issue as the general-purpose language remains unchanged. Language boundaries are more rigid than an ideal no-compromise language, as they force users to preserve the distinction between the general-purpose and the advanced features; it is precisely this compromise that gives a design of reduced complexity.
Finally, on the side of the semantics, our system is related to LNL (Benton 1994), a calculus for linear logic that, in a sense, is itself built as a multi-language system where (non-duplicable) linear types and (duplicable) intuitionistic types interact through a boundary. It is not surprising that our design contains an instance of this adjunction: for any  there is a unique
there is a unique  such that
such that  , and converting a
, and converting a  value to this
value to this  and back gives a
and back gives a  and is provably equivalent, by boundary cancellation, to just using
and is provably equivalent, by boundary cancellation, to just using  .
.
Notes
- 1.
- 2.
- 3.
Standard presentations of linear logic force contexts to be completely distinct, but have a separate rule to duplicate linear variables, which is less natural for programming.
- 4.
Thanks to Stephen Dolan for pointing out that \(\lambda f. \lambda x.\,f~x\) has several incompatible Linear Haskell types.
References
Abramsky, S., Jagadeesan, R., Malacaria, P.: Full abstraction for PCF. Inf. Comput. 163(2), 409–470 (2000)
Ahmed, A., Blume, M.: Typed closure conversion preserves observational equivalence. In: International Conference on Functional Programming (ICFP), Victoria, British Columbia, Canada, pp. 157–168, September 2008
Ahmed, A., Blume, M.: An equivalence-preserving CPS translation via multi-language semantics. In: International Conference on Functional Programming (ICFP), Tokyo, Japan, pp. 431–444, September 2011
Ahmed, A., Fluet, M., Morrisett, G.: L3: a linear language with locations. Fundamenta Informaticae 77(4), 397–449 (2007)
Balabonski, T., Pottier, F., Protzenko, J.: The design and formalization of Mezzo, a permission-based programming language. ACM Trans. Program. Lang. Syst. 38(4), 14:1–14:94 (2016)
Barrett, E., Bolz, C.F., Diekmann, L., Tratt, L.: Fine-grained language composition: a case study. In: ECOOP (2016)
Benton, P.N.: A mixed linear and non-linear logic: proofs, terms and models. In: Pacholski, L., Tiuryn, J. (eds.) CSL 1994. LNCS, vol. 933, pp. 121–135. Springer, Heidelberg (1995). https://doi.org/10.1007/BFb0022251
Bernardy, J.-P., Boespflug, M., Newton, R.R., Jones, S.P., Spiwack, A.: Linear haskell: practical linearity in a higher-order polymorphic language. PACMPL 2(POPL), 5:1–5:29 (2018). https://doi.org/10.1145/3158093
Cartwright, R., Felleisen, M.: Observable sequentiality and full abstraction. In: ACM Symposium on Principles of Programming Languages (POPL), Albuquerque, New Mexico, pp. 328–342 (1992)
Devriese, D., Patrignani, M., Piessens, F.: Fully-abstract compilation by approximate back-translation. In: ACM Symposium on Principles of Programming Languages (POPL), St. Petersburg, Florida (2016)
Fahndrich, M., DeLine, R.: Adoption and focus: practical linear types for imperative programming. In: PLDI 2002 (2002)
Felleisen, M., Findler, R.B., Flatt, M., Krishnamurthi, S.: The teachscheme! project: computing and programming for every student. Comput. Sci. Educ. 14(1), 55–77 (2004)
Garcia, R., Tanter, É., Wolff, R., Aldrich, J.: Foundations of typestate-oriented programming. TOPLAS 36, 12 (2014)
Hoffmann, J., Aehlig, K., Hofmann, M.: Resource aware ML. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 781–786. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31424-7_64
Jeffrey, A., Rathke, J.: Java JR: fully abstract trace semantics for a Core Java Language. In: Sagiv, M. (ed.) ESOP 2005. LNCS, vol. 3444, pp. 423–438. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31987-0_29
Matthews, J., Findler, R.B.: Operational semantics for multi-language programs. ACM Trans. Program. Lang. Syst. (TOPLAS) 31(3), 12 (2009)
Meyer, A.R., Sieber, K.: Towards fully abstract semantics for local variables. In: ACM Symposium on Principles of Programming Languages (POPL), San Diego, California, pp. 191–203 (1988)
Milner, R.: Fully abstract models of typed lambda calculi. Theor. Comput. Sci. 4(1), 1–22 (1977)
Morris, J.G.: The best of both worlds: linear functional programming without compromise. In: ICFP (2016)
New, M.S., Bowman, W.J., Ahmed, A.: Fully abstract compilation via universal embedding. In: International Conference on Functional Programming (ICFP), Nara, Japan, September 2016
O’Connor, L., Chen, Z., Rizkallah, C., Amani, S., Lim, J., Murray, T., Nagashima, Y., Sewell, T., Klein, G.: Refinement through restraint: bringing down the cost of verification. In: ICFP (2016)
Osera, P.M., Sjöberg, V., Zdancewic, S.: Dependent interoperability. In: Programming Languages Meets Program Verification (PLPV), January 2012
Patrignani, M., Agten, P., Strackx, R., Jacobs, B., Clarke, D., Piessens, F.: Secure compilation to protected module architectures. ACM Trans. Program. Lang. Syst. 37(2), 6:1–6:50 (2015)
Patterson, D., Perconti, J., Dimoulas, C., Ahmed, A.: FunTAL: reasonably mixing a functional language with assembly. In: ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), Barcelona, Spain, June 2017. http://www.ccs.neu.edu/home/amal/papers/funtal.pdf
Perconti, J.T., Ahmed, A.: Verifying an open compiler using multi-language semantics. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 128–148. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54833-8_8
Tov, J.A., Pucella, R.: Stateful contracts for affine types. In: Gordon, A.D. (ed.) ESOP 2010. LNCS, vol. 6012, pp. 550–569. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11957-6_29
Tov, J.A., Pucella, R.: Practical affine types. In: POPL (2011)
Wadler, P.: Linear types can change the world! In: Programming Concepts and Methods (1990)
Acknowledgments
We thank our anonymous reviewers for their feedback, as well as Neelakantan Krishnaswami, François Pottier, Jennifer Paykin, Sylvie Boldot and Simon Peyton-Jones for our discussions on this work.
This work was supported in part by the National Science Foundation under grants CCF-1422133 and CCF-1453796, and the European Research Council under ERC Starting Grant SECOMP (715753). Any opinions, findings, and conclusions expressed in this material are those of the authors and do not necessarily reflect the views of our funding agencies.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Scherer, G., New, M., Rioux, N., Ahmed, A. (2018). Fab ous Interoperability for ML and a Linear Language.
In: Baier, C., Dal Lago, U. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2018. Lecture Notes in Computer Science(), vol 10803. Springer, Cham. https://doi.org/10.1007/978-3-319-89366-2_8
ous Interoperability for ML and a Linear Language.
In: Baier, C., Dal Lago, U. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2018. Lecture Notes in Computer Science(), vol 10803. Springer, Cham. https://doi.org/10.1007/978-3-319-89366-2_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-89366-2_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89365-5
Online ISBN: 978-3-319-89366-2
eBook Packages: Computer ScienceComputer Science (R0)





 , that supports linear state (Sect.
, that supports linear state (Sect.  combining a core ML language,
combining a core ML language, 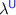 (
( for Unrestricted, as opposed to Linear) with
for Unrestricted, as opposed to Linear) with 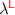 and prove that the embedding of the ML language
and prove that the embedding of the ML language  in
in  is fully abstract (Sect.
is fully abstract (Sect. 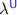 .
.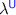 and
and 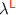 Languages
Languages

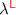



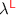
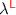 Syntax and Typing
Syntax and Typing

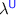 into
into