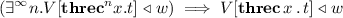Advertisement

A Syntactic View of Computational Adequacy

  • Marco Devesas Campos
  • Paul Blain Levy
Open Access
Conference paper
First Online:
Part of the Lecture Notes in Computer Science book series (LNCS, volume 10803)

Abstract

When presenting a denotational semantics of a language with recursion, it is necessary to show that the semantics is computationally adequate, i.e. that every divergent term denotes the “bottom” element of a domain.

We explain how to view such a theorem as a purely syntactic result. Any theory (congruence) that includes basic laws and is closed under an infinitary rule that we call “rational continuity” has the property that every divergent term is equated with the divergent constant. Therefore, to prove a model adequate, it suffices to show that it validates the basic laws and the rational continuity rule. While this approach was inspired by the categorical, ordered framework of Abramsky et al., neither category theory nor order is needed.

The purpose of the paper is to present this syntactic result for call-by-push-value extended with term-level recursion and polymorphic types. Our account begins with PCF, then includes sum types, then moves to call-by-push-value, and finally includes polymorphic types.

Download conference paper PDF

1 Introduction

Models of Recursion. A conventional denotational account of a language with recursion proceeds as follows. First define the syntax and operational semantics. Then give a denotational model. Lastly, prove soundness, i.e. if t evaluates to u (written \(t \mathbin {\Downarrow }u\)) then \(\llbracket t\rrbracket = \llbracket u\rrbracket \), and adequacy, i.e. if t diverges (written \(t \Uparrow \)) then \(\llbracket {t}\rrbracket =\bot \).

Because it is often convenient to structure a model categorically, Fiore and Plotkin (1994) gave categorical axioms on a model that imply (soundness and) adequacy. Crucially, in their work, as detailed by Fiore (1996), a model is required to be “\(\omega \mathbf{{Cpo}}\)-enriched”, meaning that a term denotes an element of a pointed \(\omega \)-cpo (poset with least element \(\bot \) and suprema of all increasing \(\omega \)-chains), and a term constructor is \(\omega \)-continuous (preserves suprema of \(\omega \)-chains). Thus (for a call-by-name language) a term \({x:A \vdash t:A}\) gives a continuous endofunction f, and the recursion \({\mathbf {rec}}\,x \,.\,M\) denotes the supremum of \((f^n\bot )_{n \in \mathbb {N}}\), the least (pre)fixpoint of f.

However, for the models of Abramsky et al.  (2000), Abramsky and McCusker (1997), and McCusker  (1998), the requirement of \(\omega \mathbf{{Cpo}}\)-enrichment is too restrictive, because the posets arising do not have suprema of all increasing \(\omega \)-chains (Normann 2006). So these papers use a more relaxed ordered framework where the only suprema that must be preserved are those of chains \((f^n \bot )_{n \in \mathbb {N}}\) of iterated applications. This means that any so called rational chain \((g \circ f^n \bot )_{n \in \mathbb {N}}\) has an upper bound given by \(g\left( \bigsqcup f^n \bot \right) \)—a property known as rational continuity (Wright et al. 1976; cf. also Bloom and Ésik 1993).

Recursion but Rationally. Our goal is to give an even more relaxed version of this “rational” framework for adequacy; one that uses no category theory, order or denotational model. It could be viewed as a purely syntactic result: a property of a theory (congruence) \(\approx \) rather than of a model. Thus we want \(t \Downarrow u\) to imply \(t \approx u\), and \(t \Uparrow \) to imply \(t\approx \varOmega \), where \(\varOmega \) is a divergent constant. The benefit of such a result is to modularize the narrative described at the start; we can get adequacy out of the way before we start studying categorical and denotational semantics.

Rational Continuity. Currently we have accomplished this goal for term-level recursion and polymorphic types. (Recursive and existential types are left to future work; see Sect. 6). Our result is that any theory (congruence) \(\approx \) will be sound and adequate provided it (a) contains the \(\beta \)-laws, fixpoint law and strictness laws and (b) is closed under an infinitary rule called rational continuity. This rule says (for a call-by-name language) that if \(C[{\mathbf {rec}}^{n}\, x \,.\,t] \approx D[{\mathbf {rec}}^{n}\, x\,.\,t]\) for infinitely many \(n \in \mathbb {N} \), then \(C[{\mathbf {rec}}\,x \,.\,t] \approx D[{\mathbf {rec}}\,x\,.\,t]\). Here we write \({\mathbf {rec}}^{n}\, x\,.\,t\) for the nth approximant to recursion, defined by the clauses \({\mathbf {rec}}^{0}\, x\,.\,t \mathrel {:=} \varOmega \) and \({\mathbf {rec}}^{n+1}\, x \,.\,t \mathrel {:=} t[{\mathbf {rec}}^{n}\, x\,.\,t/x]\).

Plan. To include both call-by-value (CBV) and call-by-name (CBN), we have established our result for call-by-push-value. The latter has both value types and computation types, but the treatment of value types in our proof is more complicated, so we begin in the CBN setting, which has only computation types. Our CBN account itself begins with PCF, which has only base types and function types; we then include sum types, using a proof method adapted from McCusker  (1998). Next we move to call-by-push-value, and use ultimate pattern matching of values (Lassen and Levy 2008) to treat the value types. Finally we include polymorphic types.

Related Work. Adequacy of topos models has been studied using an internal language (Simpson 2004). Other adequacy results for polymorphic models include realizability semantics (Møgelberg 2009) and game semantics (Laird 2013).

2 PCF

Language. We begin by introducing a version of Plotkin’s PCF (1997) that replaces fixpoint combinators with recursion operators and an explicit divergence construct \(\varOmega \) (Table 1). As per usual, terms are taken up to \(\alpha \)-equivalence. The set of closed terms of type T will be denoted by \(\text {CTerms}^T\) and that of normal forms by \(\text {NF}^T\). For a closed term t there is at most one v such that \(t \mathbin {\Downarrow }v\); when there is none we say it diverges and represent this by \(t \Uparrow \).
Table 2.

Rationally continuous \(\beta \)-\(\varOmega \)-fix theory of PCF

2.1 A Rationally Continuous Theory of PCF

The Theory. A congruence on terms is a type-indexed equivalence relation on closed terms of said type satisfying \(t \approx t' \implies C[t] \approx C[t']\) for any context \(C[-]\) where the hole is closed. (We omit type annotations.) A congruence is a rationally continuous \(\beta \)-\(\varOmega \)-fix theory if it also satisfies the rules in Table 2.

The basis for the theory are the obvious \(\beta \) rules that mimic the reduction rules. In a similar vein, the fixpoint rule establishes that each recursive term is the fixpoint of a substitution. These rules alone are enough to establish the soundness of the theory with respect to reduction.

Proposition 1

(Soundness). Any congruence \(\approx \) satisfying the \(\beta \) and fixpoint rules (Table 2) is sound: \( t \mathbin {\Downarrow }r \implies t \approx r \).

A Converse. Our sights now turn to proving that divergent terms are identical to \(\varOmega \). The extra requirement calls for a more refined theory that can more closely mirror the behaviour of reduction. The last two sets of equations in Table 2 fill the gaps in what the reduction rules don’t say about divergence. The first relates to the strictness of the operators: divergence of an argument leads to the divergence of the operator, e.g., \( \varOmega u \approx \varOmega \). The second is the rational continuity rule presented in the introduction.

Rational Continuity and Chains. To prove adequacy, one often has to re-write or equate certain terms built with recursion either with some constant or as the unrolling of the recursive term a few times. In cpo models, continuity and compositionality of the interpretations validate the following ruleBut this can be further weakened by requiring only equality at infinitely many n, for then one would still be able to define chains with exactly the same least upper bounds. We write \(\exists ^\infty n . P(n)\) to mean there exist infinitely many n in \(\mathbb {N} \) for which P(n) holds. This leads us to the syntactic continuity rule in Table 2. Since adequacy refers solely to closed terms, we only require this property for \(x : T \vdash t : T\)—and therefore \({\mathbf {rec}}^{n}\, x \,.\,t\) and \({\mathbf {rec}}\,x\,.\,t\) are closed. Similarly, by a rational chain we mean a chain of the form \(C[{\mathbf {rec}}\,^n x \,.\,t]\) for infinitely many \(n \in \mathbb {N} \), and by its limit we mean the term \(C[{\mathbf {rec}}\,x \,.\,t]\).

2.2 Adequacy

The Claim. We now embark on the syntactic journey towards a proof we have an adequate theory—formally, that \( t \Uparrow \implies t \approx \varOmega \). By the aforementioned reasons the proof follows the usual approaches by replacing closure under bottom elements and least upper bounds of the relevant chains with closure under divergence and limits of rational chains.

Approximations. First we define abstractly1 the notion of an approximation candidate between terms and the values they approximate; these are then extended to relations on terms. The concrete relations we use for each type are given by certain actions on approximation candidates (cf., e.g., Pitts 2000). When using the result of an action \(\phi \) on approximation candidates \(\mathrel {\triangleleft }_1,\ldots , \mathrel {\triangleleft }_n\) infix, we will sometimes surround the result with brackets, as in \(t \mathrel {\left\langle \phi (\mathrel {\triangleleft }_1,\ldots ,\mathrel {\triangleleft }_n)\right\rangle }u\), to aid readability.

Definition 1

(Approximation Candidates). An approximation candidate \(\mathrel {\triangleleft }\) for a type T is a subset of \(\text {CTerms}^T \times \text {NFs}^T\) s.t.:
  1. 1.

    \(\approx \) Extension: \( t \approx t' \text { and }t' \mathrel {\triangleleft }v \implies t \mathrel {\triangleleft }v \)

     
  2. 2.
    Rational Admissibility: for \(x : T \vdash t : T\)
    $$ (\exists ^\infty n. C[{\mathbf {rec}}^{n}\, x \,.\,t] \mathrel {\triangleleft }v) \implies C[{\mathbf {rec}}\,x \,.\,t ] \mathrel {\triangleleft }v $$
     

Proposition 2

If \(\mathrel {\triangleleft }\) is an approximation candidate for type T, then the binary relation on \(\text {CTerms}^T\) defined by
$$ t \mathrel {\triangleleft }^c u \iff t \approx \varOmega \text { or }(\exists v . u \mathbin {\Downarrow }v \text { and }t \mathrel {\triangleleft }v)$$
satisfies the following properties:
  1. 1.

    \(\varOmega \) Property: \( \varOmega \mathrel {\triangleleft }^c u\) , for any \(u \in \text {CTerms}^T\)

     
  2. 2.

    \(\approx \) Extension: \( t \approx t' \text { and }t' \mathrel {\triangleleft }^c u \implies t \mathrel {\triangleleft }^c u \)

     
  3. 3.

    \(\mathbin {\Downarrow }\) Extension: \( t \mathrel {\triangleleft }^c u \text { and }(\forall v . u \mathbin {\Downarrow }v \implies u' \mathbin {\Downarrow }v) \implies t \mathrel {\triangleleft }^c u' \)

     
  4. 4.
    Rational Admissibility: for \(x : T \vdash t : T\)
    $$ (\exists ^\infty n. C[{\mathbf {rec}}^{n}\, x\,\,.\,\,t] \mathrel {\triangleleft }^c u) \implies C[{\mathbf {rec}}\,x \,.\,t ] \mathrel {\triangleleft }^c u $$
     

Proof

To give a taste of how the proofs go using rational admissibility, assume we have \(\exists ^\infty n. C[{\mathbf {rec}}^{n}\, x \,.\,t] \mathrel {\triangleleft }^c u\). From the definition, one of two options (possibly both) is true: that an infinite number of terms on the left are identical to \(\varOmega \); or that for an infinite series of m, \(C[{\mathbf {rec}}^{m}\, x \,.\,t]\) is related to the value v that u reduces to (determinism of reduction is paramount here). Admissibility then follows by rational continuity in the first case (using the obvious constant context), and by admissibility of \(\mathrel {\triangleleft }\) (Definition 1) in the second.

Proposition 3

(Base Type Actions). The two binary relations \({\mathrel {\triangleleft }_{\text {Bool}}} \subseteq {\text {CTerms}^\text {Bool}\times \text {NFs}^\text {Bool}}\) and \({\mathrel {\triangleleft }_{\text {Nat}}} \subseteq {\text {CTerms}^\text {Nat}\times \text {NFs}^\text {Nat}}\) defined by
$$ t \mathrel {\triangleleft }_{\text {Bool}} v \iff t \approx v \quad \text { and }\quad t \mathrel {\triangleleft }_{\text {Nat}} v \iff t \approx v $$
are approximation candidates for \(\text {Bool}\) and \(\text {Nat}\).

Proposition 4

(Arrow Action). Given approximation candidates \(\mathrel {\triangleleft }_T\) for T and \(\mathrel {\triangleleft }_U\) for U, the binary relation between \(\text {CTerms}^{T \rightarrow U}\) and \(\text {NFs}^{T \rightarrow U}\)
$$ t \mathrel {\left\langle {\mathrel {\triangleleft }_T} \rightarrow {\mathrel {\triangleleft }_U}\right\rangle }\mathbf {\lambda } {x } . {u} \iff \forall p \mathrel {\triangleleft }^c_T q\ .\ t p \mathrel {\triangleleft }^c_U u[q/x]) $$
is an approximation candidate for \(T \rightarrow U\).

Definition 2

(Approximation Relation). The approximation relation \(\mathrel {\triangleleft }_T\) is the type-indexed family of approximation candidates defined by induction on types, where base types are covered by their respective actions (Proposition 3), and \(\mathrel {\triangleleft }_{T \rightarrow U} = {\mathrel {\triangleleft }_T} \rightarrow {\mathrel {\triangleleft }_U}\) (Proposition 4).

Definition 3

(Environments). Given a typing context \(\varGamma \), an environment \(\sigma \) for \(\varGamma \) is a substitution that maps each \(x : T \in \varGamma \) to a closed term of type \(\vdash \sigma (x) : T\). If \(\sigma _1\) and \(\sigma _2\) are two such, we write \(\sigma _1 \mathrel {\triangleleft }^c_\varGamma \sigma _2\) to mean \( \sigma _1(x) \mathrel {\triangleleft }^c_{T} \sigma _2(x) \) for all \(x : T \in \varGamma \).

Proposition 5

For any \(\varGamma \vdash t : T\) and environments \(\sigma _1 \mathrel {\triangleleft }^c_{\varGamma } \sigma _2\), \( t[\sigma _1] \mathrel {\triangleleft }^c_T t[\sigma _2] \).

Corollary 1

(Adequacy). For every closed \(\vdash t : T\), \( t \Uparrow \implies t \approx \varOmega \).

Proof

Applying Proposition 5 to \(\vdash t : T\) (for the empty substitution), we conclude that \(t \mathrel {\triangleleft }^c_T t\); the definition of \((-)^c\) (Proposition 2) asserts, then, that either \( t \approx \varOmega \) or \((t \mathbin {\Downarrow }v \text { and }t \mathrel {\triangleleft }_T v) \); whereby if \(t \Uparrow \), it can only be that \(t \approx \varOmega \).

3 PCF with Sums

The Extension. Sums provide a slight complication—but one which shows the adaptability of the method. The extension to call-by-name sums is presented in Table 3. With the new reduction rules come new \(\beta \) rules and divergence rules in the theory (Table 4). As before, reduction is deterministic and the theory is sound.
Table 3.

Extension of PCF with binary sums

Table 4.

Extension of the theory in Table 2 with binary sums

3.1 Adequacy

Action. The action for sums must reflect the structure of its parameters. That is for \(\mathrel {\triangleleft }_T\) we expect \(t \mathrel {\triangleleft }_{T+U} \mathop {\mathbf {inl}}\nolimits u \) exactly when (modulo the theory) t decomposes into some \(\mathop {\mathbf {inl}}\nolimits t' \) for which \(t' \mathrel {\triangleleft }_T u\). The assertion of that existence, though, causes us a small hiccup2 in proving that \( - \mathrel {\triangleleft }_{T+U} v\) is rationally admissible: If we have a series of \(C[{\mathbf {rec}}^{n}\, x \,.\,t] \mathrel {\triangleleft }_{T+U} \mathop {\mathbf {inl}}\nolimits u \), then we know that each of the terms on the left must be identical to some \(\mathop {\mathbf {inl}}\nolimits t_n\) with \(t_n \mathrel {\triangleleft }_T u\)—but do the \(t_n\) form a rational chain? It turns out that for every t, simply from the existence of \(t \approx \mathop {\mathbf {inl}}\nolimits t'\), and because each type is inhabited by \(\varOmega \), there is a context that can extract directly the \(t'\) (up to equivalence, obviously) from the original term. (An idea we borrowed from McCusker 1998)

Lemma 1

The contexts
$$ \mathcal {T} ^l[-] = {\mathbf {match}}\,- \,{\mathbf {as}}\left\{ \mathop {\mathbf {inl}}\nolimits x . x \, , \, \mathop {\mathbf {inr}}\nolimits y .\varOmega \right\} $$
$$ \mathcal {T} ^r[-] = {\mathbf {match}}\,- \,{\mathbf {as}}\left\{ \mathop {\mathbf {inl}}\nolimits x . \varOmega \, , \, \mathop {\mathbf {inr}}\nolimits y .y\right\} $$
satisfy \(t \approx \mathop {\mathbf {inl}}\nolimits u \implies \mathcal {T} ^l[t] \approx u \) and \( t \approx \mathop {\mathbf {inr}}\nolimits u \implies \mathcal {T} ^r[t] \approx u\).

Proposition 6

(Sum Action). Given approximation candidates \(\mathrel {\triangleleft }_T\) for T and \(\mathrel {\triangleleft }_U\) for U, the relation between \(\text {CTerms}^{T + U}\) and \(\text {NFs}^{T + U}\) defined by
$$ t \mathrel {\left\langle \mathrel {\triangleleft }_T + \mathrel {\triangleleft }_U\right\rangle }\mathop {\mathbf {inl}}\nolimits v \iff (\exists t' \mathrel {\triangleleft }^c_T u . t \approx \mathop {\mathbf {inl}}\nolimits t') $$
$$ t \mathrel {\left\langle \mathrel {\triangleleft }_T + \mathrel {\triangleleft }_U\right\rangle }\mathop {\mathbf {inr}}\nolimits v \iff (\exists t' \mathrel {\triangleleft }^c_U u . t \approx \mathop {\mathbf {inr}}\nolimits t') $$
is an approximation candidate for \(A + B\).

Proof

For rational admissibility, the pre-condition must hold for (at least) one of the two clauses in the definition. Say we have \(\exists ^\infty n. C[{\mathbf {rec}}^{n}\, x \,.\,t] \mathrel {\left\langle \mathrel {\triangleleft }_T + \mathrel {\triangleleft }_U\right\rangle }\mathop {\mathbf {inl}}\nolimits u\) with each term on the left equivalent to some \(\mathop {\mathbf {inl}}\nolimits t_n\); rewriting \( t_n \approx \mathcal {T} ^l[C[{\mathbf {rec}}^{n}\, x \,.\,t]] \) (Lemma 1) it follows that (Proposition 2)
$$ C[{\mathbf {rec}}^{n}\, x \,.\,t] \approx \mathop {\mathbf {inl}}\nolimits \mathcal {T} ^l[C[{\mathbf {rec}}^{n}\, x \,.\,t]] \text { and }\mathcal {T} ^l[C[{\mathbf {rec}}^{n}\, x \,.\,t]] \mathrel {\triangleleft }^c_T u $$
An application of rational continuity of the theory, and one of rational admissibility of \(\mathrel {\triangleleft }^c_T\) (again, Proposition 2) yields \( C[{\mathbf {rec}}\,x \,.\,t] \approx \mathop {\mathbf {inl}}\nolimits \mathcal {T} ^l[C[{\mathbf {rec}}\,x \,.\,t]]\) and also \(\mathcal {T} ^l[C[{\mathbf {rec}}\,x \,.\,t]] \mathrel {\triangleleft }^c_T u \) so that \( C[{\mathbf {rec}}\,x \,.\,t] \mathrel {\left\langle \mathrel {\triangleleft }_T + \mathrel {\triangleleft }_U\right\rangle }\mathop {\mathbf {inl}}\nolimits u \). (Likewise for the right injection.)

Adequacy. The rest of the proof of adequacy follows exactly as before. Approximation candidates for sums are derived by induction using the sum action; and with them we can extend Proposition 5.

4 Call-by-Push-Value

Values vs. Computations. We now turn to Call-by-push-value (Levy 2004). This language (Table 5) distinguishes between values and computations, with value types represented by A, \(A'\), etc., and computation types by \(\underline{B}\), \(\underline{B'}\), etc. The set of closed values of type A will be represented by \(\text {Vals}^A\); that of closed computations by \(\text {Comps}^{\underline{B}}\). Variables always have value type. Here we include value products and sums, products of computation types Open image in new window , types \(F A\) for computations aiming to return a value, and functions which in CBPV are computations taking values to computations. Central to CBPV, we also include value types \(U \underline{B}\) of suspended computations of type \(\underline{B}\)—which can be of one of two forms.
Table 5.

Call-by-push with recursion-value—syntax

Recursion. In addition to the usual \(\mathop {\mathbf {thunk}}\)s of computations, we also have recursively defined thunks \(\mathbf {threc}\, x . t\). An alternative would be to use recursive computations \(\varGamma \vdash ^c \mathop {\mathbf {rec}}\nolimits x . t : \underline{B}\). Although the two are equivalent via the definitions \( \mathop {\mathbf {rec}}\nolimits x . t \mathrel {:=} \mathop {\mathbf {force}}\mathbf {threc}\, x . t \) and \( \mathbf {threc}\, x . t \mathrel {:=} \mathop {\mathbf {thunk}}\mathop {\mathbf {rec}}\nolimits x . t \), there are two reasons for preferring \(\mathbf {threc}\): One is that, in some denotational models (e.g. state or continuation passing), \(\mathbf {threc}\) has a simpler denotation than \(\mathop {\mathbf {rec}}\nolimits \). The other is that a treatment based on \(\mathbf {threc}\) would be more easily adapted to call-by-value, where recursion and lambda are combined.
Table 6.

Call-by-push-value with recursion—reduction

Evaluation. Evaluation (Table 6) pertains only to computations. To those on the co-domain side of the evaluation relation \(\mathbin {\Downarrow }\), we call the terminal computations or, alternatively, the normal forms; and their (typed-indexed) set is represented by \(\text {NFs}^{\underline{B}}\). Since we have two forms of thunked computations, the action of forcing one such into execution much act accordingly; this \(\mathop { unthunk }\)ing (a derived operation on the syntax) returns the computations suspended inside \(\mathop {\mathbf {thunk}}\)s, or plucks out the computation from a Open image in new window suitably instantiated by the recursive thunk itself—i. e. Open image in new window . Note that reduction is deterministic.

4.1 Theory

Theory. By a (CBPV) congruence on closed terms we mean a type-indexed equivalence relation \(\approx \) on closed values and computations such that for all closed terms \(t \approx t'\) and (value or computation) context \(C[-]\) we have \(C[t] \approx C[t']\), respectively. A congruence is a rationally continuous \(\beta \)-\(\varOmega \)-fix theory when it satisfies the rules in Table 7. Rational chains are now those built by the application of a context \(C[-]\) to the (thunked) approximants \(\mathbf {threc}^n\) of recursive thunks and which are defined by the clauses Open image in new window and Open image in new window ; continuity is defined accordingly. Any congruence including the \(\beta \) and fixpoint rules is easily seen to be sound. We shall show that with the remaining rules it is also adequate.
Table 7.

Call-by-push-value with recursion—rationally continuous \(\beta \)-\(\varOmega \)-fix theory

4.2 Adequacy

Values: Empty Shells. In the proof of adequacy for PCF with sums we were required to introduce the tests so that we could, metaphorically, peek inside the injections and transform the rational chains there into equivalent ones with the properties we needed (cf. proof of Proposition 6). Here the problem expands to all value types. When checking rational admissibility, we need to decompose a value into its ultimate pattern and its constituent thunks (Lassen and Levy 2008, following ideas from Abramsky and McCusker 1997; also discernible in the work of Zeilberger 2008) and use those to find equivalent chains that can be used to establish adequacy.

Definition 4

(Ultimate Patterns). The set of of ultimate patterns \(\text {UP}^{A}\) for a value type A is given by induction on the following rules: \(-_{U \underline{B}} \in \text {UP}^{U \underline{B}}\), \(\left\langle \right\rangle \in \text {UP}^1\) andFor a given ultimate pattern \(p \in \text {UP}^A\) the finite sequence of hole-types in pattern p is given by induction by
$$\begin{aligned} H(-_{U \underline{B}})&= (U \underline{B})&H(\left\langle \right\rangle )&= \epsilon&H(\left\langle p , p' \right\rangle )&= H(p)\mathbin {++}H(p')\\ H(\mathop {\mathbf {inl}}\nolimits p)&= H(p)&H(\mathop {\mathbf {inr}}\nolimits p)&= H(p)\end{aligned}$$

Proposition 7

(Value Decomposition). Given \(\vdash ^v v : A\), there is a unique \(p \in \text {UP}^A\) and a unique sequence \((\vdash ^v v_i : H(p)_i)_{i < |H(p)|} \)—the filling—for which \(v = p \,@\, {(v_i)_{i < |H(p)|}} \), using the reassembly function

Tests. Ultimate patterns let us define the tests that extract the computations embedded in a given value. Like in the PCF sum case, we can use them to define values that are equivalent to a given one but make use only of the latter. If the values are derived from some family of contexts for the holes, then we can derive an equivalent context from the respective ultimate pattern.

Definition 5

For \(p \in \text {UP}^A\), and \( i < |H(p)|\), we define a context \(\mathop {\mathcal T}\nolimits ^{p }_{i}[-]\) by induction on \(p \in \text {UP}^A\) using the rules below. Note that when \(\varGamma \vdash ^v - : A\) the test has type \(\varGamma \vdash ^c \mathop {\mathcal T}\nolimits ^{p }_{i}[-] : \underline{B_i}\) where \(U \underline{B_i}= H(p)_i\).
$$\begin{aligned} \mathop {\mathcal T}\nolimits ^{-_{U B} }_0[-]&= \mathop {\mathbf {force}}-\\ \mathop {\mathcal T}\nolimits ^{\mathop {\mathbf {inl}}\nolimits p }_{i} [-]&= \mathbf {match}\,- \,\mathbf {as}\,\left\{ \mathop {\mathbf {inl}}\nolimits x . \mathop {\mathcal T}\nolimits ^{p }_{i}[x],\ \mathop {\mathbf {inr}}\nolimits y . \varOmega \right\} \\ \mathop {\mathcal T}\nolimits ^{\mathop {\mathbf {inr}}\nolimits p }_{i} [-]&= \mathbf {match}\,- \,\mathbf {as}\,\left\{ \mathop {\mathbf {inl}}\nolimits x . \varOmega ,\ \mathop {\mathbf {inr}}\nolimits y .\mathop {\mathcal T}\nolimits ^{p }_{i}[y] \right\} \\ \mathop {\mathcal T}\nolimits ^{\left\langle p , p' \right\rangle }_{i< |H(p)|}[-]&= \mathbf {match} - \mathbf {as}<{x , y}>.\, {\mathop {\mathcal T}\nolimits ^{p }_i [ x ]} \\ \mathop {\mathcal T}\nolimits ^{\left\langle p , p' \right\rangle }_{i=|H(p)| + i'}[-]&= \mathbf {match} - \mathbf {as} <{x , y}>.\, {\mathop {\mathcal T}\nolimits ^{p' }_{i'} [ y ]} \end{aligned}$$

Proposition 8

(Tests Decompose). Given a pattern \(p \in \text {UP}^A\), a sequence \((\vdash w_i : H(p)_i)_{i < |H(p)|}\), and \( i < |H(p)|\), we have \( \mathop {\mathcal T}\nolimits ^{p }_{i}[{p}\,@\,{(w_i)}_{i < |H(p)|}] \approx \mathop {\mathbf {force}}w_i \).

Proposition 9

For \(\vdash ^c t : F A\) , and \(p \in \text {UP}^{A}\), if \(t \approx \mathop {\mathbf {return\,}}p\,@\,{(v_i)_{i < |H(p)|}}\) then, successively:
  1. 1.

    \( \forall i < |H(p)| . \mathop {\mathbf {thunk}}(t \, \mathbin {\mathbf {to}} \,x.\, \mathop {\mathcal T}\nolimits ^{p }_i[x]) \approx v_i \)

     
  2. 2.

    \( p\,@\,{(v_i)_{i< |H(p)|}} \approx p\,@\,{(\mathop {\mathbf {thunk}}(t \, \mathbin {\mathbf {to}} \, x.\, \mathop {\mathcal T}\nolimits ^{p }_i[x]))_{i < |H(p)|}} \)

     
  3. 3.

    \( t \approx \mathop {\mathbf {return\,}}p\,@\,{(\mathop {\mathbf {thunk}}(t\, \mathbin {\mathbf {to}} \, x.\, \mathop {\mathcal T}\nolimits ^{p }_i[x]))_{i < |H(p)|}} \)

     

Approximation Candidates. Unlike PCF where we have computations and normal forms, CBPV has three levels of syntax: values, terminals, and computations. For the purposes of defining the needed approximation candidates, terminals (read: normal forms) and computations, behave like their PCF counterparts and have (now) familiar definitions of approximation candidates. Approximation candidates for value types enforce that: only structurally similar values are related; that they are (left) closed under equivalence of their holes; and that they are closed under the usual chains.

Definition 6

(Approximation Candidates). Given a value type A, an approximation candidate \(\mathrel {\triangleleft }\) for A is a subset of \(\text {Vals}^A \times \text {Vals}^A\) such that
  1. 1.

    Structural Matching: \( p \,@\,{(v_i)_i} \mathrel {\triangleleft }p'\,@\,{(w_i)_i} \implies p = p'\)

     
  2. 2.
    Computational \(\approx \) Extension: if \( p \,@\, (v'_i)_{i< |H(p)|} \mathrel {\triangleleft }p \,@\,{(w_i)_{i < |H(p)|}} \) then
    $$(\forall i< |H(p)| . v_i \approx v'_i) \implies p \,@\, (v_i)_{i< |H(p)|} \mathrel {\triangleleft }p \,@\, (w_i)_{i < |H(p)|} $$
     
  3. 3.
    Rational Admissibility: for \(x : U \underline{B}\vdash ^c t :\underline{B}\)
     
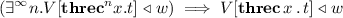
Given a computation type \(\underline{B}\), an approximation candidate \(\mathrel {\triangleleft }\) for \(\underline{B}\) is a subset of \(\text {Comps}^{\underline{B}} \times \text {NF}^{\underline{B}}\) such that
  1. 1.

    \(\approx \) Extension: \( t \approx t' \text { and }t' \mathrel {\triangleleft }r \implies t \mathrel {\triangleleft }r \)

     
  2. 2.
    Rational Admissibility: for \(x : U \underline{B}\vdash ^c t : \underline{B}\)
     

Proposition 10

Given a (computation) approximation candidate \(\mathrel {\triangleleft }\) on \(\underline{B}\), define its closure as the binary relation \(\text {Comps}^{\underline{B}} \times \text {Comps}^{\underline{B}}\) where
$$ t \mathrel {\triangleleft }^c u \iff t \approx \varOmega \text { or }(\exists r . u \mathbin {\Downarrow }r \text { and }t \mathrel {\triangleleft }r)$$
It satisfies the following properties:
  1. 1.

    \(\varOmega \) Property: \( \varOmega \mathrel {\triangleleft }^c u \) for any \(u \in \text {Comps}^{\underline{B}}\)

     
  2. 2.

    \(\approx \) Extension: \( t \approx t' \text { and }t' \mathrel {\triangleleft }^c u \implies t \mathrel {\triangleleft }^c u \)

     
  3. 3.

    \(\mathbin {\Downarrow }\) Extension: \( t \mathrel {\triangleleft }^c u' \text { and }(\forall r . u' \mathbin {\Downarrow }r \implies u \mathbin {\Downarrow }r) \implies t \mathrel {\triangleleft }^c u \)

     
  4. 4.
    Rational Admissibility: for \(x : U \underline{B}\vdash ^c t : \underline{B}\)
     

Actions. We can then define the actions on these approximation candidates associated with each type constructor. Mostly this is done by structure (for values) or by use (for computations); the exceptions are \(U \) types and \(F \) types that we define, respectively, by structure, and by use. Note that it is the existential quantification in the definition of the \(F \) action that—very much like PCF sums—requires the use of the tests. Using them, we can easily define, by induction, the approximation relation and thereby establish the adequacy of the theory.

Proposition 11

(Thunk Action). Let \(\mathrel {\triangleleft }\) be an approximation candidate for \(\underline{B}\). Then the binary relation
$$ v \mathrel {\left\langle U (\mathrel {\triangleleft })\right\rangle }w \iff \mathop {\mathbf {force}}v \mathrel {\triangleleft }^c \mathop { unthunk }w $$
is an approximation candidate for \(U \underline{B}\).

Proposition 12

(F Action). Let \(\mathrel {\triangleleft }\) be an approximation candidate for A. Then the following is an approximation candidate for \(F A\):
$$ t \mathrel {\left\langle F (\mathrel {\triangleleft })\right\rangle }\mathop {\mathbf {return\,}}w \iff \exists v \mathrel {\triangleleft }w. t \approx \mathop {\mathbf {return\,}}v $$

Definition 7

(Enviroments). Given a typing context \(\varGamma \), an environment \(\sigma \) for \(\varGamma \) is a substitution that maps each \(x : A \in \varGamma \) to a closed term of type \(\vdash ^v \sigma (x) : A\). If \(\sigma _1\) and \(\sigma _2\) are two such, we write \(\sigma _1 \mathrel {\triangleleft }_\varGamma \sigma _2\) to mean \( \sigma _1(x) \mathrel {\triangleleft }_{A} \sigma _2(x) \) for all \(x : A \in \varGamma \).

Proposition 13

For any \(\varGamma \vdash ^c t : B\) (resp. \(\varGamma \vdash ^v v : A\)), and environments \(\sigma _1 \mathrel {\triangleleft }_\varGamma \sigma _2\) we have \( t[\sigma _1] \mathrel {\triangleleft }_{\underline{B}}^c t[\sigma _2]\) (resp. \(v[\sigma _1] \mathrel {\triangleleft }_A v[\sigma _2]\)).

Corollary 2

(Adequacy). For any computation \(\vdash ^c t : \underline{B}\), if \( t \Uparrow \) then \( t \approx \varOmega \).

5 Polymorphic Call-by-Push-Value

Adequacy, Now For All. Our final extension deals with polymorphism. In Call-by-push-value, polymorphic types are computation types. We may quantify over both value and computation types. The extension is presented in Table 8.

We assume two disjoint countable sets of variables, \( X, Y, \ldots \in \text {VVars}\) and \(\underline{X}, \underline{Y}, \ldots \in \text {CVars}\), for value and computation types (resp.). Types are now also considered up to \(\alpha \)-equivalence. They will also be considered under context, \(\varTheta \vdash ^C \underline{B}\) and \(\varTheta \vdash ^V A\), where \(\varTheta \) is some finite subset of \(\text {VVars}\cup \text {CVars}\) that includes the free type variables of the A or \(\underline{B}\). (These type judgements have an obvious inductive definition). The proper extension of a type context \(\varTheta \) by a type variable \(\chi \) will be denoted by \( \chi , \varTheta \). Typing judgements also need to be annotated by a type context, as in \(\varTheta ; \varGamma \vdash ^c t :\underline{B}\) where \(\varTheta \) includes all the free type variables in the types of \(\varGamma \) and \(\underline{B}\). The previous typing rules are extended in the evident way.
Table 8.

Polymorphic Call-by-push-value with recursion

Reduction and Theory. Reduction—defined only for closed terms of closed type—is still deterministic. On the theory end of things, we equate only closed terms of closed type so that we need only extend the theory of Sect. 4 with the obvious \(\beta \) and divergence rules (Table 9). Unsurprisingly, soundness still stands.
Table 9.

Extension of the theory in Table 7 to polymorphism

5.1 Adequacy

Approximation Candidates and Actions. Throughout we have worked with approximation candidates—and now we can reap the fruits of that work. The definition of approximation candidates (Definition 6) and of their extension to computations (Proposition 10) can stay exactly the same; as can the actions for non-polymorphic type constructors. The actions of polymorphic types follow.

Proposition 14

Let \(Y \vdash ^C \underline{B}\) be a computation type, and \(\phi \) a mapping that assigns to every closed type T and approximation candidate \({\mathrel {\triangleleft }} \in \text {ACs}^{T}\) an approximation candidate \( \phi _{T,\mathrel {\triangleleft }} \in \text {ACs}^{\underline{B}[T/Y]}\); then
$$ t \mathrel {\left\langle \prod \nolimits Y.\phi \right\rangle }\varLambda Y . u \iff \text {for all }\vdash ^C T, {\mathrel {\triangleleft }} \in \text {ACs}^{T} .\, t T \mathrel {\left\langle \phi _{T,\mathrel {\triangleleft }}\right\rangle }^c u[T / Y] $$
is an approximation candidate for \(\prod \nolimits Y . \underline{B}\)—and likewise for \(\prod \nolimits \underline{Y}. \underline{B}\)

Approximations. The approximation relations need to be parametrized by the candidates that will instantiate the type variables so that in the end we arrive at a candidate for a closed type. As usual, we have that it satisfies the weakening and substitution properties that are used in the proof of adequacy for abstractions and type instantiations, respectively.

Definition 8

(Approximation Environment). An approximation environment \(\gamma \) for \(\varTheta \) is a map taking each \(\chi \in \varTheta \) to a closed type \(\gamma ^T(\chi )\) of the same kind as \(\chi \) and an adequacy candidate \(\gamma ^C(\chi ) \in \text {ACs}^{\gamma ^T(\chi )}\).

Definition 9

(Parametrized Approximation Relations). Let \(\varTheta \vdash ^V A\) (resp. \(\varTheta \vdash ^C \underline{B}\)) be a (possibly open) type and \(\gamma \) an approximation environment for \(\varTheta \). The following parametrized approximation relations, defined by induction on types, determine an approximation candidate for \(A[\gamma ^T]\)—i.e. A with each type variable \(\chi \) replaced with \(\gamma ^T(\chi )\) (resp. \(\underline{B}[\gamma ^T]\)).

Definition 10

For any \(\varTheta \) and approximation environment \(\gamma \) for \(\varTheta \), if \(\sigma _1\) and \(\sigma _2\) are environments for \(\varGamma [\gamma ^T]\), we write \( \sigma _1 \mathrel {\triangleleft }_{\varTheta ; \varGamma }^\gamma \sigma _2\) to mean \( \sigma _1(x) \mathrel {\triangleleft }^\gamma _{\varTheta \vdash ^V A} \sigma _2(x) \) for every \( x : A \in \varGamma \).

Proposition 15

For any \(\varTheta ; \varGamma \vdash ^c t : B\) (resp. \(\varTheta , \varGamma \vdash ^v v : A\)), approximation environment \(\gamma \) for \(\varTheta \), and environments \(\sigma _1 \mathrel {\triangleleft }_{\varTheta ; \varGamma }^\gamma \sigma _2\) for \(\varGamma \)
$$ t[\gamma ^T][\sigma _1] \mathrel {\left\langle \mathrel {\triangleleft }_{\varTheta \vdash ^C \underline{B}}^\gamma \right\rangle }^c t[\gamma ^T][\sigma _2] \qquad \left( \text {resp. } v[\gamma ^T][\sigma _1] \mathrel {\left\langle \mathrel {\triangleleft }_{\varTheta \vdash ^V A}^\gamma \right\rangle }v[\gamma ^T][\sigma _2]\right) $$

6 Concluding Remarks

We have thus seen how, for term-level recursion, the rational continuity rule coupled with \(\beta \), the fixpoint property of recursion, and strictness of the basic constructors of the language suffices to make a theory adequate. The recipe of the previous sections applies to both call-by-name and call-by-value languages and is compatible with polymorphic types. Along the way we used no category theory; no models were mentioned. We relied only on syntactic constructions and required no external machinery.

Two extensions are conspicuous for their absence: to existential types and to recursive types. In Call-by-push-value, existential types are value types. We conjecture our theorem holds for them but we must find a way to quantify over ultimate patterns. For recursive types, even finding suitable conditions on \(\approx \) is challenging. We would like to adapt Pitts’ (1996) method of minimal invariant relations but we will need type constructors to be functorial over suitable syntactic categories.

For term-recursion and polymorphism, however, we now know that to prove a model adequate we need only to show that it satisfies the basic laws and rational continuity.

Footnotes

  1. 1.

    Anticipating our treatment of polymorphism in Sect. 4, we have purposefully set up here a proof structure in the style of Girard  (1989).

  2. 2.

    A hiccup that will be much amplified in the proof of admissibility for \(\mathrel {\triangleleft }_{F A}\) (Sect. 4).

References

  1. Abramsky, S., Jagadeesan, R., Malacaria, P.: Full abstraction for PCF. Inf. Comput. 163(2), 409–470 (2000)MathSciNetCrossRefGoogle Scholar
  2. Abramsky, S., McCusker, G.: Call-by-value games. In: Nielsen, M., Thomas, W. (eds.) CSL 1997. LNCS, vol. 1414, pp. 1–17. Springer, Heidelberg (1998).  https://doi.org/10.1007/BFb0028004CrossRefGoogle Scholar
  3. Bloom, S.L., Ésik, Z.: Iteration Theories - The Equational Logic of Iterative Processes. EATCS Monographs on Theoretical Computer Science. Springer, Heidelberg (1993).  https://doi.org/10.1007/978-3-642-78034-9CrossRefzbMATHGoogle Scholar
  4. Fiore, M.P., Plotkin, G.D.: An axiomatization of computationally adequate domain theoretic models of FPC. In: LICS: IEEE Symposium on Logic in Computer Science (1994)Google Scholar
  5. Fiore, M.P.: Axiomatic Domain Theory in Categories of Partial Maps, Distinguished Dissertations in Computer Science, vol. 14. Cambridge University Press, Cambridge (1996)CrossRefGoogle Scholar
  6. Girard, J.Y., Lafont, Y., Taylor, P.: Proofs and Types, Cambridge Tracts in Theoretical Computer Science, vol. 7. Cambridge University Press, Cambridge (1989)Google Scholar
  7. Laird, J.: Game semantics for a polymorphic programming language. J. ACM 60(4), 29:1–29:27 (2013)MathSciNetCrossRefGoogle Scholar
  8. Lassen, S.B., Levy, P.B.: Typed normal form bisimulation for parametric polymorphism. In: Proceedings of the Twenty-Third Annual IEEE Symposium on Logic in Computer Science, LICS 2008, 24–27 June 2008, Pittsburgh, PA, USA, pp. 341–352 (2008)Google Scholar
  9. Levy, P.B.: Call-By-Push-Value: A Functional/Imperative Synthesis, Semantics Structures in Computation, vol. 2. Springer, Dordrecht (2004).  https://doi.org/10.1007/978-94-007-0954-6CrossRefGoogle Scholar
  10. McCusker, G.: Games and Full Abstraction for a Functional Metalanguage with Recursive Types. CPHC/BCS Distinguished Dissertations. Springer, London (1998).  https://doi.org/10.1007/978-1-4471-0615-9CrossRefzbMATHGoogle Scholar
  11. Møgelberg, R.E.: From parametric polymorphism to models of polymorphic FPC. Math. Struct. Comput. Sci. 19(4), 639–686 (2009)MathSciNetCrossRefGoogle Scholar
  12. Normann, D.: On sequential functionals of type 3. Math. Struct. Comput. Sci. 16(2), 279–289 (2006)MathSciNetCrossRefGoogle Scholar
  13. Pitts, A.M.: Relational properties of domains. Inf. Comput. 127(2), 66–90 (1996)MathSciNetCrossRefGoogle Scholar
  14. Pitts, A.M.: Parametric polymorphism and operational equivalence. Math. Struct. Comput. Sci. 10(3), 321–359 (2000)MathSciNetCrossRefGoogle Scholar
  15. Plotkin, G.D.: LCF considered as a programming language. Theor. Comput. Sci. 5(3), 223–255 (1977)MathSciNetCrossRefGoogle Scholar
  16. Simpson, A.K.: Computational adequacy for recursive types in models of intuitionistic set theory. Ann. Pure Appl. Log. 130(1–3), 207–275 (2004)MathSciNetCrossRefGoogle Scholar
  17. Wright, J.B., Thatcher, J.W., Wagner, E.G., Goguen, J.A.: Rational algebraic theories and fixed-point solutions. In: 1976 17th Annual Symposium on Foundations of Computer Science, pp. 147–158. IEEE (1976)Google Scholar
  18. Zeilberger, N.: Focusing and higher-order abstract syntax. In: Proceedings of the 35th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2008, pp. 359–369. ACM, New York (2008)Google Scholar

Copyright information

© The Author(s) 2018

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

Authors and Affiliations

  1. 1.School of Computer ScienceUniversity of BirminghamBirmignhamUK

Personalised recommendations

Cite paper

Download book