Abstract
The purpose of this paper is to define in a clean and conceptual way a non-deterministic and sheaf-theoretic variant of the category of simple games and deterministic strategies. One thus starts by associating to every simple game a presheaf category of non-deterministic strategies. The bicategory of simple games and non-deterministic strategies is then obtained by a construction inspired by the recent work by Melliès and Zeilberger on type refinement systems. We show that the resulting bicategory is symmetric monoidal closed and cartesian. We also define a 2-comonad which adapts the Curien-Lamarche exponential modality of linear logic to the 2-dimensional and non deterministic framework. We conclude by discussing in what sense the bicategory of simple games defines a model of non deterministic intuitionistic linear logic.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A new generation of 2-categorical and sheaf-theoretic game semantics is currently emerging in the field of programming language semantics. The games and strategies which determine them are more sophisticated mathematically, and also more difficult to define rigorously, than they were in the deterministic case. For that reason, it is timely to examine more closely the 2-categorical and sheaf-theoretic frameworks available to us in order to formulate these games and strategies in a suitably clean and conceptual way. In this investigation, one benefits from the efforts made in the past twenty-five years to give a clearer mathematical status to the previous generation of game semantics, which was (to a large extent) based on the notion of arena game. We recognize three main lines of work here:
-
1.
the logical approach advocated by Girard, and formulated in ludics [3], polarized linear logic [7] or tensorial logic [12] with its connection to continuations and string diagrams,
-
2.
the combinatorial approach advocated by Hyland, inspired by algebraic topology, and based on the combinatorial description of the structure of pointers in arena games [4],
-
3.
the concurrent and asynchronous approach advocated by Melliès, based on the description of arena games as asynchronous games, and of strategies as causal concurrent structures playing on them, either in an alternated [9,10,11] or in a non-alternated way [18].
Interestingly, all the sheaf-theoretic frameworks designed for game semantics today are offsprings of the third approach based on asynchronous games: on the one hand, the notion of concurrent strategy in [19] is a sheaf-theoretic transcription of the notion of receptive ingenuous strategy formulated in [18]; on the other hand, the sheaf-theoretic notion of non-deterministic innocent strategy in [13, 17] relies on the diagrammatic and local definition of innocence in alternated asynchronous games [11]. For that reason, our purpose in this paper is to investigate the connection with the second approach, different in spirit and design, and to define a bicategory of simple games and non-deterministic strategies in the sheaf-theoretic style of Harmer et al. [4]. As we will see, our work also integrates a number of elements coming from the first approach, and more specifically, the discovery by Melliès that strategies are presented by generators and relations, and for that reason, are prone to factorisation theorems [14, 15]. Since we are interested in sheaf-theoretic models of computations, we should not forget to mention the pioneering work by Hirschowitz and Pous on models of process calculi [5], and its recent connection to game semantics [2].
In the present paper, we start from the category  of simple games and deterministic strategies between them, and we explain how to turn
of simple games and deterministic strategies between them, and we explain how to turn  into a bicategory
into a bicategory  of simple games and non-deterministic strategies. As we will see, the construction of
of simple games and non-deterministic strategies. As we will see, the construction of  relies on the discovery of a number of elementary but fundamental fibrational properties of the original category
relies on the discovery of a number of elementary but fundamental fibrational properties of the original category  . Since our work is built on [4], let us recall that a simple game A is defined there as a contravariant presheaf \(A : \omega ^{op} \rightarrow \mathbf {Set}\) over the order category \(\omega = \begin{array}{ccccccc}0\rightarrow & {} 1\rightarrow & {} 2\rightarrow & {} \cdots \end{array}\) associated to the infinite countable ordinal \(\omega \). A simple game A is thus a family of sets \(A_{n}\) together with a function \(\pi _{n}:A_{n+1}\rightarrow A_{n}\) for all \(n\in \mathbb {N}\), depicted as:
. Since our work is built on [4], let us recall that a simple game A is defined there as a contravariant presheaf \(A : \omega ^{op} \rightarrow \mathbf {Set}\) over the order category \(\omega = \begin{array}{ccccccc}0\rightarrow & {} 1\rightarrow & {} 2\rightarrow & {} \cdots \end{array}\) associated to the infinite countable ordinal \(\omega \). A simple game A is thus a family of sets \(A_{n}\) together with a function \(\pi _{n}:A_{n+1}\rightarrow A_{n}\) for all \(n\in \mathbb {N}\), depicted as:

One requires moreover that \(A_{0}\) is the singleton set. The intuition is that \(A\) is a rooted tree; that \(A_{n}\) contains its plays (or branches) of length n; and that \(\pi _{n}\) is the prefix function which transports every play of length \(n+1\) to its prefix of length n. In particular, every simple game \(A\) contains only one play of length 0, which should be thought as the empty play. Every simple game \(A\) should be moreover understood as alternating: here, the intuition is that every play of odd length \(2n+1\) ends with an Opponent move, and that every play of even length 2n ends with a Player move if \(n>0\).
Terminology: An element \(a\in A_{n}\) is called a position of degree n in the game \(A\). The position \(a\in A_{n}\) is called a P-position when its degree n is even, and a O-position when its degree n is odd. Given a position \(a\in A_{n+1}\), we write \(\pi (a)\) for the position \(\pi _{n}(a)\); similarly, given a position \(a\in A_{n+2}\), we write \(\pi ^2(a)\) for the position \(\pi _{n}\circ \pi _{n+1}(a)\). A simple game A is called O-branching when the function \(\pi :A_{2n+2}\rightarrow A_{2n+1}\) is injective, for all \(n\in \mathbb {N}\). This means that every Opponent position \(a\in A_{2n+1}\) can be extended in at most one way into a Player position \(b\in A_{2n+2}\), for all \(n\in \mathbb {N}\).
We start the paper by formulating a sheaf-theoretic notion of non-deterministic P-strategy on a simple game A. Recall that a deterministic P-strategy \(\sigma \) of a simple game A is defined in [4] as a family of subsets \(\sigma _{2n}\subseteq A_{2n}\) of P-positions, satisfying the following properties, for all \(n\in \mathbb {N}\):
- (i) :
-
Unique empty play — \(\sigma _{0}\) is equal to the singleton set \(A_{0}\),
- (ii) :
-
Closure under even prefixes — if \(a \in \sigma _{2n+2}\) then \(\pi ^2(a) \in \sigma _{2n}\),
- (iii) :
-
Determinacy — if \(a,b \in \sigma _{2n}\) with \(\pi (a) = \pi (b)\), then \(a=b\).
In order to generalize this definition to non-deterministic P-strategies, we find convenient to consider the full subcategory \(\omega _{P}\) of \(\omega \) consisting of the strictly positive even numbers, of the form 2n for \(n>0\); and the inclusion functor \(\iota _P:\omega _P\rightarrow \omega \). Define the presheaf \(A_P=A\circ \iota _P\) as the simple game A obtained as the restriction of the presheaf \(A:\omega ^{op}\rightarrow \mathbf {Set}\) to the subcategory \(\omega _P\):

The collection \(A_P\) thus consists of all the Player positions in A, except for the initial one \(*\in A(0)\). This leads us to the following definition of (non-deterministic) P-strategy on a simple game A:
Definition 1
A P-strategy \(\sigma \) on a simple game A is a presheaf \(S:\omega _P^{\mathrm {op}}\rightarrow \mathbf {Set}\) over the category \(\omega _P\) together with a morphism of presheaves \(\sigma : S\rightarrow A_P\). We write \(\sigma :A\) in that case. The presheaf \(S\) is called the support of the strategy \(\sigma \) and the elements of \(S_{2n}\) are called the runs of degree 2n of the strategy, for \(n\ge 0\).
In other words, a P-strategy \(\sigma \) on \(A\) is a family of sets \(S_{2n}\) indexed by strictly positive numbers \(n>0\), related between them by functions \((\pi _P)_{2n}:S_{2n+2}\rightarrow S_{n}\) pictured as:

together with a family of functions \(\sigma _{2n}:S_{2n}\rightarrow A_{2n}\) making the diagram below commute, for all \(n>0\):

To every simple game A, we associate the category  of P-strategies over A, defined as the slice category
of P-strategies over A, defined as the slice category

whose objects are thus the strategies over A, and whose morphisms \(\theta :\sigma \rightarrow \tau \) between two strategies \(\sigma :S\rightarrow A\) and \(\tau :T\rightarrow A\) are the morphisms \(\theta :S\rightarrow T\) of presheaves satisfying the expected equation: \(\sigma =\tau \circ \theta \). We will call those simulations. One main contribution of the paper is the observation that the family of categories  can be organised into a pseudofunctor
can be organised into a pseudofunctor

from the category  of simple games and deterministic strategies. The pseudofunctor
of simple games and deterministic strategies. The pseudofunctor  is moreover monoidal, in the sense that there exists a family of functors
is moreover monoidal, in the sense that there exists a family of functors

indexed by simple games A, B. As a symmetric monoidal closed category, the category  is enriched over itself, with the simple game
is enriched over itself, with the simple game  constructed from the simple games A and B. Here comes the nice point of the construction: the bicategory
constructed from the simple games A and B. Here comes the nice point of the construction: the bicategory  is simply defined as the bicategory with simple games A, B as objects, and with
is simply defined as the bicategory with simple games A, B as objects, and with

as category of morphisms between two simple games A and B. In other words, a morphism \(\sigma :A\rightarrow B\) in  is a P-strategy \(\sigma :A\multimap B\), and a 2-cell \(\theta :\sigma \Rightarrow \tau : A\rightarrow B\) is a morphism \(\theta :\sigma \rightarrow \tau \) in the category
is a P-strategy \(\sigma :A\multimap B\), and a 2-cell \(\theta :\sigma \Rightarrow \tau : A\rightarrow B\) is a morphism \(\theta :\sigma \rightarrow \tau \) in the category  . At this point, the fact that
. At this point, the fact that  defines a bicategory is easily derived from the lax monoidal structure of the pseudofunctor
defines a bicategory is easily derived from the lax monoidal structure of the pseudofunctor  . Recall that, as a symmetric monoidal closed category, the category
. Recall that, as a symmetric monoidal closed category, the category  is enriched over itself. From a conceptual point of view, the construction of the bicategory
is enriched over itself. From a conceptual point of view, the construction of the bicategory  thus amounts to a change of enrichment category along the lax monoidal pseudofunctor
thus amounts to a change of enrichment category along the lax monoidal pseudofunctor  , transforming the
, transforming the  -enriched category
-enriched category  into the (weak) \(\mathbf {Cat}\)-enriched category
into the (weak) \(\mathbf {Cat}\)-enriched category  .
.
Besides the construction of  , a great care will be devoted to the analysis of the Curien-Lamarche exponential comonad ! on the category
, a great care will be devoted to the analysis of the Curien-Lamarche exponential comonad ! on the category  and to the recipe to turn it into an exponential 2-comonad on the bicategory
and to the recipe to turn it into an exponential 2-comonad on the bicategory  . The construction relies on the existence of a family of functors
. The construction relies on the existence of a family of functors

called “promotion” functors, and natural in the simple game A in the category  . In particular, the functorial part of the exponential 2-comonad
. In particular, the functorial part of the exponential 2-comonad  is defined as the composite:
is defined as the composite:

where \(n_{A,B}:{!{(A\multimap B)}} \rightarrow {!{A}}\multimap {!{B}}\) is the canonical morphism in  which provides the structure of a lax monoidal functor to the original comonad
which provides the structure of a lax monoidal functor to the original comonad  .
.
2 Non-deterministic P-strategies as P-cartesian Transductions
As explained in the introduction, a P-strategy  over a simple game A is defined as an object of the slice category (1) in the category \([\omega _P^{op},\mathbf {Set}]\) of contravariant presheaves over \(\omega _P\). We will use the fact that the slice category is equivalent to the category of contravariant presheaves
over a simple game A is defined as an object of the slice category (1) in the category \([\omega _P^{op},\mathbf {Set}]\) of contravariant presheaves over \(\omega _P\). We will use the fact that the slice category is equivalent to the category of contravariant presheaves

over the Grothendieck category \(\mathbf {tree}({A_P})\) generated by the presheaf \(A_P\in [\omega _P^{op},\mathbf {Set}]\). The category \(\mathbf {tree}({A_P})\) has the P-positions of the simple game \(A\) as objects, and a morphism \(a\rightarrow a'\) between \(a\in A_{2p}\) and \(a'\in A_{2q}\) precisely when \(p\le q\) and \(\pi ^{2q-2p}(a')=a\). In other words, it is the order category associated to the tree of P-positions of the simple game \(A\).
We find convenient for later purposes to reformulate non-deterministic P-strategies in the following way. This paves the way to a comprehension theorem for the pseudofunctor  , which will be established in the next section. A transduction \(\theta :A\rightarrow B\) between two simple games \(A,B:\omega ^{op}\rightarrow \mathbf {Set}\) is defined as a natural transformation between the presheaves A and B, given by a family of functions \(\theta _n:A_n\rightarrow B_n\) making the square \(\Box _n\) diagram below commute, for all \(n\in \mathbb {N}\):
, which will be established in the next section. A transduction \(\theta :A\rightarrow B\) between two simple games \(A,B:\omega ^{op}\rightarrow \mathbf {Set}\) is defined as a natural transformation between the presheaves A and B, given by a family of functions \(\theta _n:A_n\rightarrow B_n\) making the square \(\Box _n\) diagram below commute, for all \(n\in \mathbb {N}\):

A transduction \(\theta :A\rightarrow B\) is called P-cartesian when \(\Box _{2n}\) is a pullback square for all \(n\in \mathbb {N}\); and O-cartesian when \(\Box _{2n+1}\) is a pullback square for all \(n\in \mathbb {N}\). We write  for the category of simple games and transductions between them, and
for the category of simple games and transductions between them, and  (resp.
(resp.  ) for the subcategory of P-cartesian (resp. O-cartesian) transductions. Note that the restriction functor
) for the subcategory of P-cartesian (resp. O-cartesian) transductions. Note that the restriction functor
is a fibration, and that a transduction \(\theta :A\rightarrow B\) between simple games is P-cartesian precisely when it defines a cartesian morphism with respect to the fibration \((-)_P\). For that reason, a P-cartesian transduction \(\theta :A\rightarrow B\) is entirely characterized by the family of functions \(\theta _{2n}:A_{2n}\longrightarrow B_{2n}\) on the P-positions of the simple games A and B, for \(n\in \mathbb {N}\). From this follows easily that
Proposition 1
A P-strategy \(\sigma \) on a simple game A is the same thing as a simple game S together with a P-cartesian transduction \(S\rightarrow A\). The simple game S is uniquely determined by \(\sigma \) up to isomorphism. It is called the support (or run-tree) of \(\sigma \), and noted \(\{A\,|\,\sigma \}\), while the P-cartesian transduction is noted \(\mathsf {supp}_{\,\sigma } : \{A\,|\,\sigma \} \longrightarrow A\).
Note that the definition applies the general principle formulated in [18] that a strategy \(\sigma \) of a game A is a specific kind of map (here a P-cartesian transduction) \(S\rightarrow A\) from a given game \(S=\{A\,|\,\sigma \}\) to the game A of interest. One benefit of this principle is that it unifies the two concepts of game and of strategy, by regarding a strategy \(\sigma \) of a game A as a game S “embedded” in an appropriate way by \(S\rightarrow A\) inside the simple game A. This insight coming from [18] underlies for instance the construction in [19] of a category of non-deterministic strategies between asynchronous games.
Typically, consider the simple game \(A=\mathbb {B}_1\multimap \mathbb {B}_2\) where \(\mathbb {B}\) is the simple boolean game with a unique initial Opponent move q and two Player moves \(\mathsf {tt}\) for true and \(\mathsf {ff}\) for false; and where the indices 1, 2 are here to indicate the component of the boolean game \(\mathbb {B}\). The simple game A may be represented as the decision tree below:

where the sets of positions are defined as:
and where the branches are induced by the prefix functions \(\pi _{n}:A_{n+1}\rightarrow A_{n}\) depicted on the picture above. For the reader’s convenience, we label every edge of A by the name of the move which would be used in the more familiar definition of simple games, where plays are defined as sequences of moves [1, 6]. Note that every position \(a\in A_{n}\) of degree n is determined by its occurrence, defined as the sequence of n moves from the root \(*\) to the position a in the tree \(A\). Typically, the P-position \(b\in A_{2}\) has occurrence \(q_2\cdot q_1\) and the P-position \(b_{21}\in A_{4}\) has occurrence \(q_2\cdot q_1 \cdot \mathsf {tt}_1 \cdot \mathsf {ff}_2\).
By way of illustration, we define the P-strategy  as the presheaf below
as the presheaf below
on the Grothendieck category \(\mathbf {tree}({A_P})\) associated to the presheaf \(A_P\) of P-positions in \(A\). As explained in Proposition 1, the P-strategy \(\sigma \) may be equivalently defined as the simple game \(S=\{A\,|\,\sigma \}\) below

together with the P-cartesian transduction \(\mathsf {supp}_{\,\sigma }:\{A\,|\,\sigma \}\rightarrow A\) described as:
It is worth mentioning that the transduction \(\mathsf {supp}_{\,\sigma }\) may be recovered from the moves labelled on the run-tree \(S=\{A\,|\,\sigma \}\). This pictorial description provides a convenient way to describe how the non-deterministic P-strategy \(\sigma \) plays on A. Typically, when questioned by the initial move \(q_2\) of the game, the non-deterministic P-strategy \(\sigma \) answers \(\mathsf {tt}_2\) with the run \(x''\in S_{2}\) or asks the value of the input boolean by playing the move \(q_1\); when the Opponent answers with the move \(\mathsf {tt}_1\), the P-strategy reacts by playing the value \(\mathsf {ff}_2\) with the run \(z'\in S_{4}\) or by playing the value \(\mathsf {ff}_2\) with the runs \(z'', z'''\in S_{4}\). Note in particular that the P-strategy \(\sigma \) is allowed to play two different runs \(z'', z'''\in S_{4}\) of the same play \(b_{22}\in A_{4}\).
3 P-cartesian Transductions as Deterministic Strategies
In the previous section, we have seen how to regard every non-deterministic P-strategy  as a P-cartesian transduction \(\mathsf {supp}_{\,\sigma }:\{B\,|\,\sigma \}\rightarrow B\) into the simple game B. Our purpose here is to show that every P-cartesian transduction \(\theta :A\rightarrow B\) can be seen as a particular kind of deterministic strategy of the simple game \(A\multimap B\).
as a P-cartesian transduction \(\mathsf {supp}_{\,\sigma }:\{B\,|\,\sigma \}\rightarrow B\) into the simple game B. Our purpose here is to show that every P-cartesian transduction \(\theta :A\rightarrow B\) can be seen as a particular kind of deterministic strategy of the simple game \(A\multimap B\).
Definition 2
(Total strategies). A deterministic strategy \(\sigma \) of a simple game A is total when for every O-position s such that the P-position \(\pi (s)\) is an element of \(\sigma \), there exists a P-position t in the strategy \(\sigma \) such that \(\pi (t)=s\).
Definition 3
(Back-and-forth strategies). Given two simple games A and B, a back-and-forth strategy f of the simple game \(A\multimap B\) is a deterministic and total strategy whose positions are all of the form (c, a, b) where \(c:n\rightarrow n\) is a copycat schedule.
Back-and-forth strategies compose, and thus define a subcategory of  :
:
Definition 4
(The category  ). The category
). The category  of back-and-forth strategies is the subcategory of
of back-and-forth strategies is the subcategory of  whose objects are the simple games and whose morphisms \(f:A\rightarrow B\) are the back-and-forth strategies of \(A\multimap B\).
whose objects are the simple games and whose morphisms \(f:A\rightarrow B\) are the back-and-forth strategies of \(A\multimap B\).
As a matter of fact, we will be particularly interested here in the subcategory  of functional back-and-forth strategies in the category
of functional back-and-forth strategies in the category  .
.
Definition 5
(Functional strategies). A functional strategy f of the simple game \(A\multimap B\) is a back-and-forth strategy such that for every position \(a\in A_{n}\) of degree n in the simple game \(A\), there exists a unique position \(b\in B_{n}\) of same degree in \(B\) such that \((c,a,b)\in f\), where \(c:n\rightarrow n\) is the copycat schedule.
The following basic observation justifies our interest in the notion of functional strategy:
Proposition 2
For all simple games A, B, there is a one-to-one correspondence between the P-cartesian transductions \(A\rightarrow B\) and the functional strategies in \(A\multimap B\).
Proof
See Appendix E.
For that reason, we will identify P-cartesian transductions and functional strategies from now on. Put together with Proposition 1, this leads us to the following correspondence, which holds for every simple game A:
Proposition 3
The category  is equivalent to the slice category
is equivalent to the slice category  .
.
The result may be understood as a preliminary form of comprehension: it states that every non-deterministic P-strategy  may be equivalently seen as a functional P-strategy
may be equivalently seen as a functional P-strategy
in the category  of simple games and deterministic strategies, obtained by composing the equivalences stated in Propositions 1 and 3. Note that the simple game \(\{A\,|\,\sigma \}\) coincides with the run-tree S of the non-deterministic strategy \(\sigma \) formulated in Proposition 1 and that the functional strategy \(\mathsf {supp}_{\,\sigma }\) coincides with the P-cartesian transduction which “projects” the support S on the simple game A. The property (Proposition 3) is important from a methodological point of view, because it enables us to use the rich toolbox developed for simple games and deterministic strategies, in order to handle non-deterministic strategies inside the category
of simple games and deterministic strategies, obtained by composing the equivalences stated in Propositions 1 and 3. Note that the simple game \(\{A\,|\,\sigma \}\) coincides with the run-tree S of the non-deterministic strategy \(\sigma \) formulated in Proposition 1 and that the functional strategy \(\mathsf {supp}_{\,\sigma }\) coincides with the P-cartesian transduction which “projects” the support S on the simple game A. The property (Proposition 3) is important from a methodological point of view, because it enables us to use the rich toolbox developed for simple games and deterministic strategies, in order to handle non-deterministic strategies inside the category  .
.
4 The Pseudofunctor 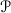
Suppose given a P-strategy  over the simple game A and a morphism \(f:A\rightarrow B\) in the category
over the simple game A and a morphism \(f:A\rightarrow B\) in the category  .
.
Definition 6
The P-strategy  over the simple game B is defined as the contravariant presheaf over \(\mathbf {tree}({B_P})\) which transports every P-position b of the simple game \(B\) to the disjoint union defined below:
over the simple game B is defined as the contravariant presheaf over \(\mathbf {tree}({B_P})\) which transports every P-position b of the simple game \(B\) to the disjoint union defined below:

The fact that (3) defines a presheaf over  and that
and that  is a pseudofunctor (see Definition 24) is established in the Appendix F.
is a pseudofunctor (see Definition 24) is established in the Appendix F.
This construction equips the family of presheaf categories  with the structure of a pseudofunctor
with the structure of a pseudofunctor  Moreover, the pseudo-functor
Moreover, the pseudo-functor  has comprehension in the sense of Lawvere [8]. For every simple game B, the comprehension functor is defined as the composite
has comprehension in the sense of Lawvere [8]. For every simple game B, the comprehension functor is defined as the composite

which transports every non-deterministic P-strategy to the morphism (2) seen as an object of  . One establishes that
. One establishes that
Theorem 1
(Comprehension). For every simple game B, the comprehension functor

has a left adjoint functor

Given a deterministic strategy \(f:A\rightarrow B\), the contravariant presheaf \(\mathsf {image}(f)\) over the category \(\mathbf {tree}({B_P})\) transports every P-position b of the game \(B\) to the set below:
Note that the presheaf \(\mathsf {image}(f)\) may be also described by the formula

where \(*_A\) is the terminal object in the category  of P-strategies over A. Note that the run-tree \(\{A\,|\,*_A\}\) of the P-strategy
of P-strategies over A. Note that the run-tree \(\{A\,|\,*_A\}\) of the P-strategy  is the simple game A itself, with \(\mathsf {supp}_{\,*_A}\) the identity \(i_A:A\rightarrow A\). In other words, the P-strategy \(*_A\) has exactly one run over each position of the simple game A.
is the simple game A itself, with \(\mathsf {supp}_{\,*_A}\) the identity \(i_A:A\rightarrow A\). In other words, the P-strategy \(*_A\) has exactly one run over each position of the simple game A.
Also note that we will occasionally note positions of \(\mathsf {image}(f)\) \(b_{(e,a)}\) when there is need to emphasize the fact that \(\mathsf {image}(f)\) is a contravariant presheaf over \(\mathbf {tree}({B_P})\).
5 The Slender-Functional Factorisation Theorem
In order to establish the comprehension theorem, we prove a factorization theorem in the original category  , which involves slender and functional strategies.
, which involves slender and functional strategies.
Definition 7
A deterministic strategy f in a simple game \(A \multimap B\) is slender when for every P-position b in the simple game B, there exists exactly one P-position a of the simple game A and exactly one schedule e such that \((e,a,b) \in f\).
By extension, we say that a morphism \(f:A\rightarrow B\) in the category  is slender when the deterministic strategy f is slender in \(A\multimap B\). Note that every isomorphism \(f:A\rightarrow B\) in the category
is slender when the deterministic strategy f is slender in \(A\multimap B\). Note that every isomorphism \(f:A\rightarrow B\) in the category  is both slender and functional.
is both slender and functional.
Proposition 4
Suppose that A and B are two simple games and that f is a deterministic strategy of \(A \multimap B\). Then, there exists a slender strategy \(g:A\rightarrow C\) and a functional strategy \(h:C\rightarrow B\) such that \(f=h \circ g\).
The simple game C is defined as \(\{B\,|\,\mathsf {image}(f)\}\) while the slender strategy \(g:A\rightarrow C\) is defined as
and \(h:C\rightarrow B\) is the functional strategy \(\mathsf {supp}_{\,\mathsf {image}(f)}\) associated in Proposition 3 to the P-strategy  .
.
Proposition 5
Suppose that \(s:U\rightarrow V\) and \(f:A\rightarrow B\) are two morphisms of the category  . Suppose moreover that s is slender and that f is functional. Then, \(s:X\rightarrow Y\) is orthogonal to \(f:A\rightarrow B\) in the sense that for all morphisms \(u:X\rightarrow A\) and \(v:Y\rightarrow B\) making the diagram (a) commute, there exists a unique morphism \(h:Y\rightarrow B\) making the diagram (b) commute in the category
. Suppose moreover that s is slender and that f is functional. Then, \(s:X\rightarrow Y\) is orthogonal to \(f:A\rightarrow B\) in the sense that for all morphisms \(u:X\rightarrow A\) and \(v:Y\rightarrow B\) making the diagram (a) commute, there exists a unique morphism \(h:Y\rightarrow B\) making the diagram (b) commute in the category  :
:

The deterministic strategy \(h:Y\rightarrow A\) is defined as
Note that the position b is uniquely determined by the position a because f is functional, and that the pair \((e',x)\) is uniquely determined by the position y because s is slender. Moreover, by determinism of \(u=h\circ s\), the schedule \(e''\) is entirely determined by the schedules e and \(e'\).
Theorem 2
(Factorization theorem). The classes  of slender morphisms and
of slender morphisms and  of functional morphisms define a factorization system
of functional morphisms define a factorization system  in the category
in the category  .
.
It is a folklore result that, in that situation, the comprehension theorem (Theorem 1) follows from the factorization theorem. The reason is that the category  is equivalent (by Proposition 3) to the full subcategory
is equivalent (by Proposition 3) to the full subcategory  of functional strategies in the slice category
of functional strategies in the slice category  . Seen from that point of view, the comprehension functor \(\{B\,|\,-\}\) coincides with the embedding of
. Seen from that point of view, the comprehension functor \(\{B\,|\,-\}\) coincides with the embedding of  into
into  . It is worth noting that for every P-strategy
. It is worth noting that for every P-strategy  , one has an isomorphism
, one has an isomorphism
in the category  , and that one has an isomorphism
, and that one has an isomorphism

in the category  , for every morphism \(f:A\rightarrow B\) in the category
, for every morphism \(f:A\rightarrow B\) in the category  . This provides an alternative way to define the pseudofunctor
. This provides an alternative way to define the pseudofunctor  .
.
6 The Bicategory  of Simple Games and Non-deterministic Strategies
of Simple Games and Non-deterministic Strategies
In this section, we explain how to construct a bicategory  of simple games and non-deterministic strategies, starting from the category
of simple games and non-deterministic strategies, starting from the category  . The first step is to equip the pseudofunctor
. The first step is to equip the pseudofunctor  with a lax monoidal structure (See Definition 25), based on the definition of tensor product in the category
with a lax monoidal structure (See Definition 25), based on the definition of tensor product in the category  formulated in [4], see Appendix B for details. We start by observing that
formulated in [4], see Appendix B for details. We start by observing that
Proposition 6
Suppose given two morphisms \(f:A\rightarrow B\) and \(g:C\rightarrow D\) in the category  of simple games and deterministic strategies. The morphism
of simple games and deterministic strategies. The morphism
is slender when f and g are slender, and functional when f and g are functional.
Proof
See Appendix G.
Note that the isomorphism \(\mathsf {image}(f \otimes g) \cong \mathsf {image}(f) \otimes \mathsf {image}(g)\) follows immediately from this statement and from the factorization theorem (Theorem 2), for every pair of morphisms \(f:A\rightarrow B\) and \(g:C\rightarrow D\) in the category  . The tensor product \(\sigma \otimes \tau \) of two P-strategies \(\sigma \) and \(\tau \) is defined in the same spirit, using comprehension:
. The tensor product \(\sigma \otimes \tau \) of two P-strategies \(\sigma \) and \(\tau \) is defined in the same spirit, using comprehension:
Definition 8
Suppose that  is a P-strategy of a simple game A and that
is a P-strategy of a simple game A and that  is a P-strategy of a simple game B. The tensor product \(\sigma \otimes \tau \) is the P-strategy of the simple game \(A\otimes B\) defined as
is a P-strategy of a simple game B. The tensor product \(\sigma \otimes \tau \) is the P-strategy of the simple game \(A\otimes B\) defined as
Here, the morphism \( \mathsf {supp}_{\,\sigma } \otimes \mathsf {supp}_{\,\tau } : \{A\,|\,\sigma \}\otimes \{B\,|\,\tau \} \rightarrow A\otimes B \) denotes the tensor product (computed in the original category  ) of the morphisms \(\mathsf {supp}_{\,\sigma }\) and \(\mathsf {supp}_{\,\tau }\). A direct description of
) of the morphisms \(\mathsf {supp}_{\,\sigma }\) and \(\mathsf {supp}_{\,\tau }\). A direct description of  is also possible, as the presheaf which transports every position (e, a, b) of the simple game \(A\otimes B\) to the set-theoretic product below:
is also possible, as the presheaf which transports every position (e, a, b) of the simple game \(A\otimes B\) to the set-theoretic product below:
As indicated in the introduction, the tensor product of P-strategies defines a family of functors  which, together with the isomorphism of categories
which, together with the isomorphism of categories  , equips the pseudofunctor
, equips the pseudofunctor  with a lax monoidal structure:
with a lax monoidal structure:
Theorem 3
The pseudofunctor  equipped with the family of functors \(m_{A,B}\) and \(m_1\) defines a lax monoidal pseudofunctor from
equipped with the family of functors \(m_{A,B}\) and \(m_1\) defines a lax monoidal pseudofunctor from  to \((\mathbf {Cat},\times ,1)\).
to \((\mathbf {Cat},\times ,1)\).
Proof
See Appendix H.
The bicategory  of simple games and non-deterministic strategies is deduced from the lax monoidal pseudofunctor
of simple games and non-deterministic strategies is deduced from the lax monoidal pseudofunctor  in the following generic way, inspired by the idea of monoidal refinement system [16].
in the following generic way, inspired by the idea of monoidal refinement system [16].
Definition 9
The bicategory  has simple games A, B, C as objects, with the hom-category
has simple games A, B, C as objects, with the hom-category  defined as
defined as

the composition functor

defined as the composite

where \(comp_{A,B,C} : (B\multimap C) \otimes (A \multimap B) \longrightarrow (A \multimap C)\) is the morphism which internalizes composition in the symmetric monoidal closed category  . In the same way, the identity in
. In the same way, the identity in  is defined as the composite
is defined as the composite

where the morphism \(id_A: 1\rightarrow (A\multimap A)\) internalizes the identity morphism in  .
.
Proposition 7
The bicategory  is symmetric monoidal closed in the sense that there exists a family of isomorphisms
is symmetric monoidal closed in the sense that there exists a family of isomorphisms

The isomorphism \(\varPhi _{A,B,C}\) is defined as the image by the pseudofunctor  of the isomorphism
of the isomorphism
in the category  between the underlying simple games. One benefit of our conceptual approach is that the monoidal closed structure of
between the underlying simple games. One benefit of our conceptual approach is that the monoidal closed structure of  is neatly deduced from the monoidal closed structure of the original category
is neatly deduced from the monoidal closed structure of the original category  .
.
7 The Exponentional Modality on the Category 
Now that the monoidal bicategory  has been defined, we analyze how the exponential modality defined in [4] adapts to our sheaf-theoretic framework.
has been defined, we analyze how the exponential modality defined in [4] adapts to our sheaf-theoretic framework.
Definition 10
Let A be a simple game. !A is the simple game whose set \((!A)_n\) of positions of degree n consists of the pairs \((\phi , \overline{a})\) such that:
-
\(\phi \) is a O-heap over n and \(\overline{a}=(a_1,\dots ,a_n)\) is a sequence of positions of A,
-
for each \(k\in \{1,\dots ,n\}\), the sequence of positions in \(\overline{a}=(a_1,\dots ,a_n)\) corresponding to the branch of k in \(\phi \) defines a play
$$\begin{aligned} \{a_k,a_{\phi (k)}, a_{\phi ^2(k)}, \dots \} \end{aligned}$$of the simple game A.
The predecessor function \(\pi _n:(!A)_{n+1}\rightarrow (!A)_{n}\) is defined as 
Definition 11
Let f be a deterministic strategy of \(A \multimap B\). The deterministic strategy !f of \({!A} \multimap {!B}\) consists of the positions \((e,(\phi ,\overline{a}), (\psi , \overline{b}))\) such that \(\phi =e^*\psi \) and, for each branch of \((\phi ,e,\pi )\), the positions associated to that branch are played by f.
It is worth observing that the construction of \({!f}:{!A}\rightarrow {!B}\) can be decomposed in the following way. Consider the morphism
obtained by currying the composite morphism

in the symmetric monoidal closed category  , where we use the coercion morphism which provides the exponential modality
, where we use the coercion morphism which provides the exponential modality  with the structure of a lax monoidal functor.
with the structure of a lax monoidal functor.
Definition 12
(\(\# f\)). Given a deterministic strategy f of a simple game A, the deterministic strategy \(\#f\) of the simple game !A has positions the pairs \((\phi ,\overline{a})\) such that for each branch of \((\phi ,\overline{a})\), the positions associated to that branch are played by the deterministic strategy f.
Proposition 8
Given a morphism \(f:A\rightarrow B\) of the category  and its curried form \(\lambda a. f\, :\, 1\rightarrow A\multimap B\), the composite morphism
and its curried form \(\lambda a. f\, :\, 1\rightarrow A\multimap B\), the composite morphism

is the curried form \(\lambda x:{!A}.\,\,{!f}\) in the category  of the morphism \({!f}:{!A}\longrightarrow {!B}\).
of the morphism \({!f}:{!A}\longrightarrow {!B}\).
More details about the original exponential modality in  will be found in Appendix C. By analogy with Proposition 6, we establish that
will be found in Appendix C. By analogy with Proposition 6, we establish that
Proposition 9
Suppose that \(f:A\rightarrow B\) is a morphism in the category  . Then, the morphism
. Then, the morphism
is slender when f is slender, and functional when f is functional.
Proof
See Appendix I.
8 The Exponential Modality on the Bicategory 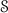
In this section, we define the linear exponential modality  on the symmetric monoidal closed bicategory
on the symmetric monoidal closed bicategory  , in order to define a bicategorical model of intuitionistic linear logic. The construction is inspired by the observation made in the previous section (Proposition 8).
, in order to define a bicategorical model of intuitionistic linear logic. The construction is inspired by the observation made in the previous section (Proposition 8).
Definition 13
Given a P-strategy  of a simple game A, the P-strategy \(\#\sigma \) of the simple game !A is defined as the image in
of a simple game A, the P-strategy \(\#\sigma \) of the simple game !A is defined as the image in  of the morphism
of the morphism
Note that the definition of \(\#\sigma \) induces a commutative diagram in the category 

where the top arrow is an isomorphism. Moreover, the definition of \(\#\sigma \) coincides with the previous definition (Definition 12) when the P-strategy \(\sigma =f\) happens to be deterministic.Consequently, for two games A, B and a deterministic strategy \(f:A\multimap B\), we have  and
and  .
.
As mentioned in the introduction, this construction \(\sigma \mapsto \#\sigma \) defines a functor

Now, remember that a morphism \(\sigma :A\rightarrow B\) of the bicategory  is defined as a P-strategy
is defined as a P-strategy

For that reason, every such morphism \(\sigma :A\rightarrow B\) induces a P-strategy

In order to turn the P-strategy \(\#\sigma \) into a P-strategy

we apply the functor

to the P-strategy \(\#\sigma \), where
denotes the structural morphism of  defined in the previous section. The construction may be summarized as follows:
defined in the previous section. The construction may be summarized as follows:
Definition 14
The morphism \({!\sigma }:{!A}\rightarrow {!B}\) of the bicategory  associated to the morphism \(\sigma :A\rightarrow B\) is defined as the P-strategy
associated to the morphism \(\sigma :A\rightarrow B\) is defined as the P-strategy

Theorem 4
With this definition,  defines a pseudofunctor from the bicategory
defines a pseudofunctor from the bicategory  to itself.
to itself.
Proof
See Appendix J.
The family of morphisms
are defined with the same deterministic strategies in  and
and  as in the original category
as in the original category  . One checks that the families \(\delta \) and \(\varepsilon \) define natural transformations between pseudonatural functors on
. One checks that the families \(\delta \) and \(\varepsilon \) define natural transformations between pseudonatural functors on  (as defined in Definition 26), and that the 2-functor
(as defined in Definition 26), and that the 2-functor  defines a 2-comonad in the appropriate bicategorical sense (see Definition 27). The family of morphisms
defines a 2-comonad in the appropriate bicategorical sense (see Definition 27). The family of morphisms
are defined with the same deterministic strategies in  and
and  as in the original category
as in the original category  , and one checks that they define natural transformations between pseudonatural functors on
, and one checks that they define natural transformations between pseudonatural functors on  . One obtains in this way that
. One obtains in this way that
Theorem 5
The bicategory p equipped with the exponential modality \(!:\) defines a bicategorical model of multiplicative intuitionistic linear logic.
The formal and rigorous verification of these facts would be extremely tedious if done directly on the bicategory  of nondeterministic strategies. Our proof relies on the fact that the constructions of the model (Definitions 9, 14) are performed by “push” functors
of nondeterministic strategies. Our proof relies on the fact that the constructions of the model (Definitions 9, 14) are performed by “push” functors  above a structural morphism f living in the original category
above a structural morphism f living in the original category  . The interested reader will find part of the detailed proof in Appendix K.
. The interested reader will find part of the detailed proof in Appendix K.
9 Conclusion
We construct a bicategory  of simple games and non-deterministic strategies, which is symmetric monoidal closed in the extended 2-dimensional sense. We then equip the bicategory
of simple games and non-deterministic strategies, which is symmetric monoidal closed in the extended 2-dimensional sense. We then equip the bicategory  with a linear exponential modality
with a linear exponential modality  which defines a bicategorical model of intuitionistic linear logic. This provides, as far as we know, the first sheaf-theoretic and non-deterministic game semantics of intuitionistic linear logic — including, in particular, a detailed description of the exponential modality.
which defines a bicategorical model of intuitionistic linear logic. This provides, as far as we know, the first sheaf-theoretic and non-deterministic game semantics of intuitionistic linear logic — including, in particular, a detailed description of the exponential modality.
References
Curien, P.-L.: On the symmetry of sequentiality. In: Brookes, S., Main, M., Melton, A., Mislove, M., Schmidt, D. (eds.) MFPS 1993. LNCS, vol. 802, pp. 29–71. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58027-1_2
Eberhart, C., Hirschowitz, T.: Justified sequences in string diagrams: a comparison between two approached to concurrent game semantics (2016)
Girard, J.Y.: Locus Solum: from the rules of logic to the logic of rules. Math. Struct. Comput. Sci. 11(03), 301–506 (2001)
Harmer, R., Hyland, J.M.E., Melliès, P.-A.: Categorical combinatorics for innocent strategies. In: LICS, pp. 379–388 (2007)
Hirschowitz, T., Pous, D.: Innocent strategies as presheaves and interactive equivalences for CCS. Sci. Ann. Comput. Sci. (2012)
Hyland, M.: Game semantics. In: Semantics of Logics and Computation, Publications of the Newton Institute, pp. 131–184. Cambridge University Press (1997)
Laurent, O.: Polarized games. Ann. Pure Appl. Logic 130(1–3), 79–123 (2004)
Lawvere, F.W.: Equality in hyperdoctrines and comprehension schema as an adjoint functor. In: Proceedings of the New York Symposium on Applications of Categorical Algebra, pp. 1–14 (1970)
Melliès, P.-A.: Asynchronous games 3: an innocent model of linear logic. In: Category Theory and Computer Science, pp. 171–192 (2004)
Melliès, P.-A.: Asynchronous games 4: a fully complete model of propositional linear logic. In: LICS 2005 (2005)
Melliès, P.-A.: Asynchronous games 2: the true concurrency of innocence. Theor. Comput. Sci. 358, 200–228 (2006)
Melliès, P.-A.: Game semantics in string diagrams. In: LICS 2012 (2012)
Melliès, P.-A.: Tensorial logic with algebraic effects. Talk at the Institut Henri Poincaré, June 2014
Melliès, P.-A.: Dialogue categories and chiralities. In: Publications of the Research Institute in Mathematical Sciences (2015)
Melliès, P.-A.: Une étude micrologique de la négation. Habilitation thesis (2017)
Mellies, P.-A., Zeilberger, N.: Functors are type refinement systems (2015)
Ong, C.H.L., Tsukada, T.: Nondeterminism in game semantics via sheaves. In: LICS 2016 (2016)
Melliès, P.-A., Mimram, S.: Asynchronous games: innocence without alternation. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 395–411. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74407-8_27
Rideau, S., Winskel, G.: Concurrent strategies. In: LICS 2011 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A The Category  of Simple Games and Deterministic Strategies
of Simple Games and Deterministic Strategies
We recall the construction of the category \(\varUpsilon \) of schedules performed in [4] and how we deduce from it the category  of simple games and deterministic strategies.
of simple games and deterministic strategies.
Definition 15
(Schedule). A schedule is defined as a function \(e:\{1,\dots ,n\}\rightarrow \{0,1\}\) verifying \(e(1)=1\) and \(e(2k+1)=e(2k)\) whenever \(1\le 2k \le n-1\). The number of 0’s and 1’s in e are noted \(|e|_0\) and \(|e|_1\) respectively. A schedule e is noted \(e: |e|_0 \rightarrow |e|_1\).
A schedule \(e:p\rightarrow q\) may be equivalently seen as a couple \(l:(p) \rightarrow (p + q) \) and \(r :(q) \rightarrow (p + q)\) of order-preserving and globally surjective functions, such that \(r(1) = 1\) and
for all \(1\le i\le p-1\) and \(1\le j\le q-1\), where (n) stands for the finite ordinal \((n)=\{1,\dots , n\}\).
Definition 16
The category of schedules \(\varUpsilon \) has the natural numbers as objects, the schedules \(e:p\rightarrow q\) as morphisms from p to q.
The identity morphism \(c:p\rightarrow p\) is the copycat schedule c characterized by the fact that \(c(2k+1)\ne c(2k+2)\) for all \(1\le 2k\le 2p\). Details on the composition of two schedules \(e:p\rightarrow r\) and \(e':r\rightarrow q\) as a schedule \(e\centerdot e':p\rightarrow q\) can be found in [4]. Now, we explain how we derive the category  from the category \(\varUpsilon \). We start by defining the simple game \(A\multimap B\) of linear maps from A to B:
from the category \(\varUpsilon \). We start by defining the simple game \(A\multimap B\) of linear maps from A to B:
Definition 17
The simple game \(A \multimap B\) is defined as the set \((A\multimap B)_n\) of all the triples (e, a, b) consisting of a schedule \(e : p\rightarrow q\) with \(p+q=n\), a position \(a \in A_{p}\) and \(b \in B_{q}\). The predecessor function \(\pi \) is defined as

Definition 18
The category  has simple games A, B as objects, and deterministic P-strategies f, g of \(A\multimap B\) as morphisms from A to B. Note that we use latin letters instead of greek letters for deterministic strategies. The identity morphism \(i_A : A \rightarrow A\) is defined as the P-strategy of \(A\multimap A\) whose positions of degree 2n are the triples (c, a, a) where \(c:n\rightarrow n\) is the copycat schedule, and \(a\in A_{n}\). The composite \(g \circ f: A \rightarrow C\) of two deterministic P-strategies \(f : A \rightarrow B\) and \(g : B \rightarrow C\) is the deterministic P-strategy whose set of positions of degree 2n is defined as
has simple games A, B as objects, and deterministic P-strategies f, g of \(A\multimap B\) as morphisms from A to B. Note that we use latin letters instead of greek letters for deterministic strategies. The identity morphism \(i_A : A \rightarrow A\) is defined as the P-strategy of \(A\multimap A\) whose positions of degree 2n are the triples (c, a, a) where \(c:n\rightarrow n\) is the copycat schedule, and \(a\in A_{n}\). The composite \(g \circ f: A \rightarrow C\) of two deterministic P-strategies \(f : A \rightarrow B\) and \(g : B \rightarrow C\) is the deterministic P-strategy whose set of positions of degree 2n is defined as
B The Tensor Product in the Category 
Definition 19
(Tensorial schedule). A \(\otimes \)-schedule is a function \(e:\{1,\dots ,n\}\rightarrow \{0,1\}\) verifying \(e(2k+1)=e(2k+2)\) whenever \(0\le 2k \le n-2\).
Definition 20
(\(A\otimes B\)). The positions of the simple game \(A \otimes B\) of degree n are the triples (e, a, b) where \(e : p\otimes q\) is a \(\otimes \)-schedule with \(p+q=n\), \(a \in A_{p}\) and \(b \in B_{q}\). The predecessor function \(\pi \) is defined as

The simple game 1 is the simple game with a unique position \(*\), of degree 0.
We can also define \(\otimes \) on strategies. Intuitively, for \(f:A\rightarrow B\) and \(g:C\rightarrow D\) two morphisms of the category  , the plays of the strategy \({f \otimes g}\) of the simple game \({(A\otimes C) \multimap (B \otimes D)}\) are obtained by combining through a tensorial schedule plays of f and g.
, the plays of the strategy \({f \otimes g}\) of the simple game \({(A\otimes C) \multimap (B \otimes D)}\) are obtained by combining through a tensorial schedule plays of f and g.
The intuition is that, once we know the structure of f and g, the structure of plays of \({f \otimes g}\) is entirely directed by what happens in \({B \otimes D}\). The only agency that Opponent really has is to decide at some points whether to play on B or D, the rest being handled by the plays of f, g and the structure of \({(A\otimes C) \multimap (B \otimes D)}\). Formally, this gives the proposition:
Proposition 10
Let \(f:A\multimap B, g:C\multimap D\) be two deterministic strategies. Assuming a valid play of \(f \otimes g: A \otimes C \multimap B \otimes D\) and the associated schedules \(e:A\otimes C \rightarrow B \otimes D ,t_1:A \times C ,t_2:B \times D,e_1:A\rightarrow B, e_2:C\rightarrow D\), the knowledge of \(t_2,e_1,e_2\) is enough to reconstruct e and \(t_1\).
Proof
The first O move of such a play is in \(B \otimes D\) to follow the structure of \(A\otimes C \multimap B \otimes D\). This is given to us by \(t_2\). Let us assume it is a move in D (The other case is handled similarly).
The P move after that will necessarily be a move in C or D, as playing a move in A, B would break the structure of \(A\multimap B, B\otimes D\) respectively. \(e_2\) gives us the information.
-
If it is a move in D, We go back to a situation equivalent to the initial one. We have also started to reconstruct e, which starts by 11.
-
If it is a move in C, we start to reconstruct both e which starts by 10 and \(t_1\) which starts by 1.
In this last case, the following O move will be a move in C as a move in A, B, D would break the structure of \(A\multimap B, B\otimes D, C \multimap D\) respectively. e is then at 100 and \(t_1\) at 11.
Finally, the following P move will be a move in either C or D as a move in A, B would break the structure of \(A\multimap B, B\otimes D\) respectively. \(e_2\) gives us this information.
-
If it is a move in D, We go back to a situation equivalent to the initial one. We have also started to reconstruct e, which starts by 1001 and \(t_1\) which starts by 11. We’ve also played the first two moves of \(t_2\) which is at 11.
-
If it is a move in C, we go back to the precedent situation (the one with a fixed O move in C) with e at 1000 and \(t_1\) at 111.
To sum up the described construction, once an opponent move in B or D is played, the play is stuck playing in either \(A \multimap B\) or \(C \multimap D\) until a player move is played in B, D respectively. \(t_2\) decides whether to play the opponent move in B or D and \(e_1\) guides the play in \(A\multimap B\) in the first case, \(e_2\) guides it in \(C \multimap D\) in the second. This guides us through the whole play and allows us to reconstruct both e and \(t_1\).
In particular, any compatible plays of \(f,g , B \otimes D\) induce a play of \(f \otimes g\).
This proposition and its proof are key in several proofs we will make in the rest of the paper.
Proposition 11
The category  is symmetric monoidal closed.
is symmetric monoidal closed.
C The Exponential Modality on the Category 
In this section, we recall the combinatorial structures introduced in [4] to construct the linear exponential comonad  on the symmetric monoidal closed category
on the symmetric monoidal closed category  .
.
Definition 21
(Pointer function). A pointer function on n is a parity-reversing function
such that \(\phi (i)<i\) for all i. A pointer function \(\phi \) is called an O-heap if \(\phi (2k) = 2k -1\) for all k, and a P-heap if \(\phi (2k +1) = 2k \) for all k. The set \(\{k, \phi (k), \phi ^2(k),...\}\) will be called the branch of \(\phi \) associated to the integer k. Note that the predecessor function \(\pi \) defined as \(\pi (i) = i-1\) for all i is both an O-heap and a P-heap.
Definition 22
Suppose that \(e:p\rightarrow q\) is a schedule, that \(\phi \) is a O-heap over q and that \(\psi \) is a P-heap over p. The O-heap \((\phi ,e,\psi )\) on \(p+q\) is defined as follows:
where the schedule e is represented as a pair (l, r) as explained in Appendix A. Intuitively, the O-heap \((\phi ,e,\psi )\) points alongside \(\phi \) when the schedule e is at 1 and alongside \(\psi \) otherwise. The fact that \((\phi ,e,\psi )\) defines an O-heap is ensured by the even case.
We recall the partial order over the set of pointer functions introduced in [4].
Definition 23
(Generalization). Given two pointer functions \(\phi \), \(\psi \), we say that \(\phi \) is a generalization of \(\psi \), and note \(\phi \succeq \psi \), if the branch of \(\phi \) associated to \(k\in \{1,..,n\}\) can be injected in the branch of \(\psi \) associated to k, or, in other words, if for all k, there exists j such that \(\phi (k) = \psi ^j(k)\).
Further in the paper, and in certain proofs, we will also need to look into the structure of !!A. Intuitively, positions of !!A are pairs \((\phi , \overline{u})\) where \(\overline{u}\) is a sequence of positions of !A and \(\phi \) an O-heap. It is equivalent to another representation using only a sequence of positions of A:
Proposition 12
A position \((\phi , \overline{u})\) of !!A is equivalent to \((\phi , \psi , \overline{a})\) with \(\phi \succeq \psi \), \(\psi \) an O-heap, \(\overline{a}\) a sequence of positions of A, verifying
The moves alongside the branches of \(\psi \) are then plays of the simple game A.
From this follows a description of the strategy
for a deterministic strategy \(f:A \multimap B\). The positions of !!f are of the form
where \(e^*\phi '=\phi , e^*\psi '= \psi \) and each thread of \((\psi ,e,\pi )\) is a play of the strategy f.
D Some Bicategorical Definitions
In this section, we recall a few definitions required by our bicategorical setting.
Definition 24
A pseudofunctor is a mapping between bicategories  and
and  where the usual functorial equations \(F(f \circ g) = F(f) \circ F(g) \) and \(F(Id_A) = Id_{F(A)}\) are only valid up to natural bijectve 2-morphisms in
where the usual functorial equations \(F(f \circ g) = F(f) \circ F(g) \) and \(F(Id_A) = Id_{F(A)}\) are only valid up to natural bijectve 2-morphisms in  .
.
Definition 25
Let  and
and  be two monoidal bicategories. A lax monoidal pseudofunctor between them is given by:
be two monoidal bicategories. A lax monoidal pseudofunctor between them is given by:
-
a pseudofunctor \(F:\)
-
a morphism
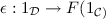
-
for every pair of objects
 , a natural transformation
, a natural transformation 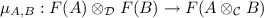
satisfying the following conditions:
-
associativity: For every triple of objects
 , the following diagram commutes:
, the following diagram commutes: 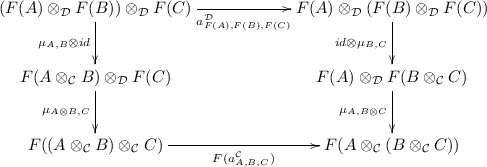
where the two morphisms
 denote the associators of the two tensor products.
denote the associators of the two tensor products. -
unality: For every object
 , the following diagram and its right symmetry both commute:
, the following diagram and its right symmetry both commute: 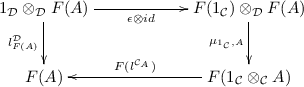
where
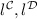 denote the left unitors of the two tensor products.
denote the left unitors of the two tensor products.
Definition 26
Let F, G be two pseudofunctors between two bicategories  and
and  . A pseudonatural transformation \(\phi : F \rightarrow G\) is given by:
. A pseudonatural transformation \(\phi : F \rightarrow G\) is given by:
-
for every object A of
 , a morphism \(\phi (A): F(A) \rightarrow G(A)\) of
, a morphism \(\phi (A): F(A) \rightarrow G(A)\) of  .
. -
for every morphism \(f:A \rightarrow B\) of
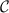 , a bijective \(2-\)morphism \(\phi (f): \phi (B) \circ F(f) \Rightarrow G(f) \circ \phi (A)\)
, a bijective \(2-\)morphism \(\phi (f): \phi (B) \circ F(f) \Rightarrow G(f) \circ \phi (A)\)
such that
-
\(\phi \) respects composition of morphisms, meaning that we have an equivalence between
$$\begin{aligned} (\phi (A) \triangleleft G(f,g) )\cdot (\phi (f) \triangleright G(g)) \cdot (F(f)\triangleleft \phi (g)) \end{aligned}$$and
$$\begin{aligned} \phi (g \circ f) \cdot (F(f,g) \triangleright \phi (C) ), \end{aligned}$$both being 2-morphisms from
$$\begin{aligned} \phi (C) \circ F(g) \circ F(f) \Rightarrow G(g \circ f) \circ \phi (A), \end{aligned}$$where \(\cdot \) is the vertical composition between 2-morphisms, \(\triangleleft , \triangleright \) the two versions of the horizontal composition between a morphism and a 2-morphism, (also called whiskering), anf \(F(f,g):F(g) \circ F(f) \Rightarrow F(g \circ f)\) is the bijective 2-morphism coming from the pseudofunctor F.
-
\(\phi \) respects the identity morphisms, meaning we have an equivalence between

and

both being 2-morphisms from
$$\begin{aligned} \phi (A) \circ F(id_A) \Rightarrow \phi (A) \end{aligned}$$where
 is the left unitor coming from the bicategory
is the left unitor coming from the bicategory  and \(\epsilon ^{F}_{id_A}: F(id_A) \Rightarrow id_{F(A)}\) is the bijective 2-morphism coming from the pseudofunctor F.
and \(\epsilon ^{F}_{id_A}: F(id_A) \Rightarrow id_{F(A)}\) is the bijective 2-morphism coming from the pseudofunctor F. -
\(\phi \) is natural in the following sense: for every 2-morphism \(\psi : f \Rightarrow g\) with \(f,g:A\rightarrow B\), we have an equivalence between
$$\begin{aligned} \phi (g) \cdot F(\psi ) \triangleright \phi (B) \end{aligned}$$and
$$\begin{aligned} \phi (A)\triangleleft G(\psi )\cdot \phi (f). \end{aligned}$$
Definition 27
A fully weak comonad G on a bicategory  is a pseudofunctor, along with pseudonatural transformations \(\delta \) and \(\epsilon \) that satisfy the usual laws of a comonad up to natural bijectiive 2-morphisms in
is a pseudofunctor, along with pseudonatural transformations \(\delta \) and \(\epsilon \) that satisfy the usual laws of a comonad up to natural bijectiive 2-morphisms in  .
.
E Proof of Proposition 2
Proof
Let A, B be two games.
Let \(\sigma \) be a P-cartesian transduction between A and B. The associated deterministic strategy \(f_\sigma \) is simply given by:
This definition clearly gives a functional strategy, the determinism being given by the fact that \(\sigma \) is P-cartesian.
Conversely, let f be a functional strategy of \(A\multimap B\). The associated P-cartesian transduction \(\sigma _f\) is given by:
Such a b is unique by functionality of f.
F Proof that  is a pseudofunctor
is a pseudofunctor
Proof
First we need to complete the definition of  by detailling why, for f a deterministic strategy of \(A\rightarrow B\) and \(\sigma \) a P-strategy over A,
by detailling why, for f a deterministic strategy of \(A\rightarrow B\) and \(\sigma \) a P-strategy over A,  is indeed a P-strategy over B, and thus a presheaf over \(\mathbf {tree}({B_P})\). For this, we need to define the collection of projector functions
is indeed a P-strategy over B, and thus a presheaf over \(\mathbf {tree}({B_P})\). For this, we need to define the collection of projector functions  as follows:
as follows:
For  over b (meaning
over b (meaning  and \(b \in B_{2n}\)), there exists by definition a unique e, a such that \((e,a,b) \in f\) and \(x \in \sigma (a)\). From this, we define:
and \(b \in B_{2n}\)), there exists by definition a unique e, a such that \((e,a,b) \in f\) and \(x \in \sigma (a)\). From this, we define:
By determinism of f, there is only one such k. Moreover, we also have \(\pi ^{k}_{\sigma }(x) \in \sigma (\pi ^{2k}_{A}(a))\). Consequently, by definition of  , we have
, we have  as expected.
as expected.
Next step is to show that, for a strategy \(f:A\rightarrow B\),  is a functor from
is a functor from  to
to  . For that, we need to define its effects on simulations. For \(\alpha : \sigma \rightarrow \tau \),
. For that, we need to define its effects on simulations. For \(\alpha : \sigma \rightarrow \tau \),  is simply defined by applying \(\alpha \) to all positions of
is simply defined by applying \(\alpha \) to all positions of  , as all those are induced from positions of \(\sigma \) by definition. With this, it is easy to verify that
, as all those are induced from positions of \(\sigma \) by definition. With this, it is easy to verify that  preserves identities and composition of simulations.
preserves identities and composition of simulations.
Finally, let us show that  is a pseudofunctor.
is a pseudofunctor.
First,  associates to a position a of A the set:
associates to a position a of A the set:

which is instantly isomorphic to \(\sigma (a)\). Factoring the effect on simulations, it is easy to build a bijective natural natural transformation between  . Thus
. Thus  .
.
Next, let \(f:A\rightarrow B\) and \(g:B \rightarrow C\) two deterministic strategies and \(\sigma \) a P-strategy of A. We have:

This is easily isomorphic to  which is given by:
which is given by:

This isomorphism is a consequence of the definition of composition for deterministic strategies, as there is only one triple \(e_1,e_2,b\) such that \((e_1,a,b) \in f\), \((e_2,b,c) \in g\) and \(e= e_1 \cdot e_2\) for a position \((e, a, c) \in g \circ f\).
This extends into a natural isomorphism between the functors  , giving us the fact that
, giving us the fact that  is indeed a pseudofunctor.
is indeed a pseudofunctor.
G Proof of Proposition 6
Proof
-
Let \(f:A\multimap B, g:C \multimap D\) be two slender strategies. Let \((t_2,b,d)\)be a player position of \(B \otimes D\). Since f and g are slender, there exist unique \(e_f,a,e_g,c\) such that \((e_f,a,b) \in f, (e_g,c,d) \in g\). Using \(t_2,e_f,e_g\) and Proposition 10, we reconstruct \(e,t_1\) such that \((e,(t_1,a,c),(t_2,b,d))\) is a position of \(f \otimes g\). This position is unique as the reconstruction of Proposition 10 is unique, and thus \(f\otimes g\) is a slender strategy.
-
Let \(f:A\multimap B, g:C \multimap D\) be two functional strategies. Let \((t_1,a,c)\) be an opponent position of \(A \otimes C\). Since f and g are functional strategies, there exist unique b, d such that \((cp_f,a,b) \in f, (cp_g,c,d) \in g\). The study of \(f \otimes g\) done in the proof of Proposition 10 gives us that any valid position of \(f \otimes g\) would have a copycat schedule (as the schedule is built from sequences \(1.0^k.1\) of \(cp_f\) and \(cp_g\). This implies immediately that the only possible position is \(cp, (t_1,a,c), (t_1,b,d)\) as no other play would verify the needed structures, and thus \(f\otimes g\) is a functional strategy.
H Proof of Theorem 3
Proof
First, we can note that the unit 1 of  has a unique P-strategy, the empty strategy. Consequently,
has a unique P-strategy, the empty strategy. Consequently,  is the singleton category, which is the unit of the cartesian product in \(\mathbf {Cat}\).
is the singleton category, which is the unit of the cartesian product in \(\mathbf {Cat}\).
Moreover, to extend  as a lax monoidal pseudofunctor, we need a transformation
as a lax monoidal pseudofunctor, we need a transformation  natural in A and B.
natural in A and B.
Since the morphisms of that transformation live in \(\mathbf {Cat}\), they are functors. We thus define:
for \(\sigma \) an object of  and \(\tau \) an object of
and \(\tau \) an object of  ,
,
for \(\alpha : \sigma \rightarrow \sigma '\) a morphism of  and \(\beta : \tau \rightarrow \tau '\) a morphism of
and \(\beta : \tau \rightarrow \tau '\) a morphism of  , \(\mu _{A,B}(\alpha , \beta ): \sigma \otimes \tau \rightarrow \sigma ' \otimes \tau '\) is defined by:
, \(\mu _{A,B}(\alpha , \beta ): \sigma \otimes \tau \rightarrow \sigma ' \otimes \tau '\) is defined by:
We now need to prove that this transformation is natural in A and B, and that it verifies the two commutative diagrams of a lax monoidal functor (associativity and unitality), up to bijective simulations. Those last two are easy to verify and use similar arguments, so we will focus on the naturality.
We need our transformation to verify the following commutative diagram for \(A,B,A',B'\) four games and \(f:A\multimap A', g:B \multimap B'\) two deterministic strategies:

Let \(\sigma \) be a P-strategy of A and \(\tau \) a P-strategy of B. Verifying the commutative diagram amounts to finding two reciprocal morphisms between:  and
and  .
.


By bifunctoriality of \(\otimes \), we have \(f \circ ~ \mathsf {supp}_{\,\sigma } \otimes \ g \circ ~ \mathsf {supp}_{\,\tau }\cong (f\otimes g) \circ ~ \mathsf {supp}_{\,\sigma } \otimes \mathsf {supp}_{\,\tau }\), giving us the equality of the images we need, up to bijective simulations.
I Proof of Proposition 9
Proof
-
Let \((\psi ,\overline{b}=b_1,...b_n)\) a P position of !B. Since f is slender, for all \(b_i\) player positions of \(\overline{b}\), there exists a unique pair \((e_i,a_i)\) such that \((e_i,a_i,b_i) \in f\). We use a method similar to the one used in the proof of Proposition 10. Instead of using the tensorial schedule to guide us in reconstructing the play of \(!A \multimap !B\), we use \(\psi \), which indicates us what is the next player move \(b_i\) to get to (starting from \(b_{i-2}\), and assuming we have reconstructed e and \(\phi \) so far), and then use the play \((e_i,a_i,b_i)\) to construct the play.
The sequence of moves we add is the suffix of the play \((e_i,a_i,b_i)\) looking like \(b_{i-1} a^{1}_i....a^{k}_i b_i\) (with \(a^{k}_i=a_i\)) as any other move in the play \((e_i,a_i,b_i)\) has already been played (since in particular any b move prior to \(b_{i-1}\) has been played.
Player cannot backtrack in the middle of the sequence \(b_{i-1} a^{1}_i....a^{k}_i b_i\) without breaking the fact that the full play is associated to a O-heap in \(!(A \multimap B)\).
This allows us to extend e into \(e.1.0^k.1\) and \(\phi \) by linking \(a^{1}_i\) to its predecessor in A of the play \((e_i,a_i,b_i)\).
This method constructs a valid position of !f as all branches are played following f and \(\phi \) is a O-Heap. It is the only possible position including \(\psi ,\overline{b}\) as everything we have done was determined by \(\psi \), f and \(\overline{b}\). Thus !f is a slender strategy.
-
Let \((\phi , \overline{a}=a_1,...a_n)\) an O position of !A. Since f is a functional strategy, for all \(a_i\) opponent positions of \(\overline{a}\), there exists a unique \(b_i\) such that \((c,a_i,b_i) \in f\). By determinism of f, it is also true for all player positions of \(\overline{a}\). By using \(\phi \) as a guide, this easily allows us to construct the position of !f: \((c, (\phi ,\overline{a}), (\phi , \overline{b}=b_1,...b_n))\).
It is the unique such position for \((\phi , \overline{a})\) for reasons similar to the ones evoked in the proof for slender strategies. Thus !f is a functional strategy.
J Proof of Theorem 4
Proof
-
For a game A, we have by construction:
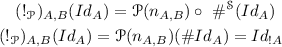
-
Let A, B, C be three games and \(\sigma \) a P-strategy of \(A\multimap B\), \(\tau \) a P-strategy of \(B \multimap C\). We need to prove that there is a natural isomorphic simulation between
 and
and  . First we will simplify those two strategies through the various properties we have seen so far:
. First we will simplify those two strategies through the various properties we have seen so far:First
 :
: 
Then,
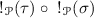 :
: 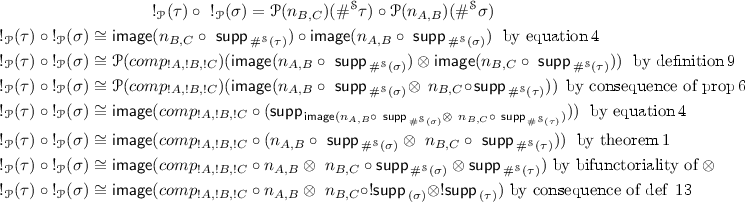
We intend to prove that those two images are isomorphic. For that, we will make the following remark: ! is lax monoidal in
 , meaning that there exists a transformation \(\mu _{A,B} : !A \otimes !B \rightarrow !(A\otimes B)\) natural in A and B. Thus we have the following diagram with the top square commuting by naturality of \(\mu \):
, meaning that there exists a transformation \(\mu _{A,B} : !A \otimes !B \rightarrow !(A\otimes B)\) natural in A and B. Thus we have the following diagram with the top square commuting by naturality of \(\mu \): 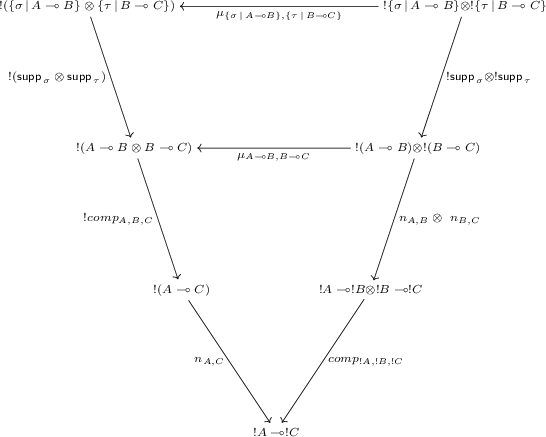
In more details, positions of \(\mu _{A,B}\) are of the form: \((e, (t, \phi ,\overline{a}, \psi , \overline{b}), (\varPhi , \overline{t',a,b}))\), where, for a position \((\varPhi , \overline{t',a,b})\) of \(!(A \otimes B)\), one can rebuild the unique associated position by playing the moves in order and building the tensorial schedule and the O-heaps incrementally, the general structure ensuring that we do get them in the end. Consequently \(\mu _{A,B}\) is slender and induces a transduction from B to A. Note that it is not bijective as the play of \(!(A \otimes B)\) where we play in B, then backtrack to play in A would produce the same play in \(!A \otimes !B\) than playing in B then in A without backtracking. Thus, we have, since \(\mu _{\{\sigma \,|\,A \multimap B\},\{\tau \,|\,B \multimap C\}}\) is slender:
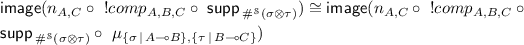
Then, by naturality,

Consequently,
$$\begin{aligned}&\mathsf {image}(n_{A,C} \circ ~!comp_{A,B,C} \circ ~ \mathsf {supp}_{\,!(\sigma \otimes \tau )})\cong \\&\mathsf {image}(comp_{!A,!B,!C} \circ n_{A,B} \otimes ~n_{B,C} \circ !\mathsf {supp}_{\,(\sigma )} \otimes !\mathsf {supp}_{\,(\tau )}) \end{aligned}$$if and only if
$$\begin{aligned}&\mathsf {image}(n_{A,C} \circ ~!comp_{A,B,C} \circ ~\mu _{A\multimap B,B\multimap C}\circ ~ \mathsf {supp}_{\,!\sigma \otimes !\tau })\cong \\&\mathsf {image}(comp_{!A,!B,!C} \circ n_{A,B} \otimes ~n_{B,C} \circ !\mathsf {supp}_{\,(\sigma )} \otimes !\mathsf {supp}_{\,(\tau )}) \end{aligned}$$meaning if and only if
$$\begin{aligned}&\mathsf {image}(n_{A,C} \circ ~!comp_{A,B,C} \circ ~\mu _{A\multimap B,B\multimap C})\cong \\&\mathsf {image}(comp_{!A,!B,!C} \circ n_{A,B} \otimes ~n_{B,C} ) \end{aligned}$$An important remark is that \(\mu _{A\multimap B,B\multimap C}\) transfers plays p of \((!(A \multimap B) \otimes !(B \multimap C))\) such that there exists \((e,(\phi ,\overline{a}),(\psi ,\overline{c}))_p \in \mathsf {image}(comp_{!A,!B,!C} \circ n_{A,B} \otimes ~n_{B,C} ) \) to plays \(p'\) of \(!(A \multimap B \otimes B \multimap C)\) such that there exists \((e,(\phi ,\overline{a}),(\psi ,\overline{c}))_p' \in \mathsf {image}(n_{A,C} \circ ~!comp_{A,B,C})\). In other words \(\mu \), when restricted to plays that play a role in the images we outlined, acts as a function from the set of plays of \((!(A \multimap B) \otimes !(B \multimap C))\) to the set of plays of \(!(A \multimap B \otimes B \multimap C)\). This can be proved by looking at the respective structures of the plays and induces one half of the isomorphism we need. We do a similar study by introducing a P-strategy of \(!(A \multimap B \otimes B \multimap C) \multimap (!(A \multimap B) \otimes !(B \multimap C))\) that acts as a converse of \(\mu _{A\multimap B,B\multimap C}\) for such plays and thus get a converse to our morphism, which will give us the second half of the isomorphism we need. Here is how we proceed: Let \((t, (\phi , \overline{e,a,b}), (\psi , \overline{f,b,c}))\) be a play of \((!(A \multimap B) \otimes !(B \multimap C))\) such that there exists
$$\begin{aligned} (e_{!A \multimap !C}, (\phi _{!A}, \overline{a}), (\phi _{!C}, \overline{c}))_{e, (t, \phi , \overline{e,a,b}, \psi , \overline{f,b,c})} \in \mathsf {image}(comp_{!A,!B,!C} \circ n_{A,B} \otimes ~n_{B,C}). \end{aligned}$$In particular, that implies that, since \(n_{A,B} \otimes ~n_{B,C}\) doesn’t change the order of moves, the sequence of moves of \((t, (\phi , \overline{e,a,b}) , (\psi , \overline{f,b,c}))\) must be able to be the left projection of \(comp_{!A,!B,!C}\). This restricts the way the moves can be played. In particular, B moves from the two components must must answer each other right away, giving sequences without backtrack of the form \(c (b_r.b_l . b_l.b_r)* c\), with similar structures for sequences starting and/or finishing with a A move. In addition, there cannot be any backtrack in A or any of the two B component that would not be initiated by a backtrack in a C component. The idea is that a backtrack in C induces a backtrack in B which is mirrored on the left component and induces a backtrack in A. Those backtracks give us a heap structure and the moves inside a sequence follow a proper tensor schedule, so it can be seen as a play of \(!(A \multimap B \otimes B \multimap C)\) and it is easy to verify that this play would produce an element of \(\mathsf {image}(n_{A,C} \circ ~!comp_{A,B,C} \circ ~\mu _{A\multimap B,B\multimap C})\) and that the P-strategy of \(!(A \multimap B \otimes B \multimap C) \multimap (!(A \multimap B) \otimes !(B \multimap C))\) built by reorganizing structure without changing order of moves is a converse to \(\mu _{A\multimap B,B\multimap C}\). Consequently, we have the bijection of images we needed and thus an isomorphic simulation between
 and
and  . It is natural since \(\mu \) and the isomorphisms involved in the manipulation of images are natural.
. It is natural since \(\mu \) and the isomorphisms involved in the manipulation of images are natural.The few additional diagrams that must be checked are easy to verify with similar methods, and thus we have that
 is a pseudofunctor.
is a pseudofunctor.
K Proof that ! Is a Pseudocomonad
In the following section, we’ll detail the construction of the pseudonatural transformations \(\delta \) and \(\epsilon \) and prove their naturality. From those definitions, verifying that ! is a pseudocomonad is easy as the morphism part of the two natural transformations coincides with their definition in the deterministic case, making the diagrams commute instantly. After that, we may do a similar study on d, e to give ! the necessary structure to be a linear exponential modality.
We will handle here the case of \(\delta _\sigma \) for a P-strategy \(\sigma :A\rightarrow B\). This is, by Definiton 26, a bijective 2-morphism between  and
and  , both being P-strategies of \(!A \multimap !!B\).
, both being P-strategies of \(!A \multimap !!B\).
First note that

and that

We want to study the structure of both images to find an isomorphic simulation between them.

What we will do is start from a position
of \(!A \multimap !!B\) and go back along the arrows to see what structure the positions that produce this position must have.
First, on the left branch, the presence of \(comp_{!A,!B,!!B}\) indicates that the position in \(!A \multimap !B \otimes !B \multimap !!B\) must be of the form
for some \(t,e_1,e_2, \varPhi _B, \overline{b'}\) such that \(e_1 \cdot e_2 = e\).
Since the right component of this position comes from \(\delta _B\), we actually have \(\overline{b'}=\overline{b}\), \(\varPhi _B=\phi _B\), \(e_2=c\) and thus \(e_1=e\) and we actually have the position
for some t which is fixed by the two components for the composition to work.
And thus, this gives us the following position of  :
:
where \(\overline{x}\) is a sequence of moves that gets projected to the sequence of moves of \((e,(\phi _A, \overline{a}),(\phi _B,\overline{b}))\). There is no modification of the order the moves are played in this step, just a reorganization of the structure.
Thus a position of  is of the form
is of the form
We apply a similar reasoning to the right branch to obtain the form of a position of  :
:
where \(t'\) is fixed by the composition and the sequence of moves \(\overline{x'}\) gets projected to the same sequence of moves than \(\overline{x}\) in the left branch. In particular, both sequences have the same length.
Since everything is fixed from the initial position \((e,(\phi _A, \overline{a}), (\psi _B,\phi _B,\overline{b}))\) but the two sequences \(\overline{x}\) and \(\overline{x'}\), we can then build \(\delta _\sigma \) as the simulation sending one position to the other one sharing that same initial structure and the same sequence \(\overline{x}\).
With a simlar study, we build \(\epsilon _\sigma \) as the simulation that sends positions of the form
to positions of the form
where \(t,t'\) are fixed by construction and \(\overline{x}\) is the branch of positions finishing in x in \(\mathcal {R}_{\sigma }\).
Proof
We will now prove the pseudonaturality of \(\epsilon \), \(\delta \) is handled in a similar way. Let us look at the naturality first. Let A, B be two games, \(\sigma ,\tau \) two P-strategies of \(A\multimap B\) and \(\alpha :\sigma \rightarrow \tau \) a simulation We require that the two following pasting diagrams are equivalent:


This amounts to the following equality of simulations:

where \(\triangleleft ,\triangleright \) indicate the whiskering that results from the composition of P-strategies and \(\cdot \) indicates the vertical composition which is simply the composition of functions. Thus, for a position
of  , we have:
, we have:

On the other hand,


And thus, we have the equivalence we require. The other diagram equalitiies we need to verify are done in a similar way.
The key point to remember from this proof and the similar ones that need to be done, is that, while the form of the positions is a bit heavy, the structures that underly them do most of the work for us, making most of the needed verifications very easy, once the positions have been properly described.
We apply those methods to verify that ! is indeed a pseudocomonad, to define and verify that \(d_A,e_A\) are proper pseudonatural transformations and to check that !, along with those transformations, does have the structure of a linear exponential modality.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Jacq, C., Melliès, PA. (2018). Categorical Combinatorics for Non Deterministic Strategies on Simple Games. In: Baier, C., Dal Lago, U. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2018. Lecture Notes in Computer Science(), vol 10803. Springer, Cham. https://doi.org/10.1007/978-3-319-89366-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-89366-2_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89365-5
Online ISBN: 978-3-319-89366-2
eBook Packages: Computer ScienceComputer Science (R0)





 of Simple Games and Non-deterministic Strategies
of Simple Games and Non-deterministic Strategies
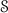
 of Simple Games and Deterministic Strategies
of Simple Games and Deterministic Strategies

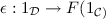
 , a natural transformation
, a natural transformation 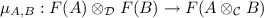
 , the following diagram commutes:
, the following diagram commutes: 
 denote the associators of the two tensor products.
denote the associators of the two tensor products. , the following diagram and its right symmetry both commute:
, the following diagram and its right symmetry both commute: 
 denote the left unitors of the two tensor products.
denote the left unitors of the two tensor products. , a morphism
, a morphism 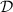 .
.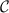 , a bijective
, a bijective 

 is the left unitor coming from the bicategory
is the left unitor coming from the bicategory  and
and  is a pseudofunctor
is a pseudofunctor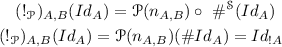
 and
and  . First we will simplify those two strategies through the various properties we have seen so far:
. First we will simplify those two strategies through the various properties we have seen so far: :
: 
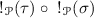 :
: 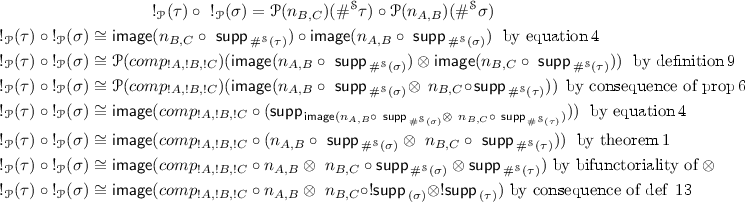
 , meaning that there exists a transformation
, meaning that there exists a transformation 
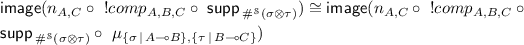

 and
and  . It is natural since
. It is natural since  is a pseudofunctor.
is a pseudofunctor.