Abstract
We show that call-by-need is observationally equivalent to weak-head needed reduction. The proof of this result uses a semantical argument based on a (non-idempotent) intersection type system called \(\mathcal {V}\). Interestingly, system \(\mathcal {V}\) also allows to syntactically identify all the weak-head needed redexes of a term.
This work was partially founded by LIA INFINIS.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
One of the fundamental notions underlying this paper is the one of needed reduction in \(\lambda \)-calculus, which is to be used here to understand (lazy) evaluation of functional programs. Key notions are those of reducible and non-reducible programs: the former are programs (represented by \(\lambda \)-terms) containing non-evaluated subprograms, called reducible expressions (redexes), whereas the latter can be seen as definitive results of computations, called normal forms. It turns out that every reducible program contains a special kind of redex known as needed or, in other words, every \(\lambda \)-term not in normal form contains a needed redex. A redex \(\mathsf {r}\) is said to be needed in a \(\lambda \)-term t if \(\mathsf {r}\) has to be contracted (i.e. evaluated) sooner or later when reducing t to normal form, or, informally said, if there is no way of avoiding \(\mathsf {r}\) to reach a normal form.
The needed strategy, which always contracts a needed redex, is normalising [8], i.e. if a term can be reduced (in any way) to a normal form, then contraction of needed redexes necessarily terminates. This is an excellent starting point to design an evaluation strategy, but unfortunately, neededness of a redex is not decidable [8]. As a consequence, real implementations of functional languages cannot be directly based on this notion.
Our goal is, however, to establish a clear connection between the semantical notion of neededness and different implementations of lazy functional languages (e.g. Miranda or Haskell). Such implementations are based on call-by-need calculi, pioneered by Wadsworth [20], and extensively studied e.g. in [3]. Indeed, call-by-need calculi fill the gap between the well-known operational semantics of the call-by-name \(\lambda \)-calculus and the actual implementations of lazy functional languages. While call-by-name re-evaluates an argument each time it is used –an operation which is quite expensive– call-by-need can be seen as a memoized version of call-by-name, where the value of an argument is stored the first time it is evaluated for subsequent uses. For example, if  , where
, where  and
and  , then call-by-name duplicates the argument
, then call-by-name duplicates the argument  , while lazy languages first reduce
, while lazy languages first reduce  to the value I so that further uses of this argument do not need to evaluate it again.
to the value I so that further uses of this argument do not need to evaluate it again.
While the notion of needed reduction is defined with respect to (full strong) normal forms, call-by-need calculi evaluate programs to special values called weak-head normal forms, which are either abstractions or arbitrary applications headed by a variable (i.e. terms of the form  where \(t_1 \ldots t_n\) are arbitrary terms). To overcome this shortfall, we first adapt the notion of needed redex to terms that are not going to be fully reduced to normal forms but only to weak-head normal forms. Thus, informally, a redex \(\mathsf {r}\) is weak-head needed in a term t if \(\mathsf {r}\) has to be contracted sooner or later when reducing t to a weak-head normal form. The derived notion of strategy is called a weak-head needed strategy, which always contracts a weak-head needed redex.
where \(t_1 \ldots t_n\) are arbitrary terms). To overcome this shortfall, we first adapt the notion of needed redex to terms that are not going to be fully reduced to normal forms but only to weak-head normal forms. Thus, informally, a redex \(\mathsf {r}\) is weak-head needed in a term t if \(\mathsf {r}\) has to be contracted sooner or later when reducing t to a weak-head normal form. The derived notion of strategy is called a weak-head needed strategy, which always contracts a weak-head needed redex.
This paper introduces two independent results about weak-head neededness, both obtained by means of (non-idempotent) intersection types [12, 13] (a survey can be found in [9]). We consider, in particular, typing system \(\mathcal {V}\) [14] and show that it allows to identify all the weak-head needed redexes of a weak-head normalising term. This is done by adapting the classical notion of principal type [17] and proving that a redex in a weak-head normalising term t is weak-head needed iff it is typed in a principally typed derivation for t in \(\mathcal {V}\).
Our second goal is to show observational equivalence between call-by-need and weak-head needed reduction. Two terms are observationally equivalent when all the empirically testable computations on them are identical. This means that a term t can be evaluated to a weak-head normal form using the call-by-need machinery if and only if the weak-head needed reduction normalises t.
By means of system \(\mathcal {V}\) mentioned so far we use a technique to reason about observational equivalence that is flexible, general and easy to verify or even certify. Indeed, system \(\mathcal {V}\) provides a semantic argument: first showing that a term t is typable in system \(\mathcal {V}\) iff it is normalising for the weak-head needed strategy (\(t \in \mathcal {W\!N}_{\mathtt {whnd}}\)), then by resorting to some results in [14], showing that system \(\mathcal {V}\) is complete for call-by-name, i.e. a term t is typable in system \(\mathcal {V}\) iff t is normalising for call-by-name (\(t \in \mathcal {W\!N}_{\mathtt {name}}\)); and that t is normalising for call-by-name iff t is normalising for call-by-need (\(t \in \mathcal {W\!N}_{\mathtt {need}}\)). Thus completing the following chain of equivalences:

This leads to the observational equivalence between call-by-need, call-by-name and weak-head needed reduction.
Structure of the paper: Sect. 2 introduces preliminary concepts while Sect. 3 defines different notions of needed reduction. The type system \(\mathcal {V}\) is studied in Sect. 4. Section 5 extends \(\beta \)-reduction to derivation trees. We show in Sect. 6 how system \(\mathcal {V}\) identifies weak-head needed redexes, while Sect. 7 gives a characterisation of normalisation for the weak-head needed reduction. Sect. 8 is devoted to define call-by-need. Finally, Sect. 9 presents the observational equivalence result.
2 Preliminaries
This section introduces some standard definitions and notions concerning the reduction strategies studied in this paper, that is, call-by-name, head and weak-head reduction, and neededness, this later notion being based on the theory of residuals [7].
2.1 The Call-by-Name Lambda-Calculus
Given a countable infinite set \(\mathcal {X}\) of variables \(x, y, z, \ldots \) we consider the following grammar:

The set of \(\lambda \)-terms is denoted by \(\mathcal {T}_{\mathtt {a}}\). We use I, K and \(\varOmega \) to denote the terms \(\lambda {x}.{x}\), \(\lambda {x}.{\lambda {y}.{x}}\) and  respectively. We use \({\mathtt {C}}\langle {t}\rangle \) (resp. \({\mathtt {E}}\langle {t}\rangle \)) for the term obtained by replacing the hole \(\Box \) of \(\mathtt {C}\) (resp. \(\mathtt {E}\)) by t. The sets of free and bound variables of a term t, written respectively \(\mathtt {fv}({t})\) and \(\mathtt {bv}({t})\), are defined as usual [7]. We work with the standard notion of \(\alpha \)-conversion, i.e. renaming of bound variables for abstractions; thus for example
respectively. We use \({\mathtt {C}}\langle {t}\rangle \) (resp. \({\mathtt {E}}\langle {t}\rangle \)) for the term obtained by replacing the hole \(\Box \) of \(\mathtt {C}\) (resp. \(\mathtt {E}\)) by t. The sets of free and bound variables of a term t, written respectively \(\mathtt {fv}({t})\) and \(\mathtt {bv}({t})\), are defined as usual [7]. We work with the standard notion of \(\alpha \)-conversion, i.e. renaming of bound variables for abstractions; thus for example  .
.
A term of the form  is called a \(\beta \)-redex (or just redex when \(\beta \) is clear from the context) and \(\lambda x\) is called the anchor of the redex. The one-step reduction relation \(\mathrel {\rightarrow _{\beta }}\) (resp. \(\mathrel {\rightarrow _{\mathtt {name}}}\)) is given by the closure by contexts \(\mathtt {C}\) (resp. \(\mathtt {E}\)) of the rewriting rule
is called a \(\beta \)-redex (or just redex when \(\beta \) is clear from the context) and \(\lambda x\) is called the anchor of the redex. The one-step reduction relation \(\mathrel {\rightarrow _{\beta }}\) (resp. \(\mathrel {\rightarrow _{\mathtt {name}}}\)) is given by the closure by contexts \(\mathtt {C}\) (resp. \(\mathtt {E}\)) of the rewriting rule  , where
, where  denotes the capture-free standard higher-order substitution. Thus, call-by-name forbids reduction inside arguments and \(\lambda \)-abstractions, e.g.
denotes the capture-free standard higher-order substitution. Thus, call-by-name forbids reduction inside arguments and \(\lambda \)-abstractions, e.g.  and
and  but neither
but neither  nor
nor  holds. We write \(\mathrel {\twoheadrightarrow _{\beta }}\) (resp. \(\mathrel {\twoheadrightarrow _{\mathtt {name}}}\)) for the reflexive-transitive closure of \(\mathrel {\rightarrow _{\beta }}\) (resp. \(\mathrel {\rightarrow _{\mathtt {name}}}\)).
holds. We write \(\mathrel {\twoheadrightarrow _{\beta }}\) (resp. \(\mathrel {\twoheadrightarrow _{\mathtt {name}}}\)) for the reflexive-transitive closure of \(\mathrel {\rightarrow _{\beta }}\) (resp. \(\mathrel {\rightarrow _{\mathtt {name}}}\)).
2.2 Head, Weak-Head and Leftmost Reductions
In order to introduce different notions of reduction, we start by formalising the general mechanism of reduction which consists in contracting a redex at some specific occurrence. Occurrences are finite words over the alphabet \(\{{\mathsf {0}, \mathsf {1}}\}\). We use \(\epsilon \) to denote the empty word and notation \(\mathsf {a^n}\) for \(\mathsf {n} \in \mathbb {N}\) concatenations of some letter \(\mathsf {a}\) of the alphabet. The set of occurrences of a given term is defined by induction as follows:  ;
;  ;
;  .
.
Given two occurrences \(\mathsf {p}\) and \(\mathsf {q}\), we use the notation \(\mathsf {p} \le \mathsf {q}\) to mean that \(\mathsf {p}\) is a prefix of \(\mathsf {q}\), i.e. there is \(\mathsf {p'}\) such that \(\mathsf {p} \mathsf {p'} = \mathsf {q}\). We denote by \({t}|_{\mathsf {p}}\) the subterm of t at occurrence \(\mathsf {p}\), defined as expected [4], thus for example  . The set of redex occurrences of t is defined by
. The set of redex occurrences of t is defined by  . We use the notation \({\mathsf {r}}:{t}\mathrel {\rightarrow _{\beta }}{t'}\) to mean that \(\mathsf {r} \in \mathtt {r}\mathtt {oc}({t})\) and t reduces to \(t'\) by contracting the redex at occurrence \(\mathsf {r}\), e.g.
. We use the notation \({\mathsf {r}}:{t}\mathrel {\rightarrow _{\beta }}{t'}\) to mean that \(\mathsf {r} \in \mathtt {r}\mathtt {oc}({t})\) and t reduces to \(t'\) by contracting the redex at occurrence \(\mathsf {r}\), e.g.  . This notion is extended to reduction sequences as expected, and noted \({\rho }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t'}\), where \(\rho \) is the list of all the redex occurrences contracted along the reduction sequence. We use \( nil \) to denote the empty reduction sequence, so that \({ nil }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t}\) holds for every term t.
. This notion is extended to reduction sequences as expected, and noted \({\rho }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t'}\), where \(\rho \) is the list of all the redex occurrences contracted along the reduction sequence. We use \( nil \) to denote the empty reduction sequence, so that \({ nil }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t}\) holds for every term t.
Any term t has exactly one of the following forms:  or
or  with \(n, m \ge 0\). In the latter case we say that
with \(n, m \ge 0\). In the latter case we say that  is the head redex of t, while in the former case there is no head redex. Moreover, if \(n = 0\), we say that
is the head redex of t, while in the former case there is no head redex. Moreover, if \(n = 0\), we say that  is the weak-head redex of t. In terms of occurrences, the head redex of t is the minimal redex occurrence of the form \(\mathsf {0^n}\) with \(\mathsf {n} \ge 0\). In particular, if it satisfies that \({t}|_{\mathsf {0^k}}\) is not an abstraction for every \(\mathsf {k} \le \mathsf {n}\), it is the weak-head redex of t. A reduction sequence contracting at each step the head redex (resp. weak-head redex) of the corresponding term is called the head reduction (resp. weak-head reduction).
is the weak-head redex of t. In terms of occurrences, the head redex of t is the minimal redex occurrence of the form \(\mathsf {0^n}\) with \(\mathsf {n} \ge 0\). In particular, if it satisfies that \({t}|_{\mathsf {0^k}}\) is not an abstraction for every \(\mathsf {k} \le \mathsf {n}\), it is the weak-head redex of t. A reduction sequence contracting at each step the head redex (resp. weak-head redex) of the corresponding term is called the head reduction (resp. weak-head reduction).
Given two redex occurrences \(\mathsf {r}, \mathsf {r'} \in \mathtt {r}\mathtt {oc}({t})\), we say that \(\mathsf {r}\) is to-the-left of \( \mathsf {r'}\) if the anchor of \(\mathsf {r}\) is to the left of the anchor of \(\mathsf {r'}\). Thus for example, the redex occurrence \(\mathsf {0}\) is to-the-left of \(\mathsf {1}\) in the term  , and \(\mathsf {\epsilon }\) is to-the-left of \(\mathsf {00}\) in
, and \(\mathsf {\epsilon }\) is to-the-left of \(\mathsf {00}\) in  . Alternatively, the relation to-the-left can be understood as a dictionary order between redex occurrences, i.e. \(\mathsf {r}\) is to-the-left of \(\mathsf {r'}\) if either \(\mathsf {r' = rq}\) with \(\mathsf {q} \ne \epsilon \) (i.e. \(\mathsf {r}\) is a proper prefix of \(\mathsf {r'}\)); or \(\mathsf {r} = \mathsf {p0q}\) and \(\mathsf {r'} = \mathsf {p1q'}\) (i.e. they share a common prefix and \(\mathsf {r}\) is on the left-hand side of an application while \(\mathsf {r'}\) is on the right-hand side). Notice that in any case this implies \(\mathsf {r'} \not \le \mathsf {r}\). Since this notion defines a total order on redexes, every term not in normal form has a unique leftmost redex. The term t leftmost reduces to \(t'\) if t reduces to \(t'\) and the reduction step contracts the leftmost redex of t. For example,
. Alternatively, the relation to-the-left can be understood as a dictionary order between redex occurrences, i.e. \(\mathsf {r}\) is to-the-left of \(\mathsf {r'}\) if either \(\mathsf {r' = rq}\) with \(\mathsf {q} \ne \epsilon \) (i.e. \(\mathsf {r}\) is a proper prefix of \(\mathsf {r'}\)); or \(\mathsf {r} = \mathsf {p0q}\) and \(\mathsf {r'} = \mathsf {p1q'}\) (i.e. they share a common prefix and \(\mathsf {r}\) is on the left-hand side of an application while \(\mathsf {r'}\) is on the right-hand side). Notice that in any case this implies \(\mathsf {r'} \not \le \mathsf {r}\). Since this notion defines a total order on redexes, every term not in normal form has a unique leftmost redex. The term t leftmost reduces to \(t'\) if t reduces to \(t'\) and the reduction step contracts the leftmost redex of t. For example,  leftmost reduces to
leftmost reduces to  and
and  leftmost reduces to
leftmost reduces to  . This notion extends to reduction sequences as expected.
. This notion extends to reduction sequences as expected.
3 Towards Neededness
Needed reduction is based on two fundamental notions: that of residual, which describes how a given redex is traced all along a reduction sequence, and that of normal form, which gives the form of the expected result of the reduction sequence. This section extends the standard notion of needed reduction [8] to those of head and weak-head needed reductions.
3.1 Residuals
Given a term t, \(\mathsf {p} \in \mathtt {oc}({t})\) and \(\mathsf {r} \in \mathtt {r}\mathtt {oc}({t})\), the descendants of \(\mathsf {p}\) after \(\mathsf {r}\) in t, written \({\mathsf {p}}/{\mathsf {r}}\), is the set of occurrences defined as follows:

For instance, given  , then \(\mathtt {oc}({t}) = \{\epsilon , \mathsf {0}, \mathsf {1}, \mathsf {00}, \mathsf {000}, \mathsf {001}, \mathsf {0000}\}\), \(\mathtt {r}\mathtt {oc}({t}) = \{{\epsilon , \mathsf {00}}\}\), \({\mathsf {00}}/{\mathsf {00}} = \varnothing \), \({\epsilon }/{\mathsf {00}} = \{{\epsilon }\}\), \({\mathsf {00}}/{\epsilon } = \{{\epsilon }\}\) and \({\mathsf {1}}/{\epsilon } = \{{\mathsf {1}, \mathsf {00}}\}\).
, then \(\mathtt {oc}({t}) = \{\epsilon , \mathsf {0}, \mathsf {1}, \mathsf {00}, \mathsf {000}, \mathsf {001}, \mathsf {0000}\}\), \(\mathtt {r}\mathtt {oc}({t}) = \{{\epsilon , \mathsf {00}}\}\), \({\mathsf {00}}/{\mathsf {00}} = \varnothing \), \({\epsilon }/{\mathsf {00}} = \{{\epsilon }\}\), \({\mathsf {00}}/{\epsilon } = \{{\epsilon }\}\) and \({\mathsf {1}}/{\epsilon } = \{{\mathsf {1}, \mathsf {00}}\}\).
Notice that \({\mathsf {p}}/{\mathsf {r}} \subseteq \mathtt {oc}({t'})\) where \({\mathsf {r}}:{t}\mathrel {\rightarrow _{\beta }}{t'}\). Furthermore, if \(\mathsf {p}\) is the occurrence of a redex in t (i.e. \(\mathsf {p} \in \mathtt {r}\mathtt {oc}({t})\)), then \({\mathsf {p}}/{\mathsf {r}} \subseteq \mathtt {r}\mathtt {oc}({t'})\), and each position in \({\mathsf {p}}/{\mathsf {r}}\) is called a residual of \(\mathsf {p}\) after reducing \(\mathsf {r}\). This notion is extended to sets of redex occurrences, indeed, the residuals of \(\mathcal {P}\) after \(\mathsf {r}\) in t are  . In particular \({\varnothing }/{\mathsf {r}} = \varnothing \). Given \({\rho }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t'}\) and \(\mathcal {P} \subseteq \mathtt {r}\mathtt {oc}({t})\), the residuals of \(\mathcal {P}\) after the sequence \(\rho \) are:
. In particular \({\varnothing }/{\mathsf {r}} = \varnothing \). Given \({\rho }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t'}\) and \(\mathcal {P} \subseteq \mathtt {r}\mathtt {oc}({t})\), the residuals of \(\mathcal {P}\) after the sequence \(\rho \) are:  and
and 
Stability of the to-the-left relation makes use of the notion of residual:
Lemma 1
Given a term t, let \(\mathsf {l}, \mathsf {r}, \mathsf {s} \in \mathtt {r}\mathtt {oc}({t})\) such that \(\mathsf {l}\) is to-the-left of \(\mathsf {r}\), \(\mathsf {s} \nleq \mathsf {l}\) and \({\mathsf {s}}:{t}\mathrel {\rightarrow _{\beta }}{t'}\). Then, \(\mathsf {l} \in \mathtt {r}\mathtt {oc}({t'})\) and \(\mathsf {l}\) is to-the-left of \(\mathsf {r'}\) for every \(\mathsf {r'} \in {\mathsf {r}}/{\mathsf {s}}\).
Proof
By case analysis using the definition of to-the-left [15]. \(\square \)
Notice that this result does not only implies that the leftmost redex is preserved by reduction of other redexes, but also that the residual of the leftmost redex occurs in exactly the same occurrence as the original one.
Corollary 1
Given a term t, and \(\mathsf {l} \in \mathtt {r}\mathtt {oc}({t})\) the leftmost redex of t, if the reduction \({\rho }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t'}\) contracts neither \(\mathsf {l}\) nor any of its residuals, then \(\mathsf {l} \in \mathtt {r}\mathtt {oc}({t'})\) is the leftmost redex of \(t'\).
Proof
By induction on the length of \(\rho \) using Lemma 1. \(\square \)
3.2 Notions of Normal Form
The expected result of evaluating a program is specified by means of some appropriate notion of normal form. Given any relation \(\mathrel {\rightarrow _{\mathcal {R}}}\), a term t is said to be in \(\mathcal {R}\)-normal form (\(\mathcal {N\!F}_{\mathcal {R}}\)) iff there is no \(t'\) such that \(t \mathrel {\rightarrow _{\mathcal {R}}} t'\). A term t is \(\mathcal {R}\)-normalising (\(\mathcal {W\!N}_{\mathcal {R}}\)) iff there exists \(u \in \mathcal {N\!F}_{\mathcal {R}}\) such that \(t \mathrel {\twoheadrightarrow _{\mathcal {R}}} u\). Thus, given an \(\mathcal {R}\)-normalising term t, we can define the set of \(\mathcal {R}\)-normal forms of t as  .
.
In particular, it turns out that a term in weak-head \(\beta \)-normal form (\(\mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\)) is of the form  (\(n \ge 0\)) or \(\lambda {x}.{t}\), where \(t, t_1, \ldots , t_n\) are arbitrary terms, i.e. it has no weak-head redex. The set of weak-head \(\beta \)-normal forms of t is
(\(n \ge 0\)) or \(\lambda {x}.{t}\), where \(t, t_1, \ldots , t_n\) are arbitrary terms, i.e. it has no weak-head redex. The set of weak-head \(\beta \)-normal forms of t is 
Similarly, a term in head \(\beta \)-normal form (\(\mathcal {H}\mathcal {N\!F}_{\beta }\)) turns out to be of the form  (\(n,m \ge 0\)), i.e. it has no head redex. The set of head \(\beta \)-normal forms of t is given by
(\(n,m \ge 0\)), i.e. it has no head redex. The set of head \(\beta \)-normal forms of t is given by  .
.
Last, any term in \(\beta \)-normal form (\(\mathcal {N\!F}_{\beta }\)) has the form  (\(n, m \ge 0\)) where \(t_1, \ldots , t_m\) are themselves in \(\beta \)-normal form. It is well-known that the set \(\mathtt {nf}_{\beta }({t})\) is a singleton, so we may use it either as a set or as its unique element.
(\(n, m \ge 0\)) where \(t_1, \ldots , t_m\) are themselves in \(\beta \)-normal form. It is well-known that the set \(\mathtt {nf}_{\beta }({t})\) is a singleton, so we may use it either as a set or as its unique element.
It is worth noticing that \(\mathcal {N\!F}_{\beta } \subset \mathcal {H}\mathcal {N\!F}_{\beta } \subset \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\). Indeed, the inclusions are strict, for instance  is in weak-head but not in head \(\beta \)-normal form, while
is in weak-head but not in head \(\beta \)-normal form, while  is in head but not in \(\beta \)-normal form.
is in head but not in \(\beta \)-normal form.
3.3 Notions of Needed Reduction
The different notions of normal form considered in Sect. 3.2 suggest different notions of needed reduction, besides the standard one in the literature [8]. Indeed, consider \(\mathsf {r} \in \mathtt {r}\mathtt {oc}({t})\). We say that \(\mathsf {r}\) is used in a reduction sequence \(\rho \) iff \(\rho \) reduces \(\mathsf {r}\) or some residual of \(\mathsf {r}\). Then:
-
1.
\(\mathsf {r}\) is needed in t if every reduction sequence from t to \(\beta \)-normal form uses \(\mathsf {r}\);
-
2.
\(\mathsf {r}\) is head needed in t if every reduction sequence from t to head \(\beta \)-normal form uses \(\mathsf {r}\);
-
3.
\(\mathsf {r}\) is weak-head needed in t if every reduction sequence of t to weak-head \(\beta \)-normal form uses \(\mathsf {r}\).
Notice in particular that \(\mathtt {nf}_{\beta }({t}) = \varnothing \) (resp. \(\mathtt {hnf}_{\beta }({t}) = \varnothing \) or \(\mathtt {whnf}_{\beta }({t}) = \varnothing \)) implies every redex in t is needed (resp. head needed or weak-head needed).
A one-step reduction \(\mathrel {\rightarrow _{\beta }}\) is needed (resp. head or weak-head needed), noted \(\mathrel {\rightarrow _{\mathtt {nd}}}\) (resp. \(\mathrel {\rightarrow _{\mathtt {hnd}}}\) or \(\mathrel {\rightarrow _{\mathtt {whnd}}}\)), if the contracted redex is needed (resp. head or weak-head needed). A reduction sequence \(\mathrel {\twoheadrightarrow _{\beta }}\) is needed (resp. head or weak-head needed), noted \(\mathrel {\twoheadrightarrow _{\mathtt {nd}}}\) (resp. \(\mathrel {\twoheadrightarrow _{\mathtt {hnd}}}\) or \(\mathrel {\twoheadrightarrow _{\mathtt {whnd}}}\)), if every reduction step in the sequence is needed (resp. head or weak-head needed).
For instance, consider the reduction sequence:

which is needed but not head needed, since redex \(\mathsf {r_1}\) might not be contracted to reach a head normal form:

Moreover, this second reduction sequence is head needed but not weak-head needed since only redex \(\mathsf {r_3}\) is needed to get a weak-head normal form:

Notice that the following equalities hold: \(\mathcal {N\!F}_{\mathtt {nd}} = \mathcal {N\!F}_{\beta }\), \(\mathcal {N\!F}_{\mathtt {hnd}} = \mathcal {H}\mathcal {N\!F}_{\beta }\) and \(\mathcal {N\!F}_{\mathtt {whnd}} = \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\).
Leftmost redexes and reduction sequences are indeed needed:
Lemma 2
The leftmost redex in any term not in normal form (resp. head or weak-head normal form) is needed (resp. head or weak-head needed).
Proof
By contradiction using the definition of needed [15]. \(\square \)
Theorem 1
Let \(\mathsf {r} \in \mathtt {r}\mathtt {oc}({t})\) and \({\rho }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t'}\) be the leftmost reduction (resp. head reduction or weak-head reduction) starting with t such that \(t' = \mathtt {nf}_{\beta }({t})\) (resp. \(t' \in \mathtt {hnf}_{\beta }({t})\) or \(t' \in \mathtt {whnf}_{\beta }({t})\)). Then, \(\mathsf {r}\) is needed (resp. head or weak-head needed) in t iff \(\mathsf {r}\) is used in \(\rho \).
Proof
By definition of needed using Lemma 2 [15]. \(\square \)
Notice that the weak-head reduction is a prefix of the head reduction, which is in turn a prefix of the leftmost reduction to normal form. As a consequence, it is immediate to see that every weak-head needed redex is in particular head needed, and every head needed redex is needed as well. For example, consider:

where \(\mathsf {r_3}\) is a needed redex but not head needed nor weak-head needed. However, \(\mathsf {r_2}\) is both needed and head needed, while \(\mathsf {r_1}\) is the only weak-head needed redex in the term, and \(\mathsf {r_4}\) is not needed at all.
4 The Type System \(\mathcal {V}\)
In this section we recall the (non-idempotent) intersection type system \(\mathcal {V}\) [14] –an extension of those in [12, 13]– used here to characterise normalising terms w.r.t. the weak-head strategy. More precisely, we show that t is typable in system \(\mathcal {V}\) if and only if t is normalising when only weak-head needed redexes are contracted. This characterisation is used in Sect. 9 to conclude that the weak-head needed strategy is observationally equivalent to the call-by-need calculus (to be introduced in Sect. 8).
Given a constant type \(\mathtt {a}\) that denotes answers and a countable infinite set \(\mathcal {B}\) of base type variables \(\alpha , \beta , \gamma , \ldots \), we define the following sets of types:

The empty multiset is denoted by \(\{\!\!\{{}\}\!\!\}_{}\). We remark that types are strict [18], i.e. the right-hand sides of functional types are never multisets. Thus, the general form of a type is \({\mathcal {M}_1}\rightarrow {{\ldots }\rightarrow {{\mathcal {M}_n}\rightarrow {\tau }}}\) with \(\tau \) being the constant type or a base type variable.
Typing contexts (or just contexts), written \(\varGamma , \varDelta \), are functions from variables to multiset types, assigning the empty multiset to all but a finite set of variables. The domain of \(\varGamma \) is given by  . The union of contexts, written \({\varGamma }\mathrel {+_{}}{\varDelta }\), is defined by
. The union of contexts, written \({\varGamma }\mathrel {+_{}}{\varDelta }\), is defined by  , where \(\sqcup \) denotes multiset union. An example is \((x:\{\!\!\{{\sigma }\}\!\!\}_{}, y:\{\!\!\{{\tau }\}\!\!\}_{}) + (x:\{\!\!\{{\sigma }\}\!\!\}_{}, z:\{\!\!\{{\tau }\}\!\!\}_{}) = (x:\{\!\!\{{\sigma , \sigma }\}\!\!\}_{}, y:\{\!\!\{{\tau }\}\!\!\}_{}, z:\{\!\!\{{\tau }\}\!\!\}_{})\). This notion is extended to several contexts as expected, so that \(+_{i \in I} \varGamma _i\) denotes a finite union of contexts (when \(I = \varnothing \) the notation is to be understood as the empty context). We write \({\varGamma }\mathrel {\setminus \!\!\setminus _{}}{x}\) for the context \(({\varGamma }\mathrel {\setminus \!\!\setminus _{}}{x})(x) = \{\!\!\{{}\}\!\!\}_{}\) and \(({\varGamma }\mathrel {\setminus \!\!\setminus _{}}{x})(y) = \varGamma (y)\) if \(y \ne x\).
, where \(\sqcup \) denotes multiset union. An example is \((x:\{\!\!\{{\sigma }\}\!\!\}_{}, y:\{\!\!\{{\tau }\}\!\!\}_{}) + (x:\{\!\!\{{\sigma }\}\!\!\}_{}, z:\{\!\!\{{\tau }\}\!\!\}_{}) = (x:\{\!\!\{{\sigma , \sigma }\}\!\!\}_{}, y:\{\!\!\{{\tau }\}\!\!\}_{}, z:\{\!\!\{{\tau }\}\!\!\}_{})\). This notion is extended to several contexts as expected, so that \(+_{i \in I} \varGamma _i\) denotes a finite union of contexts (when \(I = \varnothing \) the notation is to be understood as the empty context). We write \({\varGamma }\mathrel {\setminus \!\!\setminus _{}}{x}\) for the context \(({\varGamma }\mathrel {\setminus \!\!\setminus _{}}{x})(x) = \{\!\!\{{}\}\!\!\}_{}\) and \(({\varGamma }\mathrel {\setminus \!\!\setminus _{}}{x})(y) = \varGamma (y)\) if \(y \ne x\).
Type judgements have the form \({\varGamma }\vdash {{t}:{\tau }}\), where \(\varGamma \) is a typing context, t is a term and \(\tau \) is a type. The intersection type system \(\mathcal {V}\) for the \(\lambda \)-calculus is given in Fig. 1.
The constant type \(\mathtt {a}\) in rule \(\mathtt {({val})}\) is used to type values. The axiom \(\mathtt {({ax})}\) is relevant (there is no weakening) and the rule \(\mathtt {({{\!}\rightarrow {\!}e})}\) is multiplicative. Note that the argument of an application is typed \(\#(I)\) times by the premises of rule \(\mathtt {({{\!}\rightarrow {\!}e})}\). A particular case is when \(I = \varnothing \): the subterm u occurring in the typed term  turns out to be untyped.
turns out to be untyped.
A (type) derivation is a tree obtained by applying the (inductive) typing rules of system \(\mathcal {V}\). The notation \({}\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\) means there is a derivation of the judgement \({\varGamma }\vdash {{t}:{\tau }}\) in system \(\mathcal {V}\). The term t is typable in system \(\mathcal {V}\), or \(\mathcal {V}\)-typable, iff t is the subject of some derivation, i.e. iff there are \(\varGamma \) and \(\tau \) such that \({}\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\). We use the capital Greek letters \(\varPhi , \varPsi , \ldots \) to name type derivations, by writing for example \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\). For short, we usually denote with \(\varPhi _{t}\) a derivation with subject t for some type and context. The size of the derivation \(\varPhi \), denoted by \(\mathtt {sz}({\varPhi })\), is defined as the number of nodes of the corresponding derivation tree. We write \(\mathtt {RULE}({\varPhi }) \in \{{\mathtt {({ax})}, \mathtt {({{\!}\rightarrow {\!}i})}, \mathtt {({{\!}\rightarrow {\!}e})}}\}\) to access the last rule applied in the derivation \(\varPhi \). Likewise, \(\mathtt {PREM}({\varPhi })\) is the multiset of proper maximal subderivations of \(\varPhi \). For instance, given

we have \(\mathtt {RULE}({\varPhi }) = \mathtt {({{\!}\rightarrow {\!}e})}\) and \(\mathtt {PREM}({\varPhi }) = \{\!\!\{{\varPhi _{t}}\}\!\!\} \sqcup \{\!\!\{{\varPhi _{u}^{i} \mid i \in I}\}\!\!\}\). We also use functions \(\mathtt {CTXT}({\varPhi })\), \(\mathtt {SUBJ}({\varPhi })\) and \(\mathtt {TYPE}({\varPhi })\) to access the context, subject and type of the judgement in the root of the derivation tree respectively. For short, we also use notation \(\varPhi (x)\) to denote the type associated to the variable x in the typing environment of the conclusion of \(\varPhi \) (i.e.  ).
).
Intersection type systems can usually be seen as models [11], i.e. typing is stable by convertibility: if t is typable and \(t =_{\beta } t'\), then \(t'\) is typable too. This property splits in two different statements known as subject reduction and subject expansion respectively, the first one giving stability of typing by reduction, the second one by expansion. In the particular case of non-idempotent types, subject reduction refines to weighted subject-reduction, stating that not only typability is stable by reduction, but also that the size of type derivations is decreasing. Moreover, this decrease is strict when reduction is performed on special occurrences of redexes, called typed occurrences. We now introduce all these concepts.
Given a type derivation \(\varPhi \), the set \(\mathtt {TOC}({\varPhi })\) of typed occurrences of \(\varPhi \), which is a subset of \(\mathtt {oc}({\mathtt {SUBJ}({\varPhi })})\), is defined by induction on the last rule of \(\varPhi \).
-
If \(\mathtt {RULE}({\varPhi }) \in \{{\mathtt {({ax})}, \mathtt {({val})}}\}\), then
 .
. -
If \(\mathtt {RULE}({\varPhi }) = \mathtt {({{\!}\rightarrow {\!}i})}\) with \(\mathtt {SUBJ}({\varPhi }) = \lambda {x}.{t}\) and \(\mathtt {PREM}({\varPhi }) = \{\!\!\{{\varPhi _{t}}\}\!\!\}\), then
 .
. -
If
 and \(\mathtt {PREM}({\varPhi }) = \{\!\!\{{\varPhi _{t}}\}\!\!\} \sqcup \{\!\!\{{\varPhi _{u}^{i} \mid i \in I}\}\!\!\}\), then
and \(\mathtt {PREM}({\varPhi }) = \{\!\!\{{\varPhi _{t}}\}\!\!\} \sqcup \{\!\!\{{\varPhi _{u}^{i} \mid i \in I}\}\!\!\}\), then  .
.
Remark that there are two kind of untyped occurrences, those inside untyped arguments of applications, and those inside untyped bodies of abstractions. For instance consider the following type derivations:

Then, \(\mathtt {TOC}({\varPhi _{KI\varOmega }}) = \{{\epsilon , \mathsf {0}, \mathsf {00}, \mathsf {01}, \mathsf {000},\mathsf {0000}}\} \subseteq \mathtt {oc}({KI\varOmega })\).
Remark 1
The weak-head redex of a typed term is always a typed occurrence.
Given \(\varPhi \) and \(\mathsf {p} \in \mathtt {TOC}({\varPhi })\), we define \({\varPhi }|_{\mathsf {p}}\) as the multiset of all the subderivations of \(\varPhi \) at occurrence \(\mathsf {p}\) (a formal definition can be found in [15]). Note that \({\varPhi }|_{\mathsf {p}}\) is a multiset since the subterm of \(\mathtt {SUBJ}({\varPhi })\) at position \(\mathsf {p}\) may be typed several times in \(\varPhi \), due to rule \(\mathtt {({{\!}\rightarrow {\!}e})}\).
We can now state the two main properties of system \(\mathcal {V}\), whose proofs can be found in Sect. 7 of [9].
Theorem 2
(Weighted Subject Reduction). Let \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\). If \({\mathsf {r}}:{t}\mathrel {\rightarrow _{\beta }}{t'}\), then there exists \(\varPhi '\) s.t. \({\varPhi '}\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t'}:{\tau }}}\). Moreover,
-
1.
If \(\mathsf {r} \in \mathtt {TOC}({\varPhi })\), then \(\mathtt {sz}({\varPhi }) > \mathtt {sz}({\varPhi '})\).
-
2.
If \(\mathsf {r} \notin \mathtt {TOC}({\varPhi })\), then \(\mathtt {sz}({\varPhi }) = \mathtt {sz}({\varPhi '})\).
Theorem 3
(Subject Expansion). Let \({\varPhi '}\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t'}:{\tau }}}\). If \(t \mathrel {\rightarrow _{\beta }} t'\), then there exists \(\varPhi \) s.t. \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\).
Note that weighted subject reduction implies that reduction of typed redex occurrences turns out to be normalising.
5 Substitution and Reduction on Derivations
In order to relate typed redex occurrences of convertible terms, we now extend the notion of \(\beta \)-reduction to derivation trees, by making use of a natural and basic concept of typed substitution. In contrast to substitution and \(\beta \)-reduction on terms, these operations are now both non-deterministic on derivation trees (see [19] for discussions and examples). Given a variable x and type derivations \(\varPhi _{t}\) and \(({\varPhi _{u}^{i}})_{i \in I}\), the typed substitution of x by \(({\varPhi _{u}^{i}})_{i \in I}\) in \(\varPhi _{t}\), written  by making an abuse of notation, is a type derivation inductively defined on \(\varPhi _{t}\), only if \(\varPhi _{t}(x) = \{\!\!\{{\mathtt {TYPE}({\varPhi _{u}^{i}})}\}\!\!\}_{i \in I}\). This non-deterministic construction may be non-trivial but it can be naturally formalised in a quite straightforward way (full details can be found in [15]). Intuitively, the typed substitution replaces typed occurrences of x in \(\varPhi _t\) by a corresponding derivation \(\varPhi _u^i\) matching the same type, where such a matching is chosen in a non-deterministic way. Moreover, it also substitutes all untyped occurrences of x by u, where this untyped operation is completely deterministic. Thus, for example, consider the following substitution, where \(\varPhi _{KI}\) is defined in Sect. 4:
by making an abuse of notation, is a type derivation inductively defined on \(\varPhi _{t}\), only if \(\varPhi _{t}(x) = \{\!\!\{{\mathtt {TYPE}({\varPhi _{u}^{i}})}\}\!\!\}_{i \in I}\). This non-deterministic construction may be non-trivial but it can be naturally formalised in a quite straightforward way (full details can be found in [15]). Intuitively, the typed substitution replaces typed occurrences of x in \(\varPhi _t\) by a corresponding derivation \(\varPhi _u^i\) matching the same type, where such a matching is chosen in a non-deterministic way. Moreover, it also substitutes all untyped occurrences of x by u, where this untyped operation is completely deterministic. Thus, for example, consider the following substitution, where \(\varPhi _{KI}\) is defined in Sect. 4:

The following lemma relates the typed occurrences of the trees composing a substitution and those of the substituted tree itself:
Lemma 3
Let \(\varPhi _{t}\) and \(({\varPhi _{u}^{i}})_{i \in I}\) be derivations such that  is defined, and \(\mathsf {p} \in \mathtt {oc}({t})\). Then,
is defined, and \(\mathsf {p} \in \mathtt {oc}({t})\). Then,
-
1.
\(\mathsf {p} \in \mathtt {TOC}({\varPhi _{t}})\) iff
 .
. -
2.
\(\mathsf {q} \in \mathtt {TOC}({\varPhi _{u}^{k}})\) for some \(k \in I\) iff there exists \(\mathsf {p} \in \mathtt {TOC}({\varPhi _{t}})\) such that \({t}|_{\mathsf {p}} = x\) and
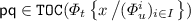 .
.
Proof
By induction on \(\varPhi _{t}\). \(\square \)
Based on the previous notion of substitutions on derivations, we are now able to introduce (non-deterministic) reduction on derivation trees. The reduction relation \(\mathrel {\rightarrow _{\beta }}\) on derivation trees is then defined by first considering the following basic rewriting rules.
-
1.
For typed \(\beta \)-redexes:

-
2.
For \(\beta \)-redexes in untyped occurrences, with \(u \mathrel {\rightarrow _{\beta }} u'\):
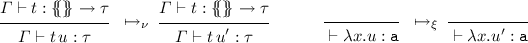
As in the case of the \(\lambda \)-calculus, where reduction is closed under usual term contexts, we need to close the previous relation under derivation tree contexts. However, a one-step reduction on a given subterm causes many one-step reductions in the corresponding derivation tree (recall \({\varPhi }|_{\mathsf {p}}\) is defined to be a multiset). Then, informally, given a redex occurrence \(\mathsf {r}\) of t, a type derivation \(\varPhi \) of t, and the multiset of minimal subderivations of \(\varPhi \) containing \(\mathsf {r}\), written \(\mathscr {M}\), we apply the reduction rules \(\mathrel {\mapsto _{\beta ,\nu ,\xi }}\) to all the elements of \(\mathscr {M}\), thus obtaining a multiset \(\mathscr {M'}\), and we recompose the type derivation of the reduct of t (see [15] for a formal definition). This gives the reduction relation \(\mathrel {\rightarrow _{\beta }}\) on trees. A reduction sequence on derivation trees contracting only redexes in typed positions is dubbed a typed reduction sequence.
Note that typed reductions are normalising by Theorem 2, yielding a special kind of derivation. Indeed, given a type derivation \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\), we say that \(\varPhi \) is normal iff \(\mathtt {TOC}({\varPhi }) \cap \mathtt {r}\mathtt {oc}({t}) = \varnothing \). Reduction on trees induces reduction on terms: when \({\rho }:{\varPhi }\mathrel {\twoheadrightarrow _{\beta }}{\varPhi '}\), then \(\mathtt {SUBJ}({\varPhi }) \mathrel {\twoheadrightarrow _{\beta }} \mathtt {SUBJ}({\varPhi '})\). By abuse of notation we may denote both sequences with the same letter \(\rho \).
6 Weak-Head Neededness and Typed Occurrences
This section presents one of our main results. It establishes a connection between weak-head needed redexes and typed redex occurrences. More precisely, we first show in Sect. 6.1 that every weak-head needed redex occurrence turns out to be a typed occurrence, whatever its type derivation is. The converse does not however hold. But, we show in Sect. 6.2 that any typed occurrence in a special kind of typed derivation (that we call principal) corresponds to a weak-head needed redex occurrence. We start with a technical lemma.
Lemma 4
Let \({\mathsf {r}}:{\varPhi _{t}}\mathrel {\rightarrow _{\beta }}{\varPhi _{t'}}\) and \(\mathsf {p} \in \mathtt {oc}({t})\) such that \(\mathsf {p} \ne \mathsf {r}\) and \(\mathsf {p} \ne \mathsf {r0}\). Then, \(\mathsf {p} \in \mathtt {TOC}({\varPhi _{t}})\) iff there exists \(\mathsf {p'} \in {\mathsf {p}}/{\mathsf {r}}\) such that \(\mathsf {p'} \in \mathtt {TOC}({\varPhi _{t'}})\).
Proof
By induction on \(\mathsf {r}\) using Lemma 3. \(\square \)
6.1 Weak-Head Needed Redexes Are Typed
In order to show that every weak-head needed redex occurrence corresponds to a typed occurrence in some type derivation we start by proving that typed occurrences do not come from untyped ones.
Lemma 5
Let \({\rho }:{\varPhi _{t}}\mathrel {\twoheadrightarrow _{\beta }}{\varPhi _{t'}}\) and \(\mathsf {p} \in \mathtt {oc}({t})\). If there exists \(\mathsf {p'} \in {\mathsf {p}}/{\rho }\) such that \(\mathsf {p'} \in \mathtt {TOC}({\varPhi _{t'}})\), then \(\mathsf {p} \in \mathtt {TOC}({\varPhi _{t}})\).
Proof
Straightforward induction on \(\rho \) using Lemma 4. \(\square \)
Theorem 4
Let \(\mathsf {r}\) be a weak-head needed redex in t. Let \(\varPhi \) be a type derivation of t. Then, \(\mathsf {r} \in \mathtt {TOC}({\varPhi })\).
Proof
By Theorem 1, \(\mathsf {r}\) is used in the weak-head reduction from t to \(t' \in \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\). By Remark 1, the weak-head reduction contracts only typed redexes. Thus, \(\mathsf {r}\) or some of its residuals is a typed occurrence in its corresponding derivation tree. Finally, we conclude by Lemma 5, \(\mathsf {r} \in \mathtt {TOC}({\varPhi })\). \(\square \)
6.2 Principally Typed Redexes Are Weak-Head Needed
As mentioned before, the converse of Theorem 4 does not hold: there are some typed occurrences that do not correspond to any weak-head needed redex occurrence. This can be illustrated in the following examples (recall \(\varPhi _{KI\varOmega }\) defined in Sect. 4):

Indeed, the occurrence \(\mathsf {0}\) (resp \(\mathsf {1}\)) in the term \(\lambda {y}.{KI\varOmega }\) (resp.  ) is typed but not weak-head needed, since both terms are already in weak-head normal form. Fortunately, typing relates to redex occurrences if we restrict type derivations to principal ones: given a term t in weak-head \(\beta \)-normal form, the derivation \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\) is normal principally typed if:
) is typed but not weak-head needed, since both terms are already in weak-head normal form. Fortunately, typing relates to redex occurrences if we restrict type derivations to principal ones: given a term t in weak-head \(\beta \)-normal form, the derivation \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\) is normal principally typed if:
-
 , and \(\varGamma = \{{{x}:{\{\!\!\{{{\overbrace{{{\{\!\!\{{}\}\!\!\}_{}}\rightarrow {\ldots }}\rightarrow {\{\!\!\{{}\}\!\!\}_{}}}^{\text {n times}}}\rightarrow {\tau }}\}\!\!\}_{}}}\}\) and \(\tau \) is a type variable \(\alpha \) (i.e. none of the \(t_i\) are typed), or
, and \(\varGamma = \{{{x}:{\{\!\!\{{{\overbrace{{{\{\!\!\{{}\}\!\!\}_{}}\rightarrow {\ldots }}\rightarrow {\{\!\!\{{}\}\!\!\}_{}}}^{\text {n times}}}\rightarrow {\tau }}\}\!\!\}_{}}}\}\) and \(\tau \) is a type variable \(\alpha \) (i.e. none of the \(t_i\) are typed), or -
\(t = \lambda {x}.{t'}\), and \(\varGamma = \varnothing \) and \(\tau = \mathtt {a}\).
Given a weak-head normalising term t such that \({\varPhi _t}\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\), we say that \(\varPhi _{t}\) is principally typed if \(\varPhi _{t} \mathrel {\twoheadrightarrow _{\beta }} \varPhi _{t'}\) for some \(t' \in \mathtt {whnf}_{\beta }({t})\) implies \(\varPhi _{t'}\) is normal principally typed.
Note in particular that the previous definition does not depend on the chosen weak-head normal form \(t'\): suppose \(t'' \in \mathtt {whnf}_{\beta }({t})\) is another weak-head normal form of t, then \(t'\) and \(t''\) are convertible terms by the Church-Rosser property [7] so that \(t'\) can be normal principally typed iff \(t''\) can, by Theorems 2 and 3.
Lemma 6
Let \(\varPhi _{t}\) be a type derivation with subject t and \(\mathsf {r} \in \mathtt {r}\mathtt {oc}({t}) \cap \mathtt {TOC}({\varPhi _{t}})\). Let \({\rho }:{\varPhi _{t}}\mathrel {\twoheadrightarrow _{\beta }}{\varPhi _{t'}}\) such that \(\varPhi _{t'}\) is normal. Then, \(\mathsf {r}\) is used in \(\rho \).
Proof
Straightforward induction on \(\rho \) using Lemma 4. \(\square \)
The notions of leftmost and weak-head needed reductions on (untyped) terms naturally extends to typed reductions on tree derivations. We thus have:
Lemma 7
Let t be a weak-head normalising term and \(\varPhi _{t}\) be principally typed. Then, a leftmost typed reduction sequence starting at \(\varPhi _{t}\) is weak-head needed.
Proof
By induction on the leftmost typed sequence (called \(\rho \)). If \(\rho \) is empty the result is immediate. If not, we show that t has a typed weak-head needed redex (which is leftmost by definition) and conclude by inductive hypothesis. Indeed, assume \(t \in \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\). By definition \(\varPhi _{t}\) is normal principally typed and thus it has no typed redexes. This contradicts \(\rho \) being non-empty. Hence, t has a weak-head redex \(\mathsf {r}\) (i.e. \(t \notin \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\)). Moreover, \(\mathsf {r}\) is both typed (by Remark 1) and weak-head needed (by Lemma 2). Thus, we conclude. \(\square \)
Theorem 5
Let t be a weak-head normalising term, \(\varPhi _{t}\) be principally typed and \(\mathsf {r} \in \mathtt {r}\mathtt {oc}({t}) \cap \mathtt {TOC}({\varPhi _{t}})\). Then, \(\mathsf {r}\) is a weak-head needed redex in t.
Proof
Let \({\rho }:{\varPhi _{t}}\mathrel {\twoheadrightarrow _{\beta }}{\varPhi _{t'}}\) be the leftmost typed reduction sequence where \(\varPhi _{t'}\) is normal. Note that \(\varPhi _{t'}\) exists by definition of principally typed. By Lemma 7, \(\rho \) is a weak-head needed reduction sequence. Moreover, by Lemma 6, \(\mathsf {r}\) is used in \(\rho \). Hence, \(\mathsf {r}\) is a weak-head needed redex in t. \(\square \)
As a direct consequence of Theorems 4 and 5, given a weak-head normalising term t, the typed redex occurrences in its principally typed derivation (which always exists) correspond to its weak-head needed redexes. Hence, system \(\mathcal {V}\) allows to identify all the weak-head needed redexes of a weak-head normalising term.
7 Characterising Weak-Head Needed Normalisation
This section presents one of the main pieces contributing to our observational equivalence result. Indeed, we relate typing with weak-head neededness by showing that any typable term in system \(\mathcal {V}\) is normalising for weak-head needed reduction. This characterisation highlights the power of intersection types. We start by a technical lemma.
Lemma 8
Let \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\). Then, \(\varPhi \) normal implies \(t \in \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\).
Proof
By induction on \(\varPhi \) analysing the last rule applied. \(\square \)
Let \({\rho }:{t_1}\mathrel {\twoheadrightarrow _{\beta }}{t_n}\). We say that \(\rho \) is a left-to-right reduction sequence iff for every \(i < n\) if \({\mathsf {r_i}}:{t_i}\mathrel {\rightarrow _{\beta }}{t_{i+1}}\) and \(\mathsf {l_i}\) is to the left of \(\mathsf {r_i}\) then, for every \(j > i\) such that \({\mathsf {r_j}}:{t_j}\mathrel {\rightarrow _{\beta }}{t_{j+1}}\) we have that \(\mathsf {r_j} \notin {\{{\mathsf {l_i}}\}}/{\rho _{ij}}\) where \({\rho _{ij}}:{t_i}\mathrel {\twoheadrightarrow _{\beta }}{t_j}\) is the corresponding subsequence of \(\rho \). In other words, for every j and every \(i < j\), \(\mathsf {r_j}\) is not a residual of a redex to the left of \(\mathsf {r_i}\) (relative to the given reduction subsequence from \(t_i\) to \(t_j\)) [7].
Left-to-right reductions define in particular standard strategies, which give canonical ways to construct reduction sequences from one term to another:
Theorem 6
([7]). If \(t \mathrel {\twoheadrightarrow _{\beta }} t'\), there exists a left-to-right reduction from t to \(t'\).
Theorem 7
Let \(t \in \mathcal {T}_{\mathtt {a}}\). Then, \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\) iff \(t \in \mathcal {W\!N}_{\mathtt {whnd}}\).
Proof
\(\Rightarrow \)) By Theorem 2 we know that the strategy reducing only typed redex occurrences is normalising, i.e. there exist \(t'\) and \(\varPhi '\) such that \(t \mathrel {\twoheadrightarrow _{\beta }} t'\), \({\varPhi '}\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t'}:{\tau }}}\) and \(\varPhi '\) normal. Then, by Lemma 8, \(t' \in \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\). By Theorem 6, there exists a left-to-right reduction \({\rho }:{t}\mathrel {\twoheadrightarrow _{\beta }}{t'}\). Let us write
such that \(t_1, \ldots , t_{n-1} \notin \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\) and \(t_n \in \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\).
We claim that all reduction steps in \(t_1 \mathrel {\twoheadrightarrow _{\beta }} t_n\) are leftmost. Assume towards a contradiction that there exists \(k < n\) such that \({\mathsf {r}}:{t_k}\mathrel {\rightarrow _{\beta }}{t_{k+1}}\) and \(\mathsf {r}\) is not the leftmost redex of \(t_k\) (written \(\mathsf {l_{k}}\)). Since \(\rho \) is a left-to-right reduction, no residual of \(\mathsf {l_{k}}\) is contracted after the k-th step. Thus, there is a reduction sequence from \(t_k \notin \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\) to \(t_n \in \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta }\) such that \(\mathsf {l_{k}}\) is not used in it. This leads to a contradiction with \(\mathsf {l_{k}}\) being weak-head needed in \(t_k\) by Lemma 2.
As a consequence, there is a leftmost reduction sequence \(t \mathrel {\twoheadrightarrow _{\beta }} t_n\). Moreover, by Lem. 2, \(t \mathrel {\twoheadrightarrow _{\mathtt {whnd}}} t_n \in \mathcal {W}\mathcal {H}\mathcal {N\!F}_{\beta } = \mathcal {N\!F}_{\mathtt {whnd}}\). Thus, \(t \in \mathcal {W\!N}_{\mathtt {whnd}}\).
\(\Leftarrow \)) Consider the reduction \({\rho }:{t}\mathrel {\twoheadrightarrow _{\mathtt {whnd}}}{t'}\) with \(t' \in \mathtt {whnf}_{\beta }({t})\). Let \({\varPhi '}\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t'}:{\tau }}}\) be the normal principally typed derivation for \(t'\) as defined in Sect. 6.2. Finally, we conclude by induction in \(\rho \) using Theorem 3, \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\). \(\square \)
8 The Call-by-Need Lambda-Calculus
This section describes the syntax and the operational semantics of the call-by-need lambda-calculus introduced in [1]. It is more concise than previous specifications of call-by-need [2, 3, 10, 16], but it is operationally equivalent to them [6], so that our results could also be presented by using alternative specifications.
Given a countable infinite set \(\mathcal {X}\) of variables \(x, y, z, \ldots \) we define different syntactic categories for terms, values, list contexts, answers and need contexts:

We denote the set of terms by \(\mathcal {T}_{\mathtt {e}}\). Terms of the form \({t}[{x}\backslash {u}]\) are closures, and \([{x}\backslash {u}]\) is called an explicit substitution (ES). The set of \(\mathcal {T}_{\mathtt {e}}\)-terms without ES is the set of terms of the \(\lambda \)-calculus, i.e. \(\mathcal {T}_{\mathtt {a}}\). The notions of free and bound variables are defined as expected, in particular,  ,
,  ,
,  and
and  . We extend the standard notion of \(\alpha \)-conversion to ES, as expected.
. We extend the standard notion of \(\alpha \)-conversion to ES, as expected.
We use the special notation \({\mathtt {N}}\langle \langle {u}\rangle \rangle \) or \({\mathtt {L}}\langle \langle {u}\rangle \rangle \) when the free variables of u are not captured by the context, i.e. there are no abstractions or explicit substitutions in the context that binds the free variables of u. Thus for example, given  , we have
, we have  , but
, but  cannot be written as \({\mathtt {N}}\langle \langle {x}\rangle \rangle \). Notice the use of this special notation in the last case of needed contexts, an example of such case being
cannot be written as \({\mathtt {N}}\langle \langle {x}\rangle \rangle \). Notice the use of this special notation in the last case of needed contexts, an example of such case being 
The call-by-need calculus, introduced in [1], is given by the set of terms \(\mathcal {T}_{\mathtt {e}}\) and the reduction relation \(\mathrel {\rightarrow _{\mathtt {need}}}\), the union of \(\mathrel {\rightarrow _{\mathtt {dB}}}\) and \(\mathrel {\rightarrow _{\mathtt {lsv}}}\), which are, respectively, the closure by need contexts of the following rewriting rules:

These rules avoid capture of free variables. An example of \(\mathtt {need}\)-reduction sequence is the following, where the redex of each step is underlined for clearness:

As for call-by-name, reduction preserves free variables, i.e. \(t \mathrel {\rightarrow _{\mathtt {need}}} t'\) implies \(\mathtt {fv}({t}) \supseteq \mathtt {fv}({t'})\). Notice that call-by-need reduction is also weak, so that answers are not \(\mathtt {need}\)-reducible.
9 Observational Equivalence
The results in Sect. 7 are used here to prove soundness and completeness of call-by-need w.r.t weak-head neededness, our second main result. More precisely, a call-by-need interpreter stops in a value if and only if the weak-head needed reduction stops in a value. This means that call-by-need and call-by-name are observationally equivalent.
Formally, given a reduction relation \(\mathcal {R}\) on a term language \(\mathcal {T}\), and an associated notion of context for \(\mathcal {T}\), we define t to be observationally equivalent to u, written \(t \cong _{\mathcal {R}} u\), iff \({\mathtt {C}}\langle {t}\rangle \in \mathcal {W\!N}_{\mathcal {R}} \Leftrightarrow {\mathtt {C}}\langle {u}\rangle \in \mathcal {W\!N}_{\mathcal {R}}\) for every context \(\mathtt {C}\). In order to show our final result we resort to the following theorem:
Theorem 8
([14]).
-
1.
Let \(t \in \mathcal {T}_{\mathtt {a}}\). Then, \({\varPhi }\rhd _{\mathcal {V}}{{\varGamma }\vdash {{t}:{\tau }}}\) iff \(t \in \mathcal {W\!N}_{\mathtt {name}}\).
-
2.
For all terms t and u in \(\mathcal {T}_{\mathtt {a}}\), \(t \cong _{\mathtt {name}} u\) iff \(t \cong _{\mathtt {need}} u\).
These observations allows us to conclude:
Theorem 9
For all terms t and u in \(\mathcal {T}_{\mathtt {a}}\), \(t \cong _{\mathtt {whnd}} u\) iff \(t \cong _{\mathtt {need}} u\).
Proof
By Theorem 8:2 it is sufficient to show \(t \cong _{\mathtt {whnd}} u\) iff \(t \cong _{\mathtt {name}} u\). The proof proceeds as follows:

\(\square \)
10 Conclusion
We establish a clear connection between the semantical standard notion of neededness and the syntactical concept of call-by-need. The use of non-idempotent types –a powerful technique being able to characterise different operational properties– provides a simple and natural tool to show observational equivalence between these two notions. We refer the reader to [5] for other proof techniques (not based on intersection types) used to connect semantical notions of neededness with syntactical notions of lazy evaluation.
An interesting (and not difficult) extension of our result in Sect. 6 is that call-by-need reduction (defined on \(\lambda \)-terms with explicit substitutions) contracts only \(\mathtt {dB}\) weak-head needed redexes, for an appropriate (and very natural) notion of weak-head needed redex for \(\lambda \)-terms with explicit substitutions. A technical tool to obtain such a result would be the type system \(\mathcal {A}\) [14], a straightforward adaptation of system \(\mathcal {V}\) to call-by-need syntax.
Given the recent formulation of strong call-by-need [6] describing a deterministic call-by-need strategy to normal form (instead of weak-head normal form), it would be natural to extend our technique to obtain an observational equivalence result between the standard notion of needed reduction (to full normal forms) and the strong call-by-need strategy. This remains as future work.
References
Accattoli, B., Barenbaum, P., Mazza, D.: Distilling abstract machines. In: Jeuring, J., Chakravarty, M.M.T. (eds.) Proceedings of the 19th ACM SIGPLAN International Conference on Functional Programming, Gothenburg, Sweden, 1–3 September 2014, pp. 363–376. ACM (2014)
Ariola, Z.M., Felleisen, M.: The call-by-need lambda calculus. J. Funct. Program. 7(3), 265–301 (1997)
Ariola, Z.M., Felleisen, M., Maraist, J., Odersky, M., Wadler, P.: The call-by-need lambda calculus. In: Cytron, R.K., Lee, P. (eds.) Conference Record of POPL 1995: 22nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, San Francisco, California, USA, 23–25 January 1995, pp. 233–246. ACM Press (1995)
Baader, F., Nipkow, T.: Term Rewriting and all That. Cambridge University Press, New York (1998)
Balabonski, T.: La pleine paresse, une certaine optimalité. Ph.D. Thesis, Université Paris-Diderot (2012)
Balabonski, T., Barenbaum, P., Bonelli, E., Kesner, D.: Foundations of strong call by need. PACMPL 1(ICFP), 20:1–20:29 (2017)
Barendregt, H.P.: The Lambda Calculus Its Syntax and Semantics, vol. 103, revised edition, North Holland (1984)
Barendregt, H.P., Kennaway, J.R., Klop, J.W., Sleep, M.R.: Needed reduction and spine strategies for the lambda calculus. Inf. Comput. 75(3), 191–231 (1987)
Bucciarelli, A., Kesner, D., Ventura, D.: Non-idempotent intersection types for the lambda-calculus. Logic J. IGPL 25(4), 431–464 (2017)
Chang, S., Felleisen, M.: The call-by-need lambda calculus, revisited. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 128–147. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_7
Coppo, M., Dezani-Ciancaglini, M.: An extension of the basic functionality theory for the \(\lambda \)-calculus. Notre Dame J. Formal Log. 21(4), 685–693 (1980)
de Carvalho, D.: Sémantiques de la logique linéaire et temps de calcul. Ph.D. thesis, Université Aix-Marseille II (2007)
Gardner, P.: Discovering needed reductions using type theory. In: Hagiya, M., Mitchell, J.C. (eds.) TACS 1994. LNCS, vol. 789, pp. 555–574. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-57887-0_115
Kesner, D.: Reasoning about call-by-need by means of types. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 424–441. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_25
Kesner, D., Ríos, A., Viso, A.: Call-by-need, neededness and all that. Extended report (2017). https://arxiv.org/abs/1801.10519
Maraist, J., Odersky, M., Wadler, P.: The call-by-need lambda calculus. J. Funct. Program. 8(3), 275–317 (1998)
Rocca, S.R.D.: Principal type scheme and unification for intersection type discipline. Theor. Comput. Sci. 59, 181–209 (1988)
van Bakel, S.: Complete restrictions of the intersection type discipline. Theor. Comput. Sci. 102(1), 135–163 (1992)
Vial, P.: Non-idempotent intersection types, beyond lambda-calculus. Ph.D. thesis, Université Paris-Diderot (2017)
Wadsworth, C.P.: Semantics and pragmatics of the lambda calculus. Ph.D. thesis, Oxford University (1971)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Kesner, D., Ríos, A., Viso, A. (2018). Call-by-Need, Neededness and All That. In: Baier, C., Dal Lago, U. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2018. Lecture Notes in Computer Science(), vol 10803. Springer, Cham. https://doi.org/10.1007/978-3-319-89366-2_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-89366-2_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89365-5
Online ISBN: 978-3-319-89366-2
eBook Packages: Computer ScienceComputer Science (R0)






 .
. .
. and
and  .
. .
.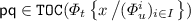 .
.
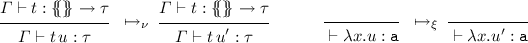
 , and
, and