Abstract
In safety-critical cyber-physical systems (CPS), a service failure may result in severe financial loss or damage in human life. Smart CPSs have complex interaction with their environment which is rarely known in advance, and they heavily depend on intelligent data processing carried out over a heterogeneous computation platform and provide autonomous behavior. This complexity makes design time verification infeasible in practice, and many CPSs need advanced runtime monitoring techniques to ensure safe operation. While graph queries are a powerful technique used in many industrial design tools of CPSs, in this paper, we propose to use them to specify safety properties for runtime monitors on a high-level of abstraction. Distributed runtime monitoring is carried out by evaluating graph queries over a distributed runtime model of the system which incorporates domain concepts and platform information. We provide a semantic treatment of distributed graph queries using 3-valued logic. Our approach is illustrated and an initial evaluation is carried out using the MoDeS3 educational demonstrator of CPSs.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A smart and safe cyber-physical system (CPS) [23, 30, 36] heavily depends on intelligent data processing carried out over a heterogeneous computation platform to provide autonomous behavior with complex interactions with an environment which is rarely known in advance. Such a complexity frequently makes design time verification be infeasible in practice, thus CPSs need to rely on run-time verification (RV) techniques to ensure safe operation by monitoring.
Traditionally, RV techniques have evolved from formal methods [24, 26], which provide a high level of precision, but offer a low-level specification language (with simple atomic predicates to capture information about the system) which hinders their use in every day engineering practice. Recent RV approaches [17] started to exploit rule-based approaches over a richer information model.
In this paper, we aim to address runtime monitoring of distributed systems from a different perspective by using runtime models (aka models@ runtime [8, 38]) which have been promoted for the assurance of self-adaptive systems in [10, 44]. The idea is that runtime models serve as a rich knowledge base for the system by capturing the runtime status of the domain, services and platforms as a graph model, which serves as a common basis for executing various analysis algorithms. Offering centralized runtime models accessible via the network, the Kevoree Modeling Framework [28] has been successfully applied in numerous Internet-of-Things applications over the Java platform. However, the use of such run-time models for analysis purposes in resource-constrained smart devices or critical CPS components is problematic due to the lack of control over the actual deployment of the model elements to the execution units of the platform.
Graph queries have already been applied in various design and analysis tools for CPSs thanks to their highly expressive declarative language, and their scalability to large industrial models [40]. Distributed graph query evaluation techniques have been proposed in [22, 34], but all of these approaches use a cloud-based execution environment, and the techniques are not directly applicable for a heterogeneous execution platform with low-memory computation units.
As a novelty in our paper, we specify safety criteria for runtime monitoring by graph queries formulated over runtime models (with domain concepts, platform elements, and allocation as runtime information) where graph query results highlight model elements that violate a safety criterion. Graph queries are evaluated over a distributed runtime model where each model element is managed by a dedicated computing unit of the platform while relevant contextual information is communicated to neighboring computing units periodically via asynchronous messages. We provide a semantic description for the distributed runtime model using 3-valued logic to uniformly capture contextual uncertainty or message loss. Then we discuss how graph queries can be deployed as a service to the computing units (i.e., low-memory embedded devices) of the execution platform of the system in a distributed way, and provide precise semantics of distributed graph query evaluation over our distributed runtime model. We provide an initial performance evaluation of our distributed query technique over the MoDeS3 CPS demonstrator [45], which is an open source educational platform, and also compare its performance to an open graph query benchmark [35].
2 Overview of Distributed Runtime Monitoring
Figure 1 is an overview of distributed runtime monitoring of CPSs deployed over heterogeneous computing platform using runtime models and graph queries.
Our approach reuses a high-level graph query language [41] for specifying safety properties of runtime monitors, which language is widely used in various design tools of CPS [37]. Graph queries can capture safety properties with rich structural dependencies between system entities which is unprecedented in most temporal logic formalisms used for runtime monitoring. Similarly, OCL has been used in [20] for related purposes. While graph queries can be extended to express temporal behavior [11], our current work is restricted to (structural) safety properties where the violation of a property is expressible by graph queries.
These queries will be evaluated over a runtime model which reflects the current state of the monitored system, e.g. data received from different sensors, the services allocated to computing units, or the health information of computing infrastructure. In accordance with the models@ runtime paradigm [8, 38], observable changes of the real system gets updated—either periodically with a certain frequency, or in an event-driven way upon certain triggers.
Runtime monitor programs are deployed to a distributed heterogeneous computation platform, which may include various types of computing units ranging from ultra-low-power microcontroller units, through smart devices to high-end cloud-based servers. These computation units primarily process the data provided by sensors and they are able to perform edge- or cloud-based computations based on the acquired information. The monitoring programs are deployed and executed on them exactly as the primary services of the system, thus resource restrictions (CPU, memory) need to be respected during allocation.
Runtime monitors are synthesized by transforming high-level query specifications into deployable, platform dependent source code for each computation unit used as part of a monitoring service. The synthesis includes a query optimization step and a code generation step to produce platform-dependent C++ source code ready to be compiled into an executable for the platform. Due to space restrictions, this component of our framework is not detailed in this paper.
Our system-level monitoring framework is hierarchical and distributed. Monitors may observe the local runtime model of the their own computing unit, and they can collect information from runtime models of different devices, hence providing a distributed monitoring architecture. Moreover, one monitor may rely on information computed by other monitors, thus yielding a hierarchical network.
Running Example. We illustrate our runtime monitoring technique in the context of a CPS demonstrator [45], which is an educational platform of a model railway system that prevents trains from collision and derailment using safety monitors. The railway track is equipped with several sensors (cameras, shunt detectors) capable of sensing trains on a particular segment of a track connected to some computing units, such as Arduinos, Raspberry Pis, BeagleBone Blacks (BBB), or a cloud platform. Computing units also serve as actuators to stop trains on selected segments to guarantee safe operation. For space considerations, we will only present a small self-contained fragment of the demonstrator.
In Fig. 1, the System Under Monitor is a snapshot of the system where train tr1 is on segment s4, while tr2 is on s2. The railroad network has a static layout, but turnouts tu1 and tu2 can change between straight and divergent states. Three BBB computing units are responsible for monitoring and controlling disjoint parts of the system. A computing unit may read its local sensors, (e.g. the occupancy of a segment, or the status of a turnout), collect information from other units during monitoring, and it can operate actuators accordingly (e.g. change turnout state) for the designated segment. All this information is reflected in the (distributed) runtime model which is deployed on the three computing units and available for the runtime monitors.
3 Towards Distributed Runtime Models
3.1 Runtime Models
Many industrial modeling tools used for engineering CPS [3, 31, 47] build on the concepts of domain-specific (modeling) languages (DSLs) where a domain is typically defined by a metamodel and a set of well-formedness constraints. A metamodel captures the main concepts in a domain as classes with attributes, their relations as references, and specifies the basic structure of graph models.
A metamodel can be formalized as a vocabulary  with a unary predicate symbol
with a unary predicate symbol  for each class, a binary predicate symbol
for each class, a binary predicate symbol  for each attribute, and a binary predicate symbol
for each attribute, and a binary predicate symbol  for each relation.
for each relation.
Example 1
Figure 2 shows a metamodel for the CPS demonstrator with Computing Units (identified on the network by hostID attribute) which host Domain Elements and communicate with other Computing Units. A Domain Element is either a Train or Railroad Element where the latter is either a Turnout or a Segment. A Train is situated on a Railroad Element which is connected to at most two other Railroad Elements. Furthermore, a Turnout refers to Railroad Elements connecting to its straight and divergent exits. A Train also knows its speed.
Objects, their attributes, and links between them constitute a runtime model [8, 38] of the underlying system in operation. Changes to the system and its environment are reflected in the runtime model (in an event-driven or time-triggered way) and operations executed on the runtime model (e.g. setting values of controllable attributes or relations between objects) are reflected in the system itself (e.g. by executing scripts or calling services). We assume that this runtime model is self-descriptive in the sense that it contains information about the computation platform and the allocation of services to platform elements, which is a key enabler for self-adaptive systems [10, 44].
A runtime model \(M = \langle { Dom _{M}}, {\mathcal {I}_{M}} \rangle \) can be formalized as a 2-valued logic structure over \(\varSigma \) where \( Dom _{M} = Obj _{M} \sqcup Data _{M}\) where \( Obj _{M}\) is a finite set of objects, while \( Data _{M}\) is the set of (built-in) data values (integers, strings, etc.). \(\mathcal {I}_{M}\) is a 2-valued interpretation of predicate symbols in \(\varSigma \) defined as follows:
-
Class predicates: If object \(o_p\) is an instance of class
 then the 2-valued interpretation of
then the 2-valued interpretation of  in M denoted by
in M denoted by  , otherwise \(0\).
, otherwise \(0\). -
Attribute predicates: If there exists an attribute of type
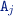 in \(o_p\) with value \(a_r\) in M then
in \(o_p\) with value \(a_r\) in M then  , and otherwise \(0\).
, and otherwise \(0\). -
Reference predicates: If there is a link of type
 from \(o_p\) to \(o_q\) in M then
from \(o_p\) to \(o_q\) in M then  , otherwise \(0\).
, otherwise \(0\).
3.2 Distributed Runtime Models
Our framework addresses decentralized systems where each computing unit periodically communicates a part of its internal state to its neighbors in an update phase. We abstract from the technical details of communication, but we assume approximate synchrony [13] between the clocks of computing units, thus all update messages regarded lost that does not arrive within given timeframe \(T_{\text {update}}\).
As such, a centralized runtime model is not a realistic assumption for mixed synchronous systems. First, each computing unit has only incomplete knowledge about the system: it fully observes and controls a fragment of the runtime model (to enforce the single source of truth principle), while it is unaware of the internal state of objects hosted by other computing units. Moreover, uncertainty may arise in the runtime model due to sensing or communication issues.
Semantics of Distributed Runtime Models. We extend the concept of runtime models to a distributed setting with heterogeneous computing units which periodically communicate certain model elements with each other via messages. We introduce a semantic representation for distributed runtime models (DRMs) which can abstract from the actual communication semantics (e.g. asynchronous messages vs. broadcast messages) by (1) evaluating predicates locally at a computing unit with (2) a 3-valued truth evaluation having a third  value in case of uncertainty. Each computing unit maintains a set of facts described by atomic predicates in its local knowledge base wrt. the objects with attributes it hosts, and references between local objects. Additionally, each computing unit incorporates predicates describing outgoing references for each object it hosts.
value in case of uncertainty. Each computing unit maintains a set of facts described by atomic predicates in its local knowledge base wrt. the objects with attributes it hosts, and references between local objects. Additionally, each computing unit incorporates predicates describing outgoing references for each object it hosts.
The 3-valued truth evaluation of a predicate \(P(v_1,\ldots ,v_n)\) on a computing unit \( cu \) is denoted by \({[\![ P(v_1,\ldots ,v_n) ]\!]}^{}\mathtt {@} cu \). The DRM of the system is constituted from the truth evaluation of all predicates on all computing units. For the current paper, we assume the single source of truth principle, i.e. each model element is always faithfully observed and controlled by its host computing unit, thus the local truth evaluation of the corresponding predicate P is always \(1\) or \(0\). However, 3-valued evaluation could be extended to handle such local uncertainties.
Example 2
Figure 3 shows a DRM snapshot for the CPS demonstrator (bottom part of Fig. 1). Computing units BBB1–BBB3 manage different parts of the system, e.g. BBB1 hosts objects s1, s2, tu1 and tr2 and the links between them. We illustrate the local knowledge bases of computing units.
Since computing unit BBB1 hosts train tr2, thus  . However, according to computing module BBB2,
. However, according to computing module BBB2,  as there is no train tr2 hosted on BBB2, but it may exist on a different one.
as there is no train tr2 hosted on BBB2, but it may exist on a different one.
Similarly,  , as BBB1 is the host of s1, the source of the reference. This means BBB1 knows that there is a (directed) reference of type connectedTo from s1 to s7. However, the knowledge base on BBB3 may have uncertain information about this link, thus
, as BBB1 is the host of s1, the source of the reference. This means BBB1 knows that there is a (directed) reference of type connectedTo from s1 to s7. However, the knowledge base on BBB3 may have uncertain information about this link, thus  , i.e. there may be a corresponding link from s1 to s7, but it cannot be deduced using exclusively the predicates evaluated at BBB3.
, i.e. there may be a corresponding link from s1 to s7, but it cannot be deduced using exclusively the predicates evaluated at BBB3.
4 Distributed Runtime Monitoring
4.1 Graph Queries for Specifying Safety Monitors
To capture the safety properties to be monitored, we rely on the VIATRA Query Language (VQL) [7]. VIATRA has been intensively used in various design tools of CPSs to provide scalable queries over large system models. The current paper aims to reuse this declarative graph query language for runtime verification purposes, which is a novel idea. The main benefit is that safety properties can be captured on a high level of abstraction over the runtime model, which eases the definition and comprehension of safety monitors for engineers. Moreover, this specification is free from any platform-specific or deployment details.
The expressiveness of the VQL language converges to first-order logic with transitive closure, thus it provides a rich language for capturing a variety of complex structural conditions and dependencies. Technically, a graph query captures the erroneous case, when evaluating the query over a runtime model. Thus any match (result) of a query highlights a violation of the safety property at runtime.
Example 3
In the railway domain, safety standards prescribe a minimum distance between trains on track [1, 14]. Query closeTrains captures a (simplified) description of the minimum headway distance to identify violating situations where trains have only limited space between each other. Technically, one needs to detect if there are two different trains on two different railroad elements, which are connected by a third railroad element. Any match of this pattern highlights track elements where passing trains need to be stopped immediately. Figure 4a shows the graph query closeTrains in a textual syntax, Fig. 4b displays it as a graph formula, and Fig. 4c is a graphical illustration as a graph pattern.
Syntax. Formally, a graph pattern (or query) is a first order logic (FOL) formula \(\varphi (v_1, \ldots , v_n)\) over variables [42]. A graph pattern \(\varphi \) can be inductively constructed (see Table 1) by using atomic predicates of runtime models  ,
,  ,
,  ,
,  , equality between variables \(v_1 = v_2\), FOL connectives \(\vee \), \(\wedge \), quantifiers \(\exists \), \(\forall \), and positive (\( call \)) or negative (\( neg \)) pattern calls.
, equality between variables \(v_1 = v_2\), FOL connectives \(\vee \), \(\wedge \), quantifiers \(\exists \), \(\forall \), and positive (\( call \)) or negative (\( neg \)) pattern calls.
This language enables to specify a hierarchy of runtime monitors as a query may explicitly use results of other queries (along pattern calls). Furthermore, distributed evaluation will exploit a spatial hierarchy between computing units.
Semantics. A graph pattern \(\varphi (v_1,\ldots ,v_n)\) can be evaluated over a (centralized) runtime model M (denoted by \({[\![ \varphi (v_1,\ldots ,v_n) ]\!]}^{M}_Z\)) along a variable binding \(Z:\{v_1,\ldots ,v_n\} \rightarrow Dom _{M} \) from variables to objects and data values in M in accordance with the semantic rules defined in Table 1 [42].
A variable binding Z is called a \(match \) if pattern \(\varphi \) is evaluated to \(1\) over M, i.e. \({[\![ \varphi (v_1,\ldots ,v_n) ]\!]}^{M}_{Z} = 1\). Below, we may use \({[\![ \varphi (v_1,\ldots ,v_n) ]\!]}^{}_{}\) as a shorthand for \({[\![ \varphi (v_1,\ldots ,v_n) ]\!]}^{M}_{Z}\) when M and Z are clear from context. Note that \(\min \) and \(\max \) take the numeric minimum and maximum values of \(0\),  and \(1\) with
and \(1\) with  .
.
4.2 Execution of Distributed Runtime Monitors
To evaluate graph queries of runtime monitors in a distributed setting, we propose to deploy queries to the same target platform in a way that is compliant with the distributed runtime model and the potential resource restrictions of computation units. If a graph query engine is deployed as a service on a computing unit, it can serve as a local monitor over the runtime model. However, such local monitors are usable only when all graph nodes traversed and retrieved during query evaluation are deployed on the same computing unit, which is not the general case. Therefore, a distributed monitor needs to gather information from other model fragments and monitors stored at different computing units.
A Query Cycle. Monitoring queries are evaluated over a distributed runtime model during the query cycle, where individual computing units communicate with each other asynchronously in accordance with the actor model [18].
-
A monitoring service can be initiated (or scheduled) at a designated computing unit cu by requesting the evaluation of a graph query with at least one unbound variable denoted as \({[\![ \varphi (v_1,\ldots ,v_n) ]\!]}^{}_{}\mathtt {@} cu = ?\).
-
A computing unit attempts to evaluate a query over its local runtime model.
-
If any links of its local runtime model point to a fragment stored at a neighboring computing unit, or if a subpattern call is initiated, corresponding query
 , \(call (\varphi )\) or \(neg (\varphi )\) needs to be evaluated at all neighbors \(cu_i\).
, \(call (\varphi )\) or \(neg (\varphi )\) needs to be evaluated at all neighbors \(cu_i\). -
Such calls to distributed monitors are carried out by sending asynchronous messages to each other thus graph queries are evaluated in a distributed way along the computing platform. First, the requester \(cu_r\) sends a message of the form “\({[\![ \varphi (v_1,\ldots ,v_n) ]\!]}^{}_{}\mathtt {@} cu_p = ?\)”. The provider \(cu_p\) needs to send back a reply which contains further information about the internal state or previous monitoring results of the provider which contains all potential matches known by \(cu_p\), i.e. all bindings
 (where we abbreviated the binding \(v_i \mapsto o_i\) into the predicate as a notational shortcut).
(where we abbreviated the binding \(v_i \mapsto o_i\) into the predicate as a notational shortcut). -
Matches of predicates sent as a reply to a computing unit can be cached.
-
Messages may get delayed due to network traffic and they are considered to be lost by the requester if no reply arrives within a deadline. Such a case introduces uncertainty in the truth evaluation of predicates, i.e. the requestor \(cu_r\) stores
 in its cache, if the reply of the provider \(cu_p\) is lost.
in its cache, if the reply of the provider \(cu_p\) is lost. -
After acquiring truth values of predicates from its neighbors, a computing unit needs to decide on a single truth value for each predicate evaluated along different variable bindings. This local decision will be detailed below.
-
At the end of the query cycle, each computing unit resets its cache to remove information acquired within the last cycle.
Example 4
Figure 5 shows the beginning of a query evaluation sequence for monitor closeTrains initiated at computing unit BBB3. Calls are asynchronous (cf. actor model), while diagonal lines illustrate the latency of network communication. Message numbers represent the order between timestamps of messages.
When the query is initiated (message 1, shortly, m1), and the first predicate  of the query is sent to the other two computing unit as requests with a free variable parameter T (m2 and m3). In the reply messages, BBB2 reports tr1 as an object satisfying the predicate (m4), while BBB1 answers that tr2 is a suitable binding to T (m5). Next BBB3 is requesting facts about outgoing references of type
of the query is sent to the other two computing unit as requests with a free variable parameter T (m2 and m3). In the reply messages, BBB2 reports tr1 as an object satisfying the predicate (m4), while BBB1 answers that tr2 is a suitable binding to T (m5). Next BBB3 is requesting facts about outgoing references of type  leading from objects tr2 and tr1 to objects stored in BBB1 and BBB2, respectively (m6 and m7). As the answer, each computing unit sends back facts stating outgoing references from the objects (m8 and m9).
leading from objects tr2 and tr1 to objects stored in BBB1 and BBB2, respectively (m6 and m7). As the answer, each computing unit sends back facts stating outgoing references from the objects (m8 and m9).
The next message (m10) asks for outgoing references of type  from object s2. To send a reply, first BBB1 asks BBB2 to ensure that a reference from s2 to s3 exists, since s3 is hosted by BBB2 (m11). This check adds tolerance against lost messages during model update. After BBB1 receives the answer from BBB2 (m12), it replies to BBB3 containing all facts maintained on this node.
from object s2. To send a reply, first BBB1 asks BBB2 to ensure that a reference from s2 to s3 exists, since s3 is hosted by BBB2 (m11). This check adds tolerance against lost messages during model update. After BBB1 receives the answer from BBB2 (m12), it replies to BBB3 containing all facts maintained on this node.
Semantics of Distributed Query Evaluation. Each query is initiated at a designated computing unit which will be responsible for calculating query results by aggregating the partial results retrieved from its neighbors. This aggregation has two different dimensions: (1) adding new matches to the result set calculated by the provider, and (2) making a potential match more precise. While the first case is a consequence of the distributed runtime model and query evaluation, the second case is caused by uncertain information caused by message loss/delay.
Fortunately, the 3-valued semantics of graph queries (see Table 1) already handles the first case: any match reported to the requester by any neighboring provider will be included in the query results if its truth evaluation is \(1\) or  . As such, any potential violation of a safety property will be detected, which may result in false positive alerts but critical situations would not be missed.
. As such, any potential violation of a safety property will be detected, which may result in false positive alerts but critical situations would not be missed.
However, the second case necessitates extra care since query matches coming from different sources (e.g. local cache, reply messages from providers) need to be fused in a consistent way. This match fusion is carried out at cu as follows:
-
If a match is obtained exclusively from the local runtime model of cu, then it is a certain match, formally \({[\![ \varphi (o_1, \dots , o_n) ]\!]}^{}\mathtt {@} cu = 1\).
-
If a match is sent as a reply by multiple neighboring computing units \(cu_i\) (with \(cu_i \in nbr(cu)\)), then we take the most certain result at cu, formally, \({[\![ \varphi (o_1, \dots , o_n) ]\!]}^{}\mathtt {@} cu := \underline{\max }\{ {[\![ \varphi (o_1, \dots , o_n) ]\!]}^{}\mathtt {@} cu_i | cu_i \in nbr(cu) \}\).
-
Otherwise, tuple \(o_1, \dots , o_n\) is surely not a match: \({[\![ \varphi (o_1, \dots , o_n) ]\!]}^{}\mathtt {@} cu = 0\).
Note that in the second case uses \(\underline{\max }\{ \}\) to assign a maximum of 3-valued logic values wrt. information ordering (which is different from the numerical maximum used in Table 1). Information ordering is a partial order  with
with  and
and  . It is worth pointing out that this distributed truth evaluation is also in line with Sobociński 3-valued logic axioms [33].
. It is worth pointing out that this distributed truth evaluation is also in line with Sobociński 3-valued logic axioms [33].
Performance Optimizations. Each match sent as a reply to a computing unit during distributed query evaluation can be cached locally to speed up the re-evaluation of the same query within the query cycle. This caching of query results is analogous to memoing in logic programming [46]. Currently, cache invalidation is triggered at the end of each query cycle by the local physical clock, which we assume to be (quasi-)synchronous with high precision across the platform.
This memoing approach also enables units to selectively store messages in the local cache depending on their specific needs. Furthermore, this can incorporate to deploy query services to computing units with limited amount of memory and prevent memory overflow due to the several messages sent over the network.
A graph query is evaluated according to a search plan [43], which is a list of predicates ordered in a way that matches of predicates can be found efficiently. During query evaluation, free variables of the predicates are bound to a value following the search plan. The evaluation terminates when all matches in the model are found. An in-depth discussion of query optimization is out of scope for this paper, but Sect. 5 will provide an initial investigation.
Semantic Guarantees and Limitations. Our construction ensures that (1) the execution will surely terminate upon reaching the end of the query time window, potentially yielding uncertain matches, (2) each local model serves as a single source of truth which cannot be overridden by calls to other computing units, and (3) matches obtained from multiple computing units will be fused by preserving information ordering. The over- and under approximation properties of 3-valued logic show that the truth values fused this way will provide a sound result (Theorem 1 in [42]). Despite the lack of total consistency, our approach still has safety guarantees by detecting all potentially unsafe situations.
There are also several assumptions and limitations of our approach. We use asynchronous communication without broadcast messages. We only assumed faults of communication links, but not the failures of computing units. We also excluded the case when computing units maliciously send false information. Instead of refreshing local caches in each cycle, the runtime model could incorporate information aging which may enable to handle other sources of uncertainty (which is currently limited to consequences of message loss). Finally, in case of longer cycles, the runtime model may no longer provide up-to-date information at query evaluation time.
Implementation Details. The concepts presented in the paper are implemented in a prototype software, which has three main components: (i) an EMF-based tool [39] for data modeling and code generation for the runtime model, (ii) an Eclipse-based tool for defining and compiling monitoring rules built on top of the VIATRA framework [41], and (iii) the runtime environment to evaluate queries.
The design tools are dominantly implemented in Java. We used EMF metamodels for data modeling, but created a code generator to derive lightweight C++ classes as representations of the runtime model. The query definition environment was extended to automatically compile queries into C++ monitors.
The runtime monitoring libraries and the runtime framework is available in C++. Our choice of C++ is motivated by its low runtime and memory overhead on almost any type of platforms, ranging from low-energy embedded microcontrollers to large-scale cloud environments. Technically, a generic query service can start query runners for each monitoring objective on each node. While query runners execute the query-specific search plan generated compile time, the network communication is handled by a query service if needed. To serialize the data between different nodes, we used the lightweight Protocol Buffers [16].
5 Evaluation
We conducted measurements to evaluate and address two research questions:
- Q1: :
-
How does distributed graph query execution perform compared to executing the queries on a single computing unit?
- Q2: :
-
Is query evaluation performance affected by alternative allocation of model objects to host computing units?
5.1 Measurement Setup
Computation Platform. We used the real distributed (physical) platform of the CPS demonstrator to answer these research questions (instead of setting up a virtual environment). It consists of 6 interconnected BBB devices (all running embedded Debian Jessie with PREEMPT-RT patch) connected to the railway track itself. This arrangement represents a distributed CPS with several computing units having only limited computation and communication resources. We used these units to maintain the distributed runtime model, and evaluate monitoring queries. This way we are able to provide a realistic evaluation, however, due to the fixed number of embedded devices built into the platform, we cannot evaluate the scalability of the approach wrt. the number of computing units.
CPS Monitoring Benchmark. To assess the distributed runtime verification framework, we used the MoDeS3 railway CPS demonstrator where multiple safety properties are monitored. They are all based on important aspects of the domain, and they have been integrated into the real monitoring components. Our properties of interest (in increasing complexity of queries) are the following:
-
Train locations: gets all trains and the segments on which trains are located.
-
Close trains: this pattern is the one introduced in Fig. 4.
-
Derailment: detects the train when approaching a turnout, but the turnout is set to the other direction (causing the train to run off from the track).
-
End of siding: detects trains approaching an end of the track.
Since the original runtime model of the CPS demonstrator has only a total of 49 objects, we scaled up the model by replicating the original elements (except for the computing units). This way we obtained models with 49–43006 objects and 114–109015 links, having similar structural properties as the original one.
Query Evaluation Benchmark. In order to provide an independent evaluation for our model query-based monitoring approach, we adapted the open-source Train Benchmark [35] that aims at comparing query evaluation performance of various tools. This benchmark defines several queries describing violations of well-formedness constraints with different complexity over graph models. Moreover, it also provides a model generator to support scalability assessment.
5.2 Measurement Results
Execution Times. The query execution times over models deployed to a single BBB were first measured to obtain a baseline evaluation time of monitoring for each rule (referred to as local evaluation). Then the execution times of system-level distributed queries were measured over the platform with 6 BBBs, evaluating two different allocations of objects (standard and alternative evaluations).
In Fig. 6 each result captures the times of 29 consecutive evaluations of queries excluding the warm-up effect of an initial run which loads the model and creates necessary auxiliary objects. A query execution starts when a node initiates evaluation, and terminates when all nodes have finished collecting matches and sent back their results to the initiator.
Overhead of Distributed Evaluation. On the positive side, the performance of graph query evaluation on a single unit is comparable to other graph query techniques reported in [35] for models with over 100 K objects, which shows a certain level of maturity of our prototype. Furthermore, the CPS demonstrator showed that distributed query evaluation yielded significantly better result than local-only execution for the Derailment query on medium size models (with 4K–43K objects reaching \(2.23\times \) – \(2.45\times \) average speed-up) and comparable runtime for Close trains and Train locations queries on these models (with the greatest average difference being 30 ms across all model sizes). However, distributed query evaluation had problems for End of siding, which is a complex query with negative application conditions, which provides clear directions for future research. Anyhow, the parallelism of even a small execution platform with only 6 computing units could suppress the communication overhead between units in case of several distributed queries, which is certainly a promising outcome.
Impact of Allocation on Query Evaluation. We synthesized different allocations of model elements to computing units to investigate the impact of allocation of model objects on query evaluation. With the CPS demonstrator model in particular, we chose to allocate all Trains to BBB1, and assigned every other node stored previously on BBB1 to the rest of the computing units. Similarly, for the Train Benchmark models, we followed this pattern with selected types, in addition to experimenting with fully random allocation of objects.
The two right-most columns of Fig. 6a and 6b show results of two alternate allocations for the same search plan with a peak difference of \(2.06\times \) (Derailment) and \(19.92\times \) (Semaphore neighbor) in the two cases. However, both of these allocations were manually optimized to exploit locality of model elements. In case of random allocations, difference in runtime may reach an order of magnitudeFootnote 1. Therefore it is worth investigating new allocation strategies and search plans for distributed queries for future work.
Threats to Validity. The generalizability of our experimental results is limited by certain factors. First, to measure the performance of our approach, the platform devices (1) executed only query services and (2) connected to an isolated local area network via Ethernet. Performance on a real network with a busy channel would likely have longer delays and message losses thus increasing execution time. Then we assessed performance using a single query plan synthesized automatically by the VIATRA framework but using heuristics to be deployed for a single computation unit. We believe that execution times of distributed queries would likely decrease with a carefully constructed search plan and allocation.
6 Related Work
Runtime Verification Approaches. For continuously evolving and dynamic CPSs, an upfront design-time formal analysis needs to incorporate and check the robustness of component behavior in a wide range of contexts and families of configurations, which is a very complex challenge. Thus consistent system behavior is frequently ensured by runtime verification (RV) [24], which checks (potentially incomplete) execution traces against formal specifications by synthesizing verified runtime monitors from provenly correct design models [21, 26].
Recent advances in RV (such as MOP [25] or LogFire [17]) promote to capture specifications by rich logic over quantified and parameterized events (e.g. quantified event automata [4] and their extensions [12]). Moreover, Havelund proposed to check such specifications on-the-fly by exploiting rule-based systems based on the RETE algorithm [17]. However, this technique only incorporates low-level events; while changes of an underlying data model are not considered as events.
Traditional RV approaches use variants of temporal logics to capture the requirements [6]. Recently, novel combinations of temporal logics with context-aware behaviour description [15, 19] (developed within the R3-COP and R5-COP FP7 projects) for the runtime verification of autonomous CPS appeared and provide a rich language to define correctness properties of evolving systems.
Runtime Verification of Distributed Systems. While there are several existing techniques for runtime verification of sequential programs available, the authors of [29] claim that much less research was done in this area for distributed systems. Furthermore, they provide the first sound and complete algorithm for runtime monitoring of distributed systems based on the 3-valued semantics of LTL.
The recently introduced Brace framework [49] supports RV in distributed resource-constrained environments by incorporating dedicated units in the system to support global evaluation of monitoring goals. There is also focus on evaluating LTL formulae in a fully distributed manner in [5] for components communicating on a synchronous bus in a real-time system. Additionally, machine learning-based solution for scalable fault detection and diagnosis system is presented in [2] that builds on correlation between observable system properties.
Distributed Graph Queries. Highly efficient techniques for local-search based [9] and incremental model queries [40] as part of the VIATRA framework were developed, which mainly builds on RETE networks as baseline technology. In [34], a distributed incremental graph query layer deployed over a cloud infrastructure with numerous optimizations was developed. Distributed graph query evaluation techniques were reported in [22, 27, 32], but none of these techniques considered an execution environment with resource-constrained computation units.
Runtime Models. The models@ runtime paradigm [8] serves as the conceptual basis for the Kevoree framework [28] (developed within the HEADS FP7 project). Other recent distributed, data-driven solutions include the Global Data Plane [48] and executable metamodels at runtime [44]. However, these frameworks currently offer very limited support for efficiently evaluating queries over a distributed runtime platform, which is the main focus of our current work.
7 Conclusions
In this paper, we proposed a runtime verification technique for smart and safe CPSs by using a high-level graph query language to capture safety properties for runtime monitoring and runtime models as a rich knowledge representation to capture the current state of the running system. A distributed query evaluation technique was introduced where none of the computing units has a global view of the complete system. The approach was implemented and evaluated on the physical system of MoDeS3 CPS demonstrator. Our first results show that it scales for medium-size runtime models, and the actual deployment of the query components to the underlying platform has significant impact on execution time. In the future, we plan to investigate how to characterize effective search plans and allocations in the context of distributed queries used for runtime monitoring.
Notes
- 1.
See Appendix A for details under http://bit.ly/2op3tdy.
References
Abril, M., et al.: An assessment of railway capacity. Transp. Res. Part E Logist. Transp. Rev. 44(5), 774–806 (2008)
Alippi, C., et al.: Model-free fault detection and isolation in large-scale cyber-physical systems. IEEE Trans. Emerg. Top. Comput. Intell. 1(1), 61–71 (2017)
AUTOSAR Tool Platform: Artop. https://www.artop.org/
Barringer, H., Falcone, Y., Havelund, K., Reger, G., Rydeheard, D.: Quantified event automata: towards expressive and efficient runtime monitors. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 68–84. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32759-9_9
Bauer, A., Falcone, Y.: Decentralised LTL monitoring. Formal Methods Syst. Des. 48(1–2), 46–93 (2016)
Bauer, A., Leucker, M., Schallhart, C.: Runtime verification for LTL and TLTL. ACM Trans. Softw. Eng. Methodol. 20(4), 14 (2011)
Bergmann, G., Ujhelyi, Z., Ráth, I., Varró, D.: A graph query language for EMF models. In: Cabot, J., Visser, E. (eds.) ICMT 2011. LNCS, vol. 6707, pp. 167–182. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21732-6_12
Blair, G.S., et al.: Models@run.time. IEEE Comput. 42(10), 22–27 (2009)
Búr, M., Ujhelyi, Z., Horváth, Á., Varró, D.: Local search-based pattern matching features in EMF-IncQuery. In: Parisi-Presicce, F., Westfechtel, B. (eds.) ICGT 2015. LNCS, vol. 9151, pp. 275–282. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21145-9_18
Cheng, B.H.C., et al.: Using models at runtime to address assurance for self-adaptive systems. In: Bencomo, N., France, R., Cheng, B.H.C., Aßmann, U. (eds.) Models@run.time. LNCS, vol. 8378, pp. 101–136. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08915-7_4
Dávid, I., Ráth, I., Varró, D.: Foundations for streaming model transformations by complex event processing. Softw. Syst. Model. 17, 1–28 (2016). https://doi.org/10.1007/s10270-016-0533-1
Decker, N., Leucker, M., Thoma, D.: Monitoring modulo theories. Int. J. Softw. Tools Technol. Transf. 18(2), 205–225 (2015)
Desai, A., Seshia, S.A., Qadeer, S., Broman, D., Eidson, J.C.: Approximate synchrony: an abstraction for distributed almost-synchronous systems. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9207, pp. 429–448. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21668-3_25
Emery, D.: Headways on high speed lines. In: 9th World Congress on Railway Research, pp. 22–26 (2011)
Gönczy, L., et al.: MDD-based design, configuration, and monitoring of resilient cyber-physical systems. Trustworthy Cyber-Physical Systems Engineering (2016)
Google: Protocol buffers. https://github.com/google/protobuf
Havelund, K.: Rule-based runtime verification revisited. Int. J. Softw. Tools Technol. Transf. 17(2), 143–170 (2015)
Hewitt, C., et al.: A universal modular ACTOR formalism for artificial intelligence. In: International Joint Conference on Artificial Intelligence, pp. 235–245 (1973)
Horányi, G., Micskei, Z., Majzik, I.: Scenario-based automated evaluation of test traces of autonomous systems. In: DECS workshop at SAFECOMP (2013)
Iqbal, M.Z., et al.: Applying UML/MARTE on industrial projects: challenges, experiences, and guidelines. Softw. Syst. Model. 14(4), 1367–1385 (2015)
Joshi, Y., et al.: Runtime verification of LTL on lossy traces. In: Proceedings of the Symposium on Applied Computing - SAC 2017, pp. 1379–1386. ACM Press (2017)
Krause, C., Tichy, M., Giese, H.: Implementing graph transformations in the bulk synchronous parallel model. In: Gnesi, S., Rensink, A. (eds.) FASE 2014. LNCS, vol. 8411, pp. 325–339. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54804-8_23
Krupitzer, C., et al.: A survey on engineering approaches for self-adaptive systems. Perv. Mob. Comput. 17, 184–206 (2015)
Leucker, M., Schallhart, C.: A brief account of runtime verification. J. Log. Algebr. Program. 78(5), 293–303 (2009)
Meredith, P.O., et al.: An overview of the MOP runtime verification framework. Int. J. Softw. Tools Technol. Transf. 14(3), 249–289 (2012)
Mitsch, S., Platzer, A.: ModelPlex: verified runtime validation of verified cyber-physical system models. In: Bonakdarpour, B., Smolka, S.A. (eds.) RV 2014. LNCS, vol. 8734, pp. 199–214. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11164-3_17
Mitschke, R., Erdweg, S., Köhler, M., Mezini, M., Salvaneschi, G.: i3QL: Language-integrated live data views. ACM SIGPLAN Not. 49(10), 417–432 (2014)
Morin, B., et al.: Kevoree Modeling Framework (KMF): efficient modeling techniques for runtime use. University of Luxembourg, Technical report (2014)
Mostafa, M., Bonakdarpour, B.: Decentralized runtime verification of LTL specifications in distributed systems. In: 2015 IEEE International Parallel and Distributed Processing Symposium, pp. 494–503, May 2015
Nielsen, C.B., et al.: Systems of systems engineering: Basic concepts, model-based techniques, and research directions. ACM Comput. Surv. 48(2), 18 (2015)
No Magic: MagicDraw. https://www.nomagic.com/products/magicdraw
Peters, M., Brink, C., Sachweh, S., Zündorf, A.: Scaling parallel rule-based reasoning. In: Presutti, V., d’Amato, C., Gandon, F., d’Aquin, M., Staab, S., Tordai, A. (eds.) ESWC 2014. LNCS, vol. 8465, pp. 270–285. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-07443-6_19
Sobociński, B.: Axiomatization of a Partial System of Three-Value Calculus of Propositions. Institute of Applied Logic (1952)
Szárnyas, G., Izsó, B., Ráth, I., Harmath, D., Bergmann, G., Varró, D.: IncQuery-D: a distributed incremental model query framework in the cloud. In: Dingel, J., Schulte, W., Ramos, I., Abrahão, S., Insfran, E. (eds.) MODELS 2014. LNCS, vol. 8767, pp. 653–669. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11653-2_40
Szárnyas, G., et al.: The Train Benchmark: cross-technology performance evaluation of continuous model queries. Softw. Syst. Model., 1–29 (2017). https://doi.org/10.1007/s10270-016-0571-8
Sztipanovits, J., et al.: Toward a science of cyber-physical system integration. Proc. IEEE 100(1), 29–44 (2012)
Sztipanovits, J., Bapty, T., Neema, S., Howard, L., Jackson, E.: OpenMETA: a model- and component-based design tool chain for cyber-physical systems. In: Bensalem, S., Lakhneck, Y., Legay, A. (eds.) ETAPS 2014. LNCS, vol. 8415, pp. 235–248. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54848-2_16
Szvetits, M., Zdun, U.: Systematic literature review of the objectives, techniques, kinds, and architectures of models at runtime. Softw. Syst. Model. 15(1), 31–69 (2013)
The Eclipse Project: Eclipse Modeling Framework. http://www.eclipse.org/emf
Ujhelyi, Z., et al.: EMF-IncQuery: an integrated development environment for live model queries. Sci. Comput. Program. 98, 80–99 (2015)
Varró, D., et al.: Road to a reactive and incremental model transformation platform: three generations of the VIATRA framework. Softw. Syst. Model 15(3), 609–629 (2016)
Varró, D., Semeráth, O., Szárnyas, G., Horváth, Á.: Towards the automated generation of consistent, diverse, scalable and realistic graph models. In: Heckel, R., Taentzer, G. (eds.) Graph Transformation, Specifications, and Nets. LNCS, vol. 10800, pp. 285–312. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-75396-6_16
Varró, G., et al.: An algorithm for generating model-sensitive search plans for pattern matching on EMF models. Softw. Syst. Model 14(2), 597–621 (2015)
Vogel, T., Giese, H.: Model-driven engineering of self-adaptive software with EUREMA. ACM Trans. Auton. Adapt. Syst. 8(4), 18 (2014)
Vörös, A., et al.: MoDeS3: model-based demonstrator for smart and safe cyber-physical systems. In: NASA Formal Methods Symposium (2018, accepted)
Warren, D.S.: Memoing for logic programs. Commun. ACM 35(3), 93–111 (1992)
Yakindu Statechart Tools: Yakindu. http://statecharts.org/
Zhang, B., et al.: The cloud is not enough: saving IoT from the cloud. In: 7th USENIX Workshop on Hot Topics in Cloud Computing (2015)
Zheng, X., et al.: Efficient and scalable runtime monitoring for cyber-physical system. IEEE Syst. J. PP, 1–12 (2016)
Acknowledgements
This paper is partially supported by MTA-BME Lendület Cyber-Physical Systems Research Group, the NSERC RGPIN-04573-16 project, the Werner Graupe International Fellowship in Engineering (as part of the MEDA program), and the ÚNKP-17-2-I New National Excellence Program of the Ministry of Human Capacities. We are grateful for Oszkár Semeráth for helping with the semantics of 3-valued logic, Gábor Szárnyas for the help with setting up Train Benchmark, the contributors of MoDeS3 for setting up the evaluation platform, and the feedback from anonymous reviewers and Gábor Bergmann.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Búr, M., Szilágyi, G., Vörös, A., Varró, D. (2018). Distributed Graph Queries for Runtime Monitoring of Cyber-Physical Systems. In: Russo, A., Schürr, A. (eds) Fundamental Approaches to Software Engineering. FASE 2018. Lecture Notes in Computer Science(), vol 10802. Springer, Cham. https://doi.org/10.1007/978-3-319-89363-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-89363-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89362-4
Online ISBN: 978-3-319-89363-1
eBook Packages: Computer ScienceComputer Science (R0)







 then the 2-valued interpretation of
then the 2-valued interpretation of  in M denoted by
in M denoted by  , otherwise
, otherwise 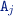 in
in  , and otherwise
, and otherwise  from
from  , otherwise
, otherwise 

 ,
,  (where we abbreviated the binding
(where we abbreviated the binding  in its cache, if the reply of the provider
in its cache, if the reply of the provider 
