Abstract
Multiple (more than 2) model synchronization is ubiquitous and important for MDE, but its theoretical underpinning gained much less attention than the binary case. Specifically, the latter was extensively studied by the bx community in the framework of algebraic models for update propagation called lenses. Now we make a step to restore the balance and propose a notion of multiary delta lens. Besides multiarity, our lenses feature reflective updates, when consistency restoration requires some amendment of the update that violated consistency. We emphasize the importance of various ways of lens composition for practical applications of the framework, and prove several composition results.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Modelling normally results in a set of inter-related models presenting different views of the system. If one of the models changes and their joint consistency is violated, the related models should also be changed to restore consistency. This task is obviously of paramount importance for MDE, but its theoretical underpinning is inherently difficult and reliable practical solutions are rare. There are working solutions for file synchronization in systems like Git, but they are not applicable in the UML/EMF world of diagrammatic models. For the latter, much work has been done for the binary case (synchronizing two models) by the bidirectional transformation community (bx) [15], specifically, in the framework of so called delta lenses [3], but the multiary case (the number of models to be synchronized is \(n\ge 2\)) gained much less attention—cf. the energetic call to the community in a recent Stevens’ paper [16].
The context underlying bx is model transformation, in which one model in the pair is considered as a transform of the other even though updates are propagated in both directions (so called round-tripping). Once we go beyond \(n=2\), we at once switch to a more general context of models inter-relations beyond model-to-model transformations. Such situations have been studied in the context of multiview system consistency, but rarely in the context of an accurate formal basis for update propagation. The present paper can be seen as an adaptation of the (delta) lens-based update propagation framework for the multiview consistency problem. We will call it multi-directional update propagation or mx following the bx-pattern. Our contributions to mx are as follows.
We show with a simple example (Sect. 2) an important special feature of mx: consistency restoration may require not only update propagation to other models but the very update created inconsistency should itself be amended (even for the case of a two-view system!); thus, update propagation should, in general, be reflective. Moreover, if even consistency can be restored without a reflective amendment, there are cases when such reflection is still reasonable. It means that Hippocraticness [15]—a major requirement for the classical bx, may have less weight in the mx world. In Sect. 3, we provide a formal definition of multiary (symmetric) lenses with reflection, and define (Sect. 4) several operations of such lens composition producing complex lenses from simple ones. Specifically, we show how n-ary lenses can be composed from n-tuples of asymmetric binary lenses (Theorems 1 and 2), thus giving a partial solution to the challenging issue of building mx synchronization via bx discussed by Stevens in [16]. We consider lens composition results important for practical application of the framework. If the tool builder has implemented a library of elementary synchronization modules based on lenses and, hence, ensuring basic laws for change propagation, then a complex module assembled from elementary lenses will automatically be a lens and thus also enjoys the basic laws.
2 Example
We will consider a simple example motivating our framework. Many formal constructs below will be illustrated with the example (or its fragments) and referred to as Running example.
2.1 A Multimodel to Play With
Suppose two data sources, whose schemas (we say metamodels) are shown in Fig. 1 as class diagrams \(M_{1}\) and \(M_{2}\) that record employment. The first source is interested in employment of people living in downtown, the second one is focused on software companies and their recently graduated employees. In general, population of classes \(\mathsf {Person}\) and \(\mathsf {Company}\) in the two sources can be different – they can even be disjoint, but if a recently graduated downtowner works for a software company, her appearance in both databases is very likely. Now suppose there is an agency investigating traffic problems, which maintains its own data on commuting between addresses (see schema \(M_{3}\)) computable by an obvious relational join over \(M_{1}\) and \(M_{2}\). In addition, the agency supervises consistency of the two sources and requires that if they both know a person p and a company c, then they must agree on the employment record (p, c): it is either stored by both or by neither of the sources. For this synchronization, it is assumed that persons and companies are globally identified by their names. Thus, a triple of data sets (we will say models) \(A_{1}\), \(A_{2}\), \(A_{3}\), instantiating the respective metamodels, can be either consistent (if the constraints described above are satisfied) or inconsistent (if they aren’t). In the latter case, we normally want to change some or all models to restore consistency. We will call a collection of models to be kept in sync a multimodel.
To talk about constraints for multimodels, we need an accurate notation. If \(A_{}\) is a model instantiating metamodel \(M_{}\) and X is a class in \(M_{}\), we write \(X^A_{}\) for the set of objects instantiating X in A. Similarly, if \(r\!:X_1\leftrightarrow X_2\) is an association in \(M_{}\), we write \(r^A_{}\) for the corresponding binary relation over \(X_1^{A_{}}\,\times \,X_2^{A_{}}\). For example, Fig. 2 presents a simple model \(A_{1}\) instantiating \(M_{1}\) with \(\mathsf {Person}^{A_{1}}=\{p_1,p_1'\}\), \(\mathsf {Company}^{A_{1}}=\{c_1\}\), \(\mathsf {empl}\text {-}\mathsf {er}^{A_{1}}=\{(p_1,c_1)\}\), and similarly for attributes, e.g.,
(\(\mathsf {lives}^{A_{1}}\) and also \(\mathsf {name}^{A_{1}}\) are assumed to be functions and \(\mathsf {Addr}\) is the (model-independent) set of all possible addresses). The triple \(({A_{1}}, {A_{2}}, {A_{3}})\) is a (state of a) multimodel over the multimetamodel \((M_{1},M_{2},M_{3})\), and we say it is consistent if the two constraints specified below are satisfied. Constraint (C1) specifies mutual consistency of models \(A_1\) and \(A_2\) in the sense described above; constraint (C2) specifies consistency between the agency’s view of data and the two data sources:


where \(^{-1}\) refers to the inverse relations and \(\bowtie \) denotes relational join (composition); using subsetting rather than equality in (C2) assumes that there are other data sources the agency can use. Note that constraint (C1) inter-relates two component models of the multimodel, while (C2) involves all three components and forces synchronization to be 3-ary.
It is easy to see that multimodel \(A_{1,2,3}\) in Fig. 2 is “two-times” inconsistent: (C1) is violated as both \(A_{1}\) and \(A_{2}\) know Mary and IBM, and (IBM, Mary)\(\,\in \) \(\mathsf {empl}\text {-}\mathsf {ee}^{A_{2}}\) but (Mary, IBM)\(\,\notin \mathsf {empl}\text {-}\mathsf {er}^{A_{1}}\); (C2) is violated as \(A_{1}\) and \(A_{2}\) show a commuting pair (a1, a15) not recorded in \(A_{3}\). We will discuss consistency restoration in the next subsection, but first we need to discuss an important part of the multimodel – traceability or correspondence mappings – held implicit so far.
A(n inconsistent) multimodel \(\mathcal{A}^\dagger \) over the multi-metamodel in Fig. 1
Indeed, classes \(\mathsf {Person}^{A_{1}}\) and \(\mathsf {Person}^{A_{2}}\) are interrelated by a correspondence relation linking persons with the same name, and similarly for \(\mathsf {Company}\). These correspondence links (we will write corr-links) may be implicit as they can always be restored. More important is to maintain corr-links between \(\mathsf {Commute}^{A_{3}}\) and \(\mathsf {empl}\text {-}\mathsf {er}^{A_{1}}\cup \mathsf {empl}\text {-}\mathsf {ee}^{A_{2}}\). Indeed, class \(\mathsf {Commute}\) together with its two attributes can be seen as a relation, and this relation can be instantiated by a multirelation as people living at the same address can work for companies located at the same address. If some of such \(\mathsf {Commute}\)-objects is deleted, and this delete is to be propagated to models \(A_{1,2}\), we need corr-links to know which employment links are to be deleted. Hence, it makes sense to establish such links when objects are added to \(\mathsf {Commute}^{A_{3}}\), and use them later for deletion propagation.
Importantly, for given models \(A_{1,2,3}\), there may be several different correspondence mappings: the same \(\mathsf {Commute}\)-object can correspond to different commute-links over \(A_{1}\) and \(A_{2}\). In fact, multiplicity of possible corr-specifications is a general story that can only be avoided if absolutely reliable keys are available, e.g., if we suppose that persons and companies can always be uniquely identified by names, then corrs between these classes are unique. But if keys (e.g., person names) are not absolutely reliable, we need a separate procedure of model matching or alignment that has to establish whether objects \(p'_1\in \mathsf {Person}^{A_{1}}\) and \(p'_2\in \mathsf {Person}^{A_{2}}\) both named Mary represent the same real world object. Constraints we declared above implicitly involve corr-links, e.g., formula for (C1) is a syntactic sugar for the following formal statement: if there are corr-links \(p=(p_1, p_2)\) and \(c=(c_1, c_2)\) with \(p_i\,{\in }\,\mathsf {Person}^{A_i}\), \(c_i~{\in }~\mathsf {Company}^{A_i}\) (\(i=1,2\)) then the following holds: \((p_1,c_1)\in \mathsf {empl}\text {-}\mathsf {er}^{A_{1}}\) iff \((c_2,p_2)\in \mathsf {empl}\text {-}\mathsf {ee}^{A_{2}}\). A precise formal account of this discussion can be found in [10].
Thus, a multimodel is actually a tuple \(\mathcal{A}=({A_{1}}, {A_{2}}, {A_{3}}, R)\) where R is a collection of correspondence relations over sets involved. This R is implicit in Fig. 2 since in this very special case it can be restored. Consistency of a multimodel is a property of the entire 4-tuple \(\mathcal{A}\) rather than its 3-tuple carrier \(({A_{1}}, {A_{2}}, {A_{3}})\).
2.2 Synchronization via Update Propagation
There are several ways to restore consistency of the multimodel in Fig. 2 w.r.t. constraint (C1). We may delete Mary from \(A_{1}\), or delete its employment with IBM from \(A_{2}\), or even delete IBM from \(A_{2}\). We can also change Mary’s employment from IBM to Google, which will restore (C1) as \(A_{1}\) does not know Google. Similarly, we can delete John’s record from \(A_{1}\) and then Mary’s employment with IBM in \(A_{2}\) would not violate (C1). As the number of constraints and the elements they involve increase, the number of consistency restoration variants grows fast.
The range of possibilities can be essentially decreased if we take into account the history of creating inconsistency and consider not only an inconsistent state \(\mathcal{A}^\dagger \) but update \(u{:}\;\mathcal{A}\rightarrow \mathcal{A}^\dagger \) that created it (assuming that \(\mathcal{A}\) is consistent). For example, suppose that initially model \(A_{1}\) contained record (Mary, IBM) (and \(A_{3}\) contained (a1, a15)-commute), and the inconsistency appears after Mary’s employment with IBM was deleted in \(A_{1}\). Then it’s reasonable to restore consistency by deleting this employment record in \(A_{2}\) too; we say that deletion was propagated from \(A_{1}\) to \(A_{2}\) (where we assume that initially \(A_{3}\) contained the commute (a1, a15)). If the inconsistency appears after adding (IBM, Mary)-employment to \(A_{2}\), then it’s reasonable to restore consistency by adding such a record to \(A_{1}\). Although propagating deletions/additions to deletions/additions is typical, there are non-monotonic cases too. Let us assume that Mary and John are spouses (they live at the same address), and that IBM follows an exotic policy prohibiting spouses to work together. Then we can interpret addition of (IBM, Mary)-record to \(A_{2}\) as swapping of the family member working for IBM, and then (John, IBM) is to be deleted from \(A_{1}\).
Now let’s consider how updates to and from model \(A_{3}\) may be propagated. As mentioned above, traceability/correspondence links play a crucial role here. If additions to \(A_{1}\) or \(A_{2}\) or both create a new commute, the latter has to be added to \(A_{3}\) (together with its corr-links) due to constraint (C2). In contrast, if a new commute is added to \(A_{3}\), we change nothing in \(A_{1,2}\) as (C2) only requires inclusion. If a commute is deleted from \(A_{3}\), and it is traced to a corresponding employment in \(\mathsf {empl}\text {-}\mathsf {er}^{A_{1}}\cup \mathsf {empl}\text {-}\mathsf {ee}^{A_{2}}\), then this employment is deleted. (Of course, there are other ways to remove a commute derivable over \(A_{1}\) and \(A_{2}\).) Finally, if a commute-generating employment in \(\mathsf {empl}\text {-}\mathsf {er}^{A_{1}}\cup \mathsf {empl}\text {-}\mathsf {ee}^{A_{2}}\) is deleted, the respective commute in \(A_{3}\) is deleted too. Clearly, many of the propagation policies above although formally correct, may contradict the real world changes and hence should be corrected, but this is a common problem of a majority of automatic synchronization approaches, which have to make guesses in order to resolve non-determinism inherent in consistency restoration.
2.3 Reflective Update Propagation
An important feature of update propagation scenarios above is that consistency could be restored without changing the model whose update caused inconsistency. However, this is not always desirable. Suppose again that violation of constraint (C1) in multimodel in Fig. 2 was caused by adding a new person Mary to \(A_{1}\), e.g., as a result of Mary’s moving to downtown. Now both models know both Mary and IBM, and thus either employment record (Mary, IBM) is to be added to \(A_{1}\), or record (IBM, Mary) is to be removed from \(A_{2}\). Either of the variants is possible, but in our context, adding (Mary, IBM) to \(A_{1}\) seems more likely and less specific than deletion (IBM, Mary) from \(A_{2}\). Indeed, if Mary has just moved to downtown, the data source \(A_{1}\) simply may not have completed her record yet. Deletion (IBM, Mary) from \(A_{2}\) seems to be a different event unless there are strong causal dependencies between moving to downtown and working for IBM. Thus, an update policy that would keep \(A_{2}\) unchanged but amend addition of Mary to \(A_{1}\) with further automatic adding her employment for IBM (as per model \(A_{2}\)) seems reasonable. This means that updates can be reflectively propagated (we also say self-propagated).
Of course, self-propagation does not necessarily mean non-propagation to other directions. Consider the following case: model \(A_{1}\) initially only contains (John, IBM) record and is consistent with \(A_{2}\) shown in Fig. 2. Then record (Mary, Google) was added to \(A_{1}\), which thus became inconsistent with \(A_{2}\). To restore consistency, (Mary, Google) is to be added to \(A_{2}\) (the update is propagated from \(A_{1}\) to \(A_{2}\)) and (Mary, IBM) is to be added to \(A_{1}\) as discussed above (i.e., addition of (Mary, Google) is amended or self-propagated).
A general schema of update propagation including reflection is shown in Fig. 3. We begin with a consistent multimodel \(({A_{1}}...A_{n},R)\)Footnote 1 one of which members is updated \(u_i{:}\;A_i\rightarrow A'_i\). The propagation operation, based on a priori defined propagation policies as sketched above, produces:
-
(a)
updates on all other models \(u'_j{:}\;A_j\rightarrow A''_j\), \(1\le j\ne i \le n\);
-
(b)
a reflective update \(u'_i{:}\;A'_i\rightarrow A''_i\);
-
(c)
a new correspondence specification \(R''\) such that the updated multimodel \((A''_1...A''_n, R'')\) is consistent.
To distinguish given data from those produced by the operation, the former are shown with framed nodes and solid lines in Fig. 3 while the latter are non-framed and dashed. Below we introduce an algebraic model encompassing several operations and algebraic laws formally modelling situations considered so far.
3 Multidirectional Update Propagation and Delta Lenses
A delta-based mathematical model for bx is well-known under the name of delta lenses; below we will say just lens. There are two main variants: asymmetric lenses, when one model is a view of the other and hence does not have any private information, and symmetric lenses, when both sides have their private data not visible on the other side [2, 3, 6]. In this section we will develop a framework for generalizing the idea for any \(n\ge 2\) and including reflective updates.
3.1 Background: Graphs and Categories
We reproduce well-known definitions to fix our notation. A (directed multi-)graph G consists of a set \({G^\bullet }\) of nodes and a set  of arrows equipped with two functions
of arrows equipped with two functions  that give arrow a its source \(\mathsf {s}(a)\) and target \(\mathsf {t}(a)\) nodes. We write \(a{:}\;N\rightarrow N'\) if \(\mathsf {s}(a)=N\) and \(\mathsf {t}(a)=N'\), and \(a{:}\;N\rightarrow \_\) or \(a{:}\;\_\rightarrow N'\) if only one of this conditions is given. Correspondingly, expressions
that give arrow a its source \(\mathsf {s}(a)\) and target \(\mathsf {t}(a)\) nodes. We write \(a{:}\;N\rightarrow N'\) if \(\mathsf {s}(a)=N\) and \(\mathsf {t}(a)=N'\), and \(a{:}\;N\rightarrow \_\) or \(a{:}\;\_\rightarrow N'\) if only one of this conditions is given. Correspondingly, expressions  ,
,  ,
,  denote sets of, resp., all arrows from N to \(N'\), all arrows from N, and all arrows into \(N'\).
denote sets of, resp., all arrows from N to \(N'\), all arrows from N, and all arrows into \(N'\).
A (small) category is a graph, whose arrows are associatively composable and every node has a special identity loop, which is the unit of the composition. In more detail, given two consecutive arrows \(a_1{:}\;\_\rightarrow N\) and \(a_2{:}\;N\rightarrow \_\), we denote the composed arrow by \(a_1;a_2\). The identity loop of node N is denoted by \(\mathsf {id}_{N}\), and equations \(a_1;\mathsf {id}_N=a_1\) and \(\mathsf {id}_N;a_2=a_2\) are to hold. A functor is a mapping of nodes and arrows from one category to another, which respects sources and targets. Having a tuple of categories \((\mathbf {A}_1...\mathbf {A}_n)\), their product is a category \(\mathbf {A}_1\,{\times }...{\times }\,\mathbf {A}_n\) whose objects are tuples \((A_1...A_n)\,\in \,{{\mathbf {A}_1^\bullet }}\,{\times }...{\times }\,{{\mathbf {A}_n^\bullet }}\), and arrows from \((A_1...A_n)\) to \((A'_1...A'_n)\) are tuples of arrows \((u_1...u_n)\) with \(u_i{:}\;A_i\rightarrow A'_i\) for all \(i\in 1...n\).
3.2 Model Spaces and Correspondences
Basically, a model space is a category, whose nodes are called model states or just models, and arrows are (directed) deltas or updates. For an arrow \(u{:}\;A\rightarrow A'\), we treat A as the state of the model before update u, \(A'\) as the state after the update, and u as an update specification. Structurally, it is a specification of correspondences between A and \(A'\). Operationally, it is an edit sequence (edit log) that changed A to \(A'\). The formalism does not prescribe what updates are, but assumes that they form a category, i.e., there may be different updates from state A to state \(A'\); updates are composable; and idle updates \(\mathsf {id}_A{:}\;A\rightarrow A\) (doing nothing) are the units of the composition.
In addition, we require every model space \(\mathbf {A}\) to be endowed with a family  of binary relations
of binary relations  indexed by objects of \(\mathbf {A}\), and specifying non-conflicting or compatible consecutive updates. Intuitively, an update u into A is compatible with update \(u'\) from A, if \(u'\) does not revert/undo anything done by u, e.g., it does not delete/create objects created/deleted by u, or re-modify attributes modified by u (see [14] for a detailed discussion). Formally, we only require
indexed by objects of \(\mathbf {A}\), and specifying non-conflicting or compatible consecutive updates. Intuitively, an update u into A is compatible with update \(u'\) from A, if \(u'\) does not revert/undo anything done by u, e.g., it does not delete/create objects created/deleted by u, or re-modify attributes modified by u (see [14] for a detailed discussion). Formally, we only require  and
and  for all \(A\in {{\mathbf {A}^\bullet }}\),
for all \(A\in {{\mathbf {A}^\bullet }}\),  and
and  .
.
Definition 1
(Model spaces). A model space is a pair  with \(|\mathbf {A}|\) a category (the carrier) of models and updates and
with \(|\mathbf {A}|\) a category (the carrier) of models and updates and  a family as specified above. A model space functor from \(\mathbf {A}\) to \(\mathbf {B}\) is a functor \(F:|\mathbf {A}|\rightarrow |\mathbf {B}|\), such that
a family as specified above. A model space functor from \(\mathbf {A}\) to \(\mathbf {B}\) is a functor \(F:|\mathbf {A}|\rightarrow |\mathbf {B}|\), such that  implies
implies  . We will denote model spaces and their carriers by the same symbol and often omit explicit mentioning of
. We will denote model spaces and their carriers by the same symbol and often omit explicit mentioning of  . \(\square \)
. \(\square \)
In the sequel, we will work with families of model spaces indexed by a finite set I, whose elements can be seen as space names. To simplify notation, we will assume that \(I=\{1,\ldots ,n\}\) although ordering will not play any role in our framework. Given a tuple of model spaces \(\mathbf {A}_1, \ldots , \mathbf {A}_n\), we will refer to objects and arrows of the product category \(\mathbf {A}_1\,{\times }\cdots {\times }\,\mathbf {A}_n\) as model tuples and update tuples or, sometimes, as discrete multimodels/multiupdates.
Definition 2
(Multispace/Multimodels). Let \(n\ge 2\) be a natural number.
-
(i)
An n-ary multimodel space or just an n-ary multispace \({\varvec{\mathcal {A}}}\) is given by a family of model spaces \(\varvec{\partial }{{\varvec{\mathcal {A}}}}=(\mathbf {A}_1, \ldots , \mathbf {A}_n)\) called the boundary of \({\varvec{\mathcal {A}}}\), and a set
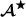 of elements called corrs along with a family of functions
of elements called corrs along with a family of functions 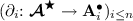 providing every corr R with its boundary \(\partial R=(\partial _1 R\ldots \partial _n R)\), i.e., a tuple of models taken from the multispace boundary one model per space. Intuitively, a corr is understood as a consistent correspondence specification interrelating models from its boundary (and for this paper, all corrs are assumed consistent).
providing every corr R with its boundary \(\partial R=(\partial _1 R\ldots \partial _n R)\), i.e., a tuple of models taken from the multispace boundary one model per space. Intuitively, a corr is understood as a consistent correspondence specification interrelating models from its boundary (and for this paper, all corrs are assumed consistent).Given a model tuple \(({A_1}...{A_{n}})\), we write
 for the set of all corrs R with \(\partial R=({A_1}...{A_{n}})\); we call models \(A_i\) feet of R. Respectively, spaces \(\mathbf {A}_i\) are feet of \({\varvec{\mathcal {A}}}\) and we write \(\varvec{\partial }_i{\varvec{\mathcal {A}}}\) for \(\mathbf {A}_i\).
for the set of all corrs R with \(\partial R=({A_1}...{A_{n}})\); we call models \(A_i\) feet of R. Respectively, spaces \(\mathbf {A}_i\) are feet of \({\varvec{\mathcal {A}}}\) and we write \(\varvec{\partial }_i{\varvec{\mathcal {A}}}\) for \(\mathbf {A}_i\). -
(ii)
An (aligned consistent) multimodel over a multispace \({\varvec{\mathcal {A}}}\) is a model tuple \(({A_1}...{A_{n}})\) along with a corr \(R\in {\varvec{\mathcal {A}}}^{\bigstar }_{}({A_1}...{A_{n}})\) relating the models. A multimodel update \(u{:}\;({A_1}...{A_{n}}, R)\rightarrow ({A'_1}...{A'_{n}}, R')\) is a tuple of updates (\(u_1{:}\;A_1\rightarrow A'_1\), ..., \(u_n{:}\;A_n\rightarrow A'_n\)). \(\square \)
Note that any corr R uniquely defines a multimodel via the corr’s boundary function \(\partial \). We will also need to identify the set of all corrs for some fixed \(A\in {{\mathbf {A}_i^\bullet }}\) for a given i: \({\varvec{\mathcal {A}}}^{\bigstar }_{i}(A,\_){\mathop {=}\limits ^{\mathrm {def}}}\,\left\{ {\,}\left| \;{R\in {\varvec{\mathcal {A}}}^{\bigstar }_{}}\right. \right\} {\partial _i R=A}\).
The Running example of Sect. 2 gives rise to a 3-ary multimodel space. For \(i\le 3\), space \(\mathbf {A}_i\) consists of all models instantiating metamodel \(M_i\) in Fig. 1 and their updates. To get a consistent multimodel \((A_1A_2A_3, R)\) from that one shown in Fig. 2, we can add to \(A_{1}\) an \(\mathsf {empl}\)-\(\mathsf {er}\)-link connecting Mary to IBM, add to \(A_{3}\) a commute with \(\mathsf {from}=a1\) and \(\mathsf {to}=a15\), and form a corr-set \(R=\{(p_1',p_2'),(c_1,c_2')\}\) (all other corr-links are derivable from this data).
3.3 Update Propagation and Multiary (Delta) Lenses
Update policies described in Sect. 2 can be extended to cover propagation of all updates \(u_i\), \(i\in 1...3\) according to the pattern in Fig. 3. This is a non-trivial task, but after it is accomplished, we have the following synchronization structure.
Definition 3
(Symmetric lenses). An n-ary symmetric lens is a pair \(\ell =({\varvec{\mathcal {A}}}, \mathsf {ppg})\) with \({\varvec{\mathcal {A}}}\) an n-ary multispace called the carrier of \(\ell \), and \((\mathsf {ppg}_i)_{i\le n}\) an n-tuple of operations of the following arities. Operation \(\mathsf {ppg}_i\) takes a corr R (in fact, a multimodel) with boundary \(\partial R=({A_1}...{A_{n}})\), and an update \(u_i{:}\;A_i\rightarrow A'_i\) as its input, and returns
-
(a)
an \((n-1)\)-tuple of updates \(u'_j{:}\;A_j\rightarrow A''_j\) with \(1\le j\not = i\le n\);
-
(b)
a reflective update \(u'_i{:}\;A'_i\rightarrow A''_i\) also called an amendment of \(u_i\),
-
(c)
a new consistent corr \(R''\in {\varvec{\mathcal {A}}}^{\bigstar }_{}({A''_1}...{A''_{n}})\).
In fact, operations \(\mathsf {ppg}_i\) complete a local update \(u_i\) to an entire multimodel update with components \((u_j')_{j\ne i}\) and \(u_i;u'_i\) (see Fig. 3). \(\square \)
Notation. If the first argument \(R\) of operation \(\mathsf {ppg}\) \(_i\) is fixed, the corresponding family of unary operations (whose only argument is \(u_i\)) will be denoted by \(\mathsf {ppg}^{R}_i\). By taking the jth component of the multi-element result, we obtain single-valued unary operations \(\mathsf {ppg}^{R}_{ij}\) producing, resp. updates \(u'_j=\mathsf {ppg}^{R}_{ij}(u_i){:}\;A'_j\rightarrow A''_j\). Note that \(A'_j=A_j\) for all \(j\not =i\) (see clause (a) of the definition) while \(\mathsf {ppg}^{R}_{ii}\) is the reflective update (b). We also have operation \(\mathsf {ppg}^{R}_{i\star }\) returning a new consistent corr \(R''=\mathsf {ppg}^{R}_{i\star }(u_i)\) according to (c).
Definition 4
(Closed updates). Given a lens \(\ell =({\varvec{\mathcal {A}}},\mathsf {ppg})\) and a corr \(R\in {\varvec{\mathcal {A}}}^{\bigstar }_{}({A_1}...{A_{n}})\), we call an update \(u_i{:}\;A_i\rightarrow A'_i\) R-closed, if \(\mathsf {ppg}^{R}_{ii}(u_i)=\mathsf {id}_{A_i'}\). An update is \(\ell \)-closed if it is R-closed for all R. Lens \(\ell \) is called non-reflective at foot \(\mathbf {A}_i\), if all updates in  are \(\ell \)-closed. \(\square \)
are \(\ell \)-closed. \(\square \)
For the Running example, update propagation policies described in Sect. 2 give rise to a lens non-reflective at space \(\mathbf {A}_3\).
Definition 5
(Well-behavedness). A lens \(\ell =({\varvec{\mathcal {A}}},\mathsf {ppg})\) is called well-behaved (wb) if the following laws hold for all \(i\le n\), \(A_i\in {{\mathbf {A}_i^\bullet }}\), \(R\in {\varvec{\mathcal {A}}}^{\bigstar }_{i}(A_i, \_)\) and \(u_i{:}\;A_i\rightarrow A'_i\), cf. Fig. 3.

where \(u_i' = \mathsf {ppg}^{R}_{ii}(u_i)\) as in Definition 3. \(\square \)
Stability says that lenses do nothing voluntarily. Reflect1 says that amendment works towards “completion” rather than “undoing”, and Reflect2-3 are idempotency conditions to ensure the completion indeed done.
Definition 6
(Invertibility). A wb lens is called (weakly) invertible, if it satisfies the following law for any i, update \(u_i{:}\;A_i\rightarrow A'_i\) and \(R\in {\varvec{\mathcal {A}}}^{\bigstar }_{i}(A_i,\_)\):

\(\square \)
This law deals with “round-tripping”: operation \(\mathsf {ppg}^{R}_{ji}\) applied to update \(u_j=\mathsf {ppg}^{R}_{ij}(u_i)\) results in update \(\hat{u_i}\) equivalent to \(u_i\) in the sense that \(\mathsf {ppg}^{R}_{ij}(\hat{u_i})=\mathsf {ppg}^{R}_{ij}(u_i)\) (see [3] for a motivating discussion).
Example 1
(Identity Lens \(\ell (n\mathbf {A})\) ). Let \(\mathbf {A}\) be an arbitrary model space. It generates an n-ary lens \(\ell (n\mathbf {A})\) as follows: The carrier \({\varvec{\mathcal {A}}}\) has n identical model spaces: \(\mathbf {A}_i=\mathbf {A}\) for all \(i\in \{1,..,n\}\), it has \({\varvec{\mathcal {A}}}^{\bigstar }_{} = {{\mathbf {A}^\bullet }}\), and boundary functions are identities. All updates are propagated to themselves (hence the name of \(\ell (n\mathbf {A})\)). Obviously, \(\ell (n\mathbf {A})\) is a wb, invertible lens non-reflective at all its feet. \(\square \)
4 Compositionality of Update Propagation: Playing Lego with Lenses
We study how lenses can be composed. Parallel constructions are easy to manage and excluded from the paper to save space (they can be found in the long version [1, Sect. 4.1]). More challenging are sequential constructs, in which different lenses share some of their feet, and updates propagated by one lens are taken and propagated further by one or several other lenses. In Sect. 4.1, we consider a rich example of such—star composition of lenses. In Sect. 4.2, we study how (symmetric) lenses can be assembled from asymmetric ones.
Since we now work with several lenses, we need a notation for lens’ components. Given a lens \(\ell = ({\varvec{\mathcal {A}}}, \mathsf {ppg})\), we write  for its set of corrs. Feet are written \(\varvec{\partial }_i^\ell \) (i-th boundary space) and \(\partial _i^\ell R\) for the i-th boundary of a corr
for its set of corrs. Feet are written \(\varvec{\partial }_i^\ell \) (i-th boundary space) and \(\partial _i^\ell R\) for the i-th boundary of a corr  . Propagation operations of the lens \(\ell \) are denoted by \(\ell .\mathsf {ppg}_{ij}^{R}\), \(\ell .\mathsf {ppg}_{i\star }^{R}\).
. Propagation operations of the lens \(\ell \) are denoted by \(\ell .\mathsf {ppg}_{ij}^{R}\), \(\ell .\mathsf {ppg}_{i\star }^{R}\).
4.1 Star Composition
Running Example Continued. Diagram in Fig. 4 presents a refinement of our example, which explicitly includes relational storage models \(B_ {1,2}\) for the two data sources. We assume that object models \(A_{1,2}\) are simple projective views of databases \(B_{1,2}\): data in \(A_i\) are copied from \(B_i\) without any transformation, while additional tables and attributes that \(B_i\)-data may have are excluded from the view \(A_i\); the traceability mappings \(R_i\!:A_i\leftrightarrow B_i\) are thus embeddings. We further assume that synchronization of bases \(B_i\) and their views \(A_i\) is realized by simple constant-complement lenses  , \(i=1,2\) (see, e.g., [9]). Finally, let
, \(i=1,2\) (see, e.g., [9]). Finally, let  be a lens synchronizing models \(A_1,A_2,A_3\) as described in Sect. 2, and
be a lens synchronizing models \(A_1,A_2,A_3\) as described in Sect. 2, and  be a corr for some \(A_3\) not shown in the figure.
be a corr for some \(A_3\) not shown in the figure.
Consider the following update propagation scenario. Suppose that at some moment we have consistency \((R_1,R,R_2)\) of all five models, and then \(B_1\) is updated with \(u_1{:}\;B_1\rightarrow B'_1\) that, say, adds to \(B_1\) a record of Mary working for Google as discussed in Sect. 2. Consistency is restored with a four-step propagation procedure shown by double-arrows labeled by x : y with x the step number and y the lens doing the propagation. Step 1: lens  propagates update \(u_1\) to \(v'_1\) that adds (Mary, Google) to view \(A_1\) with no amendment to \(u_1\) as \(v'_1\) is just a projection of \(u_1\), thus, \(B'_1=B''_1\). Note also the updated traceability mapping \(R'_1\!:B'_1\leftrightarrow A'_1\). Step 2: lens
propagates update \(u_1\) to \(v'_1\) that adds (Mary, Google) to view \(A_1\) with no amendment to \(u_1\) as \(v'_1\) is just a projection of \(u_1\), thus, \(B'_1=B''_1\). Note also the updated traceability mapping \(R'_1\!:B'_1\leftrightarrow A'_1\). Step 2: lens  propagates \(v'_1\) to \(v''_2\) that adds (Google, Mary) to \(A_2\), and amends \(v'_1\) with \(v''_1\) that adds (Mary, IBM) to \(A'_1\); a new consistent corr \(R''\) is also computed. Step 3: lens
propagates \(v'_1\) to \(v''_2\) that adds (Google, Mary) to \(A_2\), and amends \(v'_1\) with \(v''_1\) that adds (Mary, IBM) to \(A'_1\); a new consistent corr \(R''\) is also computed. Step 3: lens  propagates \(v''_2\) to \(u'''_2\) that adds Mary’s employment by Google to \(B_2\) with, perhaps, some other specific relational storage changes not visible in \(A_2\). We assume no amendment to \(v''_2\) as otherwise access to relational storage would amend application data, and thus we have a consistent corr \(R'''_2\) as shown. Step 4: lens
propagates \(v''_2\) to \(u'''_2\) that adds Mary’s employment by Google to \(B_2\) with, perhaps, some other specific relational storage changes not visible in \(A_2\). We assume no amendment to \(v''_2\) as otherwise access to relational storage would amend application data, and thus we have a consistent corr \(R'''_2\) as shown. Step 4: lens  maps update \(v''_1\) (see above in Step 2) backward to \(u'''_1\) that adds (Mary, IBM) to \(B'_1\) so that \(B'''_1\) includes both (Mary, Google) and (Mary, IBM) and a respective consistent corr \(R'''_1\) is provided. There is no amendment for \(v''_1\) by the same reason as in Step 3.
maps update \(v''_1\) (see above in Step 2) backward to \(u'''_1\) that adds (Mary, IBM) to \(B'_1\) so that \(B'''_1\) includes both (Mary, Google) and (Mary, IBM) and a respective consistent corr \(R'''_1\) is provided. There is no amendment for \(v''_1\) by the same reason as in Step 3.
Thus, all five models in the bottom line of Fig. 4 (\(A''_3\) is not shown) are mutually consistent and all show that Mary is employed by IBM and Google. Synchronization is restored, and we can consider the entire scenario as propagation of \(u_1\) to \(u'''_2\) and its amendment with \(u'''_1\) so that finally we have a consistent corr \((R'''_1,R'',R'''_2)\) interrelating \(B'''_1, A''_3, B'''_2\). Amendment \(u'''_1\) is compatible with \(u_1\) as nothing is undone and condition  holds; the other two equations required by Reflect2-3 for the pair \((u_1,u'''_1)\) also hold. For our simple projection views, these conditions will hold for other updates too, and we have a well-behaved propagation from \(B_1\) to \(B_2\) (and trivially to \(A_3\)). Similarly, we have a wb propagation from \(B_2\) to \(B_1\) and \(A_3\). Propagation from \(A_3\) to \(B_{1,2}\) is non-reflective and done in two steps: first lens
holds; the other two equations required by Reflect2-3 for the pair \((u_1,u'''_1)\) also hold. For our simple projection views, these conditions will hold for other updates too, and we have a well-behaved propagation from \(B_1\) to \(B_2\) (and trivially to \(A_3\)). Similarly, we have a wb propagation from \(B_2\) to \(B_1\) and \(A_3\). Propagation from \(A_3\) to \(B_{1,2}\) is non-reflective and done in two steps: first lens  works, then lenses
works, then lenses  work as described above (and updates produced by
work as described above (and updates produced by  are
are  -closed). Thus, we have built a wb ternary lens synchronizing spaces \(\mathbf {B}_1, \mathbf {B}_2\) and \(\mathbf {A}_3\) by joining lenses
-closed). Thus, we have built a wb ternary lens synchronizing spaces \(\mathbf {B}_1, \mathbf {B}_2\) and \(\mathbf {A}_3\) by joining lenses  and
and  to the central lens
to the central lens  .
.

Discussion. Reflection is a crucial aspect of lens composition. The inset figure describes the scenario above as a transition system and shows that Steps 3 and 4 can go concurrently. It is the non-trivial amendment created in Step 2 that causes the necessity of Step 4, otherwise Step 3 would finish consistency restoration (with Step 4 being an idle transition). On the other hand, if update \(v''_2\) in Fig. 4 would not be closed for lens  , we’d have yet another concurrent step complicating the scenario. Fortunately for our example with simple projective views, Step 4 is simple and provides a non-conflicting amendment, but the case of more complex views beyond the constant-complement class needs care and investigation. Below we specify a simple situation of lens composition with reflection a priori excluded, and leave more complex cases for future work.
, we’d have yet another concurrent step complicating the scenario. Fortunately for our example with simple projective views, Step 4 is simple and provides a non-conflicting amendment, but the case of more complex views beyond the constant-complement class needs care and investigation. Below we specify a simple situation of lens composition with reflection a priori excluded, and leave more complex cases for future work.
Formal Definition. Suppose we have an n-ary lens  , and for every \(i\le n\), a binary lens
, and for every \(i\le n\), a binary lens  , with the first model space \(\mathbf {A}_i\) being the ith model space of
, with the first model space \(\mathbf {A}_i\) being the ith model space of  (see Fig. 5, where
(see Fig. 5, where  is depicted in the center and
is depicted in the center and  are shown as ellipses adjoint to
are shown as ellipses adjoint to  ’s feet). We also assume the following Junction conditions: For any \(i\le n\), all updates propagated to \(\mathbf {A}_i\) by lens
’s feet). We also assume the following Junction conditions: For any \(i\le n\), all updates propagated to \(\mathbf {A}_i\) by lens  are
are  -closed, and all updates propagated to \(\mathbf {A}_i\) by lens
-closed, and all updates propagated to \(\mathbf {A}_i\) by lens  are
are  -closed.
-closed.
Below we will write a corr  as \(R_i\!:A_i\leftrightarrow B_i\), and the sixtuple of operations
as \(R_i\!:A_i\leftrightarrow B_i\), and the sixtuple of operations  as the family
as the family  . Likewise we write
. Likewise we write  with \(x\in \{\mathbf {A}, \mathbf {B}\}\) for the boundary functions of lenses
with \(x\in \{\mathbf {A}, \mathbf {B}\}\) for the boundary functions of lenses  .
.
The above configuration gives rise to the following n-ary lens \(\ell \). The carrier is the tuple of model spaces \(\mathbf {B}_1...\mathbf {B}_n\) and corrs are tuples \((R, R_1...R_n)\) with  and
and  , such that
, such that  for all \(i\in 1..n\). Moreover, we define
for all \(i\in 1..n\). Moreover, we define  (see Fig. 5). Operations are defined as compositions of consecutive lens’ executions as described below (we will use the dot notation for operation application and write \(x.\mathsf {op}\) for \(\mathsf {op}(x)\), where x is an argument).
(see Fig. 5). Operations are defined as compositions of consecutive lens’ executions as described below (we will use the dot notation for operation application and write \(x.\mathsf {op}\) for \(\mathsf {op}(x)\), where x is an argument).
Given a model tuple \((B_1...B_n)\in \mathbf {B}_1\,{\times }...{\times }\,\mathbf {B}_n\), a corr \((R, R_1...R_n)\), and update \(v_i{:}\;B_i\rightarrow B'_i\) in  , we define, first for \(j\ne i\),
, we define, first for \(j\ne i\),

and  for \(j=i\). Note that all internal amendments to
for \(j=i\). Note that all internal amendments to  produced by
produced by  , and to
, and to  produced by
produced by  , are identities due to the Junction conditions. This allows us to set corrs properly and finish propagation with the three steps above: \(v_i.\; \ell .\mathsf {ppg}^{(R,R_1...R_n)}_{i\star }\;{\mathop {=}\limits ^{\mathrm {def}}}\; (R', R'_1...R'_n) \) where
, are identities due to the Junction conditions. This allows us to set corrs properly and finish propagation with the three steps above: \(v_i.\; \ell .\mathsf {ppg}^{(R,R_1...R_n)}_{i\star }\;{\mathop {=}\limits ^{\mathrm {def}}}\; (R', R'_1...R'_n) \) where  ,
,  for \(j\ne i\), and
for \(j\ne i\), and  . We thus have a lens \(\ell \) denoted by
. We thus have a lens \(\ell \) denoted by  . \(\square \)
. \(\square \)
Theorem 1
(Star Composition). Given a star configuration of lenses as above, if lens  fulfills Stability, all lenses
fulfills Stability, all lenses  are wb, and Junction conditions hold, then the composed lens
are wb, and Junction conditions hold, then the composed lens  defined above is wb, too.
defined above is wb, too.
Proof
Laws Stability and Reflect1 for the composed lens are straightforward. Reflect2-3 also follow immediately, since the first step of the above propagation procedure already enjoys idempotency by Reflect2-3 for  . \(\square \)
. \(\square \)
4.2 Assembling n-ary Lenses from Binary Lenses
This section shows how to assemble n-ary (symmetric) lenses from binary asymmetric lenses modelling view computation [2]. As the latter is a typical bx, the well-behavedness of asymmetric lenses has important distinctions from well-behavedness of general (symmetric mx-tailored) lenses.
Definition 7
(Asymmetric Lens, cf. [2]). An asymmetric lens (a-lens) is a tuple  with \(\mathbf {A}\) a model space called the (abstract) view, \(\mathbf {B}\) a model space called the base, \({\mathsf {get}}\!:\mathbf {A}\leftarrow \mathbf {B}\) a functor (read “get the view”), and \(\mathsf {put}\) a family of operations
with \(\mathbf {A}\) a model space called the (abstract) view, \(\mathbf {B}\) a model space called the base, \({\mathsf {get}}\!:\mathbf {A}\leftarrow \mathbf {B}\) a functor (read “get the view”), and \(\mathsf {put}\) a family of operations  (read “put the view update back”) of the following arity. Provided with a view update \(v{:}\;{\mathsf {get}}(B)\rightarrow A'\) at the input, operation \(\mathsf {put}^{B}\) outputs a base update \({\mathsf {put}}^{B}_\mathsf {b}(v)=u'{:}\;B\rightarrow B''\) and a reflected view update \({\mathsf {put}}^{B}_\mathsf {v}(v)=v'{:}\;A'\rightarrow A''\) such that \(A''={\mathsf {get}}(B'')\). A view update \(v{:}\;{\mathsf {get}}(B)\rightarrow A'\) is called closed if \({\mathsf {put}}^{B}_\mathsf {v}(v)=\mathsf {id}_{A'}\). \(\square \)
(read “put the view update back”) of the following arity. Provided with a view update \(v{:}\;{\mathsf {get}}(B)\rightarrow A'\) at the input, operation \(\mathsf {put}^{B}\) outputs a base update \({\mathsf {put}}^{B}_\mathsf {b}(v)=u'{:}\;B\rightarrow B''\) and a reflected view update \({\mathsf {put}}^{B}_\mathsf {v}(v)=v'{:}\;A'\rightarrow A''\) such that \(A''={\mathsf {get}}(B'')\). A view update \(v{:}\;{\mathsf {get}}(B)\rightarrow A'\) is called closed if \({\mathsf {put}}^{B}_\mathsf {v}(v)=\mathsf {id}_{A'}\). \(\square \)
The following is a specialization of Definition 5.
Definition 8
(Well-behavedness). An a-lens is well-behaved (wb) if it satisfies the following laws for all \(B\in {{\mathbf {B}^\bullet }}\) and \(v{:}\;{\mathsf {get}}(B)\rightarrow A'\)

\(\square \)
In contrast to the general lens case, a wb a-lens features Reflect0—a sort of self-Hippocraticness important for bx. Another distinction is inclusion of a strong invertibility law PutGet into the definition of well-behavedness: PutGet together with Reflect2 provide (weak) invertibility: \({\mathsf {put}}^B_\mathsf {b}({\mathsf {get}}({\mathsf {put}}^B_\mathsf {b}(v)))={\mathsf {put}}^B_\mathsf {b}(v)\). Reflect3 is omitted as it is implied by Reflect0 and PutGet.
Any a-lens  gives rise to a binary symmetric lens
gives rise to a binary symmetric lens  . Its carrier consists of model spaces \(\mathbf {A}\) and \(\mathbf {B}\). Furthermore
. Its carrier consists of model spaces \(\mathbf {A}\) and \(\mathbf {B}\). Furthermore  with boundary mappings defined as follows: for
with boundary mappings defined as follows: for  ,
,  and
and  . Thus, the set of corrs
. Thus, the set of corrs  is \(\{B\}\) if \(A={\mathsf {get}}(B)\), and is empty otherwise.
is \(\{B\}\) if \(A={\mathsf {get}}(B)\), and is empty otherwise.
For a corr B, we need to define six operations  . If \(v{:}\;A\rightarrow A'\) is a view update, then \(\mathsf {ppg}^{B}_{\mathbf {A}\mathbf {B}}(v)={\mathsf {put}}^B_\mathsf {b}(v): B\rightarrow B''\), \(\mathsf {ppg}^{B}_{\mathbf {A}\mathbf {A}}(v)={\mathsf {put}}^B_\mathsf {v}(v): A'\rightarrow A''\), and \(\mathsf {ppg}^{B}_{\mathbf {A}\star }(v)=B''\). The condition \(A''={\mathsf {get}}(B'')\) for
. If \(v{:}\;A\rightarrow A'\) is a view update, then \(\mathsf {ppg}^{B}_{\mathbf {A}\mathbf {B}}(v)={\mathsf {put}}^B_\mathsf {b}(v): B\rightarrow B''\), \(\mathsf {ppg}^{B}_{\mathbf {A}\mathbf {A}}(v)={\mathsf {put}}^B_\mathsf {v}(v): A'\rightarrow A''\), and \(\mathsf {ppg}^{B}_{\mathbf {A}\star }(v)=B''\). The condition \(A''={\mathsf {get}}(B'')\) for  means that \(B''\) is again a consistent corr with the desired boundaries. For a base update \(u{:}\;B\rightarrow B'\) and corr B, \(\mathsf {ppg}^{B}_{\mathbf {B}\mathbf {A}}(u)={\mathsf {get}}(u)\), \(\mathsf {ppg}^{B}_{\mathbf {B}\mathbf {B}}(u)=\mathsf {id}_{B'}\), and \(\mathsf {ppg}^{B}_{\mathbf {B}\star }(u)=B'\). Functoriality of \({\mathsf {get}}\) yields consistency of \(B'\).
means that \(B''\) is again a consistent corr with the desired boundaries. For a base update \(u{:}\;B\rightarrow B'\) and corr B, \(\mathsf {ppg}^{B}_{\mathbf {B}\mathbf {A}}(u)={\mathsf {get}}(u)\), \(\mathsf {ppg}^{B}_{\mathbf {B}\mathbf {B}}(u)=\mathsf {id}_{B'}\), and \(\mathsf {ppg}^{B}_{\mathbf {B}\star }(u)=B'\). Functoriality of \({\mathsf {get}}\) yields consistency of \(B'\).
Lemma 1
Let  be a wb a-lens and
be a wb a-lens and  the corresponding symmetric lens. Then all base updates of
the corresponding symmetric lens. Then all base updates of  are closed, and
are closed, and  is wb and invertible.
is wb and invertible.
Proof
Base updates are closed by the definition of \(\mathsf {ppg}_{\mathbf {B}\mathbf {B}}\). Well-behavedness follows from wb-ness of  . Invertibility has to be proved in two directions: \(\mathsf {ppg}_{\mathbf {B}\mathbf {A}};\mathsf {ppg}_{\mathbf {A}\mathbf {B}};\mathsf {ppg}_{\mathbf {B}\mathbf {A}} = \mathsf {ppg}_{\mathbf {B}\mathbf {A}}\) follows from \(\mathsf {{(PutGet)}}_{}\) and \(\mathsf {{(Reflect0)}}_{,}\) the other direction follows from \(\mathsf {{(PutGet)}}_{}\) and \(\mathsf {{(Reflect2)}}_{,}\) see the remark after Definition 8. \(\square \)
. Invertibility has to be proved in two directions: \(\mathsf {ppg}_{\mathbf {B}\mathbf {A}};\mathsf {ppg}_{\mathbf {A}\mathbf {B}};\mathsf {ppg}_{\mathbf {B}\mathbf {A}} = \mathsf {ppg}_{\mathbf {B}\mathbf {A}}\) follows from \(\mathsf {{(PutGet)}}_{}\) and \(\mathsf {{(Reflect0)}}_{,}\) the other direction follows from \(\mathsf {{(PutGet)}}_{}\) and \(\mathsf {{(Reflect2)}}_{,}\) see the remark after Definition 8. \(\square \)
Theorem 2
(Lenses from Spans). An n-ary span of wb a-lenses  , \(i=1..n\) with common base \(\mathbf {B}\) of all
, \(i=1..n\) with common base \(\mathbf {B}\) of all  gives rise to a wb (symmetric) lens denoted by
gives rise to a wb (symmetric) lens denoted by  .
.
Proof
An n-ary span of a-lenses  (all of them interpreted as symmetric lenses
(all of them interpreted as symmetric lenses  as explained above) is a construct equivalent to the star-composition of Definition 4.1.3, in which lens
as explained above) is a construct equivalent to the star-composition of Definition 4.1.3, in which lens  (cf. Example 1) and peripheral lenses are lenses
(cf. Example 1) and peripheral lenses are lenses  . The junction condition is satisfied as all base updates are
. The junction condition is satisfied as all base updates are  -closed for all i by Lemma 1, and also trivially closed for any identity lens. The theorem thus follows from Theorem 1. Note that a corr in
-closed for all i by Lemma 1, and also trivially closed for any identity lens. The theorem thus follows from Theorem 1. Note that a corr in  is nothing but a single model \(B\in {{\mathbf {B}^\bullet }}\) with boundaries being the respective \({\mathsf {get}}_i\)-images. \(\square \)
is nothing but a single model \(B\in {{\mathbf {B}^\bullet }}\) with boundaries being the respective \({\mathsf {get}}_i\)-images. \(\square \)
The theorem shows that combining a-lenses in this way yields an n-ary symmetric lens, whose properties can automatically be inferred from the binary a-lenses.
Running example. Figure 6 shows a metamodel \(M^+\) obtained by merging the three metamodels \(M_{1,2,3}\) from Fig. 1 without loss and duplication of information. In addition, for persons and companies, the identifiers of model spaces, in which a given person or company occurs, can be traced back via attribute “spaces” (\(\mathsf {Commute}\)-objects are known to appear in space \(\mathbf {A}_3\) and hence do not need such an attribute). As shown in [10], any consistent multimodel \((A_1...A_n, R)\) can be merged into a comprehensive model \(A^+\) instantiating \(M^+\). Let \(\mathbf {B}\) be the space of such together with their comprehensive updates \(u^+{:}\;A^+\rightarrow A'^+\).
For a given \(i\le 3\), we can define the following a-lens  : \({\mathsf {get}}_i\) takes update \(u^+\) as above and outputs its restriction to the model containing only objects recorded in space \(\mathbf {A}_i\). Operation \({\mathsf {put}}_i\) takes an update \(v_i{:}\;A_i\rightarrow A'_i\) and first propagates it to all directions as discussed in Sect. 2, then merges these propagated local updates into a comprehensive \(\mathbf {B}\)-update between comprehensive models. This yields a span of a-lenses that implements the same synchronization behaviour as the symmetric lens discussed in Sect. 2.
: \({\mathsf {get}}_i\) takes update \(u^+\) as above and outputs its restriction to the model containing only objects recorded in space \(\mathbf {A}_i\). Operation \({\mathsf {put}}_i\) takes an update \(v_i{:}\;A_i\rightarrow A'_i\) and first propagates it to all directions as discussed in Sect. 2, then merges these propagated local updates into a comprehensive \(\mathbf {B}\)-update between comprehensive models. This yields a span of a-lenses that implements the same synchronization behaviour as the symmetric lens discussed in Sect. 2.
From lenses to spans. There is also a backward transformation of (symmetric) lenses to spans of a-lenses. Let \(\ell =({\varvec{\mathcal {A}}}, \mathsf {ppg})\) be a wb lens. It gives rise to the following span of wb a-lenses \(\ell _i^\preccurlyeq =(\varvec{\partial }_i({\varvec{\mathcal {A}}}),\mathbf {B},{\mathsf {get}}_i, {\mathsf {put}}_i)\) where space \(\mathbf {B}\) is built from consistent multimodels and their updates, and functors \({\mathsf {get}}_i:\mathbf {B}\rightarrow \mathbf {A}_i\) are projection functors. Given \(B = ({A_1}...{A_{n}}, R)\) and update \(u_i{:}\;A_i\rightarrow A'_i\), let
\({\mathsf {put}}^B_{i\mathsf {b}}(u_i){\mathop {=}\limits ^{\mathrm {def}}}(u_1',..,u'_{i-1}, (u_i;u_i'), u'_{i+1},..,u_n'){:}\;({A_1}...{A_{n}}, R)\rightarrow ({A''_1}...{A''_{n}}, R'')\)
where \(u_j'\,{\mathop {=}\limits ^{\mathrm {def}}}\,\mathsf {ppg}^R_{ij}(u_i)\) (all j) and \(R'' = \mathsf {ppg}_{i\star }^R(u_i)\). Finally, \({\mathsf {put}}^B_{i\mathsf {v}}(v_i)\,{\mathop {=}\limits ^{\mathrm {def}}}\,\mathsf {ppg}^R_{ii}(u_i)\). Validity of Stability, Reflect0-2, PutGet directly follows from the above definitions.
An open question is whether the span-to-lens transformation in Theorem 2 and the lens-to-span transformation described above are mutually inverse. The results for the binary case in [8] show that this is only the case modulo certain equivalence relations. These equivalences may be different for our reflective multiary lenses, and we leave this important question for future research.
5 Related Work
For state-based lenses, the work closest in spirit is Stevens’ paper [16]. Her and our goals are similar, but the technical realisations are different even besides the state- vs. delta-based opposition. Stevens works with restorers, which take a multimodel (in the state-based setting, just a tuple of models) presumably inconsistent, and restores consistency by changing some models in the tuple while keeping other models (from the authority set) unchanged. In contrast, lenses take a consistent multimodel and updates, and return a consistent multimodel and updates. Also, update amendments are not considered in [16] – models in the authority set are intact.
Another distinction is how the multiary vs. binary issue is treated. Stevens provides several results for decomposing an n-ary relation  into binary relations \({\varvec{\mathcal {A}}}^\bigstar _{ij}\subseteq \mathbf {A}_i\,{\times }\,\mathbf {A}_j\) between the components. For us, a relation is a span, i.e., a set
into binary relations \({\varvec{\mathcal {A}}}^\bigstar _{ij}\subseteq \mathbf {A}_i\,{\times }\,\mathbf {A}_j\) between the components. For us, a relation is a span, i.e., a set  endowed with an n-tuple of projections
endowed with an n-tuple of projections  uniquely identifying elements in
uniquely identifying elements in  . Thus, while Stevens considers “binarisation” of a relation R over its boundary \(A_1...A_n\), we “binarise” it via the corresponding span (the UML would call it reification). Our (de)composition results demonstrate advantages of the span view. Discussion of several other works in the state-based world, notably by Macedo et al. [12] can be found in [16].
. Thus, while Stevens considers “binarisation” of a relation R over its boundary \(A_1...A_n\), we “binarise” it via the corresponding span (the UML would call it reification). Our (de)composition results demonstrate advantages of the span view. Discussion of several other works in the state-based world, notably by Macedo et al. [12] can be found in [16].
Compositionality as a fundamental principle for building synchronization tools was proposed by Pierce and his coauthors, and realized for several types of binary lenses in [4, 6, 7]. In the delta-lens world, a fundamental theory of equivalence of symmetric lenses and spans of a-lenses (for the binary case) is developed by Johnson and Rosebrugh [8], but they do not consider reflective updates. The PutGetPut law has been discussed (in a different context of state-based asymmetric injective editing) in several early bx work from Tokyo, e.g., [13]. A notion close to our update compatibility was proposed by Orejas et al in [14]. We are not aware of multiary update propagation work in the delta-lens world. Considering amendment and its laws in the delta lens setting is also new.
In [11], Königs and Schürr introduced multigraph grammars (MGGs) as a multiary version of well-known triple graph grammar (TGG). Their multi-domain-integration rules specify how all involved graphs evolve simultaneously. The idea of an additional correspondence graph is close to our consistent corrs. However, their scenarios are specialized towards (1) directed graphs, (2) MOF-compliant artifacts like QVT, and (3) the global consistency view on a multimodel rather than update propagation.
6 Conclusions and Future Work
We have considered multiple model synchronization via multi-directional update propagation, and argued that reflective propagation to the model whose change originated inconsistency is a reasonable feature of the scenario. We presented a mathematical framework for such synchronization based on a multiary generalisation of binary symmetric delta lenses introduced earlier in [3], and enriched it with reflective propagation. Our lens composition results make the framework interesting for practical applications, but so far it has an essential limitation: we consider consistency violation caused by only one model change, and thus consistency is restored by propagating only one update, while in practice we often deal with several models changing concurrently. If these updates are in conflict, consistency restoration needs conflict resolution, and hence an essential development of the framework.
There are also several open issues for the non-concurrent case considered in the paper (and its future concurrent generalisation). First, our pool of lens composition constructs is far incomplete (because of both space limitations and the necessity of further research). We need to enrich it with (i) sequential composition of (reflective) a-lenses so that a category of a-lenses could be built, and (ii) a relational composition of symmetric lenses sharing several of their feet (similar to relational join). It is also important to investigate composition with weaker junction conditions than we considered. Another important issue is invertibility, which nicely fits in some but not all of our results, which shows the necessity of further investigation. It is a sign that we do not well understand the nature of invertibility. We conjecture that while invertibility is essential for bx, its role for mx may be less important. The (in)famous PutPut law is also awaiting its exploration in the case of multiary reflective propagation. And the last but not the least is the (in)famous PutPut law: how well our update propagation operations are compatible with update composition is a very important issue to explore. Finally, paper [5] shows how binary delta lenses can be implemented with TGG, and we expect that MGG could play a similar role for multiary delta lenses.
Notes
- 1.
Here we first abbreviate \(({A_{1}},\ldots ,A_{n})\) by \(({A_{1}}...A_{n})\), and then write \(({A_{1}}...A_{n},R)\) for \((({A_{1}}...A_{n}),R)\). We will apply this style in other similar cases, and write, e.g., \(i\in 1...n\) for \(i\in \{1,...,n\}\) (this will also be written as \(i\le n\)).
References
Diskin, Z., König, H., Lawford, M.: Multiple model synchronization with multiary delta lenses. Technical report. McMaster Centre for Software Certification, McSCert-2017-10-01, McMaster University (2017). http://www.mcscert.ca/projects/mcscert/wp-content/uploads/2017/10/Multiple-Model-Synchronization-with-Multiary-Delta-Lenses-ZD.pdf
Diskin, Z., Xiong, Y., Czarnecki, K.: From state- to delta-based bidirectional model transformations: the asymmetric case. J. Object Technol. 10(6), 1–25 (2011)
Diskin, Z., Xiong, Y., Czarnecki, K., Ehrig, H., Hermann, F., Orejas, F.: From state- to delta-based bidirectional model transformations: the symmetric case. In: Whittle, J., Clark, T., Kühne, T. (eds.) MODELS 2011. LNCS, vol. 6981, pp. 304–318. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24485-8_22
Foster, J.N., Greenwald, M.B., Moore, J.T., Pierce, B.C., Schmitt, A.: Combinators for bi-directional tree transformations: a linguistic approach to the view update problem. In: Palsberg, J., Abadi, M. (eds.) Proceedings of the 32nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2005, 12–14 January 2005, Long Beach, California, USA, pp. 233–246. ACM (2005). https://doi.org/10.1145/1040305.1040325
Hermann, F., Ehrig, H., Orejas, F., Czarnecki, K., Diskin, Z., Xiong, Y.: Correctness of model synchronization based on triple graph grammars. In: Whittle, J., Clark, T., Kühne, T. (eds.) MODELS 2011. LNCS, vol. 6981, pp. 668–682. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24485-8_49
Hofmann, M., Pierce, B.C., Wagner, D.: Symmetric lenses. In: Ball, T., Sagiv, M. (eds.) Proceedings of the 38th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2011, 26–28 January 2011, Austin, TX, USA, pp. 371–384. ACM (2011). https://doi.org/10.1145/1926385.1926428
Hofmann, M., Pierce, B.C., Wagner, D.: Edit lenses. In: Field, J., Hicks, M. (eds.) Proceedings of the 39th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2012, 22–28 January 2012, Philadelphia, Pennsylvania, USA, pp. 495–508. ACM (2012). https://doi.org/10.1145/2103656.2103715
Johnson, M., Rosebrugh, R.D.: Symmetric delta lenses and spans of asymmetric delta lenses. J. Object Technol. 16(1), 2:1–2:32 (2017). https://doi.org/10.5381/jot.2017.16.1.a2
Johnson, M., Rosebrugh, R.D., Wood, R.J.: Lenses, fibrations and universal translations. Math. Struct. Comput. Sci. 22(1), 25–42 (2012). https://doi.org/10.1017/S0960129511000442
König, H., Diskin, Z.: Efficient consistency checking of interrelated models. In: Anjorin, A., Espinoza, H. (eds.) ECMFA 2017. LNCS, vol. 10376, pp. 161–178. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61482-3_10
Königs, A., Schürr, A.: MDI: a rule-based multi-document and tool integration approach. Softw. Syst. Model. 5(4), 349–368 (2006). https://doi.org/10.1007/s10270-006-0016-x
Macedo, N., Cunha, A., Pacheco, H.: Towards a framework for multidirectional model transformations. In: Proceedings of the Workshops of the EDBT/ICDT 2014 Joint Conference (EDBT/ICDT 2014), 28 March 2014, Athens, Greece, pp. 71–74 (2014). http://ceur-ws.org/Vol-1133/paper-11.pdf
Mu, S.-C., Hu, Z., Takeichi, M.: An algebraic approach to bi-directional updating. In: Chin, W.-N. (ed.) APLAS 2004. LNCS, vol. 3302, pp. 2–20. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30477-7_2
Orejas, F., Boronat, A., Ehrig, H., Hermann, F., Schölzel, H.: On propagation-based concurrent model synchronization. ECEASST 57, 1–19 (2013). http://journal.ub.tu-berlin.de/eceasst/article/view/871
Stevens, P.: Bidirectional model transformations in QVT: semantic issues and open questions. Softw. Syst. Model. 9(1), 7–20 (2010)
Stevens, P.: Bidirectional transformations in the large. In: 20th ACM/IEEE International Conference on Model Driven Engineering Languages and Systems, MODELS 2017, 17–22 September 2017, Austin, TX, USA, pp. 1–11 (2017). https://doi.org/10.1109/MODELS.2017.8
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Diskin, Z., König, H., Lawford, M. (2018). Multiple Model Synchronization with Multiary Delta Lenses. In: Russo, A., Schürr, A. (eds) Fundamental Approaches to Software Engineering. FASE 2018. Lecture Notes in Computer Science(), vol 10802. Springer, Cham. https://doi.org/10.1007/978-3-319-89363-1_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-89363-1_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89362-4
Online ISBN: 978-3-319-89363-1
eBook Packages: Computer ScienceComputer Science (R0)








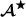 of elements called corrs along with a family of functions
of elements called corrs along with a family of functions 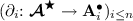 providing every corr R with its boundary
providing every corr R with its boundary  for the set of all corrs R with
for the set of all corrs R with 

