Abstract
Software product lines continuously undergo model transformations, such as refactorings, refinements, and translations. In product line transformations, the dedicated management of variability can help to control complexity and to benefit maintenance and performance. However, since no existing approach is geared for situations in which both the product line and the transformation specification are affected by variability, substantial maintenance and performance obstacles remain. In this paper, we introduce a methodology that addresses such multi-variability situations. We propose to manage variability in product lines and rule-based transformations consistently by using annotative variability mechanisms. We present a staged rule application technique for applying a variability-intensive transformation to a product line. This technique enables considerable performance benefits, as it avoids enumerating products or rules upfront. We prove the correctness of our technique and show its ability to improve performance in a software engineering scenario.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Software product line engineering [1] enables systematic reuse of software artifacts through the explicit management of variability. Representing a software product line (SPL) in terms of functionality increments called features, and mapping these features to development artifacts such as domain models and code allows to generate custom-tailored products on demand, by retrieving the corresponding artifacts for a given feature selection. Companies such as Bosch, Boeing, and Philips use SPLs to deliver tailor-made products to their customers [2].
Despite these benefits, a growing amount of variability leads to combinatorial explosions of the product space and, consequently, to severe challenges. Notably, this applies to software engineering tasks such as refactorings [3], refinements [4], and evolution steps [5], which, to support systematic management, are often expressed as model transformations. When applying a given model transformation to a SPL, a key challenge is to avoid enumerating and considering all possible products individually. To this end, Salay et al. [6] have proposed an algorithm that “lifts” regular transformation rules to a whole product line. The algorithm transforms the SPL, represented as a variability-annotated domain model, in such way as if each product had been considered individually.
Yet, in complex transformation scenarios as increasingly found in practice [7], not only the considered models include variations: The transformation system can contain variability as well, for example, due to desired optional behavior of rules, or for rule variants arising from the sheer complexity of the involved meta-models. While a number of works [8,9,10] support systematic reuse to improve maintainability, variability-based model transformation (VB) [11, 12] also aims to improve the performance when a transformation system with many similar rules is executed. To this end, these rules are represented as a single rule with variability annotations, called VB rule. During rule applications, a special VB rule application technique [13] saves redundant effort by considering common rule parts only once. In summary, for cases where either the model or the transformation system alone contains variability, solid approaches are available.
However, a more challenging case occurs when a variability-intensive transformation is applied to an SPL. In this multi-variability setting, where both the input model and the specification of a transformation contain variability, the existing approaches fall short to deal with the resulting complexity: One can either consider all rules, so they can be “lifted” to the product line, or consider all products, so they become amenable to VB model transformation. Both approaches are undesirable, as they require enumerating an exponentially growing number of artifacts and, therefore, threaten the feasibility of the transformation.
In this paper, we introduce a methodology for SPL transformations inspired by the uniformity principle [14], a tenet that suggests to handle variability consistently throughout all software artifacts. We propose to capture variability of SPLs and transformations using variability-annotated domain models and rules. Model and rule elements are annotated with presence conditions, specifying the conditions under which the annotated elements are present. The presence conditions of model and rule elements are specified over two separate sets of features, representing SPL and rule variability. Annotated domain models and rules can be created manually using available editor support [15, 16], or automatically from existing products and rules by using merge-refactoring techniques [17, 18].
Given an SPL and a VB rule, as shown in Fig. 1, we provide a staged rule application technique (black arrow) for applying a VB rule to a SPL. In contrast to the state of the art (shown in gray), enumerating products or rules upfront is not required. By adopting this technique, existing tools that use transformation technology, such as refactoring engines, may benefit from improved performance.
Specifically, we make the following contributions:
-
We introduce a staged technique for applying a VB rule to an SPL. Our technique combines core principles of VB rule applications and lifting, while avoiding their drawbacks w.r.t. enumerating all products or rules upfront.
-
We formally prove correctness of this technique by showing its equivalence to the application of each “flattened” product to each “flattened” rule.
-
We present an algorithm for implementing the rule application technique.
-
We evaluate the usefulness of our technique by studying its performance in a substantial number of cases within a software engineering scenario.
Our work builds on the underlying framework of algebraic graph transformation (AGT) [19]. AGT is one of the standard model transformation language paradigms [20]; in addition, it has recently gained momentum as an analysis paradigm for other widespread paradigms and languages such as ATL [21]. We focus on the annotative paradigm to variability. Suitable converters to and from alternative paradigms, such as the composition-based one [22], may allow our technique to be used in other cases as well.
The rest of this paper is structured as follows: We motivate and explain our contribution using a running example in Sect. 2. Section 3 revisits the necessary background. Section 4 introduces the formalization of our new rule application technique. The algorithm and its evaluation are presented in Sects. 5 and 6, respectively. In Sect. 7 we discuss related work, before we conclude in Sect. 8.
2 Running Example
In this section, we introduce SPLs and variability-based model transformation by example, and motivate and explain our contribution in the light of this example.

(adapted from [6]).
Washing machine controller product line and product
Software Product Lines. An SPL represents a collection of models that are similar, but different to each other. Figure 2 shows a washing machine controller SPL in an annotative representation, comprising an annotated domain model and a feature model. The feature model [23] specifies a root feature Wash with three optional children Heat, Delay, and Dry, where Heat and Delay are mutually exclusive. The domain model is a statechart diagram specifying the behavior of the controller SPL based on states Locking, Waiting, Washing, Drying, and UnLocking with transitions between them. Presence conditions, shown in gray labels, denote the condition under which an annotated element is present. These conditions are used to specify variations in the execution behavior.
Concrete products can be obtained from configurations, in which each optional feature is set to either true or false. A product arises by removing those elements whose presence condition evaluates to false in the given configuration. For instance, selecting Delay and deselecting Heat and Dry yields the product shown in the right of Fig. 2. The SPL has six configurations and products in total, since Wash is non-optional and Delay excludes Heat.
Variability-Based (VB) Model Transformation. In complex model transformation scenarios, developers often create rules that are similar, but different to each other. As an example, consider two rules foldEntryActions and foldExitActions (Fig. 3), called A and B in short. These rules express a “fold” refactoring for statechart diagrams: if a state has two incoming or outgoing transitions with the same action, these actions are to be replaced by an entry or exit action of the state. The rules have a left- and a right-hand side (LHS, RHS). The LHS specifies a pattern to be matched to an input graph, and the difference between the LHS and the RHS specifies a change to be performed for each match, like the removing of transition actions, and the adding of exit and entry actions.

(adapted from [24]).
Two rules and their encoding into a variability-based rule
Rules A and B are simple; however, in a realistic transformation system, the number of required rules can grow exponentially with the number of variation points in the rules. To avoid combinatorial explosion, a set of variability-intensive rules can be encoded into a single representation using a VB rule [12, 18]. A VB rule consist of a LHS, a RHS, a feature model specifying a set of interrelated features, and presence conditions annotating LHS and RHS elements with a condition under which they are present. Individual “flat” rules are obtained via configuration, i.e., binding each feature to either true or false. In the VB rule \(A+B\), the feature model specifies a root feature refactor with alternative child features foldEntry and foldExit. Since exactly one child feature has to be active at one time, two possible configurations exist. The two rules arising from these configurations are isomorphic to rules A and B.
Problem Statement. Model transformations such as foldActions are usually designed for applications to a concrete software product, represented by a single model. However, in various situations, it is desirable to extend the usage context to a set of models collected in an SPL. For example, during the batch refactoring of an SPL, all products should be refactored in a uniform way.
Variability is challenging for model transformation technologies. As illustrated in Table 1, products and rules need to be considered in manifold combinations. In our example, without dedicated variability support, the user needs to specify 6 products and 2 rules individually and trigger a rule application for each of the 12 combinations. A better strategy is enabled by VB model transformation: by applying the VB rule \(A+B\), only 6 combinations need to be considered. Another strategy is to apply rules A and B to the SPL by lifting [6] them, leading to 2 combinations and the biggest improvement so far. Still, in more complex cases, all of these strategies are insufficient. Since none of them avoids an exponential growth along the number of optional SPL features (\(\#F_P\)) or optional rule features (\(\#F_r\)), the feasibility of the transformation is threatened.
Solution Overview. To address this situation, we propose a staged rule application technique for applying a VB rule to an SPL. As shown in Fig. 4, this technique proceeds in three steps: In step 1, we consider the base rule, that is, the common portion of rules encoded in the VB rule, and match its LHS to the full domain model, temporarily ignoring its presence conditions. For example, considering rule A + B, the LHS of the base rule contains precisely states x1, x2, and x. A match to the domain model is indicated by dashed arrows. Using the presence conditions, we determine if the match can be mapped to any specific product. In step 2, we extend the identified base matches to identify full matches of the rules encoded in the VB rule. In the example, we would derive rules A and B; in general, to avoid fully flattening all involved rules, one can incrementally consider common subrules. An example match is denoted in terms of dashed lines for the mappings of transitions and actions. In step 3, to perform rule applications based on identified matches, we use lifting to apply the rule for which the match was found. Lifting transforms the domain model and its presence condition in such way as if each product was considered individually. In the example, only products for the configuration {Delay = true; Heat = false} are amenable to the foldAction refactoring. Consequently, the new entry action startWash has the presence condition Delay, and other presence conditions are adjusted accordingly. Failure to find suitable matches and to fulfill a certain condition during lifting (discussed later) allows early termination of the process.
Performance-wise, the main benefit of this technique is twofold: First, using the termination criteria, we can exit the matching process early without considering specifics of products and rule variants. This is particularly beneficial in situations where none or only few rules of a larger rule set are applicable most of the time, which is typically the case, for example, in translators. Second, even if we have to enumerate some rules in step 2, we do not have to start the matching process from scratch, since we can save redundant effort by extending the available base matches. Consequently, Table 1 gives the number of independent combinations (in the sense that rule applications are started from scratch) as 1.
3 Background
We now introduce the necessary prerequisites of our methodology, starting with the double-pushout approach to algebraic graph transformation [19]. As the underlying structure, we assume the category of graphs with graph morphisms (referred to as morphisms from here), although all considerations are likely compatible with additional graph features such as typing and attributes.
Definition 1
(Rules and applications). A rule  consists of graphs L, I and R, called left-hand side, interface graph and right-hand side, respectively, and two injective morphisms le and ri.
consists of graphs L, I and R, called left-hand side, interface graph and right-hand side, respectively, and two injective morphisms le and ri.
Given a rule r, a graph G, and a morphism \(m : L \rightarrow G\), a rule application from G to a graph H, written \(G \Rightarrow _{r,m} H\), arises from the diagram to the right, where (1) and (2) are pushouts. G, m and H are called start graph, match, and result graph, respectively.

A rule application exists iff the match m fulfills the gluing condition, which, in the category of graphs boils down to the dangling condition: all adjacent edges of a deleted node in m’s image m[L] must have a preimage in L.
Product Lines. Our formalization represents product lines on the semantic level by considering interrelations between the included graphs. The domain model is a “maximal” graph of which all products are sub-graphs. The presence-condition function maps sub-graphs (rather than elements, as done on the syntactic level) to terms in the boolean term algebra over features, written \(T_{BOOL}(F_P)\). The set of all sub-graphs of the domain model is written \(\mathcal {P}(M_P)\).
Definition 2
(Product line, configuration, product)
-
A product line \(P = (F_P,\varPhi _P,M_P,f_P)\) consists of three parts: a feature model that consists of a set \(F_P\) of features, and a set of feature constraints \(\varPhi _P \subseteq T_{BOOL}(F_P)\), a domain model \(M_P\) given as a graph, and a set of presence conditions expressed as a function \(f_P\): \(\mathcal {P}(M_P) \rightarrow T_{{\textit{BOOL}}}(F_P)\).
-
Given a set of features F, a configuration is a total function \(\textit{c} : F \rightarrow \{\textit{true}, \textit{false}\}\). A configuration \(\textit{c}\) satisfies a term \(t \in T_{BOOL}(F)\) if t evaluates to \(\textit{true}\) when each variable v in t is substituted by \(\textit{c}(v)\). A configuration \(\textit{c}\) is valid w.r.t. a set of constraints \(\varPhi \) if \(\textit{c}\) satisfies every constraint in \(\varPhi \).
-
Given a product line \(P= (F_P,\varPhi _P,M_P,f_P)\), a product \(P_c\) is derived from P under the valid configuration c if \(P_c\) is the union of all those graphs \(M^{\prime }{} \subseteq M_P\) for which \(f_P(M^{\prime }{})\) is satisfied by c: \(P_c = \bigcup \{M' \subseteq M_P| c~\textit{satisfies}~f_P(M^{\prime }{})\) \(\textit{and}~c~\textit{is valid w.r.t.}~\varPhi _P\}\). The flattening of P is the set Flat(P) of all products of P: Flat(P) = \(\{ P_c | P_c\,\text{ is } \text{ a } \text{ product } \text{ of }\,P \}\).
Definition 3
(Lifted rule application). Given a product line P, a rule r, and a match \(m: L \rightarrow M_P\), a lifted rule application \(P \Rightarrow _{r,m}^\uparrow Q\) is a construction that relates P to a product line Q s.t. \(F_P\) = \(F_Q\), \(\varPhi _P\) = \(\varPhi _Q\), and the set of products Flat(Q) is the same as if r was applied to each product \(P_i \in Flat (P)\) for which an inclusion \(j: m[L] \rightarrow P_i\) from the image of m exists.
Salay et al. [6] provide an algorithm for which it is shown that the properties required in Definition 3 apply. The algorithm extends a rule application to the domain model by a check that the match can be mapped to at least one product, and by dedicated presence condition handling during additions and deletions. A more declarative treatment is offered by Taentzer et al. [25]’s product line pushout construction, which is designed to support lifted rule application as a special case.
Variability-Based Transformation. VB rules are defined similarly to product lines, with a “maximal” rule instead of a domain model, and a notion of subrules instead of subgraphs. A subrule is a rule that can be embedded into a larger rule injectively s.t. the actions of rule elements are preserved [12], e.g., deletions are mapped to deletions. The set of all subrules of a rule r is written \(\mathcal {P}(r)\).
Definition 4
(Variability-based (VB) rule). A VB rule \(\check{r} = (F_{\check{r}},\varPhi _{\check{r}},r_{\check{r}},f_{\check{r}})\) consists of three parts: a feature model that consists of a set \(F_{\check{r}}\) of features, and a set of feature constraints \(\varPhi _{\check{r}} \subseteq T_{BOOL}(F_{\check{r}})\), a maximal rule \(r_{\check{r}}\) being a rule, and a set of presence conditions expressed as a function \(f_P\): \(\mathcal {P}(r_{\check{r}}) \rightarrow T_{{\mathrm{BOOL}}}(F_{\check{r}})\).
To later consider the base rule, that is, a maximal subrule of multiple flat rules, we define the flattening of VB rules in terms of consecutive intersection and union constructions, expressed as multi-pullbacks and -pushouts [12]. The multi-pullback \(r_0\) gives the base rule, over which the flat rule arises by multi-pushout.
Definition 5
(Flat rule). Given a VB rule \(\check{r}\), for a valid configuration c w.r.t. \(\varPhi _{\check{r}}\), there exists a unique set of n subrules \(S_c \subseteq \mathcal {P}(r_{\check{r}})\) s.t. \(\forall s \in \mathcal {P}(r_{\check{r}}):\) \(s \in S_c\) iff c satisfies \(f_{\check{r}}(s)\). Merging these subrules via multi-pullback and multi-pushout over \(r_{\check{r}}\) and \(r_0\), respectively, yields a rule \(r_c\), called flat rule induced by c. The flattening of \(\check{r}\) is the set Flat(\(\check{r}\)) of all flat rules of \(\check{r}\): Flat(\(\check{r}\)) = \(\{r_c | r_c~\textit{is a flat rule of}~\check{r}\}\).

In the example, \(r_{\check{r}}\) is the rule \(A+B\), ignoring presence conditions. Given the configuration c = {foldEntry = true, foldExit = false}, the multi-pullback over each subrule whose presence condition satisfies c yields as the base rule \(r_0\) precisely the part of rule \(A+B\) without presence conditions (i.e., only the states). The resulting flat rule \(r_c\) is isomorphic to rule A.
As a prerequisite for achieving efficiency during staged application, we revisit VB rule application. The key idea is that matches of a flat rule are composed from matches of all of its subrules. By considering the subrules during matching, we can reuse matches over several rules and identify early-exit opportunities.
Definition 6
(VB match family, VB match, VB rule application)
-
Given a variability-based rule \(\check{r}\), a graph G, and a valid configuration c, there exists a unique set of subrules \(S_c \subseteq r_{\check{r}}\) s.t. \(\forall s \in \mathcal {P}(r_{\check{r}}):\) \(s \in S_c\) iff c satisfies \(f_{\check{r}}(s)\). A variability-based match family is a family of morphisms \((m_s : L_s \rightarrow G)_{1 \le s \le |S_c|}\) s.t. \(\forall m_i, m_j\) with \(1 \le i,j \le |S_c|\) the following compatability condition holds: \(\forall x \in dom(m_i) \cap dom(m_j): m_i(x) = m_j(x)\).
-
Given a variability-based match family \((m_s)\) for \(\check{r}\), G, and c, a variability-based match \(\check{m}\) is a pair \((m_c, \textit{c})\) where the morphism \(m_c : L_{\textit{c}} \rightarrow G\) is obtained by the colimit property of \(L_\textit{c}\). If \(m_c\) is a match, \(\check{m}\) is called a variability-based match.
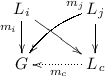
-
Given a variability-based match \(\check{m} = (m_c, c)\) for \(\check{r}\) and G, the application of \(\check{r}\) at \(\check{m}\) is the rule application \(G \Rightarrow _{r_\textit{c}, m_c}H\) of the flat rule \(r_\textit{c}\) to \(m_c\).
In the example, a VB match family is obtained: Step 1 collects matches of the LHS \(L_0\). Step 2 reuses these matches to match the flat rules: according to the compatibility condition, we may extend the matches rather than start from scratch. The set of VB rule applications for a rule \(\check{r}\) to a model G is equivalent to the set of rule applications of all flat rules in Flat(\(\check{r}\)) to G [12, Theorem 2].
4 Multi-variability of Product Line Transformations
A variability-based rule represents a set of similar transformation rules, while a product line represents a set of similar models. We consider the application of a variability-based rule to a product line from a formal perspective. Our idea is to combine two principles of maximality, which, up to now, were considered in isolation: First, by applying a rule to a “maximum” of all products, the rule can be lifted efficiently to a product line (Definition 3). Second, by reusing matches of a maximal subrule, several rules can be applied efficiently to a single model (Definition 6).
We study three strategies for applying a variability-based rule \(\check{r}\) to a product line \(P\); the third one leads to the notion of staged rule application as introduced in Sect. 2. First, we consider the naive case of flattening \(\check{r}\) and \(P\) and applying each rule to each product. Second, we take the two maximality principles into account to avoid the flattening of \(\check{r}\). Third, we use additional aspects from the first principle to avoid the flattening of \(P\) as well. We show that all strategies are equivalent in the sense that they change all of \(P\)’s products in the same way.
4.1 Fully Flattened Application
Definition 7
(Fully flattened application). Given the flattening of a product line \(P\) and the flattening of a rule family \(\check{r}\), the set of fully-flattened rule applications \(Trans_{FF}(P,\check{r})\) arises from applying each rule to each product:
In the example, there are two rules and six products; however, only for two products—the ones arising from configurations with Delay = true and Heat = false—a match, and, therefore, a rule application exists, as we saw in the earlier description of the example. \(Trans_{FF}(P,\check{r})\) comprises the resulting two rule applications.
4.2 Partially Flattened Application
We now consider a strategy that aims to avoid unflattening the variability-based rule \(\check{r}\). We use the fact that the rules in \(\check{r}\) generally share a maximal, possibly empty sub-rule \(r_0\) that can be embedded into all rules in \(\check{r}\). Moreover, we exploit the fact that each product has an inclusion into the domain model.
The key idea is as follows: each match of a flat rule to a product includes a match of \(r_0\) into the domain model \(M_P\). Absence of such a match implies that none of the rules in \(\check{r}\) has a match, allowing us to stop without considering any flat rule in its entirety. Such exit point is particularly beneficial if the VB rule represents a subset of a larger rule set in which only a few rules can be matched at one time. Conversely, if a match for \(r_0\) exists, a rule application arises if the match can be “rerouted” onto one of the products \(P_i\). In this case, we consider the flat rules, saving redundant matching effort by reusing the matches of \(r_0\).
To reuse matches to the domain model for the products, we introduce the rerouting of a morphism from its codomain onto another graph \(G'\). We omit naming the codomain and \(G'\) explicitly where they are clear from the context.
Definition 8
(Rerouted morphism). Let an inclusion \(i : G'~\rightarrow ~G\), a morphism \(m : L \rightarrow G\) with an epi-mono-factorization \((e, m')\), and a morphism \(j : m[L] \rightarrow G'\) be given, s.t. \(m' = i \circ j\). The rerouted morphism \(\textit{reroute}(m,G') : L \rightarrow G'\) arises by composition: \(\textit{reroute}(m,G') = j \circ e\).

Definition 9
(Rerouted variability-based match). Given a graph G, a variability-based rule \(\check{r}\) with a variability-based match \(\check{m}= (m_c, c)\) (Definition 6), and an inclusion \(i : G'~\rightarrow ~G\). If the epi-mono-factorization of \(m_c\) and a suitable morphism j exists, a rerouted morphism onto \(G'\) arises (Definition 8). Pairing this morphism with the configuration c induces the rerouted variability-based match of \(\check{m}_c\) onto \(G'\): \(\textit{reroute}(\check{m}, G') = (\textit{reroute}(m_c,G'),c)\).
In Fig. 5, \(m_{c,h}\) is the morphism obtained by rerouting a match \(m_{c,t}\) from the domain model \(M_p\) to product \(P_h\). For example, if \(m_{c,t}\) is the match indicated in steps 1 and 2 of Fig. 4, the morphism j and, consequently, \(m_{c,h}\) exists only for products in which all images of the mappings exist as well, e.g., the product shown in the right of Fig. 2. Note that \(m_{c,t}\) is a variability-based match to \(M_P\): In an earlier explanation, we saw that the family \((m_{i,t})\) forms a variability-based match family. Therefore, per Definition 9, pairing \(m_{c,h}\) with the configuration c induces a variability-based match to \(P_h\), which can be used as follows.
Variability-based rule application (Definition 6) allows us to save matching effort by considering shared parts of rules to a graph only once. The following definition allows us to lift this insight from graphs onto product lines. We show that the sets of partially and fully flattened rule applications are equivalent.
Definition 10
(Partially flattened application). Given a variability-based rule \(\check{r}\) and a product line \(P\), the set of partially flattened rule applications \(Trans_{PF}(P,\check{r})\) is obtained by rerouting all variability-based matches from the domain model \(M_P\) to products in \(P\) and collecting all resulting rule applications:
Theorem 1
(Equivalence of fully and partially flattened rule applications). Given a product line \(P\) and a variability-based rule \(\check{r}\), \(Trans_{FF}(P,\check{r}) = Trans_{PF}(P,\check{r})\).
Proof idea.Footnote 1 For every fully flattened (FF) rule application, we can find a corresponding partially flattened (PF) one, and vice versa: Given a FF rule application at a match \(m'\), we compose \(m'\) with the product inclusion into the domain model \(M_P\) to obtain a match \(m_c\) into \(M_P\). Per Theorem 2 in [12], \(m_c\) induces a VB match and rule application. From a diagram chase, we see that \(m'\) is the morphism arising from rerouting \(m_c\) onto the product \(P_i\). Consequently, the rule application is PF. Conversely, a PF variability-based rule application induces a corresponding FF rule application by its definition.
4.3 Staged Application
The final strategy we consider, staged application, aims to avoid unflattening the products as well. This can be achieved by employing lifting (Definition 3): Lifting takes a single rule and applies it to a domain model and its presence conditions in such a way as if the rule had been applied to each product individually. The considered rule in our case is a flat rule with a match to the domain model.
Note that we cannot compare the set of staged applications directly to the set of flattened applications, since it does not live on the product level. We can, however, compare the obtained sets of products from both sets of applications, which happens to be the same, thus showing the correctness of our approach.
Definition 11
(Staged application). Given a variability-based rule \(\check{r}\) and a product line \(P\), the set of staged applications \(Trans_{St}(P,\check{r})\) is the set of lifted rule applications obtained from VB matches to the domain model \(M_P\):
Corollary 1
(Equivalence of staged and partially flattened rule applications). Given a product line \(P\) and a variability-based rule \(\check{r}\), the sets of products obtained from \(Trans_{St}(P,\check{r})\) and \(Trans_{PF}(P,\check{r})\) are isomorphic.
Proof
Since both sets are defined over the same set of matches of flat rules, the proof follows straight from the definition of lifting.

5 Algorithm
We present an algorithm for implementing the staged application of a VB rule \(\check{r}\) to a product line P. Following the overview in Sect. 2 and the treatment in Sect. 4, the main idea is to proceed in three steps: First, we match the base rule of \(\check{r}\) to the domain model, ignoring presence conditions. Second, we consider individual rules as far as necessary to obtain matches to the domain model. Third, based on the matches, we perform the actual rule application by using the lifting algorithm from [6] in a black-box manner.
Algorithm 1 shows the computation in more detail. In line 1, \(\check{r}\)’s base rule \(r_0\) is matched to the domain model \(\textit{Model}_P\), leading to a set of base matches. If this set is empty, we have reached the first exit criterion and can stop directly. Otherwise, given a match m, in line 2, we check if at least one product \(P_i\) exists that m can be rerouted onto (Definition 8). To this end, in lines 3–4, we use a SAT solver to check if there is a valid configuration of P’s feature model for which all presence conditions of matched elements evaluate to true. In this case, we iterate over the valid configurations of \(\check{r}\) in line 5 (we may proceed more fine-grainedly by using partial configurations; this optimization is omitted for simplicity). In line 6, a flat rule is obtained by removing all elements from the rule whose presence condition evaluates to false. We match this rule to the domain model in line 7; to save redundant effort, we restrict the search to matches that extend the current base match. Absence of such a match is the second stopping criterion. Otherwise, we feed the flat rule and the set of matches to lifting in line 8. Handling dangling conditions is left to lifting; in the positive case, P is transformed afterwards.
For illustration, consider the base match \(m_1\) = {Looking, Waiting, Washing} from Fig. 4. First we calculate \(\varPhi _{pc}\). As none of the states in the domain model has a presence condition, \(\varPhi _{pc}\) is set to true and is identified as satisfiable. Two valid configurations exist, \(c_1 = \{foldEntry=true,foldExit=false\}\) and \(c_2 = \{foldEntry=false,foldExit=true\}\). Considering \(c_1\), the presence condition foldExit evaluates to false; removing the corresponding elements yield a rule isomorphic to Rule A in Fig. 3. Match \(m_1\) is now extended using this rule, leading to a match as shown in step 2 of Fig. 4. and then lifted, as discussed in the earlier explanation of the example. Step 2 is repeated for configuration \(c_2\); yet, as no suitable match in \(c_2\) exists, the shown transformation is the only possible one.
This algorithm benefits from the correctness results shown in Sect. 4. Specifically, it computes staged rule applications as per Definition 11: A configuration c is determined in line 5, and values for match \(m_c\) are collected in the set Matches. Via Corollary 1 and Theorem 1, the effect of the rule application to the products is the same as if each product had been considered individually.
In terms of performance, two limiting factors are the use of a graph matcher and a SAT solver; both of them perform an NP-complete task. Still, we expect practical improvements from our strategy of reusing shared portions of the involved rules and graphs, and from the availability of efficient SAT solvers that scale up to millions of variables [26]. This hypothesis is studied in Sect. 6.
6 Evaluation
To evaluate our technique, we implemented it for Henshin [27, 28], a graph-based model transformation language, and applied it to a transformation scenario with product lines and transformation variability. The goal of our evaluation was to study if our technique indeed produces the expected performance benefits.
Setup. The transformation is concerned with the detection of applied editing operations during model differencing [29]. This setting is particularly interesting for a performance evaluation: Since differencing is a routine software development task, low latency of the used tools is a prerequisite for developer effectiveness. The rule set, called UmlRecog, is tailored to the detection of UML edit operations. Each rule detects a specific edit operation, such as “move method to superclass”, based on a pair of model versions and a low-level difference trace. UmlRecog comprises 1404 rules, which, as shown in Table 2, fall in three main categories: Create/Set, Change/Move, and Delete/Unset. To study the effect of our technique on performance, an encoding of the rules into VB rules was required. We obtained this encoding using RuleMerger [18], a tool for generating VB rules from classic ones based on clustering and clone detection [30]. We obtained 504 VB rules; each of them representing between 1 and 71 classic rules. UmlRecog is publicly available as part of a benchmark transformation set [31].
We applied this transformation to the 6 UML-based product lines specified in Table 3. The product lines came from diverse sources and include manually designed ones (1–2), and reverse-engineered ones from open-source projects (3–6). Each product line was available as an UML model annotated with presence conditions over a feature model. To produce the model version pairs used by UmlRecog, we automatically simulated development steps by nondeterministically applying rules from a set of edit rules to the product lines, using the lifting algorithm to account for presence conditions during the simulated editing step.
As baseline for comparison, we considered the lifted application of each rule in UmlRecog. An alternative baseline of applying VB rules to the flattened set of products was not considered: The SPL variability in our setting is much greater than the rule variability, which implies a high performance penalty when enumerating products. Since we currently do not support advanced transformation features, e.g., negative application conditions and amalgamation, we used variants of the flat and the VB rules without these concepts. We used a Ubuntu 17.04 system (Oracle JDK 1.8, Intel Core i5-6200U, 8 GB RAM) for all experiments.
Results. Table 4 gives an overview of the results of our experiments. The total execution times for our technique were between 1.5 and 3.3 s, compared to 9.4 and 10.6 s for lifting, yielding a speedup by factors between 2.8 and 6.5. For both techniques, all execution times are in the same order of magnitude across product lines. A possible explanation is that the amount of applicable rules was small: if the vast majority of rules can be discarded early in the matching process, the execution time is constant with the number of rules.
The greatest speedups were observed for the Change/Move category, in which rule variability was the greatest as well, indicated by the ratio between rules and VB rules in Table 2. This observation is in line with our rationale of reusing shared matches between rules. Regarding the number of products, a trend regarding better scalability is not apparent, thus demonstrating that lifting is sufficient for controlling product-line variability. Still, based on the overall results, the hypothesis that our technique improves performance in situations with significant product-line and transformation variability can be confirmed.
Threats to Validity. Regarding external validity, we only considered a limited set of scenarios, based on six product lines and one large-scale transformation. We aim to apply our technique to a broader class of cases in the future. The version pairs were obtained in a synthetic process, arguably one that produces pessimistic cases. Our treatment so far is also limited to a particular transformation paradigm, AGT, and one variability paradigm, the annotative one. Still, AGT and annotative variability are the underlying paradigms of many state-of-the-art tools. Finally, we did not consider the advanced AGT concepts of negative application conditions and amalgamation in our evaluation; extending our technique accordingly is left as future work.
7 Related Work
During an SPL’s lifecycle, not only the domain model, but also the feature model evolves [32, 33]. To support the combined transformation of domain and feature models, Taentzer et al. [25] propose a unifying formal framework which generalizes Salay et al.’s notion of lifting [6], yet in a different direction than us: focusing on combined changes, this approach is not geared for internal variability of rules; similar rules are considered separately. Both works could be combined using a rule concept with separate feature models for rule and SPL variability.
Beyond transformations of SPLs, transformations have been used to implement SPLs. Feature-oriented development [34] supports the implementation of features as additive changes to a base product. Delta-oriented programming [35] adds flexibility to this approach: changes are specified using deltas that support deletions and modifications as well. Impact analysis in an evolving SPL can be performed by transforming deltas using higher-order deltas that encapsulate certain evolution operators [5]. For increased flexibility regarding inter-product reuse, deltas can be combined with traits [36]. Sijtema [8] introduced the concept of variability rules to develop SPLs using ATL. Conversely, SPL techniques have been applied to certain problems in transformation development. Xiao et al. [37] propose to capture variability in the backwards propagation of bidirectional transformations by turning the left-hand-side model into a SPL. Hussein et al. [10] present a notion of rule templates for generating groups of similar rules based on a data provenance model. These works address only one dimension of variability, either of a SPL or a transformation system.
In the domain of graph transformation reuse, rule refinement [9] and amalgamation [38] focus on reuse at the rule level; graph variability is not in their scope. Rensink and Ghamarian propose a solution for rule and graph decomposition based a certain accommodation condition, under which the effect of the original rule application is preserved [39, 40]. In our approach, by matching against the full domain model rather than decomposing it, we trade off compositionality for the benefit of imposing fewer restrictions on graphs and rules.
8 Conclusion and Future Work
We propose a methodology for software product line transformations in which not only the input product line, but also the transformation system contains variability. At the heart of our methodology a staged rule application technique exploits reuse potential with regard to shared portions of the involved products and rules. We showed the correctness of our technique and demonstrated its benefit by applying it to a practical software engineering task.
In the future, we aim to explore further variability dimensions, e.g., meta-model variability as considered in [41], and to extend our work to advanced transformation features, such as application conditions. We aim to address additional variability mechanisms and to perform a broader evaluation.
Notes
- 1.
A full proof is provided in the extended version of this paper: http://danielstrueber.de/publications/SPJ18.pdf.
References
Pohl, K., Boeckle, G., van der Linden, F.: Software Product Line Engineering: Foundations, Principles, and Techniques. Springer, Heidelberg (2005). https://doi.org/10.1007/3-540-28901-1
Apel, S., Batory, D., Kästner, C., Saake, G.: Feature-Oriented Software Product Lines: Concepts and Implementation. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37521-7
Schulze, S., Thüm, T., Kuhlemann, M., Saake, G.: Variant-preserving refactoring in feature-oriented software product lines. In: VaMoS, pp. 73–81 (2012)
Borba, P., Teixeira, L., Gheyi, R.: A theory of software product line refinement. Theor. Comput. Sci. 455, 2–30 (2012)
Lity, S., Kowal, M., Schaefer, I.: Higher-order delta modeling for software product line evolution. In: FOSD, pp. 39–48 (2016)
Salay, R., Famelis, M., Rubin, J., Sandro, A.D., Chechik, M.: Lifting model transformations to product lines. In: ICSE, pp. 117–128 (2014)
Kolovos, D.S., Rose, L.M., Matragkas, N., Paige, R.F., Guerra, E., Cuadrado, J.S., De Lara, J., Ráth, I., Varró, D., Tisi, M., et al.: A research roadmap towards achieving scalability in model driven engineering. In: BigMDE, p. 2. ACM (2013)
Sijtema, M.: Introducing variability rules in ATL for managing variability in MDE-based product lines. In: MtATL 2010, pp. 39–49 (2010)
Anjorin, A., Saller, K., Lochau, M., Schürr, A.: Modularizing triple graph grammars using rule refinement. In: Gnesi, S., Rensink, A. (eds.) FASE 2014. LNCS, vol. 8411, pp. 340–354. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54804-8_24
Hussein, J., Moreau, L., et al.: A template-based graph transformation system for the PROV data model. In: GCM (2016)
Strüber, D.: Model-driven engineering in the large: refactoring techniques for models and model transformation systems. Ph.D. dissertation, Philipps-Universität Marburg (2016)
Strüber, D., Rubin, J., Arendt, T., Chechik, M., Taentzer, G., Plöger, J.: Variability-based model transformation: formal foundation and application. Formal Aspects Comput. 30, 133–162 (2017)
Strüber, D., Rubin, J., Chechik, M., Taentzer, G.: A variability-based approach to reusable and efficient model transformations. In: Egyed, A., Schaefer, I. (eds.) FASE 2015. LNCS, vol. 9033, pp. 283–298. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46675-9_19
Kästner, C., Apel, S., Trujillo, S., Kuhlemann, M., Batory, D.: Language-independent safe decomposition of legacy applications into features, vol. 2. Technical report, School of Computer Science, University of Magdeburg, Germany (2008)
Di Sandro, A., Salay, R., Famelis, M., Kokaly, S., Chechik, M.: MMINT: a graphical tool for interactive model management. In: P&D@ MoDELS, pp. 16–19 (2015)
Strüber, D., Schulz, S.: A tool environment for managing families of model transformation rules. In: Echahed, R., Minas, M. (eds.) ICGT 2016. LNCS, vol. 9761, pp. 89–101. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40530-8_6
Rubin, J., Chechik, M.: Combining related products into product lines. In: de Lara, J., Zisman, A. (eds.) FASE 2012. LNCS, vol. 7212, pp. 285–300. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28872-2_20
Strüber, D., Rubin, J., Arendt, T., Chechik, M., Taentzer, G., Plöger, J.: RuleMerger: automatic construction of variability-based model transformation rules. In: Stevens, P., Wąsowski, A. (eds.) FASE 2016. LNCS, vol. 9633, pp. 122–140. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49665-7_8
Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Fundamentals of Algebraic Graph Transformation. MTCSAES. Springer, Heidelberg (2006). https://doi.org/10.1007/3-540-31188-2
Czarnecki, K., Helsen, S.: Feature-based survey of model transformation approaches. IBM Syst. J. 45(3), 621–645 (2006)
Richa, E., Borde, E., Pautet, L.: Translation of ATL to AGT and application to a code generator for Simulink. SoSyM, 1–24 (2017). https://link.springer.com/article/10.1007/s10270-017-0607-8
Kästner, C., Apel, S., Kuhlemann, M.: Granularity in software product lines. In: ICSE, pp. 311–320 (2008)
Kang, K.C., Cohen, S.G., Hess, J.A., Novak, W.E., Peterson, A.S.: Feature-oriented domain analysis (FODA) feasibility study. Technical report, Software Engineering Inst., Carnegie-Mellon Univ., Pittsburgh, PA (1990)
Chechik, M., Famelis, M., Salay, R., Strüber, D.: Perspectives of model transformation reuse. In: Ábrahám, E., Huisman, M. (eds.) IFM 2016. LNCS, vol. 9681, pp. 28–44. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-33693-0_3
Taentzer, G., Salay, R., Strüber, D., Chechik, M.: Transformations of software product lines: a generalizing framework based on category theory. In: MODELS, pp. 101–111. IEEE (2017)
Gomes, C.P., Kautz, H., Sabharwal, A., Selman, B.: Satisfiability solvers. In: Foundations of Artificial Intelligence, vol. 3, pp. 89–134 (2008)
Arendt, T., Biermann, E., Jurack, S., Krause, C., Taentzer, G.: Henshin: advanced concepts and tools for in-place EMF model transformations. In: Petriu, D.C., Rouquette, N., Haugen, Ø. (eds.) MODELS 2010. LNCS, vol. 6394, pp. 121–135. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16145-2_9
Strüber, D., Born, K., Gill, K.D., Groner, R., Kehrer, T., Ohrndorf, M., Tichy, M.: Henshin: a usability-focused framework for EMF model transformation development. In: de Lara, J., Plump, D. (eds.) ICGT 2017. LNCS, vol. 10373, pp. 196–208. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61470-0_12
Kehrer, T., Kelter, U., Taentzer, G.: A rule-based approach to the semantic lifting of model differences in the context of model versioning. In: ASE, pp. 163–172. IEEE Computer Society (2011)
Strüber, D., Plöger, J., Acreţoaie, V.: Clone detection for graph-based model transformation languages. In: Van Gorp, P., Engels, G. (eds.) ICMT 2016. LNCS, vol. 9765, pp. 191–206. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-42064-6_13
Strüber, D., Kehrer, T., Arendt, T., Pietsch, C., Reuling, D.: Scalability of model transformations: position paper and benchmark set. In: Workshop on Scalable Model Driven Engineering, pp. 21–30 (2016)
Thüm, T., Batory, D., Kästner, C.: Reasoning about edits to feature models. In: ICSE, pp. 254–264 (2009)
Bürdek, J., Kehrer, T., Lochau, M., Reuling, D., Kelter, U., Schürr, A.: Reasoning about product-line evolution using complex feature model differences. Autom. Softw. Eng. 23, 687–733 (2015)
Trujillo, S., Batory, D., Diaz, O.: Feature oriented model driven development: a case study for portlets. In: ICSE, pp. 44–53. IEEE Computer Society (2007)
Schaefer, I., Bettini, L., Bono, V., Damiani, F., Tanzarella, N.: Delta-oriented programming of software product lines. In: Bosch, J., Lee, J. (eds.) SPLC 2010. LNCS, vol. 6287, pp. 77–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15579-6_6
Damiani, F., Hähnle, R., Kamburjan, E., Lienhardt, M.: A unified and formal programming model for deltas and traits. In: Huisman, M., Rubin, J. (eds.) FASE 2017. LNCS, vol. 10202, pp. 424–441. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54494-5_25
He, X., Hu, Z., Liu, Y.: Towards variability management in bidirectional model transformation. In: COMPSAC, vol. 1, pp. 224–233. IEEE (2017)
Biermann, E., Ermel, C., Taentzer, G.: Lifting parallel graph transformation concepts to model transformation based on the eclipse modeling framework. Electron. Commun. EASST 26 (2010)
Rensink, A.: Compositionality in graph transformation. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6199, pp. 309–320. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14162-1_26
Ghamarian, A.H., Rensink, A.: Generalised compositionality in graph transformation. In: Ehrig, H., Engels, G., Kreowski, H.-J., Rozenberg, G. (eds.) ICGT 2012. LNCS, vol. 7562, pp. 234–248. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33654-6_16
Perrouin, G., Amrani, M., Acher, M., Combemale, B., Legay, A., Schobbens, P.-Y.: Featured model types: towards systematic reuse in modelling language engineering. In: MiSE, pp. 1–7. IEEE (2016)
Acknowledgement
We thank Rick Salay and the anonymous reviewers for their constructive feedback. This work was supported by the Deutsche Forschungsgemeinschaft (DFG), project SecVolution@Run-time, no. 221328183.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Strüber, D., Peldzsus, S., Jürjens, J. (2018). Taming Multi-Variability of Software Product Line Transformations. In: Russo, A., Schürr, A. (eds) Fundamental Approaches to Software Engineering. FASE 2018. Lecture Notes in Computer Science(), vol 10802. Springer, Cham. https://doi.org/10.1007/978-3-319-89363-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-89363-1_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89362-4
Online ISBN: 978-3-319-89363-1
eBook Packages: Computer ScienceComputer Science (R0)