Optimising Spectrum Based Fault Localisation for Single Fault Programs Using Specifications

Abstract

Spectrum based fault localisation determines how suspicious a line of code is with respect to being faulty as a function of a given test suite. Outstanding problems include identifying properties that the test suite should satisfy in order to improve fault localisation effectiveness subject to a given measure, and developing methods that generate these test suites efficiently.

We address these problems as follows. First, when single bug optimal measures are being used with a single-fault program, we identify a formal property that the test suite should satisfy in order to optimise fault localisation. Second, we introduce a new method which generates test data that satisfies this property. Finally, we empirically demonstrate the utility of our implementation at fault localisation on sv-comp benchmarks and the tcas program, demonstrating that test suites can be generated in almost a second with a fault identified after inspecting under 1% of the program.

This research was supported by the Innovate UK project 113099 SECT-AIR.

1 Introduction

Faulty software is estimated to cost 60 billion dollars to the US economy per year [1] and has been single-handedly responsible for major newsworthy catastrophes¹. This problem is exacerbated by the fact that debugging (defined as the process of finding and rectifying a fault) is complex and time consuming – estimated to consume 50–60% of the time a programmer spends in the maintenance and development cycle [2]. Consequently, the development of effective and efficient methods for software fault localisation has the potential to greatly reduce costs, wasted programmer time and the possibility of catastrophe.

In this paper, we advance the state of the art in lightweight fault localisation by building on research in spectrum-based fault localisation (sbfl). sbfl is one of the most prominent areas of software fault localisation research, estimated to make up 35% of published work in the field to date [3], and has been demonstrated to be efficient and effective at finding faults [4,5,6,7,8,9,10,11,12]. The effectiveness relies on two factors, (1) the quality of the measure used to identify the lines of code that are suspected to be faulty, and (2) the quality of the test suite used. Most research in the field has been focussed on finding improved measures [4,5,6,7,8,9,10,11,12], but there is a growing literature on how to improve the quality of test suites [13,14,15,16,17,18,19,20]. An outstanding problem in this field is to identify the properties that test suites should satisfy to improve fault localisation.

To address this problem, we focus our attention on improving the quality of test suites for the purposes of fault localisation on single-fault programs. Programs with a single fault are of special interest, as a recent study demonstrates that 82% of faulty programs could be repaired with a “single fix” [21], and that “when software is being developed, bugs arise one-at-a-time and therefore can be considered as single-faulted scenarios”, suggesting that methods optimised for use with single-fault programs would be most helpful in practice. Accordingly, the contributions of this paper are as follows.

• 1. We identify a formal property that a test suite must satisfy in order to be optimal for fault localisation on a single-fault program when a single-fault optimal sbfl measure is being used.

• 2. We provide a novel algorithm which generates data that is formally shown to satisfy this property.

• 3. We integrate this algorithm into an implementation which leverages model checkers to generate small test suites, and empirically demonstrate its practical utility at fault localisation on our benchmarks.

The rest of this paper is organized as follows. In Sect. 2, we present the formal preliminaries for sbfl and our approach. In Sect. 3, we motivate and describe a property of single-fault optimality. In Sect. 4, we present an algorithm which generates data for a given faulty program, and prove that the data generated satisfies the property of single fault optimality, and in Sect. 5 discuss implementation details. In Sect. 6 we present our experimental results where we demonstrate the utility of an implementation of our algorithm on our benchmarks, and in Sect. 7 we present related work.

2 Preliminaries

In this section we formally present the preliminaries for understanding our fault localisation approach. In particular, we describe probands, proband models, and sbfl.

2.1 Probands

Following the terminology in Steimann et al. [22], a proband is a faulty program together with its test suite, and can be used for evaluating the performance of a given fault localization method. A faulty program is a program that fails to always satisfy a specification, which is a property expressible in some formal language and describes the intended behaviour of some part of the program under test (put). When a specification fails to be satisfied for a given execution (i.e., an error occurs), it is assumed there exists some (incorrectly written) lines of code in the program which was the cause of the error, identified as a fault (aka bug).

Example 1

An example of a faulty c program is given in Fig. 1 (minmax.c, taken from Groce et al. [23]), and we shall use it as our running example throughout this paper. There are some executions of the program in which the assertion statement is violated, and thus the program fails to always satisfy the specification. The fault in this example is labelled C4, which should be an assignment to least instead of most.

Fig. 1.

minmax.c

Fig. 2.

Coverage matrix

A test suite is a collection of test cases whose result is independent of the order of their execution, where a test case is an execution of some part of a program. Each test case is associated with an input vector, where the n-th value of the vector is assigned to the n-th input of the given program for the purposes of a test (according to some given method of assigning values in the vector to inputs in the program). Each test suite is associated with a set of input vectors which can be used to generate the test cases. A test case fails (or is failing) if it violates a given specification, and passes (or is passing) otherwise.

Example 2

We give an example of a test case for the running example. The test case with associated input vector $\langle 0, 1, 2 \rangle$ is an execution in which input1 is assigned 0, input2 is assigned 1, and input3 is assigned 2, the statements labeled C1, C2 and C3 are executed, but C4 and C5 are not executed, and the assertion is not violated at termination, as least and most assume values of 0 and 2 respectively. Accordingly, we may associate a collection of test cases (a test suite) with a set of input vectors. For the running example the following ten input vectors are associated with a test suite of ten test cases: $\langle 1, 0, 2 \rangle$, $\langle 2, 0, 1 \rangle$, $\langle 2, 0, 2 \rangle$, $\langle 0, 1, 0 \rangle$, $\langle 0, 0, 1 \rangle$, $\langle 1, 1, 0 \rangle$, $\langle 2, 0, 0 \rangle$, $\langle 2, 2, 2 \rangle$, $\langle 1, 2, 0 \rangle$, and $\langle 0, 1, 2 \rangle$. Here, the first three input vectors result in error (and thus their associated test cases are failing), and the last seven do not (and thus their associated test cases are passing).

A unit under test uut is a concrete artifact in a program which is a candidate for being at fault. Many types of uuts have been defined and used in the literature, including methods [24], blocks [25, 26], branches [16], and statements [27,28,29]. A uut is said to be covered by a test case just in case that test case executes the uut. For convenience, it will help to always think of uuts as being labeled C1, C2, ... etc. in the program itself (as they are in the running example). Assertion statements are not considered to be uuts, and we assume that each fault in the program has a corresponding uut.

Example 3

To illustrate some uuts for the running example (Fig. 1), we have chosen the units under test to be the statements labeled in comments marked C1, $\dots$, C5. The assertion is labeled E, which is violated when an error occurs. To illustrate a proband, the faulty program minmax.c (described in Example 1), and the test suite associated with the input vectors described in Example 2, together form a proband.

2.2 Proband Models

In this section we define proband models, which are the principle formal objects used in sbfl. Informally, a proband model is a mathematical abstraction of a proband. We assume the existence of a given proband in which the uuts have already been identified for the faulty program and appropriately labeled C1, ..., Cn, and assume a total of n uuts. We begin as follows.

Definition 1

A set of coverage vectors, denoted by $\mathbf {T}$, is a set $\{ t_{1},\ldots , t_{|\mathbf {T}|} \}$ in which each $t_k \in \mathbf {T}$ is a coverage vector defined $t_k = \langle c_1^k,\ldots , c_{n+1}^k,k \rangle$, where

• for all $0 < i \leqslant n$, $c_i^k = 1$ if the i-th uut is covered by the test case associated with $t_k$, and 0 otherwise.

• $c_{n+1}^k =$ 1 if the test case associated with $t_k$ fails and 0 if it passes.

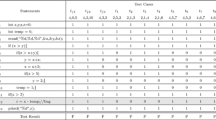
We also call a set of coverage vectors $\mathbf {T}$ the fault localisation data or a dataset. Intuitively, each coverage vector can be thought of as a mathematical abstraction of an associated test case which describes which uuts were executed/covered in that test case. We also use the following additional notation. If the last argument of a coverage vector in $\mathbf {T}$ is the number k it is denoted $t_k$ where k uniquely identifies a coverage vector in $\mathbf {T}$ and the corresponding test case in the associated test suite. In general, for each $t_k \in \mathbf {T}$, $c_i^k$ is a coverage variable and gives the value of the i-th argument in $t_k$. If $c_{n+1}^k = 1$, then $t_k$ is called a failing coverage vector, and passing otherwise. The set of failing coverage vectors/the event of an error is denoted E (such that the set of passing vectors is then $\overline{E}$). Element $c_{n+1}^k$ is also denoted $e^k$ (as it describes whether the error occurred). For convenience, we may represent the set of coverage vectors $\mathbf {T}$ with a coverage matrix, where for all $0 < i \leqslant n$ and $t_k \in \mathbf {T}$ the cell intersecting the i-th column and k-th row is $c_i^k$ and represents whether the i-th uut was covered in the test case corresponding to $t_k$. The cell intersecting the last column and k-th row is $e^k$ and represents whether $t_k$ is a failing or passing test case. Fig. 2 is an example coverage matrix. In practice, given a program and an input vector, one can extract coverage information from an associated test case using established tools².

Example 4

For the test suite given in Example 2 we can devise a set of coverage vectors $\mathbf {T} = \{t_1, \ldots , t_{10}\}$ in which $t_1 = \langle 1, 0, 1, 1,0, 1, 1 \rangle$, $t_2 = \langle 1, 0, 0, 1,1, 1, 2 \rangle$, $t_3 = \langle 1, 0, 0, 1,0, 1, 3 \rangle$, $t_4 = \langle 1, 1, 0, 0,0, 0, 4 \rangle$, $t_5 = \langle 1, 1, 0, 0,0, 0, 5 \rangle$, $t_6 = \langle 1, 0, 0, 0,1, 0, 6 \rangle$, $t_7 = \langle 1, 0, 0, 1,1, 0, 7 \rangle$, $t_8 = \langle 1, 0, 0, 0,0, 0, 8 \rangle$, $t_9 = \langle 1, 1, 0, 0,1, 0, 9 \rangle$, and $t_{10} = \langle 1, 1, 1, 0,0, 0, 10 \rangle$. Here, coverage vector $t_k$ is associated with the k-th input vector described in the list in Example 2. To illustrate how input and coverage vectors relate, we observe that $t_{10}$ is associated with a test case with input vector $\langle 0, 1, 2 \rangle$ which executes the statements labeled C1, C2 and C3, does not execute the statements labeled C4 and C5, and does not result in error. Consequently $c_1^{10} = c_2^{10} = c_3^{10} = 1$, and $c_4^{10} = c_5^{10} = e^{10} = 0$, and $k = 10$ such that $t_{10} = \langle 1, 1, 1, 0, 0, 0, 10 \rangle$ (by the definition of coverage vectors). The coverage matrix representing $\mathbf {T}$ is given in Fig. 2.

Definition 2

Let $\mathbf {T}$ be a non-empty set of coverage vectors, then $\mathbf {T}$’s program model $\mathbf {PM}$ is defined as the sequence $\langle C_1, \dots , C_{|\mathbf {PM}|} \rangle$, where for each $C_i \in \mathbf {PM}$, $C_i = \{t_k \in \mathbf {T}| c_i^k = 1\}$.

We often use the notation $\mathbf {{PM}}_{\mathbf {T}}$ to denote the program model $\mathbf {PM}$ associated with $\mathbf {T}$. The final component $C_{|\mathbf {PM}|}$ is also denoted E (denoting the event of the error). Each member of a program model is called a program component or event, and if $c_i^k = 1$ we say $C_i$ occurred in $t_k$, that $t_k$ covers $C_i$, and say that $C_i$ is faulty just in case its corresponding uut is faulty. Following the definition above, each component $C_i$ is the set of vectors in which $C_i$ is covered, and obey set theoretic relationships. For instance, for all components $C_i$, $C_j \in \mathbf {PM}$, we have $\forall t_k \in C_j.\, c_i^{k} = 1$ just in case $C_j \subseteq C_i$. In general, we assume that E contains at least one coverage vector and each coverage vector covers at least one component. Members of E and $\overline{E}$ are called failing/passing vectors, respectively.

Example 5

We use the running example to illustrate a program model. For the set of coverage vectors $\mathbf {T} = \{t_1, \dots , t_{10}\}$, we may define a program model $\mathbf {PM} = \langle C_1, C_2, C_3, C_4, C_5, E \rangle$, where $C_1 = \{t_1, \dots , t_{10}\}$, $C_2 = \{t_4, t_9, t_{10}\}$, $C_3 = \{t_1, t_{5}, t_{10}\}$, $C_4 = \{t_1, t_{2}, t_{3}, t_{7}\}$, $C_5 = \{t_2, t_{6}, t_{7}, t_{9}\}$, $E = \{t_1, t_2, t_3\}$. Here, we may think of $C_1, \dots , C_5$ as events which occur just in case a corresponding uut (lines of code labeled C1, $\dots$,C5 respectively) is executed, and E as an event which occurs just in case the assertion is violated. $C_4$ is identified as the faulty component.

Definition 3

For a given proband we define a proband model $\langle \mathbf {PM}, \mathbf {T}\rangle$, consisting of the given faulty program’s program model $\mathbf {PM}$, and an associated test suite’s set of coverage vectors $\mathbf {T}$.

Finally, we extend our setup to distinguish between samples and populations. The population test suite for a given program is a test suite consisting of all possible test cases for the program, a sample test suite is a test suite consisting of some (but not necessarily all) possible test cases for the program. All test suites are sample test suites drawn from a given population. Let $\langle \mathbf {PM}, \mathbf {T}\rangle$ be a given proband model for a given faulty program and sample test suite, we denote the population vectors, corresponding to the population test suite of the given faulty program, as $\mathbf {T}^*$ (and $E^*$ and $\overline{E}^*$ as the population failing and passing vectors in $\mathbf {T}^*$ respectively). The population program model associated with the population test suite is denoted $\mathbf {PM}^*$ (aka $\mathbf {PM}^*_{\mathbf {T}^*}$). $\langle \mathbf {PM}^*, \mathbf {T}^* \rangle$ is called the population proband model. Finally, we extend the use of asterisks to make clear that the asterisked variable is associated with a given population. Accordingly, each component in the population program model is also superscripted with a * to denote that it is a member of $\mathbf {PM}^*$ (e.g. $C_1^*$). Each vector in the population set of vectors $\mathbf {T}^*$ (e.g., $t_1^*$), and each coverage variable in each vector $t_k^* \in \mathbf {T}^*$ (e.g., $c_1^{k*}$).

It is assumed that for a given sample proband model $\langle \mathbf {PM}, \mathbf {T} \rangle$ and its population proband model $\langle \mathbf {PM}^*, \mathbf {T}^* \rangle$, we have $\mathbf {T} \subseteq \mathbf {T}^*$. Intuitively, this is because a sample test suite is drawn from the population. In addition, for each $i \in \mathbb {N}$ if $C_i \in \mathbf {{PM}}$ and $C_i^{*} \in \mathbf {PM}^*$, then $C_i \subseteq$ $C_i^{*}$. Intuitively, this is because if the i-th uut is executed by a test case in the sample then it is executed by that test case in the population.

2.3 Spectrum Based Fault Localisation

We first define what a program spectrum is, as it serves as the principle formal object used in spectrum based fault localization (sbfl).

Definition 4

For each proband model $\langle \mathbf {\textit{PM}}, \mathbf {T}\rangle$, and each component $C_i \in \mathbf {\textit{PM}}$, a component’s program spectrum is a vector $\langle |C_i \cap E|, |\overline{C_i} \cap E|, |C_i \cap \overline{E}|, |\overline{C_i} \cap \overline{E}| \rangle$.

Informally, $|C_i \cap E|$ is the number of failing coverage vectors in $\mathbf {T}$ that cover $C_i$, $|\overline{C_i} \cap E|$ is the number of failing coverage vectors in $\mathbf {T}$ that do not cover $C_i$, $|C_i \cap \overline{E}|$ is the number of passing coverage vectors in $\mathbf {T}$ that cover $C_i$, and $|\overline{C_i} \cap \overline{E}|$ is the number of passing coverage vectors in $\mathbf {T}$ that do not cover $C_i$. $|C_i \cap E|, |\overline{C_i} \cap E|, |C_i \cap \overline{E}|$ and $|\overline{C_i} \cap \overline{E}|$ are often denoted $a_{ef}^i$, $a_{nf}^i$, $a_{ep}^i$, and $a_{np}^i$ respectively in the literature [4, 7,8,9,10,11,12].

Example 6

For the proband model of the running example $\langle \mathbf {PM}, \mathbf {T} \rangle$ (where $\mathbf {PM} = \langle C_1, \dots , C_5, E \rangle$ and $\mathbf {T}$ is represented by the coverage matrix in Fig. 2), the spectra for $C_1$, ...$C_5$, and E are $\langle 3, 0, 7, 0 \rangle$, $\langle 0, 3, 3, 4 \rangle$, $\langle 1, 2, 2, 5 \rangle$, $\langle 3, 0, 1, 6 \rangle$, $\langle 1, 2, 3, 4 \rangle$, and $\langle 3, 0, 0, 7 \rangle$ respectively.

Following Naish et al. [7], we define a suspiciousness measure as follows.

Definition 5

A suspiciousness measure w is a function with signature $w : \mathbf {PM} \rightarrow \mathbb {R}$, and maps each $C_i \in \mathbf {PM}$ to a real number as a function of $C_i$’s program spectrum $\langle |C_i \cap E|, |\overline{C_i} \cap E|, |C_i \cap \overline{E}|, |\overline{C_i} \cap \overline{E}| \rangle$, where this number is called the component’s degree of suspiciousness.

The higher/lower the degree of suspiciousness the more/less suspicious $C_i$ is assumed to be with respect to being a fault. A property of some sbfl measures is single-fault optimality [7, 30]. Using our notation we can express this property as follows:

Definition 6

A suspiciousness measure w is single-fault optimal if it satisfies the following. For every program model $\mathbf {PM}$ and every $C_i \in \mathbf {PM}$:

• 1. If $E \not \subseteq C_i$ and $E \subseteq C_j$, then $w(C_j) > w(C_i)$ and

• 2. if $E \subseteq C_i$, $E \subseteq C_j$, $|{C_i} \cap \overline{E}| = k$ and $|{C_j} \cap \overline{E}| < k$, then $w(C_j) > w(C_i)$.

Under the assumption that there is a single fault in the program, Naish et al. argue that a measure must have this property to be optimal [7]. Informally, the first condition demands that uuts covered by all failing test cases are more suspicious than anything else. The rationale here is that if there is only one faulty uut in the program, then it must be executed by all failing test cases (otherwise there would be some failing test case which executes no fault – which is impossible given it is assumed that all errors are caused by the execution of some faulty uut) [7, 30]. The second demands that of two uuts covered by all failing test cases, the one which is executed by fewer passing test cases is more suspicious.

An example of a single fault optimal measure is the Naish-I measure $w(C_i) = a_{ef}^i - \frac{a_{ep}^i }{a_{ep}^i + a_{np}^i + 1}$ [31]. A framework that optimises any given sbfl measure to being single fault optimal was first given by Naish [31]. For any suspiciousness measure w scaled from 0 to 1, we can construct the single fault optimised version for w (written $Opt_w$) as follows (here, we use the equivalent formulation of Landsberg et al. [4]): $Opt_w(C_i) = a_{np}^i + 2$ if $a_{ef}^i = |E|$, and $w(C_i)$ otherwise.

We now describe the established sbfl algorithm [4, 7,8,9,10,11,12]. The method produces a list of program component indices ordered by suspiciousness, as a function of set of coverage vectors $\mathbf {T}$ (taken from a proband model $\langle \mathbf {PM}, \mathbf {T}\rangle$) and suspiciousness measure w. As the algorithm is simple, we informally describe the algorithm in three stages, as follows. First, the program spectrum for each program component is constructed as a function of $\mathbf {T}$. Second, the indices of program components are ordered in a suspiciousness list according to decreasing order of suspiciousness. Third, the suspiciousness list is returned to the user, who will inspect each uut corresponding to each index in the suspiciousness list in decreasing order of suspiciousness until a fault is found. We assume that in the case of ties of suspiciousness, the uut that comes earlier in the code is investigated first, and assume effectiveness of a sbfl measure on a proband is measured by the number of non-faulty uuts a user has to investigate before a fault is found.

Example 7

We illustrate an instance of sbfl using our running minmax.c example of Fig. 1, and the Naish-I measure as an example suspiciousness measure. First, the program spectra (given in Example 6) are constructed as a function of the given coverage vectors (represented by the coverage matrix of Fig. 2). Second, the suspiciousness of each program component is computed (here, the suspiciousness of the five components are 2.125, $-0.375$, 0.75, 2.875, 0.625 respectively), and the indices of components are ordered according to decreasing order of suspiciousness. Thus we get the list $\langle 4, 1, 3, 5, 2 \rangle$. Finally, the list is returned to the user, and the uuts in the program are inspected according to this list in descending order of suspiciousness until a fault is found. In our running example, C4 (the fault) is investigated first.

3 A Property of Single-Fault Optimal Data

In this section, we identify a new property for the optimality of a given dataset $\mathbf {T}$ for use in fault localisation. Throughout we make two assumptions: Firstly that a single bug optimal measure w is being used and secondly that there is a single bug in a given faulty program (henceforth our two assumptions). Let $\langle \mathbf {PM}, \mathbf {T} \rangle$ be a given sample proband model, then we have the following:

Definition 7

A Property of Single Fault Optimal Data. If $\mathbf {T}$ is single bug optimal, then $\forall C_i \in \mathbf {PM}_{\mathbf {T}}.$ $E \subseteq C_i \rightarrow E^* \subseteq C_i^*$.

If this condition holds, then we say the dataset $\mathbf {T}$ (and its associated test suite) satisfies this property of single fault optimality. Informally, the condition demands that if a uut is covered by all failing test cases in the sample test suite then it is covered by all failing test cases in the population. If our two assumptions hold, we argue it is a desirable that a test suite satisfies this property. This is because the fault is assumed to be covered by all failing test cases in the population (similar to the rationale of Naish et al. [7]), and as uuts executed by all failing test cases in the sample are investigated first when a single fault optimal measure is being used, it is desirable that uuts not covered by all failing test cases in the population are less suspicious in order to guarantee the fault is found earlier. An additional desirable feature of knowing one’s data satisfies this property, is that we do not have to add any more failing test cases to a test suite, given it is then impossible to improve fault localization effectiveness by adding more failing test cases under our two assumptions.

4 Algorithm

In this section we present an algorithm which outputs single fault optimal data for a given faulty program. We assume several preconditions for our algorithm.

• For the given faulty program, at least one uut is executed by all failing test cases (for C programs this could be a variable initialization in the main function).

• The population proband model is available (but as we shall see in the next section, practical implementations will not require this).

• We also assume that E is a mutable set, and shall make use of a $choose (X)$ subroutine which non-deterministically returns the set of a single a member of X (if one exists, otherwise it returns the empty set).

The algorithm is formally presented as Algorithm 1. We assume that an associated sample test suite will also be available as a by-product of the algorithm in addition to producing the data E. The intuition behind the algorithm is that failing vectors are iteratively accumulated in a set E one by one, where the next failing vector added does not cover some component which is covered by all vectors already in E (the algorithm terminates if no such vector exists). The resulting set is observed to be single-fault optimal. To illustrate the algorithm we give the example below. We then give a proof of partial correctness.

Example 8

We assume some population set of failing coverage vectors $E^*$, which we may identify with the set $\{t_1^*, t_2^*, t_3^*\} = \{ \langle 1, 0, 1, 1, 0, 1, 1 \rangle ,\langle 1, 0, 0, 1, 1, 1, 2 \rangle ,\langle 1, 0, 0, 1, 0, 1, 3 \rangle \}$ described in the coverage matrix of Fig. 2. In reality, the population set of failing coverage vectors for this faulty program is much larger than this, but this will suffice for our example. The algorithm proceeds as follows. First, we assume E is a non-empty subset of $E^*$, and thus may assume $E = \{ \langle 1, 0, 1, 1, 0, 1, 1 \rangle \}$. Now, to evaluate step 2, we first evaluate the set $\{ t_k^* \in E^* \,|\, \exists i \in \mathbb {N}. \forall t_j \in E. c_i^{j} = 1 \wedge c_i^{k*} = 0 \}$. Intuitively, this is the set of failing vectors in the population which do not cover some component which is covered by all vectors in E. We may find a member of this set as follows. First, we must evaluate the condition for when $E^* = \{t_1^*, t_2^*, t_3^*\}$. Given $c_3^{1} = 1$ holds of $t_1$, and $t_1$ is the only member of E, and given $c_3^{2*} = 0$, we have the conclusion that $t_2^*$ is a member of the set. Thus, for our example we may assume that $choose$ returns $t_2^*$ from this set such that $T = \{t_2^*\}$. So at step 3 the new version of E is $E = \{ \langle 1, 0, 1, 1, 0, 1, 1 \rangle ,\langle 1, 0, 0, 1, 1, 1, 2 \rangle \}$. Consequently, on the next iteration of the loop the set condition will be unsatisfiable – this is because there is no index to a component i such that both $\forall t_j \in E. c_i^{j} = 1$ holds (i.e., $E \subseteq C_i$), and also $c_i^{k*} = 0$ holds for some vector $t_k^*$ in the population (i.e., not $E^* \subseteq C_i$). Thus, $choose$ will return the empty set, and the algorithm will terminate returning the dataset E to the user to be used in sbfl. Using the Naish-I measure with this dataset, we have the result that C1 and C4 are associated with the largest suspicious score of 2.0. Thus, with single-fault optimal data alone we can find a fault C4 reasonably effectively in our running example.

Proposition 1

All datasets returned by Algorithm 1 are single-fault optimal.

Proof

We show partial correctness as follows. Let $\langle \mathbf {PM}^*, \mathbf {T}^* \rangle$ be a given population proband model, where $E^* \subseteq \mathbf {T}^*$ is the population set of failing vectors, and let E be returned by the algorithm. We must show that for all $C_i \in \mathbf {PM}_E$, $E \subseteq C_i \rightarrow E^* \subseteq C_i^*$ (by def. of single fault optimality). We prove this by contradiction. Assume there is some $C_i \in \mathbf {PM}_E$ (without loss of generality we may assume $i = 1$), such that $E \subseteq C_1$ but not $E^* \subseteq C_1^*$. Given we assume E has been returned by the algorithm, we may assume $T = \emptyset$ (step 4), and thus $choose$ returned $\emptyset$ at step 2 (by def. of $choose$). Accordingly, there is no $t_{k}^* \in E^*$ where $((\forall t_k \in E) c_1^{j} = 1) \wedge c_1^{k*} = 0$ (by the set condition at step 2). Thus, $(\forall t_k^* \in E^*)$ $((\forall t_j \in E) c_1^{j} = 1) \rightarrow c_1^{k*} = 1$. Now, ($(\forall t_j \in E)$ $c_1^{j} = 1$) just in case $E \subseteq C_1$ (by def. of program models). So, $(\forall t_k^* \in E^*)$, if $E \subseteq C_1$ then $c_1^{k*} = 1$ (by substitution of equivalents). Equivalently, if $E \subseteq C_1$ then $(\forall t_k^* \in E^*)$ $c_1^{k*} = 1$. Now, in general it holds that ($(\forall t_k^* \in E^*)$ $c_1^{k*} = 1$) just in case $E^* \subseteq C_1^*$ (by def. of program models). Thus $E \subseteq C_1 \rightarrow E^* \subseteq C_1^*$ (by substitution of equivalents). This contradicts the initial assumption.    $\square$

Finally, we informally observe that the maximum size of the E returned is the number of uuts. In this case E is input to the algorithm with a failing vector that covers all components, and $choose$ always returns a failing vector that covers 1 fewer uuts than the failing vector covering the fewest uuts already in E (noting that we assume at least one component will always be covered). The minimum is one. In this case E is input to the algorithm with a failing vector which covers some components and the post-condition is already fulfilled. In general, E can potentially be much smaller than $E^*$.

5 Implementation

We now discuss our implementation of the algorithm. In practice, we can leverage model checkers to compute members of $E^*$ (the population set of failing vectors) on the fly, where computing $E^*$ as a pre-condition would usually be intractable. This can be done by appeal to a SMT solving subroutine, which we describe as follows. Given a formal model of some code $F_{ code }$, a formal specification $\phi$, set of Booleans which are true just in case a corresponding uut is executed in a given execution $\{\mathtt{C1}, \dots , \mathtt{Cn}\}$, and a set $E \subseteq$ $E^*$, we can use a SMT solver to return a satisfying assignment by calling SMT($F_{ code }$ $\wedge$ $\lnot \phi$ $\wedge$ $\bigvee _{(\forall t_k \in E) c_i^{k} = 1} \texttt {Ci} = 0$), and then extracting a coverage vector from that assignment. A subroutine which returns this coverage vector (or the empty set if one does not exist) can act as a substitute for the $choose$ subroutine in Algorithm 1, and the generation of a static object $E^*$ is no longer required as an input to the algorithm. Our implementation of this is called $sfo$ (single fault optimal data generation tool).

We now discuss extensions of $sfo$. It is known that adding passing executions help in sbfl [4, 5, 7,8,9,10,11,12], thus to develop a more effective fault localisation procedure we developed a second implementation $sfo _p$ ($sfo$ with passing traces) that runs $sfo$ and then adds passing test cases. To do this, after running $sfo$ we call a SMT solver 20 times to find up to 20 new passing execution, where on each call if the vector found has new coverage properties (does not cover all the same uuts as some passing vector already computed) it is added to a set of passing vectors.

Our implementations of $sfo$ and $sfo _p$ are integrated into a branch of the model checker cbmc [32]. Our branch of the tool is available for download at the URL given in the footnote³. Our implementations, along with generating fault localisation data, rank uuts by degree of suspiciousness according to the Naish-I measure and report this fault localisation data to the user.

6 Experimentation

In this section we provide details of evaluation results for the use of $sfo$ and $sfo _p$ in fault localisation. The purpose of the experiment is to demonstrate that implementations of Algorithm 1 can be used to facilitate efficient and effective fault localisation in practice on small programs ($\le$2.5kloc). We think generation of fault localisation information in a few seconds ($\le$2) is sufficient to demonstrate practical efficiency, and ranking the fault in the top handful of the most suspicious lines of code ($\le$5) on average is sufficient to demonstrate practical effectiveness. In the remainder of this section we present our experimental setup (where we describe our scoring system and benchmarks), and our results.

6.1 Setup

For the purposes of comparison, we tested the fault localisation potential of $sfo$ and $sfo _p$ against a method named $1f$, which performes sbfl when only a single failing test case was generated by cbmc (and thus uuts covered by the test case were equally suspicious). We used the following scoring method to evaluate the effectiveness of each of the methods for each benchmark. We envisage an engineer who is inspecting each loc in descending order of suspiciousness using a given strategy (inspecting lines that appear earlier in the code first in the case of ties). We rank alternative techniques by the number of non-faulty loc that are investigated until the engineer finds a fault. Finally, we report the average of these scores for the benchmarks to give us an overall measure of fault localisation effectiveness.

We now discuss the benchmarks used in our experiments. In order to perform an unbiased experiment to test our techniques on, we imposed that our benchmarks needed to satisfy the following three properties (aside from being a C program which cbmc could be used on):

• 1. Programs must have been created by an independent source, to prevent any implicit bias caused by creating benchmarks ourselves.

• 2. Programs must have an explicit, formally stated specification that can be given as an assertion statement in order to apply a model checker.

• 3. In each program, the faulty code must be clearly identifiable, in order to be able to measure the quality of fault localisation.

Unfortunately, benchmarks satisfying these conditions are rare. In practice, benchmarks exist in verification research that satisfy either the second or third criterion, but rarely both. For instance, the available sir benchmarks satisfy the third criterion, but not the second⁴. The software verification competition (sv-comp) benchmarks satisfy the second criterion, but almost never satisfy the third⁵. Furthermore, it is often difficult to obtain benchmarks from authors even when usable benchmarks do in fact exist. Finally, we have been unable to find an instance of a C program that was not artificially developed for the purposes of testing.

The benchmarks are described in Table 1, where we give the benchmark name, the number of faults in the program, and lines of code (loc). The modified versions of tcas were made available by Alex Groce via personal correspondence and were used with the Explain tool in [33]⁶. The remaining benchmarks were identified as usable by manual investigation and testing in the repositories of sv-comp 2013 and 2017. We have made our benchmarks available for download directly from the link on footnote 4. Faults in sv-comp programs were identified by comparing them to an associated fault-free version (in tcas the fault was already identified). A series of continuous lines of code that differed from the fault free version (usually one line, and rarely up to 5 loc for larger programs) constituted one fault. loc were counted using the cloc utility.

We give further details about our application of cbmc in this experiment. For all our benchmarks, we used the smallest unwinding number that enables the bounded model checker to find a counterexample. These counterexamples were sliced, which usually results in a large improvement in fault localisation. For details about unwindings and slicing see the cbmc documentation [34]. In each benchmark each executable statement (variable initialisations, assignments, or condition statements) was determined as a uut.

6.2 Results and Discussion

In this section we discuss our experimental results. In Table 1, columns $1f$/$sfo _p$/$sfo$ give the scores for when the respective method is used. Column t gives the runtime for cbmc and $sfo _p$ respectively (we ignore the runtime for $sfo$ due to negligible difference). |E| and $|\overline{E}|$ give the number of failing and passing test cases generated by $sfo _p$. The AVG row gives averages column values. We are primarily interested in comparing the scores of $sfo _p$ and $1f$.

Table 1. Experimental results

We now discuss the results of the three techniques $1f$, $sfo$ and $sfo _p$. On average, $1f$ located a fault after investigating 17.23 lines of code (4.09% of the program on average). The results here are perhaps better than expected. We observed that the single failing test case consistently returned good fault localisation potential given the use of slicing by the technique.

We now discuss $sfo$. On average, $sfo$ located a fault after investigating 16 lines of code (3.8% of the program on average). Thus, the improvement over $1f$ is very small. When only one failing test case was available for $sfo$ (i.e. |E| = 1) we emphasise that the SMT solver could not find any other failing traces which covered different parts of the program. In such cases, $sfo$ performed the same as $1f$ (as expected). However, when there was more than one failing test case available (i.e. $|E| > 1$), $sfo$ always made a small improvement. Accordingly, for benchmarks 1, 2, 3, 5, 9, and 12 the improvements in terms fewer loc examined are 2, 6, 3, 1, 2, and 3, respectively. An improvement in benchmarks where $sfo$ generated more than one test case is to be expected, given there was always a fault covered by all failing test cases in each program (even in programs with multiple faults), thus taking advantage of the property of single fault optimal data. Finally, we conjecture that on programs with more failing test cases available in the population, and on longer faulty programs, that this improvement will be larger.

We now discuss $sfo _p$. On average, $sfo _p$ located a fault after investigating 4.08 loc (0.97% of each program on average). Thus, the improvement over the other techniques is quite large (four times as effective as $1f$). Moreover, this effectiveness came at very little expense to runtime – $sfo _p$ had an average runtime of 1.06 s, which is comparable to the runtime of $1f$ of 0.78 s. This is despite the fact that $sfo _p$ generated over 7 executions on average. We consequently conclude that implementations of Algorithm 1 can be used to facilitate efficient and effective fault localisation in practice on small programs.

7 Related Work

The techniques discussed in this paper improve the quality of data usable for sbfl. We divide the research in this field into the following areas; many other methods can be potentially combined with our technique.

Test Suite Expansion. One approach to improving test suites is to add more test cases which satisfy a given criterion. A prominent criterion is that the test suite has sufficient program coverage, where studies suggest that test suites with high coverage improve fault localisation [15,16,17, 20]. Other ways to improve test suites for sbfl are as follows. Li et al. generate test suites for sbfl, considering failing to passing test case ratio to be more important than number [35]. Zhang et al. consider cloning failed test cases to improve sbfl [13]. Perez et al. develop a metric for diagnosing whether a test suite is of sufficient quality for sbfl to take place [14]. Li et al. consider weighing different test cases differently [36]. Aside from coverage criteria, methods have been studied which generate test cases with a minimal distance from a given failed test case [18]. Baudry et al. use a bacteriological approach in order to generate test suites that simultaneously facilitate both testing and fault localisation [19]. Concolic execution methods have been developed to add test cases to a test suite based on their similarity to an initial failing run [20].

Prominent approaches which leverage model checkers for fault localisation are as follows. Groce [33] uses integer linear programming to find a passing test case most similar to a failing one and then compare the difference. Schupman and Bierre [37] generate short counterexamples for use in fault localisation, where a short counterexample will usually mean fewer uuts for the user to inspect. Griesmayer [38] and Birch et al. [39] use model checkers to find failing executions and then look for whether a given number of changes to values of variables can be made to make the counterexample disappear. Gopinath et al. [40] compute minimal unsatisfiable cores in a given failing test case, where statements in the core will be given a higher suspiciousness level in the spectra ranking. Additionally, when generating a new test, they generate an input whose test case is most similar to the initial run in terms of its coverage of the statements. Fey et al. [41] use SAT solvers to localise faults on hardware with LTL specifications. In general, experimental scale is limited to a small number of programs in these studies, and we think our experimental component provides an improvement in terms of experimental scale (13 programs).

Test Suite Reduction. An alternative approach to expanding a test suite is to use reduction methods. Recently, many approaches have demonstrated that it is not necessary for all test cases in a test suite to be used. Rather, one can select a handful of test cases in order to minimise the number of test cases required for fault localisation [42, 43]. Most approaches are based on a strategy of eliminating redundant test cases relative to some coverage criterion. The effectiveness of applying various coverage criteria in test suite reduction is traditionally based on empirical comparison of two metrics: one which measures the size of the reduction, and the other which measures how much fault detection is preserved.

Slicing. A prominent approach to improving the quality of test suites involves the process of slicing test cases. Here, sbfl proceeds as usual except the program and/or the test cases composing the test suite are sliced (with irrelevant lines of code/parts of the execution removed). For example, Alves et al. [44] combine Tarantula along with dynamic slices, Ju et al. [45] use sbfl in combination with both dynamic and execution slices. Syntactic dynamic slicing is built-in in all our tested approaches by appeal to the functionalities of cbmc.

To our knowledge, no previous methods generate data which exhibit our property of single fault optimality.

8 Conclusion

In this paper, we have presented a method to generate single fault optimal data for use with sbfl. Experimental results on our implementation $sfo _p$, which integrates single fault optimal data along with passing test cases, demonstrate that small optimized fault localisation data can be generated efficiently in practice (1.06 s on average), and that subsequent fault localization can be performed effectively using this data (investigating 4.06 loc until a fault is found). We envisage that implementations of the algorithm can be used in two different scenarios. In the first, the test suite generated can be used in standalone fault localisation, providing a small and low cost test suite useful for repeating iterations of simultaneous testing and fault localisation during program development. In the second, the data generated can be added to any pre-existing data associated with a test suite, which may be useful at the final testing stage where we may wish to optimise single fault localisation.

Future work involves finding larger benchmarks to use our implementation on and developing further properties, and methods for use with programs with multiple faults. We would also like to combine our technique with existing test suite generation algorithms in order to experiment how much test suites can be additionally improved for the purposes of fault localization.