Abstract
In 2011, Danicic et al. introduced an elegant generalization of the notion of control dependence for any directed graph. They also proposed an algorithm computing the weak control-closure of a subset of graph vertices and performed a paper-and-pencil proof of its correctness. We have performed its proof in the Coq proof assistant. This paper also presents a novel, more efficient algorithm to compute weak control-closure taking benefit of intermediate propagation results of previous iterations in order to accelerate the following ones. This optimization makes the design and proof of the algorithm more complex and requires subtle loop invariants. The new algorithm has been formalized and mechanically proven in the Why3 verification tool. Experiments on arbitrary generated graphs with up to thousands of vertices demonstrate that the proposed algorithm remains practical for real-life programs and significantly outperforms Danicic’s initial technique.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Context. Control dependence is a fundamental notion in software engineering and analysis (e.g. [6, 12, 13, 21, 22, 27]). It reflects structural relationships between different program statements and is intensively used in many software analysis techniques and tools, such as compilers, verification tools, test generators, program transformation tools, simulators, debuggers, etc. Along with data dependence, it is one of the key notions used in program slicing [25, 27], a program transformation technique allowing to decompose a given program into a simpler one, called a program slice.
In 2011, Danicic et al. [11] proposed an elegant generalization of the notions of closure under non-termination insensitive (weak) and non-termination sensitive (strong) control dependence. They introduced the notions of weak and strong control-closures, that can be defined on any directed graph, and no longer only on control flow graphs. They proved that weak and strong control-closures subsume the closures under all forms of control dependence previously known in the literature. In the present paper, we are interested in the non-termination insensitive form, i.e. weak control-closure.
Besides the definition of weak control-closure, Danicic et al. also provided an algorithm computing it for a given set of vertices in a directed graph. This algorithm was proved by paper-and-pencil. Under the assumption that the given graph is a CFG (or more generally, that the maximal out-degree of the graph vertices is bounded), the complexity of the algorithm can be expressed in terms of the number of vertices n of the graph, and was shown to be \(O(n^3)\). Danicic et al. themselves suggested that it should be possible to improve its complexity. This may explain why this algorithm was not used until now.
Motivation. Danicic et al. introduced basic notions used to define weak control-closure and to justify the algorithm, and proved a few lemmas about them. While formalizing these concepts in the Coq proof assistant [5, 24], we have discovered that, strictly speaking, the paper-and-pencil proof of one of them [11, Lemma 53] is inaccurate (a previously proven case is applied while its hypotheses are not satisfied), whereas the lemma itself is correct. Furthermore, Danicic’s algorithm does not take advantage of its iterative nature and does not reuse the results of previous iterations in order to speed up the following ones.
Goals. First, we fully formalize Danicic’s algorithm, its correctness proof and the underlying concepts in Coq. Our second objective is to design a more efficient algorithm sharing information between iterations to speed up the execution. Since our new algorithm is carefully optimized and more complex, its correctness proof relies on more subtle arguments than for Danicic’s algorithm. To deal with them and to avoid any risk of error, we have decided again to use a mechanized verification tool – this time, the Why3 proof system [1, 14] – to guarantee correctness of the optimized version. Finally, in order to evaluate the new algorithm with respect to Danicic’s initial technique, we have implemented both algorithms in OCaml (using OCamlgraph library [9]) and tested them on a large set of randomly generated graphs with up to thousands of vertices. Experiments demonstrate that the proposed optimized algorithm is applicable to large graphs (and thus to CFGs of real-life programs) and significantly outperforms Danicic’s original technique.
Contributions. The contributions of this paper include:
-
A formalization of Danicic’s algorithm and proof of its correctness in Coq;
-
A new algorithm computing weak control-closure and taking benefit from preserving some intermediary results between iterations;
-
A mechanized correctness proof of this new algorithm in the Why3 tool including a formalization of the basic concepts and results of Danicic et al.;
-
An implementation of Danicic’s and our algorithms in OCaml, their evaluation on random graphs and a comparison of their execution times.
The Coq, Why3 and OCaml implementations are all available in [17].
Outline. We present our motivation and a running example in Sect. 2. Then, we recall the definitions of some important concepts introduced by [11] in Sect. 3 and state two important lemmas in Sect. 4. Next, we describe Danicic’s algorithm in Sect. 5 and our algorithm along with a sketch of the proof of its correctness in Sect. 6. Experiments are presented in Sect. 7. Finally, Sect. 8 presents some related work and concludes.
2 Motivation and Running Example
This section informally presents weak control-closure using a running example.
The inputs of our problem are a directed graph \(G = (V, E)\) with set of vertices (or nodes) V and set of edges E, and a subset of vertices \(V' \subseteq V\). The property of interest of such a subset is called weakly control-closed in [11] (cf. Definition 3). \(V'\) is said to be weakly control-closed if the nodes reachable from \(V'\) are \(V'\)-weakly committing (cf. Definition 2), i.e. always lead the flow to at most one node in \(V'\). Since \(V'\) does not necessarily satisfy this property, we want to build a superset of \(V'\) satisfying it, and more particularly the smallest one, called the weak control-closure of \(V'\) in G (cf. Definition 5). For that, as it will be proved by Lemma 2, we need to add to \(V'\) the points of divergence closest to \(V'\), called the \(V'\)-weakly deciding vertices, that are reachable from \(V'\). Formally, vertex u is \(V'\)-weakly deciding if there exist two non-trivial paths starting from u and reaching \(V'\) that have no common vertex except u (cf. Definition 4).
Let us illustrate these ideas on an example graph \(G_0\) shown in Fig. 1. \(V'_0 = \{ u_1, u_3 \}\) is the subset of interest represented with dashed double circles ( ) in Fig. 1. \(u_5\) is reachable from \(V'_0\) and is not \(V'_0\)-weakly committing, since it is the origin of two paths \(u_5, u_6, u_0, u_1\) and \(u_5, u_6, u_0, u_2, u_3\) that can lead the flow to two different nodes \(u_1\) and \(u_3\) in \(V'_0\). Therefore, \(V'_0\) is not weakly control-closed. To build the weak control-closure, we need to add to \(V'_0\) all \(V'_0\)-weakly deciding nodes reachable from \(V'_0\). \(u_0\) is such a node. Indeed, it is reachable from \(V'_0\) and we can build two non-trivial paths \(u_0, u_1\) and \(u_0, u_2, u_3\) starting from \(u_0\), ending in \(V'_0\) (respectively in \(u_1\) and \(u_3\)) and sharing no other vertex than \(u_0\). Similarly, nodes \(u_2\), \(u_4\) and \(u_6\) must be added as well. On the contrary, \(u_5\) must not be added, since every non-empty path starting from \(u_5\) has \(u_6\) as second vertex. More generally, a node with only one child cannot be a “divergence point closest to \(V'\)” and must never be added to build the weak control-closure. The weak control-closure of \(V'_0\) in \(G_0\) is thus \(\{ u_0, u_1, u_2, u_3, u_4, u_6\}\).
) in Fig. 1. \(u_5\) is reachable from \(V'_0\) and is not \(V'_0\)-weakly committing, since it is the origin of two paths \(u_5, u_6, u_0, u_1\) and \(u_5, u_6, u_0, u_2, u_3\) that can lead the flow to two different nodes \(u_1\) and \(u_3\) in \(V'_0\). Therefore, \(V'_0\) is not weakly control-closed. To build the weak control-closure, we need to add to \(V'_0\) all \(V'_0\)-weakly deciding nodes reachable from \(V'_0\). \(u_0\) is such a node. Indeed, it is reachable from \(V'_0\) and we can build two non-trivial paths \(u_0, u_1\) and \(u_0, u_2, u_3\) starting from \(u_0\), ending in \(V'_0\) (respectively in \(u_1\) and \(u_3\)) and sharing no other vertex than \(u_0\). Similarly, nodes \(u_2\), \(u_4\) and \(u_6\) must be added as well. On the contrary, \(u_5\) must not be added, since every non-empty path starting from \(u_5\) has \(u_6\) as second vertex. More generally, a node with only one child cannot be a “divergence point closest to \(V'\)” and must never be added to build the weak control-closure. The weak control-closure of \(V'_0\) in \(G_0\) is thus \(\{ u_0, u_1, u_2, u_3, u_4, u_6\}\).
To build the closure, Danicic’s algorithm, like the one we propose, does not directly try to build the two paths sharing only one node. Both algorithms rely on a concept called observable vertex. Given a vertex \(u \in V\), the set of observable vertices in \(V'\) from u contains all nodes reachable from u in \(V'\) without using edges starting in \(V'\). The important property about this object is that, as it will be proved by Lemma 4, if there exists an edge \((u, v) \in E\) such that u is not in \(V'\), u is reachable from \(V'\), v can reach \(V'\) and there exists a vertex w observable from u but not from v, then u must be added to \(V'\) to build the weak control-closure. Figure 2a shows our example graph \(G_0\), each node being annotated with its set of observables in \(V'_0\).
\((u_0, u_1)\) is an edge such that \(u_0\) is reachable from \(V'_0\), \(u_1\) can reach \(V'_0\) and \(u_3\) is an observable vertex from \(u_0\) in \(V'_0\) but not from \(u_1\). \(u_0\) is thus a node to be added in the weak control-closure. Likewise, from the edges \((u_2, u_3)\) and \((u_4, u_3)\), we can deduce that \(u_2\) and \(u_4\) belong to the closure. However, we have seen that \(u_6\) belongs to the closure, but it is not possible to apply the same reasoning to \((u_6, u_0)\), \((u_6, u_4)\) or \((u_6, u_5)\). We need another technique. As Lemma 3 will establish, the technique is actually iterative. We can add to the initial \(V'_0\) the nodes that we have already detected and apply our technique to this new set \(V''_0\). The vertices that will be detected this way will also be in the closure of the initial set \(V'_0\). The observable sets w.r.t. to \(V''_0 = V'_0 \cup \{ u_0, u_2, u_4 \}\) are shown in Fig. 2b. This time, both edges \((u_6, u_4)\) and \((u_6, u_0)\) allow us to add \(u_6\) to the closure. Applying again the technique with the augmented set \(V'''_0 = V''_0 \cup \{ u_6 \}\) (cf. Fig. 2c) does not reveal new vertices. This means that all the nodes have already been found. We obtain the same set as before for the weak control-closure of \(V'_0\), i.e. \(\{ u_0, u_1, u_2, u_3, u_4, u_6\}\).
3 Basic Concepts
This section introduces basic definitions and properties needed to define the notion of weak control-closure. They have been formalized in Coq [17], including in particular Property 3 whose proof in [11] was inaccurate.
From now on, let \(G = (V, E)\) denote a directed graph, and \(V'\) a subset of V. We define a path in G in the usual way. We write \(u \xrightarrow {path} v\) if there exists a path from u to v. Let  be the set of nodes reachable from \(V'\). In our example (cf. Fig. 1), \(u_6, u_0, u_1, u_3\) is a (4-node) path in \(G_0\), \(u_1\) is a trivial one-node path in \(G_0\) from \(u_1\) to itself, and
be the set of nodes reachable from \(V'\). In our example (cf. Fig. 1), \(u_6, u_0, u_1, u_3\) is a (4-node) path in \(G_0\), \(u_1\) is a trivial one-node path in \(G_0\) from \(u_1\) to itself, and  .
.
Definition 1
(\(V'\)-disjoint, \(V'\)-path). A path \(\pi \) in G is said to be \(V'\)-disjoint in G if all the vertices in \(\pi \) but the last one are not in \(V'\). A \(V'\)-path in G is a \(V'\)-disjoint path whose last vertex is in \(V'\). In particular, if \(u \in V'\), the only \(V'\)-path starting from u is the trivial path u.
We write \(u \xrightarrow {V'-disjoint} v\) (resp. \(u \xrightarrow {V'-path} v\)) if there exists a \(V'\)-disjoint path (resp. a \(V'\)-path) from u to v.
Example
In \(G_0\), \(u_3\); \(u_2,u_3\); \(u_0,u_1\); \(u_0,u_2,u_3\) are \(V'_0\)-paths and thus \(V'_0\)-disjoint paths. \(u_6,u_0\) is a \(V'_0\)-disjoint path but not a \(V'_0\)-path.
Remark 1
Definition 1 and the following ones are slightly different from [11], where a \(V'\)-path must contain at least two vertices and there is no constraint on its first vertex, which can be in \(V'\) or not. Our definitions lead to the same notion of weak control-closure.
Definition 2
(\(V'\)-weakly committing vertex). A vertex u in G is \(V'\)-weakly committing if all the \(V'\)-paths from u have the same end point (in \(V'\)). In particular, any vertex \(u \in V'\) is \(V'\)-weakly committing.
Example
In \(G_0\), \(u_1\) and \(u_3\) are the only \(V'_0\)-weakly committing nodes.
Definition 3
(Weakly control-closed set). A subset \(V'\) of V is weakly control-closed in G if every vertex reachable from \(V'\) is \(V'\)-weakly committing.
Example
Since in particular \(u_2\) is not \(V'_0\)-weakly committing and reachable from \(V'_0\), \(V'_0\) is not weakly control-closed in \(G_0\). \(\varnothing \), singletons and the set of all nodes \(V_0\) are trivially weakly control-closed. Less trivial weakly control-closed sets include \(\{u_0,u_1\}\), \(\{u_4,u_5,u_6\}\) and \(\{u_0,u_1,u_2,u_3,u_4,u_6\}\).
Definition 3 characterizes a weakly control-closed set, but does not explain how to build one. It would be particularly interesting to build the smallest weakly control-closed set containing a given set \(V'\). The notion of weakly deciding vertex will help us to give an explicit expression to that set.
Definition 4
(\(V'\)-weakly deciding vertex). A vertex u is \(V'\)-weakly deciding if there exist at least two non-trivial \(V'\)-paths from u that share no vertex except u. Let  denote the set of \(V'\)-weakly deciding vertices in G.
denote the set of \(V'\)-weakly deciding vertices in G.
Property 1
If \(u \in V'\), then  (by Definitions 1, 4).
(by Definitions 1, 4).
Example
In \(G_0\), by Property 1,  . We have illustrated the definition for nodes \(u_0\) and \(u_5\) in Sect. 2. We have
. We have illustrated the definition for nodes \(u_0\) and \(u_5\) in Sect. 2. We have  .
.
Lemma 1
(Characterization of being weakly control-closed).\(V'\) is weakly control-closed in G if and only if there is no \(V'\)-weakly deciding vertex in G reachable from \(V'\).
Example
In \(G_0\), \(u_2\) is reachable from \(V'_0\) and is \(V'_0\)-weakly deciding. This gives another proof that \(V'_0\) is not weakly control-closed.
Here are two other useful properties of  .
.
Property 2

Property 3
 .
.
We can prove that adding to a given set \(V'\) the \(V'\)-weakly deciding nodes that are reachable from \(V'\) gives a weakly control-closed set in G. This set is the smallest superset of \(V'\) weakly control-closed in G.
Lemma 2
(Existence of the weak control-closure). Let  denote the set of vertices in
denote the set of vertices in  that are reachable from \(V'\). Then \(V' \cup W\) is the smallest weakly control-closed set containing \(V'\).
that are reachable from \(V'\). Then \(V' \cup W\) is the smallest weakly control-closed set containing \(V'\).
Definition 5
(Weak control-closure). We call weak control-closure of \(V'\), denoted  , the smallest weakly control-closed set containing \(V'\).
, the smallest weakly control-closed set containing \(V'\).
Property 4
Let \(V'\), \(V'_1\) and \(V'_2\) be subsets of V. Then
-
(a)
 .
. -
(b)
If \(V'_1 \subseteq V'_2\), then
 .
. -
(c)
If \(V'\) is weakly control-closed, then
 .
. -
(d)
 .
.
4 Main Lemmas
This section gives two lemmas used to justify both Danicic’s algorithm and ours.
Lemma 3
Let \(V'\) and W be two subsets of V. If  . If moreover
. If moreover  , then
, then  .
.
Proof
Assume  . Since \(V' \subseteq W\), we have by Property 2,
. Since \(V' \subseteq W\), we have by Property 2,  . Moreover,
. Moreover,  by Property 2, hence
by Property 2, hence  by Property 3. These inclusions imply
by Property 3. These inclusions imply  .
.
If now  , we deduce
, we deduce  from the previous result by intersecting with
from the previous result by intersecting with  by Property 4a. \(\square \)
by Property 4a. \(\square \)
Lemma 3 allows to design iterative algorithms to compute the closure. Indeed, assume that we have a procedure which, for any non-weakly control-closed set \(V'\), can return one or more elements of the weak control-closure of \(V'\) not in \(V'\). If we apply such a procedure to \(V'\) once, we get a set W that satisfies  . From Lemma 3,
. From Lemma 3,  . To compute the weak control-closure of \(V'\), it is thus sufficient to build the weak control-closure of W. We can apply our procedure again, this time to W, and repetitively on all the successively computed sets. Since each set is a strict superset of the previous one, this iterative procedure terminates because graph G is finite.
. To compute the weak control-closure of \(V'\), it is thus sufficient to build the weak control-closure of W. We can apply our procedure again, this time to W, and repetitively on all the successively computed sets. Since each set is a strict superset of the previous one, this iterative procedure terminates because graph G is finite.
Before stating the second lemma, we introduce a key concept. It is called \(\varTheta \) in [11]. We use the name “observable” as in [26].
Definition 6
(Observable). Let \(u \in V\). The set of observable vertices from u in \(V'\), denoted  , is the set of vertices \(u'\) in \(V'\) such that \(u \xrightarrow {V'-path} u'\).
, is the set of vertices \(u'\) in \(V'\) such that \(u \xrightarrow {V'-path} u'\).
Remark 2
A vertex \(u \in V'\) is its unique observable:  .
.
The concept of observable set was illustrated in Fig. 2 (cf. Sect. 2).
Lemma 4
(Sufficient condition for being \(V'\)-weakly deciding). Let (u, v) be an edge in G such that \(u \not \in V'\), v can reach \(V'\) and there exists a vertex \(u'\) in \(V'\) such that  and
and  . Then
. Then  .
.
Proof
We need to exhibit two \(V'\)-paths from u ending in \(V'\) that share no vertex except u. We take the \(V'\)-path from u to \(u'\) as the first one, and a \(V'\)-path connecting u to \(V'\) through v as the second one (we construct it by prepending u to the smallest prefix of the path from v ending in \(V'\) which is a \(V'\)-path). If these \(V'\)-paths intersected at a node y different from u, we would have a \(V'\)-path from v to \(u'\) by concatenating the paths from v to y and from y to \(u'\), which is contradictory. \(\square \)
Example
In \(G_0\),  and
and  (cf. Fig. 2a). Since \(u_1\) is a child of \(u_0\), we can apply Lemma 4, and deduce that \(u_0\) is \(V'_0\)-weakly deciding.
(cf. Fig. 2a). Since \(u_1\) is a child of \(u_0\), we can apply Lemma 4, and deduce that \(u_0\) is \(V'_0\)-weakly deciding.  and
and  . We cannot apply Lemma 4 to \(u_5\), and for good reason, since \(u_5\) is not \(V'_0\)-weakly deciding. But we cannot apply Lemma 4 to \(u_6\) either, since \(u_6\) and all its children \(u_0\), \(u_4\) and \(u_5\) have observable sets \(\{ u_1, u_3 \}\) w.r.t. \(V'_0\), while \(u_6\) is \(V'_0\)-weakly deciding. This shows that with Lemma 4, we have a sufficient condition, but not a necessary one, for proving that a vertex is weakly deciding.
. We cannot apply Lemma 4 to \(u_5\), and for good reason, since \(u_5\) is not \(V'_0\)-weakly deciding. But we cannot apply Lemma 4 to \(u_6\) either, since \(u_6\) and all its children \(u_0\), \(u_4\) and \(u_5\) have observable sets \(\{ u_1, u_3 \}\) w.r.t. \(V'_0\), while \(u_6\) is \(V'_0\)-weakly deciding. This shows that with Lemma 4, we have a sufficient condition, but not a necessary one, for proving that a vertex is weakly deciding.
Example
Let us apply Algorithm 1 to our running example \(G_0\) (cf. Fig. 1). Initially, \(W_0 = V'_0 = \{ u_1, u_3\}\).
-
1.
 , therefore \((u_0, u_1)\) is a \(W_0\)-critical edge. Set \(W_1 = \{ u_0, u_1, u_3 \}\).
, therefore \((u_0, u_1)\) is a \(W_0\)-critical edge. Set \(W_1 = \{ u_0, u_1, u_3 \}\). -
2.
 and
and  , therefore \((u_2, u_3)\) is a \(W_1\)-critical edge. Set \(W_2 = \{ u_0, u_1, u_2, u_3 \}\).
, therefore \((u_2, u_3)\) is a \(W_1\)-critical edge. Set \(W_2 = \{ u_0, u_1, u_2, u_3 \}\). -
3.
 and
and  , therefore \((u_4, u_3)\) is a \(W_2\)-critical edge. Set \(W_3 = \{ u_0, u_1, u_2, u_3, u_4 \}\).
, therefore \((u_4, u_3)\) is a \(W_2\)-critical edge. Set \(W_3 = \{ u_0, u_1, u_2, u_3, u_4 \}\). -
4.
 and
and  , therefore \((u_6, u_0)\) is a \(W_3\)-critical edge. Set \(W_4 = \{ u_0, u_1, u_2, u_3, u_4, u_6 \}\).
, therefore \((u_6, u_0)\) is a \(W_3\)-critical edge. Set \(W_4 = \{ u_0, u_1, u_2, u_3, u_4, u_6 \}\). -
5.
There is no \(W_4\)-critical edge.
 .
.

5 Danicic’s Algorithm
We present here the algorithm described in [11]. This algorithm and a proof of its correctness have been formalized in Coq [17]. The algorithm is nearly completely justified by a following lemma (Lemma 5, equivalent to [11, Lemma 60]).
We first need to introduce a new concept, which captures edges that are of particular interest when searching for weakly deciding vertices. This concept is taken from [11], where it was not given a name. We call such edges critical edges.
Definition 7
(Critical edge). An edge (u, v) in G is called \(V'\)-critical if:
-
(1)
 ;
; -
(2)
 ;
; -
(3)
u is reachable from \(V'\) in G.
Example
In \(G_0\), \((u_0, u_1)\), \((u_2,u_3)\) and \((u_4, u_3)\) are the \(V'_0\)-critical edges.
Lemma 5
If \(V'\) is not weakly control-closed in G, then there exists a \(V'\)-critical edge (u, v) in G. Moreover, if (u, v) is such a \(V'\)-critical edge, then  , therefore
, therefore  .
.
Proof
Let x be a vertex in  reachable from \(V'\). There exists a \(V'\)-path \(\pi \) from x ending in \(x' \in V'\). It follows that
reachable from \(V'\). There exists a \(V'\)-path \(\pi \) from x ending in \(x' \in V'\). It follows that  and
and  . Let u be the last vertex on \(\pi \) with at least two observable nodes in \(V'\) and v its successor on \(\pi \). Then (u, v) is a \(V'\)-critical edge.
. Let u be the last vertex on \(\pi \) with at least two observable nodes in \(V'\) and v its successor on \(\pi \). Then (u, v) is a \(V'\)-critical edge.
Assume there exists a \(V'\)-critical edge (u, v). Since  and
and  , \(u \not \in V'\), v can reach \(V'\) and there exists \(u'\) in
, \(u \not \in V'\), v can reach \(V'\) and there exists \(u'\) in  but not in
but not in  . By Lemma 4,
. By Lemma 4,  and thus
and thus  . \(\square \)
. \(\square \)
Remark 3
We can see in the proof above that we do not need the exact values 2 and 1. We just need strictly more observable vertices for u than for v and at least one observable for v, to satisfy the hypotheses of Lemma 4.
As described in Sect. 4, we can build an iterative algorithm constructing the weak control-closure of \(V'\) by searching for critical edges on the intermediate sets built successively. This is the idea of Danicic’s algorithm shown as Algorithm 1.
Proof of Algorithm 1. To establish the correction of the algorithm, we can prove that \(W_i\), the value of W before iteration \({i+1}\), satisfies both \(V' \subseteq W_i\) and  for any i by induction. If \(i = 0\), \(W_0 = V'\), and both relations trivially hold. Let i be a natural number such that \(V' \subseteq W_i\),
for any i by induction. If \(i = 0\), \(W_0 = V'\), and both relations trivially hold. Let i be a natural number such that \(V' \subseteq W_i\),  and there exists a \(W_i\)-critical edge (u, v). We have \(W_{i+1} = W_i \cup \{ u \}\). \(V' \subseteq W_{i+1}\) is straightforward. By Lemma 5,
and there exists a \(W_i\)-critical edge (u, v). We have \(W_{i+1} = W_i \cup \{ u \}\). \(V' \subseteq W_{i+1}\) is straightforward. By Lemma 5,  . Therefore, by Lemma 3,
. Therefore, by Lemma 3,  , and thus,
, and thus,  . At the end of the algorithm, there is no W-critical edge, therefore W is weakly control-closed by Lemma 5. Since \(V' \subseteq W\) and
. At the end of the algorithm, there is no W-critical edge, therefore W is weakly control-closed by Lemma 5. Since \(V' \subseteq W\) and  ,
,  by Lemma 3. Termination follows from the fact that W strictly increases in the loop and is upper-bounded by
by Lemma 3. Termination follows from the fact that W strictly increases in the loop and is upper-bounded by  . \(\square \)
. \(\square \)
In terms of complexity, [11] shows that, assuming that the degree of each vertex is at most 2 (and thus that \(O(|V|) = O(|E|)\)), the complexity of the algorithm is \(O(|V|^3)\). Indeed, the main loop of Algorithm 1 is run at most O(|V|) times, and each loop body computes  in O(|V|) for at most O(|V|) edges.
in O(|V|) for at most O(|V|) edges.
Remark 4
We propose two optimizations for Algorithm 1:
-
at each step, consider all critical edges rather than only one;
-
use the weaker definition of critical edge suggested in Remark 3.
Example
We can replay Algorithm 1 using the first optimization. This run corresponds to the steps shown in Fig. 2. Initially, \(W_0 = V'_0 = \{ u_1, u_3 \}\).
-
1.
\((u_0, u_1)\), \((u_2, u_3)\), \((u_4, u_3)\) are \(W_0\)-critical edges. Set \(W_1 = \{ u_0, u_1, u_2, u_3, u_4 \}\).
-
2.
\((u_6, u_0)\) is a \(W_1\)-critical edge. Set \(W_2 = \{ u_0, u_1, u_2, u_3, u_4, u_6\}\).
-
3.
There is no \(W_2\)-critical edge in \(G_0\).
The optimized version computes the weak control-closure of \(V'_0\) in \(G_0\) in only 2 iterations instead of 4. This run also demonstrates that the algorithm is necessarily iterative: even when considering all \(V'_0\)-critical edges in the first step, \(u_6\) is not detected before the second step.
6 The Optimized Algorithm
Overview. A potential source of inefficiency in Danicic’s algorithm is the fact that no information is shared between the iterations. The observable sets are recomputed at each iteration since the target set changes. This is the reason why the first optimization proposed in Remark 4 is interesting, because it allows to work longer on the same set and thus to reuse the observable sets.
We propose now to go even further: to store some information about the paths in the graph and reuse it in the following iterations. The main idea of the proposed algorithm is to label each processed node u with a node \(v\in W\) observable from u in the resulting set W being progressively constructed by the algorithm. Labels survive through iterations and can be reused.
Unlike Danicic’s algorithm, ours does not directly compute the weak control-closure. It actually computes the set  . To obtain the closure
. To obtain the closure  , W is then simply filtered to keep only vertices reachable from \(V'\) (cf. Property 4a).
, W is then simply filtered to keep only vertices reachable from \(V'\) (cf. Property 4a).
In addition to speeding up the algorithm, the usage of labels brings another benefit: for each node of G, its label indicates its observable vertex in W (when it exists) at the end of the algorithm. Recall that since  (by Property 3), each node in the graph has at most one observable vertex in W.
(by Property 3), each node in the graph has at most one observable vertex in W.
One difficult point with this approach is that the labels of the nodes need to be refreshed with care at each iteration so that they remain up-to-date. Actually, our algorithm does not ensure that at each iteration the label of each node is an observable vertex from this node in W. This state is only ensured at the beginning and at the end of the algorithm. Meanwhile, some nodes are still in the worklist and some labels are wrong, but this does not prevent the algorithm from working.
Informal Description. Our algorithm is given a directed graph G and a subset of vertices \(V'\) in G. It manipulates three objects: a set W which is equal to \(V'\) initially, which grows during the algorithm and which at the end contains the result,  ; a partial mapping obs associating at most one label obs[u] to each node u in the graph, this label being a vertex in W reachable from this node (and which is the observable from u in
; a partial mapping obs associating at most one label obs[u] to each node u in the graph, this label being a vertex in W reachable from this node (and which is the observable from u in  at the end); a worklist L of nodes of the closure not processed yet. Each iteration proceeds as follows. If the worklist is not empty, a vertex u is extracted from it. All the vertices that transitively precede vertex u in the graph and that are not hidden by vertices in W are labeled with u. During the propagation, nodes that are good candidates to be \(V'\)-weakly deciding are accumulated. After the propagation, we filter them so that only true \(V'\)-weakly deciding nodes are kept. Each of these vertices is associated to itself in obs, and is added to W and L. If L is not empty, a new iteration begins. Otherwise, W is equal to
at the end); a worklist L of nodes of the closure not processed yet. Each iteration proceeds as follows. If the worklist is not empty, a vertex u is extracted from it. All the vertices that transitively precede vertex u in the graph and that are not hidden by vertices in W are labeled with u. During the propagation, nodes that are good candidates to be \(V'\)-weakly deciding are accumulated. After the propagation, we filter them so that only true \(V'\)-weakly deciding nodes are kept. Each of these vertices is associated to itself in obs, and is added to W and L. If L is not empty, a new iteration begins. Otherwise, W is equal to  and obs associates each node in the graph with its observable vertex in the closure (when it exists).
and obs associates each node in the graph with its observable vertex in the closure (when it exists).
Note that each iteration consists in two steps: a complete backward propagation in the graph, which collects potential \(V'\)-weakly deciding vertices, and a filtering step. The set of predecessors of the propagated node are thus filtered twice: once during the propagation and once afterwards. We can try to filter as much as possible in the first step or, at the opposite, to avoid filtering during the first step and do all the work in the second step. For the sake of simplicity of mechanized proof, the version we chose does only simple filtering during the first step. We accumulate in our candidate \(V'\)-weakly deciding nodes all nodes that have at least two children and a label different from the one currently propagated, and we eliminate the false positives in the second step, once the propagation is done.
Example
Let us use our running example (cf. Fig. 1) to illustrate the algorithm. The successive steps are represented in Fig. 3. In the different figures, nodes in W already processed (that is, in \(W\backslash L\)) are represented using a solid double circle ( ), while nodes in W not already processed (that is, still in worklist L) are represented using a dashed double circle (
), while nodes in W not already processed (that is, still in worklist L) are represented using a dashed double circle ( ). A label \(u_j\) next to a node \(u_i\) (
). A label \(u_j\) next to a node \(u_i\) ( ) means that \(u_j\) is associated to \(u_i\), i.e. \(obs[u_i] = u_j\). Let us detail the first steps of the algorithm. Initially, \(W_0 = V'_0 = \{ u_1, u_3 \}\) (cf. Fig. 1).
) means that \(u_j\) is associated to \(u_i\), i.e. \(obs[u_i] = u_j\). Let us detail the first steps of the algorithm. Initially, \(W_0 = V'_0 = \{ u_1, u_3 \}\) (cf. Fig. 1).
-
1.
\(u_1\) is selected and is propagated backwards from \(u_1\) (cf. Fig. 3a). We find no candidate, the first iteration is finished, \(W_1 = \{ u_1, u_3 \}\).
-
2.
\(u_3\) is selected and is propagated backwards from \(u_3\) (cf. Fig. 3b). \(u_0\), \(u_2\), \(u_4\) and \(u_6\) are candidates, but only \(u_0\) is confirmed as a \(V'_0\)-weakly deciding node. It is stored in worklist L and its label is set to \(u_0\). Now \(W_2 = \{ u_0, u_1, u_3 \}\).
-
3–6.
\(u_0\), \(u_2\), \(u_4\) and \(u_6\) are processed similarly (cf. Fig. 3c, d, e, f). At the end, we get
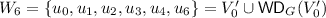 .
.
As all nodes in \(W_6\) are already reachable from \(V'_0\),  .
.
We can make two remarks on this example. First, as we can see in Fig. 3f, each node is labeled with its observable in W at the end of the algorithm. Second, in Fig. 3e, we have the case of a node labeled with an obsolete label, since \(u_5\) is labeled \(u_4\) while its only observable node in W is \(u_6\).
Detailed Description. Our algorithm is split into three functions:
-
confirm is used to check if a given node is \(V'\)-weakly deciding by trying to find a child with a different label from its own label given as an argument.
-
propagate takes a vertex and propagates backwards a label over its predecessors. It returns a set of candidate \(V'\)-weakly-deciding nodes.
-
main calls propagate on a node of the closure not yet processed, gets candidate \(V'\)-weakly deciding nodes, calls confirm to keep only true \(V'\)-weakly deciding nodes, adds them to the closure and updates their labels, and loops until no more \(V'\)-weakly deciding nodes are found.
Function Confirm. A call to \(\texttt {confirm} (G, obs, u, v)\) takes four arguments: a graph G, a labeling of graph vertices obs, and two vertices u and v. It returns true if and only if at least one child \(u'\) of u in G has a label in obs different from v, which can be written \(u' \in obs \wedge obs[u'] \ne v\). This simple function is left abstract here for lack of space. The Why3 formalization [17] contains a complete proof. Its contract is given as Algorithm 2.

Function Propagate. A call to \(\texttt {propagate} (G,W,obs,u,v)\) takes five arguments: a graph G, a subset W of nodes of G, a labeling of nodes obs, and two vertices u and v. It traverses G backwards from u (stopping at nodes in W) and updates obs so that all predecessors not hidden by vertices in W have label v at the end of the function. It returns a set of potential \(V'\)-weakly deciding vertices. Again, this function is left abstract here but is proved in the Why3 development [17]. Its contract is given as Algorithm 3.

propagate requires that, when called, only u is labeled with v (\(P_1\)) and that \(u \in W\) (\(P_2\)). It ensures that, after the call, all the predecessors of u not hidden by a vertex in W are labeled v (\(Q_1\)), the labels of the other nodes are unchanged (\(Q_2\)), C contains only predecessors of u but not u itself (\(Q_3\)), and all the predecessors that had a label before the call (different from v due to \(P_1\)) and that have at least two children are in C (\(Q_4\)).
Function Main. The main function of our algorithm is given as Algorithm 4. It takes two arguments: a graph G and a subset of vertices \(V'\). It returns  and a labeling associating to each node its observable vertex in this set if it exists. It maintains a worklist L of vertices that must be processed. L is initially set to \(V'\), and their labels to themselves (line 2). If L is not empty, a node u is taken from it and \(\texttt {propagate} (G, W, obs, u, u)\) is called (lines 3–5). It returns a set of candidate \(V'\)-weakly deciding nodes (C) that are not added to W yet. They are first filtered using confirm (lines 6–10). The confirmed nodes (\(\varDelta \)) are then added to W and to L, and the label of each of them is updated to itself (line 11). The iterations stop when L is empty (cf. lines 3, 13).
and a labeling associating to each node its observable vertex in this set if it exists. It maintains a worklist L of vertices that must be processed. L is initially set to \(V'\), and their labels to themselves (line 2). If L is not empty, a node u is taken from it and \(\texttt {propagate} (G, W, obs, u, u)\) is called (lines 3–5). It returns a set of candidate \(V'\)-weakly deciding nodes (C) that are not added to W yet. They are first filtered using confirm (lines 6–10). The confirmed nodes (\(\varDelta \)) are then added to W and to L, and the label of each of them is updated to itself (line 11). The iterations stop when L is empty (cf. lines 3, 13).

Proof of the Optimized Algorithm. We opted for Why3 instead of Coq for this proof to take advantage of Why3’s automation. Indeed, most of the goals could be discharged in less than a minute using Alt-Ergo, CVC4, Z3 and E. Some of them still needed to be proved manually in Coq, resulting in 330 lines of Coq proof. The Why3 development [17] focuses on the proof of the algorithm, not on the concepts presented in Sects. 3 and 4. Most of the concepts are proved, one of them is assumed in Why3 but was proved in Coq previously. Due to lack of space, we detail here only the main invariants necessary to prove main (cf. Algorithm 4). The proofs of \(I_1\), \(I_2\), \(I_3\), \(I_4\) are rather simple. while those of \(I_5\) and \(I_6\) are more complex.
\(I_1\) states that each node in W has itself as a label. It is true initially for all nodes in \(V'\) and is preserved by the updates.
\(I_2\) states that all labels are in W. This is true initially since all labels are in \(V'\). The preservation is verified, since all updates are realized using labels in W.
\(I_3\) states that labels in L have not been already propagated. Given a node y in L, y is the only node whose label is y. It is true initially since every vertex in \(V'\) has itself as a label. After an update, the new nodes obey the same rule, so \(I_3\) is preserved.
\(I_4\) states that if label z is associated to a node y then there exists a path between y and z. Initially, there exist trivial paths from each node in \(V'\) to itself. When obs is updated, there exists a W-path, thus in particular a path.
\(I_5\) states that W remains between \(V'\) and  during the execution of the algorithm. The first part \(V' \subseteq W\) is easy to prove, because it is true initially and W is growing. For the second part, we need to prove that after the filtering,
during the execution of the algorithm. The first part \(V' \subseteq W\) is easy to prove, because it is true initially and W is growing. For the second part, we need to prove that after the filtering,  . For that, we will prove that
. For that, we will prove that  thanks to Lemma 3. Let v be a node in \(\varDelta \). Since \(\varDelta \subseteq C\), we know that \(v \not \in W\) and
thanks to Lemma 3. Let v be a node in \(\varDelta \). Since \(\varDelta \subseteq C\), we know that \(v \not \in W\) and  . Moreover, we have \(\texttt {confirm} (G, obs, v, u) = true\), i.e. v has a child \(v'\) such that \(v' \in obs\), hence \(v'\) can reach W by \(I_4\), and \(obs[v'] \ne u\), hence
. Moreover, we have \(\texttt {confirm} (G, obs, v, u) = true\), i.e. v has a child \(v'\) such that \(v' \in obs\), hence \(v'\) can reach W by \(I_4\), and \(obs[v'] \ne u\), hence  . We can apply Lemma 4 and deduce that
. We can apply Lemma 4 and deduce that  .
.
\(I_6\) is the most complicated invariant. \(I_6\) states that if there is a path between two vertices y and z that does not intersect W, and z has a label already processed, then y and z have the same label. Let us give a sketch of the proof of preservation of \(I_6\) after an iteration of the main loop. Let us note \(obs'\) the map at the end of the iteration. Let \(y, z, z' \in V\) such that \(y \xrightarrow {(W\cup \varDelta )-disjoint} z\), \(obs'[z] = z'\) and \(z' \not \in (L \setminus \{ u \}) \cup \varDelta \). Let us show that \(obs'[y] = z'\). First, observe that neither y nor z can be in \(\varDelta \), otherwise \(z'\) would be in \(\varDelta \), which would be contradictory. We examine four cases depending on whether the conditions \(z \xrightarrow {W-path} u\) \((H_1)\) and \(y \xrightarrow {W-path} u\) \((H_2)\) hold.
-
\(H_1 \wedge H_2\): Both z and y were given the label u during the last iteration, thus \(obs'[z] = obs'[y] = u\) as expected.
-
\(H_1 \wedge (\lnot H_2)\): This case is impossible, since \(y \xrightarrow {(W\cup \varDelta )-disjoint} z\).
-
\((\lnot H_1) \wedge (\lnot H_2)\): Both z and y have the same label as before the iteration. We can therefore conclude by \(I_6\) at the beginning of the iteration.
-
\((\lnot H_1) \wedge H_2\): This is the only complicated case. We show that it is contradictory. For that, we introduce \(v_1\) as the last vertex on the \((W \cup \varDelta )\)-disjoint path connecting y and z which is also the origin of a W-path to u, and \(v_2\) as its successor on this \((W \cup \varDelta )\)-disjoint path. We can show that \(v_1 \in \varDelta \), which contradicts the fact that it lives on a \((W \cup \varDelta )\)-disjoint path.
We can now prove the assertions \(A_1\), \(A_2\), \(A_3\) and \(A_4\) at the end of main. \(A_1\) is a direct consequence of \(I_6\) since at the end \(L = \varnothing \). \(A_1\) implies that each vertex u has at most one observable in W: obs[u] if \(u \in obs\). A W-weakly deciding vertex would have two observables, thus  . \(A_3\) is a direct consequence of \(I_5\). \(A_4\) can be deduced from \(A_2\) and Lemma 3 applied to \(A_3\). This proves that at the end
. \(A_3\) is a direct consequence of \(I_5\). \(A_4\) can be deduced from \(A_2\) and Lemma 3 applied to \(A_3\). This proves that at the end  . To prove the other post-condition, we must prove that if there are two nodes u, v such that \(obs[u] = v\), then
. To prove the other post-condition, we must prove that if there are two nodes u, v such that \(obs[u] = v\), then  . By \(I_4\), there is a path from u to v. Let w be the first element in W on this path. Then \(u \xrightarrow {W-path} w\). By \(A_1\), \(obs[u]=w\). Thus, \(w=v\) and \(u \xrightarrow {W-path} v\). This proves the second post-condition. \(\square \)
. By \(I_4\), there is a path from u to v. Let w be the first element in W on this path. Then \(u \xrightarrow {W-path} w\). By \(A_1\), \(obs[u]=w\). Thus, \(w=v\) and \(u \xrightarrow {W-path} v\). This proves the second post-condition. \(\square \)
7 Experiments
We have implemented Danicic’s algorithm (additionally improved by the two optimizations proposed in Remark 4) and ours in OCaml [17] using the OCamlgraph library [9], taking care to add a filtering step at the end of our algorithm to preserve only nodes reachable from the initial subset. To be confident in their correctness, we have tested both implementations on small examples w.r.t. a certified but slow Coq-extracted implementation as an oracle. We have also carefully checked that the results returned by both implementations were the same in all experiments.
We have experimentally evaluated both implementations on thousands of random graphs with up to thousands of vertices, generated by OCamlgraph. For every number of vertices between 10 and 1000 (resp. 6500) that is a multiple of 10, we generate 10 graphs with twice as many edges as vertices and randomly select three vertices to form the initial subset \(V'\) and run both algorithms (resp. only our algorithm) on them. Although the initial subsets are small, the resulting closures nearly always represent a significant part of the set of vertices of the graph. To avoid the trivial case, we have discarded the examples where the closure is restricted to the initial subset itself (where execution time is insignificant), and computed the average time of the remaining tests. Results are presented in Fig. 4. Experiments have been performed on an Intel Core i7 4810MQ with 8 cores at 2.80 GHz and 16 GB RAM.
We observe that Danicic’s algorithm explodes for a few hundreds of vertices, while our algorithm remains efficient for graphs with thousands of nodes.
8 Related Work and Conclusion
Related Work. The last decades have seen various definitions of control dependence given for larger and larger classes of programs [6, 12, 13, 21, 22, 27]. To consider programs with exceptions and potentially infinite loops, Ranganath et al. [23] and then Amtoft [2] introduced non-termination sensitive and non-termination insensitive control dependence on arbitrary program structures. Danicic et al. [11] further generalized control dependence to arbitrary directed graphs, by defining weak and strong control-closure, which subsume the previous non-termination insensitive and sensitive control dependence relations. They also gave a control dependence semantics in terms of projections of paths in the graph, allowing to define new control dependence relations as long as they are compatible with it. This elegant framework was reused for slicing extended finite state machines [3] and probabilistic programs [4]. In both works, an algorithm computing weak control-closure, working differently from ours, was designed and integrated in a rather efficient slicing algorithm.
While there exist efficient algorithms to compute the dominator tree in a graph [8, 10, 16, 19], and even certified ones [15], and thus efficient algorithms computing control dependence when defined in terms of post-dominance, algorithms in the general case [2, 11, 23] are at least cubic.
Mechanized verification of control dependence computation was done in formalizations of program slicing. Wasserrab [26] formalized language-independent slicing in Isabelle/HOL, but did not provide an algorithm. Blazy et al. [7] and our previous work [18] formalized control dependence in Coq, respectively, for an intermediate language of the CompCert C compiler [20] and on a WHILE language with possible errors.
Conclusion and Future Work. Danicic et al. claim that weak control-closure subsumes all other non-termination insensitive variants. It was thus a natural candidate for mechanized formalization. We used the Coq proof assistant to formalize it. A certified implementation of the algorithm can be extracted from the Coq development. During formalization in Coq of the algorithm and its proof, we have detected an inconsistency in a secondary proof, which highlights how useful proof assistants are to detect otherwise overlooked cases. To the best of our knowledge, the present work is the first mechanized formalization of weak control-closure and of an algorithm to compute it. In addition to formalizing Danicic’s algorithm in Coq, we have designed, formalized and proved a new one, that is experimentally shown to be faster than the original one. Short-term future work includes considering further optimizations. Long-term future work is to build a verified generic slicer. Indeed, generic control dependence is a first step towards it. Adding data dependence is the next step in this direction.
References
Why3, a tool for deductive program verification, GNU LGPL 2.1, development version, January 2018. http://why3.lri.fr
Amtoft, T.: Slicing for modern program structures: a theory for eliminating irrelevant loops. Inf. Process. Lett. 106(2), 45–51 (2008)
Amtoft, T., Androutsopoulos, K., Clark, D.: Correctness of slicing finite state machines. Technical report RN/13/22. University College London, December 2013
Amtoft, T., Banerjee, A.: A theory of slicing for probabilistic control flow graphs. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 180–196. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_11
Bertot, Y., Castéran, P.: Interactive Theorem Proving and Program Development. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-662-07964-5
Bilardi, G., Pingali, K.: Generalized dominance and control dependence. In: PLDI, pp. 291–300. ACM (1996)
Blazy, S., Maroneze, A., Pichardie, D.: Verified validation of program slicing. In: CPP 2015, pp. 109–117 (2015)
Buchsbaum, A.L., Georgiadis, L., Kaplan, H., Rogers, A., Tarjan, R.E., Westbrook, J.: Linear-time algorithms for dominators and other path-evaluation problems. SIAM J. Comput. 38(4), 1533–1573 (2008)
Conchon, S., Filliâtre, J., Signoles, J.: Designing a generic graph library using ML functors. In: Morazán, M.T. (ed.) Trends in Functional Programming, vol. 8, pp. 124–140. Intellect, Bristol (2007)
Cooper, K.D., Harvey, T.J., Kennedy, K.: A simple, fast dominance algorithm. Softw. Pract. Exp. 4(1–10), 1–8 (2001)
Danicic, S., Barraclough, R.W., Harman, M., Howroyd, J., Kiss, Á., Laurence, M.R.: A unifying theory of control dependence and its application to arbitrary program structures. Theor. Comput. Sci. 412(49), 6809–6842 (2011)
Denning, D.E., Denning, P.J.: Certification of programs for secure information flow. Commun. ACM 20(7), 504–513 (1977)
Ferrante, J., Ottenstein, K.J., Warren, J.D.: The program dependence graph and its use in optimization. ACM Trans. Program. Lang. Syst. 9(3), 319–349 (1987)
Filliâtre, J.-C., Paskevich, A.: Why3 — where programs meet provers. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 125–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_8
Georgiadis, L., Tarjan, R.E.: Dominator tree certification and divergent spanning trees. ACM Trans. Algorithms 12(1), 11:1–11:42 (2016)
Georgiadis, L., Tarjan, R.E., Werneck, R.F.F.: Finding dominators in practice. J. Graph Algorithms Appl. 10(1), 69–94 (2006)
Léchenet, J.-C.: Formalization of weak control dependence (2018). http://perso.ecp.fr/~lechenetjc/control/
Léchenet, J.-C., Kosmatov, N., Le Gall, P.: Cut branches before looking for bugs: sound verification on relaxed slices. In: Stevens, P., Wąsowski, A. (eds.) FASE 2016. LNCS, vol. 9633, pp. 179–196. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49665-7_11
Lengauer, T., Tarjan, R.E.: A fast algorithm for finding dominators in a flowgraph. ACM Trans. Program. Lang. Syst. 1(1), 121–141 (1979)
Leroy, X.: Formal verification of a realistic compiler. Commun. ACM 52(7), 107–115 (2009)
Ottenstein, K.J., Ottenstein, L.M.: The program dependence graph in a software development environment. In: The First ACM SIGSOFT/SIGPLAN Software Engineering Symposium on Practical Software Development Environments (SDE 1984), pp. 177–184. ACM Press (1984)
Podgurski, A., Clarke, L.A.: A formal model of program dependences and its implications for software testing, debugging, and maintenance. IEEE Trans. Softw. Eng. 16(9), 965–979 (1990)
Ranganath, V.P., Amtoft, T., Banerjee, A., Hatcliff, J., Dwyer, M.B.: A new foundation for control dependence and slicing for modern program structures. ACM Trans. Program. Lang. Syst. 29(5) (2007). Article No. 27
The Coq Development Team: The Coq proof assistant, v8.6 (2017). http://coq.inria.fr/
Tip, F.: A survey of program slicing techniques. J. Prog. Lang. 3(3), 121–189 (1995)
Wasserrab, D.: From formal semantics to verified slicing: a modular framework with applications in language based security. Ph.D. thesis, Karlsruhe Inst. of Techn. (2011)
Weiser, M.: Program slicing. In: ICSE 1981 (1981)
Acknowledgements
We thank the anonymous reviewers for helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Léchenet, JC., Kosmatov, N., Le Gall, P. (2018). Fast Computation of Arbitrary Control Dependencies. In: Russo, A., Schürr, A. (eds) Fundamental Approaches to Software Engineering. FASE 2018. Lecture Notes in Computer Science(), vol 10802. Springer, Cham. https://doi.org/10.1007/978-3-319-89363-1_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-89363-1_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89362-4
Online ISBN: 978-3-319-89363-1
eBook Packages: Computer ScienceComputer Science (R0)







 .
. .
. .
. .
. , therefore
, therefore  and
and  , therefore
, therefore  and
and  , therefore
, therefore  and
and  , therefore
, therefore  .
. ;
; ;
;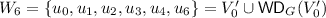 .
.
