Does the Road to Happiness Depend on the Retirement Decision? Evidence from Italy

Claudio Deiana; Gianluca Mazzarella

doi:10.1007/978-3-319-78461-8_15

Data-Driven Policy Impact Evaluation pp 237-248 | Cite as

Does the Road to Happiness Depend on the Retirement Decision? Evidence from Italy

Authors
Authors and affiliations

Claudio Deiana
Gianluca Mazzarella

Open Access

Chapter

First Online: 03 October 2018

1 Citations
7.3k Downloads

Abstract

This study estimates the causal effect of retirement decision on well-being in Italy. To do so, the authors exploit the exogenous variation provided by the changes in the eligibility criteria for pensions that were enacted in Italy in 1995 (Dini’s law) and in 1997 (Prodi’s law, from the names of the prime ministers at the time of their introduction). A sizeable and positive impact of retirement decision is found on satisfaction with leisure time and on frequency of meeting friends. Furthermore, the results are generalized, allowing for the estimation of different moments from different data sources.

Keywords

Retirement Decisions Retirement Probability Seniority Pensions First-stage Coefficients Involuntary Retirement

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Download chapter PDF

1 Introduction

Retirement is a fundamental decision in the life-cycle of a person. For this reason many studies try to assess the effect of retirement on outcomes such as consumption, health, and well-being. Due to Italy’s aging population, a trend which started in the second half of the twentieth century, it is fundamental to understand the effect of retirement on mental health and well-being. Charles (2004), among others, focuses on the effect of retirement in the United States (US), finding a positive effect of retirement on well-being. Using Canadian data, Gall et al. (1997) provide some empirical evidence in support of the theory first proposed by Atchley (1976), in which there is a positive short-term effect of retirement (defined as the honeymoon period) on well-being, but a negative mid- to long-term effect. Heller-Sahlgren (2017) identifies the short-term and longer-term effects of retirement on mental health across Europe. He shows that there is no effect in the short term, but that there is a strong negative effect in the long term. Bonsang and Klein (2012), Hershey and Henkens (2013), in Germany and in the Netherlands, respectively, try to disentangle the effects of voluntary retirement compared with those of involuntary retirement, finding that involuntary retirement has strong negative effects that are absent in the case of voluntary retirement. Börsch-Supan and Jürges (2006) analyze the German context and find a negative effect of early retirement on subjective well-being. Indeed, Coe and Lindeboom (2008) do not find any effect of early retirement on health in the US. The paper by Fonseca et al. (2015) shows a negative relationship between retirement and depression, but a positive relationship with life satisfaction. Finally, Bertoni and Brunello (2017) performed an analysis of the so-called Retired Husband Syndrome in Japan, finding a negative effect of the husband’s retirement on the wife’s health.

This chapter provides some new evidence of the effect of retirement on well-being, an effect which is characterized by self-reported satisfaction with the economic situation, health, family relationships, relationships with friends and leisure time, and by the probability of meeting friends at least once a week.

The remainder of the chapter is organized as follows: Sect. 2 illustrates the background of the literature on retirement. Section 3 details the data sources and provides some descriptive statistics. Section 4 illustrates the identification strategy and the empirical specification. Section 5 shows the effect of retirement on well-being, obtained using standard instrumental variables (IV) regression. Section 6 briefly discusses the Two-Sample Instrumental Variables estimator that will be applied to generalize result in Sect. 7. Conclusions follow.

2 Pension Reforms in Italy

Among developed economies, increasing life expectancy and reduced birth rates in the second half of the twentieth century have led to aging populations. In addition, empirical findings suggest an increase in anticipated retirement and consequently a reduction in the participation of elderly people at work (see, for example, Costa, 1998). These two trends have progressively unbalanced the ratio between retired and working people, compromising the financial sustainability of the social security system (see Galasso and Profeta, 2004).

This is primarily why policy-makers are typically deciding to increase the retirement age. Like many industrialized countries, Italy has experienced many pension reforms since the early 1990s. In Italy the first change in regulation was put in place in 1992, with the so-called Amato’s law, which modified the eligibility criteria for the old age pension. Three years later, in 1995, a new regulation was introduced under the name of Dini’s law. After a short period, the Italian government approved a new version (Prodi’s law) in 1997. Finally, Maroni’s law was implemented in 2004, which changed all of the eligibility criteria for the seniority pension.

This paper focuses on the changes made during the 1990s to the ‘seniority pension’ scheme. In particular, Dini’s law introduced two alternative rules regulating pension eligibility, stating that the pension can be drawn either (1) at the age of 57, after 35 years of contributions, or (2) after 40 years of contributions regardless of age. As with Amato’s law, the introduction of Dini’s law was gradual, with age and contribution criteria increasing from 1996 to 2006, and with further evolution of the contribution criteria from 1996 to 2008. Prodi’s law, in 1997, anticipated the changes of age and contribution criteria set by Dini’s law. Table 1 summarizes the changes in the eligibility criteria provided by these laws.

Table 1

Seniority pension: evolution of eligibility rules

	Age and	Contribution
Period	contribution (years)	only (years)
–31/12/1995	–	35
01/01/1996–31/12/1997	52 and 35	36
01/01/1998–31/12/1998	54 and 35	36
01/01/1999–31/12/2000	55 and 35	37
01/01/2001–31/12/2001	56 and 35	37
01/01/2002–31/12/2003	57 and 35	37
01/01/2004–31/12/2005	57 and 35	38
01/01/2006–31/12/2007	57 and 35	39
01/01/2008–	57 and 35	40

The progressive tightening of the pension’s requirements is associated with a decreasing retirement probability, which is evident comparing different cohorts given a certain age. However, neither law causes a drastic change in the retirement likelihood, and there is no expectation of a discontinuity at the threshold point, rather a gradual decrease provided by the progression of the law.

The individuals most likely to be affected by the reforms are those aged 52 so that we compare individuals at the same age but in different cohort. Table 1 summarizes the issue: before the reforms an individual was eligible to draw a pension after 35 years of contributions (having started work at 17, for example), but for the next 2 years would need to have 36 years’ worth of contributions, and from 1999 would need 37 years’ worth (which in the case of someone aged 52 would mean that they started work at 15, i.e. the minimum working age, and had no interruptions in their working career). Furthermore, workers cannot retire at any of the year because Dini’s law also introduced the so-called retirement windows, fixed periods in which it is possible to stop working. For this reason most retirements are on 31 December and the first day of retirement is 1 January of the following year. So one would expect the first reduction in the number of retired workers to be in 1997. Due to differences in career paths, this study concentrates on male workers because females usually register more labor market interruptions to their working careers than men, and are automatically less affected by pension reforms.

3 Data

This section introduces the data sources used to obtain the two sets of results that are shown in Sects. 5 and 7. Furthermore, it provides some descriptive statistics on the variables considered.

3.1 Survey Data: AVQ

The study exploits a survey called Aspetti della Vita Quotidiana ((Aspects of Daily Life’) (AVQ) carried out by the Italian Bureau of Statistics (Istat). It is an annual survey and each year involves about 50,000 individuals belonging to about 20,000 households, and it is a part of an integrated system of social surveys called Indagine Multiscopo sulle Famiglie (“Multipurpose Surveys on Household”). The first wave of the survey took place in 1993 and it includes different information about individual quality of life, satisfaction with living conditions, financial situation, area of residence, and the functioning of all public utilities and services.

All males aged 52 in the waves between 1993 and 2000 are selected, to give four cohorts from the pre-reform period and four from the post-reform period, for a total sample of 3143 individuals.

Table 2 presents the descriptive statistics of the outcomes involved in the analysis. Five outcome variables related to individual satisfaction were extracted from the AVQ, across various surveys. Respondents could choose from a Likert scale of four values, where a value of 1 means Very much and a value of 4 means Not at all. The authors created a set of dummy variables that are equal to 1 if the original variable is equal to 1, and 0 otherwise. A final dummy variable relates to the frequency with which individuals meet their friends, and takes a value equal to 1 if the answer is at least once a week. It is observed that almost 3% and 17% of the sample are satisfied with their economic situation and their health, respectively. More than 37% and 24% of the individuals are satisfied with their relationships with family and friends, respectively. The percentage of people who report satisfaction with leisure and meeting friends is 11% and about 70%, respectively.

Table 2

Descriptive statistics

Sample	Variable	Mean	Standard error
AVQ	Satisfaction with the economic situation	0.029	(0.168)
	Satisfaction with health	0.164	(0.371)
	Satisfaction with family relationships	0.376	(0.485)
	Satisfaction with relationships with friends	0.241	(0.428)
	Satisfaction with leisure	0.114	(0.318)
	Meet friends at least once a week	0.690	(0.463)
	Retired	0.149	(0.356)

3.2 Administrative Data: WHIP

The Work Histories Italian Panel (WHIP) is a statistical database constructed from administrative data from the National Institute of Social Security (INPS). It includes the work histories of private sector workers. INPS has extracted all the records contained in its administrative archives relating to individuals born on 24 selected dates (irrespective of the year of birth), creating a sample size of about 1∕15 of the entire INPS population. The dataset is mainly structured in three different sections: the first relates to employment records, including yearly wage and type of contract; the second collects information on unemployment periods; and the third part is wholly dedicated to pensions, including first day of retirement, initial income from pension, etc.

The full sample initially included all male individuals aged 52 in the years covered by the AVQ survey, but the sample was not comparable with the survey data, mainly because the administrative data include individuals who cannot be included in the survey data (such as foreign citizens who have worked in Italy for just a few months, Italian citizens who have moved abroad and are therefore not represented in the survey data, etc.). For this reason, all individuals who worked less than 12 months in the 4 years between 1987 and 1990 were excluded from the sample (these years were selected to obtain a window that is removed from the years implemented in the analysis). The final sample includes 90,891 individuals.

4 Empirical Strategy

Retirement is a complex choice that involves multiple factors. This is an obvious reason why it is not possible simply to compare retired people with individuals who are not retired. These two groups are probably not comparable in terms of observed and unobserved characteristics. Indeed, one needs to look for an exogenous variation to help identify the effect of the retirement decision on well-being. In this context, this study exploits the changes to the pensions rules instigated by Dini’s and Prodi’s laws to instrument the retirement decision.

As summarized in Table 1, the progression provided by the two reforms does not allow identification of the retirement effects using a standard regression discontinuity design (see Hahn et al., 2001; Lee and Lemieux, 2010, for reviews). This is the reason why the effect of retirement is identified using the change of slope (kink) in the retirement probability. The identification strategy was first proposed by Dong (2016) and it mimics a binary treatment setting (where some individuals can be considered as treated and others as not treated) the Regression Kink Design (see Card et al., 2015; Nielsen et al., 2010; Simonsen et al., 2015). This allows the identification of the local average response for a continuous treatment setting (in which all the individuals can be considered as treated, but the amount of the treatment changes following certain predetermined rules). In this setting the change in slope at the threshold point becomes the additional instrument for the endogenous treatment decision (in this case the retirement choice). Then, the first-stage regression can be illustrated as follows:

$$\displaystyle \begin{aligned} D_i= \alpha_0 + \alpha_1 (X_i-1997) + \alpha_2 (X_i-1997)Z_i + \upsilon_i, \end{aligned} $$

(1)

where D_i is a variable that is equal to 1 if the individual i is retired, 0 otherwise; X indicates the year in which the individual i reached age 52 and $Z=\b 1_{\left \{X\geq 0\right \}}$. The structural equation becomes:

$$\displaystyle \begin{aligned} Y_i= \beta_0 + \beta_1 (X_i-1997) + \beta_2 D_i + \epsilon_i,\end{aligned} $$

(2)

where Y is the outcome of interest. The coefficient β₂ that comes from this specification corresponds to the ratio γ₂∕α₂, where γ₂ is the coefficient related to (X − 1997)Z in the intention to treat equation:

$$\displaystyle \begin{aligned} Y_i= \gamma_0 + \gamma_1 (X_i-1997) + \gamma_2 (X_i-1997)Z_i + \zeta_i,\end{aligned} $$

and α₂ is as in Eq. (1) (see Appendix A in Mazzarella, 2015, for a formal proof). In this setting one can estimate Eq. (1) using both data sources, but the outcomes of interest Y are observed only in the survey data, so Eq. (2) can be computed only using AVQ data. The next sections present the results using the standard IV and TSIV estimators and then we compare the empirical evidence from the two. Specifically, we study the precision of the estimates born out from the survey and administrative data.

5 Results Using Survey Data: IV Estimates

This section discusses the main empirical results obtained using survey data. The first-stage coefficient (reported in the bottom row of Table 3) is equal to −0.0485 and is statistically significant at any level. This is consistent with the hypothesis that the reforms have progressively reduced the retirement probability. The F-statistic is equal to 18.60, which is larger than the threshold value of 10, so one can reject the hypothesis of weakness of the instrument.

Table 3

Results

Panel	Outcomes	IV (AVQ)	TSIV (AVQ + WHIP)
(A)	Satisfaction	0.1094	0.1192
	with the economic situation	(0.1212)	(0.1259)
(B)	Satisfaction	0.0089	0.0098
	with health	(0.2576)	(0.2907)
(C)	Satisfaction	−0.0761	−0.0811
	with family relationships	(0.3488)	(0.3665)
(D)	Satisfaction	0.1086	0.1206
	with relationships with friends	(0.2953)	(0.332)
(E)	Satisfaction	0.4402^∗	0.4829^∗∗
	with leisure	(0.2254)	(0.2353)
(F)	Meet friends	0.6399^∗	0.7393^∗∗
	at least once a week	(0.3283)	(0.3555)
First stage	Coeff.	− 0.0485^∗∗∗	− 0.0419^∗∗∗
	Stand. err.	(0.0112)	(0.0022)
	Test F weak instrument	18.60	369.13

Standard errors in parentheses using bootstrap

^∗p < 0.10; ^∗∗p < 0.05; ^∗∗∗p < 0.01

The discussion now turns to the second-stage results. The first row in Table 3 shows the main findings. Each row shows different outcomes. The results in the first two rows demonstrate that retirement decisions are positively associated with an increase in economic and health satisfaction, even though statistical significance is not reached at any conventional level. On the one hand, one can observe a decrease in satisfaction with family relationships, but here too the estimates are not significant (third row). On the other hand, there is a positive relationship between retirement decision and satisfaction with relationships with friends, but again this is not significant.

That the decision to retire is generally associated with increased quality of relationships with friends can be related to better use of time—leisure versus work. In fact, the fifth row shows a positive relationship between retirement and satisfaction with leisure, and the sixth row reveals that retirement is associated with a higher probability of meeting friends at least once a week. Both coefficients are significant at 10%.

6 The Two-Sample Instrumental Variables Estimator

This section explains how the two-sample instrumental variables (TSIV) estimator can be implemented, since it is used to improve the precision of the estimates presented in Sect. 5.

The TSIV estimator was first proposed by Angrist and Krueger (1992) and, more recently, improved by Inoue and Solon (2010). It allows estimation of different moments from diverse data sources which are representative of the same population but which cannot be directly merged due to the lack of a unique identifier cross-database. The idea behind the TSIV estimator is to estimate the first stage regression using one sample, then use the coefficients estimated from this sample to compute the fitted value of the endogenous variables in the second sample. Finally, it exploits the fitted values to estimate the structural equation in the second sample.

Here this is briefly discussed in formal terms. Y^(s) is defined as the (n^(s) × 1) outcome, $\mathcal {X}^{(s)}$ as the (n^(s) × p + k) matrix which includes the set of the endogenous (p) and exogenous variables (k), and lastly $\mathcal {Z}^{(s)}$ as the (n^(s) × q + k) (with q ≥ p) matrix which comprises the set of additional instruments (q) and the exogenous variables, where s = 1, 2 denotes whether they belong to the first or to the second sample. The first-stage equations estimated with the second sample are, in matrix form:

$$\displaystyle \begin{aligned}\mathcal{X}^{(2)}=\boldsymbol{\alpha}\mathcal{Z}^{(2)} + \boldsymbol{\upsilon},\end{aligned}$$

where υ is an (n⁽²⁾ × p + k) matrix with the last k columns identically equal to zero. The previous equations could be estimated using standard ordinary least squares (OLS) to recover the value $\hat {\boldsymbol {\alpha }}$, which serves to obtain the fitted values of the endogenous variables in the first sample as:

$$\displaystyle \begin{aligned}\hat{\mathcal{X}}^{(1)}=\hat{\boldsymbol{\alpha}}\mathcal{Z}^{(1)}.\end{aligned}$$

Finally, the structural equation could be estimated with the regression:

$$\displaystyle \begin{aligned}Y^{(1)}=\beta\hat{\mathcal{X}}^{(1)}+\epsilon.\end{aligned}$$

The previous equations show how it is necessary to observe $(Y;\mathcal {Z})$ in the first sample and $(\mathcal {X};\mathcal {Z})$ in the second sample, so $\mathcal {Z}$ has to be observed in both samples.

The TSIV estimator was originally proposed to allow the estimation of an IV regression when it is missing the required information of interest in both samples. In contrast, this study sheds some light on how the TSIV estimator can be used to improve the efficiency of the IV coefficient in estimating the first-stage regression with administrative data, even though the investigator can obtain the same information from survey data.

7 Results Combining Administrative and Survey Data: TSIV Estimates

This section presents results obtained by combining the survey data and the administrative data, in comparison with the standard IV results. The first-stage equation is estimated using WHIP, and the coefficients obtained with WHIP are then exploited to predict the fitted values of the endogenous retirement probability in AVQ. Finally the structural equation is estimated using AVQ. Standard errors are computed using the bootstrap method.

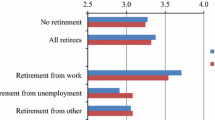
In general the estimates in Table 3 show how the TSIV estimator works with respect to the standard IV strategy. The first-stage coefficient is equal to −0.042 and it is highly statistically significant, with an associated F-statistic of 369.13. This is roughly 20 times larger than the coefficient obtained with survey data. The improvement of the precision of the first-stage estimates is also shown in Fig. 1, which compares the fitted values of the two samples, and their confidence intervals. All the sizes of the coefficients are almost unchanged, and they fall within the estimated confidence intervals of those calculated using survey data. The effects of retirement on satisfaction with economic situation, health, and relationships with family and friends are still not sizeable, and indeed the effects on satisfaction with leisure and on the probability of meeting friends at least once a week increase their significance from 10 to 5%, due to the increase of first-stage precision.

Fig. 1
First-stage comparison. (a) First stage with survey data. (b) First stage with administrative data

8 Conclusions

This study analyzes the retirement effect using as an exogenous variation the pension reforms that took place in Italy in the mid-1990s. It explains how to integrate survey and administrative data that are not directly linkable, estimating different moments from different data sources to obtain the two-sample instrumental variables estimator. In the empirical analysis all the required information is available in the survey data, but administrative data guaranteed a considerable improvement in the precision of the first-stage regression. The results from survey data are compared with those obtained by integrating the two data sources. The study shows that men increase their life satisfaction when they retire, providing further evidence that some men were adjusting their retirement decision, and that pension regulations prevented some men from locating precisely at the kink.

These results also have important implications. Administrative data have the advantage of giving detailed and precise information on large sample characteristics—in this case, retired men—over repeated periods of time. This chapter provides relevant evidence that the estimates’ precision strongly depends on big data availability. This implies that policy-makers and politicians in general should foster access to administrative data to make the policy evaluation more systematic and estimates more accurate.

Appendix: Asymptotic Variance Comparison Using Delta Method

This appendix describes the conditions under which the estimator based on TSIV is more efficient than the simple IV estimator.

The approach is intentionally simplified and is based on delta method. Furthermore, it is assumed that the two samples are representative of the same population, and so the estimators are both unbiased for the parameter of interest.

The IV estimator β_IV could be defined as:

$$\displaystyle \begin{aligned}\beta_{\mathrm{IV}}=\frac{\gamma_S}{\alpha_S},\end{aligned}$$

where γ_S is the coefficient of the intention to treat regression and α_S the coefficient of the first stage regression, both computed using survey data (represented by the subscript S). They are asymptotically distributed as:

$$\displaystyle \begin{aligned} \begin{pmatrix} \hat\gamma_S \\ \hat\alpha_S \end{pmatrix}\overset{.}{\sim} \mathcal{N} \left(\begin{pmatrix} \gamma \\ \alpha \end{pmatrix}; \begin{pmatrix} \frac{\sigma^2_{\gamma}}{n_S} & \\ \frac{\sigma_{\gamma,\alpha}}{n_S} & \frac{\sigma^2_{\alpha}}{n_S} \end{pmatrix} \right).\end{aligned}$$

So the asymptotic variance of $\hat \beta _{\mathrm {IV}}$ is equal to:

$$\displaystyle \begin{aligned} \mathbb{A}\mathbb{V}\text{ar}\left[\hat\beta_{\mathrm{IV}}\right]=\mathbb{A}\mathbb{V}\text{ar}\left[\frac{\hat\gamma_S}{\hat\alpha_S}\right]=\frac{\sigma^2_\alpha/n_S}{\alpha^2}-\frac{\gamma^2 \sigma^2_\gamma/n_S}{\alpha^4} -\frac{\gamma \sigma_{\gamma,\alpha}/n_S}{\alpha^3} \end{aligned} $$

(3)

Similarly β_TSIV could be defined as γ_S∕α_A (where the subscript A denotes the fact that it is computed with admin data), and:

$$\displaystyle \begin{aligned} \begin{pmatrix} \hat\gamma_S \\ \hat\alpha_A \end{pmatrix}\overset{.}{\sim} \mathcal{N} \left(\begin{pmatrix} \gamma \\ \alpha \end{pmatrix}; \begin{pmatrix} \frac{\sigma^2_{\gamma}}{n_S} & \\ 0 & \frac{\sigma^2_{\alpha}}{n_A} \end{pmatrix} \right),\end{aligned}$$

where the correlation between the two estimates is equal to 0 because they come from different samples.

Using similar arguments one can establish that the asymptotic variance of $\hat \beta _{\mathrm {TSIV}}$ is equal to:

$$\displaystyle \begin{aligned} \mathbb{A}\mathbb{V}\text{ar}\left[\hat\beta_{\mathrm{TSIV}}\right]=\mathbb{A}\mathbb{V}\text{ar}\left[\frac{\hat\gamma_S}{\hat\alpha_A}\right]=\frac{\sigma^2_\alpha/n_S}{\alpha^2}-\frac{\gamma^2 \sigma^2_{\gamma}/n_S}{\alpha^4}. \end{aligned} $$

(4)

From Eqs. (3) and (4) one can obtain that:

$$\displaystyle \begin{aligned} \mathbb{A}\mathbb{V}\text{ar}\left[\hat\beta_{\mathrm{TSIV}}\right]<\mathbb{A}\mathbb{V}\text{ar}\left[\hat\beta_{\mathrm{IV}}\right] \leftrightarrow \frac{\sigma^2_\alpha(n_A-n_S)}{\alpha^2 n_A}>2\frac{\gamma \sigma_{\gamma,\alpha}}{\alpha^3}. \end{aligned} $$

(5)

From Eq. (5) one can obtain the following conclusion:

1.

If the policy has no effect (i.e., γ = 0), the TSIV estimator is even more efficient than the IV estimator (obviously if the sample size of the administrative data is bigger than that of survey data.)
2.

Even if n_A →∞ it does not imply that $\mathbb {A}\mathbb {V}\text{ar}\left [\hat \beta _{\mathrm {TSIV}}\right ]<\mathbb {A}\mathbb {V}\text{ar}\left [\hat \beta _{\mathrm {IV}}\right ]$, and as a matter of fact Eq. (5) reduces to:
$$\displaystyle \begin{aligned}\frac{\sigma^2_\alpha}{\alpha^2}>2\frac{\gamma \sigma_{\gamma,\alpha}}{\alpha^3}, \end{aligned}$$
so the comparison still depends on quantities that could be both positive and negative (such as γ, α, σ_γ,α).

References

Angrist JD, Krueger AB (1992) The effect of age at school entry on educational attainment: an application of instrumental variables with moments from two samples. J Am Stat Assoc 87(418):328–336CrossRefGoogle Scholar
Atchley RC (1976) The sociology of retirement. Halsted Press, New YorkGoogle Scholar
Bertoni M, Brunello G (2017) Pappa ante portas: the effect of the husband’s retirement on the wife’s mental health in Japan. Soc Sci Med 175(2017):135–142CrossRefGoogle Scholar
Bonsang E, Klein TJ (2012) Retirement and subjective well-being. J Econ Behav Organ 83(3): 311–329CrossRefGoogle Scholar
Börsch-Supan A, Jürges H (2006) Early retirement, social security and well-being in Germany. NBER Technical Report No. 12303. National Bureau of Economic Research, CambridgeGoogle Scholar
Card D, Lee DS, Pei Z, Weber A (2015) Inference on causal effects in a generalized regression kink design. Econometrica 83(6):2453–2483CrossRefGoogle Scholar
Charles KK (2004) Is retirement depressing?: Labor force inactivity and psychological well-being in later life. Res Labor Econ 23:269–299CrossRefGoogle Scholar
Coe NB, Lindeboom M (2008) Does retirement kill you? Evidence from early retirement windows. IZA Discussion Papers No. 3817. Institute for the Study of Labor (IZA), BonnGoogle Scholar
Costa DL (1998) The evolution of retirement. In: Costa DL (ed) The evolution of retirement: an American economic history, 1880–1990. University of Chicago Press, Chicago, pp 6–31CrossRefGoogle Scholar
Dong Y (2016) Jump or kink? Regression probability jump and kink design for treatment effect evaluation. Technical report, Working paper, University of California, IrvineGoogle Scholar
Fonseca R, Kapteyn A, Lee J, Zamarro G (2015) Does retirement make you happy? A simultaneous equations approach. NBER Technical report No. 13641. National Bureau of Economic Research, CambridgeGoogle Scholar
Galasso V, Profeta P (2004) Lessons for an ageing society: the political sustainability of social security systems. Econ Policy 19(38):64–115CrossRefGoogle Scholar
Gall TL, Evans DR, Howard J (1997) The retirement adjustment process: changes in the well-being of male retirees across time. J Gerontol B Psychol Sci Soc Sci 52(3):P110–P117CrossRefGoogle Scholar
Hahn J, Todd P, Van der Klaauw W (2001) Identification and estimation of treatment effects with a regression-discontinuity design. Econometrica 69(1):201–209CrossRefGoogle Scholar
Heller-Sahlgren G (2017) Retirement blues. J Health Econ 54:66–78CrossRefGoogle Scholar
Hershey DA, Henkens K (2013) Impact of different types of retirement transitions on perceived satisfaction with life. Gerontologist 54(2):232–244CrossRefGoogle Scholar
Inoue A, Solon G (2010) Two-sample instrumental variables estimators. Rev Econ Stat 92(3): 557–561CrossRefGoogle Scholar
Lee DS, Lemieux T (2010) Regression discontinuity designs in economics. J Econ Lit 48:281–355CrossRefGoogle Scholar
Mazzarella G (2015) Combining jump and kink ratio estimators in regression discontinuity designs, with an application to the causal effect of retirement on well-being. PhD thesis, University of PadovaGoogle Scholar
Nielsen HS, Sørensen T, Taber C (2010) Estimating the effect of student aid on college enrollment: evidence from a government grant policy reform. Am Econ J Econ Policy 2(2):185CrossRefGoogle Scholar
Simonsen M, Skipper L, Skipper N (2015) Price sensitivity of demand for prescription drugs: exploiting a regression kink design. J Appl Econ 2(32):320–337Google Scholar

Copyright information

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

Authors and Affiliations

Claudio Deiana
- 1
Gianluca Mazzarella
- 1
Email author

1.European Commission, Joint Research Centre, Directorate I – CompetencesCompetence Centre on Microeconomic Evaluation (CC-ME)IspraItaly

Does the Road to Happiness Depend on the Retirement Decision? Evidence from Italy

Abstract

Keywords

1 Introduction

2 Pension Reforms in Italy

3 Data

3.1 Survey Data: AVQ

3.2 Administrative Data: WHIP

4 Empirical Strategy

5 Results Using Survey Data: IV Estimates

6 The Two-Sample Instrumental Variables Estimator

7 Results Combining Administrative and Survey Data: TSIV Estimates

8 Conclusions

References

Copyright information

Authors and Affiliations

Personalised recommendations

Cite chapter

Does the Road to Happiness Depend on the Retirement Decision? Evidence from Italy

Abstract

Keywords

1 Introduction

2 Pension Reforms in Italy

3 Data

3.1 Survey Data: AVQ

3.2 Administrative Data: WHIP

4 Empirical Strategy

5 Results Using Survey Data: IV Estimates

6 The Two-Sample Instrumental Variables Estimator

7 Results Combining Administrative and Survey Data: TSIV Estimates

8 Conclusions

References

Copyright information

Authors and Affiliations

Personalised recommendations

Cite chapter

Download book