Interactively Secure Groups from Obfuscation

Abstract

We construct a mathematical group in which an interactive variant of the very general Uber assumption holds. Our construction uses probabilistic indistinguishability obfuscation, fully homomorphic encryption, and a pairing-friendly group in which a mild and standard computational assumption holds. While our construction is not practical, it constitutes a feasibility result that shows that under a strong but generic, and a mild assumption, groups exist in which very general computational assumptions hold. We believe that this grants additional credibility to the Uber assumption.

T. Agrikola—Supported by ERC Project PREP-CRYPTO 724307.

D. Hofheinz—Supported by ERC Project PREP-CRYPTO 724307, and by DFG grants HO 4534/4-1 and HO 4534/2-2.

1 Introduction

Cyclic groups in cryptography. Cyclic groups (such as subgroups of the multiplicative group of a finite field, or certain elliptic curves) are a popular mathematical building block in cryptography. Countless cryptographic constructions are formulated in a cyclic group setting. Usually these constructions are accompanied by a security reduction that transforms any adversarial algorithm that breaks the scheme into an algorithm that solves a computational problem in that group. Among the more popular computational problems are the (computational or decisional) Diffie-Hellman problem [25], or the discrete logarithm problem.

The currently known security reductions of several relevant cryptographic schemes require somewhat more exotic computational assumptions, however. For instance, the security of the Digital Signature Algorithm is only proven in a generic model of computation [14] (see also [15]). Moreover, the semi-adaptive (i.e., IND-CCA1) security of the ElGamal encryption scheme requires a “one-more type” assumption [33]. The currently most efficient structure-preserving signature schemes require complex interactive assumptions [1, 2]. Finally, some proofs (e.g., [6, 23, 24, 31]) even require “knowledge assumptions” that essentially state that the only way to generate new group elements is as linear combinations of given group elements (with extractable coefficients).

While more exotic assumptions can thus be very helpful for constructing cryptographic schemes, their use also has a downside: reductions to more exotic (and less investigated) assumptions tend to lower our confidence in the corresponding scheme. (See [12, 32] for two very different views on this matter).

The Uber-assumption family. An example of a somewhat exotic but very general and strong class of computational assumptions in a cyclic group setting is the “Uber” assumption family ([10], see also [12]). Essentially, this assumption states that no efficient adversary $\mathcal {A}$ can win the following guessing game significantly better than with probability $1/2$. The game is formulated in a group $\mathcal {G}=\langle g\rangle$ of order $q$, and is parameterized over polynomials $P_1,\dots ,P_l,P^*\in \mathbb {Z}_q[{X}_{1}, \dots , {X}_{m}]$. Initially, the game chooses secret exponents $s_{1},\dots ,s_{m}\in \mathbb {Z}_q$ uniformly, and hands $\mathcal {A}$ the group elements $g^{P_i(s_{1},\dots ,s_{m})}$, and a challenge element $Z\in \mathcal {G}$ with either $Z=g^{P^*(s_{1},\dots ,s_{m})}$ or independently random $Z$. Given these elements, $\mathcal {A}$ has to guess if $Z$ is random or not.¹

Depending on the number $m$ of variables, and the concrete polynomials $P_i$ and $P^*$, the Uber assumption generalizes many popular existing assumptions, such as the Decisional Diffie-Hellman assumption, the $k$-Linear family of assumptions, and so-called “$q$-type assumptions”. However, it is a priori not at all clear how plausible such general assumptions are. In fact, there are indications that, e.g., $q$-type assumptions are indeed easier to break than, say, the discrete log assumption [21].

Fortunately, a number of cryptographic constructions that rely on $q$-type assumptions can be transported into composite-order groups, with the advantage that now their security holds under a simpler, subgroup indistinguishability assumption [19, 20]. However, this change of groups will not work for every cryptographic construction, and currently we only know how to perform this technique for a subclass of $q$-type assumptions.

Our contribution. In this work, we shed new light on the plausibility of Uber-style assumptions. Concretely, we construct a group in which an interactive variant of Uber-style assumptions (in which the adversary may choose the $P_i$ and $P^*$ adaptively) holds. We believe that this lends additional credibility to the Uber assumption itself, and also strengthens plausibility results obtained from the Uber assumption (see [12] for an overview).

Our construction assumes subexponentially secure indistinguishability obfuscation (iO, a very strong but generic assumption), a perfectly correct additively homomorphic encryption scheme for addition modulo a given prime, and a pairing-friendly group in which a standard assumption (SXDH, the symmetric external Diffie-Hellman assumption) holds. We stress that we consider our result as a feasibility result. Indeed, due to the use of indistinguishability obfuscation, our construction is far from practical. Still, our result shows that even interactive generalizations of the Uber assumption family are no less plausible than indistinguishability obfuscation (plus a standard assumption in cyclic groups and additively homomorphic encryption).

Before describing our results in more detail, we remark that the group we construct actually has non-unique element encodings (much like in a “graded encoding scheme” [26], only without any notion of multilinear map). It is hence possible to compare and operate with group elements, but it is not directly possible to use, e.g., the encoding of group elements to hide an encrypted message. (In particular, it is not immediately possible to implement, say, the ElGamal encryption scheme with our group as there is no obvious way to decrypt ciphertexts. Signature schemes, however, do not require unique encodings of group elements and can hence be implemented using our group.) Furthermore, due to technical reasons our construction requires the maximum degree of the adversarially chosen polynomials to be bounded a priori.

Related work. Pass et al. [36] introduce semantically secure multilinear (and graded) encoding schemes (of groups). A semantically secure encoding scheme guarantees security of a class of algebraic decisional assumptions. On a high level, the security property requires that encodings are computationally indistinguishable whenever there is no way to distinguish the corresponding elements using only generic operations. The generic multilinear encoding model implies semantic security of a multilinear encoding scheme. Furthermore, Pass et al. show that many existing iO candidates [5, 13, 27] that are proven secure in the generic multilinear encoding model can also be proven secure assuming semantically secure encoding schemes. Hence, this result relaxes the necessary assumptions to prove the security of certain iO constructions. Bitansky et al. [8] slightly strengthen the security property of encoding schemes formulated in [36]. Assuming the resulting security property allows to prove that existing obfuscation candidates [5] provide virtual grey-box security².

In [4] Albrecht et al. construct a group scheme providing a multilinear map from iO. This result complements earlier results that construct iO from multilinear maps [27, 38]. The notion of encoding schemes used in [4] is a direct adaption of the “cryptographic” multilinear group setting from [11]. In contrast to [8, 36], the encoding scheme of Albrecht et al. provides an extraction algorithm producing a unique string for all encodings that are equal with respect to the equality relation of the scheme. Furthermore, [4] requires a publicly available sampling algorithm that produces encodings for given exponents. Hence, the encoding scheme of [4] grants adversaries slightly more power.

In this paper we use a similar notion of encoding schemes as in [4]. Furthermore, [8, 36] define the security property for encoding schemes implicitly. We, in contrast, consider a concrete strong interactive hardness assumption that holds in our encoding scheme.

Technical approach. The assumption we consider is defined similarly to the Uber assumption above, only with an interactive and adaptive choice of arbitrary (multivariate) polynomials $P_i, P^*$ over $\mathbb {Z}_q$, where $q$ is the order of the group. That is, there is a secret point ${{\varvec{s}}}:=(s_{1}, \dots , s_{m})\in \mathbb {Z}_q^m$, and $\mathcal {A}$ may freely and adaptively choose the $P_i$ and $P^*$ during the course of the security game. To avoid trivialities, we require that $P^*$ does not lie in the linear span of the polynomials $P_i$. We call this assumption the Interactive Uber assumption. For convenience only, we will describe our approach assuming only univariate polynomials in the Interactive Uber assumption. However, we will see that similar techniques yield security even for multivariate polynomials.

Our starting point is a recent work by Albrecht et al. [4], which constructs a group with a multilinear map from (probabilistic) iO, an additively homomorphic encryption scheme, a dual mode NIZK proof system, and a group $\mathcal {G}$ in which (a variant of) the Strong Diffie-Hellman assumption [9] holds. For our purposes, we are not interested in obtaining a multilinear map, however, and we would also like to avoid relying on a strong (i.e., $q$-type) assumption to begin with. Moreover, [4] only proves relatively mild computational assumptions in the constructed group.

In a nutshell, a group element in the construction of [4] has the form

(1)

where $z\in \mathbb {Z}$ is the discrete logarithm of that group element, $g\in \mathcal {G}$ is a generator of the used existing group $\mathcal {G}$, ${Enc}$ is the encryption algorithm of an additively homomorphic encryption scheme, and $\pi$ is a non-interactive zero-knowledge proof of consistency. Concretely, $\pi$ proves that $C$ encrypts the discrete logarithm $z$ of $g^z$, or that $C$ encrypts a polynomial $f$ with $f(w)=z$, for a fixed value $w$ committed to in the public parameters.

In their security analysis, Albrecht et al. [4] crucially use a “switching lemma” that states that different encodings $(g^z,{Enc}(z),\pi )$ and $(g^{f(w)},{Enc}(f),\pi ')$ are computationally indistinguishable whenever $f(w)=z$. This allows to switch to, and argue about encodings with higher-degree $f$. Note, however, that any such encoding must also carry a valid $g^z=g^{f(w)}$. Hence, changing the values $z=f(w)$ in such encodings with higher-degree $f$ (as is often required to prove security) would seem to already necessitate Uber-style assumptions. Indeed, Albrecht et al. require a variant of the Strong Diffie-Hellman assumption, a $q$-type assumption.

Group elements in our group. To avoid making Uber-style assumptions in the first place, we simply omit the initial $g^z$ value in encodings of group elements, and modify the consistency proof from Eq. (1). That is, group elements in our group are of the form

(2)

where ${Enc}$ is the encryption algorithm of an additively homomorphic encryption scheme, and $\pi$ is a proof of knowledge of some (potentially constant) polynomial ${f'}$ with ${f'}(w)=z$ or ${f'}(w)=f(w)$ (in case $C$ encrypts a polynomial $f$). The value w is some point in $\mathbb {Z}_q$ that is fixed, but hidden, in the public parameters of our group, where $q$ is the group order. The proof of knowledge is realized through an additional encryption $C'$ that contains the polynomial ${f'}$. Hence, group elements are actually of the form

(3)

In a nutshell, such an encoding implicitly represents the group element $g^{f(w)}=g^{{f'}(w)}$, where $f$ and ${f'}$ are the polynomials defined by $C$ and $C'$ respectively. For clarity, we sometimes omit the component $C'$ in this overview.

More precisely, $C$ and $C'$ contain representation vectors and of the polynomials $f$ and ${f'}$ with respect to a basis $\{a_{1}$, $\dots$, $a_{d}\}$ of $\mathbb {Z}_q^{d}$. That is, given a vector that is encrypted in $C$, the coefficients of the corresponding polynomial $f$ are defined as follows

(4)

using the homomorphic mapping between polynomials over $\mathbb {Z}_q$ and vectors in $\mathbb {Z}_q^{d}$. This basis is not public, but committed to in the public parameters. The reason for using a hidden basis is that we need to deal with adaptive queries. We postpone the details to a subsequent paragraph. In this overview, however, we will pretend the ciphertexts $C$ and $C'$ contain mere polynomials.

Intuitively, the crux of the matter for the proof of security will be to remove the dependency on the point $w$. This changes the group structure to be isomorphic to $\mathbb {Z}_q^{d}$ which makes it possible to argue with linear algebra.

A public sampling algorithm allows to produce arbitrary encodings of group elements. Given an exponent $z$, the sampling algorithm produces the ciphertexts $C$ and $C'$ using the constant polynomials $f:={f'}:=z$ and produces the consistency proof accordingly. We remark that our group allows for re-randomization of encodings assuming some natural additional properties of the homomorphic encryption scheme.

The group operation is performed in a similar way to [4]. Namely, suppose we want to add two encodings $({Enc}(f_1),\pi _1)$ and $({Enc}(f_2),\pi _2)$. The resulting $({Enc}(f_3),\pi _3)$ should satisfy $f_3=f_1+f_2$ as abstract polynomials. Hence, ${Enc}(f_3)$ can be computed homomorphically from ${Enc}(f_1)$ and ${Enc}(f_2)$. To compute the proof $\pi _3$, however, we require an obfuscated circuit $C_{\textsf {Add}}$ that extracts $f_1,f_2$, and generates a fresh proof using the knowledge of $f_3=f_1+f_2$ as witness. Thus, the implementation of $C_{\textsf {Add}}$ needs to know both decryption keys for $C$ and $C'$. (The details are somewhat technical and similar to [4], so we omit them in this overview.) We prove that it is possible to implement a circuit $C''_{\textsf {Add}}$ that has almost the same functionality as $C_{\textsf {Add}}$ but produces a simulated proof of consistency that is identically distributed to a real one. Hence, the implementation of $C''_{\textsf {Add}}$ does not need to know the decryption keys. Therefore, exploiting the security of the used obfuscator, we are able to unnoticeably replace the obfuscation of $C_{\textsf {Add}}$ with an obfuscation of $C''_{\textsf {Add}}$.

We note that our modification to omit the entry $g^z$ from the encodings in Eq. (1) makes it nontrivial to decide whether two given encodings represent the same group element, or, equivalently, to decide whether a given encoding represents the identity element of the group. Recall that an encoding $(C={Enc}(f),\pi )$ represents the group element $g^{f(w)}$. (This operation is trivial in the setting of Albrecht et al., since their encodings carry a value $g^z=g^{f(w)}$.) Thus, our construction needs to provide a public algorithm that tests whether a given encoding $(C={Enc}(f),\pi )$ represents the identity element of the group, i.e. that tests whether $f(w)=0$.

At this point two problems arise. First, this public algorithm must be able to obtain at least one of the polynomials that are encrypted in $C$ and $C'$ respectively. Second, the value $w$ must not be explicitly known during the proof of security as our strategy is to remove the dependency on $w$. We solve both problems by using an obfuscated circuit $C_{\textsf {Zero}}$ for testing whether a given encoding represents the identity element. More precisely, given an encoding $(C={Enc}(f),\pi )$, $C_{\textsf {Zero}}$ decrypts $C$ (using one fixed decryption key) to obtain the polynomial $f$. In order to avoid the necessity to explicitly know the value $w$, $C_{\textsf {Zero}}$ factors the univariate polynomial $f$ (in $\mathbb {Z}_q[X]$), and obtains the small set $\{x_1,\dots ,x_n\}$ of all zeros of $f$.³ As mentioned above, the value $w$ is fixed but hidden inside the public parameters. Particularly, we store the value $w$ in form of a point function obfuscation (i.e., in form of a publicly evaluable function $\mathsf {po}:\mathbb {Z}_q\rightarrow \{0,1\}$ with $\textsf {po}(x)=1\Leftrightarrow x=w$, such that it is hard to determine the value $w$ given only the function description $\textsf {po}$). The zero testing circuit $C_{\textsf {Zero}}$ treats an encoding as the identity element if $f$ is the zero polynomial or $w\in \{x_1,\dots ,x_n\}$.

Observe that this implementation of $C_{\textsf {Zero}}$ only requires one decryption key allowing to apply the Naor-Yung strategy [35]. Furthermore, $C_{\textsf {Zero}}$ does not need to know the value w in the clear. Hence, using an obfuscation of this implementation of $C_{\textsf {Zero}}$ avoids both problems described above.

Switching of encodings. Similarly to Albrecht et al. [4] we prove a “switching lemma” that states that encodings $(C_1={Enc}(f_1),\pi _1)$ and $(C_2={Enc}(f_2),\pi _2)$ are computationally indistinguishable whenever $f_1(w)=f_2(w)$. In other words, encodings of the same group element are computationally indistinguishable. To prove this lemma, we exploit the security of the used double-encryption in a similar way as in the IND-CCA proof of Naor and Yung [35]. Particularly, when using an obfuscation of the circuit $C''_{\textsf {Add}}$, it is not necessary to know both decryption keys to produce public parameters for the group. We recall that the circuit $C_{\textsf {Zero}}$ only knows the decryption key to decrypt the first component of encodings. Furthermore, it is possible to produce a consistency proof without knowing the content of the ciphertexts $C$ and $C'$ by simply simulating it in the same way $C''_{\textsf {Add}}$ does. Therefore, we can reduce to the IND-CPA security of the encryption scheme. In order to apply the same argument for the first component of encodings, we need the circuit $C_{\textsf {Zero}}$ to forget about the first decryption key. We accomplish that by replacing the obfuscation of $C_{\textsf {Zero}}$ with an obfuscation of the circuit $\overline{C}_{\textsf {Zero}}$ that uses only the second decryption key instead of the first one. This is possible due to the security of the obfuscator and the soundness of the proof system. Then, we can use the same argument as above to reduce to the IND-CPA security of the encryption scheme.

Obtaining the Interactive Uber assumption in our group. We recall that the Interactive Uber assumption (in one variable) generates one secret point $s\in \mathbb {Z}_q$ uniformly at random at which all queried polynomials are evaluated. To show that the Interactive Uber assumption holds in our group, we first set up that secret point $s$ as $c\cdot w$ for some independent random $c$ from $\mathbb {Z}_q^{\times }$, where $w$ is the secret value of our group introduced above. Hence, a polynomial $P$ that is evaluated at $s=c\cdot w$ can be interpreted as a (different) polynomial in $w$. Particularly, given a polynomial $P(X)$, the polynomial $\overline{P}(X):=P(c\cdot X)$ satisfies the equation $P(s)=\overline{P}(w)$. Thus, an encoding that contains the polynomial $\overline{P}(X)$ determines the exponent of the represented group element to equal ${\overline{P}(w)}={P(c\cdot w)}={P(s)}$. This observation paves the way for using higher-degree polynomials $\overline{P}(X)$ to produce encodings for oracle answers and the challenge. As the resulting group elements (i.e. the corresponding exponents) remain the same, the “switching lemma” described above justifies that this modification is unnoticeable. Furthermore, by a similar argument as above, we simulate the proofs of consistency $\pi$ for every produced encoding, in particular for the encodings that are produced by the addition circuit.⁴ As the consistency proof can now be produced independently of the basis $\{a_{1}, \dots , a_{d}\}$, we are able to unnoticeably “erase” this basis from the commitment in the public parameters.

Our goal now is to alter the structure of the group in the following sense. By definition, our group is isomorphic to the additive group $\mathbb {Z}_q$. We aim to alter that structure such that our group is isomorphic to the additive group of polynomials in $\mathbb {Z}_q[X]$ (of bounded degree). Particularly, we alter the equality relation that is defined on the set of encodings such that two encodings are considered equal only if the thereby defined polynomials are equal as abstract polynomials. For that purpose, we remove the dependency on the point $w$ by altering the point function obfuscation $\textsf {po}$ such that it maps all inputs to $0$. Therefore, the zero testing circuit $C_{\textsf {Zero}}$ only treats an encoding that contains the zero polynomial as an encoding of the identity element of the group. As the value $w$ is never used explicitly in the game (as all the proofs of consistency are simulated), this modification is unnoticeable due to the security property of the point function obfuscation $\textsf {po}$. This is a crucial step paving the way for employing arguments from linear algebra to enable randomization.

The final step requires to randomize the challenge encoding such that there is no detectable difference between a real challenge and a randomly sampled one. First, we recall that encodings do not encrypt polynomials in the plain. The encodings contain the representation of polynomials with respect to some basis $\{a_{1}, \dots , a_{d}\}$. That is, given a polynomial $P(X)$, the encoding corresponding to $g^{P(s)}$ encrypts the vectors

(5)

where $P(c\cdot X)$ is interpreted as a vector of coefficients in the natural way. Therefore, the only information about the matrix $\left( a_{1} | \dots | a_{d}\right)$ is given by matrix vector products. To avoid trivialities, the challenge polynomial $P^*$ can be assumed not to lie in the span of the queries $P_1, \dots , P_l$, which is why $P^*(c\cdot X)$ does not lie in the span of $P_1(c\cdot X), \dots , P_l(c\cdot X)$. Hence, we may resort to an information-theoretic argument. More precisely, an adversary that is able to adaptively ask for matrix vector products, information-theoretically learns nothing about matrix vector products that are linearly independent of its queries. Therefore, the polynomial that is contained in the real challenge encoding information-theoretically looks like a randomly sampled polynomial (with bounded degree) given that the matrix $\left( a_{1} | \dots | a_{d}\right)$ is uniformly distributed.

Obtaining the multivariate Interactive Uber assumption. The main difficulty that arises from generalizing our results to the multivariate Interactive Uber assumption is that we do not have a polynomial-time algorithm that computes all zeros of a multivariate polynomial. Hence, the zero testing circuit $C_{\textsf {Zero}}$ needs to know the point $\mathbf {\omega }:=(\omega _{1}, \dots , \omega _{m})\in \mathbb {Z}_q^m$ in the clear to explicitly evaluate the polynomial $f$ that is defined by a given encoding. Our previous proof strategy, however, crucially relies on removing the dependency on $w$ such that $C_{\textsf {Zero}}$ only treats encodings containing the zero polynomial as encodings of the identity element. This is equivalent to altering the group structure such that it is isomorphic to the additive group of polynomials over $\mathbb {Z}_q$ (of bounded degree).

Although the zero testing circuit $C_{\textsf {Zero}}$ knows $\mathbf {\omega }$ in the clear, it is nevertheless possible to pursue a similar strategy. Our solution is to gradually alter $C_{\textsf {Zero}}$ such that it “forgets” the components $\omega _{i}$ of $\mathbf {\omega }$ one by one. Particularly, we define intermediate circuits $C^{(i)}_{\textsf {Zero}}$ that test if the polynomial

$$\begin{aligned} F^{(f)}_{i}({X}_{1}, \dots , {X}_{i}) := f({X}_{1}, \dots , {X}_{i}, \omega _{i+1}, \dots , \omega _{m}) \end{aligned}$$

(6)

equals the zero polynomial in $\mathbb {Z}_q[{X}_{1}, \dots , {X}_{i}]$. Observe that the original circuit $C_{\textsf {Zero}}$ tests whether $F^{(f)}_{0}\equiv 0$. Our goal is to unnoticeably establish $C^{(m)}_{\textsf {Zero}}$ as zero testing circuit, as it realizes the stricter equality relation we aim for.

In order to unnoticeably replace an obfuscation of $C^{(i)}_{\textsf {Zero}}$ with an obfuscation of $C^{(i+1)}_{\textsf {Zero}}$, we first alter the implementation of $C^{(i)}_{\textsf {Zero}}$ such that it performs the test whether $F^{(f)}_{i}$ is the zero polynomial by evaluating it at a randomly sampled point ${{\varvec{r}}}{}\in \mathbb {Z}_q^{i}$. Applying the Schwartz-Zippel lemma upper bounds the statistical distance of the output distributions of the two circuits enabling to reduce this step to the security of the obfuscator.

Furthermore, the condition that $F^{(f)}_{i}({{\varvec{r}}}{})=F^{(f)}_{i+1}({{\varvec{r}}}{}, \omega _{i+1})=0$ is equivalent to the condition that the univariate polynomial $F^{(f)}_{i+1}({{\varvec{r}}}{}, {X}_{i+1})$ is zero at the point $\omega _{i+1}$. This can be implemented in a similar manner as in the univariate case using a point function obfuscation of $\omega _{i+1}$. In addition, this circuit contains a conceptional logical or statement testing whether the polynomial $F^{(f)}_{i+1}({{\varvec{r}}}{}, {X}_{i+1})$ equals the zero polynomial. Using a similar argument as above we are able to alter the point function obfuscation for $\omega _{i+1}$ to a point function obfuscation that never triggers.

Hence, our zero testing circuit effectively only tests whether $F^{(f)}_{i+1}({{\varvec{r}}}{}, {X}_{i+1})$ equals the zero polynomial in $\mathbb {Z}_q[{X}_{i+1}]$. Applying the Schwartz-Zippel lemma again, we are able to unnoticeably alter the implementation of the zero testing circuit such that it tests whether $F^{(f)}_{i+1}$ equals the zero polynomial in ${X}_{1}, \dots , {X}_{i+1}$ concluding the argument.

Roadmap. After fixing notation and recalling some basic definitions in Sect. 2, we present our main group construction in Sect. 3. Our main theorem, Theorem 1, states the validity of (our variant of) the Interactive Uber assumption relative to the group construction from Sect. 3. For the detailed proofs we refer the reader to the full version [3].

2 Preliminaries

2.1 Notation

For $n\in \mathbb {N}$, let $1^n$ denote the string consisting of n times the digit 1. For a probabilistic algorithm A, let $y\leftarrow A(x)$ denote that y is the output of A on input x. The randomness which A uses during the computation can be made explicit by $y\leftarrow A(x; r)$, where r denotes the randomness. Let $\lambda$ denote the security parameter. We assume that the security parameter is implicitly given to all algorithms as $1^{\lambda }$.

Let $\mathcal {G}$ be a group and let h be a fixed generator of $\mathcal {G}$. Then, [n] denotes the group element $h^n$.

Let $n\in \mathbb {N}$ be a number, let $\mathbb {K}$ be a field, and let $\mathbb {K}^n$ denote the vector space of n-tuples of elements of $\mathbb {K}$. Further, for any $i\in \{1$, $\dots$, $n\}$, let $e_i\in \mathbb {K}^n$ be the vector such that the i-th entry of $e_i$ equals 1 and any remaining entry equals 0. Then, the set $\{e_1$, $e_2$, $\dots$, $e_n\}$ denotes the standard basis of $\mathbb {K}^n$. Let $b_1$, $\dots$, $b_i\in \mathbb {K}^n$, then $\langle b_1$, $\dots$, $b_i\rangle \subseteq \mathbb {K}^n$ denotes the span of those vectors.

2.2 Assumptions

Let $(\mathcal {G}_{\lambda })_{\lambda \in \mathbb {N}}$ be a family of finite cyclic groups. If it is clear from the context, we write $\mathcal {G}$ instead of $\mathcal {G}_{\lambda }$. We assume that the order $q:={|* |}{\mathcal {G}}$ of the group is known and prime. Let $\textsf {Gens}_{\mathcal {G}}$ be the set of generators of $\mathcal {G}$. We assume that we can efficiently sample elements uniformly at random from $\textsf {Gens}_{\mathcal {G}}$.

A very basic and well-established cryptographic assumption is the decisional Diffie-Hellman (DDH) assumption. The DDH assumption states that the distributions ([x], [y], $[x\cdot y])$ and ([x], [y], [z]) are computationally indistinguishable for x, y, $z\leftarrow \mathbb {Z}_q$.

Definition 1

(Decisional Diffie-Hellman (DDH) assumption). For any PPT adversary $\mathcal {A}$, the advantage $Adv^{\text {ddh}}_{\mathcal {G}, \mathcal {A}}(\lambda )$ is negligible in $\lambda$, where

$$\begin{aligned} Adv^{\text {ddh}}_{\mathcal {G}, \mathcal {A}}(\lambda ):= {\text {Pr}}\left[ \mathcal {A}(1^{\lambda }, [x], [y], [x\cdot y])=1|x, y\leftarrow \mathbb {Z}_q \right] \\ -{\text {Pr}}\left[ \mathcal {A}(1^{\lambda }, [x], [y], [z])=1|x, y, z\leftarrow \mathbb {Z}_q \right] \text {} \end{aligned}$$

and q is the order of the group $\mathcal {G}$.

Let $(\mathcal {G}_1$, $\mathcal {G}_2$, e) be finite cyclic groups of prime order ${|* |}{\mathcal {G}_1}={|* |}{\mathcal {G}_2}$ and let $e:\mathcal {G}_1\times \mathcal {G}_2\rightarrow \mathcal {G}_T$ be a pairing (i.e. a non-degenerate and bilinear map). The groups $\mathcal {G}_1$, $\mathcal {G}_2$, $\mathcal {G}_T$, as well as the pairing e depend on the security parameter. For greater clarity, we omit this dependency in this setting.

A natural extension of the DDH assumption to the bilinear setting is the symmetric external Diffie-Hellman (SXDH) assumption. The SXDH assumption states that the DDH assumption holds in both groups $\mathcal {G}_1$ and $\mathcal {G}_2$.

2.3 Point Obfuscation

In our construction we employ a cryptographic primitive that is called point obfuscation [16, 37]. A point obfuscation serves the purpose to hide a certain point, but to enable a test whether a given value is hidden inside. Equivalently, this notion can be seen as an “obfuscation” of a point-function that evaluates to 1 at exactly this given point and to 0 everywhere else. We require that it is infeasible to distinguish a point obfuscation that triggers at a randomly sampled point from a point obfuscation that never triggers. This security requirement is rather weak compared to similar notions [7].

Definition 2

(Point obfuscation). A point obfuscation for message space $\mathcal {M}_{\lambda }$ is a PPT algorithm ${PObf}$.

• ${PObf}(1^{\lambda }, x)\rightarrow \textsf {po}$ On input a message $x\in \mathcal {M}_{\lambda }\cup \{\bot \}$, ${PObf}$ produces a description of the point function

  

We require the following two properties to hold:

• Correctness: For any x, $y\in \mathcal {M}_{\lambda }$ and any $\textsf {po}\leftarrow {PObf}(1^{\lambda }$, x), $\textsf {po}(y)\mapsto 1$ if and only if $x=y$.

• Soundness: For any PPT adversary $\mathcal {A}$, the advantage $Adv^{\text {po}}_{{PObf}, \mathcal {A}}(\lambda )$ is negligible in $\lambda$, where

  $$\begin{aligned} Adv^{\text {po}}_{{PObf}, \mathcal {A}}(\lambda ):=&{\text {Pr}}\left[ \mathcal {A}(1^{\lambda }, \textsf {po})=1|\textsf {po}\leftarrow {PObf}(1^{\lambda }, x)\text {,}x\leftarrow \mathcal {M}_{\lambda } \right] \\&- {\text {Pr}}\left[ \mathcal {A}(1^{\lambda }, \textsf {po})=1|\textsf {po}\leftarrow {PObf}(1^{\lambda }, \bot ) \right] \text {.} \end{aligned}$$

An adaption of a construction proposed in [16] yields a point obfuscation ${PObf}$ with message space $\mathbb {Z}_{p}$ based on the DDH assumption. Furthermore, a point obfuscation with message space $\mathbb {Z}_{p}$ can be used to construct a point obfuscation for message space $\mathbb {Z}_q$, where q is a prime such that $\frac{p}{q}$ is negligible in $\lambda$. For further details, we refer the reader to the full version [3].

Remark 1

According to a reviewer of TCC 2017, a point obfuscation with message space $\{0, 1\}^{\textsf {poly}(\lambda )}$ can be constructed from an injective one-way function F together with a corresponding hardcore bit B.

Given a string x, the tuple (F(x), B(x)) is the obfuscation of x. The tuple $(F(y), 1-B(y))$ is an obfuscation of $\bot$, where y is a random element from the message space.

2.4 Subset Membership Problems

The notion of subset membership problems was introduced in [22]. Informally, a hard subset membership problem specifies a set, such that it is intractable to decide whether a value is inside this set or not. Let $\mathcal {L}=(\mathcal {L}_{\lambda })_{\lambda \in \mathbb {N}}$ be a family of families of languages $L\subseteq \mathcal {X}_{\lambda }$ in a universe $\mathcal {X}_{\lambda }=\mathcal {X}$. Further, let $\mathcal {R}$ be an efficiently computable witness relation, such that $x\in L$ if and only if there exists a witness $w\in \{0, 1\}^{\textsf {poly}({|x |})}$ with $\mathcal {R}(x$, $w)=1$, where $\textsf {poly}$ is a fixed polynomial. We assume that we are able to efficiently and uniformly sample elements from L together with a corresponding witness, and that we are able to efficiently and uniformly sample elements from $\mathcal {X}\setminus L$.

Definition 3

(Hard subset membership problem). The subset membership problem (SMP) $L\subseteq \mathcal {X}$ is hard, if for any PPT adversary $\mathcal {A}$, the advantage

$$\begin{aligned} Adv^{\text {smp}}_{\mathcal {L}, \mathcal {A}}(\lambda ):={\text {Pr}}\left[ \mathcal {A}(1^{\lambda }, x)=1|x\leftarrow L \right] -{\text {Pr}}\left[ \mathcal {A}(1^{\lambda }, x)=1|x\leftarrow \mathcal {X}\setminus L \right] \end{aligned}$$

is negligible in $\lambda$.

For our construction we need a family $\mathcal {L}=(\mathcal {L}_{\lambda })_{\lambda \in \mathbb {N}}$ such that for any $L\in \mathcal {L}_{\lambda }$ and any $x\in L$, there exists exactly one witness $r\in \{0,1\}^*$ with $\mathcal {R}(x$, $w)=1$.

Let $\mathcal {G}=\{\mathcal {G}_{\lambda }\}$ be a family of finite cyclic groups of prime order such that the DDH assumption holds. A possible instantiation of a hard SMP meeting our requirements is the Diffie-Hellman language $\mathcal {L}^{\text {dh}}:=(\mathcal {L}^{\text {dh}}_{\lambda })_{\lambda \in \mathbb {N}}$. For any $\lambda \in \mathbb {N}$, , $\mathcal {X}_{\lambda }=\textsf {Gens}_{\mathcal {G}}\times \textsf {Gens}_{\mathcal {G}}$, and , where $q={|* |}{\mathcal {G}_k}$. The SMP $L_{g, h}\subseteq \mathcal {X}$ is hard for randomly chosen generators g, $h\leftarrow \textsf {Gens}_{\mathcal {G}}$. Given $(g^r$, $h^r)\in L_{g, h}$, the corresponding unique witness is $r\in \mathbb {Z}_q$.

2.5 Non-interactive Commitments

Non-interactive commitment schemes are a commonly used cryptographic primitive [29]. They enable to commit to a chosen value without revealing this value. Additionally, once committed to a value, this value cannot be changed. In contrast to the notion of point obfuscations, a commitment scheme prevents to test whether a particular value is hidden inside a commitment.

Definition 4

(Perfectly binding non-interactive commitment scheme (syntax and security)). A perfectly binding non-interactive commitment scheme for message space $\mathcal {M}_{\lambda }$ is a triple of PPT algorithms $\mathrm{C}\textsc {om}=(\mathrm{C}\textsc {om}\mathrm{S}\textsc {etup}$, $\mathrm{C}\textsc {ommit}$, $\mathrm{O}\textsc {pen})$.

• $\mathrm{C}\textsc {om}\mathrm{S}\textsc {etup}(1^{\lambda })\rightarrow ck$ On input the unary encoded security parameter, the algorithm $\mathrm{C}\textsc {om}\mathrm{S}\textsc {etup}$ outputs a commitment key $ck$.

• $\mathrm{C}\textsc {ommit}_{ ck }(m)\rightarrow ( com , op )$ On input the commitment key ck and a message $m\in \mathcal {M}_{\lambda }$, $\mathrm{C}\textsc {ommit}$ outputs a tuple $( com$, $op )$.

• $\mathrm{O}\textsc {pen}_{ ck }( com , op )\rightarrow \widetilde{m}$ On input the commitment key $ck$ and a commitment-opening pair $( com$, $op )$, $\mathrm{O}\textsc {pen}$ outputs the committed message m if $op$ is a valid opening for $com$. Otherwise, $\mathrm{O}\textsc {pen}$ outputs $\bot$.

We require $\mathrm{C}\textsc {om}$ to be perfectly correct, perfectly binding, and computationally hiding.

• Correctness $\mathrm{C}\textsc {om}$ is correct if for any $\lambda \in \mathbb {N}$, any $ck \leftarrow \mathrm{C}\textsc {om}\mathrm{S}\textsc {etup}(1^{\lambda })$, and any $m\in \mathcal {M}_{\lambda }$, $\mathrm{O}\textsc {pen}_{ ck }(\mathrm{C}\textsc {ommit}_{ ck }(m))=m$.

• Perfectly binding $\mathrm{C}\textsc {om}$ is perfectly binding if it is not possible to find a commitment that has valid openings for more than one message, i.e. for any (possibly unbounded) adversary $\mathcal {A}$, $Adv^{\text {binding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda )=0$, where

  $$\begin{aligned} Adv^{\text {binding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda ):={\text {Pr}}\left[ Exp^{\text {binding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda )=1 \right] \text {.} \end{aligned}$$

• Computationally hiding $\mathrm{C}\textsc {om}$ is computationally hiding if commitments for different messages are computationally indistinguishable, i.e. for any PPT adversary $\mathcal {A}$, $Adv^{\text {hiding}}_{\mathcal {A}}(\lambda )$ is negligible, where

  $$\begin{aligned} Adv^{\text {hiding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda ):={\text {Pr}}\left[ Exp^{\text {hiding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda )=1 \right] -\frac{1}{2}\text {.} \end{aligned}$$

The games $Exp^{\text {binding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda )$ and $Exp^{\text {hiding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda )$ are defined in Fig. 1.

Fig. 1.

The description of the Binding game $Exp^{\text {binding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda )$ (left) and the Hiding game $Exp^{\text {hiding}}_{\mathrm{C}\textsc {om}, \mathcal {A}}(\lambda )$ (right).

Such a commitment scheme can be obtained from a group in which the DDH assumption holds.

2.6 Dual Mode NIWI Proof System

The notion of dual mode NIWI proof systems abstracts from the NIWI proof system proposed in [30]. A similar abstraction was used in [4].

Definition 5

(Dual mode NIWI proof system (syntax and security)). A dual mode non-interactive witness-indistinguishable (NIWI) proof system for a relation $\mathcal {R}$ is a tuple of PPT algorithms $\varPi =(\textsf {Setup}_\varPi$, $\textsf {K}$, $\textsf {S}$, $\textsf {Prove}$, $\textsf {Verify}$, $\textsf {Extract})$.

• $\textsf {Setup}_\varPi (1^{\lambda })\rightarrow (gpk, gsk)$ On input the unary encoded security parameter, $\textsf {Setup}_\varPi$ outputs a group key gpk and, additionally, may output some related information gsk. The relation $\mathcal {R}$ is an efficiently computable ternary relation consisting of triplets of the form (gpk, x, w) and defines a group-dependent language L. The language L consists of the statements x, such that there exists a witness w with (gpk, x, $w)\in \mathcal {R}$.

• $\textsf {K}(gpk, gsk)\rightarrow ( crs , td_{\text {ext}})$ On input the group keys gpk and gsk, $\textsf {K}$ outputs a binding common reference string (CRS) $crs$ and a corresponding extraction trapdoor $td_{\text {ext}}$.

• $\textsf {S}(gpk, gsk)\rightarrow ( crs , \bot )$ On input the group keys gpk and gsk, $\textsf {S}$ outputs a hiding CRS $crs$.

• $\textsf {Prove}(gpk, crs , x, w)\rightarrow \pi$ On input the public group key gpk, the CRS $crs$, a statement x, and a corresponding witness w, $\textsf {Prove}$ produces a proof $\pi$.

• $\textsf {Verify}(gpk, crs , x, \pi )\rightarrow \{0, 1\}$ On input the public group key gpk, the CRS $crs$, a statement x, and a proof $\pi$, $\textsf {Verify}$ outputs 1 if the proof is valid and 0 if the proof is rejected.

• $\textsf {Extract}(td_{\text {ext}}, x, \pi )\rightarrow w$ On input the extraction trapdoor $td_{\text {ext}}$, a statement x, and a proof $\pi$, $\textsf {Extract}$ outputs a witness w.

We require $\varPi$ to meet the following requirements:

• CRS indistinguishability. Common reference strings generated via $\textsf {K}(gpk$, gsk) and $\textsf {S}(gpk$, gsk) are computationally indistinguishable, i.e.

  

  is negligible in $\lambda$, where $Exp^{\text {crs}}_{\varPi , \mathcal {A}}(\lambda )$ is defined as in Fig. 2.

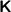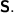• Perfect completeness under and For any $\lambda \in \mathbb {N}$, any (gpk, $gsk)\leftarrow \textsf {Setup}_\varPi (1^{\lambda })$, any CRS $( crs , \cdot )\leftarrow \textsf {K}(gpk$, gsk), any (x, w) such that (gpk, x, $w)\in \mathcal {R}$, and any $\pi \leftarrow \textsf {Prove}(gpk$, $crs$, x, w), $\textsf {Verify}(gpk$, $crs$, x, $\pi )\rightarrow 1$. The same holds for any $( crs , \cdot )\leftarrow \textsf {S}(gpk$, gsk).

• Perfect soundness under For any $\lambda \in \mathbb {N}$, any (gpk, $gsk)\leftarrow \textsf {Setup}_\varPi (1^{\lambda })$, any $( crs , \cdot )$ $\leftarrow \textsf {K}(gpk$, gsk), any statement x such that there exists no witness w with (gpk, x, $w)\in \mathcal {R}$, and any $\pi \in \{0,1\}^*$, $\textsf {Verify}(gpk$, $crs$, x, $\pi )\rightarrow 0$.

• Perfect extractability under For any $\lambda \in \mathbb {N}$, any key pair (gpk, $gsk)\leftarrow \textsf {Setup}_\varPi (1^{\lambda })$, any $( crs$, $td_{\text {ext}})\leftarrow \textsf {K}(gpk$, gsk), any (x, $\pi )$ such that $\textsf {Verify}(gpk$, $crs$, x, $\pi )\rightarrow 1$, and for any $w\leftarrow \textsf {Extract}(td_{\text {ext}}$, x, $\pi )$, w is a satisfying witness for the statement x, i.e. $(gpk, x, w)\in \mathcal {R}$.

• Perfect witness-indistinguishability under 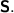For any $\lambda \in \mathbb {N}$, any (gpk, $gsk)\leftarrow$ $\textsf {Setup}_\varPi (1^{\lambda })$, any $( crs , \cdot )\leftarrow \textsf {S}(gpk$, gsk), any (x, $w_0)$ and (x, $w_1)$ with (gpk, x, $w_0)$, (gpk, x, $w_1)\in \mathcal {R}$, the output of $\textsf {Prove}(gpk$, $crs$, x, $w_0)$ and the output of $\textsf {Prove}(gpk$, $crs$, x, $w_1)$ are identically distributed.

Fig. 2.

The description of the CRS inistinguishability game $Exp^{\text {crs}}_{\varPi , \mathcal {A}}(\lambda )$.

An exemplary dual mode NIWI proof system satisfying computational CRS indistinguishability, perfect completeness, perfect soundness, perfect extractability, and perfect witness-indistinguishability is the proof system proposed by Groth and Sahai in [30]. The soundness, in particular the indistinguishability of common reference strings, of this construction can for instance be based on the SXDH assumption. The Groth-Sahai proof system allows perfect extractability for group elements, however, does not provide a natural way to extract scalars. Nevertheless, perfect extractability can be achieved by using the proof system for the bit representation of the particular scalars [34].

2.7 Probabilistic Indistinguishability Obfuscation

The notion of probabilistic circuit obfuscation was proposed in [17]. Informally, probabilistic circuit obfuscation enables to conceal the implementation of probabilistic circuits while preserving their functionality. Let $\mathcal {C}=(\mathcal {C}_{\lambda })_{\lambda \in \mathbb {N}}$ be a family of sets $\mathcal {C}_{\lambda }$ of probabilistic circuits. The set $\mathcal {C}_{\lambda }$ contains circuits of polynomial size in $\lambda$. A circuit sampler for $\mathcal {C}$ is defined as a set of (efficiently samplable) distributions $S=(S_{\lambda })_{\lambda \in \mathbb {N}}$, where $S_{\lambda }$ is a distribution over triplets $(C_0$, $C_1$, z) with $C_0$, $C_1\in \mathcal {C}_{\lambda }$ such that $C_0$ and $C_1$ take inputs of the same length and $z\in \{0, 1\}^{\textsf {poly}(\lambda )}$.

Definition 6

(Probabilistic indistinguishability obfuscation for a class of samplers $\varvec{\mathcal {S}}$ , [4, 17]). A probabilistic indistinguishability obfuscator (pIO) for a class of samplers $\mathcal {S}$ over the probabilistic circuit family $\mathcal {C}=(\mathcal {C}_{\lambda })_{\lambda \in \mathbb {N}}$ is a uniform PPT algorithm $pi \mathcal {O}$, such that the following properties hold:

• Correctness. On input the unary encoded security parameter $1^{\lambda }$ and a circuit $C\in \mathcal {C}_{\lambda }$, $pi \mathcal {O}$ outputs a deterministic circuit $\varLambda$ of polynomial size in ${|* |}{C}$ and $\lambda$. For any $\lambda \in \mathbb {N}$, any $C\in \mathcal {C}_{\lambda }$, any $\varLambda \leftarrow pi \mathcal {O}(1^{\lambda }$, C), and any inputs $m\in \{0, 1\}^*$ (of matching length), there exists a randomness r, such that $C(m; r)=\varLambda (m)$.

  Furthermore, for every non-uniform PPT distinguisher $\mathcal {D}$, every $\lambda \in \mathbb {N}$, every $C\in \mathcal {C}_{\lambda }$, and every auxiliary input $z\in \{0, 1\}^{\textsf {poly}(\lambda )}$, the advantage

  $$\begin{aligned} Adv^{\text {pio-c}}_{C, z, \mathcal {D} }(\lambda ):={\text {Pr}}\left[ Exp^{\text {pio-c}}_{C, z, \mathcal {D} }(\lambda )=1 \right] -\frac{1}{2} \end{aligned}$$

  is negligible in $\lambda$, where $Exp^{\text {pio-c}}_{C, z, \mathcal {D} }(\lambda )$ is defined as in Fig. 3.

• Security with respect to ${\mathbf {\mathsf{{S.}}}}$ For any circuit sampler $S=\{S_{\lambda }\}_{\lambda \in \mathbb {N}}$, for any non-uniform PPT adversary $\mathcal {A}$, the advantage

  $$ Adv^{\text {pio-ind}}_{ pi \mathcal {O}, S, \mathcal {A}}(\lambda ):={\text {Pr}}\left[ Exp^{\text {pio-ind}}_{ pi \mathcal {O}, S\mathcal {A}}(\lambda )=1 \right] -\frac{1}{2} $$

  is negligible in $\lambda$, where $Exp^{\text {pio-ind}}_{ pi \mathcal {O}, S\mathcal {A}}(\lambda )$ is defined as in Fig. 3.

Fig. 3.

The descriptions of the games $Exp^{\text {pio-c}}_{C, z, \mathcal {D} }(\lambda )$ (left), $Exp^{\text {pio-ind}}_{ pi \mathcal {O}, S, \mathcal {A}}(\lambda )$ (middle), and $Exp^{\text {sel-ind}}_{S, \mathcal {A}}(\lambda )$ (right). In $Exp^{\text {pio-c}}_{C, z, \mathcal {D} }(\lambda )$, $\mathcal {D}$ has oracle access to either a probabilistic circuit $C_0$ using fresh randomness for every oracle query or to a deterministic circuit $C_1$. $\mathcal {D}$ can make an unbounded number of oracle queries with the restriction that no input is queried twice.

We remark that the construction proposed in [17] also satisfies our definition of correctness.

Let $X:\mathbb {N}\rightarrow \mathbb {N}$ be a function. For our purposes we use a class of circuit samplers, such that the sampled circuits are functionally equivalent for all inputs outside of a set $\mathcal {X}$, and the outputs of the circuits are indistinguishable for inputs inside of this set $\mathcal {X}$. The set $\mathcal {X}$ is a subset of the circuits’ domain of cardinality at most $X(\lambda )$. Two circuits $C_0$ and $C_1$ are functionally equivalent if for any input x of matching length and any randomness r, $C_0(x; r)=C_1(x; r)$.

Definition 7

( X -Ind sampler, [4, 17]). Let $X:\mathbb {N}\rightarrow \mathbb {N}$ be a function with $X(\lambda )\le 2^{\lambda }$, for all $\lambda \in \mathbb {N}$. The class $\mathcal {S}^{X\text {-ind}}$ of X-Ind samplers for a circuit family $\mathcal {C}$ contains all circuit samplers $S$ for $\mathcal {C}$ satisfying, that for any $\lambda \in \mathbb {N}$, there exists a set $\mathcal {X}=\mathcal {X}_{\lambda }\subseteq \{0, 1\}^*$ with ${|* |}{\mathcal {X}}\le X(\lambda )$, such that the following two properties hold:

• $\varvec{X}$ -differing inputs. For any (possibly unbounded) deterministic adversary $\mathcal {A}$, the advantage

  

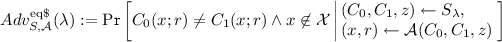
  is negligible in $\lambda$.

• $\varvec{X}$ -indistinguishability. For any non-uniform PPT distinguisher $\mathcal {A}=(\mathcal {A}_1$, $\mathcal {A}_2)$, the advantage

  $$ X(\lambda )\cdot Adv^{\text {sel-ind}}_{S, \mathcal {A}}(\lambda ):=X(\lambda )\cdot \left( {\text {Pr}}\left[ Exp^{\text {sel-ind}}_{S, \mathcal {A}}(\lambda )=1 \right] - \frac{1}{2}\right) $$

  is negligible in $\lambda$, where $Exp^{\text {sel-ind}}_{S, \mathcal {A}}(\lambda )$ is defined as in Fig. 3.

For our construction we use an obfuscator for the class $\mathcal {S}^{X\text {-ind}}$.

According to Theorem 2 in the proceedings of [17], a pIO which is secure with respect to $\mathcal {S}^{X\text {-ind}}$ for a circuit family $\mathcal {C}$ that only contains circuits of size at most $\lambda$ can be obtained from sub-exponentially secure indistinguishability obfuscation (IO) for deterministic circuits in conjunction with sub-exponentially secure puncturable PRF. The construction given in [17] satisfies this security requirement even if the circuit family $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ contains circuits with polynomial size in $\lambda$ as long as the input length of those circuits is at most $\lambda$.

2.8 Fully Homomorphic Encryption Scheme

Let $\mathcal {C}=(\mathcal {C}_{\lambda })_{\lambda \in \mathbb {N}}$ be a family of sets of polynomial sized circuits of arity $a(\lambda )$, i.e. the set $\mathcal {C}_{\lambda }$ contains circuits of polynomial size in $\lambda$. We assume that for any $\lambda \in \mathbb {N}$ the circuits in $\mathcal {C}_{\lambda }$ share the common input domain $(\{0, 1\}^{\textsf {poly}(\lambda )})^{a(\lambda )}$ for a fixed polynomial $\textsf {poly}(\lambda )$. A homomorphic encryption scheme enables evaluation of circuits on encrypted data. The first fully homomorphic encryption scheme was proposed in [28]. In this paper, we abide by the notation used in [4].

Definition 8

(Homomorphic public-key encryption (HPKE) scheme (syntax and security)). A homomorphic public-key encryption scheme with message space $\mathcal {M}\subseteq \{0, 1\}^{*}$ for a deterministic circuit family $\mathcal {C}=(\mathcal {C}_{\lambda })_{\lambda \in \mathbb {N}}$ of arity $a(\lambda )$ and input domain $(\{0, 1\}^{\textsf {poly}(\lambda )})^{a(\lambda )}$ is a tuple of PPT algorithms $\mathrm{H}\textsc {pke}=(\mathrm{G}\textsc {en}$, $\mathrm{E}\textsc {nc}$, $\mathrm{D}\textsc {ec}$, $\mathrm{E}\textsc {val})$.

• $\mathrm{G}\textsc {en}(1^{\lambda })\rightarrow (pk, sk)$ On input the unary encoded security parameter $1^{\lambda }$, $\mathrm{G}\textsc {en}$ outputs a public key pk and a secret key sk.

• $\mathrm{E}\textsc {nc}(pk, m)\rightarrow c$ On input the public key pk and a message $m\in \mathcal {M}$, $\mathrm{E}\textsc {nc}$ outputs a ciphertext $c\in \{0, 1\}^{\textsf {poly}(\lambda )}$ for message m.

• $\mathrm{D}\textsc {ec}(sk, c)\rightarrow m$ On input the secret key sk and a ciphertext $c\in \{0, 1\}^{\textsf {poly}(\lambda )}$, $\mathrm{D}\textsc {ec}$ outputs the corresponding message $m\in \mathcal {M}$ (or $\bot$, if the ciphertext is not valid).

• $\mathrm{E}\textsc {val}(pk, C, c_1, \dots , c_{a(\lambda )})\rightarrow c$ On input the public key pk, a deterministic circuit $C\in \mathcal {C}_{\lambda }$, and ciphertexts $(c_1$, $\dots$, $c_{a(\lambda )})\in (\{0, 1\}^{\textsf {poly}(\lambda )})^{a(\lambda )}$, $\mathrm{E}\textsc {val}$ outputs a ciphertext $c\in \{0, 1\}^{\textsf {poly}(\lambda )}$.

We require $\mathrm{H}\textsc {pke}$ to meet the following requirements:

• Perfect correctness. The triple $(\mathrm{G}\textsc {en}$, $\mathrm{E}\textsc {nc}$, $\mathrm{D}\textsc {ec})$ is perfectly correct as a PKE scheme, i.e. for any $\lambda \in \mathbb {N}$, any (pk, $sk)\leftarrow \mathrm{G}\textsc {en}(1^{\lambda })$, any $m\in \mathcal {M}$, and any $c\leftarrow \mathrm{E}\textsc {nc}(pk$, m), $\mathrm{D}\textsc {ec}(sk$, $c) = m$. Furthermore, the evaluation algorithm $\mathrm{E}\textsc {val}$ is perfectly correct in the sense that for any $\lambda \in \mathbb {N}$, any (pk, $sk)\leftarrow \mathrm{G}\textsc {en}(1^{\lambda })$, any $m_1$, $\dots$, $m_{a(\lambda )}\in \mathcal {M}$, any $c_i\leftarrow \mathrm{E}\textsc {nc}(pk$, $m_i)$, any $C\in \mathcal {C}_{\lambda }$, and any $c\leftarrow \mathrm{E}\textsc {val}(pk$, C, $c_1$, $\dots$, $c_{a(\lambda )})$, $\mathrm{D}\textsc {ec}(sk$, $c)=C(m_1$, $\dots$, $m_{a(\lambda )})$.

• Compactness. The size of the output of $\mathrm{E}\textsc {val}$ is polynomial in $\lambda$ and independent of the size of the circuit C.

• Security. For any legitimate PPT adversary $\mathcal {A}$, the advantage

  $$\begin{aligned} Adv^{\text {ind-cpa}}_{\mathrm{H}\textsc {pke}, \mathcal {A}}(\lambda ):=Exp^{\text {ind-cpa}}_{\mathrm{H}\textsc {pke}, \mathcal {A}}(\lambda )-\frac{1}{2} \end{aligned}$$

  is negligible in $\lambda$, where $Exp^{\text {ind-cpa}}_{\mathrm{H}\textsc {pke}, \mathcal {A}}$ is defined as in Fig. 4. An adversary $\mathcal {A}$ is legitimate if it outputs two messages $m_0$, $m_1$ of identical length.

Fig. 4.

The description of the IND-CPA game $Exp^{\text {ind-cpa}}_{\mathrm{H}\textsc {pke}, \mathcal {A}}(\lambda )$.

Without loss of generality, we assume that the secret key is the randomness that was used during the key generation. This enables to test whether key pairs are valid.

3 Construction

3.1 Group Scheme

A group scheme is an abstraction from the properties of groups formalized via a tuple of PPT algorithms. For our purposes, we further abstract this notion to suit groups where group elements do not necessarily have unique encodings. We adapt the notion described in [4] which in turn generalizes the notion introduced in [11]. As demonstrated in [4], such group schemes benefit from the fact that group elements can be represented with many different encodings. This allows to add auxiliary information inside encodings of group elements in order to add more structure to the group. In our case, however, we exploit that group schemes with non-unique encodings can be used to conceal the structure of the group.

Definition 9

(Group scheme with non-unique encodings). A group scheme with non-unique encodings $\varGamma$ is a tuple of PPT algorithms $\varGamma =({Setup}$, ${Val}$, ${Sam}$, ${Add}$, ${Equal})$.

• ${Setup}(1^{\lambda })\rightarrow pp$ On input the unary encoded security parameter $1^{\lambda }$, ${Setup}$ outputs public parameters $pp$. In particular, $pp$ contains the group order q. We assume that $pp$ is given implicitly to the following algorithms.

We assume that any encoding is represented as a bit string. In order to decide, whether a given bit string is a valid encoding of a group element, $\varGamma$ provides a validation algorithm ${Val}$. We refer to bit strings causing ${Val}$ to output 1 as (valid) encodings of group elements.

• ${Val}(h)\rightarrow \{0, 1\}$ On input a bit string $h\in \{0, 1\}^*$, ${Val}$ outputs 1 if h is a valid encoding with respect to $pp$, otherwise ${Val}$ outputs 0.

In general, it is not sufficient to compare encodings as bit strings in order to decide whether they represent the same group element. Hence, a group scheme needs to define an algorithm that provides this functionality. This algorithm is called ${Equal}$. We require ${Equal}$ to realize an equivalence relation on the set of valid encodings. For any valid encoding $h\in \{0, 1\}^*$, let $\mathcal {G}(h)$ denote the equivalence class of this encoding. In other words, $\mathcal {G}(h)$ contains all encodings that correspond to the same group element as the encoding h. For any valid encoding h, we require that is the order of the group. We refer to the equivalence classes in as group elements.

• ${Equal}(a, b)\rightarrow \{0, 1, \bot \}$ On input two valid encodings a and b, ${Equal}$ outputs 1 if a and b represent the same group element, otherwise ${Equal}$ outputs 0. If either a or b is invalid, ${Equal}$ outputs $\bot$.

In order to perform the group operation on two given encodings, we define an addition algorithm ${Add}$.

• ${Add}(a, b)$ On input two valid encodings a and b, ${Add}$ outputs an encoding corresponding to the group element that results from the addition of the group elements represented by a and b. If either a or b is invalid, ${Add}$ outputs $\bot$.

The sampling algorithm ${Sam}$ enables to produce an encoding of a group element and only uses information that is part of the public parameters pp. Let h be a bit string produced via ${Sam}(1)$.

For any $z\in \mathbb {N}$, let [z] denote the group element corresponding to the equivalence class $\mathcal {G}(h^z)$, where the group operation is performed using ${Add}$. We require the distribution of ${Sam}(z)$ to be computationally indistinguishable from uniform distribution over [z].

• ${Sam}(z)\rightarrow a$ On input an exponent $z\in \mathbb {N}$, ${Sam}$ outputs an encoding a from the equivalence class $\mathcal {G}(h^z)$.

Given the order q of the group, it is sufficient to provide an addition algorithm to enable inversion of group elements. To invert a given group element, we use the square-and-multiply approach to add the given encoding $q-1$ times to itself. Further, it suffices to define an algorithm ${Zero}$ that tests whether a given encoding corresponds to the identity element of the group instead of an algorithm ${Equal}$ as above. To implement the algorithm ${Equal}$ on input two encodings a and b, we invert b, add the result to a and test whether the result corresponds to the identity element using ${Zero}$.

According to [4], a group scheme with non-unique encodings, in addition to the algorithms defined above, provides an extraction algorithm. The extraction algorithm, given a valid encoding, produces a bit string such that all encodings that represent the same group element lead to the same bit string. However, we omit this algorithm, as our construction does not provide one. It remains an open problem to extend our construction with an extraction algorithm such that the validity of the (m, n)-Interactive Uber assumption (see Definition 10) can still be proven.

3.2 Interactive Uber Assumption

The Uber assumption is a very strong cryptographic assumption in bilinear groups first proposed in [10] and refined in [12]. It provides a natural framework that enables to assess the plausibility of cryptographic assumptions in bilinear groups.

In contrast to the original definition, we consider adaptive attacks (in which an adversary may ask adaptively for more information about the game secrets and choose his challenge).

Definition 10

((m, n)-Interactive Uber assumption for group schemes). Let $m=m(\lambda )$ and $n=n(\lambda )$ such that $d:=\left( {\begin{array}{c}n+m\\ m\end{array}}\right)$ is a polynomial⁵ in $\lambda$, and let $\varGamma$ be a group scheme. The (m, n)-Interactive Uber assumption holds for $\varGamma$ if for any legitimate PPT adversary $\mathcal {A}$, the advantage $Adv^{\text {uber}}_{\varGamma , \mathcal {A}}(\lambda )$ is negligible in $\lambda$, where

$$ Adv^{\text {uber}}_{\varGamma , \mathcal {A}}(\lambda ):={\text {Pr}}\left[ Exp^{\text {uber}}_{\varGamma , \mathcal {A}}(\lambda )=1 \right] -\frac{1}{2}\text {.} $$

The game $Exp^{\text {uber}}_{\varGamma , \mathcal {A}}(\lambda )$ is described in Fig. 5. An adversary $\mathcal {A}$ is legitimate, if and only if it always guarantees $P^*({{\varvec{X}}})\not \in \langle 1$, $P_1({{\varvec{X}}})$, $\dots$, $P_l({{\varvec{X}}}) \rangle$ and for any $P({{\varvec{X}}})\in \{P^*({{\varvec{X}}})$, $P_1({{\varvec{X}}})$, $\dots$, $P_l({{\varvec{X}}})\}$, $\deg (P({{\varvec{X}}}))\le n$ in $Exp^{\text {uber}}_{\varGamma , \mathcal {A}}(\lambda )$, where $\{P_1({{\varvec{X}}})$, $\dots$, $P_l({{\varvec{X}}})\}$ are the polynomials that $\mathcal {A}$ requests from its oracle $\mathcal {O}$.

Fig. 5.

The description of the (m, n)-Interactive Uber game $Exp^{\text {uber}}_{\varGamma , \mathcal {A}}(\lambda )$. The oracle $\mathcal {O}$ on input a polynomial $P({{\varvec{X}}})$, returns an encoding of the group element $[P({{\varvec{s}}})]$. We refer to $P^*({{\varvec{X}}})$ as “challenge polynomial” and to $z_b$ as “challenge encoding”. Further, we call the polynomials that $\mathcal {A}$ requests from the oracle $\mathcal {O}$ “query polynomials”.

For technical reasons, we need the maximum total degree n of the polynomials appearing in $Exp^{\text {uber}}_{\varGamma , \mathcal {A}}(\lambda )$ and the number of unknowns m to be bounded a priori.

3.3 Our Construction

Inspired by the construction in [4], an encoding of a group element includes two ciphertexts each encrypting a vector determining an m-variate polynomial over $\mathbb {Z}_q$ of maximum total degree n with respect to some randomly sampled basis $\{a_{1}$, $\dots$, $a_{d}\}$. That basis is hidden inside the public parameters of the group scheme via a perfectly binding commitment. An encoding corresponds to the group element whose discrete logarithm equals the evaluation of the thus determined polynomial at a random point $\mathbf {\omega }\in \mathbb {Z}_q^m$. That random point $\mathbf {\omega }$ is fixed in the public parameters via a point obfuscation $\textsf {po}$.

For our construction we employ the following building blocks: (i) a dual mode NIWI proof system $\varPi$, (ii) a homomorphic encryption scheme $\mathrm{H}\textsc {pke}$ with message space $\mathcal {M}=\mathbb {Z}_q^{d}$ for a family of circuits of arity $a(\lambda )=2$ adding two tuples in $\mathbb {Z}_q^{d}$ component-by-component modulo q, (iii) a point obfuscation ${PObf}$ for message space $\mathcal {M}_k=\mathbb {Z}_q$, (iv) a family $\mathcal {TD}=(\mathcal {TD}_{\lambda })_{\lambda \in \mathbb {N}}$ of families $\mathcal {TD}_{\lambda }$ of languages $\text {TD}$ in a universe $\mathcal {X}=\mathcal {X}_{\lambda }$ with unique witnesses for $y\in \text {TD}$ such that the subset membership problem $\text {TD}\subseteq \mathcal {X}$ is hard, (v) a perfectly binding non-interactive commitment scheme $\mathrm{C}\textsc {om}$ for message space $\mathbb {Z}_q^{d\times d}$, and (vi) a general purpose X-Ind pIO $pi \mathcal {O}$ (i.e. a pIO that is secure with respect to $\mathcal {S}^{X\text {-ind}}$ for a circuit family that only contains circuits with input length at most l, where l is the security parameter used for $pi \mathcal {O}$). Let $n=n(\lambda )$ and let $m=m(\lambda )$ such that $\left( {\begin{array}{c}n+m\\ m\end{array}}\right)$ is a polynomial in $\lambda$. The group scheme we construct depends on n and m. We emphasize this fact by calling it $\varGamma _{m, n}:=({Setup}$, ${Val}$, ${Sam}$, ${Add}$, ${Equal})$. As mentioned above, we provide an algorithm that tests if a given encoding is an encoding of the identity group element, instead of implementing ${Equal}$.

Fig. 6.

The implementation of the ${Setup}$ algorithm producing public parameters $pp$.

In Fig. 6 we describe the algorithm ${Setup}$ of our construction. The number q is a prime number that is greater than $2^{p(\lambda )}$ and will serve as the order of our group scheme. We require $p$ to be a polynomial such that $p(\lambda )\ge poly (\lambda )$, where $poly$ is used to scale the security parameter of $pi \mathcal {O}$. We emphasize that our construction allows to arbitrarily choose the group order q as long as q is greater than $2^{p(\lambda )}$ and prime. Therefore, q can be understood as an input of the algorithm ${Setup}$. For the sake of simplicity, we do not write q as input and assume that ${Setup}$ generates a suitable group order.

We remark that the circuits $C_{\textsf {Add}}$ and $C^{(0)}_{\textsf {Zero}}$ that appear in the algorithm ${Setup}$ implement the addition of two group elements and a test for the identity element respectively. For a description of these circuits we refer the reader to Fig. 7. The polynomial $poly (\lambda )\ge \lambda$ that is used to scale the security parameter for the obfuscator $pi \mathcal {O}$ upper bounds the input length of these circuits $C_{\textsf {Add}}$ and $C^{(0)}_{\textsf {Zero}}$. All versions of addition circuits and all versions zero testing circuits that appear during the proofs are padded to the same length respectively. We emphasize that it is necessary to scale the used security parameter as the pIO $pi \mathcal {O}$ we rely on is secure with respect to $\mathcal {S}^{X\text {-ind}}$ for a circuit family that only contains circuits with input length at most $\lambda ^\prime$, where $\lambda ^\prime$ denotes the security parameter that is used to invoke $pi \mathcal {O}$.

Encodings of Group Elements. Encodings of group elements are of the form $h=(C$, $C'$, $\pi )$. The first two entries $C$ and $C'$ are ciphertexts encrypting vectors and respectively under the public keys $pk$ and $pk '$ respectively, where $d$ is the dimension of the $\mathbb {Z}_q$ vector space of m-variate polynomials over $\mathbb {Z}_q$ with total degree at most n, i.e. $d=\left( {\begin{array}{c}n+m\\ m\end{array}}\right)$. We require the dimension $d$ of the vector space to grow at most polynomially in $\lambda$. The last entry $\pi$ is the so-called consistency proof. We refer to the vectors and as representation vectors of the group element and to the tuple , as representation of the group element. Let $\alpha =(\alpha _1$, $\dots$, $\alpha _m)\in \mathbb {N}^m$ denote tuples with $\sum _{i=1}^m\alpha _i\le n$ and let

$$\begin{aligned} \varphi _\text {pol}:\mathbb {Z}_q^{d}\rightarrow \mathbb {Z}_q[{{\varvec{X}}}]\text {,}(\dots , v_{\alpha }, \dots )^T\mapsto \sum _{\alpha } v_{\alpha }\cdot X_1^{\alpha _1}\cdots X_m^{\alpha _m} \end{aligned}$$

be the vector space homomorphism mapping the standard basis of $\mathbb {Z}_q^{d}$ to a natural basis of the vector space of m-variate polynomials of degree at most n. For well-definedness we use the lexicographical order on the tuples $(\alpha _1$, $\dots$, $\alpha _m)\in \mathbb {N}^m$, particularly, the first vector of the standard basis of $\mathbb {Z}_q^{d}$ is mapped to the constant polynomial 1. The image of $\varphi _\text {pol}$ is and the kernel is $\mathrm {ker}(\varphi _\text {pol})=\{0\}$. Hence, $\varphi _\text {pol}$ is an isomorphism between the vector spaces $\mathbb {Z}_q^{d}$ and $\mathrm {Im}(\varphi _\text {pol})$.

We recall that ${Setup}(1^{\lambda })$ samples the matrix $A$ uniformly at random from ${{\mathrm{GL}}}_{d}(\mathbb {Z}_q)$ such that the first column equals $e_1$. Hence, the matrix $A^{-1}$ exists and has the form $A^{-1}=\left( a_{1}\;|\;a_{2}\;|\;\dots \;|\;a_{d}\right)$ such that $a_{1}=e_1$. The columns $a_{1}$, $\dots$, $a_{d}\in \mathbb {Z}_q^{d}$ form a basis of the vector space $\mathbb {Z}_q^{d}$.

The coefficients of the representation vectors , $\dots$, $f_{d})^T$ and , $\dots$, $f_{d}')^T$ of a group element define the polynomials $f({{\varvec{X}}})$, ${f'}({{\varvec{X}}})\in \mathrm {Im}(\varphi _\text {pol})$ via

In other words, the representation vectors and are the representations of the abstract polynomials $f({{\varvec{X}}})$ and ${f'}({{\varvec{X}}})$ respective to the basis $\{\varphi _\text {pol}(a_{1})=\varphi _\text {pol}(e_1)$, $\varphi _\text {pol}(a_{2})$, $\dots$, $\varphi _\text {pol}(a_{d})\}$. Intuitively, a valid encoding that contains the representation vector corresponds to the group element $[f(\mathbf {\omega })]$, where $\mathbf {\omega }$ is the value that is fixed in the public parameters of the group scheme via $\textsf {po}$. The same holds for the representation vector resulting in a redundant encoding. This approach is similar to the Naor-Yung paradigm [35].

We call the representation , consistent if both representation vectors correspond to the same group element, i.e. the evaluation of the corresponding polynomials $f({{\varvec{X}}})$ and ${f'}({{\varvec{X}}})$ at $\mathbf {\omega }$ are equal. Otherwise, we call such a representation inconsistent. If the representation , is consistent, we call this representation constant if the corresponding polynomials $f({{\varvec{X}}})$ and ${f'}({{\varvec{X}}})$ are constant (i.e. are of total degree at most 0). If a consistent representation is not constant we call this representation non-constant. The purpose of the so-called consistency proof is to ensure consistency of encodings, i.e. to ensure that the corresponding representation is consistent. Further, we use the terms constant, non-constant, consistent, and inconsistent to characterize encodings if the associated representation has the respective properties.

Consistency Proof and Validation Algorithm. The above mentioned consistency proof ensures that the representations, that are encrypted inside of encodings, are consistent. In other words, the consistency proof ensures that both representation vectors and used for an encoding lead to the same group element. We realize this by using the dual mode NIWI proof system $\varPi$ to produce the consistency proof $\pi$ for a relation $\mathcal {R}$. The relation $\mathcal {R}$ is a disjunction of three main statements $\mathcal {R}=\mathcal {R}_1\vee \mathcal {R}_2\vee \mathcal {R}_3$:

The relation $\mathcal {R}_1$ is satisfied for representations that are constant and consistent. We formalize this via relation $\mathcal {R}_{1.a}$:

We recall the convention that the degree of the zero polynomial is defined to be $-\infty$. For technical reasons, we need to make sure that the knowledge of the secret decryption keys $( sk$, $sk ')$ and the knowledge of the used encryption randomness are both sufficient as witnesses. Thus, additionally to $\mathcal {R}_{1.a}$ we define the two relations $\mathcal {R}_{b}$ and $\mathcal {R}_{c}$. The relations $\mathcal {R}_{b}$ and $\mathcal {R}_{c}$ connect the ciphertexts $C$, $C'$ of the encoding with the corresponding representation vectors , appearing in relation $\mathcal {R}_{1.a}$.

At this point we make use of the assumption that a secret decryption key equals the randomness that was used to produce the corresponding public encryption key. The relation $\mathcal {R}_1$ is defined as follows:

$$\begin{aligned} \mathcal {R}_1 := \mathcal {R}_{1.a} \wedge \left( \mathcal {R}_{b}\vee \mathcal {R}_{c}\right) \text {.} \end{aligned}$$

(7)

Given a consistent and constant representation , and resulting ciphertexts $C$ and $C'$, there are two possible witnesses to produce the consistency proof for the relation $\mathcal {R}_1$: using the secret decryption keys $( sk$, $sk '$, , and using the encryption randomness , $R)$, , $R'))$.

The relation $\mathcal {R}_2$ is satisfied for representations that are consistent. Again, we formalize this via a relation $\mathcal {R}_{2.a}$:

The relation $\mathcal {R}_2$ is defined as follows:

$$\begin{aligned} \mathcal {R}_2 := \mathcal {R}_{2.a} \wedge \left( \mathcal {R}_{b}\vee \mathcal {R}_{c}\right) \text {.} \end{aligned}$$

(8)

Given a consistent representation , and resulting ciphertexts $C$ and $C'$, there are two possible witnesses to produce the consistency proof for the relation $\mathcal {R}_2$: using the secret decryption keys $( sk$, $sk '$, , , $\mathbf {\omega }$, $op )$ and using the encryption randomness , $R)$, , $R')$, $\mathbf {\omega }$, $op )$. To be precise, the matrix $A$ also is part of these witnesses. However, as we can assume that $A$ is a part of $op$, we omit this fact in our notation.

The relation $\mathcal {R}_3$ introduces a trapdoor enabling production of consistency proofs for inconsistent encodings.

$$\begin{aligned} \mathcal {R}_3 := \bigl [y\in \text {TD}\bigr ]\text {.} \end{aligned}$$

(9)

This relation only depends on the instance $(\text {TD}$, y) of the subset membership problem $\text {TD}\subseteq \mathcal {X}$ defined in the public parameters. We recall that if $y\in \text {TD}$, there exists a unique witness $w_y$ satisfying the witness relation for the SMP. Hence, the witness for the relation $\mathcal {R}_3$ is $(w_y)$. Given public parameters $pp$ that are generated via ${Setup}(1^{\lambda })$, y is not in $\text {TD}$. Therefore, there exists no trapdoor if $pp$ is generated honestly.

Let rp denote the parts of the public parameters that are necessary to produce consistency proofs, i.e. $rp:=(q$, $pk$, $pk '$, $\textsf {po}$, $ck$, $com$, $\text {TD}$, y). To be precise, the corresponding language L has the following form:

where . For the sake of clarity, we henceforth omit the parameters rp and treat the tuple $(C$, $C')$ as the statement.

The validation algorithm ${Val}$, on input a bit string $h\in \{0, 1\}^*$, parses h into $(C$, $C'$, $\pi )$ and executes $\textsf {Verify}(gpk$, $crs$, x, $\pi )$ of the underlying NIWI proof system $\varPi$ for the relation $\mathcal {R}$.

Addition and Zero Algorithm. The implementations of the algorithms ${Add}$ and ${Zero}$ need to know secret information that is associated with the public parameters, for instance the secret decryption keys. Therefore, we implement these algorithms as probabilistic circuits and “hard-code” the necessary secret parameters inside. The security requirement of the employed obfuscator $pi \mathcal {O}$ enables to conceal the implementation of these circuits and, hence, conceals the secret parameters that are hard-coded. The PPT algorithms ${Add}$ and ${Zero}$ simply execute the respective obfuscated circuit $\varLambda _{\text {add}}$ and $\varLambda _{\text {zero}}$.

Fig. 7.

Circuit $C_{\textsf {Add}}$ (left) for addition of two group elements, and circuit $C^{(0)}_{\textsf {Zero}}$ (right) for testing whether a given encoding is an encoding of the identity element. Additionally to the publicly available parameters gpk and rp, $C_{\textsf {Add}}$ has the secret decryption keys $sk$, $sk '$, the values $\mathbf {\omega }$, the opening $op$, and the extraction trapdoor $td_{\text {ext}}$ hard-coded. The circuit $C^{(0)}_{\textsf {Zero}}$ knows the publicly available parameter q and additionally has the secret parameters $sk$, $\mathbf {\omega }$, and $A$ hard-coded. The circuit $\oplus$ realizes addition in $\mathbb {Z}_q^{d}$.

In Fig. 7 we present the implementation of the circuit $C_{\textsf {Add}}$ and the implementation of the circuit $C^{(0)}_{\textsf {Zero}}$. We remark that $C_{\textsf {Zero}}$ only uses the representation vector and ignores the representation vector . This enables to exploit the Naor-Yung like double encryption.

The addition circuit $C_{\textsf {Add}}$ is similar to the one constructed in [4]. The difference is limited to the fact that in our case $C_{\textsf {Add}}$ differentiates between three instead of two different possibilities to produce the new consistency proof. The encodings of group elements in the construction of [4] are of the form (h, C, $C'$, $\pi )$, where C and $C'$ are some ciphertexts and $\pi$ is a corresponding consistency proof. The value h is the group element in an underlying group that is represented by the encoding. As h uniquely identifies the represented group element, the equality test simply compares these values of the given encodings. In our case, however, the encodings do not contain a similar entry. Therefore, the implementation of the equality test, or rather the zero test, needs to decrypt the ciphertext $C$ in order to be able to make a statement about the represented group element.

Sampling Algorithm. The sampling algorithm ${Sam}$, on input an exponent $z\in \mathbb {N}$, uses the representation , , 0, $\dots$, $0)^T$, (z, 0, $\dots$, $0)^T)$ to produce an encoding of the requested group element. The consistency proof is produced for relation $\mathcal {R}_1$ using the witness , $R)$, , $R'))$, where $R$ and $R'$ are the randomnesses that are used to encrypt and respectively. If the sampling algorithm does not receive any input, it samples the exponent z from $\{0$, $\dots$, $q-1\}$ uniformly at random and proceeds as above. Due to the IND-CPA security of $\mathrm{H}\textsc {pke}$, the distribution of the output of ${Sam}(z)$ is computationally indistinguishable from uniform distribution over the equivalence class $\mathcal {G}({Sam}(z))$.

We remark that our group scheme allows for re-randomization of encodings. To re-randomize a given encoding, we sample an encoding of the identity element and use the addition algorithm to add it to the encoding to be randomized. We require the employed homomorphic encryption scheme to satisfy an additional natural property. Namely, we require that ciphertexts can be re-randomized by homomorphically adding a fresh ciphertext of 0. This property is also known as circuit privacy.

3.4 Main Theorem

Theorem 1

Let $\varGamma _{m, n}$ be the group scheme constructed in Sect. 3.3. Further, let $pi \mathcal {O}$ be a probabilistic indistinguishability obfuscator with respect to $\mathcal {S}^{X\text {-ind}}$ for a circuit family containing circuits with input length at most $poly (\lambda )$, let $\mathcal {TD}=(\mathcal {TD}_{\lambda })_{\lambda \in \mathbb {N}}$ be a family of families $\mathcal {TD}_{\lambda }=\{\text {TD}\}$ of languages $\text {TD}\subseteq \mathcal {X}_{\lambda }$ such that the subset membership problem is hard, let $\varPi$ be a dual mode NIWI proof system, let $\mathrm{H}\textsc {pke}$ be an IND-CPA secure HPKE scheme, let $\mathrm{C}\textsc {om}$ be a perfectly binding non-interactive commitment scheme, and let ${PObf}$ be a point obfuscation. Then, the (m, n)-Interactive Uber assumption (cf. Definition 10) holds for $\varGamma _{m, n}$.

In Table 1 we give an overview on the proof of Theorem 1. Informally, the “Switching lemma” states that encodings containing different representations of the same group element are hard to distinguish. The distribution $\widetilde{ pp }$ denotes the distribution of public parameters that are sampled according to ${Setup}$ with the difference that y is sampled from within the trapdoor language $\text {TD}$. The distribution $\widehat{ pp }$ denotes the same distribution as $\widetilde{ pp }$ with the difference that the CRS is sampled in hiding mode and $\varLambda _{\text {add}}$ is computed for an addition circuit that simulates consistency proofs and, hence, does not need to know the matrix $A$ or the value $\mathbf {\omega }$. On a high level, the “Swap lemma” states that these two distributions of public parameters are computationally indistinguishable.

The distribution $\overline{ pp }^{(i)}$ (for $i\in \{0$, $\dots$, $m\}$) denotes the same distribution as $\widehat{ pp }$ with the difference that $\varLambda _{\text {zero}}$ is an obfuscation of a zero testing circuit that tests whether the polynomial $f({X}_{1}$, $\dots$, ${X}_{i}$, $\omega _{i+1}$, $\dots$, $\omega _{m})$ equals the zero polynomial. Furthermore, the point obfuscations in $\widehat{ pp }$ obfuscate $\bot$ whereas the point obfuscations in $\overline{ pp }^{(i)}$ obfuscate the values $\omega _{i+1}$, $\dots$, $\omega _{m}$. The distribution $\underline{ pp }$ is the same as $\overline{ pp }^{(m)}$ with the difference that $\varLambda _{\text {zero}}$ is produced for a zero testing circuit that simply tests whether the representation vector equals zero in $\mathbb {Z}_q^{d}$ and, hence, does not need to know the matrix $A$ and anymore.

The “Randomization lemma” basically states that the images of a certain subspace under a randomly sampled vector space isomorphism do not leak any information on the behavior of that isomorphism on pre-images that do not lie in that span.

For the formal definitions and the full proofs we refer the reader to the full version [3].

Table 1. An overview on the steps of the proof of 1. The emphasize changes compared to the previous game. Let $W_i$ denote the witness that is used to prove relation $\mathcal {R}_i$ for $i\in \{1$, 2, $3\}$. The witnesses $W_1$ and $W_2$ contain the used encryption randomness. Further, for a polynomial $P({{\varvec{X}}})$, let $R_{P}:=A\cdot \varphi _\text {pol}^{-1}(P({{\varvec{c}}}\circ {{\varvec{X}}}))$, and for a vector $v^*\in \mathbb {Z}_q^{d}$, let .