Approximation Algorithm for Scheduling a Chain of Tasks on Heterogeneous Systems

Abstract

This paper presents an efficient approximation algorithm to solve the task scheduling problem on heterogeneous platform for the particular case of the linear chain of tasks. The objective is to minimize both the total execution time (makespan) and the total energy consumed by the system. For this purpose, we introduce a constraint on the energy consumption during execution. Our goal is to provides an algorithm with a performance guarantee. Two algorithms have been proposed; the first provides an optimal solution for preemptive scheduling. This solution is then used in the second algorithm to provide an approximate solution for non-preemptive scheduling. Numerical evaluations demonstrate that the proposed algorithm achieves a close-to-optimal performance compared to exact solution obtained by CPLEX for small instances. For large instances, CPLEX is struggling to provide a feasible solution, whereas our approach takes less than a second to produce a solution for an instance of 10000 tasks.

1 Introduction

Today, our daily life requires massive calculations on different computing systems (desktop, data centers) to perform various needs such as physical simulations or google searches. In order to improve the performance of these systems while keeping their energy consumption reasonable, heterogeneous system has merged. This heterogeneous architecture combines both processing elements (such as CPUs, GPUs), and reconfigurable logic (FPGAs).

However, taking advantage of such heterogeneous systems requires efficient use of resources to make profit from the performance of each part for application execution. Thus efficient scheduling of task’s applications is difficult problem often faced by designers and engineers using these complex systems. In fact, with the complexity of applications and architectures, it becomes increasingly difficult to distribute the tasks application effectively. More than a simple load balancing problem, heterogeneity leads to consider efficient scheduling techniques to take account of the different resources specificities. The objective of this work is to determine an efficient scheduling of a parallel application on a heterogeneous resources system in order to minimize both the total execution time (makespan) and the energy consumption. For this purpose, we introduce a constraint on the total energy consumed by the system. We consider in this work, a chain of tasks and communication delay. We conducted this research using the fully heterogeneous micro-server system Christmann RECS$\copyright |$BOX [3]. The rest of the paper is organized as follows. Section 2 discusses some previous efforts in scheduling parallel application on heterogeneous systems, with a focus on makespan and energy minimization. Section 3 presents a detailed description of the mathematical model proposed. In Sect. 4, we present an optimal algorithm for a chain of preemptive task. In Sect. 5 we describe the proposed algorithm for non-preemptive scheduling and approximation ratio we obtain. Section 6 shows some preliminary numerical results. The paper ends with a conclusion in Sect. 7.

2 Related Work

Due to its key importance on performance, the task scheduling problem on heterogeneous platform has been extensively studied and numerous methods have been reported in the literature. They proposed various models and techniques such as dynamical voltage scaling (DVS), list algorithms and genetic heuristics to optimize essentially two main objectives: makespan and energy consumption. Xie et al. [12], demonstrate that minimizing schedule length of a DAG-based parallel application with energy consumption constraint on heterogeneous distributed systems is a nondeterministic polynomial-hard optimization problem. They decompose the problem in two sub-problems beginning by treating the problem of the energy constraint. At each task assignment phase, the energy consumption constraint of the application can always be satisfied by supposing that the unassigned tasks are assigned to the processor with the minimum energy consumption. Then, they proceed to the minimization of makespan, assigning tasks to processors using the earliest finish time (EFT).

Authors in [13], considered the objective of maximizing the probability of completing tasks before a deadline D and to satisfy an energy constraint with execution times and stochastic communications delays. Zhang et al. [15] have treated the problem of robustness under energy constraint. The aim is to maximize system reliability by repairing runtime errors caused by various reasons such as hardware flaws and program bugs while maintaining the energy constraint. Authors in [16] began by giving an IP (Integer Programming) formulation of the problem, then a three-phase algorithm is proposed using the Dynamic Power Management (DPM) and DVS techniques. Several heuristics (iterative, Greedy, random, ...) are proposed in [8] for the problem of scheduling on heterogeneous processors that can change their frequencies among a set of possible values. The objective is to minimize the temperature more than performance and energy of the system. A three-phase list algorithm is proposed by Fard et al. [2]. They began by analyzing and classifying the different objectives and their impacts on the optimization process. The objective is to find a solution that minimizes up to four objectives (energy, makespan, reliability, economic cost).

Many works have also been done using genetic algorithms. Authors in [5], proposed the ECS heuristic (Energy Concious Heuristic) which is used in [7] to form a hybrid approach with the multi-objective genetic algorithm. This approach provides a set of Pareto solutions. More recently in [14], authors proposed a new genetic algorithm to study both objectives at once. Authors in [9,10,11] also use game theory strategies to prove the existence of Nash equilibrium and find a Pareto point.

However, all the aforementioned works did not consider approximation techniques. To the best of our knowledge, we propose the first algorithm with a guarantee of performance. Our model is inspired by [1], where authors seek to minimize the energy consumed during execution by imposing a Deadline D on completion time. In addition, we consider in this work communication cost between tasks and processing elements. Preliminary results on modeling applications and heterogeneous platforms have been presented in [6], we focus in this work on tasks chain to determine a performance guarantee algorithm.

3 Model

This study considers a fully connected heterogeneous multiprocessor platform in which M is a set of m heterogeneous processing elements (GPU, CPU, FPGA...) noted PE. Each element $PE_{k}\in M$ is characterized by its execution frequency $f_{j}\geqslant 1$, $j=\overline{1..m}$. The processing elements are sorted by increasing order of their frequencies ($f_{1}\leqslant f_{2}\leqslant \ldots \leqslant f_{m}$). An application A of n tasks is modeled using a DAG graph G(V, E, w). V represents set of nodes in G, and each node $v_{i}\in V$ represents a task $t_{i}$ which is characterized by its weight $w_{i}$, $i=\overline{1..n}$. We note by W the total sum of the weights $W=\sum _{i=1}^{n} w_{i}$. E is set of communication edges. Each edge $e_{i,j} \in E$ represents a precedence constraint between two tasks $t_{i}$ and $t_{j}$ and refers to the volume of communication from $t_{i}$ to $t_{j}$ denoted by $Ct_{i,j}$ if they are not assigned to the same processing element. Communication cost between each pair of processing elements ($PE_{k}$, $PE_{l}$) is denoted by $Cm_{k,l}$ with $Cm_{k,l}\geqslant$ $Max_{i} \ execut_{i,k}, \forall i\in \lbrace 1,2, \ldots ,n\rbrace$ and $\forall k,l\in \lbrace 1,2, \ldots ,m\rbrace$ as in [6].

A task $t_{i}$ can be executed only after the execution of all its predecessors. We do not allow duplication of tasks or preemption. A task can be executed by all processing units. Execution of task $t_{i}$ on $PE_{k}$ generates execution time equal to $execut_{i,k}=\frac{w_{i}}{f_{k}}$ and power $p_{i,k}=w_{i}*f_{k}^{2}$. We denote by E the allowed quantity of energy consumed during the execution. E represents in our case an energy bound that should not be exceeded during the execution.

We focus this work to a chain of tasks. Our problem can be modeled by mixed integer quadratic constrained program (P). The first constraint simply expresses that each task must be executed only once and on a single processing element. Constraint (2) keeps energy consumption during execution less than E. The third constraint describes that the task $t_{i+1}$ must be carried out after the starting time of the task $t_{i}$ ($i=\overline{1..n-1}$) plus the execution time of $t_{i}$. The communication cost $(Ct_{i,i+1} + Cm_{j1,j2})$ is added if both tasks are executed on two different processing elements ($PE_{j1}$ and $PE_{j2}$) s.t $x_{i,j{1}}=1$ and $x_{i+1,j{2}}=1$.

$$\begin{aligned}&x_{i,j}=\left\{ \begin{array}{ll} 1 &{} \text {if task } t_{i}\,\text {is placed on the processing element} PE_j, i=\overline{1..n},\,j=\overline{1..m}\\ 0 &{} \text {otherwise} \end{array} \right. \\&start_{i} = \text {the starting time of the task }t_{i}, i=\overline{1..n}. \end{aligned}$$

$$\begin{aligned} (P)\left\{ \begin{array}{ll} \sum \nolimits _{j=1}^{m} x_{i,j}=1, \forall i=\overline{1..n} &{} (1) \\ \sum \nolimits _{i=1}^{n} \sum \nolimits _{j=1}^{m} x_{i,j}*p_{i,j}\le E &{} (2)\\ start_{i}+x_{i,j_{1}}*execut_{i,j_{1}}+x_{i,j_{1}}*x_{i+1,j_{2}}(Ct_{i,i+1}+Cm_{j_{1},j_{2}})\leqslant start_{i+1} \quad &{} (3) \\ \qquad \qquad \forall j_{1}=\overline{1..m}, \quad \forall j_{2}= \overline{1..m} \qquad \forall i=\overline{1..n-1}\quad j_{1}\ne j_{2} &{}\\ Z(min)=start_{n}+\sum \nolimits _{j=1}^{m} x_{n,j}*execut_{n,j}&{} \end{array} \right. \end{aligned}$$

4 Optimal Scheduling Algorithm for a Chain of Preemptive Tasks

In this section we propose an algorithm to find the optimal solution of the preemptive scheduling without communication cost for a chain of n tasks on a set of m processing elements.

Lemma 1

The set of schedules that saturate energy constraint is dominant.

Proof

Let $\widehat{C}_{max}$ be the makespan of a solution such that $\widehat{C}_{max}=\frac{P_{1}}{f_{1}}+\frac{P_{2}}{f_{2}}+\ldots +\frac{P_{m}}{f_{m}}$, $P_{i}\geqslant 0$ is the quantity of work put on the processing element $PE_{i}$, $i=\overline{1..m}$. $\sum _{i=1}^{m}P_{i}=W$. We assume that $\sum _{j=1}^{m}P_{j}\,*\,f_{j}^{2}<E$. We construct another solution such that: $l=max\lbrace j\in \lbrace 1..m\rbrace , \ \sum _{i=1}^{j} P_{i}f_{m}^{2}+\sum _{i=j+1}^{m}P_{i}f_{i}^{2}<E \rbrace$ and $P_{1}^{'}=0$, $P_{2}^{'}=0$, $\ldots$, $P_{l}^{'}=0$, $P_{l+1}^{'}=\frac{E-\sum _{j=1}^{l+1}P_{j}f_{m}^{2}-\sum _{j=l+2}^{m} P_{j}f_{j}^{2}}{f_{l+1}^{2}-f_{m}^{2}}$, $P_{l+2}^{'}=P_{l+2}$, $\ldots$, $P_{m}^{'}=P_{m}+\sum _{j=1}^{l} P_{j}+(P_{l+1}-P_{l+1}^{'})$. We obtain a new solution $\widehat{C}^{'}_{max}=\sum _{j=1}^{m}\frac{P_{j}^{'}}{f_{j}}$ with $\sum _{j=1}^{m} P_{j}^{'} f_{j}^{2}=E$. $\widehat{C}^{'}_{max}=\sum _{j=1}^{m}\frac{P_{j}^{'}}{f_{j}}=\frac{P_{l+1}^{'}}{f_{l+1}}+\sum _{j=l+2}^{m}\frac{P_{j}}{f_{j}} +\frac{\sum _{j=1}^{l}P_{j}+(P_{l+1}-P_{l+1}^{'})}{f_{m}}$. Since $f_{m}>f_{j}$, $j=\overline{1..l+1}$, induces $\frac{P_{l+1}^{'}}{f_{l+1}}+\frac{(P_{l+1}-P_{l+1}^{'})}{f_{m}}\leqslant \frac{P_{l+1}}{f_{l+1}}$ and $\frac{\sum _{j=1}^{l}P_{j}}{f_{m}}\leqslant \sum _{j=1}^{l}\frac{P_{j}}{f_{j}}$. Then, we obtain $\sum _{j=1}^{m}\frac{P_{j}^{'}}{f_{j}}\leqslant \sum _{j=1}^{m}\frac{P_{j}}{f_{j}}$. Finally, $\widehat{C}^{'}_{max}\leqslant \widehat{C}_{max}$.   $\square$

Theorem 1

The following Algorithm 2 gives the optimal solution for preemptive scheduling without communication cost with a complexity of $\theta (m)$.

We start by finding the fastest processing element $PE_{j}$, on which we can perform all the tasks. Then we look for the weight of tasks that can be put on the next processing element ($PE_{j+1}$) in order to saturate the energy constraint. We denote by $W_{j}$ the quantity of work put on the processing element $PE_{j}$, $W_{j+1}$ on $PE_{j+1}$. The best solution is obtained when the energy constraint is saturated s.t $W_{j}f_{j}^{2}+W_{j+1}f_{j+1}^{2}=E$ with $W_{j}+W_{j+1}=W$. The solution of the system of two equations with two unknowns is $W_{j}=\frac{E-W\,*\,f_{j+1}^{2}}{f_{j}^{2}-f_{j+1}^{2}}$ and $W_{j+1}=W-W_{j}$. This keeps the realizability of the solution: $E-W*f_{j+1}^{2}\leqslant 0$ because $W*f_{j+1}^{2}\geqslant E$ and $f_{j}^{2}-f_{j+1}^{2}<0$ because $f_{j}<f_{j+1}$. Then $W\geqslant W_{j}>0$ induces $W_{j+1}\geqslant 0$.

We show in the following that Algorithm 2 gives an optimal solution. Let $\widehat{C}_{max}$ be the makespan of the solution obtained by the Algorithm 2: $\widehat{C}_{max}=\frac{W_{j}}{f_{j}}+\frac{W_{j+1}}{f_{j+1}}$ due to the precedence constraint. Let $\widehat{C}_{max}^{'}=\frac{P_{1}}{f_{1}}+\frac{P_{2}}{f_{2}}+\ldots +\frac{P_{k}}{f_{k}}$ be another solution on a set of $k>2$ processing elements, $\sum _{i=1}^{k}P_{i}=W$. We distinguish three possible cases. The first case corresponds to all frequencies are lower than $f_{j}$ s.t $f_{1}\leqslant f_{2}\leqslant \ldots \leqslant f_{k}\leqslant f_{j}$. Hence, $\frac{1}{f_{i}}\geqslant \frac{1}{f_{j}}$ induces $\frac{P_{i}}{f_{i}}\geqslant \frac{P_{i}}{f_{j}}$, $\forall$ $i=\overline{1..k}$. Follows $\sum _{i=1}^{k} \frac{P_{i}}{f_{i}}\geqslant \frac{\sum _{i=1}^{k}P_{i}}{f_{j}}=\frac{W}{f_{j}}$. Finally, since $f_{j}<f_{j+1}$ induces $\sum _{i=1}^{k} \frac{P_{i}}{f_{i}}\geqslant \frac{W}{f_{j}}\geqslant \frac{W_{j}}{f_{j}} +\frac{W_{j+1}}{f_{j+1}}$. Then, $\widehat{C}_{max}^{'} \geqslant \widehat{C}_{max}$.

The second case corresponds to all frequencies are greater than $f_{j+1}$ such that $f_{j+1} \leqslant f_{1}\leqslant f_{2}\leqslant \ldots \leqslant f_{k}$. Hence, $\sum _{i=1}^{k} P_{i}\,*\,f_{i}^{2}\geqslant \sum _{i=1}^{k} P_{i}\,*\,f_{j+1}^{2} = W\,*\,f_{j+1}^{2}>E$. The last case corresponds to $f_{1}\leqslant \ldots \leqslant f_{j}<f_{j+1}\leqslant \ldots \leqslant f_{k}$. To study this case, we start with the following Lemma 2.

Lemma 2

Let A, B, C be three positive integers such as $1\le A< B< C$ and $W_{1}$, $W_{2}$ be two non negative integers such as $W_{1}+W_{2}=W$. If $W_{1}\,*\,A^{2}+W_{2}\,*\,C^{2}=W*B^{2}$ then $\frac{W_{1}}{A}+\frac{W_{2}}{C}>\frac{W}{B}$.

Proof

By replacing $W_{2}$ by $(W-W_{1})$ in $W_{1}*A^{2}+W_{2}*C^{2}=W*B^{2}$, we obtain $W_{1}=W(\frac{C^{2}-B^{2}}{C^{2}-A^{2}})$. Then, by replacing $W_{1}$ by $(W-W_{2})$ we obtain $W_{2}=W(\frac{B^{2}-A^{2}}{C^{2}-A^{2}})$. Follows, $\frac{W_{1}}{A}+\frac{W_{2}}{C}=\frac{W(C^{2}-B^{2})}{A(C^{2}-A^{2})}+\frac{W(B^{2}-A^{2})}{C(C^{2}-A^{2})}$.

Let $\varDelta =\frac{W_{1}}{A}+\frac{W_{2}}{C}-\frac{W}{B}$, we prove in the following that $\varDelta >0$.

$\varDelta =\frac{W(C^{2}-B^{2})}{A(C^{2}-A^{2})}+\frac{W(B^{2}-A^{2})}{C(C^{2}-A^{2})}-\frac{W}{B}=\frac{W}{C^{2}-A^{2}}(\frac{C^{2}-B^{2}}{A}+\frac{B^{2}-A^{2}}{C}-\frac{(C^{2}-A^{2})}{B})$.

We set $X=\frac{B}{A}$ and $Y=\frac{C}{A}$. Observe that $X>1$ and $Y>X$. Follows:

$\varDelta =\frac{W}{Y^{2}A^{2}-A^{2}}(\frac{Y^{2}A^{2}-X^{2}A^{2}}{A}+\frac{X^{2}A^{2}-A^{2}}{YA}-\frac{(Y^{2}A^{2}-A^{2})}{XA})$.

$\varDelta =\frac{W}{Y^{2}A-A}(\frac{XY^{3}-X^{3}Y+X^{3}-X-Y^{3}+Y}{XY})=\frac{W}{Y^{2}A-A}(\frac{-(X-1)(Y-1)(X-Y)(X+Y+1)}{XY})$.

Since $X>Y>1$ we have $(Y-1)>0$, $(X-1)>0$ and $(X-Y)<0$.

Therefore $\frac{-(X-1)(Y-1)(X-Y)(X+Y+1)}{XY}> 0$. Furthermore, $\frac{W}{Y^{2}A-A}> 0$ because $Y>1$. Finally, $\varDelta >0$ induces $\frac{W_{1}}{A}+\frac{W_{2}}{C}> \frac{W}{B}$.   $\square$

Proposition 1

If $\sum _{i=1}^{k} P_{i}*f_{i}^{2}= W_{j}*f_{j}^{2}+W_{j+1}*f_{j+1}^{2}$ and $\sum _{i=1}^{k} P_{i}=W_{j}+W_{j+1}$, then $\sum _{i=1}^{k} \frac{P_{i}}{f_{i}}> \frac{W_{j}}{f_{j}}+\frac{W_{j+1}}{f_{j+1}}$.

Proof

Let $\varphi$ be a sequence of real such as $\varphi _{1}=f_{1}$ and $\varphi _{i}=\sqrt{\frac{\sum _{\alpha =1}^{i-1}P_{\alpha }\,*\,\varphi _{i-1}^{2}+P_{i}\,*\,f_{i}^{2}}{\sum _{\alpha =1}^{i}P_{\alpha }}}$,

for $i=\overline{ 2..j }$. This sequence guarantees that $\varphi _{i-1}<\varphi _{i}<f_{i}$, $\forall$ $i=\overline{2..j}$. Indeed, since $\varphi _{1}=f_{1}$, $\varphi _{2}^{2}=\frac{P_{1}\,*\,\varphi _{1}^{2}+P_{2}\,*\,f_{2}^{2}}{P_{1}+P_{2}} > \frac{P_{1}\,*\,f_{1}^{2}+P_{2}\,*\,f_{1}^{2}}{P_{1}+P_{2}} = f_{1}^{2}$.

Furthermore, $\frac{P_{1}\,*\,f_{1}^{2}+P_{2}\,*\,f_{2}^{2}}{P_{1}+P_{2}}<\frac{P_{1}\,*\,f_{2}^{2}+P_{2}\,*\,f_{2}^{2}}{P_{1}+P_{2}} < f_{2}^{2}$ induces $\varphi _{1}<\varphi _{2}<f_{2}$.

We assume that this is true for $i= j-1$ i.e. $\varphi _{j-2}<\varphi _{j-1}<f_{j-1}$.

$\varphi _{j}^{2}=\frac{\sum _{\alpha =1}^{j-1}P_{\alpha }\,*\,\varphi _{j-1}^{2}+P_{j}\,*\,f_{j}^{2}}{\sum _{\alpha =1}^{j}P_{\alpha }}<\frac{\sum _{\alpha =1}^{j-1}P_{\alpha }\,*\,f_{j-1}^{2}+P_{j}\,*\,f_{j}^{2}}{\sum _{\alpha =1}^{j}P_{\alpha }}<\frac{\sum _{\alpha =1}^{j-1}P_{\alpha }\,*\,f_{j}^{2}+P_{j}\,*\,f_{j}^{2}}{\sum _{\alpha =1}^{j}P_{\alpha }}=f_{j}^{2}$.

$\varphi _{j}^{2}=\frac{\sum _{\alpha =1}^{j-1}P_{\alpha }\,*\,\varphi _{j-1}^{2}+P_{j}\,*\,f_{j}^{2}}{\sum _{\alpha =1}^{j}P_{\alpha }}>\frac{\sum _{\alpha =1}^{j-1}P_{\alpha }\,*\,\varphi _{j-1}^{2}+P_{j}\,*\,\varphi _{j}^{2}}{\sum _{\alpha =1}^{j}P_{\alpha }}$ induces $\varphi _{j}^{2}>\varphi _{j-1}^{2}$.

Finally, $\varphi _{j-1}<\varphi _{j}<f_{j}$. By recurrence, we deduce that $\varphi _{i-1}<\varphi _{i}<f_{i}$.

From Lemma 2 we have:

$\frac{P_{1}}{f_{1}}+\frac{P_{2}}{f_{2}}> \frac{P_{1}+P_{2}}{\varphi _{2}}$,$\frac{P_{1}+P_{2}}{\varphi _{2}}+\frac{P_{3}}{f_{3}}>\frac{ \sum _{i=1}^{3} P_{i}}{\varphi _{3}}$ and then, $\forall$ $l\in \lbrace 1..j\rbrace$ $\frac{\sum _{i=1}^{l-1}P_{i}}{\varphi _{l-1}}+\frac{P_{l}}{f_{l}}> \frac{ \sum _{i=1}^{l} P_{i}}{\varphi _{l}}$. Follows, $\sum _{i=1}^{j} \frac{P_{i}}{f_{i}}> \frac{\sum _{i=1}^{j} P_{i}}{\varphi _{j}}$.

Let another sequence of real $\phi$ such as $\phi _{k}=f_{k}$ and $\phi _{i}=\sqrt{\frac{\sum _{\alpha =i+1}^{k}P_{\alpha }\,*\,\phi _{i+1}^{2}+P_{i}\,*\,f_{i}^{2}}{\sum _{\alpha =i}^{k}P_{\alpha }}}$

for $i\in \lbrace j+1..k-1 \rbrace$. In the same way, we get $f_{i}<\phi _{i}<\phi _{i+1}$, $\forall$ $i\in \lbrace j+1..k-1 \rbrace$. And from Lemma 2, we obtain $\sum _{i=j+1}^{k} \frac{P_{i}}{f_{i}}> +\frac{\sum _{i=j+1}^{k} P_{i}}{\phi _{j+1}}$.

It result that $\sum _{i=1}^{k} \frac{P_{i}}{f_{i}}> \frac{\sum _{i=1}^{j} P_{i}}{\varphi _{j}}+\frac{\sum _{i=j+1}^{k} P_{i}}{\phi _{j+1}}$.

In order to apply once again Lemma 2, we have to decompose $\sum _{i=1}^{j} P_{i}$ and $\sum _{i=j+1}^{k} P_{i}$ into 4 values $W_{L1}, W_{L2}, W_{R1}, W_{R2}$ such that:

$\left\{ \begin{array}{l} W_{L1}+W_{L2}= \sum _{i=1}^{j} P_{i} \\ W_{R1}+W_{R2}=\sum _{i=j+1}^{k} P_{i} \\ W_{L1}+W_{R1}=W_{j} \\ W_{L2}+W_{R2}=W_{j+1} \\ W_{L1}*\varphi _{j}^{2}+W_{R1}*\phi _{j+1}^{2}=W_{j}*f_{j}^{2} \\ W_{L2}*\varphi _{j}^{2}+W_{R2}*\phi _{j+1}^{2}=W_{j+1}*f_{j+1}^{2} \end{array} \right.$ $\Longrightarrow$ $\left\{ \begin{array}{l} W_{L1}=W_{j}*\frac{(\phi _{j+1}^{2}-f_{j}^{2})}{(\phi _{j+1}^{2}-\varphi _{j}^{2})} \\ W_{L2}=W_{j+1}*\frac{(\phi _{j+1}^{2}-f_{j+1}^{2})}{(\phi _{j+1}^{2}-\varphi _{j}^{2})} \\ W_{R1}=W_{j}*\frac{(f_{j}^{2}-\varphi _{j}^{2})}{(\phi _{j+1}^{2}-\varphi _{j}^{2})} \\ W_{R2}=W_{j+1}*\frac{(f_{j+1}^{2}-\varphi _{j}^{2})}{(\phi _{j+1}^{2}-\varphi _{j}^{2})} \end{array} \right.$

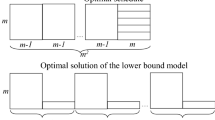
This part of proof is illustrated by Fig. 1. Observe that the result values are all positive. From Lemma 2, we obtain $\frac{W_{L1}}{\varphi _{j}}+\frac{W_{R1}}{\phi _{j+1}}>\frac{W_{j}}{f_{j}}$ and $\frac{W_{L2}}{\varphi _{j}}+\frac{W_{R2}}{\phi _{j+1}}>\frac{W_{j+1}}{f_{j+1}}$.

Hence $\frac{W_{L}}{\varphi _{j}}+\frac{W_{R}}{\phi _{j+1}}=\frac{W_{L1}}{\varphi _{j}}+\frac{W_{R1}}{\phi _{j+1}}+\frac{W_{L2}}{\varphi _{j}}+ \frac{W_{R2}}{\phi _{j+1}}>\frac{W_{1}}{f_{j}}+\frac{W_{2}}{f_{j+1}}$.

Follows, $\sum _{i=1}^{k} \frac{P_{i}}{f_{i}}>\frac{W_{j}}{f_{j}}+\frac{W_{j+1}}{f_{j+1}}$.   $\square$

Now, from Proposition 1, $\widehat{C}_{max}^{'}=\sum _{i=1}^{k} \frac{P_{i}}{f_{i}}>\widehat{C}_{max}=\frac{W_{j}}{f_{j}}+\frac{W_{j+1}}{f_{j+1}}$.

Remark 1

The proof remains valid if $\sum _{i=1}^{k} P_{i}*f_{i}^{2}\leqslant W_{j}*f_{j}^{2}+W_{j+1}*f_{j+1}^{2}$. Indeed, from Lemma 1, we can construct another solution with $P_{1}^{'},P_{2}^{'},\ldots ,P_{k}^{'}$ such as $\sum _{i=1}^{k} P_{i}^{'}=\sum _{i=1}^{k} P_{i}$ and $\sum _{i=1}^{k} P_{i}^{'}*f_{i}^{2}=W_{j}*f_{j}^{2}+W_{j+1}*f_{j+1}^{2}$. Hence, we obtain $\frac{W_{j}}{f_{j}}+\frac{W_{j+1}}{f_{j+1}}<\sum _{i=1}^{k} \frac{P_{i}^{'}}{f_{i}}<\sum _{i=1}^{k} \frac{P_{i}}{f_{i}}$.

Fig. 1.

Resume of the first part of the proof.

5 An Approximation Scheduling Algorithm for Chain of Non-preemptive Tasks with Communication Costs

We assume here a communication cost $Cm_{j,j+1}$ between $PE_{j}$ and $PE_{j+1}$ and communication cost $Ct_{i,i+1}$ between each pair of tasks $t_{i}$ and $t_{i+1}$ with $2\,*\,min_{i}\ Ct_{i,i+1}\geqslant max_{j}\ Ct_{j,j+1}$, $\forall$ $i,j \in \{ 1..n-1\}$. We do not allow preemption of tasks and we transform the previous solution of preemptive scheduling, using the processing elements $PE_{j}$ and $PE_{j+1}$ only.

Proposition 2

If only two processing elements $PE_{j}$ and $PE_{j+1}$ are available, the schedules with only one communication between them are dominant.

Proof

Let {$t_{k+2}\ldots t_{n}$} be the set of uncut tasks of the preemptive solution on $PE_{j+1}$ and $S_{1}$ the sum of their weights. Let $C_{max1}$ the makespan of a feasible solution obtained by processing tasks {$t_{1}\ldots t_{k+1}$} on $PE_{j}$ and {$t_{k+2}\ldots t_{n}$} on $PE_{j+1}$. By contradiction, let suppose that there exists a feasible solution with at least two displacements such as $S_{1}\leqslant S_{2}$, where $S_{2}$ is the sum of the tasks weights on $PE_{j+1}$ with this solution, let $C_{max2}$ be its makespan. We prove that $C_{max2}\geqslant C_{max1}$. Since the second solution is feasible, $S2 \leqslant W_{j+1}$. By the previous algorithm, $W_{j+1}\leqslant S_{1}+w_{k+1}\leqslant S_{1}+max\ w_{i}$ with $i \in \{1\ldots n\}$, and thus $S_{2}\leqslant S_{1} +\text {Max } w_{i}, i=\overline{1..n}.$ $C_{max1}=\frac{W-S_{1}}{f_{j}}+\frac{S_{1}}{f_{j+1}}+Cm_{j,j+1}+Ct_{k+1,k+2}$ and $C_{max2}\geqslant \frac{W-S_{2}}{f_{j}}+\frac{S_{2}}{f_{j+1}}+2*Cm_{j,j+1}+2\,*\,min\ Ct_{i,i+1}$, $i\in \{1 \ldots n-1\}$. Follows, $C_{max2}-C_{max1}=\frac{S_{2}-S_{1}}{f_{j+1}} -\frac{S_{2}-S_{1}}{f_{j}}+Cm_{j,j+1} +2\,*\,min\ Ct_{i,i+1}-Ct_{k+1,k+2}.$ Since $\frac{S_{2}-S_{1}}{f_{j+1}}\geqslant 0$ and $2\,*\,min\ Ct_{i,i+1}-Ct_{k+1,k+2}\geqslant 0$, $\forall$ $i=\overline{1..n-1}$, induce $C_{max2}-C_{max1} \geqslant Cm_{j,j+1}-\frac{S_{2}-S_{1}}{f_{j}}$. Finally, $Cm_{j,j+1}-\frac{S_{2}-S_{1}}{f_{j}} \geqslant Cm_{j,j+1}-\frac{Max \ w_{i}}{f_{j}}$, $i=\overline{1..n}.$ According to the hypothesis, $Cm_{j,j+1}-\text {Max }\frac{ w_{i}}{f_{j}}\geqslant 0$, $\forall$ $i=\overline{1..n}$.

Therefore $C_{max2}-C_{max1}\geqslant 0$ $\Longrightarrow$ $C_{max2}\geqslant C_{max1}$.   $\square$

Theorem 2

The following Algorithm 2 provides a solution for non-preemptive scheduling starting from the preemptive scheduling solution obtained by Algorithm 2 with a complexity of $\theta (n+m)$.

The two variables $\alpha$ and $\beta$ are used to determine the assignment of tasks. In the case $W_{j+1}=0$, we put all the tasks on $PE_{j}$. Otherwise, let $Cost_{1}(v)$ be the cost of executing the first tasks ($t_{1}$ to $t_{v}$) on $PE_{j}$ with $\sum _{i=1}^{v} w_{i}\geqslant W_{j}$, then the rest on $PE_{j+1}$. $Cost_{1}(v)=\lbrace Ct_{v,v+1}+\frac{\sum _{i=1}^{v} w_{i}}{f_{j}}+\frac{\sum _{i=v+1}^{n} w_{i} }{f_{j+1}}+Cm_{j,j+1}\rbrace$. Let $Cost_{2}(v)$ be the cost of executing the first tasks ($t_{1}$ to $t_{v}$) on $PE_{j+1}$, then the rest on $PE_{j}$ with $\sum _{i=v+1}^{n} w_{i}\geqslant W_{j}$. $Cost_{2}(v)=\lbrace Ct_{v,v+1}+\frac{\sum _{i=1}^{v} w_{i}}{f_{j+1}}+\frac{\sum _{i=v+1}^{n} w_{i} }{f_{j}}+Cm_{j,j+1}\rbrace$.

We start by finding the tasks $v_{1}$ and $v_{2}$ that give the best respective scheduling makespan ($Cost_{1}$) and ($Cost_{2}$), and keeping the best one. Finally, we check if the cost generated by using both processing elements $PE_{j}$ and $PE_{j+1}$ is less than the scheduling makespan obtained by performing all tasks on $PE_{j}$.

Example 1

Consider the task graph given by Figure 2. It contains ten task nodes $(n=10)$ labeled from $t_{1}$ to $t_{10}$ with two additional nodes S and E (beginning and end of the application). The edges are labeled with the communication cost between tasks. The nodes are labeled with the weight of each task.

Consider a heterogeneous platform with 3 processing elements, their frequencies are given in Table 1. The communication cost between processing elements are given in Table 2. The maximum energy consumption is E = 1350.

Fig. 2.

Task chain graph.

The application of preemptive scheduling Algorithm 2 gives $PE_{j}=PE_{2}$ and $PE_{j+1}=PE_{3}$ with $W_{2}=0,5625$ and $W_{3}=37,4375$. Since $W_{3}>0$, we obtain $Cost_{1}=Ct_{1,2}+\frac{w_{1}}{f_{2}}+\frac{\sum _{i=2}^{10} w_{i}}{f_{3}}+Cm_{2,3}=17$, $v_{1}=1$. $Cost_{2}=Ct_{7,8}+\frac{\sum _{i=1}^{7}w_{i}}{f_{2}}+\frac{\sum _{i=8}^{10}w_{i}}{f_{3}}+Cm_{2,3}=19$, $v_{2}=7$. $Cost_{1}<Cost_{2}$, induces $Cost=Cost_{1}=17$, $\beta =1$ and $\alpha =1$. Finally, $\frac{W}{f_{2}}=\frac{38}{2}=19>Cost$. We put the task $t_{1}$ on the processing element $PE_{2}$ and tasks $t_{2}$ to $t_{10}$ on $PE_{3}$. $\widehat{C}_{max}=Cost=17$. For this instance, our approach gives the optimal solution.

Table 1. Frequencies of processing elements.

Table 2. Communication cost between processing elements.

Proposition 3

Let $C_{max}^{\star }$ be the optimal solution for non-preemptive scheduling and $\widehat{C}_{max}$ the solution obtained by Algorithm 2, then $\frac{\widehat{C}_{max}}{C_{max}^{\star }}\leqslant \frac{W}{W_{j}+\frac{f_{j}W_{j+1}}{f_{j+1}}}$.

Proof

The optimal solution $C_{max}^{'}$ of the preemptive scheduling is given by $C_{max}^{'}=\frac{W_{j}}{f_{j}}+\frac{W_{j+1}}{f_{j+1}}$. In the worst case for our algorithm, all tasks are executed on the processing element $f_{j}$, thus we get $\widehat{C}_{max}\leqslant \frac{W}{f_{j}}$. Follows $\frac{\widehat{C}_{max}}{C_{max}^{'}}\leqslant \frac{\frac{W}{f_{j}}}{\frac{W_{j}}{f_{j}}+\frac{W_{j+1}}{f_{j+1}}}\leqslant \frac{W}{W_{j}+\frac{f_{j}W_{j+1}}{f_{j+1}}}$. By optimality of Algorithm 2, $C_{max}^{'}\leqslant C_{max}^{\star }$ induces $\frac{\widehat{C}_{max}}{C_{max}^{\star }}\leqslant \frac{\widehat{C}_{max}}{C_{max}^{'}}$, then $\frac{\widehat{C}_{max}}{C_{max}^{\star }}\leqslant \frac{W}{W_{j}+\frac{f_{j}W_{j+1}}{f_{j+1}}}$.   $\square$

Remark 2

This ratio is reached, let consider an instance which generates $W_{j+1}=0$ and $W_{j}=W$ for the preemptive solution, then, $1\leqslant \frac{\widehat{C}_{max}}{C_{max}^{\star }}\leqslant \frac{W}{W_{j}+\frac{f_{j}W_{j+1}}{f_{j+1}}}=\frac{W}{W}=1.$ So, we obtain the optimal solution, $\widehat{C}_{max}=C_{max}^{\star }.$

Remark 3

Since $\frac{f_{j}}{f_{j+1}}< 1$, $\frac{W}{W_{j}+\frac{f_{j}W_{j+1}}{f_{j+1}}}< \frac{W}{\frac{f_{j}}{f_{j+1}}(W_{j}+W_{j+1})}=\frac{f_{j+1}}{f_{j}}$, and finally, $\frac{\widehat{C}_{max}}{C_{max}^{\star }}<\frac{f_{j+1}}{f_{j}}$.

6 Experimental Results

In order to measure the efficiency of our algorithm, we performed several tests on randomly generated instances with different dimensions. For this purpose, we developed a random instances generator in C++ adjustable with several parameters.

General settings are number of tasks n and processing elements m. We denote by $test\_n\_m$ instance defined by these two parameters. The weights of the tasks are generated randomly over an interval [$w_{min},w_{max}$]. The frequencies of the processing elements are randomly generated over an interval [$f_{min}, f_{max}$] while ensuring the heterogeneity of the system by generating different values. The communication costs between tasks are generated randomly over an interval [$Ct_ {min}, Ct_ {max}$] and between processing elements over an interval [$Cm_ {min}, Cm_ {max}$] in accordance with the hypothesis described in Sect. 3. The bound E is randomly generated with respect to $W*f_{1}^{2}<E<W*f_{m}^{2}$.

Our proposed Algorithm 2 were implemented in C++. The exact solution is obtained by solving the model (P) with CPLEX 12.5.0 [4] and the OPL script language. The following Table 3 shows the results of tests on different instance sizes. We have generated 30 instances for the first four rows (from instance $test\_8\_3$ to $test\_20\_4$) and then one instance for the others due to the large running time on CPLEX.

The PS (Preemptive Scheduling) columns present the makespan average solution obtained by the Algorithm 2. The NPS (Non-Preemptive Scheduling) columns present the makespan average solution obtained by the Algorithm 2 and its average execution time. The CPLEX columns present the average makespan solution of the resolution of the model (P) with CPLEX and the average computation cost required as well as the optimality of the solutions. Finally, the columns $GAP_{1}$ and $GAP_{2}$ present the average ratio between the solution obtained by $Bound_{1}=\textit{CPLEX}$ solution and $Bound_{2}=\text {Preemtive solution}$ with NPS solutions which is calculated as follow:

$\text { } \text { }\text { }\text { }\text { }\text { }\text { }\text { }\text { }\text { }\text { }\text { }\text { }\text { }GAP_{i} = \frac{\text {Heuristic Solution} - Bound_{i} }{Bound_{i}} * 100, i\in \{1,2\}.$

Since the execution time of a quadratic model is generally too large, we have therefore limited the running time for CPLEX to 60 min. In Table 3, we can notice that for most of the instances with less than 30 tasks, our algorithm gives an optimal solution with smaller running time than CPLEX. Moreover, for larger instances, CPLEX takes much longer to find a solution, whereas NPS gives a solution in less than one second for an instance with 10000 tasks.

Table 3. Evaluation of the NPS heuristic compared to CPLEX.

7 Conclusion and Future Work

This paper presents an efficient approximation algorithm to solve the task scheduling problem on heterogeneous platform for the particular case of linear chain of tasks. Our objective is to minimize both the total execution time (makespan) and the energy consumption by imposing a constraint on the total energy consumed by the system. This work has shown that finding an efficient scheduling is not easy. Tests on large instances close to reality shows the limits of solving the problem with a solver such as CPLEX.

The main contribution of this work is to give an algorithm which provides a solution with small running time, and also guarantee the quality of the solution obtained compared to the optimal solution. The ratio obtained depends on the frequencies of two successive processing elements $PE_{j}$ and $PE_{j+1}$ used in preemptive scheduling. The performance ratio of our algorithm is bounded by $\frac{f_{j+1}}{f_{j}}$. As part of the future, we will focus on the extension to more general classes of graphs to handle real application.