Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The understanding behind managing and conserving the environment, including water resources, has an important role in worldwide development strategy. The high priority given to reestablishing and maintaining good ecological status is reflected in multiple national legislations in Europe as well as in the EU Water Framework Directive (WFD). However, despite these emerging institutional protections, water withdrawal and, among other economic uses, continue to claim large fractions of the goods and services provided by aquatic ecosystems in the world’s river basins. Consequently, much research and experimentation is needed to reestablish the ecological integrity of aquatic ecosystems, their habitats, and flow conditions.

What Is Habitat?

Habitat is where aquatic organisms prefer to live or the living characteristics of a river that aquatic organisms are using. Although habitat is fundamentally a description of what animals use and where animals are found, most ecologists assume that habitat also is what animals need to survive and reproduce. Field experiments sensu “habitat modeling” give the most reliable data what animals need, and ecologists regularly engage in discussions about best available concepts, scales, and whether our habitat studies are properly designed and interpreted. However, in this chapter we assume that habitat is the part of a river that fish or benthic invertebrates and their life stages prefer for a successful survival and reproduction.

Habitat modeling can contribute to meeting the ongoing challenge of wisely balancing demands for the environmental services between society and nature (Bain 1995). This is especially so for those environmental services that sustain the integrity of ecosystems, e.g., environmental flows (e-flow). Habitat modeling offers a tool to apply e-flow concepts for science research and management policy. The concept of e-flows is used to mitigate the impacts of altered flow regime, often by assigning compensation flow releases to maintain ecological integrity and a good ecological status (see Chap. 4).

Ideally, attempts to establish or maintain environmental flow regimes will take into consideration the quantity, timing, duration, frequency, and quality of water flows needed to maintain ecosystems and the services they sustain. Prescriptions to reestablish ecologically suitable compensation flows can be based on hydrological metrics, e.g., percentage of average flow and/or hydraulic habitat algorithms. The latter link hydraulic descriptions of rivers with “preference” models of fish life stage responses to microhabitat hydraulics (Linnansaari et al. 2012). There is a growing consensus to combine these approaches, because hydrological metrics characterize temporal variations in the aquatic environment but are poorly suited to analyze spatial variations, whereas the opposite is true for hydraulic habitat models (e.g., Poff 2009; Poff and Zimmerman 2010). Furthermore, approaches have been proposed to model the ecological effects of flow regime on population processes (e.g., growth and survival; Armstrong and Nislow 2012) and dynamics rather than time-averaged population abundance (Shenton et al. 2012).

Hydrologically based methods are still the most widely used approaches internationally (Tharme 2003). This is probably due to their ease of use and low cost, since such methods use only “stream real” or simulated flow data series. A naturally variable regime of flow, rather than just a minimum low flow, is required to sustain freshwater ecosystems (Poff et al. 1997; Bunn and Arthington 2002; Poff 2009), and this understanding has contributed to the implementation of environmental flow management on thousands of river kilometers worldwide (Lobb and Orth 1991; Linnansaari et al. 2012).

The flow regime is regarded by many aquatic ecologists to be a key driver of ecological processes that sustain the integrity of river ecosystems. Flow is a major determinant of the parameters that constitute physical habitat in streams, which in turn, is a major determinant of biotic composition. Consequently, flow dynamics play an important role for aquatic organisms (see Chap. 4). Aquatic organisms have evolved life history strategies primarily in direct response to natural flow regimes (Schmutz et al. 2000; Bunn and Arthington 2002). River discharge typically varies significantly during the annual cycle, depending on climate and catchment conditions. Aside from natural phenomena, long- and short-term flow fluctuations can be altered by human activities. Therefore, flow/habitat relationships have to be established for all relevant species and life stages in order to cover the entire variability of responses to the natural flow.

2 Principles of Habitat Modeling

Habitat models allow one to assess the quality and quantity of habitat for a species within the study area or a river reach and provide the basic information required for environmental (flow) assessment. Aquatic habitat suitability models relate suitability to individual maps that are divided into uniform, spatially discrete units, e.g., rasters. These maps are digitally stored as raster-based layers, wherein each raster contains data, such as abiotic topographic descriptors. Current methods assume that the hydraulic measure is directly or indirectly related to habitat quantity for a target species, almost exclusively fish (e.g., Bovee 1982; Reiser et al. 1989), or in some instances the ecological function of the river (e.g., Gippel and Stewardson 1998).

All habitat modeling approaches depend on spatial scales and incorporate biological data based on standardized sampling methods for ecological assessment. These approaches use hydromorphological indicators for habitat assessment, which relies on correlative relations between habitat suitability for biota and hydrological features of river stretches on different scales (e.g., micro- or mesohabitat; Parasiewicz and Walker 2007).

The primary components of the physical habitat in running waters are water depth, velocity, substrate size, and cover, and most habitat models for aquatic organisms are based on these parameters (e.g., IFIM; Bovee 1982). After Jowett (2003) habitat modeling can be generally subdivided into two main categories:

  1. 1.

    Empirically based habitat suitability models are based on a description of the abiotic environment that is subsequently linked to the biotic system of flora and fauna that are described based on the concept of their available habitat. Univariate or multivariate functions link abiotic characteristics to habitat suitability. Univariate functions consider individual parameters, while multivariate analysis takes into account the interaction of physical variables and determines species response to cumulative effects of a number of environmental characteristics.

  2. 2.

    Process-based population or bioenergetic models describe biological processes based on knowledge of species population dynamics and/or energy budgets for feeding, growth, or other functions. These models can either be linked to the results of a physical habitat model or be directly linked with data describing the physiographic environment. Bioenergetic models are a special type of biological process model where optimal fish or benthic invertebrate location is based on energy budgets. These models compute how much energy a fish uses as a function of water velocity or turbulence and of food intake. Optimal locations for indicator species are denoted by budget excesses of energy intake over energy loss due to the current.

While a suite of different types in habitat simulation methods can be identified, the general approach to evaluate effects of flow on habitat quantity is the same across different habitat modeling methods. The objective is to establish a relationship between river discharge and, typically, the amount of wetted perimeter and/or the wetted usable area (WUA), and then use this relationship to identify a “critical threshold.” Briefly, this means finding a discharge level below which a drastically increasing amount of river bed becomes unsuitable for biota or even dry. A typical application measures the response in hydraulic variables across a number of “representative” cross sections of the river channel over a range of different discharges (measured or simulated using a 1D hydrodynamic model).

In general, a number of state-of-the-art habitat models focusing at different scales (micro, meso, and macro) with various implementing statistics and modeling techniques are available for e-flow assessment. Mostly these are based on the principles of PHABSIM (physical habitat simulation) technique which is used currently all over the world (e.g., Fausch et al. 1988; Harby et al. 2004a, b).

The PHABSIM technique enables the quantitative prediction of suitable physical microhabitat in a river reach for chosen species and life stages under different river flow scenarios, similar to that are mesohabitat models (e.g., MesoHABSIM or MEM (Mesohabitat Evaluation Model); Parasiewicz 2001 and Hauer et al. 2008). Other alternative methods are available, but their predominant emphasis on hydrology does not support a comprehensive assessment of both the hydrological and morphological conditions (e.g., Hauer et al. 2011). A short overview of the implementation on micro- and mesohabitat scale is given in Sect. 3.

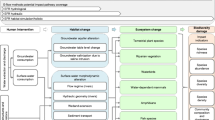
Consequently, such indicator-based habitat model consists of several integrative parts (Fig. 7.1) that are linked together:

  1. 1.

    Biotic habitat modeling: The aim is to model and assess the biological species occurrence with their physical environment. This includes sampling and analyses of habitat and the morphological characteristics: fish or benthic invertebrate ecological assessment, determination of standardized habitat use, and habitat preference curves for key indicator species and their live stages.

    1. (a)

      Standardized biotic sampling of species abundance:

      1. (i)

        Microscale: point abundance sampling (e.g., electrofishing, snorkeling)

      2. (ii)

        Mesoscale: mesohabitat sampling (e.g., electrofishing)

    2. (b)

      Hydromorphological parameter sampling across a range of discharges: water depth and flow velocity, substrate size, embeddedness and stability, cross-sectional geometry, slope, river type, topology, channel or bank stability, sinuosity, width-depth ratio, presence of barriers, land-use activity, geology-lithology, geomorphology, altitude, Froude number, etc.

    3. (c)

      The most important factors are flow (discharge), flow velocity, water depth, substrate, and cover. Within each of these categorical parameters, several to many classes (factors) are included.

  2. 2.

    Abiotic habitat modeling: Physical factors, or hydraulic modeling, provide information of changes in the physical habitat as a function of discharge (hydraulic model). The objective is to quantify changes of the physical environment in relation to changes in flow or even morphological adjustments (natural or man-made). This includes physical and spatial measurement (sampling) and analyses of:

    1. (a)

      Hydrologic characteristics: base flow, peak flow and duration, drought events, inter-annual variation of flow, flood and drought regime, spatial variation of discharge, longitudinal variation of cumulative water yield, seasonal variability in runoff, mean and maximum monthly water temperature, drainage area, stream order, branching degree, and distribution.

    2. (b)

      Hydraulic characteristics: local flow velocity, mean cross-sectional velocity, water depths, shear stress, wetted perimeter, surface-subsurface lateral linkage, and turbulence.

    3. (c)

      Morphological characteristics: see biotic part.

  3. 3.

    Integrative habitat assessment: The aim is to merge biotic habitat assessment with the abiotic flow and hydromorphological part and, as a management tool, to determine an adapted and suitable environmental flow for aquatic organism. The metrics are determined as reach-related averages, e.g., weighted useable area (WUA) derived from biota-specific habitat preferences and hydraulic 1D or 2D/3D model simulations.

Fig. 7.1
figure 1

A conceptual example for aquatic habitat modeling in rivers illustrating the process and main steps: (1) biotic and (2) abiotic habitat modeling which lead to (3) integrative habitat assessment. The colors in (1) and (3) show the optimum (green), the useable (brown and yellow), and not useable (red) water depth-based HSI (habitat suitability index) for a certain indicator species (e.g., adult European grayling)

Full size image

2.1 Biotic Habitat Modeling

For multiple reasons, fish and their life stages have proven to be one of the most suitable impact indicators of human activities related to flow and habitat modifications. This is so, because fish populations are significantly affected by all human impact types on rivers, especially by water withdrawals. Fish identification is relatively easy and their taxonomy, ecological requirements, esp. for complex migration patterns and life histories, are generally better known than for other taxa. The longevity of many fish species enables assessments to be sensitive to disturbance over relatively longtime scales. Finally, fish are valuable economic resources and are of public concern. Using fish as indicators confers an easy and intuitive understanding of cause-effect relationships to stakeholders beyond the scientific community. However, also other indicator groups such as macroinvertebrates or macrophytes might be appropriate depending on the questions to be answered.

There are two common technical ways to build these models:

  1. 1.

    Literature review and expert opinion-based habitat suitability models.

  2. 2.

    Empirical and statistical techniques for estimating habitat suitability.

Literature Review and Expert Opinion-Based Habitat Suitability Models

A common habitat suitability modeling technique is based on literature review and expert opinion and generally follows the ideas established in 1980 by the US Fish and Wildlife Service publication “Habitat as a basis for Environmental Assessment.” While literature-based models are subject to uncertainty and errors when transforming literature-based habitat studies to a specific river, they are relatively easy to create, because they do not require new collection of detailed field data and can be applied to multiple study areas and allow rapid analyses and modeling designs.

The procedure assigns a weight to each factor (parameter) and a habitat suitability score to each class within this factor. Suitability scores for all habitat factors are then combined to form a single habitat suitability map with a suitability score for each point on the sampling grid.

Combining habitat factors, the two most common methods of combining factors are arithmetic mean and geometric mean models. Further details on these models can be found in the Standards for Development of HSI Models section of the Habitat Evaluation Procedures Handbook.

Empirical and Statistical Techniques for Estimating Habitat Suitability

Sampling design

If presence-absence or species occurrence data are available in a study area, then empirical statistical models can be created by relating the species occurrence data to habitat factors. Sampling is the prerequisite for any related impact assessment and therefore takes a crucially important role for any modeling considerations. Generally, a distinction between (i) qualitative and (ii) quantitative sampling methods can be made. Depending on the scope or aim of a specific project and/or research hypothesis, it can be desirable to quantify the exact number of individuals, e.g., population number or density, in a certain area, or just to gain knowledge of the occurring species and their relative abundances (Bozeck and Rahel 1992). The main advantage of qualitative fishing is the reduced effort compared to that required for quantitative population estimates. In order to achieve the best possible results, several fish sampling methods can be applied and combined such that they are aligned to the methods selected for habitat modeling and e-flow assessments:

Fish data, obtained by electrofishing, can be used to assess ecological impacts and the sufficiency of e-flows. Standardized electric fishing procedures are described in detail in the European CEN Directive on Water Analysis—Fishing with Electricity (EN 14011; CEN 2003) for rivers. Fishing procedures and equipment differ depending upon the water depth and wetted width of the sampling site. Point abundance sampling by electrofishing (PASE) is a frequently used sampling method to define fish habitat; however, size selectivity and fish escapement patterns might be of concern (e.g., Persat and Copp 1988; Brosse et al. 1999).

Snorkeling is a prime method for underwater observation and study of fish in flowing waters. Snorkel surveys are widely used to monitor fish populations in streams and to estimate both relative and total abundance (Slaney and Martin 1987). Snorkeling can also be used to assess fish distribution, presence/absence surveys, species assemblages (i.e., diversity), some stock characteristics (e.g., fish length estimation), and habitat use. Snorkeling gear is worn by biologists who, individually or in small teams, survey fish abundance, distribution, size, and habitat use while slowly working in (generally) an upstream direction. This technique is most commonly used to survey juvenile salmonid populations but can also be used to assess other species groups. Snorkel survey programs have been designed and implemented so as to standardize procedures for underwater techniques to survey fish species in streams (Thurow 1994; Greenberg et al. 1996; O’Neal 2007).

Visual observation is an appropriate method to conduct daily surveys of fish species’ presence, number of individuals, and habitat size, e.g., in their spawning habitat. Very clear water and shallow habitats are required to count spawning individuals by visual observation. Habitat features, i.e., flow velocity, water depth, shading, cover, flow protection, type of structure, substrate, and embeddedness, are recorded at spawning grounds.

As an example, Melcher and Schmutz (2010) monitored spawning habitats of 1250 nase (Chondrostoma nasus) in the river Pielach, Lower Austria. Spawning took place in April and fish spawned in shoals on shallow gravel bars that are easy to identify from the river bank. A grid of equally spaced points was laid over the spawning area (grid size 1 m2; see Fig. 7.2). Additionally, representative sites were sampled with different morphological characteristics within the study area to describe the entire available habitat. Furthermore, point measurements were taken interspersed at 2 m intervals along transects, resulting in hundreds of microhabitat measurements as graphically explained in Fig. 7.2.

Fig. 7.2
figure 2

Description of a sampling design on microhabitat scale, using transects to measure hydromorphological parameters at each habitat where fish have been observed (grey dots) and remaining habitat with no fish habitat observed (white dots) (after Schneider et al. 2008 and Melcher et al. 2012)

Full size image

Statistical techniques

In general statistical techniques such as generalized linear or generalized additive models (e.g., logistic or Poisson regression), artificial neural networks, classification and regression trees (CARTs), and genetic algorithms can all be used to create a map of a species probability of occurrence at any point of interest (e.g., standardized sampling grid) in a river.

With these models, data observed at each site is typically extracted from a “habitat database” and assembled by occurrence hierarchy; analyzed with statistics packages such as R, SPSS, or SAS; and then fed back into the database to create a table and map storing each probability of occurrence of a certain species.

While empirical models are probably more accurate than rule-based or literature-review based models, they require gathering a good set of field observations for every species and life stage in the linkage area, which can require a considerable amount of resources.

All habitat approaches have a fundamental, sometimes untested, assumption that, e.g., fish species make decisions about how to move along a river using the same rules they use to select habitat. It is reasonable to assume that a species prefers to move through areas that provide food, sufficient water, cover, and reproductive opportunities. But it is important to admit that we never know for sure, e.g., if reproductive individuals were trapped in a river reach by dams and their presence implies that they breed there. Only a small fraction of papers on movement describe the type of movement we are most interested in, namely, why, how, and when animals move between patches of suitable and unsuitable habitat.

Univariate suitability functions

Biological habitat models describe deterministic relations that link biological responses to physical habitat. The models interpret the species presence or abundance in areas with particular characteristics (e.g., depth, velocity) as the measure of the habitat’s suitability for any given species. Originally each characteristic was analyzed individually, and algorithms selected a priori were used to account for this information. In these univariate suitability functions, the suitability of a habitat is a function of one variable characterizing one physical characteristic of the habitat. Usually, the function gets values between 0 and 1, so that for the least suitable conditions the function has the value 0, and at the most suitable conditions the value 1 (Fig. 7.1).

Three different types of habitat suitability indices are distinguished after Bovee (1986):

Category I indices are based on information other than field observations made specifically for the purpose of suitability index development. They can be derived from life history studies in the literature or from professional judgment. This latter case may involve round table discussions, the Delphi technique (which overcomes some disadvantages of traditional committee meetings), or hybrid techniques such as “habitat recognition,” where the experts are taken to a stream and asked to assess the suitability of various habitats.

Category II indices use data collected specifically for habitat studies, based on frequency analysis of the actual habitat conditions used by different species and life stages in a stream. Location of target species may be by one of a number of methods—direct observation (from the bank, snorkeling, or scuba) video, telemetry, trapping/physical capture, or electric fishing. Location of target species is accompanied by measurement of the relevant physical habitat variables at the point of observation.

Category III data combine a category II frequency analysis with additional information on the availability of habitat combinations in the sampling reaches. It has been suggested that this methodology can correct for bias caused by habitat availability in the source stream(s) and thus make indices more generic. It is clear that calculation of preference cannot take into account habitats that are not present in a stream and that occupancy/non-occupancy of low-availability habitat may significantly alter calculated preference. However, so long as care is taken not to undertake surveys on rivers with low physical diversity, calculation of preference provides the best way of removing the complicating problem of differing habitat availability between sites.

Univariate preference curves can be derived using a number of ratio formula or preference indices. The simplest is a ratio where preference (P) = use (U)/availability (A). The preference functions can be delimited to take account of time of day, seasonal, life history, and activity factors. When a physical habitat is described by more than one parameter, a combination of several preference curves has to be made. Several combinatory techniques can be chosen here, for example, to use the minimum value of each preference outcome or to use a mean or sum of all parameters or more elaborated statistical methods (see below).

Multidimensional statistical analyses for biological modeling

Numerous habitat modeling studies have been undertaken over time in North America and Europe, first mainly for salmonids (e.g., Northcote 1984; Shirvell 1989; Wollebaek et al. 2008; Moir and Pasternack 2010) but later for non-salmonids also (e.g., Melcher and Schmutz 2010). Predominantly these studies applied univariate habitat use and preference curves. In order to assess anthropogenic alterations on riverine systems, most attention was focused on morphological habitat attributes.

It was recognized that functional processes in riverine environments depend on the interactions of many factors, such as flow velocity and/or riparian vegetation (Melcher and Schmutz 2010). As a result, a more sophisticated analytical toolset is required to quantify the biological consequences of impacted multi-metric environments and to assess fish habitat improvements in river activities. Multidimensional analyses are needed to better identify and understand habitat requirements (Melcher et al. 2012). Until now parametric methods such as classical variance, regression, or discriminant function analyses (Ahmadi-Nedushan et al. 2006) have been the main statistical methods used for habitat modeling. Due to their specific statistical presumptions and requirements, their use is frequently limited in comparison to nonparametric methods (e.g., CHAID tree).

Logistic regression is a multiple regression model used in habitat modeling in the way that the probability of occurrence is regressed against a number of potential habitat characteristics. It requires field observations of habitat characteristics available and utilized by indicator species. Habitat choice is described by the probability of a specific choice occurring along a habitat gradient. Using the stepwise procedure, all significant parameters to describe the habitat are listed (Melcher et al. 2012). The result can be a map that shows the probability of fish occurrence for each location, each area, or each computational grid cell. The probability of occurrence can be converted to an HSI (habitat suitability index score).

Classification trees, often referred to as decision trees, predict the value of a discrete dependent variable with a finite set of values (called classes) from the values of a set of independent variables (called attributes), which may be either continuous or discrete (Breiman et al. 1984; Quinlan 1986). Data describing a real system, represented in the form of a table, can be used to “learn” or automatically construct a decision tree. Decision trees thus constitute a multivariate statistical method of exploration and data analysis by classification. This approach can be applied to predict the presence/absence of fish species from habitat characteristics described by a set of independent variables. The habitat modeling CHAID tree method describes specific fish habitat on microhabitat to reach scales. The method allows one to highlight the importance of and interactions among hydromorphological parameters, e.g., flow velocity or substrate for typical fish habitats (Melcher et al. 2012).

Fuzzy rule-based preference functions

Another approach to evaluate habitat quality is fuzzy rule-based modeling (Jorde et al. 2001; Schneider et al. 2001). Fuzzy modeling allows working with imprecise or “fuzzy” information. This comes with the significant advantage that expert knowledge readily available from experienced fish biologists and supported by local investigations (electrofishing, observation) can easily be transferred into preference data sets by setting up checklists. These lists or so-called fuzzy rule systems (e.g., CASiMiR (computer- aided simulation model for instream flow and riparian), http://www.casimir-software.de) offer a range of possible combinations of relevant physical criteria and let experts define if habitat quality is good or low.

2.2 Abiotic Habitat Modeling

All habitat modeling techniques require some information about hydraulic characteristics. The most commonly used method is the “wetted perimeter method” that predicts wetted area of a cross section as a function of discharge at a location (one point) in the river (Tharme 2003). Hydraulic factors may come directly from measurements or from hydraulic models and hydraulic assessment methods (e.g., Harby et al. 2004a, b).

Direct measurements of hydraulic factors: By sampling several times over a range of flows, it is possible to construct an empirical relationship between physical conditions and discharge. Habitat suitability’s are calculated for measured flow rates, and habitat suitability’s for different discharges are derived by interpolating from the measured range of flow data. Such a method does not require the investigator to accept any underlying requirements or assumptions of a particular hydraulic modeling technique. The predictability of this model is limited to the range of measured discharges.

Hydraulic rating methods, which are also known as habitat retention or hydraulic geometry methods (Tharme 2003), are based on a relationship between some hydraulic parameters of a river (usually wetted perimeter or depth) and discharge (e.g., Jowett 1993, 1997). Leopold and Maddock (1953) described simple power functions that can be used in describing changes in hydraulic variables as a function of discharge. The constants and the exponents in these equations should be empirically developed for each river or region, as the general form of river channels is variable (Linnansaari et al. 2012).

An alternative approach is to use statistically based models of river hydraulics. While empirical models of variation in broad morphometric channel variables have been in existence for many years, it is only recently that these statistically based techniques have been applied to model habitat hydraulics at the reach or “mesohabitat” scale. It has been suggested that at the reach scale, statistical hydraulic models can provide estimates of the frequency distribution of hydraulic variables, when given simple inputs such as mean river velocity, depth, and width (Lamouroux et al. 1995, 1999). Statistical techniques have shown that consistent patterns of such distributions appear among different streams. Based on power laws or multiple measurements, both depth-discharge and width-discharge relationships can be obtained, linking discharge to existing hydraulic distribution patterns. This method requires a wide range of input data from different streams in various catchment areas. Once a “library” of occurring patterns is established, the effort necessary for obtaining depth/width-discharge relations is relatively low. It should be also noted that current models are most suited to rivers with relative natural morphology. Their value lies in their ability to analyze broad trends in habitat hydraulics, rather than the specific description of a particular reach (Linnansaari et al. 2012).

Additionally, hydrodynamic-numerical models have been used in habitat modeling for many years. Hydrodynamic-numerical modeling strongly relies on using a range of river stretches with catchment typical hydromorphological characteristics (hydrology, bed substratum, bed structures, degree of braiding, sinuosity of the river course, mean bed width, and bed slope). As a result, a set of model equations enables the simulation of fish habitat conditions in river stretches as a function of flow and morphology. The habitat suitability of selected river sections is assessed mainly in terms of the needs of the life stages of important indicator fish species.

Flow calculations based on the conservation of mass, momentum, and energy provide the foundations of hydrodynamic-numerical modeling. These calculations can be generalized as nonlinear, partial differential equations, e.g., Navier–Stokes, which can be solved in the general case only by approximation with numerical methods. Navier–Stokes equations include no simplifications. That means, if no errors are introduced by the numerical solution, complex flow phenomena can even be correctly calculated to the last detail.

The Navier–Stokes and Reynolds equations can be simplified in various ways, namely, by reducing the dimensionality or through neglect or simplification of terms of output equations. Especially for habitat modeling (e-flow studies), most applications allow a dimension to be neglected only if the flow components in the corresponding direction are negligible (e.g., cross distribution of flow velocity).

In computational fluid dynamics, high-resolution techniques are applicable, e.g., direct numerical solutions (DNS) (Lin and Liu 1998), Reynolds-averaged Navier–Stokes (RANS) (Sinha et al. 1998), large eddy simulation (LES) models (Wu 2004), and smoothed particle hydrodynamics (Monaghan and Kos 1999). Those numerical codes can be used for environmental flow assessments, such as detailed studies on the impacts of turbulence phenomena on macroinvertebrates. For reach-scale environmental flow assessments, however, computational time and the required modeling boundaries make this kind of analysis mostly impracticable.

According to the computed resolution of flow velocity, three-dimensional, two-dimensional, and one-dimensional hydrodynamic-numerical models can be applied for hydraulic and environmental flow studies. The simplest form of numerical modeling is the one-dimensional modelling approach with the assumption that there is no variability of the flow velocity in the vertical and lateral direction in the cross section.

These simplifying assumptions of a one-dimensional model represent often a limit to the applicability of such ecohydraulic studies. Local differences in flow velocity (especially in cross-sectional distribution) cannot be determined with the assumptions of one-dimensional, shallow water equations. To apply simplifications to the 2D-shallow water equations requires two assumptions: (i) the velocities in the x and y directions are taken into account and (ii) the speeds are averaged over the water depth. Two- and three-dimensional models are predictive models in a sense that they also require calibration and validation. An important new development in two- and three-dimensional modeling is the capacity of using a nested grid, i.e., different spatial resolutions in the same model application. This allows for using fine grids in ecologically important areas, while coarser grids can be used in areas that do not require such resolution (Olsen 2000).

Two-dimensional and three-dimensional hydraulic models apply the principles of conservation of mass and momentum on a spatial, computational grid. Two-dimensional horizontal models use depth-averaged velocity, where three-dimensional models have computational layers in the vertical dimension. These models also include empirical or stochastic representation of water turbulence. The model schematization is based on detailed topographic input from the study area in combination with data on bed roughness and boundary conditions for water level and discharge. Velocity and water level measurements are usually used for validation.

A key aspect in numerical (habitat) modeling is the modeler’s own considerations of simplifications and assumptions concerning the physics involved. The (habitat) modeler has to decide which numerical approach fits best according to the requirements of the project to describe the abiotic environment. If the near-bottom velocity needs to be addressed (e.g., benthic habitats), a three-dimensional code would be required. If the cross section’s variability is important to characterize river morphological characteristics on the meso-unit (mesohabitat scale), then depth-averaged two-dimensional modeling should be selected. For aspects of minimum flow depths in a longitudinal view of the river, the one-dimensional model could deliver the required information for various discharges (e.g., residual flow studies), just to name some aspects of needs for a decision. Here, expert knowledge of this decision-making process is a mandatory in pre-project steps.

2.3 Integrative Habitat Assessment

Once the (hydraulic) model has been calibrated and the species-habitat relationships have been established, the two separate components need to be combined into a composite flow-habitat relationship (sometimes referred to as habitat-discharge rating curves). Usually this is done by applying the weighted usable area (WUA) (Bovee 1982) concept used in the PHABSIM family of fish habitat models. The WUA is calculated as an aggregate of the product of a composite suitability index (CSI, range 0.0–1.0). The CSI is calculated as a combination of the separate suitability indices for every single physical parameter. The suitability index for each parameter is evaluated by linear interpolation from an appropriate preference curve to be supplied separately. Velocities and depths are usually taken directly from the hydrodynamic model, while substrate and cover derives from additional mapped data. For quantitative assessment of habitat suitability as a function of flow rate, hydraulic rating curves (flow vs. habitat relationship) for the different key species are generated.

A specific WUA can only be seen as an index because perceived physical area is multiplied by unit-less habitat suitability attributes (Payne 2003). These attributes were originally termed “elective criteria” (Bovee and Cochnauer 1977) under the assumption that species will elect to leave an area when conditions become unfavorable. Electivity is variously expressed as probability of use (or nonuse), preference, suitability, or utilization over the possible range of conditions. Electivity indices range between 0 and 1, have no units, and are most commonly derived from frequency analysis of field observations.

To combine multiple habitat factors into one aggregate habitat suitability model assessment, first it is useful to assign weights to each factor that reflect their relative importance. If a habitat factor is not important for a species, it is assigned a weight of 0%.

Weighting is one of the weakest parts of the models if lacking any underlying theory or hard data. One theoretical issue, for example, is this: When the scores are combined across factors, does the overall score still have the same biological interpretation we established when scoring suitability for each factor? Therefore, habitat assessment should be built on a model that uses weights based on empirical data.

Further criteria to consider are anthropogenic reductions of the mean flow velocity in the cross section along the river stretch; anthropogenic migration obstacles occurring in the natural fish habitat must be passable by fish all year long and stream bed stabilization (river-bottom sills, bank dynamics, and local protections) in context to open substrate und dynamics.

Physical habitat units on the mesoscale (hydromorphological units) are addressed at an intermediate level between microhabitats and reach-scale habitat characteristics and hence are most commonly termed as mesohabitats (Maddock 1999; see also case studies River Ybbs and MEM below). Although, various hydromorphological studies have yet to find consistent numbers of distinctly mesohabitat types for the aquatic environment (e.g., Bain and Knight 1996), variable descriptions of abiotic parameters exist to determine the different habitats on the mesoscale and have served mainly to distinguish between pool, riffle, and run habitats. For characterizing mesohabitats, the Froude number, the water surface slope, the range of water depth and velocities, and the bed material size have been used. Based on the importance of mesohabitats for instream studies and river restoration, various parameters have been developed and implemented as different modeling approaches for mesohabitat description and quantification (e.g., Parasiewicz 2001; Le Coarer 2005; Hauer et al. 2009).

3 Managing River Systems Through Habitat Assessment

The following sections describe examples of implementation of habitat modeling at micro- and mesohabitat spatial scales.

3.1 Case Study on Microhabitat Scale: E-Flow Study at River Ybbs, Austria

As part of an environmental flow study on the River Ybbs (Zeiringer et al. 2010), a microhabitat modeling approach was carried out as an integrative assessment method to identify ecologically reasonable minimum flows. For the appropriate ecological evaluation of the current situation, quantitative fish surveys (after Haunschmid et al. 2010) and hydromorphological measurements were carried out along the residual flow stretch as well as in unaffected stretches further upstream of the water abstraction inlet for the power plant (see Fig. 7.3). The fishing results formed the basis for deficit analysis and habitat modeling. Within the residual flow stretch, two sections were surveyed and mapped in order to enable numerical modeling of flow. These sections constitute a basic requirement for evaluating the habitat suitability depending on different flow rates. Further, the hydrological conditions along the 30 km long river section were quantified using several water level logger and stage-discharge relationships. Thus, precise residual flow along the river section could be derived over long periods.

Fig. 7.3
figure 3

Case study area and study sites are located at River Ybbs in Lower Austria. (WLL = water level logger, Ref = reference/fully discharged river stretch, RF = residual flow)

Full size image

For the habitat modeling approach, the habitat requirements of the key species in this river section, e.g., brown trout (Salmo trutta) and European grayling (Thymallus thymallus), for different age stages (0+, 1+, 2+>) were defined. This was done using preference functions (univariate and multivariate, see Fig. 7.4, 2a, b, c) of the indicator species for different seasons (summer and fall) derived from unaffected river stretches further upstream (Fig. 7.3). Fish were observed via snorkeling in the fully discharged sections (Thurow 1994; Greenberg et al. 1996), and the abiotic characteristic (water depth, flow velocity, substrate, and cover) of used and available habitat depended on species and life stage were measured.

Fig. 7.4
figure 4

Concept of a case study on microhabitat scale, which combines abiotic and biotic information (after Maddock 1999). The overall physical habitat simulation shows the integration of (1) hydraulic measurement and modeling and (2) biotic habitat suitability criteria to define the (3) flow versus habitat relationship, which is combined with (4) flow time series to produce (5) habitat time series (example of WUA for brown trout older than 2 years), whereas examples for brown trout life stages habitat use are given in 2a for water depth, in 2b for flow velocity, and in 2c as a CHAID tree method selecting specific fish habitat preferences

Full size image

The hydraulics were modeled using the software River2D, which is a two-dimensional depth-averaged model of river hydrodynamics and can also be used for fish habitat modeling (Steffler and Blackburn 2002). The habitat suitability of the modeled river stretches was calculated by linking the physical (habitat descriptive) parameters with the habitat requirements of selected indicator species. The fish habitat component of River2D is based on the weighted usable area (WUA). For the quantitative assessment of habitat suitability as a function of flow rate, hydraulic rating curves (flow vs. habitat relationship) for the different key species were generated (Fig. 7.4). This was then combined with a historical flow time series to produce a physical habitat time series and hence a physical habitat duration curve (Maddock 1999).

3.2 Example at Mesohabitat Scale: Mesohabitat Evaluation Model (MEM)

The conceptual MEM model was developed and validated by Hauer et al. (2008, 2011) and allows evaluation of six different hydromorphological units (mesohabitats) according to their abiotic characteristics. Three abiotic parameters (flow velocity, water depth, and bottom shear stress) were incorporated into the MEM analysis. For practical purposes, the MEM concept was implemented using a Java software application, which enables MEM evaluation based on one of three different two-dimensional (CCHE2D, River2D, Hydro_AS-2D) and two different three-dimensional models (RSim-3D, SSIIM) (Tritthart et al. 2008).

Recently, the MEM approach was successfully applied for the evaluation of various anthropogenic pressures and the habitat quality assessment of restored river sites in Austria. For example, hydropeaking impact studies (unsteady dynamics in mesohabitat patterns) are significant recent applications. Here, the MEM results were used as a fundamental basis for the discussion of future mitigation measure design (Hauer et al. 2013). Moreover, the MEM concept was used to evaluate the habitat quality of larger river systems like the Drava (Drau) river or the Danube (Fig. 7.5). Here, the distribution of mesohabitats could be linked to the presence of fish guilds, which enables habitat evaluation not only for single fish species, but for groups with similar preferences for the aquatic environment. Using the fish guild concept, the model evaluates habitat suitability for spawning, juveniles, subadult, and adult life stages of rheophilic, indifferent, and stagnophilic fish species (see for details: Hauer et al. 2011, 2014).

Fig. 7.5
figure 5

Visualization of the mesohabitat evaluation model (MEM) featuring calibrated mesohabitats under low flow conditions for a restored section of the Drava River (left) and the regulated Danube east of Vienna (right) (Hauer et al. 2011) (reproduced from: Hauer et al. 2011. Variability of mesohabitat characteristics in riffle-pool reaches: Testing an integrative evaluation concept (FGC) for MEM-application. River Research and Applications 27(4):403–430, © 2010 John Wiley & Sons, Ltd.)

Full size image