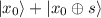Quantum Key-Recovery on Full AEZ

Abstract

AEZ is an authenticated encryption algorithm, submitted to the CAESAR competition. It has been selected for the third round of the competition. While some classical analysis on the algorithm have been published, the cost of these attacks is beyond the security claimed by the designers.

In this paper, we show that all the versions of AEZ are completely broken against a quantum adversary. For this, we propose a generalisation of Simon’s algorithm for quantum period finding that allows to build efficient attacks.

1 Introduction

Post-quantum cryptography studies the weaknesses of cryptographic systems against quantum adversaries. The consequences of a quantum computer would be catastrophic in cryptography. Indeed, due to Shor’s algorithm [17], most widely used cryptographic primitives would be completely broken. The situation is different in symmetric cryptography. We know since 1996 that Grover’s algorithm [9] gives a quadratic speedup on exhaustive search, which lead to the common belief that doubling the key length would be enough to attain a suitable level of security against quantum computers. The work on dedicated cryptanalysis is much more recent, with many results [2, 11, 13] showing that we need to study further the implications of quantum computation in symmetric cryptography.

Authenticated encryption aims at providing both secrecy and authenticity. It can be achieved by a classical symmetric primitive in a specific mode of operation (OCB, GCM) [14, 16], or with a dedicated primitive. The CAESAR competition, launched in 2014, aims to standardise a portfolio of authenticated encryption algorithms. It has been quite successful in driving the community to work on this subject, with more than 50 submissions, and many cryptanalytic results on these submissions, like for instance [5, 6]. AEZ [10] is one of these proposals, still in the competition in the 3rd round of the selection process. The candidate AEZ has been tweaked several times to counter some proposed analysis [6, 8]. The current version is AEZ version 5, denoted AEZv5. AEZ claims to be a robust authenticated encryption scheme, being secure even in nonce misuse scenarios. The designers however limited their security claims to $2^{44}$ blocks of data used with the same key. This unusually small limit renders the attacks from [6, 8] inapplicable, and their security claims remain unaffected. The published analysis consider only a classical adversary. In this paper, we study the resistance against quantum adversaries.

There has been some previous work on authenticated encryption in a quantum setting, for instance SPHINCS, by Berstein et al. [3]. Kaplan et al. [11] showed some existential forgeries in OCB, GCM and many CAESAR candidates(including AEZ). Soukharev et al. have proposed a security model for authenticated encryption against quantum adversaries [19], where the challenges are classical, but the adversary can make queries in quantum superposition to an encryption (or decryption, if available) oracle, with a classical chosen randomness. Our attacks performs in this model, where the chosen queries are quantum, except for the nonce, which should be classical (it can be chosen or known, this has no impact on our quantum attacks).

Table 1. Summary of the attacks on AEZ since version 3

This is a strong model, as the attacker has not only quantum computation capabilities, but can perform quantum queries to an oracle that computes a classical function f: that is, from an arbitrary superposition , get . It has the advantage of encompassing any other, more constrained, model, and if a primitive is safe in this model, it is safe in the others. Moreover, it may become plausible. We can for example think of white-box cryptography: if you have access to a program that computes a function, you can implement it on a quantum computer. Finally, this model is non-trivial: it is possible to build constructions secure in this model.

In this paper, we show how the key-recovery of [6] can be dramatically accelerated in a quantum setting to break AEZv4. We also show of to adapt the attack for a key-recovery of AEZv5 and a universal forgery with AEZ10. All these attacks use quantum period finding and have a cost in data of around $2^{10}$ blocks, which is far below the $2^{44}$ limit claimed by the designers.

From a quantum algorithmic’s point of view, we propose a more powerful and precise analysis than the one in [11]. We also show how to take advantage of a quantum multiple period finding, that allows to reduce even more the data complexity in some cases. The results are summarised in Table 1.

2 Preliminaries

In this section, we describe the primitive we’re attacking and our main cryptanalytic tool, Simon’s algorithm.

2.1 Description of AEZ

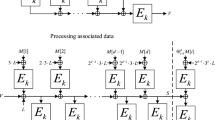
AEZ [10] (Fig. 1) is a tweakable block cipher for authenticated encryption, and its components have been tweaked in the different versions of the algorithm. It uses a master key K of 384 bits, decomposed in 3 subkeys (I, J, L) of 128 bits each. AEZ has at its core a tweakable function $E_K^{i,j}$ used in the intermediate function AEZ-hash (Fig. 2). The user calls the external function Encrypt, that calls, depending on the message length, AEZ-prf, AEZ-tiny or AEZ-core. AEZ-tiny and AEZ-core are symmetric ciphers, AEZ-tiny is used for messages of less than 32 bytes (one block), AEZ-core is used for longer messages. AEZ-prf is a pseudo-random function (PRF) called when the message is empty that takes some associated data and a length $\tau$ in argument, and that outputs a tag of the desired length that can be used to authentify the associated data. Our attacks will use AEZ-prf, and its components are described below. We also need AEZ-core for a part of the attack against AEZ version 4, but as its description is more complex and the attack uses the same principles, we refer to [6] for a description of AEZ-core.

Fig. 1.

High-level view of the components of AEZ

Associated Data. The associated data is seen as a bidimensional vector of 128-bit blocks. An example for 7 blocks can be represented as:

$$\begin{array}{l} A_1^1\\ A_2^1\\ A_3^1A_3^2A_3^3\\ A_4^1A_4^2 \end{array} \text { that we note } (A_1^1, A_2^1, (A_3^1, A_3^2, A_3^3), (A_4^1, A_4^2)).$$

The associated data can contain any number of lines, and each line can have any length. In practice, we have two constraints. The first line $A_1$ contains the output length $\tau$ of the PRF, in bits. As we’ll only have output lengths smaller than $2^{128}$ bits, the first line will only contain one block. The second line contains the nonce N. The specification recommends a nonce smaller than 128 bits, which also limits this line to one block. However, as this is only a recommendation, we can also study what happens if we allow longer nonces.

Finite Field. AEZ uses a multiplication in $\mathbb {F}_{2^{128}}$, seen as $\mathbb {F}_2[X]/(X^{128}+X^7+X^2+X+1)$. As we are in a field, we can invert any non-zero number. Moreover, knowing the polynomial, we can do it efficiently.

Core Function. The core of the algorithm is the function $E_K^{i,j}$, which is a permutation on 128 bits. It is concretely a tweaked version of 4 or 10 rounds of AES [7] ($\texttt {AES4}$ and $\texttt {AES10}$). The exact function depends on the version of the algorithm and the values of i and j. These versions of AES don’t use the normal key schedule but one of the subkeys (I, J, L) at each round.

Table 2 shows the value of $E_K^{i,j}$ in AEZv4, depending on the parameters i and j, with $\alpha _j = 2^{3+\lfloor (j-1)/8\rfloor }+((j-1) \mod 8)$ and $\beta _i = 2^{i-3}$. The multiplication is done in the finite field.

Table 2. $E_K^{i,j}$ in AEZv4

The function is simpler in AEZv5:

• $E_K^{-1,j}(X) = \texttt {AES10}(X\oplus jL)$

• $E_K^{i,j}(X) = \texttt {AES4}(X\oplus iJ\oplus 2^{\lceil j/8\rceil }I\oplus (j\mod 8)L)$

Since version 2, AEZ also proposes an alternative algorithm named AEZ10 where the master key K has 128 bits and is directly used as an AES key, $I = \texttt {AES}_K(0)$, $J = \texttt {AES}_K(1)$ and $E_K^{i,j} = \texttt {AES}_K(X\oplus jI \oplus iJ)$.

AEZ-hash . This function takes as input the associated data A and the key K and outputs 128 bits.

Fig. 2.

AEZ-hash scheme

$$\begin{aligned} \texttt {AEZ-hash}(K,A) = \varDelta = \bigoplus _{i,j} E_K^{i+2,j}(A_i^j) \text { in both v4 and v5.} \end{aligned}$$

AEZ-prf . This function is a PRF of arbitrary output length which can be used to authentify the associated data. It takes as input an output length $\tau$, some associated data A and the key K, and outputs $\tau$ bits.

It computes $\varDelta = \texttt {AEZ-hash}(K, A)$, and outputs the first $\tau$ bits of the sequence $E_K^{-1,3}(\varDelta ), E_K^{-1,3}(\varDelta \oplus 1), E_K^{-1,3}(\varDelta \oplus 2)\dots$ The most interesting property of this function is that its value (for $\tau$ fixed) depends only on the value of $\texttt {AEZ-hash}$, and in particular, that a collision in $\texttt {AEZ-hash}$ implies a collision in $\texttt {AEZ-prf}$.

Encrypt. This function takes as input the key K, the associated data A and a variable-length message M. For empty messages, it is a direct call to $\texttt {AEZ-prf}(K,A,\tau )$.

2.2 Simon’s Algorithm

Simon’s algorithm [18] aims at solving the following problem:

Simon’s problem. Given a function $f : \{0,1\}^n \rightarrow \{0,1\}^n$ and the promise that there exists $s\in \{0,1\}^n$ such that for all $(x,y)\in \left( \{0,1\}^n\right) ^2$, $f(x) = f(y) \Leftrightarrow x\oplus y \in \{0,s\}$, find s.

We say that f has the period s. We have a 2-to-1 function such that for each output, the xor of the 2 preimages is always the same value, and we want to find this value. Classically, we can solve this problem by searching for collisions, in time $\varOmega \left( 2^{n/2}\right)$. In our quantum model, where we allow quantum queries to the function, Simon’s algorithm solves that problem in O(n) quantum queries and time, using the circuit in Fig. 3. It also needs a polynomial-time classical post-processing, that we will neglect. We have access to the oracle . We also use the Hadamard transform , with $\cdot$ the inner product in $\{0,1\}^n$, and some measurements.

Fig. 3.

Simon’s algorithm quantum circuit

This circuits has five steps:

• 1. Starting with 2 n-qbits registers , we apply the Hadamard transform on the first register, which gives us the superposition

  

• 2. With the oracle, we get the quantum superposition of all input-outputs through f:

  

• 3. We measure the second register. This gives us an $f(x_0)$ for an unknown $x_0$, and collapses the first register to the compatible preimages, that are, thanks to the promise

  

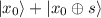
• 4. We then reapply the Hadamard transform to the first register, which becomes

  

• 5. We measure that register. Any x such that $x\cdot s = 1$ has a null amplitude, and we can’t measure it. Therefore, we’ll measure a random value satisfying $x\cdot s = 0$.

One application of this circuit gives us a random vector orthogonal to s. We can retrieve the hyperplane orthogonal to s with $n-1$ independent equations in O(n) queries, and then retrieve s.

3 Extending Simon’s Algorithm

In this section, we’ll study what happens in the circuit in various interesting situations that occur in the applications we have considered.

s is 0 [18]. The behaviour is slightly different if $s = 0$ (f is injective): we have only one element at step 3, and we measure a random value at step five, wich means we’ll get n independent values in O(n) queries. This case was already treated by Simon in his original paper.

More Preimages [11]. If f fulfils $f(x) = f(x\oplus s)$ for all x, but can also verify $f(x) = f(y)$ for different values, that is, f can have more than 2 preimages by image, the routine still works and gives us a vector orthogonal to the secret, but we won’t get a uniform distribution. This problem has been addressed in [11], Theorem 1, where they bound the error probability of the algorithm, depending on the probability of occurence of a given parasite period, that is, with

$$\begin{aligned} p_0 = \max _{t\notin \{0,s\}} \Pr [f(x) = f(x\oplus t)], \end{aligned}$$

we get an error probability with cn queries of at most

$$\begin{aligned} \left( 2\left( \frac{1+p_0}{2}\right) ^c\right) ^n. \end{aligned}$$

Taking the log in base 2, with $p_e$ the error bound, we get

$$\begin{aligned} n(1+c(\log (p_0+1)-1)) = \log (p_e). \end{aligned}$$

We can rewrite it as

$$\begin{aligned} cn = \frac{1}{\log \left( \frac{2}{p_0+1}\right) }(n-\log (p_e)). \end{aligned}$$

This allows us to compute directly the needed number of queries for a given success probability. We see that $p_e$ diminishes exponentially with the number of queries. For our numerical applications, we can be very conservative for $p_0$ and take 1 / 8. As this shows an unwanted differential property, this bound is unlikely to be tight for our applications, which are xors of 4 AES rounds. With such a $p_0$, we get $cn = 1.2(n-\log (p_e))$. For our numerical applications, we’ll consider a $p_e$ such that the total success probability of the attack is greater than one half.

Multiple Periods [21]. If f satisfies $f(x) = f(x\oplus s)$ for multiple values of s, the routine will spawn some vectors orthogonal to all the periods. We will then be able to recover the vector space generated by these periods [21]. If we have n bits and s independent periods, it is equivalent to Simon’s problem with $n - s+1$ bits (the post-processing is a bit different, as we get a vector space instead of a value). In the most degenerate case, if f is constant, we can only measure 0 (this can also be detected in a few classical queries).

Different Functions [11]. The original problem requires an oracle identical for each query. However, as one query gives one equation, we don’t need to have the same oracle call for each query, as long as the hidden periods are the same in all the functions. This will allow us to apply our cryptanalysis with a different nonce at each oracle call. This was used in some of the applications in [11].

4 Previous Classical Attack

Chaigneau and Gilbert presented at FSE’17 a key-recovery attack on AEZv4 [6]. The attacker can query the functions of AEZ with a fixed unknown key, and chosen authenticated data and plaintexts. The attack is done in two parts: first, they apply 3 independent birthday sub-attacks that retrieve one of the 3 subkeys, and next they perform a diffential attack that retrieves the 2 remaining subkeys once one is known. The first part needs a quantity of data at the birthday bound ($2^{64}$ blocks), wich is beyond the security claimed by AEZs designers, who limited the data to $2^{44}$ blocks for a given key. We’ll describe here only that part, as it is sufficient to perform efficient quantum attacks. Moreover, the second part doesn’t gain much in a quantum setting, and would lead to less efficient attacks.

For each of the 3 attacks, they seek for a collision in a specific function we construct with some functions of AEZ, and such a collision, with a high probability, will give them a subkey if they xor the colliding inputs. The functions are described in Table 3. The functions $f_I$ and $f_J$ need a fixed nonce N for each input, but not $f_L$, as for this function the queried nonce depends on the input value.

Table 3. Collision functions in [6]

For example, for $f_L$, the value of $\texttt {AEZ-hash}(K,(\tau ,x,x))$ is $\varDelta = E_K^{3,1}(\tau )\oplus E_K^{4,1}(x)\oplus E_K^{5,1}(x)$, which gives us, when we expand:

$$\begin{aligned} \varDelta = E_K^{3,1}(\tau )\oplus \texttt {AES4}(x\oplus 2L\oplus 8J)\oplus \texttt {AES4}(x\oplus 4L\oplus 8J). \end{aligned}$$

For $x' = x\oplus 6L$, we get

$$\begin{aligned} \varDelta = E_K^{3,1}(\tau )\oplus \texttt {AES4}(x\oplus 6L\oplus 2L\oplus 8J)\oplus \texttt {AES4}(x\oplus 6L\oplus 4L\oplus 8J). \end{aligned}$$

As we are in $\mathbb {F}_{2^{128}}$, it reduces to

$$\begin{aligned} \varDelta = E_K^{3,1}(\tau )\oplus \texttt {AES4}(x\oplus 4L\oplus 8J)\oplus \texttt {AES4}(x\oplus 2L\oplus 8J). \end{aligned}$$

Hence, we get the same $\varDelta$ (which implies the same value of $f_L(x)$) if $x\oplus x' = 6L$, that is, $f_L(x) = f_L(x\oplus 6L)$. We have similar properties for $f_J$ and $f_I$: $f_J(x) = f_J(x\oplus J)$ and $f_I(x) = f_I(x\oplus I)$.

Then, for $f_L$ (and similarly for $f_I$ and $f_J$), the attack is:

• Query $f_L(x)$ for $2^{64}$ different values of x.

• Search for a collision $f_L(x) = f_L(x')$

• With high probability, $x\oplus x' = 6L$.

We’ll see how to use these properties to dramatically accelerate this attack in a quantum setting in the next section.

5 Quantum Cryptanalysis of AEZ

In this section, we’ll show how to use Simon’s algorithm to efficiently recover the subkeys in AEZv4, AEZv5 and AEZ10. We’ve chosen to restrain ourselves to a classical known nonce for each quantum query.

All these attacks make use of a function f, of the form $f(x) = a\oplus g(x\oplus b) \oplus g(x\oplus b \oplus s)$, with g a xor of AES4 with various inputs. Simon’s algorithm will retrieve efficiently s, except if $s = 0$. In this case, f is a constant function, and the corresponding key is weak, as such a property can easily be detected classically. However, the proportion of such weak keys, which corresponds to the subkeys I, J, L (or some multiples of the subkeys) being linearly dependent, is too small to be exploited (this occurs with a probability of around $2^{-125}$ for one f).

5.1 AEZv4

We can directly use the functions of [6], described in Table 3, in Simon’s algorithm. There is however a slight difference for $f_I$, as the period is not on the full AEZ-core but only on the last block. We can construct an oracle of $f_I$ from an oracle of AEZ-core by uncomputing and taking only the last block. With this method, one query to $f_I$ costs two queries to $\texttt {AEZ-core}$. For each case, we query functions of $n = 128$ bits. In order to get a success probability of 0.5, we need $80\%$ of success for each subkey, which is attained in 157 queries. The total query complexity of the attack is $628 = 2^{9.3}$. We use respectively 2, 3 and $2\times 6$ block of data for each query. We need $2669 = 2^{11.4} \ll 2^{44}$ blocks of data.

The complete attack is:

• For $k \in \{I,J,L\}$:

  • Query 157 times Simon’s routine with $f_k$.

  • Solve classically the boolean equation system to get the period of $f_k$.

  • If this period was a multiple of k, invert to retrieve k.

In the original attack, $f_I$ and $f_J$ needed a nonce reuse. This is not the case with the quantum attack, as the different functions have the same hidden period. The only constraint for the nonce is to be non-entangled with the input value. For $f_L$, we need to perform a quantum query with a nonce superposition. If we want to disallow this, we can still use $f'_L =\texttt {AEZ-prf}(K,(\tau ,N,x,x),\tau )$, which satisfies $f'_L(x) = f'_L(x\oplus 12L)$. This has the same query complexity, but a slightly larger data complexity ($2^{11.5}$).

But we can go even further, if we look at

$$\begin{aligned} f_{JL}(x) = \texttt {AEZ-prf}(K,(\tau ,N,(x,x),(x,x)),\tau ). \end{aligned}$$

The associated $\varDelta$ is

$$\begin{aligned} A\oplus \texttt {AES4}(x\oplus 4L\oplus 8J)\oplus \texttt {AES4}(x\oplus 4L\oplus 9J)\oplus \texttt {AES4}(x\oplus 8L\oplus 8J)\oplus \texttt {AES4}(x\oplus 8L\oplus 9J). \end{aligned}$$

This function has a hidden period of J and 12L (and also $J\oplus 12L$). As seen in Sect. 3, this means we can retrieve the vector space with this function. J and 12L need to be independent for the function to be non-constant. In that case, we can retrieve the value of J and L with an exhaustive (classical) research, as it has only 6 possibilities (for example by checking for collisions in $f_J$ and $f_L$). This diminishes even more the query complexity to $471 = 2^{8.9}$, using the same number of block of quantum data. We then need to identify J and L. We can do an exhaustive search, in one classical query and 6 tests (we only need to test pairs of linearly independent vectors of the subspace we retrieved), or check for collisions, in 6 classical queries (one for a reference, 3 to try to collide with the reference on the first subkey, 2 to try to collide on the second).

We can also use these multiple periods in the classical attack: we use $f_{JL}$ for our collisions, but as one query of this function has the same data complexity as the queries of $f_J$ and $f_L$, it won’t change much on the overall complexity.

5.2 AEZv5

The functions in Table 4 allow to perform the same attack on AEZv5, with a quantum query complexity of $2^{8.9}$, and a data complexity of $2464 = 2^{11.3}$ blocks.

Table 4. Collision functions for AEZv5

We can even be more efficient in queries and recover the vector space in one go, with the function

$$\begin{array}{clc}f_{IJL}(x) = \texttt {AEZ-prf}(K,(\tau ,N,&{}(x,x,A,B,C,D,E,F,x,x),&{}\\ {} &{}(x,x,A',B',C',D',E',F',x,x)&{}),\tau ). \end{array}$$

Here, any non-x value in argument can be anything as long as it is not entangled with x. This f has the 3 periods of $f_I, f_J$ and $f_L$, and allows us to recover the vector space in $155 = 2^{7.3}$ queries, and a data complexity of $3255 = 2^{11.7}$ blocks. Once we know the vector space, we can use one classical query and check the $7\times 6\times 4 = 168$ possible triplets, or check for collisions in the classical version of $f_I$, $f_J$ and $f_K$, which can be done in $1+7+6+4 = 18$ classical queries.

Using the same principle, we can also define and use $f_{IJ}$, $f_{JL}$ or $f_{IL}$, which all have comparable complexities,

$$\begin{aligned} f_{IL}(x) = \texttt {AEZ-prf}(K,(\tau ,N,(x,x,B,C,D,E,F,G,x,x),\tau ) \end{aligned}$$

and $f_J(x)$ giving the best data complexity of $2^{11.1}$ blocks.

5.3 AEZ10

The core function is even simpler in this variant: $E_K^{i,j}(X) = \texttt {AES(}X\oplus iJ\oplus jI)$. Hence, we can do the attack with the functions in Table 5. With two functions, we can recover I and J in 312 quantum queries and 936 quantum blocks of data. If we choose to get the vector space spawned by I and J, we only need 155 queries and 775 blocks of data. In this case, we don’t get a full key recovery, but the knowledge of the tweaks I and J allows to make forgeries for any non-empty authenticated data.

Table 5. Collision functions for AEZ10

5.4 Variants of the Attack

We can gain one block per query if we allow the nonce to be in quantum superposition and if the nonce can be more than 128 bits (which is not recommended, but isn’t forbidden by the specification). Indeed, this would allow to suppress the nonce line in the associated data in each of the queried functions. The new functions would have a hidden period for some other multiples of the subkeys.

The attack from Chaigneau and Gilbert [6] can also be applied to all the versions we have considered here classically, and the cost will be at the birthday bound ($2^{64}$ queries, for around $2^{66}$ blocks of data, depending on the amount of associated data in the functions). If we want to gain in data complexity, we can reuse the second part of the attack in [6]. Once the subkey I is known, we can get J and L by attacking 3 rounds of AES (we can probably also make use of the knowledge of J or L, but this would need another dedicated analysis).

5.5 Thwarting the Attack

There are different ways to counter this specific attack. As Simon’s algorithm uses a specific structure, the simplest solution would be to change the way offsets are used, from a xor with the data to another operation (see [1]). However, if this is still a commutative group operation, the algorithm would be vulnerable to some other quantum algorithms like Kuperberg’s algorithm [12], and it may not lead to a satisfactory level of security.

A more conservative approach would be to change a bit the way the associated data is processed. We can currently see it as 4 rounds of an AES with a custom key schedule, with the first round key that depends on the position of the block, the other ones being fixed. If the variable key is one of the inner AES keys (or if there are variable keys on multiple rounds), this quantum attack would not work. This could however lead to some kind of related-key attacks on this 4-round AES, and it would require a dedicated analysis to ensure it does not lead to some other classical attacks.

Moreover, these changes would prevent the quantum exponential gain of Simon’s algorithm, but the collision analysis from Chaigneau and Gilbert [6] would remain.

6 Conclusion

We’ve shown that all the versions of AEZ are deeply broken in the quantum superposition model. This is an example of an exponential speedup of a classical attack on a real primitive, that went from costly to almost-free. We’ve also presented a way to exploit multiple hidden periods in order to reduce the number of quantum oracle calls, and provide more flexibility in the attack, and discussed how to avoid these kinds of attacks.