Abstract
In this chapter we show how multihadron production can be related to thermodynamical considerations. Following a general introduction to the topic, we discuss the statistical hadronization model, in which each species is produced according to its phase space weight, and show that this leads to a universal hadronization temperature found in e + e − annihilation as well as in hadron-hadron and nucleus-nucleus collisions. In the final part we address deviations from a universal statistical hadronization description.
Es wurde schon vor längerer Zeit geschlossen, daß bei einem sehr energiereichen Stoß eines Kernteilchens auf ein anderes viele Mesonen mit einem Schlag erzeugt werden können Werner Heisenberg, Zeitschrift für Physik 126 (1949) 569 (It was concluded quite some time ago that in an energetic collision of one nuclear particle with another, many mesons could be created with one bang) (Werner Heisenberg)
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
This is no longer correct in the presence of exactly conserved charges, see “Appendix 2: Exact Charge Conservation”.
- 2.
The data are taken in a unit interval at midrapidity. In principle, statistical hadronization applies to full (
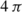 ) production rates; at high energies, however, the rapidity distributions are sufficiently flat to allow midrapidity studies.
) production rates; at high energies, however, the rapidity distributions are sufficiently flat to allow midrapidity studies. - 3.
We note here that over the years, both the deconfinement temperature T c obtained in lattice studies for μ ≃ 0 and the hadronization temperature determined in the analysis of species abundances have shown some slight fluctuations. The ideal resonance gas is, of course, a priori a model. Nevertheless, all versions have remained in the range between 150 and 170 MeV, and this range is in accord with the lattice results.
References
W. Heisenberg, Z. Phys. 113, 61 (1939)
E. Fermi, Progr. Theor. Phys. (Japan) 5, 570 (1950)
P.P. Srivastava, G. Sudarshan, Phys. Rev. 110, 765 (1958)
H. Satz, Il Nuovo Cim. 37, 1407 (1965)
L.D. Landau, Izv. Akad. Nauk SSSr 17, 51 (1953)
V.N. Gribov, Sov. Phys. JETP 29, 483 (1969)
R. Hagedorn, Nuovo Cim. Suppl. 3, 147 (1965)
R. Hagedorn, Nuovo Cim. A 56, 1027 (1968)
W.-M. Yao et al., Rev. Part. Phys. J. Phys. G 33, 1 (2006)
E. Beth, G.E. Uhlenbeck, Physica 4, 915 (1937)
R. Dashen, S.-K. Ma, H.J. Bernstein, Phys. Rev. 187, 345 (1969)
J.D. Bjorken, Lect. Notes Phys. (Springer) 56, 93 (1976)
F. Becattini, G. Passaleva, Eur. Phys. J. C 23, 551 (2002)
See also e.g., P. Braun-Munzinger, K. Redlich, J. Stachel, in Quark-Gluon Plasma 3, ed. by R.C. Hwa, X.-N. Wang (World Scientific, Singapore, 2003)
F. Becattini, R. Fries, arXiv:0907.1031 [nucl-th], and Landolt-Boernstein 1–23
F. Cerulus, Nuovo Cim. 19, 528 (1961)
K. Redlich, L. Turko, Z. Phys. C 5, 201 (1980)
For a general summary, see e.g., K. Redlich, F. Karsch, A. Tounsi
F. Becattini, U. Heinz, Z. Phys. C 76, 268 (1997)
J. Cleymans, M. Marais, E. Suhonen, Phys. Rev. C 56, 2747 (1997)
J. Letessier, J. Rafelski, A. Tounsi, Phys. Rev. C 64, 406 (1994)
J.S. Hamieh, K. Redlich, A. Tounsi, Phys. Lett. B 486, 61 (2000)
R. Hagedorn, Thermodynamics of Strong Interactions, CERN Yellow Report 71–12, 1971
F. Becattini, Z. Phys. C 69, 485 (1996)
F. Becattini et al., Eur. Phys. J. C 56, 493 (2008)
A. Andronic et al., Phys. Lett. B 675, 312 (2009)
F. Becattini et al., Eur. Phys. J. C 66, 377 (2010)
J. Cleymans et al., Phys. Lett. B 242, 111 (1990)
J. Cleymans, H. Satz, Z. Phys. C 57, 135 (1993)
K. Redlich et al., Nucl. Phys. A 566, 391 (1994)
P. Braun-Munzinger et al., Phys. Lett. B 344, 43 (1995)
F. Becattini, M. Gazdzicki, J. Sollfrank, Eur. Phys. J. C 5, 143 (1998)
F. Becattini et al., Phys. Rev. C 64, 024901 (2001)
B.I. Abelev et al. [STAR Collaboration], Phys. Rev. C 79, 034909 (2009)
B.I. Abelev et al. [STAR Collaboration], Phys. Rev. C 75, 064901 (2007)
J. Adams et al. [STAR Collaboration], Phys. Rev. Lett. 92, 092301 (2004)
B.I. Abelev et al. [STAR Collaboration], Phys. Rev. C 79, 034909 (2009)
J. Adams et al. [STAR Collaboration], Phys. Lett. B 612, 181–189 (2005)
J. Adams et al. [STAR Collaboration], Phys. Rev. Lett. 98, 062301 (2007)
B.I. Abelev et al. [STAR Collaboration], Phys. Rev. Lett. 97, 132301 (2006)
P. Castorina, H. Satz, Eur. Phys. J. CA 52, 200 (2016)
The γ s values were obtained in the following data analyses, where also the original experimental references are given: F. Becattini, J. Manninen, M. Gazdzicki, Phys. Rev. C 73, 044905 (2006)
F. Becattini et al., Eur. Phys. J. CC 66, 377 (2010)
F. Becattini, J. Manninen, Phys. Rev. C 78, 054901 (2008)
F. Becattini et al., Eur. Phys. J. CC 66, 377 (2010)
M. Floris et al., Nucl. Phys. A 931, 103 (2014)
F. Becattini, hep-ph/9701275
F. Becattini et al., Phys. Rev. Lett. 111, 082302 (2013)
P. Castorina, S. Plumari, H. Satz, Int. J. Mod. Phys. E 26, 1750081 (2017)
K. Aamodt et al. (ALICE Coll.), Phys. Rev. Lett. 105, 252301 (2010)
A. Bazazov et al. (HotQCD), Phys. Rev. D90, 094503 (2014)
A. Majumdar, B. Müller, Phys. Rev. Lett. 105, 252002 (2010)
H. Satz, Phys. Rev. D 19, 1912 (1979)
M.M. Aggarwal et al. (STAR Collaboration), Phys. Rev. Lett. 105, 22302 (2010)
F. Karsch, K. Redlich, Phys. Lett. B 695, 136 (2011)
O. Kaczmarek et al., Phys. Rev. D 83, 014504 (2011)
Christian Schmidt, Nucl. Phys. A904–905 2013, 865c (2013)
A. Andronic et al., Phys. Lett. B 678, 350 (2009)
S. Jacobs, M.G. Olsson, C. Suchyta, Phys. Rev. 33, 3338 (1986)
See e.g., L. Kluberg, H. Satz, arXiv:0901.3831 [hep-ph] and Landolt-Boernstein
See e.g., N. Brambilla et al., Heavy Quarkonium Physics, CERN Yellow Report CERN-2005-005
See e.g., N. Brambilla et al., Phys. Rev. D 78, 014017 (2008)
R. Baier, R. Rückl, ZP C 19, 251 (1983)
R.V. Gavai et al., Int. J. Mod. Phys. A 10, 3043 (1995)
P. Braun-Munzinger, J. Stachel, Nucl. Phys. A 690, 119 (2001)
R.L. Thews et al., Phys. Rev. C 63, 054905 (2001)
L. Grandchamp, R. Rapp, Nucl. Phys. A 709, 415 (2002)
T. Matsui, H. Satz, Phys. Lett. B 178, 416 (1986)
E. Fermi, Progr. Theor. Phys. (Japan) 5, 570 (1950)
H. Satz, Il Nuovo Cim. 37, 1407 (1965)
R. Hagedorn, Thermodynamics of Strong Interactions, CERN Yellow Report 71–12, 1971
F. Cerulus, Nuovo Cim. 19, 528 (1961)
K. Redlich, L. Turko, Z. Phys. C 5, 201 (1980)
K. Redlich, F. Karsch, A. Tounsi, hep-ph/0302245; published in Physical and Mathematical Aspects of Symmetries, Paris (2002)
P. Braun-Munzinger, K. Redlich, J. Stachel, in Quark-Gluon Plasma 3, ed. by R.C. Hwa, X.-N. Wang (World Scientific, Singapore, 2003)
Author information
Authors and Affiliations
Appendices
Appendix 1: Scattering Matrix and Phase Space
The probability for the production of N particles in the collision of two incident hadrons of four-momenta q 1 and q 2 is determined by

where W 2 = (q 1 + q 2)2 is the (squared) center-of-mass collision energy and p 1, …, p N are the four-momenta of the final hadrons. For simplicity, we assume here for the time being only one species of identical scalar hadrons of mass m 0 and neglect any effects of quantum statistics. The unitary scattering matrix S maps the initial state onto the final state. The Fermi model [69] is obtained by assuming that the squared S-matrix element is proportional to the probability of finding the N final hadrons as free particles inside a spatial volume V ,
With plane wave states
for the final hadrons we obtain the standard form for the relativistic N-particle phase space volume,

with W 2 = E 2 −P 2 for the invariant center of mass energy of the system. The delta functions project the N-particle state onto fixed total energy E and momentum P. The production probability can then be expressed in terms of the phase space volume Q N (W) as
where the normalization Q(W) is given by the sum over all states at fixed energy and volume
assuming, as mentioned, that all particles are identical.
The Laplace transforms of Q N (W) and Q(W) are just the canonical and grand canonical partition functions of an ideal gas in the Boltzmann limit,
and
with

here K 2(x) is the Hankel function of purely imaginary argument. For small x, K 2(x) ≃ (2/x 2), so that for high temperatures

This can be used to invert the Laplace transform (11.32), leading to [70]

Hence the average multiplicity

increases as W 3/4, so that the average energy per secondary grows as W 1/4.
Appendix 2: Exact Charge Conservation
The phase space integral (11.28) specifies the totality of allowed states consisting of a fixed number N of constituents, subject to the conservation of overall energy and momentum and contained in a volume V . The corresponding partition function (11.30) then provides the grand canonical sum over all N-body states, with the temperature T determining the average overall energy; the effect of momentum conservation actually becomes asymptotically negligible [71]. Quantum-mechanically, we write the grand canonical partition function as
where the trace runs over all possible N-particle states and \({\mathcal {H}}\) denotes the Hamiltonian. In the grand canonical framework, the conservation of a discrete charge Q (for simplicity, we restrict ourselves to only one additive conserved charge) is taken into account through fugacities \(\exp \{-\mu {\mathcal {Q}}\}\), with \( {\mathcal {Q}}\) for the charge operator and μ for the corresponding chemical potential,
For illustration, consider a system containing particles of charge zero and mass m 0, together with particles of charge ± 1 and a common mass m 1. The grand canonical partition function then becomes
and the average charge density q = 〈Q〉/V is given by
with
for the weight factor of a single particle of mass m i and degeneracy d i , in the Boltzmann limit. For a system of vanishing average charge density, Eq. (11.40) thus implies μ = 0, and from Eq. (11.39) we see that the system contains an equal number of positive and negative particles, in addition to the neutral ones. We thus have
for the corresponding grand canonical partition function.
Such a grand canonical formulation provides a correct description of the system only if it contains sufficiently many charged particles, so that fluctuations can be neglected. If there are only very few such particles, charge conservation has to be implemented exactly, not on the average. One thus has to “project” out the section of phase space associated to a fixed quantum number. We define the partition function at fixed Q as
where \({\mathcal {P}}_Q\) is the corresponding projection operator onto a fixed charge Q [72,73,74,75]. The partition function \({\mathcal {Z}}_Q(T,V)\) is thus a sum over all possible N = 2, 3, … particle clusters of fixed total charge Q. Using it, the grand canonical partition function (11.30) can be “re-organized”, i.e., rewritten as a sum over Q instead of as sum over N,
where
is the corresponding fugacity. Each term in the sum (11.44) is grand-canonical in terms of particle number, but canonical in charge. The series (11.44) can be inverted to obtain the partition function Z Q (T, V ) at fixed charge Q, using the Cauchy formula. The result is

with the function \({\tilde {Z}}(T,V,\phi )\) obtained from the grand canonical partition function Z(T, V, μ) by a Wick rotation μ s /T → iϕ, so that \(\lambda \to \exp \{i \phi \}\).
For our system containing charges 0, ±1, we thus obtain

so that the “charge-canonical” partition function for exactly vanishing overall charge Q = 0 becomes

where I 0(x) is the Bessel function of purely imaginary argument. From this we get
Comparing Eq. (11.45) to the grand canonical form (11.39), we see that the exact conservation of charge leads to the replacement
Since for large argument
the two forms become identical in the large volume limit, as expected. For small V , corresponding to small particle numbers, the contribution of the charged particles is suppressed relative to that of the neutral particles, if the overall charge is fixed to zero. It can be shown, in fact, that the canonical (c) and grand canonical (gc) densities n Q of particles of charge Q are related by [75]
This relation is approximate, since it neglects the possibility of multiply-charged states; the role of these is addressed in [75]. Since I 1(x)/I 0(x) → 1 for x →∞, exact charge conservation leads to an effective charge suppression by a factor approaching unity in the large volume limit. Since the volume V is determined by the overall multiplicity, which in turn grows with the collision energy, the suppression of the form (11.52) disappears with increasing \(\sqrt {s}\).
The formalism just sketched for the case of an Abelian (additive) charge 0, ±1 can be extended to several Abelian as well as non-Abelian charges [72,73,74,75]; for details, we refer to the cited works. We note here only that while exact baryon number conservation does lead to the correct non-strange abundances in elementary hadron-hadron collisions and in e + e − annihilation, the strangeness reduction obtained through exact strangeness conservation is not sufficient to account for the reduced strange particle production observed in these reactions. This requires an additional suppression, as given, e.g., by the suppression factor γ s applied per strange quark in the hadron in question, as discussed above.
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this chapter
Cite this chapter
Satz, H. (2018). The Fireball Paradigm. In: Extreme States of Matter in Strong Interaction Physics. Lecture Notes in Physics, vol 945. Springer, Cham. https://doi.org/10.1007/978-3-319-71894-1_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-71894-1_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-71893-4
Online ISBN: 978-3-319-71894-1
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


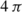 ) production rates; at high energies, however, the rapidity distributions are sufficiently flat to allow midrapidity studies.
) production rates; at high energies, however, the rapidity distributions are sufficiently flat to allow midrapidity studies.