Abstract
An attribute-based credential scheme allows a user, given a set of attributes, to prove ownership of these attributes to a verifier, voluntarily disclosing some of them while keeping the others secret. A number of such schemes exist, of which some additionally provide unlinkability: that is, when the same attributes were disclosed in two transactions, it is not possible to tell if one and the same or two different credentials were involved. Recently full-fledged implementations of such schemes on smart cards have emerged; however, these need to compromise the security level to achieve reasonable transaction speeds. In this paper we present a new unlinkable attribute-based credential scheme with a full security proof, using a known hardness assumption in the standard model. Defined on elliptic curves, the scheme involves bilinear pairings but only on the verifier’s side, making it very efficient both in terms of speed and size on the user’s side.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
- 2.
As in Idemix and U-Prove, our
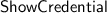 protocol can easily be extended to simultaneously show multiple credentials that have the same secret key, and to proving that the hidden attributes satisfy arbitrary linear combinations [10].
protocol can easily be extended to simultaneously show multiple credentials that have the same secret key, and to proving that the hidden attributes satisfy arbitrary linear combinations [10]. - 3.
Combining the verification of the elements S, \(S_i\) in this fashion achieves with overwhelming probability the same as separately verifying \(e(S,Q){\mathop {=}\limits ^{?}}e(K,A)\) and \(e(S_i,Q){\mathop {=}\limits ^{?}}e(K,A_i)\) [17], reducing the amount of necessary pairings from \(n+3\) to 2. In implementations it will probably suffice to choose these numers from \(\{1,\dots ,2^{\ell _{r}}\}\) (with, say, \(\ell _{r} = 80\)), resulting in a probability of \(2^{\ell _{r}}\) that the \(S,S_i\) are the correct powers \(a,a_i\) of K. We are very grateful to I. Goldberg for suggesting this improvement.
- 4.
We could have eased the notation somewhat by denoting the number \(\kappa \) as an extra attribute \(k_{n+1}\), but because it plays a rather different role than the other attributes (it is part of the signature), we believe this would create more confusion than ease.
- 5.
Credential owners already have such a tuple; verifiers can obtain one simply by executing the
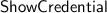 protocol; and issuers can of course create such tuples by themselves. Therefore in practice, each party participating in the scheme will probably already have such a tuple, so that including it in the public key may not be necessary in implementations.
protocol; and issuers can of course create such tuples by themselves. Therefore in practice, each party participating in the scheme will probably already have such a tuple, so that including it in the public key may not be necessary in implementations. - 6.
See gmplib.org.
- 7.
References
Ateniese, G., Camenisch, J., de Medeiros, B.: Untraceable RFID tags via insubvertible encryption. In: Proceedings of the 12th ACM Conference on Computer and Communications Security (CCS 2005), pp. 92–101. ACM, New York (2005)
Au, M.H., Susilo, W., Mu, Y.: Constant-size dynamic k-TAA. In: De Prisco, R., Yung, M. (eds.) SCN 2006. LNCS, vol. 4116, pp. 111–125. Springer, Heidelberg (2006). https://doi.org/10.1007/11832072_8
Baldimtsi, F., Lysyanskaya, A.: Anonymous credentials light. In: Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security (CCS 2013), pp. 1087–1098. ACM, New York (2013)
Baldimtsi, F., Lysyanskaya, A.: On the security of one-witness blind signature schemes. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 82–99. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_5
Barki, A., Brunet, S., Desmoulins, N., Traoré, J.: Improved algebraic MACs and practical keyed-verification anonymous credentials. In: Avanzi, R., Heys, H. (eds.) SAC 2016. LNCS, vol. 10532, pp. 360–380. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-69453-5_20
Beuchat, J.-L., González-Díaz, J.E., Mitsunari, S., Okamoto, E., Rodríguez-Henríquez, F., Teruya, T.: High-speed software implementation of the optimal ate pairing over Barreto–Naehrig curves. In: Joye, M., Miyaji, A., Otsuka, A. (eds.) Pairing 2010. LNCS, vol. 6487, pp. 21–39. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17455-1_2
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again. In: Proceedings of the 3rd Innovations in Theoretical Computer Science Conference (ITCS 2012), pp. 326–349. ACM, New York (2012)
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Cryptol. 21(2), 149–177 (2008)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Brands, S.: Rethinking Public Key Infrastructures and Digital Certificates: Building in Privacy. MIT Press, Cambridge (2000)
Camenisch, J., Hohenberger, S., Pedersen, M.Ø.: Batch verification of short signatures. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 246–263. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_14
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_7
Camenisch, J., Lysyanskaya, A.: Signature schemes and anonymous credentials from bilinear maps. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 56–72. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_4
Camenisch, J., Stadler, M.: Efficient group signature schemes for large groups. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 410–424. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052252
Cramer, R., Damgård, I., MacKenzie, P.: Efficient zero-knowledge proofs of knowledge without intractability assumptions. In: Imai, H., Zheng, Y. (eds.) PKC 2000. LNCS, vol. 1751, pp. 354–372. Springer, Heidelberg (2000). https://doi.org/10.1007/978-3-540-46588-1_24
Damgård, I.: Towards practical public key systems secure against chosen ciphertext attacks. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 445–456. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_36
Ferrara, A.L., Green, M., Hohenberger, S., Pedersen, M.Ø.: Practical short signature batch verification. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 309–324. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00862-7_21
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fuchsbauer, G., Hanser, C., Slamanig, D.: Structure-preserving signatures on equivalence classes and constant-size anonymous credentials. Cryptology ePrint Archive, Report 2014/944 (2014). https://eprint.iacr.org/2014/944
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
Hajny, J., Malina, L.: Unlinkable attribute-based credentials with practical revocation on smart-cards. In: Mangard, S. (ed.) CARDIS 2012. LNCS, vol. 7771, pp. 62–76. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37288-9_5
Hanzlik, L., Kluczniak, K.: A short paper on how to improve U-Prove using self-blindable certificates. In: Christin, N., Safavi-Naini, R. (eds.) FC 2014. LNCS, vol. 8437, pp. 273–282. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45472-5_17
Hoepman, J.-H., Lueks, W., Ringers, S.: On linkability and malleability in self-blindable credentials. In: Akram, R.N., Jajodia, S. (eds.) WISTP 2015. LNCS, vol. 9311, pp. 203–218. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24018-3_13
IBM Research Zürich Security Team: Specification of the identity mixer cryptographic library, version 2.3.0. Technical report, IBM Research, Zürich, February 2012. https://tinyurl.com/idemix-spec
Lenstra, A.K., Verheul, E.R.: Selecting cryptographic key sizes. J. Cryptol. 14(4), 255–293 (2001)
Lysyanskaya, A.: Pseudonym systems. Master’s thesis, Massachusetts Institute of Technology (1999). https://groups.csail.mit.edu/cis/theses/anna-sm.pdf
Lysyanskaya, A., Rivest, R.L., Sahai, A., Wolf, S.: Pseudonym systems. In: Heys, H., Adams, C. (eds.) SAC 1999. LNCS, vol. 1758, pp. 184–199. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46513-8_14
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Paquin, C., Zaverucha, G.: U-Prove cryptographic specification v1.1 (revision 3), December 2013. http://research.microsoft.com/apps/pubs/default.aspx?id=166969. Released under the Open Specification Promise
Ringers, S., Verheul, E., Hoepman, J.H.: An efficient self-blindable attribute-based credential scheme. Cryptology ePrint Archive, Report 2017/115 (2017). https://eprint.iacr.org/2017/115
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Verheul, E., Ringers, S., Hoepman, J.-H.: The self-blindable U-Prove scheme from FC’14 is forgeable (short paper). In: Grossklags, J., Preneel, B. (eds.) FC 2016. LNCS, vol. 9603, pp. 339–345. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54970-4_20
Verheul, E.R.: Self-blindable credential certificates from the weil pairing. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 533–551. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_31
Vullers, P., Alpár, G.: Efficient selective disclosure on smart cards using Idemix. In: Fischer-Hübner, S., de Leeuw, E., Mitchell, C. (eds.) IDMAN 2013. IAICT, vol. 396, pp. 53–67. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37282-7_5
Wachsmann, C., Chen, L., Dietrich, K., Löhr, H., Sadeghi, A.-R., Winter, J.: Lightweight anonymous authentication with TLS and DAA for embedded mobile devices. In: Burmester, M., Tsudik, G., Magliveras, S., Ilić, I. (eds.) ISC 2010. LNCS, vol. 6531, pp. 84–98. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18178-8_8
Wei, V.K., Yuen, T.H.: More short signatures without random oracles. IACR Cryptology ePrint Archive 2005, 463 (2005). http://eprint.iacr.org/2005/463
Acknowledgments
We are very grateful to the anonymous referees for their helpful and constructive feedback, and to I. Goldberg for suggesting the method from [17] for reducing the verification pairing count.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Unforgeability and Unlinkability Games
A Unforgeability and Unlinkability Games
Unforgeability of a credential scheme is defined using the following game (resembling the signature scheme unforgeability game).
Definition 14
(unforgeability game). The unforgeability game of an attribute-based credential scheme between a challenger and an adversary \(\mathcal {A}\) is defined as follows.
- Setup.:
-
For a given security parameter \(\ell \), the adversary decides on the number of attributes \(n\ge 1\) that each credential will have, and sends n to the challenger. The challenger then runs the
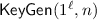 algorithm from the credential scheme and sends the resulting public key to the adversary.
algorithm from the credential scheme and sends the resulting public key to the adversary. - Queries.:
-
The adversary \(\mathcal {A}\) can make the following queries to the challenger.
 :
:-
The challenger and adversary engage in the
 protocol, with the adversary acting as the user and the challenger acting as the issuer, over the attributes \((k_{1,j},\dots ,k_{n,j})\). It may choose these adaptively.
protocol, with the adversary acting as the user and the challenger acting as the issuer, over the attributes \((k_{1,j},\dots ,k_{n,j})\). It may choose these adaptively. 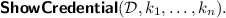 :
:-
The challenger creates a credential with the specified attributes \(k_1,\dots ,k_n\), and engages in the
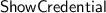 protocol with the adversary, acting as the user and taking \(\mathcal {D}\) as disclosure set, while the adversary acts as the verifier.
protocol with the adversary, acting as the user and taking \(\mathcal {D}\) as disclosure set, while the adversary acts as the verifier.
- Challenge.:
-
The challenger, now acting as the verifier, and the adversary, acting as the user, engage in the
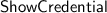 protocol. The adversary chooses a disclosure set \(\mathcal {D}\), and if it manages to make the verifier accept then it wins if one of the following holds:
protocol. The adversary chooses a disclosure set \(\mathcal {D}\), and if it manages to make the verifier accept then it wins if one of the following holds:
-
If the adversary made no
 queries then it wins regardless of the disclosure set (even if \(\mathcal {D}=\emptyset \));
queries then it wins regardless of the disclosure set (even if \(\mathcal {D}=\emptyset \)); -
Otherwise \(\mathcal {D}\) must be nonempty, and if \((k_i)_{i\in \mathcal {D}}\) are the disclosed attributes, then there must be no j such that \(k_i = k_{i,j}\) for all \(i \in \mathcal {D}\) (i.e., there is no single credential issued in an
 query containing all of the disclosed attributes \((k_i)_{i \in \mathcal {D}}\)).
query containing all of the disclosed attributes \((k_i)_{i \in \mathcal {D}}\)).
We say that the credential scheme is unforgeable if no probabilistic polynomial-time algorithm can win this game with non-negligible probability in the security parameter \(\ell \).
Next we turn to the unlinkability game.
Definition 15
(unlinkability game). The unlinkability game of an attribute-based credential scheme between a challenger and an adversary \(\mathcal {A}\) is defined as follows.
- Setup.:
-
For a given security parameter \(\ell \), the adversary decides on the number of attributes \(n\ge 1\) that each credential will have, and sends n to the challenger. The adversary then runs the
 algorithm from the credential scheme and sends the resulting public key to the challenger.
algorithm from the credential scheme and sends the resulting public key to the challenger. - Queries.:
-
The adversary \(\mathcal {A}\) can make the following queries to the challenger.
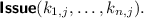 :
:-
The adversary chooses a set of attributes \((k_{1,j},\dots ,k_{n,j})\), and sends these to the challenger. Then, acting as the issuer, the adversary engages in the
 protocol with the challenger, issuing a credential j to the challenger having attributes \((k_{1,j},\dots ,k_{n,j})\).
protocol with the challenger, issuing a credential j to the challenger having attributes \((k_{1,j},\dots ,k_{n,j})\).  :
:-
The adversary and challenger engage in the showing protocol on credential j, the challenger acting as the user and the adversary as the verifier. Each time the adversary may choose the disclosure set \(\mathcal {D}\).
 :
:-
The challenger sends the entire internal state, including the secret key \(k_0\), of credential j to the adversary.
- Challenge.:
-
The adversary chooses two uncorrupted credentials \(j_0\), \(j_1\) and a disclosure set \(\mathcal {D}\subset \{1,\dots ,n\}\). These have to be such that the disclosed attributes from credential \(j_0\) coincide with the ones from credential \(j_1\), i.e., \(k_{i,j_0} = k_{i,j_1}\) for each \(i \in \mathcal {D}\). It sends the indices \(j_0\), \(j_1\) and \(\mathcal {D}\) to the challenger, who checks that this holds; if it does not then the adversary loses.
Next, the challenger flips a bit \(b \in _R\{0,1\}\), and acting as the user, it engages in the
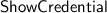 with the adversary on credential \(j_b\). All attributes whose index is in \(\mathcal {D}\) are disclosed.
with the adversary on credential \(j_b\). All attributes whose index is in \(\mathcal {D}\) are disclosed. - Output.:
-
The adversary outputs a bit \(b'\) and wins if \(b = b'\).
We define the advantage of the adversary \(\mathcal {A}\) as \(\textsf {Adv}_\mathcal {A}:= \left| \Pr [b=b']-1/2\right| \). When no probabilistic polynomial-time algorithm can win this game with non-negligible advantage in the security parameter \(\ell \), then we say that the credential scheme is unlinkable.
Rights and permissions
Copyright information
© 2017 International Financial Cryptography Association
About this paper
Cite this paper
Ringers, S., Verheul, E., Hoepman, JH. (2017). An Efficient Self-blindable Attribute-Based Credential Scheme. In: Kiayias, A. (eds) Financial Cryptography and Data Security. FC 2017. Lecture Notes in Computer Science(), vol 10322. Springer, Cham. https://doi.org/10.1007/978-3-319-70972-7_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-70972-7_1
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70971-0
Online ISBN: 978-3-319-70972-7
eBook Packages: Computer ScienceComputer Science (R0)


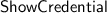 protocol can easily be extended to simultaneously show multiple credentials that have the same secret key, and to proving that the hidden attributes satisfy arbitrary linear combinations [
protocol can easily be extended to simultaneously show multiple credentials that have the same secret key, and to proving that the hidden attributes satisfy arbitrary linear combinations [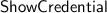 protocol; and issuers can of course create such tuples by themselves. Therefore in practice, each party participating in the scheme will probably already have such a tuple, so that including it in the public key may not be necessary in implementations.
protocol; and issuers can of course create such tuples by themselves. Therefore in practice, each party participating in the scheme will probably already have such a tuple, so that including it in the public key may not be necessary in implementations.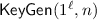 algorithm from the credential scheme and sends the resulting public key to the adversary.
algorithm from the credential scheme and sends the resulting public key to the adversary. :
: protocol, with the adversary acting as the user and the challenger acting as the issuer, over the attributes
protocol, with the adversary acting as the user and the challenger acting as the issuer, over the attributes 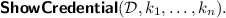 :
: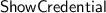 protocol with the adversary, acting as the user and taking
protocol with the adversary, acting as the user and taking 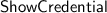 protocol. The adversary chooses a disclosure set
protocol. The adversary chooses a disclosure set  queries then it wins regardless of the disclosure set (even if
queries then it wins regardless of the disclosure set (even if  query containing all of the disclosed attributes
query containing all of the disclosed attributes  algorithm from the credential scheme and sends the resulting public key to the challenger.
algorithm from the credential scheme and sends the resulting public key to the challenger.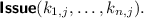 :
: protocol with the challenger, issuing a credential j to the challenger having attributes
protocol with the challenger, issuing a credential j to the challenger having attributes  :
: :
: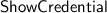 with the adversary on credential
with the adversary on credential