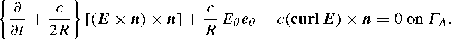Abstract
The aim of this first chapter is to present the physics framework of electromagnetism, in relation to the main sets of equations, that is, Maxwell’s equations and some related approximations. In that sense, it is neither a purely physical nor a purely mathematical point of view. The term model might be more appropriate: sometimes, it will be necessary to refer to specific applications in order to clarify our purpose, presented in a selective and biased way, as it leans on the authors’ personal view. This being stated, this chapter remains a fairly general introduction, including the foremost models in electromagnetics. Although the choice of such applications is guided by our own experience, the presentation follows a natural structure.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Unless otherwise specified, in this chapter, a domain is an open region of space. Another meaning is given for the mathematical studies, starting in Chap. 2.
- 2.
H is sometimes called the magnetizing field.
- 3.
The standard differential operators
 , div, \( \operatorname {\mathrm {\mathbf {grad}}}\), and Δ are mathematically defined in Sect. 1.5.1.
, div, \( \operatorname {\mathrm {\mathbf {grad}}}\), and Δ are mathematically defined in Sect. 1.5.1. - 4.
By definition, δ Σ is the surface Dirac mass on Σ, so one has \(\int \varrho v = \int _\varSigma \sigma _\varSigma v_{|\varSigma } \,dS\) for ad hoc functions v.
- 5.
See the end of the section.
- 6.
By definition, \(\delta _{{\boldsymbol {x}}_0}\) is the Dirac mass in x 0, so one has \(\int \varrho _0 v = q_0 v({\boldsymbol {x}}_0)\) for ad hoc functions v.
- 7.
Or: electrostatically.
- 8.
To deserve the label fixed frequency problem, one assumes a non-vanishing value of the pulsation. Otherwise, one solves a static problem, cf. Sect. 1.4.1.
- 9.
The fields
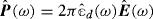 and
and 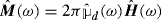 are respectively called electric and magnetic polarizations
.
are respectively called electric and magnetic polarizations
. - 10.
Other conditions on
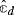 lead to the same conclusion. For instance, if
lead to the same conclusion. For instance, if 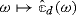 is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition
is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition  for large |ω|.
for large |ω|. - 11.
In particular, this is the case for the Lorentz force (1.75). As a matter of fact, div v F(t, x, v) = q (div v E + div v (v ×B)) = 0, since the electromagnetic fields are independent of v in the phase space.
- 12.
- 13.
It can happen that, in Maxwell’s equations, parts of ϱ and J are due to external charge and current sources. In this case, E and B depend in an affine way on f.
- 14.
Id est, consider \(f_\alpha ({\boldsymbol {v}})\approx A_\alpha \exp (-B_\alpha |{\boldsymbol {v}}-\boldsymbol {u}_\alpha |{ }^2)\), with A α , B α > 0.
- 15.
See the upcoming Sect. 1.5 for a precise definition.
- 16.
More precisely, ω is a pulsation and the corresponding frequency is ω∕(2π).
- 17.
One may also use the interface conditions to describe electromagnetic fields globally in \(\mathbb {R}^3\): this is an integral representation. More precisely [167, §5.5], consider that \(\mathbb {R}^3\) is split into two media M + and M −, one of them being bounded, and let Σ be the interface between the two media. If one is interested in the electromagnetic fields that are governed by the homogeneous time-harmonic equations in M + and M −, then, assuming that the jump j Σ = −[H ×n Σ ] Σ (condition (1.12 right)) is known, one can use integral representation formulas for the values of E(x) and H(x), for all \({\boldsymbol {x}}\in \mathbb {R}^3\setminus \varSigma \). The integrals are taken over Σ and depend only on j Σ . In the same spirit, one can represent the (different) values of E ±(x Σ ) and H ±(x Σ ) for all x Σ ∈ Σ. Within this framework, one may generalize these results in the presence of magnetic polarization by assuming that the magnetic current on Σ, m Σ = [E ×n Σ ] Σ , is also different from 0. In this case, one ends up with integral representation formulas of E and H, with integrals over Σ that depend on j Σ and m Σ . In the same manner, one may use the jump relation σ Σ = [D ⋅n Σ ] Σ (1.11 left) to solve a diffraction problem expressed as a scalar Helmholtz equation, assuming σ Σ is known, where the unknown is the scalar electric potential.
- 18.
Instead of B(O, R), one can choose any reasonable volume in which the computations ought to be performed: a cube, as in Fig. 1.3 (right, rightmost Γ A ), etc.
- 19.
For instance (see [187]), if the artificial boundary Γ A is a cylinder of radius R and axis Oz, one gets
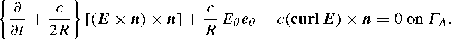
with E = E r e r + E θ e θ + E z e z in cylindrical coordinates.
- 20.
Manipulating Maxwell’s equations thusly is certainly admissible, since one is dealing with artificial media, in which the electromagnetic fields are artifacts…
- 21.
Indeed, the unit outward normal vector to ∂B(O, R) is n = e r . Moreover, since x = r e r on ∂B(O, R), for an outgoing plane wave that propagates normally to ∂B(O, R) (k out = k e r ), one finds k out ⋅x = kr. Respectively, for an incoming plane wave that propagates normally to ∂B(O, R) (k in = −k e r ), k in ⋅x = −kr.
References
S. Abarbanel, D. Gottlieb, J.S. Hestaven, Non-linear PML equations for time-dependent electromagnetics in three dimensions. J. Sci. Comput. 28, 125–137 (2006)
J.J. Ambrosiano, S.T. Brandon, E. Sonnendrücker, A finite element formulation of the Darwin PIC model for use on unstructured grids. J. Comput. Phys. 121, 281–297 (1995)
X. Antoine, H. Barucq, A. Bendali, Bayliss-Turkell-like radiation conditions on surfaces of arbitrary shape. J. Math. Anal. Appl. 229, 184–211 (1999)
A.A. Arseneev, Local uniqueness and existence of classical solution of Vlasov’s system of equations. Sov. Math. Dokl. 15, 1223–1225 (1974)
A.A. Arseneev, Global existence of a weak solution of Vlasov’s system of equations. U.S.S.R. Comput. Math. Math. Phys. 15, 131–143 (1975)
F. Assous, P. Degond, E. Heintzé, P.-A. Raviart, J. Segré, On a finite element method for solving the three-dimensional Maxwell equations. J. Comput. Phys. 109, 222–237 (1993)
F. Assous, F. Tsipis, A PIC method for solving a paraxial model of highly relativistic beams. J. Comput. Appl. Math. 227, 136–146 (2008)
F.V. Atkinson, On Sommerfeld’s radiation condition. Philos. Mag. 40, 645–651 (1949)
A. Bachelot, V. Lange, Time dependent integral method for Maxwell’s equations with impedance boundary condition, in Boundary Element Technology, vol. 10, ed. by C.A. Brebbia, M.H. Aliabadah (Wessex Institute of Technology, Southampton, 1995), pp. 137–144
E. Bécache, S. Fauqueux, P. Joly, Stability of perfectly matched layers, group velocities and anisotropic waves. J. Comput. Phys. 188, 399–433 (2003)
E. Bécache, P. Joly, On the analysis of Bérenger’s perfectly matched layers for Maxwell’s equations. Math. Model. Numer. Anal. 36, 87–119 (2002)
S. Benachour, F. Filbet, P. Laurençot, E. Sonnendrücker, Global existence for the Vlasov-Darwin system in \(\mathbb {R}^3\) for small initial data. Math. Methods Appl. Sci. 26, 297–319 (2003)
A. Bendali, P. Guillaume, Non-reflecting boundary conditions for waveguides. Math. Comput. 68, 123–144 (1999)
A. Bendali, L. Halpern, Conditions aux limites absorbantes pour le système de Maxwell dans le vide en dimension 3. C. R. Acad. Sci. Paris Ser. I 307, 1011–1013 (1988)
J.-P. Bérenger, A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 114, 185–200 (1994)
J.-P. Bérenger, Three-dimensional perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 127, 363–379 (1996)
A.J. Berkhout, Seismic Migration (Elsevier, Amsterdam, Oxford, New York, Tokyo, 1984)
C.K. Birdsall, A.B. Langdon, Plasmas Physics via Computer Cimulation (McGraw-Hill, New York, 1985)
V.A. Bokil, M.W. Buksas, Comparison of finite difference and mixed finite element methods for perfectly matched layer models. Commun. Comput. Phys. 2, 806–826 (2007)
F. Bouchut, F. Golse, M. Pulvirenti, Kinetic Equations and Asymptotic Theory. Series in Applied Mathematics (Gauthier-Villars, 2000)
M. Cessenat, Mathematical Methods in Electromagnetism. Linear Theory and Applications. Advances in Mathematics for Applied Sciences, vol. n41 (World Scientific, Singapore, 1996)
F.F. Chen, Introduction to Plasma Physics (Plenum Press, New York, London, 1974)
W.C. Chew, W.H. Weedon, A 3D perfectly matched medium from modified Maxwell’s equations with stretched coordinates. Microw. Opt. Technol. Lett. 7, 599–604 (1994)
P. Ciarlet, Jr., E. Sonnendrücker, A decomposition of the electric field. Application to the Darwin model. Math. Methods Appl. Sci. 7(8), 1085–1120 (1997)
J.F. Claerbout, Imaging the Earth’s Interior (Blackwell Scientific Publications, Oxford, 1985)
D. Colton, R. Kress, Inverse Acoustic and Electromagnetic Theory (Springer, Berlin, 1998)
C.G. Darwin, The dynamical motion of particles. Philos. Mag. 39, 537–551 (1920)
R. Dautray, J.-L. Lions, Analyse mathématique et calcul numérique pour les sciences et les techniques (Masson, Paris, 1987)
R. Dautray, J.-L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology (Springer, Berlin, 1990)
P.A. Davidson, An Introduction to Magnetohydrodynamics (Cambridge University Press, Cambridge, 2001)
P. Degond, Local existence of the solutions of the Vlasov-Maxwell equations and convergence to the Vlasov-Poisson equations for infinite light velocity. Math. Methods Appl. Sci. 8, 533–558 (1986)
P. Degond, P.-A. Raviart, An analysis of the Darwin model of approximation to Maxwell’s equations. Forum Math. 4, 13–44 (1992)
L. Desvillettes, Quelques outils d’analyse pour les équations de Vlasov et de Landau, in Ecole CEA-EDF-INRIA, Equations cinétiques et applications à la physique (2005)
R.J. DiPerna, P.-L. Lions, Global weak solutions of Vlasov-Maxwell systems. Commun. Pure Appl. Math. 42, 729–757 (1989)
E. Durand, Electrostatique (Masson, Paris, 1964)
D.M. Eidus, The principle of limiting absorption. Russ. Math. Surv. 24, 97–167 (1969)
B. Engquist, A. Majda, Absorbing boundary conditions for acoustic and elastic wave equations. Math. Comput. 31, 629–651 (1977)
X. Feng, Absorbing boundary conditions for electromagnetic wave propagation. Math. Comput. 68, 145–168 (1999)
R. Feynman, Leighton, Sands, The Feynman Lectures on Physics: Electromagnetism (Addison-Wesley, Reading, 1964)
S.D. Gedney, An anisotropic perfectly-matched layer absorbing medium for the truncation of FT-TD lattices. IEEE Trans. Antennas Propag. 44, 1630–1639 (1996)
S.D. Gedney, The perfectly matched layer absorbing medium, in Advances in Computational Electrodynamics, ed. by A. Taflove (Artech House, 1998), pp. 263–344
D. Givoli, A spatially exact non-reflecting boundary condition for time dependent problems. Comput. Methods Appl. Mech. Eng. 95, 97–113 (1992)
R.T. Glassey, W. Strauss, Singularity formation in a colisionless plasma could only occur at high velocities. Arch. Ration. Mech. Anal. 92, 56–90 (1986)
P.W. Gross, P.R. Kotiuga, Electromagnetic Theory and Computation: A Topological Approach. MSRI Publications Series (Cambridge University Press, Cambridge, 2004)
M.J. Grote, J.B. Keller, On nonreflecting boundary conditions. J. Comput. Phys. 122, 231–243 (1995)
Y. Guo, Global weak solutions of the Vlasov-Maxwell system with boundary conditions. Commun. Math. Phys. 154, 245–263 (1993)
C. Hazard, M. Lenoir, On the solution of time-harmonic scattering problems for Maxwell’s equations. SIAM J. Math. Anal. 27, 1597–1630 (1996)
A.D. Ioannidis, I.G. Stratis, A. Yannacopoulos, Electromagnetic wave propagation in dispersive bianisotropic media, in Proc. of the 6th Int. Workshop on Advances in Scattering and Biomedical Engineering, ed. by D. Fotiadis et al. (World Scientific, 2003), pp. 295–304
J.D. Jackson, Classical Electrodynamics, 3rd edn. (Wiley, New York, 1999)
B. Jensen, The quantum extension of the Drude-Zener theory in polar semiconductors, in Handbook of Optical Constants of Solids, ed. by E.D. Palik (Academic Press, New York, 1998), pp. 169–188
P. Joly, An elementary introduction to the construction and the analysis of perfectly matched layers for time domain wave propagation. SeMA J. 57, 5–48 (2012)
P. Joly, B. Mercier, Une nouvelle condition transparente d’ordre 2 pour les équations de Maxwell en dimension 3. Technical Report INRIA, vol. 1047 (1989)
D.S. Jones, Methods in Electromagnetic Wave Propagation (Clarendon Press, Oxford, 1998)
A. Karlsson, G. Kristensson, Constitutive relations, dissipation and reciprocity for the Maxwell equations in the time domain. Technical Report (Revision No. 2: August 1999) Lund Institute of Technology, CODEN:LUTEDX/(TEAT-7005)/1-36/(1989), Lund (1999)
N.A. Krall, A.W. Trivelpiece, Principles of Plasma Physics (McGraw-Hill, New York, 1973)
A. Lakhtakia, V.K. Varadan, V.V. Varadan, Time-Harmonic Electromagnetic Fields in Chiral Media. Lecture Notes in Physics (Springer, Berlin, 1989)
G. Laval, Matière et rayonnement (Ecole Polytechnique, Palaiseau, 1986)
A.E. Lifschitz, Magnetohydrodynamics and Spectral Theory (Kluwer Academic, 1989)
I. Lindell, A. Shivola, S. Tertyakov, A. Viitanen, Electromagnetic Waves in Chiral and Bi-isotropic Media (Artech House, Boston, 1994)
S.A. Maier, Plasmonics: Fundamentals and Applications (Springer, 2007)
C. Müller, Foundations of the Mathematical Theory of Electromagnetic Waves (Springer, Berlin, 1969)
J.-C. Nédélec, Acoustic and Electromagnetic Equations. Applied Mathematical Sciences, vol. 144 (Springer, New York, 2001)
H.M. Nussenzveig, Causality and Dispersion Relations (Academic Press, New York, 1972)
C. Rappaport, Perfectly matched absorbing boundary conditions based on anisotropic lossy mapping of space. IEEE Microw. Guid. Wave Lett. 5, 90–92 (1995)
P.-A. Raviart, E. Sonnendrücker, A hierarchy of approximate models for the Maxwell equations. Numer. Math. 73, 329–372 (1996)
Z. Sacks, D. Kinsland, R. Lee, J.F. Lee, A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE Trans. Antennas Propag. 43, 1460–1463 (1995)
J. Sanchez Hubert, E. Sanchez Palencia, Vibration and Coupling of Continuous Systems (Springer, 1989)
M. Sesques, Conditions aux limites artificielles pour le système de Maxwell, PhD Thesis, Bordeaux I University, France, 1990 (in French)
S. Silver, Microwave Antenna Theory and Design. M.I.T. Radiation Laboratory Series, vol. 12 (McGraw-Hill, New York, 1949)
F. Simpson, K. Bahr, Practical Magnetotellurics (Cambridge University Press, Cambridge, 2005)
A. Sommerfeld, Die Greensche Funktion der Schwingungsgleichung. Jber. Deutsch. Math. Verein. 21, 309–353 (1912)
T.H. Stix, Waves in Plasmas (American Institute of Physics, New York, 1992)
S. Ukai, T. Okabe, On classical solution in the large in time of two dimensional Vlasov’s equation. Osaka J. Math. 15, 245–261 (1978)
J. Van Bladel, Electromagnetic Fields (McGraw-Hill, New York, 1985)
C.H. Wilcox, An expansion theorem for electromagnetic fields. Commun. Pure Appl. Math. 9, 115–134 (1956)
S. Wollman, An existence and uniqueness theorem for the Vlasov-Maxwell system. Commun. Pure Appl. Math. 37, 457–462 (1984)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Assous, F., Ciarlet, P., Labrunie, S. (2018). Physical Framework and Models. In: Mathematical Foundations of Computational Electromagnetism. Applied Mathematical Sciences, vol 198. Springer, Cham. https://doi.org/10.1007/978-3-319-70842-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-70842-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70841-6
Online ISBN: 978-3-319-70842-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 , div,
, div, 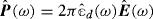 and
and 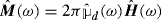 are respectively called electric and magnetic polarizations
.
are respectively called electric and magnetic polarizations
.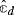 lead to the same conclusion. For instance, if
lead to the same conclusion. For instance, if 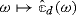 is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition
is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition  for large |ω|.
for large |ω|.