Abstract
This paper summarizes the ideas and background of a combinatorics research and teaching project, including historical reforms in school curriculum in 1978 in Hungary and T. Varga’s work. Thereafter we discuss the main elements of our current project: pretest and developed teaching materials, including worksheets with some examples and some tools for teaching combinatorics such as Poliuniversum. In choosing the problems of the worksheets we were led by two research questions: (1) how students handle open tasks (which are presented in many combinatorial problems) and (2) how they use various manipulatives at different ages.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Beregszászi, E. (2016). Development of combinatorial thinking. Unpublished dissertation [in Hungarian]. Eötvös Lóránd University, Budapest, Hungary.
Bruner, J., Olver, R., & Greenfield, P. (1966). Studies in cognitive growth. Oxford, England: Wiley.
Fenyvesi, K., Oláhné Téglási, I., & Prokajné Szilágyi, I. (2014). Adventures on paper math-art activities for experience-centered education of mathematics. Eger: Eszterházy Károly College (http://vismath.ektf.hu/index.php?l=en&m=311).
Fenyvesi, K., & Stettner, E. (Eds.) (2011). Hidak, Matematikai kapcsolatok a művészetben, a tudományban és az élményközpontú oktatásban. Kaposvár.
Freudenthal, H. (1973). Mathematics as an educational task. Dordrecht-Holland: D. Riedel Publishing Company.
Halmos, M., & Varga, T. (1978). Change in mathematics education since the late 1950’s—Ideas and realization, Hungary. Educational Studies in Mathematics, 9, 225–244.
Kosztolányi, J., Pintér, K., Bagota, M., & Dancs, G. (2016). How do students solve combinatorial problems: Some results of a research about difficulties and strategies of Hungarian students. In C. Csíkos, A. Rausch, & J. Szitanyi (Eds.), Proceedings of the 40th conference of the international group for the psychology of mathematics education (Vol. 3, pp. 115–122). Szeged, Hungary: PME.
Lockwood, E., Swinyard, C. A., & Caughman, J. S. (2015). Modeling outcomes in combinatorial problem solving: The case of combinations. In T. Fukawa-Connelly, N. Infante, K. Keene, & M. Zandieh (Eds.), Proceedings for the eighteenth special interest group of the MAA on research on undergraduate mathematics education (pp. 601–696). Pittsburgh, PA: West Virginia University.
Stettner, E., & Emese, G. (2016). Teaching combinatorics with “poly-universe”, bridges Finland conference proceedings, 2016 (pp. 553–556). Phoenix, Arizona: Tessellations Publishing.
Szitányi, J., & Csíkos, Cs. (2015). Performance and strategy use in combinatorial reasoning among pre-service elementary teachers. In Proceedings of the 39th conference of the international group for the psychology of mathematics education (Vol. 4, pp. 225–232), Hobart.
Varga, T. (1967). Combinatorials and probability for young children. Canada: Sherbrooke Mathematics Project, University of Sherbrooke.
Varga, T. (1969). Matematika születőfélben [Mathematics at birth], Élet és irodalom, 1.
Varga, T. (1988). Mathematics education in Hungary today. Educational Studies in Mathematics, 19, 291–298.
Acknowledgements
This study was funded by the Content Pedagogy Research Program of the Hungarian Academy of Sciences.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Pretest
Appendix: Pretest
Sixty minutes are allocated to answer the following questions. Give reasons to your answers in detail. Make sure that you indicate your final answer. Have fun.
-
1.
Robert, John, Kate and Elizabeth are sitting on a bench next to each other.
-
(a)
How many sitting arrangements are possible?
-
(b)
Another boy, called Michael joined them. How many different ways can they be seated on the bench if a girl can sit next to a boy and a boy can sit next to a girl only (if girls and boys alternate)?
-
(c)
Robert, Michael, John, Kate, Maria, Elizabeth and Susanne line up (in a row) in the schoolyard. How many ways is it possible?
-
(d)
How many different ways could this be done if boys and girls alternate? (A girl can stand next to a boy and a boy can stand next to a girl only.)
-
(a)
-
2.
Consider clowns.
-
(a)
A clown has 3 buttons on each leg of his trousers, 3 on each arm of his coat and 3 in the middle of his coat. There were three colors used on each place: one red, one yellow and one green button. Is it possible that the order of the colors of the five places is different?
-
(b)
A class of the Riverside Clown School has students with a special uniform. Their uniform has 5 buttons on each leg of their trousers, 5 on each arm of their coats and 5 in the middle of their coats. There were 5 colors used on each place: one red, one yellow, one green, one blue and one purple. (See diagram.) We know that each student has a different dress (uniform). It means that the order of the colors on each of the 5 places is different. What is the maximum number of students in a class under the given conditions?
-
(a)
-
3.
Mary made towers by using colored cubes of the same size.
-
(a)
How many four-story towers can be made by using 4 cubes if each cube has different color?
-
(b)
How many five-story towers can be made by using 5 cubes if 3 of them are red and 2 cubes are blue?
-
(c)
How many eight-story towers can be made by using 8 cubes if 3 of them are red and 5 of them are green?
-
(a)
-
4.
Consider the numbered cards below.
-
(a)
How many five digit numbers can be formed by using all these cards if each of them is used exactly once?

-
(b)
How many five-digit numbers can be formed by using all these cards if each of them is used exactly once?

-
(c)
How many seven-digit numbers can be formed by using all these cards if each of them is used exactly once?

-
(a)
-
5.
Consider a magician.
-
(a)
A magician put 2 red and 5 blue balls of the same size onto a table where the table can be turned around. (See diagram.) Two arrangements of the balls are identical if they match when the table turns. How many different arrangements of the balls are possible?
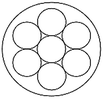
-
(b)
This time the magician put 2 red and 17 blue balls of the same size onto a table where the table can be turned around. (See diagram.) Two arrangements of the balls are identical if they match when the table turns. How many different arrangements of the balls are possible this way?
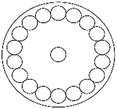
-
(a)
-
6.
We put 1, 2, 3 and 4 into the boxes by using the following rules:

-
Firstly 1 is placed in a box, followed by 2. Then 3 comes. Finally, 4 is put into the leftover place.
-
We put a single number into each square.
-
The first number can be put anywhere.
-
Then you can put each leftover number into a box which has already a number NEXT to it.
-
(a)
How many ways can you fill the boxes in? (Two arrangements are different if you find at least one box with two different numbers.)
-
(b)
How will your answer change if you must use 1, 2, 3, 4, 5, 6 and 7 under the same conditions (see list above)?

-
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this chapter
Cite this chapter
Vancsó, Ö., Beregszászi, E., Burian, H., Emese, G., Stettner, E., Szitányi, J. (2018). Complex Mathematics Education in the 21st Century: Improving Combinatorial Thinking Based on Tamás Varga’s Heritage and Recent Research Results. In: Hart, E., Sandefur, J. (eds) Teaching and Learning Discrete Mathematics Worldwide: Curriculum and Research. ICME-13 Monographs. Springer, Cham. https://doi.org/10.1007/978-3-319-70308-4_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-70308-4_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70307-7
Online ISBN: 978-3-319-70308-4
eBook Packages: EducationEducation (R0)








