New Second Preimage Attacks on Dithered Hash Functions with Low Memory Complexity

Abstract

Dithered hash functions were proposed by Rivest as a method to mitigate second preimage attacks on Merkle-Damgård hash functions. Despite that, second preimage attacks against dithered hash functions were proposed by Andreeva et al. One issue with these second preimage attacks is their huge memory requirement in the precomputation and the online phases. In this paper, we present new second preimage attacks on the dithered Merkle-Damgård construction. These attacks consume significantly less memory in the online phase (with a negligible increase in the online time complexity) than previous attacks. For example, in the case of MD5 with the Keränen sequence, we reduce the memory complexity from about $2^{51}$ blocks to about $2^{26.7}$ blocks (about 545 MB). We also present an essentially memoryless variant of Andreeva et al. attack. In case of MD5-Keränen or SHA1-Keränen, the offline and online memory complexity is $2^{15.2}$ message blocks (about 188–235 KB), at the expense of increasing the offline time complexity.

The first and second authors were supported in part by the Israeli Science Foundation through grant No. 827/12.

1 Introduction

Cryptographic hash functions have many information security applications, notably in digital signatures and message authentication codes (MACs). The need for hash functions renders its security as one of the important topics in the design analysis of cryptographic primitives.

Designing hash function usually consists of two parts:

• Designing a compression function (or a secure permutation, in the case of sponge functions [4]).

• Designing the mode of iteration (also called domain extension).

These two parts complement one another, and to create a secure hash function, a secure compression function and a secure mode of iteration are needed.

The most common and used mode of iteration is Merkle-Damgård [6, 14]. Though believed to be secure, the Merkle-Damgård construction was found vulnerable to different multi-collision and second preimage attacks [1,2,3, 7,8,9,10,11]. One of the alternatives that was suggested to replace Merkle-Damgård and to increase Merkle-Damgård security, is the dithered Merkle-Damgård [18]. Dithered Merkle-Damgård was designed by Rivest to overcome the Expandable Message attack of [11]. The main idea of dithered Merkle-Damgård is to add a third input (derived from some sequence) to the compression function to perturb the hashing process. However, dithered Merkle-Damgård was found vulnerable to two second preimage attacks by Andreeva et al. [1, 3]. While taking less than $2^n$ time to find a second preimage, these attacks consume a huge amount of memory.

1.1 Related Work

Andreeva et al. described in [1, 3] two second preimage attacks on dithered Merkle-Damgård. The first attack, the “adapted Kelsey-Kohno”, uses a diamond structure (similarly to our attack). Assume that the dithering sequence z (over alphabet $\mathcal{A}$) is used, the compression function $f:\{0,1\}^n \times \{0,1\}^b \times \mathcal{A}\rightarrow \{0,1\}^n$ and that the target message is $2^k$ blocks. The online time complexity of the first attack is¹ $\frac{{2^{n-k}}}{Freq_{z}(w^{\ell +1}_{mc})}+ 2^{n-\ell }$, and the offline and the online memory complexities are $2^{n/2+\ell /2+1/2}$ and $2^{\ell +1}$, respectively.

The second attack, the “Kite Generator”, requires $2 \cdot |\mathcal{A} |\cdot 2^n$ time complexity in the offline phase, and $max(2^k,2^{(n-k)/2})$ time complexity in the online phase. Its memory complexity is $|\mathcal {A}|\cdot 2^{n-k}$ in both the offline and the online phases.

To summarize both attacks require a tremendous amount of memory in the online phase. In this paper we reduce the memory complexity (of the online and offline phases) of second preimage attacks on dithered.

1.2 Our Results

This paper describes novel second preimage attacks on dithered Merkle-Damgård hash function with very low memory complexities. We first explore attacks that have low online memory complexity with almost no increase in the time complexities compared with the attacks of [1, 3]. The online and offline memory complexities of the basic attack are $|\mathcal{A}| \cdot Fact_z(\ell ) \cdot (\ell + 1)$ and $Fact_z(\ell ) \cdot 2^{\ell +1} + 2^{n/2+\ell /2+1/2}$, respectively. For example, the memory time complexity of the attack, in case of MD5-Keränen for $\ell = 50$ is about $2^{26.7}$ blocks (about 507 MB).

Then, we introduce ideas and optimizations of the attack that reduce the offline time and memory complexities. Lastly, we use these ideas to present an essentially memoryless attack, again without increasing the online time complexity. The online and the offline memory complexity of the attack is $(\ell + 1) \cdot Fact_z(\ell +1)$ blocks. However, for this reduced memory attack, the offline time complexity is increased.

In Table 1, we compare the complexities of second preimage attacks on dithered Merkle-Damgård. In Table 2, we compare the complexities of the second preimage attacks on real hash functions with concrete parameters.²

Table 1. Comparison of the second preimage attacks on dithered hash functions.

Table 2. Comparison of the second preimage attacks on dithered hash functions which uses the Keränen sequence. $\ell$ was chosen as an optimal value for “adapted Kelsey-Kohno”. The analysis in [1, 3] about dithering sequence, showed that for Keränen sequence and $\ell =50$ holds and .

1.3 Organization of the Paper

We introduce some terminology, describe the Merkle-Damgård construction, and the dithered Merkle-Damgård construction in Sect. 2. We describe the previous attacks in Sect. 3. We then present our new basic attack (which has comparable time complexity to the attack of [1, 3]) in Sect. 4. We show optimizations and improvements for the offline time complexity of this attack in Sect. 5. In Sect. 6, we show offline memory optimizations. We then show an essentially memoryless attack on dithered hash functions in Sect. 7. Finally, we conclude the paper in Sect. 8.

2 Background and Notations

2.1 General Notations

• $\{0,1\}^n$ — all the strings over ‘0’ and ‘1’ of length n.

• $\{0,1\}^*$ — all the strings of finite length.

• m — a message $m \in \{0,1\}^*$.

• $|m |_b$ — the length of m in b-bit block units.

• $\mathcal A$ — a finite alphabet.

• w[i] — the ith letter of w.

• $w^{\ell }_{mc}$ — the most common word (or factor) of length $\ell$ in a sequence z.

• $Freq_z(w)$ is the frequency of the word w over the sequence z.

• $Fact_z(\ell )$ — the sequence’s complexity of a sequence z, given an integer $\ell$, as the number of different factors in z of length $\ell$.

• $P_{w_h}$ — given a binary tree w, the path $P_{w_h}$ is the sequence of edges which connects the leaf h to the root of w.

2.2 Merkle-Damgård

Let $f:\{0,1\}^n \times \{0,1\}^b \rightarrow \{0,1\}^n$ be a compression function, then the Merkle-Damgård hash function $H^f:\{0,1\}^*\rightarrow \{0,1\}^n$ is:

• $m_1, m_2,\ldots ,m_L \leftarrow pad_{MD}(m)$.

• $h_0 = IV$.

• For $i = 1$ to L, compute $h_i = f(h_{i-1}, m_i)$.

• $H^f(m) \triangleq h_L$.

where $pad_{MD}(m)$ is the conventional Merkle-Damgård padding function, also called Merkle-Damgård Strengthening: Given a message m, it pads a single ‘1’ to the end of the message m also up to $b-1$ zeros, and an embedding the original length of the message at the end, such that the length of the padded message will be a multiple of b.

2.3 Dithering Sequence

To overcome the attack of [11], which is based on Expandable Message, Rivest suggested to add a third input (dithered symbol) to the compression function derived from an infinite sequence [18]. Rivest proposed to use one of two sequences:

• Keränen sequence.³

• His concrete proposal (a combination of the Keränen sequence and a counter) [18].

Let $f:\{0,1\}^n \times \{0,1\}^b \times \mathcal{A} \rightarrow \{0,1\}^n$ be a compression function that accepts an n-bit chaining value, b-bit message block, and $\mathcal A$ dither symbol taken from the sequence z. The Dithered Merkle-Damgård hash function $H^f:\{0,1\}^*\rightarrow \{0,1\}^n$ is:

• $m_1, m_2,\ldots ,m_L \leftarrow pad_{MD}(m)$.

• $h_0 = IV$.

• For $i = 1$ to L, compute $h_i = f(h_{i-1}, m_i, z[i])$.

• $H^f(m) \triangleq h_L$.

In [2], second preimage attacks were shown on dithered hash functions, and the conclusion was that the more complex the sequence is, the more secure the dithered hash function is against second preimage attacks.

2.4 Diamond Structure

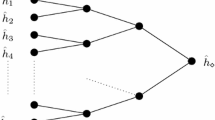
The diamond structure was introduced in [10]. It was used in the attacks of [2, 10], and also in the second preimage attack on dithered Merkle-Damgård in [1, 3]. A diamond structure is a tree T of depth $\ell$, where the $2^\ell$ leafs are the possible chaining values, denoted by $D_T=\{h^\ell _i\}$. The nodes in the tree are labeled by digest values and the edges are labeled by message blocks. The adversary builds the diamond structure starting from the $2^\ell$ leafs, she tries to map the $2^\ell$ leafs to $2^{\ell -1}$ digest values (to the next level in the structure). She does so by generating about $2^{n/2+1/2-\ell /2}$ message blocks from each leaf, then she detects collisions in the generated values. She repeats the process until she reaches the root (with adjusted number of message blocks from each node in each level). The expected time complexity of building a diamond structure is $2^{n/2+\ell /2+2}$.

The diamond structure has the interesting property that there is a path of message blocks from any chaining value leaf $h^\ell _i$ to the the digest value $h_T$ (the root). See an example in Fig. 1.

The diamond structure was introduced at first to attack classic Merkle-Damgård hash functions [10]. But it can be easily adapted for dithered Merkle-Damgård, by labeling the tree edges with a dither symbol $\alpha \in \mathcal A$ as well.

We say that a diamond structure “uses” a sequence $w'$ when all the edges between level i and level $i+1$ in the structure are labeled in addition to the message block also with w[i]. We denote the diamond structure T that uses the sequence $w'$ by $T_{w'}$.

Fig. 1.

A diamond structure that uses the dithering sequence w.

3 Previous Attacks on Merkle-Damgård Hash Functions

3.1 Dean’s Attack

Dean showed in [7] a second preimage attack on Merkle-Damgård hash functions. The idea is to generate an expandable message using a fixed point of the compression function, to connect to the targeted message. Consider a message $M=m_1m_2 \ldots m_L$, an initial value IV, and let $H(M) = h$. Denote the intermediate values of processing the message M by $h_1, h_2, \ldots ,h_L=h$, i.e., $f(h_{i-1}, m_i) = h_i$ (where $h_0 = IV$).

At the first step of the attack, the adversary generates $2^{n/2}$ random block messages, denoted by $m^r_1, m^r_2,\ldots ,m^r_{2^{n/2}}$. Then, she computes $\mathcal{X}_1 = \{f(IV, m^r_j) | \forall j \in \{1, 2, \ldots ,2^{n/2}\}\}$. She then generates $2^{n/2}$ random fixed points of the compression function,⁴ denoted by $\mathcal{X}_2 = \{(h^f_k,m^c_k) | f(h^f_k, m^f_k) = h^f_k \}$. Due to the birthday paradox, with non-negligible probability there is $m^r_j$ such that $f(IV, m^r_j)=h^f_k$ (which also means that $f(IV, m^r_j)=f(h^f_k, m^f_k)$). Now, she tries to connect $h^f_k$ to the message, so she generates $2^n / L$ random message blocks, denoted by $m_z$, $1 \le z \le {{2^n} / L}$. With a non–negligible probability, there is a $h_i$, such that $f(h^f_k, m_z) = h_i$. At this stage the adversary can output the message $M' =m'_j\underbrace{m^f_k \ldots m^f_k}_ \text {i -2 times} m_z m_{i+1} \ldots m_L$ as a second preimage for M. Note that $|M' |= |M |$, which means that after processing the messages, the Merkle-Damgård Strengthening has a similar affect on the digest value in both messages.

The time complexity of the attack is $2^{n/2+1}+2^n/L$ compression function calls.⁵

3.2 Kelsey and Schneier’s Expandable Messages Attack

Kelsey and Schneier showed in [11] a second preimage attack on Merkle-Damgård hash functions. They presented a new technique to build expandable messages without any assumption about the compression function (unlike in Dean’s attack), the new technique is based on Joux’s multi-collision technique [9], producing multiple messages of varying lengths, with the same digest value. The time complexity of the attack is about $k \cdot 2^{n/2+1}+2^{n-k+1}$, for a $2^k$-block length message.

3.3 Adapted Kelsey-Kohno

One of the second preimage attacks presented in [1, 3], is against Merkle-Damgård hash functions. The attack depends heavily on diamond structures which were introduced in [10]. The adversary generates a diamond structure of depth $\ell$ and tries to connect the diamond structure to the message by a connecting message block. After a successful attempt, she generates a prefix P which connects the IV to the diamond structure of appropriate length. The second preimage message is the concatenation of the prefix P, the path in the diamond structure (which connects the prefix to the root) and the remaining of the original message blocks (what come after the connecting message block). The complexity of the attack is $2^{n/2+\ell /2+2} + 2^{n-k} + 2^{n-\ell }$.

The attack can also be adapted to the dithered Merkle-Damgård hash functions, which we refer to as “Adapted Kelsey-Kohno”. Most of the attack steps are similar to the original attack. The adversary generates a diamond structure of depth $\ell$. The diamond structure uses the first $\ell$ symbols of the most common factor of length $\ell +1$ of the dithering sequence z. The last symbol of the most common factor of length $\ell +1$ is used to connect the diamond structure’s root to the message in appropriate location. The number of possible points to connect the diamond structure is equal to $\frac{{1}}{Freq_{z}(w^{\ell +1}_{mc})}$. So, the time complexity of the attack $2^{n/2+\ell /2+2} + \frac{{2^{n-k}}}{Freq_{z}(w^{\ell +1}_{mc})}+ 2^{n-\ell }$, and the online memory complexity is $2^{\ell +1}$.

Fig. 2.

Illustration of Andreeva’ et al.’s attack: (i) Build the diamond structure T (ii) Connect the root to the message (iii) Connect the message to the leafs of T.

3.4 Kite Generator and More Second Preimage Attacks

The “Kite Generator” was introduced in [1, 3]. It is a labeled directed graph of $2^{n-k}$ vertices. Every vertex labeled by a chaining value (including the IV) and every edge is labeled by a message block and a symbol from the alphabet of the dithering sequence. For any symbol in the dithering alphabet (i.e., $\alpha \in \mathcal A$) there are two edges labeled by the symbol $\alpha$. The result is that every vertex has $2 \cdot |\mathcal A |$ outgoing edges. The structure is highly connected, that is to say, there is an exponential number of paths for any dithering sequence that starts from a single vertex. The time complexity of building such a structure is $2\cdot |\mathcal{A} |\cdot 2^n$ and it requires $|A |\cdot 2^{n-k}$ memory.

For a given message m of $2^k$ blocks and $2^k$ intermediate digest values, there is a non-negligible probability that there is an intermediate digest value which is also a label of a vertex in the kite generator structure. Denote this value by $h_i$. The adversary picks a path in the kite generator starting from the IV of length $i-(n-k)$ with the dithering sequence $z[0 \ldots (i-(n-k))]$. Then, from the last chaining value of the generated path, build a binary tree of depth $(n-k)/2$ that uses the dithering sequence $z[(i-(n-k)+1) \ldots (i-(n-k)/2)]$ (this is achieved by traversing all possible routes in the graph corresponding the required dithering sequence). In the last step, she builds a binary tree from $h_i$ of depth $(n-k)/2$ that uses the dithering sequence $z[(i-(n-k)/2+1) \ldots i]^R$. With a non-negligible probability there is a collision in the leafs of the two trees. The second preimage is the concatenation the the generated path, the path which connects the two roots of the trees, and the remaining blocks of the original message (the message blocks which come after $h_i$). The online time and memory complexities of the attack are $max(2^{n/2},2^{n-k})$ and $|\mathcal {A}|\cdot 2^{n-k}$, respectively.

4 A New Second Preimage Attack on Dithered Merkle-Damgård

We now present a new second preimage attack on dithered Merkle-Damgård. The new attack has a slightly longer precomputation time, but in exchange, the online memory complexity of the attack is significantly reduced to practical levels.

Similarly to the attacks of [1, 3], the attack consists of two phases: the precomputation (the offline) and the online phase. In the offline phase, we generate $Fact_z(\ell )$ diamond structures, every structure with a unique factor of the sequence z of length $\ell$. Then, we connect every diamond structure to all diamond structures (including itself). We then purge unnecessary paths from the memory. These purged structures are then used in the online phase to find a second preimage by connecting one of the purged diamond structures to the message, and starting from the IV traversing through the purged diamond structures to reach the connecting point. The total amount of memory that is needed for keeping the purged diamond structures is significantly smaller than the amount of memory needed for storing a full diamond structure.

4.1 Adapting Diamond Structure to Dithered Merkle-Damgård

We now give the details of the attack:

• Offline phase:

  • 1. Build $Fact_z(\ell )$ diamond structures of depth $\ell$ each (denoted by $\{T_i |1 \le i \le Fact_z(\ell ) \}$), where every $T_i$ uses a different factor of z of length $\ell$. Every diamond structure $T_i$ has a digest value $h_{T_i}$. Note that the IV is a leaf in all the generated diamond structures.

  • 2. Connect every diamond structure $T_i$ to every diamond structure $T_j$ ($T_i$ may be $T_j$) with all $|\mathcal A|$ possible dithering symbols. Namely, for every pair of $T_i,T_j$ and any dithering symbol $\alpha$, find $m^{\alpha }_{i \rightarrow j}$ such that $f(h_{T_i}, m^{\alpha }_{i \rightarrow j}, \alpha )$ is a leaf of $T_j$.

  • 3. Prune (reduce) the diamond structures by removing all unnecessary nodes and edges that do not belong to any path that connects two roots $h_{T_i}$ and $h_{T_j}$. Formally, let $\mathcal{G}_{i} = \{P_{j,i} | \exists T_j$ such that $P_{j,i}$ is a path from a $h_{T_{j}}$ to $h_{T_{i}}\}$. Then, for all $T_{i'}$, remove the nodes $\{n' \in T_{i'} | n' \notin P_{j',i'}$ for any $P_{j',i'} \in \mathcal{G}_i\}$.

    Between two diamond structures, there are $|\mathcal A|$ such paths. So overall, keep $|\mathcal{A}| \cdot Fact_z^2(\ell )$ paths (of length $\ell + 1$ each, as we also store the connecting message block $m^{\alpha }_{j \rightarrow i}$).

  Fig. 3.

  

  Connecting diamond structure $T_i$ to diamond structure $T_j$

Complexity Analysis: Constructing $Fact_z(\ell )$ diamond structures takes $Fact_z(\ell ) \cdot 2^{n/2+\ell /2 + 2}$ compression function calls. Connecting one diamond structure to another takes $2^{n - \ell }$ compression function calls for a given dither sequence. Therefore, connecting all the diamond structures to each other takes $|\mathcal{A}| \cdot Fact_z(\ell )^2 \cdot 2^{n-\ell }$ time. Finally, pruning the diamond structures takes $|\mathcal{A}| \cdot Fact_z^2(\ell ) \cdot (\ell + 1)$ time and memory.

Therefore, the overall time complexity of the offline phase is $Fact_z(\ell ) \cdot 2^{n/2+\ell /2 + 2} + |\mathcal{A}| \cdot Fact_z(\ell )^2 \cdot 2^{n-\ell }$ compression function calls, and it passes $|\mathcal{A}| \cdot Fact_z(\ell )^2 \cdot (\ell + 1)$ memory blocks to the online phase.

• Online phase: In the online phase, given a message m, such that $|m |= 2^k$ blocks. Let $w' = w_r\alpha$ ($|w' |= \ell +1$) be the most common factor in positions $0, \ell +1, 2(\ell +1), \ldots$ (positions that are multiple of $\ell +1$) of the sequence z. Let Range be $\{i \in \mathcal{N} | i \le 2^k \wedge z[i - (\ell +1)] \ldots z[i]=w' \}$, namely, Range is the set of all indexes of chaining values which were produced of hashing of any consecutive $\ell +1$ blocks with $w_r$, perform:

  • Find a connecting block $B_r$ such that $f(h_{T_{w_{r}}}, B_r, \alpha ) = h_{i_{0}}$ for $i_{0}\in Range$.

  • Traverse the structures and find a path from IV to $B_r$ while preserving the dithering sequence order.

  • The second preimage is generated by concatenating the path that was found in the previous step, with the rest of the original m from the block after the connecting point till the end.

The complexity of the online phase is $\frac{{2^{n-k}}}{Freq_{z}(w')}+ 2^k$, which is essentially the same as the adapted Kelsey-Schneier’s attack [1, 3] (we note that the connection “into” the diamond structure is eliminated).

Fig. 4.

Illustration of the attack.

4.2 Generalization

The previous attack worked with the most common factor of length $\ell + 1$ in positions $0,\ell +1, 2 \cdot (\ell + 1), \ldots$ (i.e., a multiple of $\ell +1$). Traversing the diamond structures gives always a path whose length is a multiple of $\ell +1$. Therefore, it is limited to work with the most common factor in specific positions, which may not be the most common factor of the whole sequence.

To overcome this issue, we generate from the IV a chain of length $\ell$. We pick at random a message $m'=m'_1m'_2 \ldots m'_\ell$ and evaluate $h'_1=h(IV,m'_1,z[1]), h'_2=h(IV,m'_1m'_2,z[1,2]), h'_3=h(IV,m'_1m'_2m'_3,z[1,2,3])$. etc. until $h'_\ell$. We then, use $h'_1$ as one of the leafs in $T_{z[1\ldots ]}$, $h'_2$ as one of the leafs in $T_{z[2\ldots ]}$, etc.

In the online phase, let $w'$ be the most common word of length $\ell +1$. We connect $T_{w'}$ to the message in position t. Let $d = t \mod (\ell + 1)$, and use $m'_1m'_2\ldots m'_d$ to connect the IV to the diamond structure $T_{z[d..(d+\ell )}]$, then traverse from $T_{z[d..(d+\ell )}]$ to $T_{w'}$.

Complexity Analysis: The additional complexity of the new algorithm is $\ell$ compression function calls (generating $h_1',h_2',\ldots , h_\ell '$). This amount of complexity is negligible, and does not affect the offline time complexity. However, it does improve the online time complexity, as we now use the global most common factor in the sequence, which may allow for more connecting points, instead of a most common factor in specific positions. Therefore, the new complexity of the online phase is $\frac{{2^{n-k}}}{Freq_{z}(w^{\ell +1}_{mc})}+ 2^k$.

5 Optimizations and Improvements

In this section, we present several optimizations and improvements. Some ideas reduce the offline time complexity, while other ideas reduce the offline memory complexity. All these improvements do not increase the online time and memory complexities.

5.1 Reducing Offline Time Complexity

Optimization I - Use the Diamond Structure Roots as Leafs. A major factor in the offline phase is connection of the diamond structures to each other. We now present a simple way to reduce the time to connect the diamond structures by about half: After generating a structure, let its root and all other previous structures’ roots be part of the $2^\ell$ leafs of the following generated structures.

Namely,

• Set $D_1 = {\{IV\}}$.

• For $i = 1$ to $Fact_z(\ell )$:

  • Generate the diamond structure $T_i$, such that $D_i$ is a subset of the leafs of $T_i$, i.e., make sure that $D_i \subseteq D_{T_i}$.

  • Set $D_{i+1} = D_i \cup \{h_{T_i}\}$.

As the IV is a leaf in all the diamond structures, one can start the exploration of the dither sequence factor from it, independently of the first factor. Similarly, when generating a new diamond structure, if all the roots of the previously generated diamond structures are leafs in the new diamond structure, then they are already connected to it, and there is no need in connecting the previous diamond structures to the new one.

After the generation of the diamond structures, every pair of different diamond structures is already connected in one direction, but needs to connect in the other direction. This reduces the connection time from $|\mathcal{A}| \cdot Fact^2_z(\ell ) \cdot 2^{n - \ell }$ to $|\mathcal{A}| \cdot \big ({Fact_z(\ell ) \atopwithdelims ()2}+\ell \big )\cdot 2^{n - \ell }$, and the total offline time complexity to $Fact_z(\ell ) \cdot 2^{n/2+\ell /2 + 2}+ |\mathcal{A}| \cdot \big ({Fact_z(\ell ) \atopwithdelims ()2}+\ell \big )\cdot 2^{n - \ell }$.

Optimization II - All the Diamond Structures Have the Same Leafs. Another simple optimization which reduces the offline time complexity by a factor of $Fact_z(\ell )$, is to let the leafs of all the diamond structures be the same. In other words, choose $2^\ell$ random values, and let those values be the leafs of all the diamond structures. This way, when connecting a diamond structure to another, it connects the diamond structure to all the other diamond structures. This reduces the diamond structures connection time complexity to $|\mathcal{A}| \cdot Fact_z(\ell ) \cdot 2^{n - \ell }$, and the total offline time complexity to $Fact_z(\ell ) \cdot 2^{n/2+\ell /2 + 2}+|\mathcal{A}| \cdot Fact_z(\ell ) \cdot 2^{n - \ell }$.

Optimization III - Validate the Connections Between the Diamond Structures. Another simple observation that reduces the time complexity of the offline phase is that not all the factors of length $\ell$ (or any length greater than 1) are sequential. Meaning, if a factor x of length $\ell$ in sequence z, does not appear before another factor y of length $\ell$, then there is no need to connect $T_x$ to $T_y$. In fact, the number of the needed connections is $Fact_z(\ell +1)$ (the number of the factors of length $\ell + 1$). So the overall diamond structures connection time complexity is $Fact_z(\ell +1) \cdot 2^{n-\ell }$.

Note that as a result of this improvement (together with optimization II), the online memory complexity is also reduced to $Fact_z(\ell +1) \cdot (\ell +1)$.

5.2 Treating (Almost)-Regular Sequences

Our attacks were designed for any possible sequence z over a dithering alphabet$\mathcal A$. However, some sequences, such as the Keränen show some regular behavior. Namely, the Keränen sequence is built by taking a sequence over a 4-letter alphabet $\{a,b,c,d\}$ and replacing each character by its own 85-character sequence.⁶ We now show how to use the “regularity” of this sequence in reducing the complexities of attacking the sequence.

The basic idea is that if $\ell \le 84$, the most frequent factor necessarily starts at the beginning of one of the 85-character chunks. Moreover, the sequence itself is divided into four such chunks, and thus, one can build in advance only four diamond structures (of depth $\ell \le 84$) and connect each of them to the others by paths of length $85-\ell$. We note that the online time complexity is not affected by this change (as one of the most frequent factors starts at the first character of the chunk), whereas the offline time complexity is reduced to $4\cdot 2^{n/2+\ell +2} + 12 \cdot 2^{n-\ell }$ (compared with $732 \cdot 2^{n/2+\ell /2+2} + 2928 \cdot 2^{n-\ell }$ for the best general attack).

The idea also reduces the memory complexities (both offline and online). For example, the attack of Sect. 5.1 takes $(\ell +1)\cdot Fact_z(\ell +1)$ which are $732\cdot (\ell +1)$ blocks of memory (for $\ell <85$), or merely $12 \cdot 85 = 1020$ blocks of memory when the regularity of the sequence is used.

For $84<\ell <169$, the attack spans over two dither chunks. The offline time complexity is thus $12 \cdot 2^{n/2+\ell +2} + 132\cdot 2^{n-\ell }$, and the memory complexity is $36 \cdot 170 = 6120$ blocks of memory.

6 Memory Optimizations

In this section, we discuss how to reduce the increased memory complexity in the offline phase in exchange for additional offline computations.

6.1 Reducing Memory in the Offline Phase

The offline memory complexity could be reduced from storing $Fact_z(\ell )$ diamond structures to only one diamond structure. The basic idea is to generate only one diamond structure at a time, and reconstruct it in the preprocessing when needed. The improvement is based on optimization methods II and III, where all diamond structures share leafs. Below we describe the algorithm and then explain it:

• Let D be the leafs of the diamond structures with cardinality of $2^{\ell }$.

• For $i=1$ to $Fact_z(\ell )$:

  • Generate the diamond structure $T_i$.

  • Find and save $(h_{T_i}, {\mathcal M}_i)$, where ${\mathcal M}_i = \{ m^\alpha _{h_{T_i}\rightarrow D} | \forall \alpha \in A, h(h_{T_i}, m^\alpha _{h_{T_i}\rightarrow D},\alpha ) \in D$ and $w_i\alpha$ is a factor of z $\}$.

  • Delete $T_i$.

• For $i=1$ to $Fact_z(\ell )$:

  • Regenerate the diamond structure $T_i$.

  • Compute and save $\mathcal{G}_i$ (recall that $\mathcal{G}_i$ are the paths from the leafs connected to the root from other diamonds).

  • Delete $T_i$.

After the offline phase, pass the paths ($\mathcal{G}_i$’s) to the online phase.

We first note that when generating a diamond structure $T_i$, the leafs of other diamond structure $T_j$ should be predictable to allow the connection from $T_i$ to $T_j$. By fixing the leafs of all the diamond structures to be the same, we can overcome this obstacle, and we also reduce the time complexity, because connecting $T_i$ to $T_j$ is also connecting $T_i$ to all other diamond structures under the same dithering symbol.

To enable regenerating the same diamond structure twice independently, we can use a fixed pseudo-random sequence (e.g., by seeding some PRNG) to determine the message blocks used (and their order) along with any randomness needed for other decisions.

This reduces the offline memory complexity to $Fact_z(\ell +1) \cdot 2^{n-\ell }$. In exchange, the diamond structure generation time complexity is increased to $2 \cdot Fact_z(\ell ) \cdot 2^{n/2+1/2+\ell /2}$, and the total offline time complexity to $2 \cdot Fact_z(\ell ) \cdot 2^{n/2+\ell /2 + 2}+ Fact_z(\ell +1) \cdot 2^{n-\ell }$.

6.2 Time-Memory Trade-Off

It is possible to balance the offline memory complexity with the offline time complexity. One could store in memory x diamond structures that are computed only once. The offline memory and time complexities are $x\cdot 2^{\ell +1}$ and $(2 \cdot Fact_z(\ell ) - x)\cdot 2^{n/2+\ell /2+2} + Fact_z(\ell +1) \cdot 2^{n-\ell }$, respectively.

7 Memoryless Diamond Structure Generation

We now show that it is possible to essentially eliminate the memory used in the offline phase: By building the diamond structure as a Merkle hash tree [15] (i.e., deciding in advance which leaf collides with which leaf), and using memoryless collision search [13, 16, 17], we can reduce the offline memory completely to the online complexity.

Each diamond structure has $2^{\ell +1}-1$ collisions, each can be found in time $\mathcal{O}(2^{n/2})$ without additional memory, allowing for a memoryless diamond structure generation in time $2^{n/2+\ell +1}$. Obviously, the randomness in the generation needs to be replaced with a pseudo-random sequence (the same as in Sect. 6.1). The total offline time complexity of the attack is $2 \cdot Fact_z(\ell ) \cdot 2^{n/2+\ell }+Fact_z(\ell +1) \cdot 2^{n - \ell }$. The online time complexity does not change, and remains at $(\ell +1)\cdot Fact_z(\ell +1)$. The total (offline and online) memory complexity is $(\ell +1)\cdot Fact_z(\ell +1)$.

8 Summary

In this work we present a series of second preimage attacks on dithered Merkle-Damgård hash functions. The proposed attacks have the same online time complexity as the previous works of [1, 3], but enjoy a significantly reduced memory complexity.

The first set of attacks concentrate on reducing the memory complexity in the online phase (while maintaining, or slightly increasing, the offline memory complexity). This set is motivated by the fact that an adversary may be willing to spend some extra memory (or time) in the offline phase, so the online phase could use a smaller amount of memory (which may be more suitable for FPGA-based cryptanalytic efforts). We believe that this line of research (reducing online memory complexity, possibly at the expense of an increased offline complexities), would open up a new way to look at cryptanalytic problems.

The last attack we present offers an essentially memoryless attack on dithered hash functions which is still considerably better than generic attacks. To conclude, it seems that any dithered hash function should use as complex sequences (namely, with as many different factors) as possible.

A Compact Representations of Message Blocks in the Considered Attacks

We now turn our attention to a small constant improvement in the memory consumption of both the generation and the online storage of the diamond structures (similar ideas can be applied to the kite generator, though we do not discuss these in detail). Recall the generation of a diamond structure: $2^\ell$ chaining values are chosen (or given). For each such chaining value, we compute $^{n/2-\ell /2+1/2}$ calls to the compression function using different message blocks. To find collisions among the $2^{n/2+\ell /2+1/2}$ chaining values one can use several data structures, where the easiest one is a hash table (indexed by the chaining value). Such a hash table can store all the (chaining value, message block) pairs, and allow for an easy and efficient detection of collisions.

The main question is what is the entry size that needs to be stored in such a table. The trivial solution requires n bits for the chaining value and b bits for the message block, i.e., a total of $n+b$ bits (e.g., 640 for MD5). One can immediately note that as there are only $2^\ell$ different chaining values, it is possible to assign to each chaining value an index of $\ell$ bits, and store only the index. Another trivial improvement is to note that one can use the same message blocks for all chaining values (or determine given the chaining values the message blocks in a pseudo-random manner), and thus, one needs to store only $n/2-\ell /2+1/2$ bits for describing the message block in use. Hence, one can easily use a simpler and more compact representation of $n/2+\ell /2+1/2$ bits (i.e., 90 bits in our attacks on MD5).

We devise an even more compact representation, which is based on storing only the chaining value in the hash table. Then, once a collision is found, one can try all message blocks sequentially to recover the message blocks that led to the collision. While this doubles the computational effort of the generation of the diamond structure, by storing a few additional bits of the message block along the chaining value, is sufficient to make this approach quite computationally efficient. Hence, one can use $\ell +t$ bits, where even a small t (of 3–4 bits) can ensure the reconstruction does not affect the time complexity by much.

We note that when $\ell > n/2-\ell /2$ i.e., when $3\cdot \ell > n$, it is possible to store in the table the message blocks themselves, and then in the reconstruction try all possible message blocks. The resulting representation in this case is $n/2-\ell /2+t$ bits.

Finally, we briefly discuss the online data structure. For that structure one needs to store only the message block that connects the current chaining value to the next one. Hence, in the online phase, the memory block size is $n/2-\ell /2$.