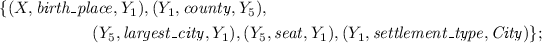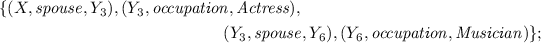Entity Comparison in RDF Graphs

Abstract

In many applications, there is an increasing need for the new types of RDF data analysis that are not covered by standard reasoning tasks such as SPARQL query answering. One such important analysis task is entity comparison, i.e., determining what are similarities and differences between two given entities in an RDF graph. For instance, in an RDF graph about drugs, we may want to compare Metamizole and Ibuprofen and automatically find out that they are similar in that they are both analgesics but, in contrast to Metamizole, Ibuprofen also has a considerable anti-inflammatory effect. Entity comparison is a widely used functionality available in many information systems, such as universities or product comparison websites. However, comparison is typically domain-specific and depends on a fixed set of aspects to compare. In this paper, we propose a formal framework for domain-independent entity comparison over RDF graphs. We model similarities and differences between entities as SPARQL queries satisfying certain additional properties, and propose algorithms for computing them.

Work supported by the Royal Society under a University Research Fellowship and the EPSRC under an IAA award and the projects DBOnto, MaSI$^3$, ED$^3$, and VADA(EP/M025268/1).

1 Introduction

The Resource Description Framework (RDF) is the standard format for representing and integrating information on the Web. The canonical reasoning task over RDF data exploited in applications is query answering, where SPARQL is the standard query language developed for that purpose [10]. There is, however, an increasing need in many applications for non-standard analysis tasks that do not directly correspond to SPARQL query answering. One such important task is entity comparison—that is, to determine what are the similarities and differences between the information about two given entities in an RDF graph.

Let us consider two example use cases. In the first one, a startup company is developing a toolkit for analysing widely-used biomedical RDF repositories, such as Bio2RDF [5]. The tool being developed should provide a drug comparison functionality; in particular, when given two drugs described in an RDF graph from the repository, such as Ibuprofen and Metamizole, the tool should be able to automatically report that “both drugs are analgesics and can reduce fever; however, Metamizole can also act as a spasm reliever, whereas Ibuprofen has an anti-inflammatory function”. The second use case concerns the development of an analysis tool on top of IMDB data; such tool should allow users to compare arbitrary aspects of movie-making, such as directors, producers, actors and so on. For example, when comparing Quentin Tarantino to Martin Scorsese, the tool should report that they are similar in that they are both male directors who won both an Oscar and a Golden Globe and who have also acted in their own movies; in turn, they are different in that Tarantino won the Palme d’Or at the Cannes Film Festival, while Scorsese won an Emmy award, to which Tarantino was only nominated.

Entity comparison is conventionally seen in the Information Retrieval community as a type of exploratory search [15, 22]. It is an important task which is implemented in a wide range of tools and web portals, in domains as diverse as hotels,¹ cars,² universities,³ or online shopping⁴. Existing entity comparison tools typically perform a side-by-side comparison of items based on a fixed (often hard-coded) template of features to compare (e.g., price, location, rating, and so on in the case of hotels). Relying on a fixed set of features is a reasonable solution for tabular, domain specific data whose structure is relatively rigid and stable. It is even appropriate in the context of graph data, provided that a limited set of relevant features can be specified beforehand; for instance, Facebook Friendship pages allow for the comparison of two Facebook users by displaying their shared information based on a limited set of features specific to social networks (e.g., “likes”, mutual friends, relationship status).

A more flexible approach to entity comparison is, however, needed in the context of Linked Data, where loosely structured RDF graphs (often describing overlapping domains) are merged and updated. Up to now, such approaches have mainly been based on the structure of the graph, e.g., finding a path that connects the two entities (see Sect. 7 for a discussion of related work). In this paper we propose a novel approach based on the semantics of the graph.

In Sect. 3 we propose a logical framework for our approach, where similarities and differences between entities are formalised as conjunctive SPARQL queries. Specifically, a similarity query (resp. a difference query) for given entities in an RDF graph is a query having both entities as answers (resp. having one entity as answer but not the other). In the case of similarity queries, we are interested in the most specific ones, e.g., knowing that Tarantino and Scorsese are both American-born film directors is more informative than reporting only that they are both film directors. In turn, in the case of difference queries we are interested in the most general ones, e.g., knowing that Brad Pitt is an actor, whereas George Lucas is a producer is more informative than knowing that the former is an American actor while the latter is an American producer, since being American is irrelevant to differentiating them.

In Sect. 4, we focus on similarities, and propose a polynomial-time algorithm for computing a most specific similarity query. As a by-product of the properties of our algorithm, we are also able to show that most specific similarity queries for two given entities in an RDF graph are unique modulo equivalence. The problem we consider in this section is strongly related to the Query Reverse Engineering problem in RDF [2], as well as to that of computing Least Common Subsumers in Description Logic ontologies [3].

In Sect. 5, we focus on difference queries. We first argue that this is a hard problem; specifically, we argue that simply checking existence of a difference query for two given entities in a graph is $\textsc {coNP}$-complete. We then propose an exponential-time algorithm for computing a most general difference query, should one exist.

Finally, we describe a prototype implementation of the algorithm for computing a most specific similarity query and present a proof of concept case study using the data from Wikipedia infoboxes.

2 Preliminaries

We follow [16] in the definition of RDF graphs and triple patterns. Let $\mathbf {U}$, $\mathbf {L}$ and $\mathbf {B}$ be pairwise disjoint, countably infinite sets of URIs, literals and blank nodes, respectively. An RDF triple (or simply a triple) is a tuple $(s,p,o) \in (\mathbf {U} \cup \mathbf {B}) \times \mathbf {U} \times (\mathbf {U} \cup \mathbf {L} \cup \mathbf {B})$. In such a triple, s is the subject, p the predicate and o the object. An RDF graph G is a finite set of triples. Any URI or literal from G is called an entity.

Let $\mathbf {V}$ be a countably infinite set of variables disjoint from $\mathbf {U}$ and $\mathbf {L}$. A term is an element from $\mathbf {U}\cup \mathbf {L} \cup \mathbf {V}$. The basic building block of our queries is a triple pattern, which is an element from $(\mathbf {U} \cup \mathbf {V}) \times (\mathbf {U} \cup \mathbf {V}) \times (\mathbf {U} \cup \mathbf {L} \cup \mathbf {V})$. A basic graph pattern is a non-empty finite set P of triple patterns. For any basic graph pattern P, we denote with $\mathrm{\mathsf {term}}(P)$ and $\mathrm{\mathsf {var}}(P)$ the sets of terms and variables occurring in P, respectively.

We define a query Q as a pair $(\bar{X}, P)$, where P is a basic graph pattern and $\bar{X} \subseteq \mathrm{\mathsf {var}}(P)$ is the set of answer variables of Q. Such queries capture the fragment of SPARQL queries of the form $\mathsf {SELECT} \; ?\bar{X} \; \mathsf {WHERE}\ P$, with P a basic graph pattern. We define $\mathrm{\mathsf {term}}(Q) = \mathrm{\mathsf {term}}(P)$ and $\mathrm{\mathsf {var}}(Q) = \mathrm{\mathsf {var}}(P)$. We say that Q is monadic if its set of answer variables is a singleton. A basic graph pattern P is connected if for every $t, t'\in \mathrm{\mathsf {term}}(P)$ there is a sequence of triple patterns $tp_1, \ldots , tp_n$ in P such that $t\in \mathrm{\mathsf {term}}(tp_1)$, $t' \in \mathrm{\mathsf {term}}(tp_n)$ and $\mathrm{\mathsf {term}}(tp_i)\cap \mathrm{\mathsf {term}}(tp_{i\,+\,1}) \ne \emptyset$, for $1\le i < n$. Query $Q = (\bar{X}, P)$ is connected if so is P. For brevity, in examples we will write a query $Q = (\bar{X}, P)$ simply as P and adopt the convention that $X_{(i)}$ represent answer variables, whereas $Y_{(j)}$ represent the remaining variables.

We next recapitulate the semantics of queries. A valuation over variables $\bar{X}$ is a mapping $\nu$ from $\bar{X}$ to $\mathbf {U} \cup \mathbf {L} \cup \mathbf {B}$. For $\nu$ a valuation over $\bar{X}$ and $\bar{Y} \subseteq \bar{X}$, let $\nu \vert _{\bar{Y}}$ be the restriction of $\nu$ to $\bar{Y}$. Valuations are applied to triple patterns and basic graph patterns in the obvious way. Let $Q = (\bar{X}, P)$ be a query, let G be an RDF graph, and $\nu$ a valuation over $\bar{X}$. Then, G satisfies Q under $\nu$, denoted $G,\nu \,\models \, Q$ if $\nu = \mu \vert _{\bar{X}}$ for some valuation $\mu$ over $\mathrm{\mathsf {var}}(Q)$ satisfying $\mu (P) \subseteq G$. The semantics $[Q]_{G}$ of a query $Q = (\bar{X}, P)$ over G is

$$\begin{aligned}{}[Q]_{G} = \{ \nu (\bar{X}) \mid G,\nu \,\models \, Q \text { and } \nu \text { is a valuation over } \bar{X} \}. \end{aligned}$$

Let G be an RDF graph. The canonical graph pattern of G is the set $\mathsf {Can}(G)$ of triple patterns $(X_s, X_p, X_o)$ for each triple (s, p, o) in G, where $X_s$, $X_p$ and $X_o$ are variables uniquely assigned to s, p and o in G. A canonical query of G is any query of the form $(\bar{X}, \mathsf {Can}(G))$.

Let $Q_1 =(\bar{X}_1, P_1)$ and $Q_2 = (\bar{X}_2, P_2)$ be queries. We say that $Q_1$ is subsumed by $Q_2$, denoted as $Q_1 \subseteq Q_2$, if $[Q_1]_{G} \subseteq [Q_2]_{G}$ for every RDF graph G. The subsumption relation between two queries with equal number of answer variables can be characterised by existence of a homomorphism—a mapping $h: \mathrm{\mathsf {term}}(Q_2) \rightarrow \mathrm{\mathsf {term}}(Q_1)$ that is the identity on URIs, literals and answer variables and satisfying $(h(t_s) , h(t_p), h(t_o)) \in P_1$ whenever $(t_s, t_p, t_o) \in P_2$ and $h(\bar{X}_2) = \bar{X}_1$. It is well-known that $Q_1 \subseteq Q_2$ if and only if there exists a homomorphism from $Q_2$ to $Q_1$. Subsumption allows us to compare queries relative to their specificity. We say that $Q_1$ is more specific than $Q_2$ if $Q_1 \subseteq Q_2$; it is strictly more specific, denoted as $Q_1 \subset Q_2$, if $Q_1 \subseteq Q_2$ and $Q_2 \not \subseteq Q_1$. Finally, $Q_1$ and $Q_2$ are equivalent, denoted $Q_1 \equiv Q_2$, if $Q_1 \subseteq Q_2$ and $Q_2 \subseteq Q_1$.

3 A Framework for Entity Comparison

In this section, we present our formalisation of entity comparison. As a running example, consider a small subset $G_{mov}$ of the YAGO graph [18] about the movie industry depicted in Fig. 1. In our example, we would like to compare Quentin Tarantino and Martin Scorsese. By inspecting $G_{mov}$ we can observe, for instance, that Tarantino and Scorsese are similar in that both of them are male, they both won an Academy Award and a Golden Globe Award, and they both acted in some of their own movies. In turn, they are different in that Tarantino directed Reservoir Dogs, whereas Scorsese directed Taxi Driver; furthermore, unlike Scorsese, Tarantino also won the Palme d’Or at the Cannes Film Festival, while Scorsese won an Emmy award, to which Tarantino was only nominated.

Fig. 1.

An example RDF graph $G_{mov}$.

How can we formalise and automatically identify such similarities and differences? There has been significant recent work in the literature on discovering relationships between entities in an RDF graph [7, 11, 14]. Existing approaches describe such relationships by means of explicit paths in the graph, which are then grouped and ranked. Using such an approach, we could view a similarity between entities as paths originating in those entities and converging into the same node; for instance, we could justify as a similarity the fact that both Tarantino and Scorsese are male by two paths leading to the node for male and starting from the nodes for Scorsese and Tarantino, respectively. In turn, we could justify a difference through the absence of such paths; for instance, the node for Emmy Award is reachable from the node for Scorsese but not from that for Tarantino. An important limitation of existing approaches, however, is that they cannot capture comparison at a higher level of abstraction; for instance, we cannot justify by means of explicit converging paths in a graph the fact that both Scorsese and Tarantino participated in a film as both actors and directors, where the specific names of those films are irrelevant.

In our framework we propose to capture similarities and differences using queries rather than explicit paths, where the presence of variables allows us to represent information at a higher level of abstraction. We start by formalising similarities. Given two entities in a graph, we view a similarity as a query having both entities as answers.

Definition 1

(Similarity query). A similarity query for entities a and b in an RDF graph G is a monadic connected query Q satisfying $\{a,b\} \subseteq [Q]_{G}$.

For instance, the following queries $Q_1$–$Q_3$ are similarity queries for Tarantino and Scorsese in our example graph $G_{mov}$:

$$\begin{aligned} Q_1(X) =&~ \lbrace (X, wonPrize , Academy\_Award )\rbrace ; \\ Q_2(X) =&~ \lbrace (X, hasGender , male), (X, wonPrize , Academy\_Award )\rbrace ; \\ Q_3(X) =&~ \lbrace (X, directed , Y),(X, actedIn , Y), ( H\_Keitel , actedIn , Y)\rbrace . \end{aligned}$$

These similarity queries can be interpreted as follows: $Q_1$ says that both Scorsese and Tarantino received an Academy award, whereas $Q_2$ additionally states that they are both male; in turn, $Q_3$ states that they are both directors who acted in their own movies, in which Harvey Keitel was also part of the cast.

We next formalise the notion of a difference. Intuitively, given two entities in an RDF graph, a difference is a query having one of the entities as answer, but not the other. Furthermore, we are specially interested in differences that are relevant to an identified similarity, in the sense that they distinguish the entities based on an aspect that they have in common.

Definition 2

(Difference query). Let a and b be entities in an RDF graph G. A difference query for a relative to b is a monadic connected query Q satisfying $a\in [Q]_{G}$ and $b\not \in [Q]_{G}$.

Additionally, let $Q'$ be a similarity query for a and b in G. Then, we say that Q is a difference query modulo $Q'$ if Q is a difference query for a relative to b and it holds that $Q \subseteq Q'$.

For instance, the following query $Q_4(X)$ is a difference query for Scorsese relative to Tarantino and modulo the similarity query $Q_1(X)$ given before.

$$\begin{aligned} Q_4(X) = \lbrace (X, wonPrize , Academy\_Award ), (X, wonPrize , Emmy\_Award )\rbrace . \end{aligned}$$

In turn, the following query is also a difference query for Scorsese relative to Tarantino, but it does not relate to any (non-trivial) similarity between them.

$$\begin{aligned} Q_5(X) = \lbrace&(X, marriedTo , Y)\rbrace . \end{aligned}$$

As we can see from the aforementioned examples, there may be multiple (even infinitely many) similarity and difference queries for a given pair of entities. Some of them are, however, more informative than others. In the case of similarity queries, it is natural to expect more specific queries to be more informative; for instance, it is natural to prefer our example query $Q_2$ over $Q_1$ since it better differentiates Tarantino and Scorsese from other directors, by ruling out those who won an Emmy but are female. In contrast, in the case of difference queries it is natural to favour more general queries over more specific ones; for instance, $Q_5$ is more informative that the following query $Q_6$ since it conveys the information that Scorsese is married, but Tarantino is not (or at least not known to be).

$$\begin{aligned} Q_6(X) = \lbrace&(X, marriedTo , I\_Rossellini )\rbrace . \end{aligned}$$

We now define these notions formally.

Definition 3

Query Q is a most specific similarity query (MSSQ) for a and b in G if Q is a similarity query for a and b in G, and there is no similarity query $Q'$ for a and b in G such that $Q' \subset Q$.

Query Q is a most general difference query (MGDQ) for a relative to b in G if Q is a difference query for a relative to b in G, and there is no difference query $Q'$ for a relative for b in G such that $Q \subset Q'$. This definition extends to the notion of difference query modulo a similarity query in the obvious way.

Intuitively, given two similarity queries Q and $Q'$ for the same pair of entities, their conjunction is also a similarity query that is more specific than both of them. We will show in the following section that MSSQs for given entities and graph are unique modulo equivalence over the given input graph. As an example, consider the following query, which combines $Q_2$ and $Q_3$; it can be checked that it is a MSSQ for Scorsese and Tarantino in $G_{mov}$:

$$\begin{aligned} Q_7(X) = \lbrace&(X, hasGender , male ), (X, wonPrize , Academy\_Award ), \\&(X, wonPrize , Golden\_Globe\_Award ), (X, actedIn , Y), \\&(X, directed , Y), ( H\_Keitel , actedIn , Y)\rbrace . \end{aligned}$$

Indeed, query $Q_8 = Q_7 \cup \lbrace (X, actedIn , Z) \rbrace$ is also a MSSQ but it is equivalent to $Q_7$. In turn, both query $Q_5$ and the following query $Q_9$ are both MGDQs for Scorsese relative to Tarantino:

$$\begin{aligned} Q_9(X) = \lbrace&(X, Y, Emmy\_Award ) \rbrace . \end{aligned}$$

Furthermore, they are incomparable with respect to subsumption and hence, in contrast to MSSQs, we cannot formulate a uniqueness result for MGDQs.

4 Computing a Most Specific Similarity Query

In this section, we tackle the problem of computing a most specific similarity query. In particular, we present a polynomial time algorithm and then show, as a byproduct of the correctness proof, that MSSQs are unique up to equivalence.

Our algorithm relies on the notion of the (tensor) product graph, which is commonly exploited in Graph Theory and in Databases (under the name of direct product [19]). Given graphs $G_1$ and $G_2$, the product $G_1 \otimes G_2$ is a graph whose vertex set is the cartesian product of the vertices of $G_1$ and $G_2$, and where two vertices in the product graph are connected by an edge if and only if their component elements are also related by an edge in the original graph. We next adapt the standard notion of product to RDF graphs. Intuitively, given entities a, b and graph G, the connected subgraph of the product $G \otimes G$ of G with itself represents the “largest common pattern” in the neighbourhoods of a and b.

Definition 4

(Product graph). Let $t_1 = (s_1, p_1, o_1)$ and $t_2 = (s_2, p_2, o_2)$ be triples. The product of $t_1$ and $t_2$, denoted as $t_1 \otimes t_2$, is the triple

$$\begin{aligned} (\langle s_1, s_2\rangle , \langle p_1, p_2\rangle , \langle o_1, o_2\rangle ). \end{aligned}$$

The product graph $G_1 \otimes G_2$ of RDF graphs $G_1$ and $G_2$ is the set

$$\begin{aligned} \{t_1 \otimes t_2 \mid t_1 \in G_1 \text { and } t_2 \in G_2 \}. \end{aligned}$$

For instance, the self-product $G_{mov} \otimes G_{mov}$ of our example graph $G_{mov}$ contains triples such as the following:⁵

which is the product of triples $( Q\_Tarantino , wonPrize , Palme\_d'Or )$ and  $( M\_Scorsese , wonPrize , Emmy\_Award )$.

We are now ready to describe our algorithm (see Algorithm 1). Given a, b and G as input, the first step is to compute the product graph $G \otimes G$ and check whether $\langle a, b \rangle$ occurs in a triple; if it doesn’t then the algorithm fails and we can conclude that there is no query having both a and b as answers. If $\langle a,b \rangle$ occurs in the product graph, then the algorithm computes the connected component $G'$ in which it occurs. Given $G'$, we are interested in its canonical query having as answer variable the variable $X_{\langle a,b \rangle }$ corresponding to $\langle a,b \rangle$ in $\mathsf {Can}(G')$. The result of this step is already a similarity query. In the last step, the algorithm grounds all variables $X_{\langle c,c \rangle }$ corresponding to nodes $\langle c,c \rangle$ to c itself; this step is essential to ensure that the output similarity query is a most specific one.

Correctness of the algorithm follows from the following lemma.

Lemma 1

Algorithm Compute-MSSQ satisfies the following properties on input a, b and G:

• 1. It fails if and only if there is no similarity query for a and b in G.

• 2. The output query Q is a similarity query for a and b in G such that any similarity query $Q'$ for a, b and G is homomorphically embeddable into Q.

Proof

1. It is easy to see that a similarity query for a and b exists if and only if a and b appear as subjects, properties, or objects at the same time in G. This is equivalent to the fact that $\langle a, b\rangle$ appears in a triple in $G\otimes G$. Compute-MSSQ returns “fail” iff the latter is not the case.

2. We first show that $\{a, b\} \subseteq [Q]_{G}$. Define two valuations over $\mathrm{\mathsf {var}}(Q)$, $\nu _1$ and $\nu _2$, as follows: for every variable $X_{\langle c,c'\rangle }$ in Q, $\nu _1(X_{\langle c,c'\rangle }) = c$, and $\nu _2(X_{\langle c,c'\rangle }) = c'$. We now show that G satisfies Q under both $\nu _1$ and $\nu _2$. Let $(X_{\langle s_1,s_2\rangle }, X_{\langle p_1,p_2\rangle }, X_{\langle o_1, o_2\rangle })$ be in Q, then it follows by definition of Q that $(\langle s_1,s_2\rangle , \langle p_1,p_2\rangle , \langle o_1, o_2\rangle ) \in G'$. Then by construction of $G'$ we know that both $(s_1, p_1, o_1)$ and $(s_2, p_2, o_2) \in G$. We then obtain that by definition of $\nu _1$ and $\nu _2$: $(\nu _i(X_{\langle s_1,s_2\rangle }), \nu _i(X_{\langle p_1,p_2\rangle }), \nu _i(X_{\langle o_1, o_2\rangle })))\in G$, for $i=1, 2$. Hence, $\nu _1$ and $\nu _2$ are satisfying for Q in G. We have $\nu _1(X_{\langle a,b\rangle }) = a$ and $\nu _2(X_{\langle a,b\rangle }) = b$. Therefore, $\{a, b\} \subseteq [Q]_{G}$.

Let $Q'(X)$ be an arbitrary similarity query for a and b. There are two satisfying valuations $\nu _1$ and $\nu _2$ over $\mathrm{\mathsf {var}}(Q')$ for $Q'$ in G that map X to a and b respectively. We define $\nu (Y) = \langle \nu _1(Y), \nu _2(Y)\rangle$ for Y a variable and $\nu (e) = \langle e, e\rangle$ for e an entity. Since $Q'$ is connected and $\nu (X) = \langle a,b\rangle$, the image of $Q'$ under $\nu$ is a connected subgraph in $G \otimes G$ and thus is contained in $G'$. Since $G'$ and Q are isomorphic, $\nu$ can be considered as a homomorphism from $Q'$ to Q.    $\square$

Clearly, our algorithm works in polynomial time; in particular the size of the product graph $G \otimes G$ is cubic in the size of G. Hence, using the previous Lemma we conclude the following.

Theorem 1

Compute-MSSQ is a polynomial time algorithm that returns a MSSQ for its input if one exists, and “fail” otherwise.

Finally, note that the second statement in Lemma 1 ensures that the return query is, in fact, more specific than any other similarity query. Thus, it also follows from the lemma that MSSQs are unique up to equivalence.

Corollary 1

If Q and $Q'$ are MSSQs for a and b in RDF graph G, then $Q \equiv Q'$.

We conclude by observing that the algorithm Compute-MSSQ will compute, on our running example, a query that is significantly larger than (yet equivalent to) $Q_7$ in the previous section. Indeed, $Q_7$ is a core query in the sense that it cannot be further minimised while preserving equivalence.

5 Computing Most General Difference Queries

We now turn our attention to MGDQs. As already pointed out, MGDQs are not unique modulo equivalence and hence we focus on providing an algorithm that computes one of them.

In contrast to the case of computing MSSQs, we will not be able to provide a polynomial-time algorithm. In fact, we show that the associated decision problem of checking whether a MGDQ exists is $\textsc {coNP}$-complete. This result stems from a characterisation of existence of MGDQs in terms of (non-)existence of homomorphisms.

In what follows we fix arbitrary entities a and b in an arbitrary RDF graph G. We denote with $Q_b$ to be the query $(X_b,\mathsf {Can}(G))$ and $Q_a$ to be the query $(X_a, P_{X_a})$ with $P_{X_a}$ the connected component of $\mathsf {Can}(G)$ containing $X_a$.

Lemma 2

A difference query for a relative to b in G exists if and only if there is no homomorphism from $Q_a$ to $Q_b$.

Proof

$(\Leftarrow )$. The following properties hold for $Q_a$. It is (1) connected and (2) $a\in [Q_a]_{ G}$. Moreover, since there is no homomorphism from $Q_a$ to $Q_b$, it holds that (3) $b\not \in [Q_a]_{G}$. Indeed, otherwise a satisfying valuation $\nu$ for $Q_a$ over $\mathrm{\mathsf {var}}(Q_a)$ with $\nu (X_a) = b$ can be seen as a homomorphism from $Q_a$ to $Q_b$, as $\mathsf {Can}(G)$ and G are isomorphic. Thus, $Q_a$ is a difference query for a relative to b in G.

$(\Rightarrow )$. Let Q(X) be a difference query for a relative to b in G. It implies there is a satisfying valuation $\nu$ over $\mathrm{\mathsf {var}}(Q)$ for Q in G which can be regarded as a homomorphism from Q to $Q_a$ (since Q is connected) with $\nu (X) = X_a$. For the sake of contradiction, suppose there is a homomorphism h from $Q_a$ to $Q_b$. This homomorphism can be regarded as a satisfying valuation for $Q_a$ in G with $h(X_a) = b$. Hence, the mapping $h\circ \nu$ is a satisfying valuation for Q(X) in G with $h\circ \nu (X) = b$ which implies $b\in [Q]_{G}$, a contradiction with the fact that Q is a difference query for a relative to b in G.    $\square$

Since homomorphism checking is a well-known $\textsc {NP}$-complete problem, the following result follows.

Theorem 2

The problem of checking whether a difference query for a relative to b in G exists is $\textsc {coNP}$-complete.

Proof

It is known that checking existence of a homomorphism is in $\textsc {NP}$. Together with Lemma 2 it implies that existence of a difference query can be checked in $\textsc {coNP}$. We show the lower bound by reducing from the homomorphism problem for graphs to the complement of our problem. Let $\mathsf {G}_1 = (V_1, E_1)$ and $\mathsf {G}_2 = (V_2, E_2)$ be graphs which we can assume to be disjoint. We then construct an RDF graph G over the set of URIs $V_1 \cup V_2\cup \{a, b, e, e'\}$, where $\{a, b, e, e'\} \cap V_i = \emptyset , i =1, 2$, as the following set:

$$\begin{aligned} G = \{ (u, e, v) \mid \langle u, v\rangle \in E_1 \cup E_2\} \cup \{(a, e', u) \mid u \in V_1\} \cup \{(b, e', v)\mid v\in V_2\}. \end{aligned}$$

It is straightforward to show that there exists a homomorphism from $\mathsf {G}_1$ to $\mathsf {G}_2$ if and only there is a homomorphism from $Q_a$ to $Q_b$ (note that this homomorphism must map $X_a$ to $X_b$). Lemma 2 implies that this is equivalent to non-existence of a difference query for a relative to b in G.    $\square$

In light of this result, there is no hope for a polynomial time algorithm for computing a MGDQ unless $\textsc {PTime} = \textsc {NP}$. Therefore, we present a naive, non-deterministic algorithm Compute-MGDQ for acyclic graphs. In the first step, the algorithm computes $Q_a$ (feasible in polynomial time). Then, it checks (using the oracle as per Lemma 2) whether $Q_a$ is already a difference query. If it is not, then none can exist. If it is, then it may not be a most general one. Hence, the algorithm tries to make it more general by relaxing the query while checking (again using the oracle as per Lemma 2) whether the result is still a difference query.

Correctness is established in the following theorem.

Theorem 3

Algorithm Comptute-MGDQ returns a MGDQ if one exists, and “fail” otherwise.

Proof

The algorithm fails if and only if there is a homomorphism from $Q_a$ to $Q_b$. By Lemma 2 this is equivalent to the fact that no (most general) difference query for a relative to b exists.

Let Q be the output of Comptute-MGDQ different from “fail”. The for-loop on Line 5 tries to greedily relax the query. Namely, for each variable Y we introduce a set of fresh variables $Y_i$ that replace Y in Q (thus relaxing it) as long as the result is still a difference query for a relative to b. Note that for each intermediate query $Q'$ it holds $a\in [Q']_{G}$ since the result of Line 9 is homomorphically embeddable into the original query. Therefore, we have $a\in [Q]_{G}$. The if-condition ensures that $b\not \in [Q]_{G}$ as per Lemma 2. Therefore, Q is a difference query for a relative to b.

Suppose there is a difference query $Q''$ for a relative to b that is strictly more general than Q. This means there is a homomorphism h from $Q''$ to Q but not vice versa. If h is injective, then there is a triple pattern in Q that is not in the image of $Q''$ under h but connected to it. But then the commands in the for-loop are applicable to a variable Y that connects the image of $Q''$ and the triple pattern (with the following partition: the occurrence of Y replaced with $Y_1$ and the occurrence of Y in the triple pattern with $Y_2$), a contradiction. Now suppose h is not injective. Then let $\{Z_1, \ldots , Z_n\}$ be variables in $Q''$ that are mapped by h to the same variable Y in Q. We claim that the for-loop in Line 5 is applicable to Y with $\{Z_1, \ldots , Z_n\}$ defining a partition, a contradiction.    $\square$

6 Case Study

We have implemented a prototype system in Java that implements our Algorithm 1 for computing MSSQs. As a proof of concept, we have run the algorithm on a fragment of DBpedia [13] that captures the information corresponding to Wikipedia infoboxes—tables with a fixed structure used in Wikipedia to present the key information about an entity in a concise and structured way.⁶ Infoboxes are located on the right-hand-side of Wikipedia pages that correspond to certain categories, such as people, organisations or geographical locations.

Entity comparison in Wikipedia could be implemented by comparing their infoboxes directly; such a tool would provide analogous functionality to that in existing comparison tools in Web portals, in the sense that the features to compare would be considered fixed. Figure 2 displays side by side the infoboxes corresponding to Brad Pitt and Tom Cruise, which are both fairly detailed. We can observe similarities such as their occupations and country of birth, or the fact that they have both been married and have children.

Fig. 2.

Wikipedia infoboxes for actors Brad Pitt (left) and Tom Cruise (right).

We tried our algorithm for Brad Pitt and Tom Cruise and the aforementioned fragment of DBpedia. We observed that the computed MSSQ provides much richer information than what can be obtained by direct inspection of the infoboxes. Since the resulting MSSQ is rather large, we concentrate on its subqueries of special interest. First, we notice that we generated all the aforementioned similarities that could be obtained by manual inspection of the infoboxes. In particular, we found that both Brad Pitt and Tom Cruise are:

• both actors and producers, as witnessed by the subquery

  $$\begin{aligned} \{(X, occupation , Actor ), (X, occupation , Producer )\}; \end{aligned}$$

• were born in the U.S., as witnessed by

  $$\begin{aligned} \{(X, birth\_place , Y_1), (Y_1, country , United\_States )\}; \end{aligned}$$

• were married, have kids and relatives, as witnessed by

  $$\begin{aligned} \{(X, children , Y_2), (X, spouse , Y_3), (X, relatives , Y_4)\}. \end{aligned}$$

However, the computed MSSQ also contains plenty of additional useful information. For instance, both Pitt and Cruise:

• were married to U.S. actresses, as witnessed by

  $$\begin{aligned} \{(X, spouse , Y_3), (Y_3, nationality , United\_States ), (Y_3, occupation , Actress )\}; \end{aligned}$$

• were born in cities that are both the administrative centers and largest cities of their respective counties:

  

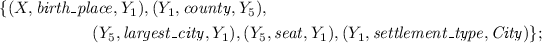
• were married to actresses who were also married to musicians:

  

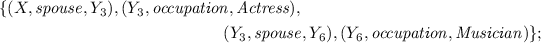
To sum up, even using only DBpedia data capturing Wikipedia infoboxes, we are able to significantly enhance the explicit contents of fairly comprehensive infoboxes and exploit the graph nature of the data to discover “deeper-level” similarities between the entities of interest. We envision that our approach could even be more useful if the whole of DBpedia had been considered, especially in the case where the infoboxes corresponding to the entities of interest are rather minimalistic and hence do not provide sufficiently many features to compare.

7 Related Work

There is a growing interest in techniques for discovering and explaining relationships between entities in an RDF graph [7, 11, 14]. These approaches are based on computing paths in the input graph connecting the input entities. Such paths are first computed via standard graph traversal algorithms, and then ranked according to certain structural and/or statistical measures [7]. We note that the problem of finding connections between entities is orthogonal to that of computing similarities and differences between them. Furthermore, as already argued, the natural adaptations of such techniques to our setting do not allow for entity comparison at a sufficiently high level of abstraction.

Computation of both similarity and difference queries can be seen as an instance of the more general problem of Query Reverse Engineering (QRE) in databases. An input to QRE is a database instance, a set of positive examples (i.e., elements that must be in the query result) and also in some cases a set of negative examples (i.e., elements that must not be included in the query result). The QRE problem for a query language $\mathcal {L}$ is to decide whether an $\mathcal {L}$-query exists whose answers satisfy the given constraints imposed by positive and negative examples over the input database instance. This problem has been studied for regular languages over strings [1], queries over relational databases [20, 21, 23, 25], XML queries [9, 17], graph database queries [6] and SPARQL queries over RDF graphs [2]. QRE is known to be coNExpTime-complete for conjunctive queries over relational databases [4, 19]. When applied to our setting, this result implies coNExpTime-completeness of the following problem: given an RDF graph, and sets of entities A and B in G, does there exist a difference query for A relative to B in G, where the definition of a difference query is extended to sets of entities in the obvious way. QRE for RDF graphs was first studied in [2], where the complexity analysis of different variations of the problem is provided for SPARQL queries allowing for the AND, FILTER and OPT operators.

Computing MSSQs is also related to (a variant of) the problem of computing the Least Common Subsumer between concepts in Description Logics (DLs) [3]. Specifically, given entities a and b, we could cast our problem as that of finding the least (i.e., most specific modulo subsumption) DL concept that contains both a and b as instances. An important difference with our setting is that DL concepts in logics such as $\mathcal {EL}$ and $\mathcal {ALC}$ can only capture conjunctive queries that are both constant-free and tree-shaped. In this sense, our query language is more expressive, as it allows for arbitrarily-shaped connected CQs. The additional expressivity turns out to be critical: while a least DL concept may not exist (e.g., if the input graph has cycles then the least concept could be infinite), our algorithm in Sect. 4 ensures that a MSSQ is always finite and can be computed in polynomial time.

Finally, it is worth mentioning that there has been a lot of work on similarity measures for computing a numeric score that estimates how similar two entities in a graph are [8, 12, 24]; this has applications, for instance, in discovering entities that are similar to a given one (i.e., those with the highest similarity score). Please note that we are considering a very different problem since our focus is on describing similarities and differences in a declarative way.

8 Conclusion and Future Work

We have investigated the problem of entity comparison over RDF graphs and proposed a logical framework that models comparison through similarity and difference queries. In particular, we have studied most specific similarity queries (MSSQs) and most general difference queries (MGDQs) as the most informative such queries. We have shown that, for a given graph and a pair of entities, there always exists a unique MSSQ modulo equivalence, which can be computed in polynomial time. In contrast, computing MGDQs is a harder problem; indeed, the underpinning decision problem is $\textsc {coNP}$-hard. Finally, we have discussed an initial implementation of the algorithm that computes a MSSQ.

An immediate step of future research would be to extend the prototype implementation of the framework into a comprehensive entity comparison tool that would account for both similarity and difference queries. This would imply, firstly, creating practical algorithms for computing MGDQs, possibly of bounded size. As for MSSQs, a practical implementation of the tool would effectively address the problem of large-sized MSSQs and how they can be presented to a user in an easy-to-read manner. One possible solution would be to split the output MSSQs into comprehensible subqueries (similar to the ones presented in Sect. 6); another solution would involve partially verbalizing MSSQs into natural language explanations. For example, a query $\lbrace (X, livesIn , London )$, $(X, friendsWith , Y)$, $(Y, worksAt , Oracle )\rbrace$ could be transformed into a natural language explanation “Both input entities live in London and are friends with someone who works at Oracle”. In addition, an interesting problem would be to consider more expressive query languages, in particular conjunctive queries with inequalities and numeric comparisons. As the example infoboxes from Sect. 6 suggests, such extensions to the query language would allow for similarity queries such as “Both Brad Pitt and Tom Cruise have at least 3 children”. Lastly, our approach to entity comparison should be thoroughly evaluated.