Abstract
The previous chapter established that neighborhood structures with the basic propositional modal language is an interesting and well-motivated logical framework. This chapter moves away from questions of motivation to explore the logical theory of neighborhood structures. Much of the mathematical theory of modal logic with respect to relational structures can be adapted to the more general setting involving neighborhood structures. For instance, there is a well-behaved notion of structural equivalence between neighborhood models matching the expressivity of the basic modal language, and the canonical model method for proving axiomatic completeness can be adapted to the more general setting. However, there are some important differences between neighborhood semantics and relational semantics for modal logic. In this chapter, I introduce the core logical theory of neighborhood structures highlighting the similarities and differences with relational structures.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This result can be generalized to the class of modally saturated neighborhood models (Hansen 2003; Hansen et al. 2009).
- 2.
The analogue of a bounded morphism for relational models is a p -morphism (Blackburn et al. 2001, Sect. 2.1).
- 3.
I write \(X^n\) for the n-fold cross product of the set X. That is, \(X^n\) consists of all tuples \(\langle x_1, \ldots , x_n\rangle \) of length n where each \(x_i\in X\).
- 4.
In fact, we have
 ,
, 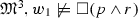 , and
, and  .
. - 5.
Note that Kripke called impossible worlds “non-normal”.
- 6.
For Modus Ponens this means that there is \(j, k <i\) such that \(\alpha _k\) is of the form \(\alpha _j\rightarrow \alpha _i\).
- 7.
This is the terminology found in Segerberg (1971) and Chellas (1980). However, this is a somewhat unfortunate name. Starting with Fitch (1948), there is a line of research studying intuitionistic modal logics (see, for instance, Artemov and Protopopescu (2016) for an interesting epistemic interpretation of intuitionistic modal logic touching on some of the issues discussed in this book). These are modal logics that extend intuitionistic propositional logics. In this literature, a “classical modal logic” is a modal logics that extends classical propositional logic (as opposed to intuitionistic propositional logic). One may be interested in both normal and non-normal modal logics that extend either classical or intuitionistic propositional logics.
- 8.
This is a small digression that can easily be skipped by readers not already familiar with relational semantics for modal logic (see Appendix A for the relevant definitions).
- 9.
I am using the definition of a deduction from assumptions found in Goldblatt (1992a, p. 17) and Blackburn et al. (2001, p. 36). See Hakli and Negri (2011) for a discussion of the issues surrounding this definition related to the deduction theorem and the proper use of inference rules.
- 10.
The proof is provided in the solution manual. Consult Chellas (1980) and Blackburn et al. (2001) for a discussion of this proof and a more complete discussion of maximally consistent sets.
- 11.
See Blackburn et al. (2001), Chap. 4, for an extended discussion of canonical properties for relational models.
- 12.
See Chellas (1980, Sects. 7.5 and 9.5) for an extended discussion.
- 13.
Of course, there are infinitely many variations of the finite \(\varphi \)-canonical model. However, we can ignore irrelevant differences, such as isomorphic copies or models that differ in their interpretation of formulas not among the subformulas of \(\varphi \).
- 14.
Consult Halpern and Rêgo (2007) and Spaan (1993) for discussions of the curious fact that the satisfiability problem for modal logics seems to be either \(\mathbf {NP}\)-complete or \(\mathbf {PSPACE}\)-hard.
- 15.
See Fitting (2006), Wansing (1998), and Negri (2011) for surveys of this literature.
- 16.
I have been using capital Greek letters to denote sets of formulas (c.f. Sect. 2.3.2). For the purposes of this section, it does not matter much whether the components of a sequent are sets or sequences. However, it is standard practice to define sequents using sequences of formulas. So, I will adopt the convention that capital Greek letters denote sequences of formulas in this section.
- 17.
This makes sense since these formulas are semantically equivalent on the class of relational frames (i.e., they are true at exactly the same points in all relational models).
- 18.
Recall that a frame \(\mathcal {F}=\langle W, N\rangle \) is said to be closed under finite intersection provided that for all \(w\in W\), N(w) is closed under finite intersections. See the discussion after Remark 1.10.
- 19.
- 20.
Swanson (2011) has an extensive discussion of incomparability when modeling conditionals.
- 21.
To keep things simple, I assume that the set of worlds is finite, so this maximal set always exists. One needs a (converse) well-foundedness condition to guarantee this when there are infinitely many states.
- 22.
This was first discussed by Boutilier (1992).
- 23.
This means that atomic propositions are nominals (cf. Sect. 3.1 and Areces and ten Cate 2007) with respect to elements in the domain of the model that correspond to subsets.
- 24.
Another option would be to let atomic propositions be undefined at all \(U\in \wp (W)\).
- 25.
I am not using ‘N’ since that is used to denote neighborhood functions.
- 26.
This should be contrasted with the standard translation of relational models for normal modal logic. Consult Blackburn et al. (2001), Sect. 2.4, for details.
- 27.
In this context, an isomorphism between \(\mathcal {L}_{\mathrm {fo}}\)-models \(\mathscr {M}=\langle D,\{P_i\ |\ i\in \mathbb {N}\}, R, E\rangle \) and \(\mathscr {M'}=\langle D',\{P_i'\ |\ i\in \mathbb {N}\}, R', E'\rangle \) is a 1-1 and onto function \(f:D\rightarrow D'\) satisfying the structural conditions: \(w\in P_i\) iff \(f(w)\in P_i'\), \(w \mathrel {R} u\) iff \(f(w)\mathrel {R'}f(u)\) and \(u\mathrel {E}w\) iff \(f(u)\mathrel {E'}f(w)\).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Pacuit, E. (2017). Core Theory. In: Neighborhood Semantics for Modal Logic. Short Textbooks in Logic. Springer, Cham. https://doi.org/10.1007/978-3-319-67149-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-67149-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-67148-2
Online ISBN: 978-3-319-67149-9
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


 ,
, 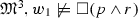 , and
, and  .
.