Heat Transfer by Conduction

Ruocco, Gianpaolo

doi:10.1007/978-3-319-66822-2_2

Heat Transfer by Conduction

Gianpaolo Ruocco²

Chapter
First Online: 13 February 2018

1188 Accesses

The original version of this chapter was revised: Belated corrections have been incorporated. The correction to this chapter is available at https://doi.org/10.1007/978-3-319-66822-2_7

Abstract

Being this the first mode that traditionally is encountered in the study of heat transfer, with the analysis of conduction the ground will be set for more complicated transfer phenomena. After a brief reference to the basic physical mechanism, as we recognize that heat transport in stationary media is driven by a temperature difference, we start by exploiting first the macroscopic balance for heat conduction. Then, the opportunity is seized to develop proper analytical skills by deriving and integrating the governing differential equations in various cases, following the microscopic balance leading to the distribution of the temperature scalar. With this mechanism, the subject medium participates only through the heat source or sink. Next, some graphical tools will be presented that are of some use for the solution of transient cases, and finally a numerical solution of the governing equations is proposed and initiated, to cast the base for a discussion on more complex transfer phenomena.

This is a preview of subscription content, log in via an institution.

Chapter: USD 29.95; Price excludes VAT (USA)

eBook: USD 49.99; Price excludes VAT (USA)

Softcover Book: USD 64.99; Price excludes VAT (USA)

Hardcover Book: USD 99.99; Price excludes VAT (USA)

Tax calculation will be finalised at checkout

Purchases are for personal use only

Learn about institutional subscriptions

Change history

31 March 2019
In the original version of the book, the belated corrections from author.

Notes

1.
The thick line in Fig. 2.2a is normal to the T axis.
2.
The temperature profile will be linear with y or otherwise, depending on the material characteristic with respect to conduction.
3.
Note that this fact agrees with the Second Law of Thermodynamics.
4.
The unit of power, watt, is named after Scottish engineer j. watt (beginning of the nineteenth century).
5.
The Kelvin scale is named after the Northern Irish mathematical physicist and engineer w. thomson, Ist Baron Kelvin (beginning of the nineteenth century).
6.
As proposed by French mathematician and physicist j.-b. fourier, in the early nineteenth century.
7.
Also called a discrete form.
8.
Tensors are important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as elasticity and fluid mechanics, among others.
9.
For many media in the biosciences, thermal conductivity $\lambda $ will take an intermediate value between those of liquid water and air.
10.
Strictly speaking, pressure-constant and volume-constant specific heats arise, when dealing with the variations of internal energy e and enthalpy h: for example, for an ideal gas it is
$$\begin{aligned}\mathrm {d}e\equiv c_v\mathrm {d}T\quad \mathrm {d}h\equiv c_p\mathrm {d}T\end{aligned}$$
For solids and liquids, as incompressible matter, there is no distinction between specific heats at constant pressure and constant volume; therefore, the subscripts can be omitted: $c_p\equiv c_v\equiv c$. For an incompressible liquid it is
$$\begin{aligned} \mathrm {d}e\equiv c\mathrm {d}T\quad \mathrm {d}h\equiv c\mathrm {d}T+\frac{V}{m}\mathrm {d}p \end{aligned}$$
with V, m, and p the volume, mass, and pressure, respectively, at the given thermodynamic state.
11.
For many substrates in the biosciences, specific heat $c_p$ will take an intermediate value between those of liquid water and air.
12.
Beside the familiar rectangular coordinate system (also called a Cartesian coordinate system, as proposed by French philosopher and mathematician r. descartes in the early seventeenth century), other frequent coordinate systems are the cylindrical system (of length L and radius R) and the spherical system (of radius R), as reported here at right with the representations of point P and its coordinates.
13.
When applied to a scalar, $\nabla $ gives its gradient (i.e., a vector). When using a rectangular 3-D coordinate system:
$$\begin{aligned} \nabla \equiv \frac{\partial }{\partial x}\mathbf {i}+\frac{\partial }{\partial y}\mathbf {j}+\frac{\partial }{\partial z}\mathbf {k} \end{aligned}$$
In cylindrical coordinates, it is
$$\nabla \equiv \frac{\partial }{\partial r}\mathbf {r}+\frac{1}{r}\frac{\partial }{\partial \phi }\varvec{\phi }+\frac{\partial }{\partial z}\mathbf {z}$$
In spherical coordinates, it is
$$\nabla \equiv \frac{\partial }{\partial r}\mathbf {r}+\frac{1}{r}\frac{\partial }{\partial \phi }\varvec{\phi }+\frac{1}{r\sin \phi }\frac{\partial }{\partial \theta }\varvec{\theta }$$
The disposition of versors are those illustrated by the axes directions in the schemes of Note 12.
14.
The nature and significance of the average coefficient $\overline{h}$ will be scrutinized in Chap. 4. The definition of average implies that its value is constant and uniform. In addition to convection heat transfer, radiation heat transfer with the surroundings may well be also present.
15.
As proposed by German physicist g.s. ohm, in the early nineteenth century.
16.
Let us recall here some parameters used in the electrical engineering. First of all, the electrical power P is defined by:
$$\begin{aligned}P=\Delta VI=RI^2\end{aligned}$$
The electrical current I is measured in ampere (A), a fundamental unit in SI (named after the French mathematician and physicist a.-m.- ampère, beginning of the nineteenth century). The electric charge is measured in coulomb (C), a derived unit in SI (named after the French physicist c.-a.- de coulomb, beginning of the eighteenth century) as $1~\mathrm {C}=1~\mathrm {A}\times \mathrm {s}$. The potential tension or voltage, and the electromotive force are measured in volt (V), a derived unit (named after the Italian physicist and chemist a.g.a.a. volta , beginning of the eighteenth century): the voltage between two points of a conductor when a current of $1~\mathrm {A}$ dissipates $1~\mathrm {W}$ between those points: $1~\mathrm {V}=1~\mathrm {W}/\mathrm {A}$. The electrical resistance R is measured in ohm ($\varOmega $), a derived unit: the resistance between two points of a conductor when a constant potential difference of $1~\mathrm {V}$, applied to these points, produces in the conductor a current of $1~\mathrm {A}$, the conductor not being the seat of any electromotive force: $1~\varOmega = 1~\mathrm {V}/\mathrm {A}$.
17.
In accordance with Kirchhoff’s Law of current, proposed by German physicist g.r. kirchhoff at mid-nineteenth century.
18.
We also note the typical curvilinear variation of T by the wall sides, due to the convective boundary layer which we will deal with when studying Chap. 4: in this case, the temperature drop due to the thermal resistance defined by Eq. (2.14) is smaller where the forced convection is applied (at side i), being this mechanism stronger than the external free convection (at side $\infty $) in transferring the heat from/to the side.
19.
With this choice of a rectangular reference system, lengths along z can be taken as unitary.
20.
The three primes $'''$ are purposeful to the fact that $\dot{e}'''$ refers to the unit volume. Therefore, $[\dot{e}''']$=W/m$^3$.
21.
Phase-change-related heat flux, such as for evaporation/condensation, is common in biosubstrate processing, in presence of an internal phase-changing constituent, and deserves a dedicated formulation. As a frequent example, evaporation of liquid water may well occur directly within water-saturated substrates, subject to heat supply. In this case, $\dot{e}'''$ represents the latent cooling rate due to evaporation and can be computed as
$$\begin{aligned} \dot{e}'''=-\dot{m}'''\Delta h_{\mathrm {vap}} \end{aligned}$$
where $\dot{m}'''$ is the volumetric flux of water vapor or evaporation rate, in kg/m$^3$s, and $\Delta h_{\mathrm {vap}}$ is the latent heat of evaporation of water, in kJ/kg.
One such applicative case is presented in Sect. 6.3.
22.
Named after English mathematician b. taylor (early eighteenth century), this series dictates that
$$\dot{Q}_x\left( x+\mathrm {d}x\right) \equiv \dot{Q}_x\left( x\right) +\frac{\partial \dot{Q}_x\left( x_0\right) }{\partial x}\mathrm {d}x+\text {a}\,truncation \,error \,\text {due to higher-order terms}\,[6]$$
This expansion can be generalized for functions of more variables.
23.
Also called the heat equation.
24.
$\nabla ^2$ is the Laplace operator (after French physicist, mathematician, astronomer, and statesman p.-s. laplace, early nineteenth century). When applied to a scalar, gives its Laplacian. See also Note 13. When using the rectangular 3-D coordinates, the Laplace operator is given by
$$\nabla ^2\equiv \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}$$
In cylindrical coordinates, it is
$$\nabla ^2\equiv \frac{\partial ^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial ^2}{\partial \phi ^2}+\frac{\partial ^2}{\partial z^2}$$
Finally, in spherical coordinates, it is
$$\nabla ^2\equiv \frac{\partial ^2}{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r}+\frac{1}{r^2\sin \gamma }\frac{\partial }{\partial \gamma }\left( \sin \gamma \frac{\partial }{\partial \gamma }\right) +\frac{1}{r^2\sin ^2\gamma }\frac{\partial ^2}{\partial \phi ^2}\,.$$
25.
PDEs can be usefully classified in parabolic, hyperbolic, and elliptic types, in analogy with second-order equations appearing in analytic geometry [3]. In addition to the parabolic type, an example of hyperbolic PDE is the wave equation used for the description of waves such as sound, light, and in liquid at interface
$$\begin{aligned}\frac{\partial ^2u}{\partial \theta ^2}=c^2\nabla ^2u\end{aligned}$$
with u the subject scalar (e.g., the wave’s mechanical displacement) and c the propagation speed. Elliptic PDEs are typically used in equilibrium phenomena, such the one that would result in the steady state, when dropping the transient term in the heat equation, Eq. (2.22).
26.
After German mathematician p.g.l. lejeune dirichlet (mid-nineteenth century).
27.
After German mathematician c. neumann (late nineteenth century).
28.
After French mathematician v.g. robin (late nineteenth century).
29.
This nomenclature stems from the Stefan–Boltzmann Law
$$\begin{aligned} E_\mathrm {b}=\sigma T^4 \end{aligned}$$
which describes the power radiated $E_\mathrm {b}$ from a so-called black body based on its absolute temperature to the fourth power, $\sigma $ being a constant. This Law was formulated jointly by the Slovenian-Austrian mathematician and physicist j. stefan and the Austrian physicist l. boltzmann (late nineteenth century).
30.
All of the governing equations in this book are elliptic in space and parabolic in time. For space-elliptic PDEs, the second space derivatives (term 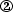in Eq. (2.22)) require two boundary conditions to be assigned in each spatial coordinate. In principle, this could be done by prescribing conditions at two locations or by prescribing two conditions at one location: only the former is appropriate. For example, prescribing both the function and its derivative at the same location, i.e., the so-called Cauchy boundary condition (after French mathematician a.-l. cauchy), leads to BCs overspecification and improperly-posed problems. See discussion in [Morse, P.M., Feshbach, H.: Methods of Theoretical Physics. McGraw-Hill, New York (1953) p. 690] and in [Jaluria, Y., Torrance, K. E.: Computational Heat Transfer. Hemisphere Publishing, Washington (1986) p. 18].
31.
Note that, due to the nature of angular coordinate $\phi $, all three fluxes are dimensionally homogeneous.
32.
Also called the Laplace’s equation .
33.
Also called the Poisson’s equation, after French mathematician and physicist s.d. poisson (early nineteenth century).
34.
As proposed by French physicist j.-b. biot, in the early nineteenth century.
35.
The first assumption is valid, that is, neglecting the effect of extremal sides along z (Figure at left in Note 12) when the height L is at least one OoM greater than the radius R. With the second assumption, this case is called the circular coordinates geometry.
36.
If the material has electrical conductivity $\lambda _\mathrm {e}$ ($1/\varOmega \mathrm {cm}$), and is subject to a current density I ($\mathrm {A/cm}^2$), the heat generation due to the Joule heating effect (after English physicist j.p. joule, at mid-nineteenth century) is $\dot{e}'''=I^2/\lambda _\mathrm {e}$ ($\varOmega \mathrm {A}^2/\mathrm {cm}^3$).
37.
It is easy to verify that, in case of two Dirichlet BCs in Eq. (2.59), the solution is simply
$$\begin{aligned} T(r)=T_1-\frac{\left( T_1-T_\infty \right) }{\ln \frac{r_2}{r_1}}\ln \frac{r}{r_1}. \end{aligned}$$
38.
Practically, it is seen that all the possible $T=T(x,\theta )$ profiles are similar, that is, have the same shape.
39.
erf and erfc have a sigmoidal shape, as explained in Abramowitz, M., Stegun, I.A.: Handbook of mathematical functions: with formulas, graphs, and mathematical tables. Dover Publications, Mineola (1965). Thus
$$\begin{aligned} \mathrm {erf}(x)\equiv \frac{2}{\sqrt{\pi }}\int _0^x\exp \left( -t^2\right) \,\mathrm {d}t\quad \text {and}\quad \mathrm {erfc}(x)\equiv 1-\mathrm {erf}(x)=\frac{2}{\sqrt{\pi }}\int _x^{\infty }\exp \left( -t^2\right) \,\mathrm {d}t \end{aligned}$$
Some properties apply: $\mathrm {erf}(0)=0$; $\mathrm {erf}(0)=0$; $\mathrm {erf}(\infty )=1$; $\mathrm {erf}(-x)=-\mathrm {erf}(x)$.
We can approximate $\mathrm {erf}(x)$ [5]:
$$\begin{aligned} \mathrm {erf}(x)\approx 1-\frac{1}{(1+a_1x+a_2x^2+a_3x^3+a_4x^4)^4}\quad (\text {maximum error:}~5\times 10^{-4}) \end{aligned}$$
with $a_1=0.278393$, $a_2=0.230389$, $a_3=0.000972$, $a_4=0.078108$.
40.
Another technique can be employed, arriving to the same results, consisting in finding pertinent dimensionless numbers from experimental data, through application of the Buckingham $\pi $ theorem [5] (named after American physicist e. buckingham, but first proved in the late nineteenth century by French mathematician j. bertrand).
41.
After the aforementioned scientist j.-b. fourier.
42.
Numerical solution of heat conduction is particularly useful when the shape of the CV is irregular, when its properties vary with space and position, and for nonlinear or non-uniform boundary conditions.
43.
This data structure will be exploited later to study the numerical solution of fluid flow.
44.
For a non-uniform medium, $\lambda $ should be evaluated at the faces w and e; if $\dot{e}'''$ is no longer uniform, it should be subject to integration across the CV. Non-uniformity can be healed by proper gridding increase across the interface.
45.
Let us recall the definition of the derivative of T(x) at $x=x_0$: $\frac{\mathrm {d}T}{\mathrm {d}x}\equiv \lim _{\Delta x\rightarrow 0}\frac{T\left( x_0+\Delta x\right) -T\left( x_0\right) }{\Delta x}$. Here, if T is continuous, it is expected that $\frac{T\left( x_0+\Delta x\right) -T\left( x_0\right) }{\Delta x}$ (also called a forward difference scheme) will be a “reasonable” approximation to $\frac{\mathrm {d}T}{\mathrm {d}x}$ for a “sufficiently” small but finite $\Delta x$. Indeed, just like in Eq. (2.22) but across a finite $\Delta x$ interval this time, the Taylor’sa series expansion is written as $T\left( x_0+\Delta x\right) =T\left( x_0\right) +\frac{\mathrm {d}T\left( x_0\right) }{\mathrm {d}x}\Delta x+\text {a truncation error}$ [3].
46.
It is clear, from inspection of coefficient equations like Eq. (2.108), that the matrix is diagonally dominant (also called the Scarborough criterion, as proposed by the American j.b. scarborough, at mid-twentieth century), with coefficients that must be always discordant with those of the lateral nonzero diagonals.
47.
After English physicist and mathematician l.h. thomas in mid-twentieth century.
48.
This number should not be confused with the one introduced earlier with Eq. (2.93). The grid Fo is used in computational stability criteria when schemes other than the fully implicit one are adopted.
49.
For 3-D geometries, the coefficient matrix Eq. (2.115) will have nonzero values aligned along 7 diagonals, to include the contributions of the CVs along the z coordinate.

References

Liley, P.E., Thomson, G.H., Friend, D.G., Daubert, T.E., Buck, E.: Physical and chemical data. In: Green, D.W., Maloney, J.O. (Eds.) Perry’s Chemical Engineers’ Handbook, Chap. 2 (1997)
Google Scholar
Irvine Jr., T.F.: Thermophysical properties. In: Rohsenow, W.M., Hartnett, J.P., Cho, Y.I. (eds.) Handbook of Heat Transfer. McGraw-Hill, New York (1998)
Google Scholar
Anderson, D.A., Tannehill, J.C., Pletcher, R.H.: Computational Fluid Dynamics and Heat Transfer. Hemisphere Publishing, Washington (1984)
MATH Google Scholar
Bejan, A.: Heat Transfer. Wiley, New York (1993)
MATH Google Scholar
Mills, A.F.: Heat Transfer. Richard D. Irwin, Boston (1992)
MATH Google Scholar
Bergman, T.L., Incropera, F.P., Lavine, A.: Fundamentals of Heat and Mass Transfer. Wiley, New York (2011)
Google Scholar
Patankar, S.V.: Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing, Washington (1980)
MATH Google Scholar

Download references

Author information

Authors and Affiliations

College of Engineering, University of Basilicata, Potenza, Italy
Gianpaolo Ruocco

Authors

Gianpaolo Ruocco
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gianpaolo Ruocco .

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Ruocco, G. (2018). Heat Transfer by Conduction. In: Introduction to Transport Phenomena Modeling. Springer, Cham. https://doi.org/10.1007/978-3-319-66822-2_2

Download citation

DOI: https://doi.org/10.1007/978-3-319-66822-2_2
Published: 13 February 2018
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66820-8
Online ISBN: 978-3-319-66822-2
eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics