Hiding Secrecy Leakage in Leaky Helper Data

Abstract

PUFs provide cryptographic keys for embedded systems without dedicated secure memory. Practical PUF implementations often show a bias in the PUF responses, which leads to secrecy leakage in many key derivation constructions. However, previously proposed mitigation techniques remove the bias at the expense of discarding large numbers of PUF response bits. Instead of removing the bias from the input sequence, this work reduces the secrecy leakage through the helper data. We apply the concept of wiretap coset coding to add randomness to the helper data such that an attacker cannot isolate significant information about the key anymore.

Examples demonstrate the effectiveness of coset coding for different bias parameters by computing the exact leakage for short code lengths and applying upper bounds for larger code lengths. In our case study, we compare a secrecy leakage mitigation design with coset coding and Differential Sequence Coding (DSC). It reduces the number of required PUF response bits by $60\%$ compared to state-of-the-art debiasing approaches.

1 Introduction

Silicon Physical Unclonable Functions (PUFs) measure physical manufacturing variations inside integrated circuits to derive a unique behavior for each device. Typical silicon PUFs can be implemented in a standard CMOS manufacturing process such that they provide cryptographic keys for embedded devices without dedicated secure key storage in non-volatile memory [1]. This makes them a suitable solution to protect a wide span of devices, starting from lightweight IoT sensors up to complex high-end circuits such as FPGAs.

PUF responses are noisy and often not fully random such that postprocessing steps are necessary to derive stable and secure cryptographic keys from PUFs. The syndrome encoder computes helper data that is stored off-chip, e.g. in unsecured external non-volatile memory. The helper data maps the PUF response to codewords of an Error-Correcting Code (ECC) to enable error correction, but it must not leak information about the derived key. Several error correction schemes were proposed and implemented over the last decade, e.g. [2,3,4,5,6,7,8,9,10].

Early work such as [11] already acknowledged the fact that PUF implementations can have imperfections that result in a reduced entropy of the PUF response. As the field matured, the security implications of the imperfections in the PUF responses, and especially bias, were analyzed and addressed in more detail [5, 10, 12,13,14,15].

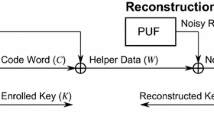
Looking at a fuzzy commitment [16] in Fig. 1 there are two ways to reduce the leakage within this setting: The approaches in [5, 10] reshape the input distribution in a debiasing step such that an unbiased sequence is processed in the syndrome encoder. This comes at the expense that the unbiased sequence is significantly shorter than the input PUF response. In contrast, we operate on the ECC encoding to mask the leakage on the secret. While [7] proposed a method to store multiple instances of helper data and thus hide the correct value, we create the ambiguity within one single instance of helper data in this work.

Fig. 1.

Helper data generation for a fuzzy commitment and a biased PUF

Another recent line of work relaxed the security argument from an information theoretical setting to a complexity theoretical argument [17,18,19,20] where no secrecy leakage is observed. However, to be able to quantify the actual statistical correlation, we stay in the stricter information theoretical setting in the following.

1.1 Contributions

• We show that the problem of secure key storage with PUFs relates closely to the wiretap channel [21]. To the best of our knowledge, we are therefore the first to apply coset coding [22] to PUFs. Instead of embedding only the secret key, we add mask bits that are encoded by the ECC together with the secret key and thus contribute to the helper data as well. Due to the bias, the helper data inevitably leaks information about the key and the mask. Since the attacker is not able to isolate the leakage on the key, this leakage cannot be exploited.

• Examples demonstrate and quantify the leakage reduction that is achieved by assigning mask bits for coset coding. We compute the exact leakage for short code lengths and apply an upper bound for long code lengths for Reed–Muller (RM) codes and a wide range of bias parameters.

• We provide design parameters for a practical design with Differential Sequence Coding (DSC) and compare it to state-of-the-art debiasing approaches with Index-Based Syndrome coding (IBS) and the von Neumann corrector (VN). The comparison shows that our approach reduces the number of PUF response bits by $60\%$ for a moderately biased PUF with a bias of 0.54 and only has a negligible secrecy leakage of less than 0.06 bit for the entire key.

1.2 Organization

Section 2 introduces the state of the art related to this work. The wiretap channel and corresponding codes which are the foundation of our new leakage reduction method are summarized in Sect. 3. Section 4 describes the correspondence between the wiretap channel model and PUF key storage, and Sect. 5 introduces coset coding for PUFs. The new approach is compared to the state of the art in Sect. 6. Section 7 concludes this work.

1.3 Notation

Capital letters indicate random variables or values that are functions of random variables, while small letters represent numbers and specific instantiations of random variables. Matrices are given by bold capital letters, and calligraphic letters represent sets. C is a codeword of a linear ECC $\mathcal {C}$ with code length n, code size k, minimum distance d, generator matrix $\mathbf {G}$, and parity check matrix $\mathbf {H}$ [23]. The helper data W is computed from PUF response X and secret S. Superscripts define the lengths of vectors.

Let ${{\mathrm{\mathbb {E}}}}[\cdot ]$ be the expectation operator and $\Pr [\cdot ]$ the probability of an event. Further, let $\mathrm {hw}(\cdot )$ be the Hamming weight of a vector.

2 State of the Art Debiasing Approaches for PUFs

A simple approach of removing bias is to XOR multiple PUF response bits [24], which reduces the bias for independent and identically distributed (i.i.d) PUF responses according to the piling-up lemma [25]. However, each XOR also reduces the number of PUF response bits so that only a fraction of the input length remains and the output error probability is increased at the same time. Therefore, we take a closer look at more sophisticated alternatives, namely Index-Based Syndrome Coding (IBS) and the von Neumann Corrector (VN) in the following.

For high input bit error probabilities in the range $>20\%$, the multi-bit symbol-based approach discussed in [26] can also be used to generate keys from biased PUFs without secrecy leakage.

2.1 Index-Based Syndrome Coding

IBS computes pointers to reliable PUF response bits and stores the pointers in helper data [5]. Going back to Fig. 1, the IBS pointer generation acts as debiasing and syndrome encoding at once. IBS decreases the output error probability but it cannot correct any errors. To enable error correction, IBS is typically concatenated with ECCs such as BCH or Reed–Muller codes [23].

Fig. 2.

Helper data generation with index-based syndrome coding

Figure 2 shows an example for helper data generation with IBS. The PUF response sequence is divided into blocks of fixed size q (here, $q = 4$). The ECC encoder maps k-bit secrets into n-bit codewords $C^n$. The inputs of the IBS encoder are a codeword bit $C_i$, a block of PUF response bits $X^q$ and reliability information, e.g. the bit error probability, for each of the PUF bits. It generates a pointer $W^s$, $s=\left\lceil \log q \right\rceil$ to index the bit which is equal to the secret bit with the highest probability. The other bits of the block are discarded. This process is repeated for each $C_i$. The indexing operation selects the PUF response bits according to the distribution of input C. As proven in [5], IBS does not leak secret information for i.i.d PUF response bits as long as no additional reliability information is published. Complementary IBS adds an intermediate error correction step to increase the efficiency of IBS [6]. However, it was shown in [9], that larger block sizes are required for more efficient indexing of reliable PUF response bits.

2.2 Von Neumann Corrector

In [10], another debiasing step was proposed to overcome the leakage caused by biased PUF responses. It is based on the von Neumann (VN) corrector [27] and evaluates pairs of consecutive PUF response bits. (1,0) and (0,1) pairs occur with the same probability but differ in the order of the numbers such that a uniform random process is sampled while the pairs (1,1) and (0,0) are ignored. Figure 3 shows the helper data generation with the VN corrector as debiasing scheme and the fuzzy commitment as syndrome encoder [16].

Fig. 3.

Helper data generation with the fuzzy commitment and the von Neumann corrector

The encoder scans the PUF response $X^m$ sequentially and maps it to a sequence $T^n$ $(m>n)$. If two consecutive PUF bits of $X^m$ differ, the first bit is added to the debiased output $T^n$ and the position of the pair is stored as additional helper data $U^l$, as shown in Fig. 3. For i.i.d PUF response bits, the VN approach provides perfectly random outputs. The efficiency of the approach is enhanced in [10] by searching $X^m$ in multiple passes for patterns of different size. For the fuzzy commitment, helper data $W^n$ is computed as XOR between $T^n$ and the codeword $C^n$. Neither $W^n$ nor $U^l$ leak secret information. However, a high number of discarded PUF response bits causes an overhead in PUF size. In addition, an implementation of the multi-pass version would require either multiple readouts of the PUF or buffering the entire PUF response.

IBS and the VN corrector both address only the debiasing and syndrome coding blocks in Fig. 1. In the following, we also take the ECC encoder into account.

3 Wiretap Channel and Coset Codes

Before going into our new leakage countermeasure for PUFs, we briefly discuss the information theoretical problem that forms the foundation of our work. In 1975, Wyner introduced the wiretap channel model which represents a communication system that is wiretapped by an adversary [21], as shown in Fig. 4.

Fig. 4.

The wiretap channel

Alice encodes a k-bit secret message $S^k$ to an n-bit codeword $C^n$ and transmits it to Bob through the main channel. Due to noise, Bob receives a distorted version $Y^n$ of $C^n$ and recovers message $\hat{S}^k$. The attacker Eve also observes a noisy version $Z^n$ of $C^n$ through the wiretapper’s channel.

The challenge is to develop a coding scheme that allows a reliable communication from Alice to Bob while preventing Eve from recovering any information. In a reliable system, Bob can decode message $\hat{S}^k$ from his received vector $Y^n$ correctly with a high probability. For security reasons, we need to limit the information that $Z^n$ provides to Eve about $S^k$. The delicate challenge is to encode the message such that it has just enough structure to be decoded correctly by Bob while it still must resemble ambiguous to Eve. Note that the wiretap channel has to be noisier than the main channel to be able to achieve any secret communication at all. The current research field of physical-layer security also makes extensive use of the wiretap channel model [28, 29].

The basic idea of wiretap coding is to introduce randomness to the encoding process by assigning multiple codewords to each message. Alice selects a message $S^k$ and encodes it as a codeword of code $\mathcal {C}_1$. Instead of a bijective and deterministic encoding, $\mathcal {C}_1$ contains a set of multiple possible codewords for each message and the encoder selects one of the corresponding codewords at random.

Bob recovers the message correctly, if $\mathcal {C}_1$ contains a sufficient amount of redundancy such that the error probability

$$\begin{aligned} P_e = \Pr [\hat{S}^k \ne S^k] < \epsilon _1 \end{aligned}$$

(1)

for an $\epsilon _1 >0$. For large block lengths, it was shown that there exist codes such that ${\lim _{n \rightarrow \infty } P_e = 0}$ [28].

Eve’s channel has a higher noise level so that she has multiple possible solutions instead of one unique solution for the decoding problem. If the code is designed properly, codeword candidates for all possible $2^k$ messages are suitable, and ideally equiprobable, for her received message $Z^n$. In other words, according to [28]

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{n} I(S^k;Z^n) = 0 \end{aligned}$$

(2)

The noise level on the main channel determines the amount of redundancy that has to be spent to achieve a reliable decoding for Bob. The difference between the noise levels of the main channel and the wiretap channel defines the maximum size of the secret information $S^k$ that can be transmitted from Alice to Bob in n transmitted symbols while keeping Eve ignorant. However, determining the noise levels can be challenging in practice.

The secrecy capacity $C_S$ is thus given by [28]

$$\begin{aligned} C_S = I(C;Y) - I(C;Z) \end{aligned}$$

(3)

Most wiretap codes discussed in the information theory community use random codes, where random numbers are generated and then assigned to different codebooks. Random coding arguments are highly suitable to prove that a problem can be solved with some asymptotic behavior or to show that a problem cannot be solved better than some bound. However storing and searching large random codebooks, e.g. with more than $2^{32}$ entries, in an embedded system is not feasible. After understanding the general theoretical behavior of a problem by analyzing the behavior of random codes, work on deterministic algorithms is the next step to bring an approach closer towards implementations in practical systems.

In 1984, Ozarow and Wyner proposed a practical wiretap coding scheme called coset coding [22]. A coset of a set is computed by adding a constant to all elements of the original set [23]. In coset coding, a coset is selected according to the secret message. Then, the encoder selects one element of the coset at random as transmitted message. Coset coding achieves secrecy for a wiretap channel model where the main channel is noiseless and the wiretapper observes the message through a binary erasure channel, which is a stochastic channel that replaces a transmitted symbol with an erasure symbol with a given fixed probability. Later, this scheme was extended to other channel models, e.g. Binary Symmetric Channels (BSCs) in [30].

Let $\mathbf {G}_1$ be a $k_1 \times n$ generator matrix of linear code $\mathcal {C}_1$ and $\mathbf {H}_1$ be the parity check matrix of the same code. Similarly, $\mathbf {G}_2$ and $\mathbf {H}_2$ are the generator and parity check matrices of a linear code ${\mathcal {C}_2 \subset \mathcal {C}_1}$ with message length $k_2$ and code length n. The code space $\mathcal {C}_1$ is partitioned into $2^k$ sets containing cosets of $\mathcal {C}_2$, where $k=k_1-k_2$.

$$\begin{aligned} \mathbf {G}_1 = \begin{bmatrix} \mathbf {G}_2 \\ \mathbf {G} \end{bmatrix} \end{aligned}$$

(4)

A uniform random vector $R^{k_2}$ is added as mask to disguise the secret message $S^k$. The encoding is formalized by

$$\begin{aligned} C^n&= \begin{bmatrix} R^{k_2}&S^k \end{bmatrix} \cdot \begin{bmatrix} \mathbf {G}_2 \\ \mathbf {G} \end{bmatrix} \end{aligned}$$

(5)

$$\begin{aligned}&= R^{k_2}\cdot \mathbf {G}_2 + S^k\cdot \mathbf {G} \end{aligned}$$

(6)

The coset $S^k\cdot \mathbf {G}$ contains the secret message while codeword ${R^{k_2}\cdot \mathbf {G}_2}$ adds randomness to prevent Eve from decoding code $\mathcal {C}$ correctly.

The effectiveness of the coset coding countermeasure is measured by the mutual information $I(S^k;Z^n)$. However, computing the exact mutual information in Eq. 2 is practically infeasible for large codes. Chen and Han Vinck provide an upper bound on the information leakage for the case that the main channel and the wiretapper’s channel both are BSCs and linear codes are used for the coset coding construction [30]. For a main channel with bit error probability $p_m$ and a wiretap channel with a bit error probability of $p_w$, the secrecy leakage is bounded by

$$\begin{aligned} I(S^k;Z^n) \le \log \left( 2^n \ P_{\mathcal {C}_2}(p_w)\right) , \end{aligned}$$

(7)

where

$$\begin{aligned} P_{\mathcal {C}_2}(p_w)=\frac{1}{|\mathcal {C}_2|} \sum _{c^n \in \mathcal {C}_2} {p_w}^{\mathrm {hw}(c^n)} (1-p_w)^{(n-\mathrm {hw}(c^n))} \end{aligned}$$

(8)

for code space $\mathcal {C}_2$ with cardinality $|\mathcal {C}_2|$ and elements $c^n$ with Hamming weight $\mathrm {hw}(c^n)$. Note that code $\mathcal {C}$ is important for the reliability while the secrecy leakage in Eq. 7 only depends on $\mathcal {C}_2$.

Equation 8 iterates over all codewords. A good code design minimizes the product ${p_w}^{\mathrm {hw}(c^n)} (1-p_w)^{(n-\mathrm {hw}(c^n))}$ to tighten the bound in Eq. 7. Since the error probability ${p_w}$ is given by the channel, one can only optimize the code. ${p_w}$ is smaller than $(1-p_w)$ such that the Hamming weight $\mathrm {hw}(c^n)$ of the codewords in $\mathcal {C}_2$ is maximized. When $\mathcal {C}_1$ is partitioned into $\mathcal {C}$ and $\mathcal {C}_2$, it is therefore important to assign components with high Hamming weights to $\mathcal {C}_2$ to maximize the impact of the mask.

4 Wiretap Channel Model for PUFs

To apply coset coding to PUFs, we first need to show that key derivation with PUFs also corresponds to the wiretap channel model.

In the following, we apply the fuzzy commitment scheme [16]. However the code-offset fuzzy extractor or the syndrome construction, both [2], or systematic low leakage coding [8] could also be used in a similar way. Figure 5 shows the PUF key generation and reproduction with an attacker that has access to the public helper data.

Fig. 5.

Fuzzy commitment PUF model with an attacker

The ECC encoder maps the secret $S^k$ to a codeword $C^n$ and the fuzzy commitment XORs $C^n$ with PUF response $X^n$ to generate helper data $W^n$. $W^n$ is public, so both the legitimate decoder and the attacker can access it. The legitimate receiver observes a noisy version of the PUF response $\tilde{X}^n = X^n \oplus E^n$ with error pattern $E^n$. If the distortion is within the error correction capability of code $\mathcal {C}_1$, the decoder can recover the secret successfully with a high probability. The attacker tries to extract information regarding the secret from the helper data $W^n$.

To map this PUF model to the wiretap channel model, one has to leave the procedure-centric view which is typically applied in PUF key generation and look at the information flows. The source outputs secret $S^k$, while $\hat{S}^k$ and $\hat{S}_A^k$ are the inputs of the sinks at the receiver and the attacker side. In both cases, the information is modified on the way from the source to the sink.

Fig. 6.

Wiretap channel model for PUFs

Figure 6 shows the wiretap channel model for PUFs, where the main and wiretapper’s channels are modeled as BSCs. Bob’s ECC decoder receives a noisy codeword $\tilde{C}^n$ with error pattern $E^n$, i.e., ${\tilde{C}^n = C^n \oplus E^n}$. In Fig. 5, $X^n$ is added twice to the codeword which is transmitted over the main channel, so that only the noise $E^n$ remains.

$$\begin{aligned} \tilde{C}^n&= C^n \oplus X^n \oplus \tilde{X}^n \end{aligned}$$

(9)

$$\begin{aligned}&= C^n \oplus X^n \oplus X^n \oplus E^n \end{aligned}$$

(10)

$$\begin{aligned}&= C^n \oplus E^n \end{aligned}$$

(11)

The attacker’s path in Fig. 6 does not show a decoder since we assume an unbounded attacker. Therefore, $W^n$ must not leak any information regardless of any subsequent processing steps.

$W^n$ also is a distorted version of $C^n$, since

$$\begin{aligned} W^n= C^n \oplus X^n \end{aligned}$$

(12)

The PUF response $X^n$ is interpreted as the wiretapper’s error pattern that is added to codeword $C^n$ in the wiretap channel. Assuming independent errors for each position, the error patterns $E^n$ and $X^n$ can therefore be modeled by BSCs with crossover probabilities $p_m = \frac{1}{n} {{\mathrm{\mathbb {E}}}}[E^n]$ and $p_w= \frac{1}{n} {{\mathrm{\mathbb {E}}}}[X^n]$, respectively.

So, we have shown that secure key storage with PUFs can also be interpreted as a wiretap channel. In contrast to the wireless wiretap channel setting, the PUF setting has the advantage that $p_w$ can be measured and characterized precisely in practice, as e.g. in [31].

5 Wiretap Coset Codes for PUFs

This section introduces coset coding to PUFs as a new practical tool to address helper data leakage, based on an example first and then provides a generic approach.

Let the PUF response bits $X^n$ be i.i.d with $\Pr [x=1]=b$, $b \in [0,1]$. Then, the probability distribution of $X^n$ is a binomial distribution with $\mathrm {hw}(x^n)$ successes out of n Bernoulli trials with success probability b.

$$\begin{aligned} \Pr [X^n=x^n] = b^{\mathrm {hw}(x^n)} \cdot (1-b)^{(n-\mathrm {hw}(x^n))} \end{aligned}$$

(13)

If $b\ne 0.5$, the response bits are said to be biased and information leakage through the helper data is observed, e.g. [15]. In the following, we discuss a toy example to explain the leakage and its mitigation for a biased PUF.

Let us consider a fuzzy commitment scheme and 4-bit PUF responses $X^4$ with bias $b=0.25$. For error correction, exemplarily a (4, 3, 2) error detecting code is applied whose generator matrix is given by

$$\begin{aligned} \mathbf {G}_1= \left( \begin{array}{cccc} 1&{}1&{}1&{}1\\ 0&{}0&{}1&{}1\\ 0&{}1&{}0&{}1\\ \end{array} \right) \end{aligned}$$

Let us assume that for a specific instance helper data $w^4 = 0001$ is stored and observed by the attacker. Table 1 shows all key candidates and assigns the conditional probability of occurrence for the given helper data to each candidate.

Table 1. Probability of different key candidates for the given helper data ${w^4=0001}$ and bias $b=0.25$.

Recalling the notation from Sect. 3, we start with secret length $k=3$ and no masking, so $k_2=0$. The first three columns show the mapping between the key candidates $s^3$, codewords $c^4$ and PUF responses $x^4$. Key candidates $s^3$ are encoded to codewords $c^4$ by $\mathbf {G}_1$, i.e. ${c^4= s^3\cdot \mathbf {G}_1}$. For a given $w^4$, there is an exact one-to-one mapping between a PUF response $x^4$ and a secret $s^3$, since

$$\begin{aligned} x^4 = w^4 \oplus c^4 = w^4 \oplus s^3 \cdot \mathbf {G}_1. \end{aligned}$$

(14)

The probabilities of all $x^4$ are listed in the fourth column of the table.

The fifth column shows that one half of the possible PUF responses contains three zeros and a single one, while the other half contains one zero and three ones. Due to the bias towards zero, the PUF responses with more ones, highlighted in gray in the table, have a lower probability of occurrence than the other half. This gives the attacker an advantage to guess the secret correctly.

Previous work focused on debiasing the PUF response to avoid leakage. In contrast, we now assign multiple PUF responses to each key candidate.

By interpreting the first bit of each key candidate as mask, so $k_2=1$, we reduce k to $k=2$. Now, we obtain four different key candidates whereas each candidate can be derived from two different PUF responses. For example, key candidates ${s^3=000}$ and ${s^3=100}$ now both lead to ${s^2=00}$ whose corresponding PUF responses are ${x^4=0001}$ and ${x^4=1110}$. So,

$$\begin{aligned} \Pr [s^2=00|W^4=0001]&= \Pr [s^3=000|W^4=0001] \end{aligned}$$

(15)

$$\begin{aligned}&+ \Pr [ s^3=100|W^4=0001] \nonumber \\&= 0.25. \end{aligned}$$

(16)

After shortening $s^3$ to $s^2$ and interpreting the first bit as mask, all four key candidates ${s^2 \in \{00, 01, 10, 11\}}$ occur with probability 0.25. As a result, the probability ${\Pr [S^2= s^2|W^4=0001]}$ is uniformly distributed and the attacker has no advantage from observing the helper data.

Generalizing the example, let $\mathbf {G}_1$ be the generator matrix of an $(n,k_1,d)$ linear block code $\mathcal {C}_1$. We mask k secret key bits with $k_2$ mask bits according to Eq. 4. Again, $\mathbf {G}_1$ is constructed as

$$\begin{aligned} \mathbf {G}_1 = \begin{bmatrix} \mathbf {G}_2 \\ \mathbf {G} \end{bmatrix} \end{aligned}$$

(17)

where $\mathbf {G}_2$ is a $k_2\times n$ generator matrix encoding the mask bits and $\mathbf {G}$ is $k\times n$ generator matrix encoding the secret key bits. As in the wiretap coset codes, $\mathcal {C}_1$ has a generator matrix $G_1$ and is partitioned by cosets of $\mathcal {C}_2$ with generator matrix $G_2$.

Applying $k_2$ mask bits maps $2^{k_2}$ PUF responses to each key. As the number of assigned PUF responses increases, $\Pr [S^k|W^n]$ gets closer to a uniform distribution which prevents the attacker from deriving secret information. Therefore, increasing the number of mask bits reduces the information leakage.

The mutual information $I(S^k;W^n)$ between the secret and the helper data quantifies the leakage. So, the leakage is upper bounded by

$$\begin{aligned} I(S^k;W^n)&= H(S^k) - H(S^k|W^n) \end{aligned}$$

(18)

$$\begin{aligned}&\le k - \tilde{H}_{\infty }(S^k|W^n) \end{aligned}$$

(19)

The conditional min entropy¹ $\tilde{H}_{\infty }(S^k|W^n)$ is given by [2]

$$\begin{aligned} \tilde{H}_{\infty }(S^k|W^n) = - \log _2 \left( \mathop {{{\mathrm{\mathbb {E}}}}}\limits _{w^n}\left[ \max _{s^k} \Pr _{S^k|W}[s^k|w^n]\right] \right) . \end{aligned}$$

(20)

The distribution of probability $P_{S^k|W}(s^k|w^n)$ was already discussed in detail in the previous example and Table 1. Now, we iterate over all $w^n$ and in each iteration all values $x^n$ with $x^n = c^n \oplus w^n$ for $c^n \in \mathcal {C}_1$, are listed. According to $\Pr [X^n=x^n]$ for the listed $x^n$, $\max _{s^k} \Pr [S^k|W^n=w^n]$ is computed. For larger code length, computing $\tilde{H}_{\infty }(S^k|W^n)$ becomes infeasible, but it can be bounded, e.g. according to [15].

6 Evaluation

After introducing the new leakage countermeasure for biased PUFs, this section evaluates its effectiveness. In Sect. 6.1, we compute and discuss the exact leakage for small codes with $n=8$. Bounded results for a larger code with length $n=64$ are provided in Sect. 6.2. Section 6.3 compares our approach to the state of the art in a practical setting.

In the following, we analyze coset code designs based on Reed–Muller (RM) codes [23]. RM codes are a popular code class that was already used several times in the PUF context, e.g. [3, 4, 6, 32]. They have a highly regular structure and are well-suited for compact hardware implementations. $\mathrm {RM}(r,m)$ codes with parameters r and m have code length $n = 2^m$, message length $k = \sum _{i=0}^r \left( {\begin{array}{c}m\\ i\end{array}}\right)$, and code distance $d = 2^{(m-r)}$. Area-optimized FPGA implementations of RM codes for PUF error correction can be found e.g. in [4, 32].

The generator matrix $\mathbf {G}$ of an $\mathrm {RM}(r,m)$ code, is built from m base vectors $v_{(i)}^n$ of length $n=2^m$ and the all ones vector $v_{(0)}^n$ of form

$$\begin{aligned} v_{(0)}^n&= 11111111\cdots 11111111 \\ v_{(m)}^n&= 00000000\cdots 11111111 \\&\vdots \\ v_{(3)}^n&= 00001111\cdots 00001111 \\ v_{(2)}^n&= 00110011\cdots 00110011 \\ v_{(1)}^n&= 01010101\cdots 01010101 \end{aligned}$$

For $r' = \{1,...,r\}$ all linear combinations of $r'$ base vectors $v_{(1)}^n$ to $v_{(m)}^n$ are added to $\mathbf {G}$. Note that combining $r'$ base vectors always results in a vector with Hamming weight $d = 2^{(m-r')}$. The generator matrix consists of $v_{(0)}^n$ and all linear combinations of 1 to r vectors in the set $\{v_{(1)}^n, v_{(2)}^n \cdots v_{(m)}\}$.

6.1 Exact Computations for Short Codes

Figure 7 presents the results for different bias values b in terms of total leakage according to Eqs. 19 and 20. To show the impact of coset coding, we used RM codes and a fuzzy commitment. Increasing the number of mask bits reduces the total leakage, as expected. $b=0.5$ refers to a uniform distribution of PUF response bits so the leakage is always 0. High b values refer to a high bias, which cause an increased secrecy leakage.

Fig. 7.

Computed total information leakage of wiretap coset coding for PUFs with bias b and $\mathrm {RM}(1,3)$ and $\mathrm {RM}(2,3)$ codes.

The RM(1,3) code in Fig. 7a has parameters (8,4,4) such that it carries 4 information bits if no bits are assigned to the mask. Depending on the bias, between 1.3 and 3.8 of the 4 secret bits are leaked. As expected, the total leakage is reduced as more secret bits are interpreted as mask bits.

The first row of its generator matrix $\mathbf {G}$ has Hamming weight 8 while the other three rows have a Hamming weight of 4. The steepness of the curves changes after one bit is assigned to the mask which is consistent with the behavior given in Eq. 7, where the Hamming weight also plays a critical role in reducing the leakage.

The second example, presented in Fig. 7b, is an $\mathrm {RM}(2,3)$ code with parameters (8,7,2). It shows significantly more secrecy leakage for high b since it also contains more information that could be leaked. In contrast to the first example, the $\mathrm {RM}(2,3)$ code is able to generate nearly leakage-free secret bits. For example for $b=0.6$, after interpreting 3 bits as mask only less than 0.2 bit leak in total about the remaining 4 secret bits.

The curves have three areas of different steepness because the generator matrix has three more rows with Hamming weight 2 in addition to the four rows of the RM(1,3) code. Therefore, each additional bit after 4 mask bits has less impact than the bits 1 to 4.

6.2 Upper Bounds for Long Codes

After discussing fundamental properties of coset coding with short code lengths in the previous section, this section shows the secrecy leakage reduction through coset coding for a code length of 64, which is also used in practical implementations.

The exhaustive computation discussed in the previous subsection becomes infeasible for longer code lengths. We therefore upper bound the leakage with the bound presented in [30]. From a security point of view, it is important to prove that the leakage is lower than a given threshold. In the following, we set this threshold to less than 1 bit total leakage. The previous figures demonstrated that this strongly depends on the bias at the input.

Figure 8 realigns the plots such that all start at a secrecy leakage around one. The offset in x direction is given by m. The RM(2,6) code has parameters (64,22,16) and the bias is narrowed down to parameters between $b=0.52$ and $b=0.60$. When interpreting the results, it is important to take into account that the results are conservative upper bounds and the actual values are always lower.

For a small bias of $b=0.52$, roughly 4 mask bits are sufficient. Going to $b=0.56$ already requires more than 11 mask bits. However, even for $b=0.60$ the bias can be brought down close to zero.

6.3 Comparison with the State of the Art

Several previous publications demonstrated that code concatenation or a combination of error reduction and ECC facilitate to achieve key error probabilities of $10^{-6}$ for low implementation complexities [3,4,5,6, 9]. In addition, we have shown in Sect. 6.1 that codes with a high ratio of key bits per codeword bit show more promising masking properties. We therefore follow general experience of previous work and coset coding specific behavior to refrain from providing a stand-alone wiretap coset coding solution and directly combine it with Differential Sequence Coding (DSC) [9].

Fig. 8.

Bounded total information leakage of wiretap coset coding for PUFs with bias b and $\mathrm {RM}(2,6)$. m refers to the initial offset of mask bits.

DSC stores differential pointers $U_i$ that indicate reliable PUF bits X, as shown in Fig. 9. Each reliable PUF bit is mapped to a codeword bit $C_i$ while unreliable PUF response bits are ignored. If the indexed PUF response bit is likely to be equal to its corresponding codeword bit, the inversion bit $V_i$ is set to zero. Otherwise it is set to one. The pointers and the inversion bits are stored as helper data.

Fig. 9.

Helper data generation with differential sequence coding

It was shown in [9] that DSC performs very efficient error reduction for unbiased PUFs. For biased PUFs, two new aspects have to be considered: First, the inversion bits V start to leak secret information, and second the bias even increases if the PUF response is reduced to its more reliable bits. This relation between bias and reliability was discussed in detail in [12].

To mitigate this leakage and derive a reliable key, we combine DSC and coset coding in this work. First, $S^k$ is encoded to $C^n$ by coset encoding, and then $C^n$ is embedded into reliable PUF responses $X^m$ by DSC.

Table 2. Design comparison of a code-offset fuzzy extractor, DSC, IBS, VN debiasing and DSC with wiretap coset coding for an SRAM PUF with $P_{in} = 10\%$ and $b=0.54$, and $P_e \le 10^{-6}$ and 128 bit key length.

Table 2 presents the result of DSC + wiretap RM coset coding (CC) and compares it with previous leakage mitigation approaches. We computed all results in Table 2 for an SRAM PUF with average bit error $P_{in} = 10\%$, i.i.d PUF response bits with bias 0.54 and reliability distribution according to [4, 12]. A key error probability $P_e \le 10^{-6}$ is targeted for 128 bit key length. The error correction relies on two ECC stages. We used repetition codes with parameters $(n_3, k_3, n_3)$ as inner codes for the code-offset fuzzy extractor, VN and IBS. For DSC, the inner repetition code is replaced by DSC with the rate $(n_3, 1)$, denoted by a star. The code-offset fuzzy extractor, and IBS and VN debiasing schemes use BCH codes as outer code with $(n_1, k_1,d_1)$ whereas wiretap coset coding uses RM codes. z refers to the number of BCH or RM codewords that are used to generate the entire key.

First of all, the Fuzzy Extractor and DSC results without debiasing clearly demonstrate that there exists significant leakage, even for the relatively low bias of 0.54. Removing this leakage with the state-of-the-art approaches IBS or VN increases the number of PUF bits from 640 with DSC to 1,778 and 2,471, respectively, which is an increase of over 1,100 PUF response bits or $178\%$.

Our new approach with DSC and wiretap coset coding only requires 704 PUF response bits for a negligible upper bounded total leakage of 0.06. Therefore, the debiasing overhead is reduced by almost $170\%$ from $178\%$ to $10\%$, or roughly 1, 000 PUF bits such that the overall number of PUF response bits is reduced by $60\%$ compared to IBS and VN.

We also provide a more conservative value for a secrecy leakage $\le 0.01$. As already discussed in Sects. 6.1 and 6.2, the efficiency of coset coding decreases as the number of mask bits increases. Removing the last 0.05 bit in the conservative estimate of the secrecy leakage doubles the number of PUF response bits.

7 Conclusion

Biased PUF responses lead to secrecy leakage. We introduce wiretap coset coding to PUFs to mitigate the leakage through the helper data. In contrast to previous work that eliminates the bias at the input, we modify the ECC.

This work applies the wiretap channel model to PUFs to reduce the secrecy leakage with coset coding. The typical one-to-one mapping between information and codeword is changed to a one-to-many mapping so that all secrets show a similar probability again for a given helper data candidate.

The exact secrecy leakage can be computed for short codes while bounds also provide leakage results for longer codes. Our design for a practical scenario reduces the overall number of required PUF response bits by roughly 1, 000 or $60\%$ compared to the reference approaches VN and IBS.