Efficient Non-blocking Radix Trees

Abstract

Radix trees belong to the class of trie data structures, used for storing both sets and dictionaries in a way optimized for space and lookup. In this work, we present an efficient non-blocking implementation of radix tree data structure that can be configured for arbitrary alphabet sizes. Our algorithm implements a linearizable set with contains, insert and remove operations and uses single word compare-and-swap (CAS) instruction for synchronization. We extend the idea of marking the child edges instead of nodes to improve the parallel performance of the data structure. Experimental evaluation indicates that our implementation out-performs other known lock-free implementations of trie and binary search tree data structures using CAS by more than 100% under heavy contention.

1 Introduction

A trie is an efficient information retrieval data structure which stores keys with a common prefix under the same sequence of edges, eliminating the need for storing the same prefix each time for each key. Radix trees are space optimized tries in which any node that is the only child is merged with its parent. They are widely used in practical applications like IP address lookup in routing systems [6], memory management in Linux kernel [3] etc.

The search complexity of a radix tree is O(k) where k is the key length. For fixed length key sets like integers, this becomes $O(\log {}U)$ where U is the size of integer universe. In a sequential setting, other balanced tree data structures like AVL or red-black trees offer a better search complexity of $O(\log {}n)$ (where n is the number of keys in the set) as $n < U$. These data structures re-balance the tree after updates to guarantee logarithmic search complexity. In a concurrent scenario, re-balancing the data structure requires complex synchronization as nodes move higher up the tree which can significantly impact the parallel performance of these data structures.

Radix trees do not require re-balancing and still guarantee logarithmic search complexity for integer key sets. For variable length key sets like strings, radix trees have a better search complexity of O(k) compared to AVL and red-black trees whose complexity is $O(k\log {}n)$. The simplicity of the structure and better search complexity makes radix trees good candidates for concurrent applications.

Various constructions for concurrent non-blocking tries exist in the literature. Non-blocking implementations ensure that system-wide progress is guaranteed even in presence of multiple thread failures making them desirable for concurrent applications. Shafiei [10] proposed a non-blocking implementation of Patricia trie data structure using compare-and-swap (CAS) instruction. A Patricia trie is a binary radix tree or a radix tree with radix value equal to 2. They extend the node level marking scheme from Ellen et al. [4] to tries. Each node in their algorithm has a structure linked to it which will be updated with the necessary information required to complete an operation. Any thread that is blocked by an on-going operation reads this structure to help finish the operation thereby achieving non-blocking progress. Even though this approach guarantees non-blocking progress, not more than one thread can simultaneously update a node limiting the parallelism of the structure. This can significantly influence the parallel performance of the structure especially with large number of operating threads.

Prokopec et al. [9] proposed a non-blocking hash trie data structure using CAS instruction. Hash tries are space efficient tries which combine the features of hash tables and tries. Each node in the hash trie maintains an invariant that the length of array containing the child pointers is always equivalent to the number of non-null children in the node. This eliminates sparse child arrays with null values, making them space efficient. The index of the child that needs to be traversed is calculated using a hash function. Non-blocking progress is achieved using the node level marking scheme from Ellen et al. [4] because of which the algorithm does not support simultaneous updates at a node limiting the amount of parallelism in the structure. Repetti et al. [11] proposed a non-blocking radix tree data structure using restricted transactional memory (RTM) extensions. The limited availability of transactional memory extensions in commercial processor architectures restricts the applicability of their algorithm.

In this work, we propose a concurrent non-blocking implementation of a radix tree data structure using single word compare-and-swap (CAS) instruction. Our algorithm can be configured to support arbitrary alphabet sizes and implements a linearizable set with Contains, Insert, and Remove operations. We extend the idea of marking the individual child pointers from Natarajan and Mittal [7] to radix trees. This allows threads to simultaneously update a node which can significantly improve the parallel performance of the structure. To the best of our knowledge, this is the first non-blocking implementation of a radix tree data structure using single word CAS that can be configured for arbitrary alphabet sizes and supports simultaneous updates on a node.

We implemented our algorithm in C++ and compared its performance with other non-blocking tries, binary search tree (BST) and k-ary tree data structures. Experimental results indicate that our algorithm performs better and scales best among other known lock-free algorithms. Due to space constrains, only a brief outline of the correctness proof is presented in this paper and the complete proof is provided elsewhere [12]. In the next few sections, we discuss our algorithm in detail and later present the experimental evaluation of our implementation.

2 Overview

We assume an asynchronous shared memory multiprocessor system that supports atomic compare-and-swap (CAS) instruction along with atomic read and write instructions. A CAS(ptr, old, new) instruction compares the value in memory referenced by ptr to old value and if they are same, then updates the memory referenced by ptr with new value atomically. Duplicate keys are not considered in our model. The size of an alphabet that is used to represent the key (e.g. binary, hexadecimal or ASCII) can be configured at the beginning of algorithm and it remains constant throughout.

Each node in our tree stores the prefix of a key, the size of the prefix in number of symbols and a boolean value to distinguish between leaf and internal nodes. Additionally, internal nodes have an array of child pointers. Leaf nodes store the key with all its symbols i.e. the actual or full key. This means that a key is considered to be present in the tree only if it matches the key in a leaf node.

The Contains(k) validates the presence of key k in the tree and returns true if k is found to be present in a leaf node. Otherwise, it returns false. An Insert(k) operation updates the data structure with a leaf node containing key k only if k is not already present in the tree. It returns false if the target key is found in the tree at the time of traversal. A suitable location for insertion is identified by traversing the tree and a leaf node containing the target key is updated into the tree using a CAS instruction. On a successful CAS, insert operation returns true.

A Remove(k) operation removes key k from the tree only if a leaf node containing k is found to be present in the tree at the time of traversal. Otherwise, remove operation returns false. The leaf node containing k is removed from the tree by updating the memory referenced by the parent pointer to NULL value using CAS instruction. After removing the leaf node, the number of non-null child pointers of the parent node is counted and if it is found to have ‘0’ or ‘1’ non-null child pointers, then the parent node is removed from the tree and remove operation returns true. This ensures that any internal node with zero or one child will always be removed thereby maintaining the space efficiency of radix trees.

If Insert or Remove operations are blocked by an on-going update operation, they will first help finish the on-going update to complete and then restart their operation. Also, if the CAS instruction that is used to update the tree fails because of simultaneous updates by other threads, the corresponding operation is restarted. For simplicity, we assume that the memory allocated to nodes that are not a part of the tree is not reclaimed. This allows us to assume that all the new nodes have unique addresses and ignore the ABA problem.

3 Algorithm

In this section, we present the structures used in our algorithm and the implementation details of Contains, Insert and Remove operations.

3.1 Data Structures

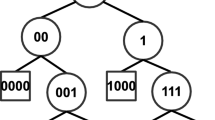
The declarations of various structures used are presented as pseudo-code in Algorithm 1. Our data structure is built using leaf (lNode) and internal (iNode) node objects which are subtypes of Node object. Each node in our data structure contains three fields: label of type KEY to store the prefix, size of type integer to store the size of label in number of symbols and isLeaf of type boolean to distinguish between leaf nodes and internal nodes. The value of isLeaf is set to true for leaf nodes and false for internal nodes. For fixed length key sets like integers, KEY refers to an integer and for variable length key sets like strings, KEY refers to an array of characters. The fields label, isLeaf, and size of a node are immutable i.e. their value will not change after initialization. Each internal node additionally has an array of child pointers with the size of array equivalent to the size of the alphabet (ALPHABET_SIZE) i.e. 16 for a hexadecimal alphabet and 2 for a binary alphabet.

Two bits from each of the child pointers are used to represent the state of an on-going remove operation. On most modern machines, memory is aligned on a 4/8-byte boundary leaving the lower 2/3 bits of the address unused. These bits can be used to store auxiliary information like the state of an operation which can be used by other threads to help complete the operation in case of contention. Two of these bits represented by boolean values flag and freeze are used from each of the child pointers to represent the state of an remove operation.

For a pointer, if the value of freeze bit is set to ‘1’, it means that the node containing the pointer is undergoing removal from the tree and the pointer is considered frozen. Similarly for a pointer, if the value of flag bit is set to ‘1’, it means that the node referred by the pointer is being removed from the tree and the pointer is considered flagged. For the tree shown in Fig. 1c, node B is undergoing removal and therefore, node A’s child pointer has the flag bit set to ‘1’ and all the child pointers of B has the freeze bit set to ‘1’. In the pseudo-code presented, we use the notation $ptr, flag, freeze$ to represent the value of pointer, flag and freeze bits. E.g., $ptr, 1, *$ implies that the value of pointer is ptr, the value of flag bit is ‘1’ and the value of freeze bit can either be ‘0’ or ‘1’.

The SeekRecord structure is used to store the result of tree traversal. It contains 5 members: (i) curr: Last traversed node in the tree (ii) par: Parent node of curr (iii) currIndex: Index of the curr node in the child pointer array of par node (iv) gPar: Grandparent of curr node or parent of par node (v) parIndex: Index of the par node in the child pointer array of gPar node.

The root node always points to the head of the tree. It is initialized as an internal node with an empty label ($\epsilon$) and zero label size. Two leaf nodes lMin and lMax are always assumed to be present in the tree and are never deleted. This ensures that the root node has at least two leaf nodes always present and is never removed from the tree. We use the SizeOf(k) method to count the number of symbols present in key k.

3.2 Search

Search is a helper method used by Contains, Insert and Remove operations to locate the position of a node containing the target key (key) or a target node (node) in the tree. The pseudo-code is presented in Algorithm 2. Starting from the root node, Search method traverses the tree one node at a time by comparing the node’s label with first ‘size’ number of symbols from target key’s prefix. The MatchPrefix method (Line 27) performs this comparison and returns true if there is a match. Otherwise, MatchPrefix method returns false and Search terminates the traversal.

On a successful prefix match, the search proceeds further by traversing through a child pointer located at the index corresponding to the ‘size+1’ symbol in the target key. The GetIndex method (Line 29) computes the index of child pointer that needs to be traversed. It takes the target key and the size of current node’s label as inputs and returns the index corresponding to the symbol at prefix location ‘size+1’ in the target key.

Search method continues with the traversal until a NULL child pointer or a leaf node is encountered i.e. the nodes after which the tree does not exist. Also, if the location of the target node is found, Search method will terminate the traversal. The results of traversal are updated in the record object (Line 31).

3.3 Contains

The pseudo-code for Contains method is presented in Algorithm 2. It uses the results of traversal by Search method to validate the presence of a key in the tree. If the last traversed node (i.e. curr) is either NULL or an internal node, then Contains method returns false as all valid keys are stored in the leaf nodes of the tree. Otherwise, it returns the result of comparison between curr node’s label and target key (Line 36).

3.4 Remove

The pseudo-code for Remove operation is presented in Algorithm 3. It first validates the presence of a key using the Contains method (Line 39) and returns false if the key is not found to be present in the tree. Otherwise, it tries to remove the leaf node containing the target key from the tree using CAS (Line 46) by updating memory referenced by the parent pointer to NULL value. If this CAS fails due to simultaneous updates on the node, Remove operation is restarted to locate the new position of the node containing target key.

Fig. 1.

Removal of internal node and simultaneous insertion

On a successful CAS, the MakeConsistent method is called to count the number of non-null child pointers of par node and remove it from the tree if it has less than two non-null child pointers. This ensures that any internal node with zero or one child will always be removed thereby maintaining the space efficiency of radix trees. The pseudo-code for MakeConsistent method is presented in Algorithm 4.

Removal of an internal node begins by updating the flag bit of the parent pointer to ‘1’ using CAS (Line 70). Note that, the flag bit is set to ‘1’ only for pointers referring to internal nodes and pointers referring to leaf nodes will never be flagged. Also, we maintain an invariant that both the flag and freeze bits of a pointer can not have the value ‘1’ at the same time. This means that, if the parent pointer of curr node is flagged, the node containing parent pointer i.e. par node can not be removed from the tree until the flag bit is cleared which can happen only during the successful removal of curr node from the tree.

After successfully flagging the parent pointer, the HelpFreeze method is called (Line 71) to set the freeze bit of all the child pointers to ‘1’ using CAS. Once the freeze bit of a pointer is set to ‘1’, it can not be undone. This prevents any further insertions at the internal node and therefore the node can safely be removed from the tree. HelpFreeze returns only after all the child pointers have the freeze bit set to ‘1’. This means that once a thread decides to freeze the node, by calling HelpFreeze method it can not be undone. When freezing the child pointers, if any of the pointer is observed to have the flag bit set to ‘1’, then HelpFreeze helps the removal of the node referred by child pointer and then attempts to set the freeze bit again. Freezing the child pointers begins only after flagging the parent. This means that if a child pointer has freeze bit set to ‘1’, then it’s parent is already flagged.

The RemoveNode method presented in Algorithm 6 removes an internal node from the tree. It updates the parent pointer to point to the new child or to a NULL value if all the child pointers are NULL. A particularly tricky case can arise when removing an internal node from the tree which is illustrated in Fig. 1. Thread T1 finds the leaf node of interest i.e. node C and removes it from the tree. As node B has only one non-null child, T1 decides to freeze the child pointers of node B. Simultaneously, thread T2 successfully inserts new leaf node D as child of B. After freezing all the child pointers, node B contains more than one non-null child pointer and therefore should not be removed from the tree.

This scenario is taken care by checking the non-null pointer values after freezing the child array. If more than one non-null pointer value exists, then a new internal node is created and all the child pointer values are copied to the new internal node (Lines 102–105). Otherwise, the parent pointer is updated to point to the only leaf node or to a NULL value (if all the pointer values in child array are NULL) using CAS (Line 106). The MakeConsistent method repeats this process recursively until an internal node with more than one non-null child pointer is encountered and only then the Remove operation returns true.

When flagging the parent pointer, the CAS (Line 70) can succeed only if the parent pointer is not frozen for deletion and it refers to the node of interest (i.e. curr node). If the parent pointer is frozen, MakeConsistent will first remove the parent node from the tree (Lines 61–69) and then tries to remove the node of interest. If the information about parent node is not available, then its location is identified by traversing down the tree using Search method. Similarly, when removing the leaf node from the tree, if the parent pointer is frozen for deletion, the remove operation will first help removal of the parent node from the tree before trying to remove the leaf node of interest.

3.5 Insert

The pseudo code for Insert method is presented in Algorithm 7. An Insert(k) operation updates the tree with a node containing key k only if it is not already present in the tree. The presence of a key is validated using the Contains method (Line 109) and Insert operation returns false if target key is found to be present in the tree. Otherwise, it creates a new node(s) and adds them to the tree using CAS (Line 128). The location for insertion is obtained from the record structure which is updated with the result of traversal during Contains operation.

If the traversal has terminated at a null child, a new leaf node is created with the label as target key (Line 113). If the traversal has terminated at a non-null child, then it implies that there exists a prefix mismatch between the label of last traversed node and the target key. In this case, two nodes are created: an internal node containing the largest common prefix between the target key and the last traversed node, a leaf node containing the target key (Lines 117–121). The GetCommonPrefix method (Line 115) computes the largest common prefix between the node’s label and target key. The child pointers of the newly created internal node are updated to point to the curr node and new leaf node (Line 121).

CAS at line 128 adds the newly created node(s) into the tree. A successful CAS implies that the node with target key is now reachable from the root node and therefore Insert method returns true. CAS (Line 128) can succeed only if the parent pointer is not flagged or frozen for deletion. If the parent pointer is already flagged or frozen, then Insert will help the corresponding remove operation before trying to update the node(s). The status of the parent pointer is retrieved from the result of traversal (Line 111).

The status flagged implies that the curr node is undergoing removal and status frozen implies that the par node undergoing removal. In both the cases, Insert method will help the removal of the corresponding node by freezing all its child pointers and later removing it from the tree. After the removal, Insert restarts its operation to locate the new position for insertion. If the CAS at line 128 fails due to a simultaneous insertion at the same location by another thread, Insert will restart the operation to locate the new position of target key in the tree.

4 Correctness

In this section, we define the linearization points for each of Contains, Insert and Remove operations and prove the non-blocking nature of our implementation. Due to space constraints, we only provide a brief sketch of proof and the complete proof is presented in [12].

4.1 Linearizability

The Contains operation has two possible outcomes, either the key is present in tree or not. For a successful Contains, if the leaf node returned by the Search method is still a part of the tree, then its linearization point is defined to be the point at which the Search method terminates the traversal. Otherwise, its linearization point is defined to be the point just before the leaf node is removed from the tree. For an unsuccessful Contains, the linearization point is the point at which the Search method terminates the traversal.

The linearization point of an successful Insert operation is defined to be the point at which it performs CAS instruction (Line 128) successfully. For an unsuccessful Insert, the linearization point is same as that of a successful Contains where the target key is already found to be present in the tree. The linearization point of Remove operation is defined to be the point at which the CAS instruction successfully removes the leaf node containing target key from the tree (Line 46). For an unsuccessful Remove, the linearization point is same as that of an unsuccessful Contains, where the target key is not found in the tree. It can be proved that, when the operations are ordered according to their linearization points, then the resulting sequence of operations is legal.

4.2 Non-blocking Progress

The non-blocking property of our algorithm is proved by describing various interactions between reading and writing threads. If the system reaches a state in which no update operation completes, then a non-faulty thread performing Contains will always return as the tree does not undergo any structural changes.

A non-faulty thread trying to modify the tree can remain blocked in two scenarios: (i) An infinite number of insert operations succeed adding new nodes to the tree. This means that other threads are able to make progress by adding new nodes (i.e. achieving system-wide progress) making the implementation non-blocking (ii) The state of the pointer is not normal i.e. either the flag or freeze bit is set to ‘1’. It is easy to observe from the Insert and Remove methods that, during update if a thread encounters a pointer whose flag or freeze bit is set to ‘1’, it first helps the removal of the corresponding node and then restarts its operation only after the node is removed from the tree. This ensures that next time the thread is traversing the tree, the node containing the pointer is no longer present in the tree.

If all the pointers in the thread’s path have then flag or freeze bits set to ‘1’, then Insert or Remove methods will help the removal of all the corresponding nodes. As root node is never removed from the tree, the operation will eventually complete unless other threads update the tree. In either cases, at least one thread makes a progress with its operation making the implementation non-blocking.

5 Experimental Evaluation

For our experiments, we considered four different alphabet sizes: binary (2-RT), quaternary (4-RT), octal (8-RT) and hexadecimal (16-RT). The source code of our implementation is available at [12]. We compared the results of our implementation with three other implementations: (i) PatTrie: Patricia trie from Shafiei [10] (ii) NBBST: Non-blocking binary search tree from Natarajan and Mittal [7] (iii) K4AryTree: Non-blocking k-ary free from Brown and Helga [2] with k = 4. The source code for NBBST is taken from syncrobench [5] test suite, for PatTrie the Java version of the source code is taken from the author and ported to C++. For K4AryTree, the Java version of the source code is taken from [1] and was ported to C++.

Fig. 2.

Experimental results for different workloads

The experiments were conducted on a machine equipped with Ubuntu 14.04 OS, 64 GB RAM and two Intel Xeon E5-2680 v2 processors each clocked at 2.80 GHz with 32 KB L1D cache per core and 2.5 MB LLC. Each processor has 10 physical cores with hyperthreading enabled yielding 40 logical cores in total. Hyperthreading is enabled prior to a simulation run and thread binding to cores is disabled to facilitate context switching. All our implementations are written in C/C++ and compiled using g++ 4.8.4 with optimization level set to O3. Random integers were considered for keys which were generated using a Mersenne twister generator from the C++11 random library on 32-bit word length.

Each experiment was run for fifty seconds, and the total number of operations completed by end of the run were calculated to determine the system throughput. The results were averaged over five runs. To capture the steady state behavior, the tree is pre-populated with 50% of its maximum size prior to starting a simulation run. The cache performance of the data structure is analyzed using cachegrind from Valgrind [8] toolchain. To compare the performance of different implementations, we considered four different key ranges from one thousand to one million and the number of threads was varied from 1 to 256. Three different workloads i.e. write-dominated (0% contains, 50% inserts and 50% removes), mixed (70% contains, 20% inserts and 10% removes) and read-dominated (90% contains, 5% inserts and 5% removes) were considered.

Table 1. Comparison of D1 cache miss percentage

The results of our experiments are presented in Fig. 2. Table 1 presents the comparison of cache performance for a mixed workload with 32 threads. From the graphs, it is clear that our algorithm has better throughput (by more than 100% in some scenarios) compared to other implementations. This is because our algorithm supports simultaneous updates on a node and has better cache performance compared to other implementations (Table 1). For smaller key ranges in all the workloads, the performance of 4-RT is better compared to 8-RT and 16-RT as nodes in 8-RT and 16-RT were spread across multiple cache lines resulting in higher cache miss percentage. For the 2-RT implementation, the number of pointer accesses were relatively high which contributed to higher cache miss percentage and slowdown in performance. For larger key ranges, 16-RT performed better as the impact of contention is reduced which resulted in less cache miss percentage and the number of pointer accesses required to traverse the leaf node are also reduced because of high branching factor.

Table 2. CAS instructions

In write dominated workload, for smaller key ranges, it can be see than NBBST performs slightly better compared to the 2-RT implementation as they use fewer atomic CAS instructions (Table 2) for synchronization compared to our implementation. However, for larger key ranges, the maximum height of the tree was observed to be twice more than log N (N being the maximum key range) which resulted in more pointer accesses and slowed down the implementation. High synchronization cost and serialization of update operations in PatTrie and K4AryTree resulted in slowness of their implementation. Also, the cache miss percentage of K4AryTree was observed to be relatively high. This is because, in their algorithm, during insert operations each k-ary node is replaced with a new k-ary node. Similar behavior is also observed in remove operations in some cases. Therefore, even though the nodes individually support good cache locality, updating the nodes resulted in higher cache miss percentage. This is not the case in our implementation as we update only the child pointers in most of the scenarios.

6 Conclusion

We presented a concurrent, non-blocking and linearizable design for radix tree data structure. We implemented it using C++ and measured its performance against Shafiei [10] Patricia trie, BST from Natarajan and Mittal [7] and k-ary search tree from Brown and Helga [2]. Experimental results indicated that our implementation performs better and scales best for small and large key ranges under all types of workloads. The cache performance of our implementation was also analyzed and the D1 cache miss percentage is observed to be less compared to other implementations which contributed to the better performance of our algorithm.