Abstract
Correlated private randomness, or correlation in short, is a fundamental cryptographic resource that helps parties compute securely over their private data. An offline preprocessing step, which is independent of the eventual secure computation, generates correlated secret shares for the parties and the parties use these shares during the final secure computation step. However, these secret shares are vulnerable to leakage attacks.
Inspired by the quintessential problem of privacy amplification, Ishai, Kushilevitz, Ostrovsky, and Sahai (FOCS 2009) introduced the concept of correlation extractors. Correlation extractors are interactive protocols that take leaky correlations as input and produce secure independent copies of oblivious transfer (OT), the building blocks of secure computation protocols. Although their initial feasibility result is resilient to linear leakage and produces a linear number of “fresh” OTs, the constants involved are minuscule. The output of this correlation extractor can be used to perform only small secure computation tasks, because the number of OTs needed to evaluate a functionality securely is roughly proportional to its circuit size. Recently, Gupta, Ishai, Maji, and Sahai (CRYPTO 2015) constructed an extractor that is resilient to 1/4 fractional leakage and has near-linear production rate. They also constructed an extractor from a large correlation that has 1/2 fractional resilience but produces only one OT, which does not suffice to compute even constant size functionalities securely.
In this paper, we show the existence of a correlation that produces n-bit shares for the parties and allows the extraction of \(n^{1-o(1)}\) secure OTs, despite n/2 bits of leakage. The key technical idea is to embed several multiplications over a field into one multiplication over an extension field. The packing efficiency of this embedding directly translates into the production rate of our correlation extractor. Our work establishes a connection between this problem and a rich vein of research in additive combinatorics on constructing dense sets of integers that are free of arithmetic progressions, a.k.a. 3-free sets. We introduce a new combinatorial problem that suffices for our multiplication embedding, and produces concrete embeddings that beat the efficiency of the embeddings inspired by the reduction to 3-free sets.
Finally, the paper introduces a graph-theoretic measure to upper-bound the leakage resilience of correlations, namely the simple partition number. This measure is similar in spirit to graph covering problems like the biclique partition number. If the simple partition number of a correlation is \(2^\lambda \), then it is impossible to extract even one OT if parties can perform \(\lambda \)-bits of leakage. We compute tight estimates of the simple partition number of several correlations that are relevant to this paper, and, in particular, show that our extractor and the extractor for the large correlation by Gupta et al. have optimal leakage resilience and (qualitatively) optimal simulation error.
A.R. Block, H.K. Maji and H.H. Nguyen—The research effort is supported in part by an NSF CRII Award CNS–1566499, an NSF SMALL Award CNS–1618822, and an REU CNS–1724673.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Secure multi-party computation [22, 71] helps mutually distrusting parties to compute securely over their private data. Unfortunately, it is impossible to securely compute most functionalities in the information-theoretic plain model even against parties who honestly follow the protocol but are curious to find additional information about the other parties’ private input [2, 19, 32, 38, 41,42,43]. However, we can securely compute any functionality if honest parties are in the majority [5, 12, 16, 56], parties use some trusted setup [10, 11, 17, 23, 35, 37, 49] or correlated private randomness [15, 39, 44, 68], or there are bounds on the computational power of the parties [22, 35].
The study of secure computation using correlated private randomness, primarily initiated due to efficiency concerns, has produced several success stories, for example FairPlay [4, 45], TinyOT [50] and SPDZ [18] (pronounced Speedz). These secure computation protocols offload most of the computational and cryptographic complexity to an offline preprocessing phase. During this preprocessing phase, a trusted dealer samples two shares \((r_A,r_B)\) from the joint distribution \((R_A,R_B)\), namely the correlated private randomness, or correlation in short, and provides the secret shares \(r_A\) to Alice and \(r_B\) to Bob. During the online secure computation phase, parties use their respective secret shares in an interactive protocol to securely compute the intended functionality. Note that the preprocessing phase is independent of the functionality or the inputs fed to the functionality by the parties.
A prominent and extremely well-studied correlation is the random oblivious transfer correlation, represented by \( \mathsf {ROT} \). It samples three bits \(x_0,x_1,b\) independently and uniformly at random, and provides the secret shares \((x_0,x_1)\) to Alice and \((b,x_b)\) to Bob. Note that Alice does not know the choice bit b, and Bob does not know the other bit \(x_{\overline{b}}\). Intuitively, \( \mathsf {ROT} \) is an input-less functionality that implements a randomized version of oblivious transfer functionality, where the sender sends \((x_0,x_1)\) as input to the functionality and the receiver picks \(x_b\) out of the two input bits. Given m independent samples from this distribution, parties can securely compute any functionality with circuit complexity (roughly) m. For example, we can utilize the randomized self-reducibility of oblivious transfer to reimagine the GMW protocol [22] in this framework naturally.
However, the storage of the secret shares by the parties brings to fore several vulnerabilities. For instance, parties can leak additional information from the secret shares of the other parties. We emphasize that the leakage need not necessarily reveal individual bits of the other party’s share. The leakage can be on the entire share and encode crucial global information that can potentially jeopardize the security of the secure computation protocol.
To address these concerns, Ishai, Kushilevitz, Ostrovsky, and Sahai [33] introduced the notion of correlation extractors. Correlation extractors distill leaky correlations into independent samples of the \( \mathsf {ROT} \) correlation that are secure. That is, for each of the new samples Alice does not know Bob’s choice bit and Bob does not know Alice’s other bit. This problem is a direct analog of the quintessential problems of privacy amplification and randomness extraction problems in the secure computation setting. With the exception that, correlation extractors ensure security against insider attacks, i.e., the parties who perform the leakage are participants in the secure protocol itself. This additional requirement makes the task of correlation extraction significantly more challenging. It is, thus, not surprising that relatively few results are known in the field of correlation extractor construction.
For example, in the setting of privacy amplification, if Alice and Bob start with a secret n-bit random string then, in the presence of t-bits of arbitrary leakage to an eavesdropper, parties can re-establish a fresh m-bit secret key such that the advantage of the eavesdropper in guessing the secret key is roughly \(2^{-\varDelta } \approx 2^{-(n-t-m)}\). Intuitively, the sum of “entropy deficiency” (t), “entropy of production” (m), and “\(-\log \) of the adversarial advantage” (\(\varDelta \)) is roughly n, the initial entropy of the secret. Analogous results also exist in the setting of randomness extraction, where we can extract nearly all of the min-entropy of a source. But similar tight extraction results are not known for correlation extractors. In fact, the task of designing correlations that simultaneously support high leakage resilience and production rate with exponential security has been elusive.
A qualitative summary of prior relevant works in correlation extractors and a comparison to our correlation extractor construction. All correlations have been normalized so that each party gets an n-bit secret share. The positive constants \(\alpha ,\beta ,\) and \(\gamma \) are minuscule. And \(g<1/2\) is an arbitrary positive constant.
The number of the output \( \mathsf {ROT} \) samples and their high security are crucial for the secure computation protocol. For example, protocols with exponential security can reduce the \( \mathsf {ROT} \) production or increase the statistical security parameter only slightly to prohibitively increase the effort needed by adversaries to break them. Furthermore, the number of these \( \mathsf {ROT} \) samples limit the size of the eventual functionality that can be securely computed, because the number of \( \mathsf {ROT} \) samples needed to implement a functionality securely is directly proportional to its circuit size. As highlighted in [26], the initial feasibility result of Ishai et al. [33], though asymptotically linear in leakage resilience and production rate, has unsatisfactorily low resilience and production rate for realistic values of n, the size of the original share of the parties. The subsequent work of Gupta et al. [26], improves the resilience to (roughly) n/4 but trades-off the security of the protocol for high production rate and, consequently, achieves only negligible (and, not exponentially low) insecurity. They also consider a new correlation, namely the inner-product correlation where the secret shares of the parties are random n-bit binary vectors subject to the constraint that they are orthogonal to each other.Footnote 1 They construct a correlation extractor for the inner-product correlation with resilience n/2 and exponential security. However, it is inherently limited to producing one \( \mathsf {ROT} \) sample as output, which is not adequate for the end goal of performing interesting secure computations. Our work shows that the inner-product correlation over an appropriately large field admits a correlation extractor that is resilient to n/2 bits of leakage, has high concrete production rate, and has exponentially high security. Figure 1 summarizes the entire preceding discussion tersely. Finally, similar to Gupta et al. [26], although our construction is stated in the information-theoretic setting, it is also relevant to the setting where computationally secure protocol generate the correlations or use the output \( \mathsf {OT} \)s.
However, is the upper-bound of n/2 resilience inherent to the inner-product correlation? For example, n/2 samples of the \( \mathsf {ROT} \) correlation cannot be resilient to more than n/4 bits of leakage. A partition argument can demonstrate this upper bound of the maximum resilience of this correlation [34]. In this partition argument, Alice emulates the generation of n/4 (i.e., half of n/2) independent samples \((x_0,x_1)\) and \((c,x_c)\) from the \( \mathsf {ROT} \) correlation and sends the corresponding \((c,x_c)\) to Bob. Moreover, Bob emulates the generation of the remaining n/4 samples and sends the corresponding \((x_0,x_1)\) shares to Alice. Finally, we reimagine any correlation extractor that is resilient to n/4 bits of leakage and produces even one secure \( \mathsf {ROT} \) sample as a secure \( \mathsf {ROT} \) protocol in the plain model where Alice implements n/4 \( \mathsf {ROT} \) samples, and Bob implements the remaining n/4 \( \mathsf {ROT} \) samples; which is impossible. Typically, the partition argument applies to “multiple independent samples of small correlations,” but its extension to one huge global correlation is not apparent.
To address this question, we introduce a new graph-theoretic measure for the maximum resilience of a correlation, namely its simple partition number. In particular, a correlation with simple partition number \(\leqslant \)2\(^\lambda \) cannot be resilient to \(\lambda \) bits of leakage (refer to Fig. 2 for a summary of these estimates). Finally, we prove the optimality of the resilience demonstrated by the correlation extractors for the inner-product correlation presented in [26] and our work. Refer to Sect. 5.7 for a discussion on how the relation between simple partition number and maximum resilience is similar to the connection between biclique partition number and Wyner’s common information [69]. The existence of correlation extractors for a slightly lesser amount of leakage implies the tightness of our upper bounds on leakage resilience. Finally, we leverage the simple partition number bounds and use an averaging argument to show that the decay in simulation security with entropy gap as achieved by [26] and our correlation extractor are qualitatively optimal.
1.1 Model
This section presents the standard model of Ishai et al. [33] for correlation extractors, which subsequent works also use. We consider 2-party semi-honest secure computation in the preprocessing model. In the preprocessing step, a trusted dealer draws a sample \((r_A,r_B)\) from the joint distribution \((R_A,R_B)\). The joint distribution \((R_A,R_B)\) is referred to as the correlated private randomness, and \(r_A\) and \(r_B\), respectively, are the secret shares of Alice and Bob. The dealer provides the secret share \(r_A\) to Alice and \(r_B\) to Bob. An adversarial party can perform arbitrary t-bits of leakage on the secret share of the other party at the end of the preprocessing step. We represent this leaky correlation hybrid as \(\left( {R_A,R_B}\right) ^{[t]} \).Footnote 2
In the leaky correlation \(\left( {R_A,R_B}\right) ^{[t]} \) hybrid, during the secure computation phase, parties perform an interactive protocol to realize their target functionality securely. No leakage occurs during the execution of the secure computation protocol. In this work, we consider the functionality that implements m independent oblivious transfers between the parties, referred to as the \( \mathsf {OT} ^{m} \) functionality.
Definition 1
(Correlation Extractor). Let \((R_A,R_B)\) be a correlated private randomness such that the secret share size of each party is n-bits. An \((n,m,t,\varepsilon )\) -correlation extractor for \((R_A,R_B)\) is a two-party interactive protocol in the \(\left( {R_A,R_B}\right) ^{[t]}\) hybrid that securely implements the \(\mathsf {OT} ^m\) functionality against information-theoretic semi-honest adversaries with \(\varepsilon \)-simulation error.
1.2 Our Contribution
Our work makes a two-fold contribution regarding correlation extractors. First, we construct a highly resilient correlation extractor that produces a large number of secure OTs as output and has exponential security. Finally, we provide a general graph-theoretic measure that upper bounds the maximal resilience of any correlation.
Correlation Extraction Construction. For any field \(({\mathbb F},+,\cdot )\), the inner-product correlation over \({\mathbb F} ^{n+1}\), represented by \( \mathsf {IP} \,\left( {{\mathbb F} ^{n+1}}\right) \), is a correlation that samples random \(r_A=(x_0,x_1,\cdots ,x_n)\in {\mathbb F} ^{n+1}\) and \(r_B=(y_0,y_1,\cdots ,y_n)\in {\mathbb F} ^{n+1}\) such that \(x_0 + y_0 = \sum _{i=1}^n x_iy_i\). That is, \(x_0\) and \(y_0\) are the additive secret shares of the inner product of  and
and  . Gupta et al. [26] consider a special case of the inner-product correlation, where \({\mathbb F} ={\mathbb G} {\mathbb F} \left[ 2\right] \). Note that each party receives \((n+1)\) field elements as its secret share. In particular, if \({\mathbb F} ={\mathbb G} {\mathbb F} \left[ 2^a\right] \), then each party gets an \(a(n+1)\)-bit secret share.
. Gupta et al. [26] consider a special case of the inner-product correlation, where \({\mathbb F} ={\mathbb G} {\mathbb F} \left[ 2\right] \). Note that each party receives \((n+1)\) field elements as its secret share. In particular, if \({\mathbb F} ={\mathbb G} {\mathbb F} \left[ 2^a\right] \), then each party gets an \(a(n+1)\)-bit secret share.
Theorem 1
(High Resilience High Production Correlation Extractor). For all constants \(0<\delta<g<1/2\), there exists a correlation \((R_A,R_B)\), where each party gets n-bit secret share, such that there exists a two-round \((n,m,t,\varepsilon )\)-correlation extractor for \((R_A,R_B)\), where \(m=(\delta n)^{1-o(1)}\), \(t=(\nicefrac 12-g)n\), and \(\varepsilon =2^{-(g-\delta )n/2}\).
We use \((R_A,R_B)= \mathsf {IP} \,\left( {{\mathbb G} {\mathbb F} \left[ 2^{\delta n}\right] ^{1/\delta }}\right) \) in this theorem. Note that we maintain the dependence on \(\delta \) explicitly in the theorem statement to enable computation of concrete efficiency. As we shall see later, this theorem achieves high production rate of \((\delta n)^{\log 10/\log 38} \approx (\delta n)^{0.633}\) even for realistic values of n. The simulation error is exponentially low in the difference between the entropy gap gn and the parameter \(\delta n\). Our construction achieves \((\delta n)^{1-o(1)}\) production asymptotically, which is close to the ideal target of \(\delta n\) production. Qualitatively, the decay in our simulation error is near optimal as demonstrated by Theorem 2 and Corollary 1.
The crux of our construction is the composition of two technical contributions. First, we observe that the correlation extractor for \( \mathsf {IP} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] ^n}\right) \) constructed by Gupta et al. [26] extends to the \( \mathsf {IP} \,\left( {{\mathbb F} ^{1/\delta }}\right) \) correlation, where \({\mathbb F} \) is a large field. However, in this case, instead of producing a secure \( \mathsf {OT} \), it produces a generalization of oblivious transfer, namely oblivious linear-function evaluation over \({\mathbb F}\) [68] (represented as \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) \)). An oblivious linear-function evaluation is a 2-party functionality that takes \((A,B)\in {\mathbb F} ^2\) as input from Alice and \(X\in {\mathbb F} \) as input from Bob, and provides \(Z=AX+B\) as output to Bob. Note that oblivious transfer is equivalent to oblivious linear-function evaluation over \({\mathbb G} {\mathbb F} \left[ 2\right] \), because \(x_b = (x_1-x_0)b + x_0\), for \(x_0,x_1,b\in {\mathbb G} {\mathbb F} \left[ 2\right] \).
Finally, we embed m \( \mathsf {OT} \) evaluations simultaneously into one \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) \) evaluation. Note that, this is not an asymptotic reduction. Asymptotically, there are several techniques to construct multiple copies of \( \mathsf {OT} \) using multiple copies of \( \mathsf {OLE} \) at a good rate. Our focus is on securely implementing multiple \( \mathsf {OT} \) evaluations from only one \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) \) evaluation. Development of more efficient embeddings will directly improve the production rate of our construction. We demonstrate that dense sets of integers that avoid any arithmetic progressions, 3-free sets, provide such embedding of multiplications. We formulate a relaxed version of this combinatorial problem (see Fig. 5) that suffices for our embedding problem and obtain more efficient embeddings than those that are inspired by the 3-free set constructions.
We emphasize that although we state our correlation extractor for the bounded leakage model, i.e. an adversary can perform at most t-bits of leakage, it also extends to the noisy leakage setting. As long as the noise is high enough to maintain \((n-t)\) bits of (average) min-entropy in the secret share of the parties, our extractor construction remains secure.
Bound on the Maximum Resilience. The construction of Theorem 1 and the correlation extractor of Gupta et al. [26], with fractional resilience 1/2, lead naturally to a fascinating question. Can there exist a correlation extractor for \( \mathsf {IP} \,\left( {{\mathbb F} ^n}\right) \) that achieves over 1/2 fractional resilience? In fact, more generally, can we meaningfully upper-bound the maximum leakage resilience of an arbitrary correlation?
Note that if parties obtain multiple independent samples from identical correlations, then the partition argument can be leveraged to deduce an upper bound. For example, either Alice or Bob by getting adequate information on half of the other party’s secret shares can break the security of the correlation extractor protocol. As discussed earlier, this argument implies that the correlation \( \mathsf {ROT} ^{n/2} \) is not resilient to \(\left\lceil {n/4}\right\rceil \) bits of leakage, because every \( \mathsf {ROT} \) hides only one bit of information from each party [34]. However, this approach does not apply to correlation extractors for secret shares drawn from one large correlation, for example, \( \mathsf {IP} \,\left( {{\mathbb F} ^n}\right) \). We prove the following main result.
Theorem 2
(Hardness of Correlation Extraction). Let \(({\mathbb F},+,\cdot )\) be an arbitrary field. There exists a universal constant \(\varepsilon ^*>0\) such that, for \((R_A,R_B)= \mathsf {IP} \,\left( {{\mathbb F} ^k}\right) \), any \((n,1,(n/k)\left\lceil {(k+1)/2}\right\rceil ,\varepsilon )\)-correlation extractor for \((R_A,R_B)\) has \(\varepsilon \geqslant \varepsilon ^*\), where \(n=k\log \left| {{\mathbb F}}\right| \).
This result proves the optimality of the leakage resilience achieved by our extractor in Theorem 1 and the correlation extractor for \( \mathsf {IP} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] ^n}\right) \) proposed by Gupta et al. [26]. In fact, a more general version of this result (using averaging arguments) shows that any \((n,1,n/2-gn,\varepsilon )\)-correlation extractor for \( \mathsf {IP} \,\left( {{\mathbb F} ^k}\right) \) has \(\varepsilon \geqslant \varepsilon ^*2^{-gn}\) (see Corollary 1). This result proves the qualitative optimality of simulation error achieved by these two correlation extractors.
The technical heart of this result is a new graph-theoretic measure for maximum leakage resilience in correlations, namely simple partition number (see Definition 4 in Sect. 2). Theorem 2 is a consequence of precise estimation of this quantity for the \( \mathsf {IP} \,\left( {{\mathbb F} ^n}\right) \) correlation. This quantity is similar in spirit to the biclique partition number of a graph [24, 25], the minimum number of bicliques needed to partition the edges of a graph. Moreover, the connection of simple partition number to maximum resilience is intuitively analogous to the link between biclique partition number and Wyner’s common information [69]. Section 5.7 provides details on this connection.
1.3 Prior Relevant Works
This work lies at the intersection of several fields like correlation extractors, additive combinatorics, graph covering problems, and information theory. In this section, we provide only a summary of the work on combiners and extractors. The prior relevant works related to the remaining topics are covered in appropriate sections later.
Combiners and Extractors. A closely related concept is the notion of OT combiners, which are a restricted variant of OT extractors in which the leakage is limited to local information about individual OT correlations, and there is no global leakage. The study of OT combiners was initiated by Harnik et al. [28]. Since then, there has been work on several variants and extensions of OT combiners [27, 35, 47, 48, 55]. Recently, Ishai et al. [34] constructed OT combiners with nearly optimal leakage parameters. However, combiners consider a restricted variant of leakage where the leakage function leaks only individual bits of the secret shares.
To address general leakage, Ishai, Kushilevitz, Ostrovsky, and Sahai [33], proposed the notion of correlation extractors. Their construction has a linear leakage resilience, production rate, and exponential security. However, as indicated by Gupta et al. [26], all the constants involved are minuscule. To address this concern, they [26] construct correlation extractor for \( \mathsf {ROT} ^{n/2} \) that has optimal leakage resilience with only a negligible (not exponentially-low) simulation error. They also provide a correlation extractor construction from a large correlation that exhibits 1/2 leakage resilience but outputs only one \( \mathsf {OT} \). Our work will achieve (roughly) the best of both these constructions, i.e., fractional resilience 1/2, (near) linear production rate, and exponential security.
1.4 Technical Overview
In this section we present a brief overview of our correlation extractor construction and the graph-theoretic measure of the maximum resilience of an arbitrary correlation.
Correlation Extractor Construction. Suppose we are given \(0<\delta<g<1/2\), and parties are in the \( \mathsf {IP} \,\left( {{\mathbb K} ^{1/\delta }}\right) ^{[t]}\)-hybrid, where \(t = (1/2-g)n\) and \({\mathbb K} ={\mathbb G} {\mathbb F} \left[ 2^{\delta n}\right] \). For \(m=(\delta n)^{1-o(1)}\), we want to implement the \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) ^m\) functionality. Figure 4 presents the outline of our correlation extractor construction. The extraction protocol \(\pi \) is similar to the correlation extractor of Gupta et al. [26]. Except that, in their case the inner-product correlation was over \({\mathbb G} {\mathbb F} \left[ 2\right] \) instead of a large field \({\mathbb K} \). The security of the protocol is argued in Sect. 3. Our correlation extractor securely computes a sample from the \( \mathsf {ROLE} \,\left( {{\mathbb K}}\right) \) correlation. The protocol \(\rho \) is the standard protocol that implements the \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) functionality in the \( \mathsf {ROLE} \,\left( {{\mathbb K}}\right) \)-hybrid with perfect security. So, all that remains is to simultaneously embed \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) ^m\) into one \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \). This embedding relies on finding solutions to a combinatorial problem that is summarized in Fig. 5. Section 4 outlines the technique of choosing the inputs to the \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) functionality so that the parties can implement the \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) ^m\) functionality with perfect security.
Hardness of Computation Result. The starting point of this result is the observation that we know the exact characterization of the correlations which do not suffice to construct \( \mathsf {OT} \) asymptotically [2, 32, 38, 41,42,43], namely simple correlations. Constructing one \( \mathsf {OT} \) given a single sample from a simple correlation is even more restrictive, and, hence, the hardness of computation result carries over.Footnote 3 This result holds true even when there is no leakage on \((R_A,R_B)\). In fact, there exists a universal constant \(\varepsilon ^*>0\) such that any \( \mathsf {OT} \) protocol using any simple correlation has simulation error at least \(\varepsilon ^*\).
Intuitively, the simple partition number of a correlation \((R_A,R_B)\), represented by \(\mathsf {sp} \,\left( R_A,R_B\right) \), is the minimum \(\Lambda \) such that \((R_A,R_B)\) can be “decomposed into a union of” \(\Lambda \) simple correlations. Section 5 formalizes this notion of decomposition. Next, we prove in Lemma 4 that for any correlation \((R_A,R_B)\), in the presence of \(t=\log \mathsf {sp} \,\left( R_A,R_B\right) \) bits of leakage, any protocol \(\pi \) for \( \mathsf {OT} \) has simulation error at least \(\varepsilon ^*\). Using this result, we translate tight upper bounds on the simple partition number of relevant correlations into corresponding meaningful upper bounds on their maximum resilience. Figure 2 summarizes our results. We construct a smoother version of this technical lemma using averaging arguments, see Corollary 1. For example, if the leakage bound \(t\geqslant \left( \log \mathsf {sp} (G)\right) -gn\), then any \((n,1,t,\varepsilon )\)-correlation extractor for \((R_A,R_B)\) has \(\varepsilon \geqslant \varepsilon ^* \cdot 2^{-gn}\).
2 Preliminaries
We represent the set \(\{1,\cdots ,n\}\) by [n]. For a vector \((x_1,\cdots ,x_n)\) and \(S=\{i_1,\cdots ,i_{\left| {S}\right| }\}\subseteq [n]\), the set \(x_S\) represents \((x_{i_1},\cdots ,x_{i_{\left| {S}\right| }})\). In this work we work with fields \({\mathbb F} = {\mathbb G} {\mathbb F} \left[ p^a\right] \), where p is a prime and a is a positive integer. An extension field \({\mathbb K}\) of \({\mathbb F}\) of degree n is interpreted as the field of all polynomials of degree \(<n\) and coefficients in \({\mathbb F}\).
2.1 Functionalities and Correlations
We introduce some useful functionalities and correlations.
Oblivious Transfer. Oblivious transfer, represented by \( \mathsf {OT} \), is a two-party functionality that takes as input \((x_0,x_1)\in {\{0,1\}} ^2\) from Alice and \(b\in {\{0,1\}} \) from Bob and outputs \(x_b\) to Bob.
Oblivious Linear-function Evaluation. For a field \(({\mathbb F},+,\cdot )\), oblivious linear-function evaluation over \({\mathbb F}\), represented by \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) \), is a two-party functionality that takes as input \((a,b)\in {\mathbb F} ^2\) from Alice and \(x\in {\mathbb F} \) from Bob and outputs \(z=ax+b\) to Bob. In particular, \( \mathsf {OLE} \) refers to the \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) \) functionality. Note that \( \mathsf {OT} \) is identical (functionally equivalent) to \( \mathsf {OLE} \) because \(x_b = (x_1-x_0)b + x_0\).
Random Oblivious Transfer Correlation. Random oblivious transfer, represented by \( \mathsf {ROT} \), is a correlation that samples \(x_0,x_1,b\) uniformly and independently at random. It provides Alice the secret share \(r_A=(x_0,x_1)\) and provides Bob the secret share \(r_B=(b,x_b)\).
Random Oblivious Linear-function Evaluation. For a field \(({\mathbb F},+,\cdot )\), random oblivious linear-function evaluation over \({\mathbb F}\), represented by \( \mathsf {ROLE} \,\left( {{\mathbb F}}\right) \), is a correlation that samples \(a,b,x\in {\mathbb F} \) uniformly and independently at random. It provides Alice the secret share \(r_A=(a,b)\) and provides Bob the secret share \(r_B=(x,z)\), where \(z=ax+b\). In particular, \( \mathsf {ROLE} \) refers to the \( \mathsf {ROLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) \) correlation. Note that \( \mathsf {ROT} \) and \( \mathsf {ROLE} \) are identical (functionally equivalent) correlations.
Inner-product Correlation. For a field \(({\mathbb F},+,\cdot )\) and \(n\in {\mathbb N} \), inner-product correlation over \({\mathbb F}\) of size n, represented by \( \mathsf {IP} \,\left( {{\mathbb F} ^n}\right) \), is a correlation that samples random \(r_A=(x_0,\cdots ,x_{n-1})\in {\mathbb F} ^n\) and \(r_B=(y_0,\cdots ,y_{n-1})\in {\mathbb F} ^n\) subject to the constraint that \(x_0 + y_0 = \sum _{i=1}^{n-1} x_iy_i\). The secret shares of Alice and Bob are, respectively, \(r_A\) and \(r_B\).
For \(m\in {\mathbb N} \), the functionality \({\mathcal F} ^m\) represents the functionality that implements m independent copies of any functionality/correlation \({\mathcal F} \).
2.2 Toeplitz Matrix Distribution
Given a field \({\mathbb F}\), the distribution \({\mathbb T} _{(k,n)}\) represents a uniform distribution over all matrices of the form \(\left[ I_{k\times k} \vert P_{k\times n-k}\right] \), where \(I_{k\times k}\) is the identity matrix and \(P_{k\times n-k}\) is a Toeplitz matrix with each entry in \({\mathbb F}\). The distribution \({\mathbb T} _{\perp ,(k,n)}\) is the uniform distribution over all matrices of the form \(\left[ P_{n-k\times k} \vert I_{{n-k\times n-k}} \right] \), where \(I_{n-k\times n-k}\) is the identity matrix and \(P_{n-k\times k}\) is a Toeplitz matrix with each entry in \({\mathbb F}\).
2.3 Graph Representation of Correlations
We introduce a graph-theoretic representation of correlations for a more intuitive presentation.
Definition 2
(Graph of a Correlation). Let \((R_A,R_B)\) be the joint distribution for a correlation. The graph of the correlation \((R_A,R_B)\) is the weighted bipartite graph \(G=(L,R,E)\) defined as follows.
-
1.
The left partite set L is the set of all possible secret shares \(r_A\) for Alice,
-
2.
The right partite set R is the set of all possible secret shares \(r_B\) for Bob, and
-
3.
The weight connecting the vertices \(r_A\) and \(r_B\) is the probability of sampling the shares \((r_A,r_B)\) according to the distribution \((R_A,R_B)\).
In this paper, the notation \((R_A,R_B)\) also represents the bipartite graph corresponding to it. If the correlation is a uniform distribution over a subset E of all possible edges, then we normalize the entire graph such that the weights on each edge is 1. For example, consider the correlations presented in Fig. 3. Henceforth, for the ease of presentation, we assume that the graph of a correlation is an unweighted bipartite graph. The left-most graph in Fig. 12 is the graph of the \( \mathsf {ROLE} \) correlation.
A bipartite graph \(G=(L,R,E)\) is a biclique if there exists \(L'\subseteq L\) and \(R'\subseteq R\) such that that edge-set \(E(G)=L'\times R'\).
Definition 3
(Simple Graph). A simple graph is a bipartite graph such that each of its connected components is a biclique.
For example, consider the graph in Fig. 6.Footnote 4 A simple correlation is a correlation whose graph is simple.
Definition 4
(Simple Partition Number). The simple partition number of a graph G, represented by \(\mathsf {sp} (G)\), is the minimum number of simple graphs needed to partition its edges.
Figures 12 and 13 show that the simple partition number for both \( \mathsf {ROLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) \) and \( \mathsf {ROLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) ^2\) is 2.
In this work, we use the tensor product of bipartite graphs defined as follows.
Definition 5
(Tensor Product Graph). For bipartite graphs \(G=(L_G,R_G,E_G)\) and \(H=(L_H,R_H,E_H)\) the tensor product of G and H is the bipartite graph \(J=(L_J,R_J,E_J)\) defined as follows.
-
1.
The left partite set
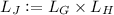 , the right partite set
, the right partite set  , and
, and -
2.
The vertices \((u,v)\in L_J\) and \((u',v') \in R_J\) are connected if \((u,u')\in E_G\) and \((v,v')\in E_H\).
Applying this definition recursively, we define  .
.
3 Extracting One OLE over a Large Field
In this section we will build some of the building blocks needed to construct the correlation extractor claimed in Theorem 1. In particular, we outline the extraction protocol that, given a leaky \( \mathsf {IP} \,\left( {{\mathbb K} ^{\eta +1}}\right) ^{[t]}\) correlation, realizes a secure \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) functionality.
-
1.
First, given the \( \mathsf {IP} \,\left( {{\mathbb K} ^{\eta +1}}\right) \) correlation where parties can perform t-bits of arbitrary leakage, we construct a secure sample of an \( \mathsf {ROLE} \,\left( {{\mathbb K}}\right) \) correlation. This protocol \(\pi ({\mathbb K},\eta )\) is presented in Fig. 7. At the end of the protocol Alice has \((\widetilde{A} _0,\widetilde{B} _0)\in {\mathbb K} ^2\) and Bob has \((\widetilde{X} _0,\widetilde{Z} _0)\in {\mathbb K} ^2\), such that \(\widetilde{A} _0,\widetilde{B} _0,\widetilde{X} _0\) are uniformly random elements in \({\mathbb K} \) and \(\widetilde{Z} _0 = \widetilde{A} _0\widetilde{X} _0+\widetilde{B} _0\). The simulation error of this protocol is \(\frac{1}{2}\sqrt{\frac{\left| {{\mathbb K}}\right| 2^t}{\left| {{\mathbb K}}\right| ^{\eta /2}}}\), refer to Lemma 2.
-
2.
Next, starting with the private shares \((\widetilde{A} _0,\widetilde{B} _0)\) with Alice and \((\widetilde{X} _0,\widetilde{Z} _0)\) with Bob, we implement a protocol \(\rho ({\mathbb K},A^*,B^*,X^*)\). Alice has private inputs \((A^*,B^*)\) that are arbitrary elements in \({\mathbb K} ^2\). Bob has private input \(X^*\) that is an arbitrary element in \({\mathbb K}\). The protocol \(\rho ({\mathbb K},A^*,B^*,X^*)\), described in Fig. 8 is a perfectly secure protocol where Bob outputs \(Z^*=A^*X^*+B^*\).
We emphasize that both \(\pi ({\mathbb K},\eta )\) and \(\rho ({\mathbb K},A^*,B^*,X^*)\) are 2-round protocols and we can compose these two protocols in parallel. The resultant protocol \(\sigma ({\mathbb K},\eta ,A^*,B^*,X^*)\) is an extraction protocol that takes as input a leaky \( \mathsf {IP} \,\left( {{\mathbb K} ^{\eta +1}}\right) ^{[t]}\) correlation where parties can perform t-bits of arbitrary leakage and implements the \( \mathsf {ROLE} \,\left( {{\mathbb K}}\right) \) functionality with simulation error \(\frac{1}{2}\sqrt{\frac{\left| {{\mathbb K}}\right| 2^t}{\left| {{\mathbb K}}\right| ^{\eta /2}}}\). This is formalized in the following lemma and the proof is included below.
Lemma 1
(Security of Correlation Extractor). The protocol \(\sigma ({\mathbb K},\eta ,A^*,B^*,X^*)\) obtained by the parallel composition of the protocols \(\pi ({\mathbb K},\eta )\) (see Fig. 7) and \(\rho ({\mathbb K},A^*,B^*,X^*)\) (see Fig. 8) is a secure protocol in the \( \mathsf {IP} \,\left( {{\mathbb K} ^{\eta +1}}\right) ^{[t]}\) hybrid that implements the \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) functionality with simulation error at most \(\frac{1}{2}\sqrt{\frac{\left| {{\mathbb K}}\right| 2^t}{\left| {{\mathbb K}}\right| ^{\eta /2}}}\).
Section 4 elaborates the exact technique to choose appropriate \({\mathbb K},\eta ,A^*,B^*,X^*\) to imply Theorem 1.
3.1 Extraction of One Secure \( \mathsf {ROLE} \,\left( {{\mathbb K}}\right) \) Correlation
The protocol is provided in Fig. 7. The security of the protocol is analogous to the proof in [26] that reduces to the unpredictability lemma over fields. We state this lemma in our context.
Lemma 2
(Unpredictability Lemma). Let \({\mathcal G} \in \left\{ {\mathbb T} _{\left( k,\eta +1\right) }, {\mathbb T} _{\perp ,\left( k,\eta +1\right) } \right\} \). Consider the following game between an honest challenger and an adversary:

The adversary \({\mathcal A} \) wins the game if \(b = \tilde{b}\). For any \({\mathcal A} \), the advantage of the adversary is \(\leqslant \frac{1}{4}\sqrt{\frac{\left| {{\mathbb K}}\right| 2^t}{\left| {{\mathbb K}}\right| ^{k}}}\).
Similar to the security proof provided by Gupta et al. [26], the simulation error of the protocol in Fig. 7 is the bound provided by the unpredictability lemma over fields (Lemma 2). Refer to the full version of the paper [6] for a proof of correctness.
3.2 Securely Realizing \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) Using \( \mathsf {ROLE} \,\left( {{\mathbb K}}\right) \) Correlation
The protocol presented in Fig. 8 is a perfectly semi-honest secure protocol for \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) in the \( \mathsf {ROLE} \,\left( {{\mathbb K}}\right) \) correlation hybrid. Note that the protocols \(\pi ({\mathbb K},\eta )\) in Fig. 7 and \(\rho ({\mathbb K},A^*,B^*,X^*)\) in Fig. 8 can be composed in parallel. Let \(\sigma ({\mathbb K},\eta ,A^*,B^*,X^*)\) be the parallel composition of the protocols \(\pi ({\mathbb K},\eta )\) and \(\rho ({\mathbb K},A^*,B^*,X^*)\). This completes the proof of Lemma 1.
4 Embedding Multiple \( \mathsf {OLE} \)s into an \( \mathsf {OLE} \) over an Extension Field
One of the primary goals in this section is to prove the following lemma.
Lemma 3
(Embedding Multiple small \( \mathsf {OLE} \) into a Large \( \mathsf {OLE} \) ). Let \({\mathbb K}\) be an extension field of \({\mathbb F}\) of degree n. There exists a perfectly secure protocol for \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) ^m\) in the \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \)-hybrid that makes only one call to the \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) functionality and \(m=n^{1-o(1)}\).
Proof
Section 4.3 provides this lemma and proves Theorem 1.
4.1 Intuition of the Embedding
We illustrate the main underlying ideas of this embedding problem and our proposed solution using the representative field \({\mathbb F} ={\mathbb G} {\mathbb F} \left[ 2\right] \) and its extension field \({\mathbb K} = {\mathbb G} {\mathbb F} \left[ 2^n\right] \). Suppose we are provided with an oracle that takes as input \(A^*,B^*\in {\mathbb K} \) from Alice and \(X^*\in {\mathbb K} \) from Bob, and outputs  to Bob. Our aim is to implement the following functionality. Alice has inputs \((a_0,\cdots ,a_{m-1})\in {\mathbb F} ^m\) and \((b_0,\cdots ,b_{m-1})\in {\mathbb F} ^m\), and Bob has inputs \((x_0,\cdots ,x_{m-1})\in {\mathbb F} ^m\). We want Bob to obtain \((z_0,\cdots ,z_{m-1})\in {\mathbb F} ^m\), where each \(z_i = a_i\cdot x_i + b_i\), for \(i\in \{0,\cdots ,m-1\}\). Intuitively, we want maximize m and embed \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) ^m\) into one \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \).
to Bob. Our aim is to implement the following functionality. Alice has inputs \((a_0,\cdots ,a_{m-1})\in {\mathbb F} ^m\) and \((b_0,\cdots ,b_{m-1})\in {\mathbb F} ^m\), and Bob has inputs \((x_0,\cdots ,x_{m-1})\in {\mathbb F} ^m\). We want Bob to obtain \((z_0,\cdots ,z_{m-1})\in {\mathbb F} ^m\), where each \(z_i = a_i\cdot x_i + b_i\), for \(i\in \{0,\cdots ,m-1\}\). Intuitively, we want maximize m and embed \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) ^m\) into one \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \).
Preliminary Idea. Consider the following simple preliminary embedding. Let \(m=\sqrt{n}\). Alice defines \(A^* = a_0 + a_1\zeta + \cdots + a_{m-1}\zeta ^{m-1}\), where \(a_0,\cdots ,a_{m-1}\in {\mathbb F} \). And, Alice defines \(B^* = \sum _{i=0}^{n-1} r_i\zeta ^i\), where each \(r_i\) is a random element in \({\mathbb F}\); except when \((m + 1)\) divides i, then we set \(r_{t(m + 1)} = b_t\), for \(t\in \{0,\cdots ,m-1\}\). Bob defines \(X^* = x_0 + x_1\zeta ^m + \cdots + x_{m-1}\zeta ^{(m-1)m}\), where \(x_0,\cdots ,x_{m-1}\in {\mathbb F} \).
Now, the parties compute \(Z^* = A^* X^* + B^*\) using one oracle call to \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) and Bob obtains the output \(Z^*\). Note that the intended \(z_i=a_i\cdot x_i + b_i\) is the coefficient of \(\zeta ^{i(m+1)}\) in \(Z^*\), for each \(i\in \{0,\cdots ,m-1\}\). Coefficients of all other powers of \(\zeta \) contain no information about \(a_0,\cdots ,a_{m-1},b_0,\cdots ,b_{m-1}\), because they are masked with random elements in \({\mathbb F}\). So, for \(m=\sqrt{n}\), we have embedded \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) ^m\) into one \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \).
Better Embedding. Observe that \((a_0 + a_1\zeta )\cdot (x_0+x_1\zeta ) = a_0x_0 + (a_0x_1+a_1x_0)\zeta + a_1x_1\zeta ^2\). So, we can embed \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) ^2\) into one \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \), where \({\mathbb K}\) is an extension field of \({\mathbb F}\) of degree 3, as follows. Alice chooses \(A^* = a_0 + a_1\zeta \in {\mathbb G} {\mathbb F} \left[ 2^2\right] \) and \(B^* = b_0 + r\zeta + b_1\zeta ^2\) (where r is a random element from \({\mathbb F}\)), and Bob chooses \(X^*=x_0+x_1\zeta \). Note that the coefficients of \(\zeta ^0\) and \(\zeta ^2\) in \(Z^*\), respectively, correspond to \(a_0x_0+b_0\) and \(a_1x_1+b_1\). Recursively applying this idea, we can construct an embedding of \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) ^{2^k}\) into one \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2^{3^k}\right] }\right) \). Asymptotically, this scheme embeds \(m = n^{\log 2/\log 3} \approx n^{0.631}\) copies of \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) \) into one \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2^n\right] }\right) \).
Generalization to 3-free sets. Consider the previous solution when \(n = 3^k\). Let \(S=\{s_0< s_1< \cdots < s_{m-1}\}\) be the set of indices. The set S corresponding to the previous solution contains all integers less than \(3^k\) whose ternary representation does not contain the digit 2. This is the famous greedy sequence of integers that does not include an arithmetic progression of length 3; namely, 3-free sets. In fact, there is nothing sacrosanct about the S chosen in the previous embedding, and any 3-free set suffices.
For example, let \(S=\{s_0< s_1< \cdots < s_{m-1}\}\) be any 3-free set such that each entry is in the range [0, n / 2), \({\mathbb F} ={\mathbb G} {\mathbb F} \left[ 2\right] \), and \({\mathbb K} ={\mathbb G} {\mathbb F} \left[ 2^n\right] \). Alice prepares \(A^* = \sum _{i=0}^{m-1} a_i\zeta ^{s_i}\) and \(B^*=\sum _{k=0}^{n-1} r_k\zeta ^k\), where \(r_{2s_i}=b_i\); otherwise it is a random element in \({\mathbb F}\). Bob prepares \(X^* = \sum _{i=0}^{m-1} x_i\zeta ^{s_i}\). Using one call to \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) Bob obtains \(Z^*\). The coefficient of \(\zeta ^{2s_i}\) is \(a_ix_i+b_i\), because no other \(s_j + s_k = 2s_i\). Now, we can embed \(m= n^{1-o(1)}\) copies of \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) \) into \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) using the state-of-the-art constructions of 3-free sets [3, 20]. However, this approach cannot give us \(m=\varTheta (n)\) due to sub-linear upper bounds on m [8, 9, 29, 58, 60, 61].
New Problem. Note that although solutions to the 3-free set problem imply embeddings in our setting, our embedding problem is potentially less restrictive. For example, the solution for \(m=\sqrt{n}\) presented above is not obtained by the reduction to 3-free sets. Are we missing something?
Suppose \(S=(s_0,\cdots ,s_{m-1})\) and \(T=(t_0,\cdots ,t_{m-1})\) be tuples of indices in the range [0, n/2). Consider the combinatorial problem proposed in Fig. 5.
Given S and T that are solutions to the problem in Fig. 5, Alice and Bob use the strategy explained in Fig. 9. Note that the initial solution for \(m=\sqrt{n}\) indeed corresponds to the solution \(S=\{0,\cdots ,m-1\}\) and \(T=\{0,m,\cdots ,(m-1)m\}\). Restricted to \(S=T\), our combinatorial problem is identical to the 3-free set problem. We numerically solve this problem for small values of n and, indeed, it produces more efficient embeddings than the embedding based on the optimal 3-free set constructions. We emphasize that we compare our solutions against the largest 3-free set computed by exhaustive search. We summarize our observations in Fig. 10.
Let \({\mathbb K}\) be an extension field of \({\mathbb F}\) of degree n. Our goal is to embed m copies of \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) \) into one \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) using minimum n. The number n(m) represents the minimum n obtained by using solutions to our combinatorial problem in Fig. 5. The number \(n'(m)\) represents the minimum n obtained by using the optimum solutions to the 3-free set problem.
4.2 Relevant Prior Work on 3-Free Sets
Our asymptotic construction for Theorem 1 relies on constructing a dense subset S of \( \{0,1, \cdots , n-1\} \) that does not contain any arithmetic progression, namely 3-free sets. Erdős and Turán introduced this problem in 1936 and presented a greedy construction with \( \left| {S}\right| = \varOmega \left( n^{\log 2/\log 3}\right) \approx n^{0,631} \). Salem and Spencer [59] showed that the surface of high-dimensional convex bodies can be embedded in the integers to construct 3-free sets of size \( n^{1- o(1)} \). Later, Behrend [3] noticed that points lying on the surface of a sphere of suitable radius are a particularly good choice, and gave a construction with \( \left| {S}\right| = \varOmega \left( \frac{n}{2^{2 \sqrt{2 \log n}} \cdot \log ^{1/4} n}\right) \). Recently, after a gap of over sixty years, Elkin [20] improved this further by a factor of \( \varTheta (\sqrt{\log n}) \) by thickening the spheres to produce the largest known 3-free set. The proofs of Behrend [3] and Elkin [20] are constructive in nature and the sets can be constructed in \({{\mathrm{poly}}}(n)\) time. Although the greedy construction is asymptotically worse than these two constructions, it performs well for realistic values of n. See Fig. 11 for details.
Roth [58] provided the first nontrivial upper bound of \( O\left( \frac{n}{\log \log n}\right) \) on the size of 3-free sets. More than thirty years later, Heath-Brown [29] showed that \( \left| {S}\right| = O\left( \frac{n}{\log ^ c n}\right) \), for some constant \( c >0 \), and then Szemeredi [61] produced an explicit value \( c = 1/20 \). Bourgain [8, 9] improved the upper bound by \({{\mathrm{polylog}}}\) factors. Currently, the best known upper bound is \(O\left( \frac{n(\log \log n)^4}{\log n} \right) \) [7, 60]. Nathan [46] provides a comprehensive summary for both 3-free set size constructions and upper bounds.
4.3 Generating Explicit Embedding and Proof of Theorem 1
First, we prove Lemma 3. Let S(n) be a 3-free set with elements in the range [0, n / 2). Behrend [3] and Elkin [20] provide constructions for S(n) such that \(\left| {S(n)}\right| \geqslant n^{1-o(1)}\). Note that \(S=T=S(n)\) is a solution to the combinatorial problem proposed in Fig. 5. Now, we use the protocol described in Fig. 9.
It is clear that the protocol is correct. The coefficients of all other \(\zeta ^i\) in \(Z^*\) are random elements in \({\mathbb F}\), if \(i\ne s_k+t_k\), for all \(k\in \{0,\cdots ,m-1\}\). It is, therefore, easy to see that this is a perfectly secure protocol for \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) ^m\) in the \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \)-hybrid.
Remark. We provide a short discussion on how to pick the 3-free set S for concrete values of n. The greedy construction is the fastest and runs in \(O(n\log n)\) time. It picks all numbers that do not have 2 in their ternary representation, and \(\left| {S(n)}\right| = n^{\log 2/\log 3}\approx n^{0.631}\). The proofs of Behrend [3] and Elkin [20] are also constructive in nature and the set can be constructed in \({{\mathrm{poly}}}(n)\) time. However, their performance for realistic values of n are worse than the greedy algorithm.
Further, for concrete values of n, one of the solutions to our combinatorial problem generates better embeddings than the greedy solution. Note that, Fig. 10 presents a solution that enables the embedding of 10 independent \( \mathsf {OLE} \,\left( {{\mathbb F}}\right) \) evaluations into one \( \mathsf {OLE} \,\left( {{\mathbb K}}\right) \) evaluation, where \({\mathbb K}\) is an extension field of \({\mathbb F}\) of degree 38. Recursively applying this embedding, we embed \(m = n^{\log 10/\log 38} \approx n^{0.633} \gg n^{0.631} \approx n^{\log 2/\log 3}\) independent \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) \) evaluations into one \( \mathsf {OLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2^n\right] }\right) \) evaluation.
Proof of Theorem 1 . Suppose we given n, \(0<\delta<g<1/2\), and \(t=(1/2 - g)n\). Let \({\mathbb K} = {\mathbb G} {\mathbb F} \left[ 2^{\delta n}\right] \) and \({\mathbb F} ={\mathbb G} {\mathbb F} \left[ 2\right] \). We construct \(A^*,B^*,X^*\in {\mathbb K} \) using Lemma 3 and \(m\geqslant (\delta n)^{1-o(1)}\). Perform the protocol \(\sigma ({\mathbb K},1/\delta -1,A^*,B^*,X^*)\) in the \( \mathsf {IP} \,\left( {{\mathbb K} ^{1/\delta }}\right) ^{[t]}\)-hybrid.Footnote 5 The simulation error is
This is an \((n,m,t,\varepsilon )\)-correlation extractor for the correlation \( \mathsf {IP} \,\left( {{\mathbb K} ^{1/\delta }}\right) \).
5 Simple Partition Number
This section defines the simple partition number of a graph, provides estimates of this quantity for correlations relevant to our work, and proves Theorem 2.
5.1 Intuition of the Hardness of Computation Result
We know that if parties have multiple independent samples of secret shares sampled according to a simple correlation, then the parties cannot securely compute \( \mathsf {OT} \) [2, 32, 38, 41,42,43]. Constructing one \( \mathsf {OT} \) given a single sample from such a correlation is even more restrictive, and, hence, the hardness of computation result carries over. This result holds true even when there is no leakage on \((R_A,R_B)\). More precisely, we import the following result that we restate in our context.
Imported Theorem 1
[43]. Let \((R_A,R_B)\) be a simple correlation with n-bit secret shares for each party. There exists a universal constant \(\varepsilon ^*>0\), such that any \((n,1,0,\varepsilon )\)-correlation extractor for \((R_A,R_B)\) has \(\varepsilon \geqslant \varepsilon ^*\).
Suppose \((R_A,R_B)\) is a correlation that has simple partition number \(\mathsf {sp} (G)=2^\lambda \) and \(G = G^{{\left( 1\right) }} + \cdots + G^{{\left( 2^\lambda \right) }} \), where each \(G^{{\left( i\right) }} \) is a simple graph. Then we consider the leakage function \({\mathcal L} (r_A,r_B)=\ell \), where \(\ell \in \{1,\cdots ,2^\lambda \}\) is the unique index such that \((r_A,r_B) \in E(G^{{\left( \ell \right) }})\). Note that \({\mathcal L}\) is a \(\lambda \)-bit leakage function and conditioned on the leakage being \(\ell \), for any \(\ell \in \{1,\cdots ,2^\lambda \}\), the correlation \((R_A,R_B \vert \ell )\) is a simple correlation. So, one of the parties can break the security of any purported \( \mathsf {OT} \) protocol where parties get secret shares sampled from the \((R_A,R_B \vert \ell )\) correlation. Overall, with probability half, one of the parties can break the security of any purported \( \mathsf {OT} \) protocol where parties get secret shares sampled from the \((R_A,R_B)\) by performing the leakage \({\mathcal L}\) described above. This technique upper-bounds the leakage resilience of \((R_A,R_B)\) and we summarize it as follows.
Lemma 4
(Connection between Maximum Leakage Resilience and Simple Partition Number). Let \((R_A,R_B)\) is a correlated private randomness that provides n-bit private shares to Alice and Bob. Let G be the bipartite graph corresponding to the correlation \((R_A,R_B)\). There exists a universal constant \(\varepsilon ^*>0\) such that any \((n,1,t,\varepsilon )\)-correlation extractor for \((R_A,R_B)\) with \(t\geqslant \left\lceil {\lg \mathsf {sp} (G)}\right\rceil \) has \(\varepsilon \geqslant \varepsilon ^*\).
We construct a smoother version of this technical lemma using averaging arguments. For example, if the leakage bound t is roughly \(\left( \log \mathsf {sp} (G)\right) -gn\), then we consider a subset of simple graphs of size \(\mathsf {sp} (G)\cdot 2^{-gn}\) from the set \(\left\{ G^{{\left( 1\right) }},\cdots ,G^{{\left( \mathsf {sp} (G)\right) }} \right\} \) that covers at least \(2^{-gn}\) fraction of the edges of G. Applying the previous lemma, we can conclude that \((n,1,t,\varepsilon )\)-correlation extractor for \((R_A,R_B)\) with \(t\geqslant \left\lceil {\log \mathsf {sp} (G)-gn}\right\rceil \) has \(\varepsilon \geqslant \varepsilon ^* \cdot 2^{-gn}\).
Corollary 1
((Smooth Version of the) Connection between Maximum Leakage Resilience and Simple Partition Number). Let \((R_A,R_B)\) is a correlated private randomness that provides n-bit private shares to Alice and Bob. Let G be the bipartite graph corresponding to the correlation \((R_A,R_B)\). There exists a universal constant \(\varepsilon ^*>0\) such that any \((n,1,t,\varepsilon )\)-correlation extractor for \((R_A,R_B)\) with \(t\geqslant \left\lceil {\lg \mathsf {sp} (G)-gn}\right\rceil \) has \(\varepsilon \geqslant \varepsilon ^*\cdot 2^{-gn}\).
5.2 Relevant Prior Work on Graph Covering Problems
The graph-theoretic measure proposed in our work to measure the maximum resilience of correlations in best presented in the framework of graph covering problems. Several problems in graph theory, for example, clique partition number, biparticity, arboricity, edge-chromatic number, vertex cover number and biclique partition number, can be expressed as covering a graph with subgraphs from a family of graphs. Of these representative examples, the concept of biclique partition number is most relevant to our paper. For a graph G, its biclique partition number, represented by \(\mathsf {bp} \,\left( G\right) \), is the minimum number of bicliques that suffice to partition it.
Refer to [40] for a comprehensive survey on graph covering problems. Motivated by network addressing problem and graph storage problem, Graham and Pollak [24, 25] introduced the biclique partition problem (see also [1, 63, 64, 70]). The celebrated Graham-Pollak Theorem states that \(\mathsf {bp} \,\left( K_n\right) =(n-1)\) [25, 52, 62, 65, 66], but all proofs are algebraic, and no purely combinatorial proof is known. In general, \(\mathsf {bp} \,\left( G\right) \geqslant \max \{n_+(G),n_-(G)\}\) [25, 30, 52, 62], where \(n_+(\cdot )\) and \(n_-(\cdot )\), respectively, represents the number of positive and negative eigenvalues of the adjacency matrix of the graph. Determining the \(\mathsf {bp} \,\left( G\right) \) of a general graph is a hard problem [40], but it admits a trivial upper bound \(\mathsf {bp} \,\left( G\right) \leqslant \) the size of the smallest vertex cover of G. Variants of this quantity have been considered recently by [14].
This quantity is closely related to the recently disproved [13, 31] Alon-Saks-Seymour Conjecture [36] that \(\mathsf {bp} \,\left( G\right) +1\) colors suffice to color a graph. This conjecture can be interpreted as a generalization of the Graham-Pollak Theorem and has close relations to computational complexity [31, 51, 57]. In the context of this paper, intuitively, the biclique partition number is a combinatorial version of the Wyner’s Common Information [69] that corresponds to the minimum description complexity of the information that kills the mutual information of correlations. We interpret a correlation as a weighted bipartite graph with the left-partite set being all possible values of \(r_A\), and the right partite set being all possible values of \(r_B\). The weight on an edge joining \(r_A\) and \(r_B\) represents the probability of jointly sampling \((r_A,r_B)\). This graph-theoretic interpretation of correlations helps establish connections between combinatorial and information-theoretic concepts.
5.3 Relation to Leakage Resilience: Proof of Lemma 4
In this section we prove Lemma 4, i.e. the maximum leakage resilience of a correlation \((R_A,R_B)\) is at most \(\lg \mathsf {sp} \,\left( R_A,R_B\right) \).
Let G be the bipartite graph corresponding to the correlation \((R_A,R_B)\). Let \(\pi \) be a \((n,1,t,\varepsilon )\)-correlation extractor for G, where \(t=\left\lceil {\log \mathsf {sp} \,\left( G\right) }\right\rceil \). Let \(G = G^{{\left( 1\right) }} + \cdots + G^{{\left( \mathsf {sp} \,\left( G\right) \right) }} \) be the simple partition of G. Define the leakage function \({\mathcal L} :E(G)\rightarrow \{1,\cdots ,\mathsf {sp} \,\left( G\right) \}\) as follows. For \(e\in E(G)\), we have \({\mathcal L} (e)=\ell \), where \(\ell \) is the unique index in \(\{1,\cdots ,\mathsf {sp} \,\left( G\right) \}\) such that \(e\in E(G^{{\left( \ell \right) }})\).
Consider an interactive protocol that runs \(\pi \) between Alice and Bob with secret samples drawn from the correlation G, and both parties receive the leakage \({\mathcal L} (r_A,r_B)\).
Note that this is identical to the interactive protocol, where the correlation \(G^+\) that samples \(\ell \in \{1,\cdots ,\mathsf {sp} \,\left( G\right) \}\) with probability proportional to \(\left| {E(G^{{\left( \ell \right) }})}\right| \), samples  , and provides \((u,\ell )\) to Alice and \((v,\ell )\) to Bob.
, and provides \((u,\ell )\) to Alice and \((v,\ell )\) to Bob.
The functionality \(G^+\) itself is simple, because each \(G^{{\left( \ell \right) }} \) is simple. So, we can use Imported Theorem 1. Therefore, one of the parties’ view cannot be simulated with less than \(\varepsilon ^*>0\) simulation error when the parties follow the protocol \(\pi \). Suppose, that party is Alice, without loss of generality. That is, the view of the party Alice\(^*\) (to represent the semi-honest adversarial strategy) in the interactive protocol between Alice\(^*\) and B incurs at least \(\varepsilon ^*\) simulation error.
Now consider the case where only Alice\(^*\) receives the leakage from the correlation and not Bob. The view of Alice\(^*\) remains identical to the previous hybrid. Therefore, this protocol also incurs a simulation error at least \(\varepsilon ^*\)
This implies that for any \((n,1,t,\varepsilon )\)-correlation extractor for \((R_A,R_B)\), if \(t\geqslant \log \mathsf {sp} \,\left( R_A,R_B\right) \), then \(\varepsilon \geqslant \varepsilon ^*\).
Intuitively, Lemma 4 can be summarized as follows. A small simple partition number of the correlated private randomness \((R_A,R_B)\) implies a low maximum leakage-resilience of \((R_A,R_B)\).
Proof of Corollary 1 . Suppose \(2^t=\mathsf {sp} \,\left( G\right) /2^{gn}\) and \(\pi \) is an \((n,1,t,\varepsilon )\)-correlation extractor for \((R_A,R_B)\). Now, we choose the \(\mathsf {sp} \,\left( G\right) /\left( 2^{gn} - 1\right) \) simple graphs among \(\{G^{{\left( 1\right) }},\cdots ,G^{{\left( \mathsf {sp} \,\left( G\right) \right) }} \}\) that cover a subset \(E'\subset E(G)\) such that \(\left| {E'}\right| /\left| {E(G)}\right| \geqslant \left( 2^{gn} - 1\right) ^{-1}\). The leakage function \({\mathcal L} (r_A,r_B)\) outputs the index of the simple graph from which the edge \(e=(r_A,r_B)\) comes, if \(e\in E'\); otherwise, it returns \(\bot \). Using the same proof as Lemma 4 we can conclude that the simulation error is \(\varepsilon \geqslant \varepsilon ^*\left( 2^{gn} - 1\right) ^{-1} \approx \varepsilon ^* 2^{-gn}\).
5.4 Estimates of Simple Partition Number and Proof of Theorem 2
In this section we present the lemma that provides the estimates of the simple partition number of relevant correlations.
Lemma 5
(Simple Partition Number Estimates). The following holds true for arbitrary field \({\mathbb F}\).
-
1.
\(\mathsf {sp} \,\left( \mathsf {IP} \,\left( {{\mathbb F} ^n}\right) \right) \leqslant \left| {{\mathbb F}}\right| ^{\left\lceil {(n+1)/2}\right\rceil }\), and
-
2.
For even n, \(\mathsf {sp} \,\left( { \mathsf {ROLE} \,\left( {{\mathbb F}}\right) }^{n/2}\right) \leqslant \left| {{\mathbb F}}\right| ^{\left\lceil {n/4}\right\rceil }\).
Refer to the full version [6] for a proof of the first part. The proof outline of the second part is provided in Sect. 5.5. The simple decomposition we construct for the correlations mentioned above have an additional property. Given an edge \((r_A,r_B)\sim (R_A,R_B)\), we can efficiently compute the index of the simple graph in the decomposition that contains it. Thus, the leakage that demonstrates the upper bound of the maximal resilience in Lemma 4 is computationally efficient.
The proof of Theorem 2 is a direct application of Lemmas 4 and 5.
5.5 Subsuming the Partition Argument
In this section, using a particular example, we want to illustrate that the simple partition number is sophisticated enough to subsume partition argument based impossibility results. To begin, let us consider an example. Let \((R_A,R_B)\) be the random oblivious linear-function evaluation over \({\mathbb G} {\mathbb F} \left[ 2\right] \). So, the correlation samples \(a,b,x\in {\mathbb G} {\mathbb F} \left[ 2\right] \) independently and uniformly at random. The secret share of Alice is \(r_A=(a,b)\) and the secret share of Bob is \(r_B=(x,z)\), where \(z=ax+b\). The secrecy of \( \mathsf {ROLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) \) ensures that Alice has no advantage in guessing x and Bob has no advantage in guessing a. The graph of the correlation is provided in Fig. 12. The figure presents the simple decomposition corresponding to the leakage \(\ell =x-a\).
Now, let us consider \( \mathsf {ROLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) ^2\), i.e. two independent samples from the \( \mathsf {ROLE} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] }\right) \) correlation. Alice gets secret share \((a_1,b_1,a_2,b_2)\) and Bob gets secret share \((x_1,z_1,x_2,z_2)\), where \(z_1=a_1x_1+b_1\) and \(z_2=a_2x_2+b_2\). Suppose in the partition argument Alice implements the first correlation and Bob implements the second correlation. This implies that Alice knows \(x_1\) and Bob knows \(a_2\). We want to achieve this effect using only one-bit leakage that is provided to both the parties.
Given the decomposition in Fig. 12, note that we can define a two-bit leakage to achieve this. For example the first leakage bit represents \(\ell _1=x_1-a_1\), and the second leakage bit represents \(\ell _2=x_2-a_2\). We show in Fig. 13 that even a one-bit leakage suffices. In particular, we use \({\mathcal L} (r_A,r_B) = x_1-a_2\). In the full version [6], we show that \(\mathsf {sp} \,\left( \mathsf {ROLE} \,\left( {{\mathbb F}}\right) ^2\right) \leqslant \left| {{\mathbb F}}\right| \).
Using this observation and the fact that \(\mathsf {sp} \,\left( G\times H\right) \leqslant \mathsf {sp} \,\left( G\right) \cdot \mathsf {sp} \,\left( H\right) \) (see full version [6] for the proof), Lemma 5 shows that \(\mathsf {sp} \,\left( \mathsf {ROLE} \,\left( {{\mathbb F}}\right) ^n\right) \leqslant {\left| {{\mathbb F}}\right| }^{\left\lceil {n/2}\right\rceil }\). This demonstrates that the simple partition number subsumes the partition argument.
5.6 Relevant Prior Work on Common Information and Assisted Common Information
We briefly introduce a few relevant information-theoretic measures for maximum resilience and maximum production rate. For a joint distribution, the mutual information \(I(R_A;R_B)\) measures the distance (KL-divergence) between the joint probability distribution \(p(r_A,r_B)\) and the distribution \(p(r_A)\cdot p(r_B)\). The mutual information between \((R_A,R_B)\) represents the number of bits of the secret key that the two parties can agree. The Gács-Körner [21] common information, represented by \(K(R_A;R_B)\), represents the largest entropy of the common random variable that each party can generate based on their respective secret share. Intuitively, this corresponds to the number of connected components in a bipartite graph representing the correlation. The Wyner common information [69], represented by \(J(R_A;R_B)\), is the minimum information that, when leaked to the eavesdropper, ensures that the parties cannot establish a secret key. This quantity roughly corresponds to the biclique partition number of a bipartite graph for the correlation, where the correlation is a uniform distribution over the edges of the bipartite graph. Prabhakaran and Prabhakaran [53, 54], generalizing [67], introduced the concept of assisted common information that, among its various applications, helps characterize an upper bound on the number of \( \mathsf {OT} \)s that a correlation can produce.
Relation to Mutual Information. In the setting of key-agreement, the mutual information \(I(R_A;R_B)\) of a correlation \((R_A,R_B)\) measures the length of the secret key that the two parties can agree on. We emphasize that this is a measure of production, and not a measure of resilience. For example, \(I( \mathsf {IP} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] ^n}\right) ) = 1\). Since, secure \( \mathsf {OT} \) implies one-bit key-agreement, mutual information is also an upper bound on the \( \mathsf {OT} \) production that a correlation can support. However, production capacity and resilience to leakage are extremely disparate quantities. For example, in the secure computation setting, the correlation \( \mathsf {IP} \,\left( {{\mathbb G} {\mathbb F} \left[ 2\right] ^n}\right) \) is resilient to n/2 bits of leakage but can only produce one \( \mathsf {OT} \). Additionally, mutual information significantly overestimates the maximum \( \mathsf {OT} \) production capacity. For example, n-bit shared private key cannot produce one \( \mathsf {OT} \) even without any leakage. However, it has n-bits of mutual information.
We emphasize that the simple partition number is only a measure for the maximum leakage resilience of correlations in the setting of secure computation. Our measure does not provide any estimates on the \( \mathsf {OT} \) production. The most relevant measure for \( \mathsf {OT} \) production is the notion of assisted common information proposed by Prabhakaran and Prabhakaran [53, 54].
5.7 Analogy of Biclique Partition Number and Wyner’s Common Information
A correlation that is a biclique has no mutual-information and, hence, is useless for parties to agree on a secret key even asymptotically. In particular, one sample from a correlation that is a biclique is also useless for key-agreement. Suppose \((R_A,R_B)\) is an arbitrary correlation and has biclique partition complexity \(\mathsf {bp} \,\left( R_A,R_B\right) \). Similar to Lemma 4, in the presence of \(t=\log \mathsf {bp} \,\left( R_A,R_B\right) \) bits of leakage there is not even a one-bit secure key-agreement protocols using \((R_A,R_B)\). The random variable J for the leakage function \({\mathcal L} (R_A,R_B)\) outputs the index of the biclique that contains the edge \(e=(r_A,r_B)\).
Wyner’s common information [69] is defined to be the minimum entropy random variable J that suffices to ensure \(I(R_A;R_B|J)=0\). If the bicliques that partition G have roughly equal number of edges then these two concepts are identical. Analogously, \(\mathsf {sp} \,\left( R_A,R_B\right) \) can be interpreted as the analog for Wyner’s common information in the secure computation setting.
However, we cannot use biclique partition number or Wyner’s Common Information to meaningfully measure the resilience of a correlation against leakage in the secure computation setting. The biclique partition number \(\mathsf {bp} \,\left( R_A,R_B\right) \) can be significantly higher than the simple partition number \(\mathsf {sp} \,\left( R_A,R_B\right) \), which is an upper bound on the maximum resilience. For example, the biclique partition number \(\mathsf {bp} \,\left( \mathsf {IP} \,\left( {{\mathbb F} ^n}\right) \right) \approx {\left| {{\mathbb F}}\right| }^{n-1}\) while its simple partition number \(\mathsf {sp} \,\left( \mathsf {IP} \,\left( {{\mathbb F} ^n}\right) \right) \approx {\left| {{\mathbb F}}\right| }^{n/2}\) is exponentially small. This example demonstrates the non-trivial utility of the new measure introduced by us in the secure computation setting.
Notes
- 1.
The actual inner-product correlation is defined slightly differently. Parties get shares \((x_0,x_1,\cdots ,x_n)\) and \((y_0,y_1,\cdots ,y_n)\) such that \(x_0+y_0 = \sum _{i=1}^n x_iy_i\). That is, \(x_0\) and \(y_0\) are additive secret shares of the inner product of \((x_1,\cdots ,x_n)\) and \((y_1,\cdots ,y_n)\). But for intuition, it suffices to consider the correlation where the secret shares of the parties are orthogonal vectors instead.
- 2.
That is, the functionality samples secret shares \((r_A,r_B)\) according to the correlation \((R_A,R_B)\). The adversarial party sends a t-bit leakage function \({\mathcal L}\) to the functionality and receives the leakage \({\mathcal L} (r_A,r_B)\) from the functionality. The functionality sends \(r_A\) to Alice and \(r_B\) to Bob. Note that the adversary does not need to know its secret share to construct the leakage function because the leakage function gets the secret shares of both parties as input.
- 3.
The problem of characterizing correlations whose single sample suffice to construct \( \mathsf {OT} \) is a fascinating open problem that lies beyond the purview of this study.
- 4.
This definition naturally generalizes to weighted graphs. Suppose \(p(r_A,r_B)\) represents the probability of jointly sampling \((r_A,r_B)\) from the correlation \((R_A,R_B)\). Then a simple graph has \(p(r_A,r_B)=p(r_A)\cdot p(r_B)\), for every \((r_A,r_B)\) edge with positive weight.
- 5.
Recall that in the protocol \(\pi ({\mathbb K},\eta )\), all parties have share size \((\eta +1)\log \left| {{\mathbb K}}\right| \).
References
Babai, L., Frankl, P.: Linear Algebra Methods in Combinatorics: With Applications to Geometry and Computer Science. Department of Computer Science, University of Chicago (1992). 23
Beaver, D.: Perfect privacy for two-party protocols. In: Feigenbaum, J., Merritt, M. (eds.) Proceedings of DIMACS Workshop on Distributed Computing and Cryptography, vol. 2, pp. 65–77. American Mathematical Society (1989). 4, 12, 22
Behrend, F.A.: On sets of integers which contain no three terms in arithmetical progression. Proc. Natl. Acad. Sci. 32(12), 331–332 (1946). 18, 19, 20, 21
Ben-David, A., Nisan, N., Pinkas, B.: FairplayMP: a system for secure multi-party computation. In: Ning, P., Syverson, P.F., Jha, S. (eds.) ACM CCS 08, pp. 257–266. ACM Press, October 2008. 4
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: 20th ACM STOC, pp. 1–10. ACM Press, May 1988. 4
Block, A.R., Maji, H.K., Nguyen, H.H.: Secure computation based on leaky correlations: high resilience setting. https://www.cs.purdue.edu/homes/hmaji/papers/C:BloMajNgu17.pdf. (Full Version). 16, 24, 25
Bloom, T.F.: A quantitative improvement for Roth’s theorem on arithmetic progressions. J. Lond. Math. Soc. 93(3), 643–663 (2016). 20
Bourgain, J.: On triples in arithmetic progression. Geom. Funct. Anal. 9(5), 968–984 (1999). 18, 20
Bourgain, J.: Roth’s theorem on progressions revisited. J. d’Analyse Math. 104(1), 155–192 (2008). 18, 20
Canetti, R., Lindell, Y., Ostrovsky, R., Sahai, A.: Universally composable two-party and multi-party secure computation. In: 34th ACM STOC, pp. 494–503. ACM Press, May 2002. 4
Chandran, N., Goyal, V., Sahai, A.: New constructions for UC secure computation using tamper-proof hardware. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 545–562. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_31. 4
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: 20th ACM STOC, pp. 11–19. ACM Press, May 1988. 4
Cioaba, S.M., Tait, M.: More counterexamples to the Alon-Saks-Seymour and rank-coloring conjectures. Electron. J. Comb. 18(P26), 1 (2011). 23
Cioabă, S.M., Tait, M.: Variations on a theme of Graham and Pollak. Discret. Math. 313(5), 665–676 (2013). 23
Crépeau, C., Morozov, K., Wolf, S.: Efficient unconditional oblivious transfer from almost any noisy channel. In: Blundo, C., Cimato, S. (eds.) SCN 2004. LNCS, vol. 3352, pp. 47–59. Springer, Heidelberg (2005). doi:10.1007/978-3-540-30598-9_4. 4
Damgård, I., Ishai, Y.: Scalable secure multiparty computation. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 501–520. Springer, Heidelberg (2006). doi:10.1007/11818175_30. 4
Damgård, I., Nielsen, J.B., Wichs, D.: Isolated proofs of knowledge and isolated zero knowledge. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 509–526. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_29. 4
Damgård, I., Pastro, V., Smart, N., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_38. 4
Dolev, D.: The Byzantine generals strike again. J. Algorithms 3(1), 14–30 (1982). 4
Elkin, M.: An improved construction of progression-free sets. In: Proceedings of the Twenty-first Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 886–905. Society for Industrial and Applied Mathematics (2010). 18, 19, 20, 21
Gács, P., Körner, J.: Common information is far less than mutual information. Probl. Control Inf. Theory 2(2), 149–162 (1973). 26
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th ACM STOC, pp. 218–229. ACM Press, May 1987. 4
Goyal, V., Ishai, Y., Sahai, A., Venkatesan, R., Wadia, A.: Founding cryptography on tamper-proof hardware tokens. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 308–326. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11799-2_19. 4
Graham, R.L., Pollak, H.O.: On the addressing problem for loop switching. Bell Syst. Tech. J. 50(8), 2495–2519 (1971). 10, 23
Graham, R.L., Pollak, H.O.: On embedding graphs in squashed cubes. In: Alavi, Y., Lick, D.R., White, A.T. (eds.) Graph Theory and Applications. LNM, vol. 303, pp. 99–110. Springer, Heidelberg (1972). doi:10.1007/BFb0067362. 10, 23
Gupta, D., Ishai, Y., Maji, H.K., Sahai, A.: Secure computation from leaky correlated randomness. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 701–720. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_34. 6, 7, 8, 9, 10, 11, 16
Harnik, D., Ishai, Y., Kushilevitz, E., Nielsen, J.B.: OT-combiners via secure computation. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 393–411. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78524-8_22. 10
Harnik, D., Kilian, J., Naor, M., Reingold, O., Rosen, A.: On robust combiners for oblivious transfer and other primitives. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 96–113. Springer, Heidelberg (2005). doi:10.1007/11426639_6. 10
Heath-Brown, D.R.: Integer sets containing no arithmetic progressions. J. Lond. Math. Soc. (2) 35(3), 385–394 (1987). 18, 20
Hoffman, A.J.: Eigenvalues and partitionings of the edges of a graph. Linear Algebra Appl. 5(2), 137–146 (1972). 23
Huang, H., Sudakov, B.: A counterexample to the alon-saks-seymour conjecture and related problems. Combinatorica 32(2), 205–219 (2012). 23
Impagliazzo, R., Luby, M.: One-way functions are essential for complexity based cryptography (extended abstract). In: 30th FOCS, pp. 230–235. IEEE Computer Society Press, October/November 1989. 4, 12, 22
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Extracting correlations. In: 50th FOCS, pp. 261–270. IEEE Computer Society Press, October 2009. 5, 6, 7, 10
Ishai, Y., Maji, H.K., Sahai, A., Wullschleger, J.: Single-use OT combiners with near-optimal resilience. In: 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014, pp. 1544–1548. IEEE (2014). 6, 9, 10
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_32. 4, 10
Kahn, J.: Recent results on some not-so-recent hypergraph matching and covering problems. DIMACS, Center for Discrete Mathematics and Theoretical Computer Science (1991). 23
Katz, J.: Universally composable multi-party computation using tamper-proof hardware. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 115–128. Springer, Heidelberg (2007). doi:10.1007/978-3-540-72540-4_7. 4
Kilian, J.: Founding cryptography on oblivious transfer. In: 20th ACM STOC, pp. 20–31. ACM Press, May 1988. 4, 12, 22
Kilian, J.: More general completeness theorems for secure two-party computation. In: 32nd ACM STOC, pp. 316–324. ACM Press, May 2000. 4
Kratzke, T., Reznick, B., West, D.: Eigensharp graphs: decomposition into complete bipartite subgraphs. Trans. Am. Math. Soc. 308(2), 637–653 (1988). 23
Künzler, R., Müller-Quade, J., Raub, D.: Secure computability of functions in the IT setting with dishonest majority and applications to long-term security. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 238–255. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_15. 4, 12, 22
Kushilevitz, E.: Privacy and communication complexity. In: 30th FOCS, pp. 416–421. IEEE Computer Society Press, October/November 1989. 4, 12, 22
Maji, H.K., Prabhakaran, M., Rosulek, M.: Complexity of multi-party computation problems: the case of 2-party symmetric secure function evaluation. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 256–273. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_16. 4, 12, 22
Maji, H.K., Prabhakaran, M., Rosulek, M.: A unified characterization of completeness and triviality for secure function evaluation. In: Galbraith, S., Nandi, M. (eds.) INDOCRYPT 2012. LNCS, vol. 7668, pp. 40–59. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34931-7_4. 4
Malkhi, D., Nisan, N., Pinkas, B., Sella, Y.: Fairplay - secure two-party computation system. In: Blaze, M. (ed.) Proceedings of the 13th USENIX Security Symposium, San Diego, CA, USA, 9–13 August 2004, pp. 287–302. USENIX (2004). 4
McNew, N.: Avoiding geometric progressions in the integers, 02 May 2017. https://math.dartmouth.edu/graduate-students/works/2013-14/McNew-GradPosterSession.pdf. 20
Meier, R., Przydatek, B.: On robust combiners for private information retrieval and other primitives. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 555–569. Springer, Heidelberg (2006). doi:10.1007/11818175_33. 10
Meier, R., Przydatek, B., Wullschleger, J.: Robuster combiners for oblivious transfer. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 404–418. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70936-7_22. 10
Moran, T., Segev, G.: David and Goliath commitments: UC computation for asymmetric parties using tamper-proof hardware. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 527–544. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_30. 4
Nielsen, J.B., Nordholt, P.S., Orlandi, C., Burra, S.S.: A new approach to practical active-secure two-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 681–700. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_40. 4
Nisan, N., Wigderson, A.: On rank vs. communication complexity. Combinatorica 15(4), 557–565 (1995). 23
Peck, G.W.: A new proof of a theorem of Graham and Pollak. Discret. Math. 49(3), 327–328 (1984). 23
Prabhakaran, V.M., Prabhakaran, M.: Assisted common information. In: 2010 IEEE International Symposium on Information Theory, ISIT Proceedings, Austin, Texas, USA, 13–18 June 2010, pp. 2602–2606. IEEE (2010). 26
Prabhakaran, V.M., Prabhakaran, M.: Assisted common information: further results. In: Kuleshov, A., Blinovsky, V., Ephremides, A. (eds.) 2011 IEEE International Symposium on Information Theory Proceedings, ISIT 2011, St. Petersburg, Russia, 31 July–5 August 2011, pp. 2861–2865. IEEE (2011). 26
Przydatek, B., Wullschleger, J.: Error-tolerant combiners for oblivious primitives. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008. LNCS, vol. 5126, pp. 461–472. Springer, Heidelberg (2008). doi:10.1007/978-3-540-70583-3_38. 10
Rabin, T., Ben-Or, M.: Verifiable secret sharing and multiparty protocols with honest majority (extended abstract). In: 21st ACM STOC, pp. 73–85. ACM Press, May 1989. 4
Razborov, A.A.: The gap between the chromatic number of a graph and the rank of its adjacency matrix is superlinear. Discret. Math. 108(1), 393–396 (1992). 23
Roth, K.F.: On certain sets of integers. J. Lond. Math. Soc. 1(1), 104–109 (1953). 18, 20
Salem, R., Spencer, D.C.: On sets of integers which contain no three terms in arithmetical progression. Proc. Natl. Acad. Sci. 28(12), 561–563 (1942). 19
Sanders, T.: On Roth’s theorem on progressions. Ann. Math. 174, 619–636 (2011). 18, 20
Szemerédi, E.: Integer sets containing no arithmetic progressions. Acta Math. Hung. 56(1–2), 155–158 (1990). 18, 20
Tverberg, H.: On the decomposition of kn into complete bipartite graphs. J. Graph Theory 6(4), 493–494 (1982). 23
van Lint, J.H., Wilson, R.M.: A Course in Combinatorics. Cambridge University Press, Cambridge (2001). 23
Van Lint, J.H.: \(\{\)0, 1,*\(\}\) distance problems in combinatorics (1985). 23
Vishwanathan, S.: A polynomial space proof of the Graham-Pollak theorem. J. Comb. Theory Ser. A 115(4), 674–676 (2008). 23
Vishwanathan, S.: A counting proof of the Graham-Pollak theorem. Discret. Math. 313(6), 765–766 (2013). 23
Wolf, S., Wullschleger, J.: New monotones and lower bounds in unconditional two-party computation. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 467–477. Springer, Heidelberg (2005). doi:10.1007/11535218_28. 26
Wolf, S., Wullschleger, J.: Oblivious transfer is symmetric. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 222–232. Springer, Heidelberg (2006). doi:10.1007/11761679_14. 4, 8
Wyner, A.D.: The common information of two dependent random variables. IEEE Trans. Inf. Theory 21(2), 163–179 (1975). 7, 10, 23, 26, 27
Yan, W., Yeh, Y.-N.: A simple proof of Graham and Pollak’s theorem. J. Comb. Theory Ser. A 113(5), 892–893 (2006). 23
Yao, A.C.-C.: Protocols for secure computations (extended abstract). In: 23rd FOCS, pp. 160–164. IEEE Computer Society Press, November 1982. 4
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Block, A.R., Maji, H.K., Nguyen, H.H. (2017). Secure Computation Based on Leaky Correlations: High Resilience Setting. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10402. Springer, Cham. https://doi.org/10.1007/978-3-319-63715-0_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-63715-0_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63714-3
Online ISBN: 978-3-319-63715-0
eBook Packages: Computer ScienceComputer Science (R0)








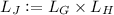 , the right partite set
, the right partite set  , and
, and






