Abstract
We present two practically efficient functional encryption schemes for a large class of quadratic functionalities. Specifically, our constructions enable the computation of so-called bilinear maps on encrypted vectors. This represents a practically relevant class of functions that includes, for instance, multivariate quadratic polynomials (over the integers). Our realizations work over asymmetric bilinear groups and are surprisingly efficient and easy to implement. For instance, in our most efficient scheme the public key and each ciphertext consist of \(2n+1\) and \(4n+2\) group elements respectively, where n is the dimension of the encrypted vectors, while secret keys are only two group elements. Our two schemes build on similar ideas, but develop them in a different way in order to achieve distinct goals. Our first scheme is proved (selectively) secure under standard assumptions, while our second construction is concretely more efficient and is proved (adaptively) secure in the generic group model.
As a byproduct of our functional encryption schemes, we show new predicate encryption schemes for degree-two polynomial evaluation, where ciphertexts consist of only O(n) group elements. This significantly improves the \(O(n^2)\) bound one would get from inner product encryption-based constructions.
R. Gay—Supported by ERC Project aSCEND (639554).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Traditional public key encryption allows the owner of a secret key \(\mathsf{sk}\) to decrypt ciphertexts created with respect to a (matching) public key \(\mathsf{mpk}\). At the same time, without \(\mathsf{sk}\), ciphertexts should not reveal any non trivial information about encrypted messages. This all-or-nothing nature of encryption is becoming insufficient in applications where a more fine-grained access to data is required. Functional Encryption (FE) allows to overcome this user-centric access to data of encryption in a very elegant way. Intuitively, given \(\mathsf{Encrypt}(m)\) and a key \(\mathsf{sk}_f\) corresponding to some function f, the owner of \(\mathsf{sk}_f\) learns f(m) and nothing else. Apart from being an interesting theoretical object, Functional Encryption has many natural applications. Think about cloud storage scenarios where users can rely on powerful external servers to store their data. To preserve their privacy, users might want to store their files encrypted. At the same time, the users may wish to let the service providers perform basic data mining operations on this data for commercial purposes, without necessarily disclosing the whole data. Functional Encryption allows to reconcile these seemingly contradicting needs, as service providers can get secret keys that allow them to perform the desired computations while preserving, as much as possible, the privacy of users.
In terms of security, the standard notion for functional encryption is indistinguishability. Informally, this notion states that an adversary who is allowed to see the secret keys for functionalities \(f_1, \ldots f_n\) should not be able to tell apart which of the challenge messages \(m_0\) or \(m_1\) has been encrypted, under the restriction that \(f_i(m_0)=f_i(m_1)\), for all i. This notion was studied in [13, 35] and shown inadequate for certain, complex, functionalitiesFootnote 1. They also explored an alternative, simulation-based, definition, which however cannot be satisfied, in general, without resorting to the random oracle heuristic.
Background on Functional Encryption. The idea of functional encryption originates from Identity Based Encryption (IBE) [11, 37] and the closely related concept of Searchable Encryption [1, 10]. In IBE, the encrypted message can be interpreted as a pair \((\mathsf{I},m)\), where \(\mathsf{I}\) is a public string and m is the actual message (often called the “payload”). More in general, the index \(\mathsf I\) can be interpreted as a set of attributes that can be either public or private. Public index schemes are often referred to as attribute based encryption [27, 36], a primitive that is by now very well understood [25]. For private index schemes, the situation is more intricate. A first distinction is between weakly and fully attribute hiding schemes [5]. The former notion refers to schemes where the set of secret keys the adversary is allowed to see in the security games is significantly restricted. The adversary is allowed to ask only keys corresponding to functions that cannot be used to decrypt the challenge message. Examples of these schemes are Anonymous Identity based encryption [11, 22], Hidden Vector Encryption [15] and (private index) predicate encryption [26, 28].
Things are less well established for the setting of private index, fully attribute hiding schemes, a notion that turns out to be equivalent to full fledged functional encryption [13]. Indeed, all known constructions supporting arbitrary circuits, either work for the case of bounded collusions [23, 24] or rely on powerful, but poorly understood, assumptions (e.g., [20]). Moreover, they are all terribly inefficient from a practical point of view.
To improve efficiency, a very natural approach is to try to realize schemes using a different, bottom up, perspective. Rather than focusing on generality, one might focus on devising efficient realizations for specific functionalities of practical interest. In 2015, Abdalla et al. [2] addressed this question for the case of linear functionalities. In particular, they show a construction which is both very simple and relies on standard, well studied assumptions (such as LWE and DDH). The construction was proved secure in the so-called selective setting where the adversary is expected to choose the messages on which she wants to be challenged in advance, even before the public key is set up. Not too surprisingly, this result sparkled significant interest in this bottom-up approach, with several results proposing new schemes [6], models [4, 9] and improved security [3, 6].
Still, none of these results managed to efficiently support more than linear functionalities. In particular, the technical barrier is to find FE schemes in which ciphertexts have size linear in the number of encrypted elements, in contrast to quadratic, as it can be achieved by using a scheme for linear functions.Footnote 2 This motivates the following question:
-
Can we construct a practically efficient functional encryption scheme
supporting more than linear functionalities?
1.1 Our Contribution
In this paper we answer the question above in the affirmative. We build two efficient functional encryption schemes for quadratic functions with linear-size ciphertexts. In terms of security, our first scheme is proven selective-secure under standard assumptions (Matrix Decisional Diffie Hellman [18] and 3-party DDH [12]), whereas our second scheme is proven adaptively secure in the generic group model, and is more efficient. In terms of functionality, to be more specific, our schemes allows to compute bilinear maps over the integers: messages are expressed as pairs of vectors \((\varvec{x}, \varvec{y}) \in \mathbb {Z}^n \times \mathbb {Z}^m\), secret keys are associated with (\(n \times m\)) matrices \(\mathbf {F}\), and decryption allows to compute \(\varvec{x}^{\top } \mathbf{F}\varvec{y}=\sum _{i,j}f_{ij} x_i y_j\). Bilinear maps represent a very general class of quadratic functions that includes, for instance, multivariate quadratic polynomials. These functions have several practical applications. For instance, a quadratic polynomial can express many statistical functions (e.g., (weighted) mean, variance, covariance, root-mean-square), the euclidean distance between two vectors, and the application of a linear or quadratic classifier (e.g., linear or quadratic regression).
In addition to the above applications of quadratic functions, we also show that our FE for bilinear maps can be used to construct new Predicate Encryption schemes (PE for short) that satisfy the fully attribute hiding property, and yield efficient solutions for interesting classes of predicates, such as constant-depth boolean formulas and comparisons. In a nutshell, in our PE scheme ciphertexts are associated with a set of attributes \((x_1,\ldots ,x_n)\) and a plaintext M, secret keys are associated with a degree-two polynomial P, and the decryption of a ciphertext \(\mathsf{Ct}_{(x_1,\ldots ,x_n) \in \mathbb {Z}^n}\) with a secret key \(\mathsf{sk}_{P \in \mathbb {Z}[X_1,\ldots ,X_n], \ \mathsf {deg}(P) \le 2}\) recovers M if, and only if, \(P(x_1,\ldots ,x_n)=1\). The attribute-hiding property refers to the fact that \(\mathsf{Ct}_{(x_1,\ldots ,x_n) \in \mathbb {Z}^n}\) leaks no information on its attribute \((x_1,\ldots ,x_n)\), beyond what is inherently leaked by the boolean value \(P(x_1,\ldots ,x_n)\mathop {=}\limits ^{?} 1\). Using our new functional encryption schemes as underlying building blocks, we obtain PE constructions for quadratic polynomials where ciphertexts consist of only O(n) group elements. This is in sharp contrast with the \(O(n^2)\) solutions one would get via inner product encryption schemes (e.g., [28]).
An Informal Description of Our FE Schemes. Our solutions work over asymmetric bilinear groups \(\mathbb G_1, \mathbb G_2, \mathbb G_T\) and are quite efficient. They are both essentially optimal in communication size: public key and ciphertexts are both linear in the size of the encrypted vectors; secret keys are only two group elements. Both our schemes share similar underlying ideas. These ideas are however developed in different ways to achieve different security and efficiency goals. Our first scheme, can be proved (selectively) secure under standard intractability assumptions but achieves somewhat worse performances in practice. The second construction, on the other hand, is (concretely) more efficient but it can be proved (adaptively) secure only in the generic group model. In what follows we will highlight some of the core ideas underlying both schemes. How these ideas are implemented and developed in the two cases will be discussed when introducing each specific scheme.
Let us recall that the functionality provided by our FE scheme is that one encrypts pairs of vectors \(\varvec{x}, \varvec{y}\), functions are matrices \(\mathbf{F}\), and decryption allows to obtain \(\varvec{x}^{\top } \mathbf{F}\varvec{y}\). The initial idea of the construction is to encrypt the two vectors \(\varvec{x} \in \mathbb {Z}^{n}\) and \(\varvec{y} \in \mathbb {Z}^{m}\) in a sort of “matrix” ElGamal in the two groups \(\mathbb G_1\) and \(\mathbb G_2\) respectively. Namely, we set
where: \(\rho , \sigma \) are randomly chosen, \(\{\mathbf {A}\varvec{r}_{i}, \mathbf {B}\varvec{s}_{j}\}_{i,j}\) are in the public key, and are constructed from two random matrices \(\mathbf {A}\) and \(\mathbf {B}\) and a collection of random vectors \(\{\varvec{r}_{i}, \varvec{s}_{j}\}_{i,j}\), and \(\varvec{a}, \varvec{b}\) are more carefully chosen vectors (see below)Footnote 3. Towards finding a decryption method, we first observe that, given \(\mathsf{Ct}_{(\varvec{x},\varvec{y})}\) and a function \(\mathbf{F}\), one can use the bilinear map to compute
Moreover, if we let \([\sum _{ij} f_{ij} \varvec{r}_i^{\top } \mathbf {A}^{\top } \mathbf {B}\varvec{s}_j]_1\) be the secret key for function \(\mathbf {F}\) and include \([\rho \sigma ]_2\) in the ciphertext, one can remove the first term in U.
Our two schemes then extend this basic blueprint with additional (but different!) structure so as to enable the extraction from U of the value \([\varvec{x}^{\top } \mathbf{F}\varvec{y}]_T\). From this, in turn, the function’s result can be obtained via a brute force discrete log computationFootnote 4. At a very intuitive level (and deliberately ignoring many important details) a key difference between the two schemes lies in the way \(\mathbf {A}\), \(\mathbf {B}\), \(\varvec{a}\) and \(\varvec{b}\) are constructed.
In our first scheme, \(\mathbf {A}\) and \(\mathbf {B}\) are carefully sampled so that to be able to prove (selective) security under standard intractability assumptions (e.g. Matrix Decisional Diffie-Hellman). Moreover \(\varvec{a}\) and \(\varvec{b}\) are chosen such that \(\mathbf {A}^{\top } \varvec{a}= \mathbf {B}^{\top } \varvec{b}=\varvec{0}\) and \(\varvec{b}^{{\!\scriptscriptstyle {\top }}} \varvec{a}=1\). This ensures that the intermediate values \(\rho \sum _{ij} f_{ij} \varvec{r}_i^{\top } \mathbf {A}^{\top }\varvec{a} y_j\), \(\sigma \sum _{ij} f_{ij} \varvec{s}_j^{\top } \mathbf {B}^{\top }\varvec{b} x_i\) cancel out at decryption time.
In our second scheme, on the other hand, the public key values \(\mathbf {A}\varvec{r}_i\) and \(\mathbf {B}\varvec{s}_j\) are simple scalars, and the “canceling” is performed via an appropriate choice of vectors \(\varvec{a}, \varvec{b}\) and simple algebraic manipulations. This makes the resulting construction (concretely) more efficient. At the same time, we lose the possibility to rely on (general) matrix assumptions and we are able to prove (adaptive) security in the generic group model. To this end, as a contribution that can be of independent interest, we state and prove a master theorem that shows hardness in the generic bilinear group model for a broad family of interactive decisional problems (notably, a family that includes our FE scheme), extending some of the tools and results of the generic group framework recently developed by Barthe et al. [8].
Concurrent and Independent Work. In concurrent and independent work, Lin [31], and Ananth and Sahai [7] present constructions of private-key functional encryption schemes for degree-D polynomials based on D-linear maps. As a special case for \(D=2\), these schemes support quadratic polynomials from bilinear maps, as ours. Also, in terms of security, the construction of Lin is proven selectively secure based on the SXDH assumption, while the scheme of Ananth and Sahai is selectively secure based on ad-hoc assumptions that are justified in the multilinear group model. In comparison to these works, our schemes have the advantage of working in the (arguably more challenging) public key setting.
We provide a summary of the existing solutions for (efficient) functional encryption for quadratic functions in Table 1.
2 Preliminaries
Notation. We denote with \(\lambda \in \mathbb N\) a security parameter. A probabilistic polynomial time (PPT) algorithm \(\mathcal{A}\) is a randomized algorithm for which there exists a polynomial \(p(\cdot )\) such that for every input x the running time of \(\mathcal{A}(x)\) is bounded by p(|x|). We say that a function \(\epsilon : \mathbb N\rightarrow \mathbb R^+\) is negligible if for every positive polynomial \(p(\lambda )\) there exists \({\lambda }_0 \in \mathbb N\) such that for all \(\lambda > {\lambda }_0\): \(\epsilon (\lambda ) < 1/p(\lambda )\). If S is a set, \(x \leftarrow _{\textsc {r}}S\) denotes the process of selecting x uniformly at random in S. If \(\mathcal{A}\) is a probabilistic algorithm, \(y \leftarrow _{\textsc {r}}\mathcal{A}(\cdot )\) denotes the process of running \(\mathcal{A}\) on some appropriate input and assigning its output to y. For a positive integer n, we denote by [n] the set \(\{1,\ldots , n\}\). We denote vectors \(\varvec{x} = (x_i)\) and matrices \(\mathbf{A}= (a_{i,j})\) in bold. For a set S (resp. vector \(\varvec{x}\)) |S| (resp. \(|\varvec{x}|\)) denotes its cardinality (resp. number of entries). For any prime p and any matrix \(\mathbf {A}\in \mathbb {Z}_p^{n \times m}\) with \(n \ge m\), we denote by \(\mathsf {orth}(\mathbf {A}) := \{ \varvec{a}^{\bot }\in \mathbb {Z}^n_p : \mathbf {A}^{\!\scriptscriptstyle {\top }}\varvec{a}^{\bot }= \mathbf {0}\}\). For all square matrices \(\mathbf {A}\in \mathbb {Z}_p^{n \times n}\), we denote by \(\det (\mathbf {A})\) the determinant of \(\mathbf {A}\). For any \(n \in \mathbb {N}^*\), we denote by \(\mathsf {GL}_n\) the general linear group of degree n, that is, the set of all \(n \times n\) invertible matrices over \(\mathbb {Z}_p\). By \(\equiv \), we denote the equality of statistical distribution, and for any \(\varepsilon >0\), we denote by \(\approx _\varepsilon \) the \(\varepsilon \)-statistical of two distributions.
Bilinear Groups. Let \(\mathcal{G}(1^\lambda )\) be an algorithm (that we call a bilinear group generator) which takes as input the security parameter and outputs the description of a bilinear group setting \(\mathsf{bgp}= (p, \mathbb G_1, \mathbb G_2, \mathbb G_T, e, g_1, g_2)\), where \(\mathbb G_1\), \(\mathbb G_2\) and \(\mathbb G_T\) are groups of the same prime order \(p > 2^\lambda \), \(g_1 \in \mathbb G_1\) and \(g_2 \in \mathbb G_2\) are two generators, and \(e: \mathbb G_1 \times \mathbb G_2 \rightarrow \mathbb G_T\) is an efficiently computable, non-degenerate, bilinear map. We define \(g_{T} = e(g_1, g_2)\) as the canonical generator of \(\mathbb G_{T}\). In the case \(\mathbb G_1 = \mathbb G_2\), the groups are said symmetric, else they are said asymmetric. In this paper we work with asymmetric bilinear groups in which there is no efficiently computable isomorphisms between \(\mathbb G_1\) and \(\mathbb G_2\) (these are also known as Type-III groups [19]).
We use implicit representation of group elements as introduced in [18]. For \(s \in \{1,2,T\}\) and \(x \in \mathbb {Z}_p\), we let \([x]_s = g_s^{x} \in \mathbb G_{s}\). This notation is extended to matrices (and vectors) as follows. For any \(\mathbf{A}= (a_{i,j}) \in \mathbb {Z}_p^{m \times n}\) we define
Note that from an element \([x]_s \in \mathbb G_s\) and a scalar a it is possible to efficiently compute \([ax] \in \mathbb G_s\). Also, given group elements \([a]_1 \in \mathbb G_1\) and \([b]_2 \in \mathbb G_2\), one can efficiently compute \([ab]_{T} = e([a]_1, [b]_2)\). Furthermore, given a matrix of scalars \(\mathbf{F}= (f_{i,j}) \in \mathbb {Z}_p^{n \times n}\) and two n-dimensional vectors of group elements \([\varvec{a}]_1, [\varvec{b}]_2\), one can efficiently compute
As above, for an easier and more compact presentation, in our work we slightly abuse notation and treat all groups \(\mathbb G_1, \mathbb G_2, \mathbb G_T\) as additive groups.
2.1 Complexity Assumptions
We recall the definitions of the Matrix Decision Diffie-Hellman (\(\mathsf {mddh}\)) Assumption [18].
Definition 1
(Matrix Distribution). Let \(k \in \mathbb {N}\). We call \(\mathcal {D}_k\) a matrix distribution if it outputs in polynomial time matrices in \(\mathbb {Z}_p^{(k+1)\times k}\) of full rank k, and satisfying the following property,
Property 1
where \(\mathbf {A},\mathbf {B}\leftarrow _{\textsc {r}}\mathcal {D}_k\).
Without loss of generality, we assume the first k rows of \(\mathbf {A}\leftarrow _{\textsc {r}}\mathcal {D}_k\) form an invertible matrix. Note that the basis property is not explicit in [18], but, as noted in [16, Lemma 1 (basis lemma)], all examples of matrix distribution presented in [18, Sect. 3.4], namely \(\mathcal {U}_k\), \(\mathcal {L}_k\), \(\mathcal {SC}_k\), \(\mathcal {C}_k\) and \(\mathcal {IL}_k\), satisfy this property.
The \(\mathcal {D}_k\)-Matrix Diffie-Hellman problem in \(\mathbb G_s\) for \(s \in \{1,2,T\}\) is to distinguish the two distributions \(([\mathbf {A}]_s, [\mathbf {A}\varvec{w}]_s)\) and \(([\mathbf {A}]_s,[\varvec{u}]_s)\) where \(\mathbf {A}\leftarrow _{\textsc {r}}\mathcal {D}_k\), \(\varvec{w}\leftarrow _{\textsc {r}}\mathbb {Z}_p^k\) and \(\varvec{u}\leftarrow _{\textsc {r}}\mathbb {Z}_p^{k+1}\).
Definition 2
( \(\mathcal {D}_k\) -Matrix Diffie-Hellman Assumption \(\mathcal {D}_k\)-\(\mathsf {mddh}\) ). Let \(\mathcal {D}_k\) be a matrix distribution. The \(\mathcal {D}_k\)-Matrix Diffie-Hellman (\(\mathcal {D}_k\)-\(\mathsf {mddh}\)) Assumption holds relative to \(\mathcal {G}\) in \(\mathbb G_s\), for \(s \in \{1,2,T\}\), if for all PPT adversaries \(\mathcal {A}\),
is \(\mathsf {negl}(\lambda )\), where probabilities are over the choices of \(\mathsf{bgp}\leftarrow _{\textsc {r}}\mathcal {G}(1^\lambda )\), \(\mathbf {A}\leftarrow _{\textsc {r}}\mathcal {D}_k, \varvec{w}\leftarrow _{\textsc {r}}\mathbb {Z}_p^k, \varvec{u}\leftarrow _{\textsc {r}}\mathbb {Z}_p^{k+1}\).
For each \(k \ge 1\), [18] specifies distributions (\(\mathcal {U}_k\), \(\mathcal {L}_k\), \(\mathcal {SC}_k\), \(\mathcal {C}_k\) and \(\mathcal {IL}_k\)) over \(\mathbb {Z}_p^{(k+1)\times k}\) such that the corresponding \(\mathcal {D}_k\)-\(\mathsf {mddh}\) assumptions are generically secure in bilinear groups and form a hierarchy of increasingly weaker assumptions. \(\mathcal {L}_k\)-\(\mathsf {mddh}\) is the well known k-Linear Assumption k-\(\mathsf {Lin} \) with 1-\(\mathsf {Lin} \) = \(\mathsf {DDH}\).
Let \(Q \ge 1\). For \(\mathbf {W}\leftarrow _{\textsc {r}}\mathbb {Z}_q^{k \times Q},\mathbf {U}\leftarrow _{\textsc {r}}\mathbb {Z}_q^{(k+1) \times Q}\), we consider the Q-fold \(\mathcal {D}_k\)-\(\mathsf {mddh}\) Assumption which consists in distinguishing the distributions \(([\mathbf {A}], [\mathbf {A}\mathbf {W}])\) from \(([\mathbf {A}], [\mathbf {U}])\). That is, a challenge for the Q-fold \(\mathcal {D}_k\)-\(\mathsf {mddh}\) Assumption consists of Q independent challenges of the \(\mathcal {D}_k\)-\(\mathsf {mddh}\) Assumption (with the same \(\mathbf {A}\) but different randomness \(\varvec{w}\)). In [18] it is shown that the two problems are equivalent.
Lemma 1
(Random self-reducibility of \(\mathcal {U}_{\ell ,k}\)-\(\mathsf {mddh}\), [18]). Let \(k,Q \in \mathbb {N}\), and \(s \in \{1,2,T\}\). For any PPT adversary \(\mathcal {A}\), there exists a PPT adversary \(\mathcal {B}\) such that
where \(\mathbf {Adv}^{Q \text {-} \mathcal {D}_k \text {-} \mathsf {mddh}}_{\mathcal {G},\mathbb G_s,\mathcal {A}}(\lambda ) :=| \Pr [\mathcal {B}(\mathsf{bgp},[\mathbf {A}]_s, [\mathbf {A}\mathbf {W}]_s)=1]-\Pr [\mathcal {B}(\mathsf{bgp},[\mathbf {A}]_s,[\mathbf {U}]_s) =1] |\) and the probability is taken over \(\mathsf{bgp}\leftarrow _{\textsc {r}}\mathcal {G}(1^\lambda )\), \(\mathbf {A}\leftarrow _{\textsc {r}}\mathcal {U}_k, \mathbf {W}\leftarrow _{\textsc {r}}\mathbb {Z}_q^{k \times Q}, \mathbf {U}\leftarrow _{\textsc {r}}\mathbb {Z}_q^{(k+1) \times Q}\).
We also recall the definition of 3-party Decision Diffie-Hellman (3-\(\mathsf {pddh}\)) Assumption introduced in [12]. We give a variant in the asymmetric-pairing setting.
Definition 3
(3-party Decision Diffie-Hellman Assumption 3-\(\mathsf {pddh}\) ). We say that the 3-party Decision Diffie-Hellman (3-\(\mathsf {pddh}\)) Assumption holds relative to \(\mathcal {G}\) if for all PPT adversaries \(\mathcal {A}\),
where the probability is taken over \(\mathsf{bgp}\leftarrow _{\textsc {r}}\mathcal {G}(1^\lambda )\), \(a,b,c,d \leftarrow _{\textsc {r}}\mathbb {Z}_p\).
2.2 Functional Encryption
We recall the definitions of Functional Encryption as given by Boneh et al. [13].
Definition 4
(Functionality). A functionality F defined over \((\mathcal{K}, \mathcal{M})\) is a function \(F: \mathcal{K}\times \mathcal{M}\rightarrow \mathcal{Y}\cup \{\bot \}\) where \(\mathcal{K}\) is a key space, \(\mathcal{M}\) is a message space and \(\mathcal{Y}\) is an output space which does not contain the special symbol \(\bot \).
Definition 5
(Functional Encryption). A functional encryption scheme \(\mathsf {FE}\) for a functionality F is defined by a tuple of algorithms \(\mathsf {FE}= (\mathsf{Setup}, \mathsf{KeyGen}, \mathsf{Encrypt}, \mathsf{Decrypt})\) that work as follows.
-
\(\mathsf{Setup}(1^{\lambda },F)\) takes as input a security parameter \(1^{\lambda }\), the functionality \(F: \mathcal {K}\times \mathcal{M}\rightarrow \mathcal {Y}\), and outputs a master secret key \(\mathsf {msk}\) and a master public key \(\mathsf {mpk}\).
-
\(\mathsf{KeyGen}(\mathsf {msk}, K)\) takes as input the master secret key and a key \(K \in \mathcal{K}\) of the functionality (i.e., a function), and outputs a secret key \(\mathsf{sk}_{K}\).
-
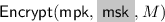 takes as input the master public key \(\mathsf {mpk}\) and a message \(M \in \mathcal{M}\), and outputs a ciphertext \(\mathsf{Ct}\). It can take as an additional input the master secret key, in which case, we talk about
takes as input the master public key \(\mathsf {mpk}\) and a message \(M \in \mathcal{M}\), and outputs a ciphertext \(\mathsf{Ct}\). It can take as an additional input the master secret key, in which case, we talk about  functional encryption. By opposition, when \(\mathsf {msk}\) is not an input of the encryption, algorithm, we say that \(\mathsf {FE}\) is public-key.
functional encryption. By opposition, when \(\mathsf {msk}\) is not an input of the encryption, algorithm, we say that \(\mathsf {FE}\) is public-key. -
\(\mathsf{Decrypt}(\mathsf{sk}_K, \mathsf{Ct})\) takes as input a secret key \(\mathsf{sk}_{K}\) and a ciphertext \(\mathsf{Ct}\), and returns an output \(Y \in \mathcal{Y}\cup \{\bot \}\).
For correctness, it is required that for all \((\mathsf {mpk}, \mathsf {msk}) \leftarrow _{\textsc {r}}\mathsf{Setup}(1^{\lambda })\), all keys \(K \in \mathcal{K}\) and all messages \(M \in \mathcal{M}\), if \(\mathsf{sk}_K \leftarrow _{\textsc {r}}\mathsf{KeyGen}(\mathsf {msk}, K)\) and  , then it holds with overwhelming probability that \(\mathsf{Decrypt}(\mathsf{sk}_{K}, \mathsf{Ct}) = F(K,M)\) whenever \(F(K, M) \ne \bot \).
, then it holds with overwhelming probability that \(\mathsf{Decrypt}(\mathsf{sk}_{K}, \mathsf{Ct}) = F(K,M)\) whenever \(F(K, M) \ne \bot \).
Indistinguishability-Based Security. For a functional encryption scheme \(\mathsf {FE}\) for a functionality F over \((\mathcal{K}, \mathcal{M})\), security against chosen-plaintext attacks (IND-FE-CPA, for short) is defined via the following experiment, denoted \(\mathbf {Exp}_{\mathsf {FE}, \mathcal{A}}^{\mathsf{ind\text {-}fe\text {-}cpa}\text {-}\beta }(\lambda )\), which is parametrized by an adversary \(\mathcal{A}\), a bit \(\beta \in \{0,1\}\), and a security parameter \(\lambda \).
-
Setup: run \((\mathsf {mpk}, \mathsf {msk}) \leftarrow _{\textsc {r}}\mathsf{Setup}(1^{\lambda })\) and give \(\mathsf {mpk}\) to \(\mathcal{A}\).
-
Query: \(\mathcal{A}\) adaptively makes secret key queries. At each query, \(\mathcal{A}\) specifies a key K and obtains \(\mathsf{sk}_K \leftarrow _{\textsc {r}}\mathsf{KeyGen}(\mathsf {msk}, K)\) from the challenger.
-
Challenge: \(\mathcal{A}\) chooses a pair of messages \(M_0, M_1 \in \mathcal{M}\) such that \(F(K, M_0) = F(K, M_1)\) holds for all keys K queried in the previous phase. The challenger computes \(\mathsf{Ct}^* \leftarrow _{\textsc {r}}\mathsf{Encrypt}(\mathsf {mpk}, M_\beta )\) and returns \(\mathsf{Ct}^*\) to \(\mathcal{A}\).
-
Query: \(\mathcal{A}\) makes more secret key queries. At each query \(\mathcal{A}\) can adaptively choose a key \(K \in \mathcal{K}\), but under the requirement that \(F(K, M_0) = F(K, M_1)\).
-
Guess: \(\mathcal{A}\) eventually outputs a bit \(\beta ' \in \{0,1\}\), and the experiment outputs the same bit.
For any stateful adversary \(\mathcal{A}\), any functional encryption scheme \(\mathsf {FE}\) for a functionality F over \((\mathcal{K}, \mathcal{M})\), any bit \(\beta \in \{0,1\}\), and any security parameter \(\lambda \), we give a compact description of experiment \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\), and its selective version \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\), in Fig. 1.
Experiments \(\mathbf {Exp}_{\mathsf {FE}, \mathcal{A}}^{\mathsf{ind\text {-}fe\text {-}cpa}\text {-}\beta }(\lambda )\) and \(\mathbf {Exp}_{\mathsf {FE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}fe\text {-}cpa}\text {-}\beta }(\lambda )\) for \(b \in \{0,1\}\), used to define adaptive, and selective security of FE, respectively. In each procedure, the components inside a solid (dotted) frame are only present in the games marked by a solid (dotted) frame, and the components inside a gray frame only appears for  FE schemes. In both games, the oracle \(\mathsf {EncO}(\cdot ,\cdot )\) is queries at most once (by \(\mathcal {A}\) or the game itself), on \(M_0,M_1\), such that for all queries K to \(\mathsf {KeyGenO}(\cdot )\), we have: \(F(K,M_0)=F(K,M_1)\). Note that in the case of private-key FE, this corresponds to single-ciphertext security (which does not imply many-ciphertext security).
FE schemes. In both games, the oracle \(\mathsf {EncO}(\cdot ,\cdot )\) is queries at most once (by \(\mathcal {A}\) or the game itself), on \(M_0,M_1\), such that for all queries K to \(\mathsf {KeyGenO}(\cdot )\), we have: \(F(K,M_0)=F(K,M_1)\). Note that in the case of private-key FE, this corresponds to single-ciphertext security (which does not imply many-ciphertext security).
We define the advantage of \(\mathcal{A}\) for adaptive security as:
We define the advantage \(\mathbf {Adv}_{\mathsf {FE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}fe\text {-}cpa}}(\lambda )\) for selective security similarly, with respect to experiments \(\mathbf {Exp}_{\mathsf {FE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}fe\text {-}cpa}\text {-}\beta }(\lambda )\) for \(\beta \in \{0,1\}\).
Definition 6
(Indistinguishability-Based Security). A functional encryption scheme \(\mathsf {FE}\) is adaptively secure (resp. selectively secure) against chosen-plaintext attacks if for every PPT algorithm \(\mathcal{A}\), \(\mathbf {Adv}_{\mathsf {FE}, \mathcal{A}}^{\mathsf{ind\text {-}fe\text {-}cpa}}(\lambda )\) (resp. \(\mathbf {Adv}_{\mathsf {FE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}fe\text {-}cpa}}(\lambda )\)) is negligible.
2.3 Bilinear Maps Functionality
In this work we consider functional encryption schemes for the following bilinear map functionality. Let \(\mathsf{bgp}=(p,\mathbb G_1,\mathbb G_2, g_1, g_2,\mathbb G_T,e) \leftarrow _{\textsc {r}}\mathcal {G}(1^\lambda )\) be a bilinear group setting, and let \(n, m \in \mathbb N^{+}\) be positive integers. We let the message space \(\mathcal{M}:= \mathbb {Z}_p^{n} \times \mathbb {Z}_p^{m}\) – every message M is a pair of vectors \((\varvec{x}, \varvec{y})\) – the key space \(\mathcal{K}:=\mathbb {Z}_p^{n \times m}\) consists of matrices – every key \(K \in \mathcal{K}\) is a matrix \(\mathbf{F}= (f_{i,j})\) – and the output space is \(\mathcal{Y}:= \mathbb G_T\). The functionality F(K, M) is the one that computes the value \([\varvec{x}^{\top } \, \mathbf{F}\, \varvec{y}]_T \in \mathbb G_T\). As we discuss below, this functionality allows for interesting applications.
Bilinear maps over the integers. We note that for appropriate choices of \(\mathcal{M}\subset \mathbb {Z}_p^{n} \times \mathbb {Z}_p^{m}\) and \(\mathcal{K}\subset \mathbb {Z}_p^{n \times m}\), the output space of \(F(\mathcal{K}, \mathcal{M})\) can be made of size polynomial in the security parameter. In this case, there exist efficient methods to extract \(\varvec{x}^{\top } \, \mathbf{F}\, \varvec{y}\in \mathbb {Z}_p\) from \([\varvec{x}^{\top } \, \mathbf{F}\, \varvec{y}]_T \in \mathbb G_T\).
For example, one can fix integers \(B_x, B_y, B_f \in \mathbb N\), and define \(\mathcal{M}:= \{0,\ldots , B_x\}^n \times \{0,\ldots , B_y\}^m\), \(\mathcal{K}:= \{0,\ldots , B_f\}^{n \times m}\). Then the quantity \(B=m n B_x B_y B_f < p\) must be small enough to allow for efficient discrete logarithm computation.
Multivariate quadratic polynomials. We also note that bilinear maps over the integers capture an interesting class of quadratic functions, such multivariate quadratic polynomials:
This can be captured by setting \(\varvec{x} = \varvec{y} = (1, \varvec{m}) \in \mathbb {Z}_p^{n+1}\) and by encoding p’s coefficients in an upper triangular matrix \(\mathbf{F}= (f_{i,j}) \in \mathbb {Z}_p^{(n+1) \times (n+1)}\) where: \(f_{1,1} = p_0\), \(f_{1,i} = p_{i-1}\) for all \(i \in [2,n+1]\), \(f_{i,j} = 0\) for all \(i>j\), and \(f_{i,j} = p_{i-1,j-1}\) for all \(i \in [2, n+1]\) and \(j \ge i\).
2.4 Predicate Encryption
We recall the definition of predicate encryption, as originally defined in [28, 29].
Definition 7
(Predicate). A predicate \(\mathsf {P}\) defined over \((\mathcal {X},\mathcal {Y})\) is a boolean function: \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\).
Definition 8
(Predicate Encryption). A predicate encryption (PE) scheme for a predicate \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) consists of four algorithms \((\mathsf{Setup}, \mathsf{Encrypt},\) \({\mathsf {KeyGen}}, \mathsf{Decrypt})\):
-
\(\mathsf{Setup}(1^\lambda ,\mathsf {P},\mathcal {M})\rightarrow (\mathsf {mpk}, \mathsf {msk})\). The setup algorithm gets as input the security parameter \(\lambda \), the predicate \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\), the message space \(\mathcal {M}\) and outputs the public parameter \(\mathsf {mpk}\), and the master key \(\mathsf {msk}\).
-
\(\mathsf{Encrypt}(\mathsf {mpk},x,M)\rightarrow \mathsf{Ct}_x\). The encryption algorithm gets as input \(\mathsf {mpk}\), an attribute \(x \in \mathcal {X}\) and a message \(M \in \mathcal {M}\). It outputs a ciphertext \(\mathsf{Ct}_{x}\).
-
\({\mathsf {KeyGen}}(\mathsf {mpk},\mathsf {msk},y)\rightarrow \mathsf{sk}_{y}\). The key generation algorithm gets as input \(\mathsf {msk}\) and a value \(y \in \mathcal {Y}\), and outputs a secret key \(\mathsf{sk}_{y}\). Note that y is public in \(\mathsf{sk}_y\).
-
\(\mathsf{Decrypt}(\mathsf {mpk},\mathsf{sk}_{y},\mathsf{Ct}_x ) \rightarrow M\). The decryption algorithm gets as input \(\mathsf{sk}_y\) and \(\mathsf{Ct}_x\) such that \(\mathsf {P}(x,y)=1\). It outputs a message M.
For correctness, it is requires that for all \((x,y) \in \mathcal {X}\times \mathcal {Y}\) such that \(\mathsf {P}(x,y)=1\) and all \(M \in \mathcal {M}\), \(\Pr [ \mathsf{Decrypt}(\mathsf {mpk},\mathsf{sk}_y,\mathsf{Encrypt}(\mathsf {mpk},x,M)) = M]= 1,\) where the probability is taken over \((\mathsf {mpk},\mathsf {msk}) \leftarrow \mathsf{Setup}(1^\lambda ,\mathcal {X},\mathcal {Y},\mathcal {M})\), \( \mathsf{sk}_{y}\leftarrow {\mathsf {KeyGen}}(\mathsf {mpk}, \mathsf {msk}, y)\), and the coins of \(\mathsf{Encrypt}\).
Fully Attribute-Hiding Security. We recall the notion of fully attribute-hiding security for predicate encryption as defined in [28]. The fully attribute hiding property refers to the fact that an adversary cannot distinguish a ciphertext for attribute \(x^{(0)}\) from a ciphertext for \(x^{(1)}\), as long as it only queries keys \(\mathsf{sk}_y\) where \(\mathsf {P}(x^{(0)},y) = \mathsf {P}(x^{(1)},y)\). This is stronger than the so-called weakly attribute hiding property, which requires the adversary to only query keys \(\mathsf{sk}_y\) where \(\mathsf {P}(x^{(0)},y) = \mathsf {P}(x^{(1)},y)=0\).
Fully attribute hiding security is essentially the specialization of the indistinguishability based security notion for functional encryption, for the functionality \(F_{\mathsf {P}}(y, (x, M))\) that outputs M if \(\mathsf {P}(x,y)=1\) and \(\bot \) otherwise.
For any stateful adversary \(\mathcal{A}\), any predicate encryption scheme \(\mathsf {PE}\), any bit \(\beta \in \{0,1\}\), and any security parameter \(\lambda \), we define experiments \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\) and \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\) in Fig. 2. We define the advantage of \(\mathcal{A}\) for adaptive security as:
We define the advantage \(\mathbf {Adv}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}pe\text {-}cpa}}(\lambda )\) for selective security similarly, with respect to experiments \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\) for \(\beta \in \{0,1\}\).
Experiments \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\) and \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\) for \(b \in \{0,1\}\), used to define adaptive, and selective security of PE, respectively. In each procedure, the components inside a solid (dotted) frame are only present in the games marked by a solid (dotted) frame. In both games, the oracle \(\mathsf {EncO}(\cdot ,\cdot ,\cdot ,\cdot )\) is queried at most once (by \(\mathcal {A}\) or the game itself), on \(x^{(0)},M_0,x^{(1)},M_1\), such that for all queries y to \(\mathsf {KeyGenO}(\cdot )\), we have: \(\mathsf {P}(x^{(0)},y)=P(x^{(1)},y)\). Moreover, if \(\mathsf {P}(x^{(0)},y)=1\) for some query y to \(\mathsf {KeyGenO}(\cdot )\), then \(M_0=M_1\).
Definition 9
(Fully Attribute-Hiding Security). A predicate encryption scheme \(\mathsf {PE}\) is fully attribute hiding, adaptively secure (resp. selectively secure) against chosen-plaintext attacks if for every PPT algorithm \(\mathcal{A}\), \(\mathbf {Adv}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{ind\text {-}pe\text {-}cpa}}(\lambda )\) (resp. \(\mathbf {Adv}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{sel\text {-}ind\text {-}pe\text {-}cpa}}(\lambda )\)) is negligible.
3 Our Functional Encryption for Bilinear Maps from MDDH
In this Section we present a functional encryption scheme that supports the bilinear maps functionality described in Sect. 2.3, and is proven selectively secure under standard assumptions.
To begin with, in Sect. 3.1 we describe a simple FE scheme that works in the private-key setting, and is only single-ciphertext secure.
This private-key scheme is used as a building block in the security proof of our main public-key FE scheme that we present in Sect. 3.2.
3.1 Private-Key, Single-Ciphertext Secure FE for Bilinear Maps
In this section, we present a family of private-key, single-ciphertext secure functional encryption schemes for bilinear maps, parametrized by an integer \(k \ge 1\) and a matrix distribution \(\mathcal {D}_k\) (see Definition 1). That is, for each \(k \in \mathbb {N}\), and each matrix distribution \(\mathcal {D}_k\), the scheme \(\mathsf {FE}_\mathsf {one}(k,\mathcal {D}_k)\), presented in Fig. 3, is single-ciphertext, selectively secure under the \(\mathcal {D}_k\)-MDDH assumption, on asymmetric pairings.
Technical overview. Before describing the scheme in full detail in Fig. 3, we give an informal exposition of our techniques. The basic idea in our private-key, single ciphertext secure FE is to create the ciphertext and the secret keys of the form:
where \(\mathbf {A}, \mathbf {B}\leftarrow _{\textsc {r}}\mathcal {D}_k\), and \((\mathbf {A}| \varvec{b}^{\bot })\), \((\mathbf {B}| \varvec{a}^{\bot })\) are bases of \(\mathbb {Z}_p^{k+1}\) such that \(\varvec{a}^{\bot }\in \mathsf {orth}(\mathbf {A})\) and \(\varvec{b}^{\bot }\in \mathsf {orth}(\mathbf {B})\), à la [16]. The vectors \([\mathbf {A}\varvec{r}_i]_1\) and \([\mathbf {B}\varvec{s}_j]_2\) for \(i \in [n], j \in [m]\), \(\varvec{a}^{\bot }\) and \(\varvec{b}^{\bot }\) are part of a master secret key, used to (deterministically) generate \(\mathsf{Ct}_{\varvec{x},\varvec{y}}\) and \(\mathsf{sk}_\mathbf {F}\). Correctness follows from the orthogonal property: decryption computes \(\sum _{i,j} f_{i,j} e([\mathbf {A}\varvec{r}_i + \varvec{b}^{\bot }x_i]^{\!\scriptscriptstyle {\top }}_1,[\mathbf {B}\varvec{s}_j + \varvec{a}^{\bot }y_j]_2) = \mathsf{sk}_{\mathbf {F}} + (\varvec{a}^{\bot })^{\!\scriptscriptstyle {\top }}\varvec{b}^{\bot }\cdot [F(\mathbf {F}, (\varvec{x}, \varvec{y}))]_T\), from which one can extract \(F(\mathbf {F}, (\varvec{x}, \varvec{y}))=0\) since \([(\varvec{a}^{\bot })^{\!\scriptscriptstyle {\top }}\varvec{b}^{\bot }]_{T}\) is public. Security relies on the \(\mathcal {D}_k\)-MDDH Assumption [18], which stipulates that given \([\mathbf {A}]_1, [\mathbf {B}]_2\) drawn from a matrix distribution \(\mathcal {D}_k\) over \(\mathbb {Z}_p^{(k+1)\times k}\),
where \(\varvec{r},\varvec{s}\leftarrow _{\textsc {r}}\mathbb {Z}_p^{k}\), and \(\varvec{u}, \varvec{v}\leftarrow _{\textsc {r}}\mathbb {Z}_p^{k+1}\). This allows to change \(\mathsf{Ct}_{(\varvec{x}^{(0)},\varvec{y}^{(0)})}\) into \(\mathsf{Ct}_{(\varvec{x}^{(1)},\varvec{y}^{(1)})}\), but creates an extra term \(\left[ \varvec{x}^{(1) {\!\scriptscriptstyle {\top }}} \mathbf {F}\varvec{y}^{(1)} - \varvec{x}^{(0) {\!\scriptscriptstyle {\top }}} \mathbf {F}\varvec{y}^{(0)}\right] _T\) in the secret keys \(\mathsf{sk}_\mathbf {F}\). We conclude the proof using the fact that for all \(\mathbf {F}\) queried to \({\mathsf {KeyGen}}\), \( F(\mathbf {F}, (\varvec{x}^{(0)},\varvec{y}^{(0)})) = F(\mathbf {F}, (\varvec{x}^{(1)},\varvec{y}^{(1)}))\), as required by the security definition for FE (see Sect. 2.2 for the definition of FE), which cancels out the extra term in all secret keys.
In the following theorem we prove the correctness of the scheme \(\mathsf {FE}_\mathsf {one}\).
Theorem 1
(Correctness). For any \(k \in \mathbb {N}^*\) and any matrix distribution \(\mathcal {D}_k\), the functional encryption scheme \(\mathsf {FE}_\mathsf {one}(k,\mathcal {D}_k)\) defined in Fig. 3 has perfect correctness.
Proof of Theorem 1 . Correctness follows from the fact that for all \(i \in [n],j \in [m]\),
since \(\mathbf {A}^{\!\scriptscriptstyle {\top }}\varvec{a}^{\bot }= \mathbf {B}^{\!\scriptscriptstyle {\top }}\varvec{b}^{\bot }= \mathbf {0}\). Therefore, the decryption computes
Property 1 in Definition 1 implies that \((\varvec{b}^{\bot })^{\!\scriptscriptstyle {\top }}\varvec{a}^{\bot }\ne 0\) with probability \(1-\frac{1}{\varOmega (p)}\) over the choices of \(\mathbf {A}, \mathbf {B}\leftarrow _{\textsc {r}}\mathcal {D}_k\), \(\varvec{a}^{\bot }\leftarrow _{\textsc {r}}\mathsf {orth}(\mathbf {A})\), and \(\varvec{b}^{\bot }\leftarrow _{\textsc {r}}\mathsf {orth}(\mathbf {B})\). Therefore, one can enumerate all possible \(v \in \mathcal {Y}\) and check if \(v \cdot [(\varvec{b}^{\bot })^{\!\scriptscriptstyle {\top }}\varvec{a}^{\bot }]_T = D\). This can be done in time \(|\mathcal {Y}|\), thus, we need to set \(\mathcal {Y}\) to be of size \(\mathsf {poly}(\lambda )\). \(\square \)
Next, we show that \(\mathsf {FE}_\mathsf {one}\) is selective-secure, for adversaries that make a single challenge encryption query, under the MDDH assumption.
Theorem 2
(Security). For any \(k \in \mathbb {N}^*\) and any matrix distribution \(\mathcal {D}_k\), if the \(\mathcal {D}_k\)-MDDH assumptions hold in \(\mathbb G_1\) and \(\mathbb G_2\), then the functional encryption scheme \(\mathsf {FE}_\mathsf {one}(k,\mathcal {D}_k)\) defined in Fig. 3 is selectively secure, in a single-ciphertext setting (see Definition 6). Namely, for any PPT adversary \(\mathcal {A}\), there exist PPT adversaries \(\mathcal {B}_1\) and \(\mathcal {B}_2\) such that:
Games \({\mathrm {G}}_0\), \({\mathrm {G}}_1\), \({\mathrm {G}}_2\), for the proof of selective security of \(\mathsf {FE}_\mathsf {one}(k,\mathcal {D}_k)\) in Fig. 3. In each procedure, the components inside a solid (dotted) frame are only present in the games marked by a solid (dotted) frame.
Proof of Theorem 2 . We prove the security of \(\mathsf {FE}_\mathsf {one}(k,\mathcal {D}_k)\) via a series of games that is compactly presented in Fig. 4. Before going to the details of the proof and proving the indistinguishability of each consecutive pair of games, we provide below a high level view of the game transitions:
-
Game \({\mathrm {G}}_0\) is the selective security experiment for scheme \(\mathsf {FE}_\mathsf {one}\) with only some syntactic changes. This is shown in Lemma 2.
-
Game \({\mathrm {G}}_1\) is the same as game \({\mathrm {G}}_0\) except that the \(\varvec{c}_{i}\) ciphertext components are uniformly random over \(\mathbb G_1^{k+1}\). In Lemma 3 we show that \({\mathrm {G}}_0\) is computationally indistinguishable from \({\mathrm {G}}_1\) under the MDDH assumption.
-
Game \({\mathrm {G}}_2\) is the same as game \({\mathrm {G}}_1\) except that the \(\widehat{\varvec{c}}_{j}\) ciphertext components are uniformly random over \(\mathbb G_2^{k+1}\). In Lemma 4 we show that \({\mathrm {G}}_1\) is computationally indistinguishable from \({\mathrm {G}}_2\) under the MDDH assumption. Finally, we show in in Lemma 5 that the adversary’s view in this game is independent of the bit \(\beta \), and thus the adversary’s advantage in this game is zero.
More formally, in what follows, we use \(\mathsf {Adv}_i\) to denote the advantage of \(\mathcal {A}\) in game \({\mathrm {G}}_i\), that is \(\mathsf {Adv}_i := |1-2\Pr [{\mathrm {G}}_i \text { returns } 1]|\).
Lemma 2
( \({\mathrm {G}}_0\) ). \(\mathsf {Adv}_0 = \mathbf {Adv}_{\mathsf {FE}_\mathsf {one}, \mathcal{A}}^{\mathsf{ind\text {-}fe\text {-}cpa}}(\lambda )\).
Proof
of Lemma 2 . We show that \({\mathrm {G}}_0\) corresponds to the game for selective security of the functional encryption scheme, in the private-key, single-ciphertext setting, as defined in Definition 6. It is clear that the output of the \(\mathsf{Setup}\) algorithm is identically distributed in both of these games. We show that this is also the case for the outputs of the \(\mathsf {KeyGenO}\) oracle. Indeed, for all \(i \in [n]\), \(j \in [m]\), we have:
Thus, in game \({\mathrm {G}}_0\), for all \(\mathbf {F}\in \mathbb {Z}_p^{n \times m}\), \(\mathsf {KeyGenO}(\mathbf {F})\) computes:
which is exactly as in the security game for selective security. \(\square \)
Lemma 3
( \({\mathrm {G}}_0\) to \({\mathrm {G}}_1\) ). There exists a PPT adversary \(\mathcal {B}_0\) such that
Proof
of Lemma 3 . Here, we use the MDDH assumption on \([\mathbf {A}]_1\) to change the distribution of the challenge ciphertext, after arguing that one can simulate the game without knowing \(\varvec{a}^{\bot }\) or \([\mathbf {A}]_2\).
Namely, we build a PPT adversary \(\mathcal {B}'_0\) against the n-fold \(\mathcal {D}_k\)-MDDH assumption in \(\mathbb G_1\) such that \(|\mathsf {Adv}_0 - \mathsf {Adv}_1| \le 2 \cdot \mathbf {Adv}^{n \text {-} \mathcal {D}_k \text {-} \mathsf {mddh}}_{\mathcal {G},\mathbb G_1,\mathcal {B}'_0}(\lambda ) + 2^{-\varOmega (\lambda )}\). Then, by Lemma 1, this implies the existence of a PPT adversary \(\mathcal {B}_0\) such that \(|\mathsf {Adv}_0 - \mathsf {Adv}_1| \le 2 \cdot \mathbf {Adv}^{\mathcal {D}_k \text {-} \mathsf {mddh}}_{\mathcal {G},\mathbb G_1,\mathcal {B}_0}(\lambda ) + 2^{-\varOmega (\lambda )}\).
Adversary \(\mathcal {B}'_0\) simulates the game to \(\mathcal {A}\) as described in Fig. 5. Finally, it outputs 1 if the bit \(\beta '\) output by the adversary \(\mathcal {A}\) is equal to \(\beta \), 0 otherwise. We show that when \(\mathcal {B}'_0\) is given a real MDDH challenge, that is, \([\varvec{h}_1| \cdots | \varvec{h}_n]_1 := \mathbf {A}\mathbf {R}\) for \(\mathbf {R}\leftarrow _{\textsc {r}}\mathbb {Z}_p^{k \times n}\), then it simulates the game \({\mathrm {G}}_0\), whereas it simulates the game \({\mathrm {G}}_1\) when given a fully random challenge, i.e. when \([\varvec{h}_1| \cdots | \varvec{h}_n]_1 \leftarrow _{\textsc {r}}\mathbb G_1^{(k+1)\times n}\), which implies the lemma.
Adversary \(\mathcal {B}'_0\) against the n-fold \(\mathcal {D}_k\)-\(\mathsf {mddh}\) assumption, for the proof of Lemma 3.
We use the following facts.
-
1.
For all \(\varvec{s}\in \mathbb {Z}_p^{k}\), \(\mathbf {B}\in \mathbb {Z}_p^{(k+1) \times k}\), \(\varvec{b}^{\bot }\in \mathsf {orth}(\mathbf {B})\), and \(\varvec{a}^{\bot }\in \mathbb {Z}_p^{k+1}\), we have:
$$\begin{aligned} (\varvec{b}^{\bot })^{\!\scriptscriptstyle {\top }}\varvec{a}^{\bot }= (\varvec{b}^{\bot })^{\!\scriptscriptstyle {\top }}(\mathbf {B}\varvec{s}+ \varvec{a}^{\bot }). \end{aligned}$$ -
2.
For all \(y_j^{(\beta )} \in \mathbb {Z}_p\), \(\varvec{s}\in \mathbb {Z}_p^k\):
$$\left( \{\varvec{s}_j\}_{j \in [m]}\right) _{\varvec{s}_j \leftarrow _{\textsc {r}}\mathbb {Z}^k_p} \equiv \left( \{\varvec{s}_j + y_j^{(\beta )} \varvec{s}\}_{j \in [m]}\right) _{\varvec{s}_j \leftarrow _{\textsc {r}}\mathbb {Z}^k_p}.$$ -
3.
$$\begin{aligned} \left( \mathbf {B}\varvec{s}+ \varvec{a}^{\bot }\right) _{\mathbf {A}, \mathbf {B}\leftarrow _{\textsc {r}}\mathcal {D}_k,\varvec{a}^{\bot }\leftarrow _{\textsc {r}}\mathsf {orth}(\mathbf {A}),\varvec{s}\leftarrow _{\textsc {r}}\mathbb {Z}_p^k} \approx _{\frac{1}{\varOmega (p)}} (\varvec{z})_{\varvec{z}\leftarrow _{\textsc {r}}\mathbb {Z}_p^{k+1}}, \end{aligned}$$
since \((\mathbf {B}| \varvec{a}^{\bot })\) is a basis of \(\mathbb {Z}_p^{k+1}\), with probability \(1-\frac{1}{\varOmega (p)}\) over the choices of \(\mathbf {A}, \mathbf {B}\), and \(\varvec{a}^{\bot }\) (this is implied by Property 1).
Therefore, we have for all \(\varvec{y}^{(\beta )} \in \mathbb {Z}_p^{m}\):

When \(\mathcal {B}'_0\) is given a real MDDH challenge, i.e., when for all \(i \in [n]\), \(\varvec{h}_i := \mathbf {A}\varvec{r}_i\), for \(\varvec{r}_i \leftarrow _{\textsc {r}}\mathbb {Z}_p^k\), we have \(\varvec{c}_i := \mathbf {A}\varvec{r}_i + x_i^{(\beta )} \varvec{b}^{\bot }\), exactly as in game \({\mathrm {G}}_0\), whereas \(\varvec{c}_i\) is uniformly random over \(\mathbb {Z}_p^{k+1}\) when \(\mathcal {B}'_0\) is given a random challenge, i.e., when for all \(i \in [n]\), \(\varvec{h}_i \leftarrow _{\textsc {r}}\mathbb {Z}_p^{k+1}\), as in game \({\mathrm {G}}_1\). As shown in the equation above, the rest of \(\mathcal {A}\)’s view, namely, \(\mathsf {mpk}\), \(\{\widehat{\varvec{c}}_j\}_{j \in [m]}\) computed by \(\mathcal {B}'_0\), and its simulation of \(\mathsf {KeyGenO}\), are statistically close to those of \({\mathrm {G}}_0\) (resp. \({\mathrm {G}}_1\)) when \(\mathcal {B}'_0\) is given a real MDDH challenge (resp. a uniformly random challenge). \(\square \)
Lemma 4
( \({\mathrm {G}}_1\) to \({\mathrm {G}}_2\) ). There exists a PPT adversary \(\mathcal {B}_1\) such that
Proof
of Lemma 4 . Here, we use the MDDH assumption on \([\mathbf {B}]_2\) to change the distribution of the challenge ciphertext, after arguing that one can simulate the game without knowing \(\varvec{b}^{\bot }\) or \([\mathbf {B}]_1\).
Namely, we build a PPT adversary \(\mathcal {B}'_1\) against the m-fold \(\mathcal {D}_k\)-MDDH assumption in \(\mathbb G_2\) such that \(|\mathsf {Adv}_1 - \mathsf {Adv}_2| \le 2 \cdot \mathbf {Adv}^{m \text {-} \mathcal {D}_k \text {-} \mathsf {mddh}}_{\mathcal {G},\mathbb G_2,\mathcal {B}'_1}(\lambda )\). Then, by Lemma 1, this implies the existence of a PPT adversary \(\mathcal {B}_1\) such that \(|\mathsf {Adv}_1 - \mathsf {Adv}_2| \le 2 \cdot \mathbf {Adv}^{\mathcal {D}_k \text {-} \mathsf {mddh}}_{\mathcal {G},\mathbb G_2,\mathcal {B}_1}(\lambda ) + \frac{2}{p-1}\).
Adversary \(\mathcal {B}'_1\) simulates the game to \(\mathcal {A}\) as described in Fig. 6. Finally, it outputs 1 if the bit \(\beta '\) output by the adversary \(\mathcal {A}\) is equal to \(\beta \), 0 otherwise. We show that when \(\mathcal {B}'_1\) is given a real MDDH challenge, that is, \([\varvec{h}_1| \cdots | \varvec{h}_m]_2 := [\mathbf {B}\mathbf {S}]_2\) for \(\mathbf {S}\leftarrow _{\textsc {r}}\mathbb {Z}_p^{k \times m}\), then it simulates the game \({\mathrm {G}}_1\), whereas it simulates the game \({\mathrm {G}}_2\) when given a uniformly random challenge, i.e. when \([\varvec{h}_1| \cdots | \varvec{h}_m]_2 \leftarrow _{\textsc {r}}\mathbb G_2^{(k+1)\times m}\), which implies the lemma.
Adversary \(\mathcal {B}_1\) against the \(\mathcal {D}_k\)-MDDH assumption, for the proof of Lemma 4.
We use the fact that for all \(\mathbf {A}, \mathbf {B}\in \mathbb {Z}_p^{(k+1) \times k}\),
Note that the leftmost distribution corresponds to \(\mathsf{mpk}\), \(\{\varvec{c}_i\}_{i \in [n]}\), and \(\mathsf {KeyGenO}\) distributed as in games \({\mathrm {G}}_1\) or \({\mathrm {G}}_2\) (these are identically distributed in these two games), while the last distribution corresponds to \(\mathsf{mpk}\), \(\{\varvec{c}_i\}_{i \in [n]}\), and \(\mathsf {KeyGenO}\) simulated by \(\mathcal {B}'_1\).
Finally, when \(\mathcal {B}'_1\) is given a real MDDH challenge, i.e., when for all \(j \in [m]\), \(\varvec{h}_j := \mathbf {B}\varvec{s}_j\), for \(\varvec{s}_j \leftarrow _{\textsc {r}}\mathbb {Z}_p^k\), we have \(\widehat{\varvec{c}}_j := \mathbf {B}\varvec{s}_j + y_j^{(\beta )} \varvec{a}^{\bot }\), exactly as in game \({\mathrm {G}}_1\), whereas \(\widehat{\varvec{c}}_j\) is uniformly random over \(\mathbb {Z}_p^{k+1}\) when \(\mathcal {B}'_1\) is given a random challenge, i.e., when for all \(j \in [m]\), \(\varvec{h}_j \leftarrow _{\textsc {r}}\mathbb {Z}_p^{k+1}\), as in game \({\mathrm {G}}_2\). \(\square \)
Lemma 5
( \({\mathrm {G}}_2\) ). \(\mathsf {Adv}_2 =0\).
Proof
of Lemma 5 . By definition of the security game, for all \(\mathbf {F}\) queried to \(\mathsf {KeyGenO}\), we have: \(\varvec{x}^{(\beta ){\!\scriptscriptstyle {\top }}} \mathbf {F}\varvec{y}^{(\beta )} = \varvec{x}^{(0){\!\scriptscriptstyle {\top }}} \mathbf {F}\varvec{y}^{(0)}\). Therefore, the view of the adversary in \({\mathrm {G}}_2\) is completely independent from the random bit \(\beta \leftarrow _{\textsc {r}}\{0,1\}\). \(\square \)
Combining Lemmas 3, 4, and 5 gives Theorem 2. \(\square \)
3.2 Public-Key FE for Bilinear Maps
In this section, we propose a family of public-key functional encryption schemes for the bilinear map functionality, that is \(F: \mathcal {K}\times \mathcal{M}\rightarrow \mathcal {Y}\), where \(\mathcal {K}:= \mathbb {Z}_p^{n \times m}\), \(\mathcal{M}:= \mathbb {Z}_p^n \times \mathbb {Z}_p^m\), and \(\mathcal {Y}:= \mathbb G_T\). The family of schemes is parametrized by an integer \(k \ge 1\) and a matrix distribution \(\mathcal {D}_k\) (see Definition 1) so that, for each \(k \in \mathbb {N}\), and each matrix distribution \(\mathcal {D}_k\), the scheme \(\mathsf {FE}(k,\mathcal {D}_k)\), presented in Fig. 7, is selectively secure under the \(\mathcal {D}_k\)-MDDH and the 3-\(\mathsf {pddh}\) assumptions, on asymmetric pairings.
Technical overview. We first give a high level view of our techniques. Our public-key FE builds on the private-key, single ciphertext secure FE presented in Sect. 3.1, but differs from it in the following essential way.
-
In the public-key setting, for the encryption to compute \([\mathbf {A}\varvec{r}_i + \varvec{b}^{\bot }x_i]\) and \([\mathbf {B}\varvec{s}_j + \varvec{a}^{\bot }y_j]\) for \(i \in [n], j\in [m]\) and any \(\varvec{x}\in \mathbb {Z}_p^n, \varvec{y}\in \mathbb {Z}_p^m\), the vectors \([\varvec{a}^{\bot }]_2\) and \([\varvec{b}^{\bot }]_1\) would need to be part of the public key, which is incompatible with the MDDH assumption on \([\mathbf {A}]_1\) or \([\mathbf {B}]_2\). To solve this problem, we add an extra dimension, namely, we use bases \(\left( \begin{array}{c|c} \mathbf {A}| \varvec{b}^{\bot }&{} 0 \\ \hline \mathbf {0}&{} 1 \end{array}\right) \) and \(\left( \begin{array}{c|c} \mathbf {B}| \varvec{a}^{\bot }&{} 0 \\ \hline \mathbf {0}&{} 1 \end{array}\right) \) where the extra dimension will be used for correctness, while \((\mathbf {A}| \varvec{b}^{\bot })\) and \((\mathbf {B}| \varvec{a}^{\bot })\) will be used for security (using the MDDH assumption, since \(\varvec{a}^{\bot }\) and \(\varvec{b}^{\bot }\) are not part of the public key anymore).
-
To avoid mix and match attacks, the encryption randomizes the bases
$$\left( \begin{array}{c|c} \mathbf {A}| \varvec{b}^{\bot }&{} 0 \\ \hline \mathbf {0}&{} 1 \end{array}\right) \text { and } \left( \begin{array}{c|c} \mathbf {B}| \varvec{a}^{\bot }&{} 0 \\ \hline \mathbf {0}&{} 1 \end{array}\right) $$into
$$\mathbf {W}^{-1}\left( \begin{array}{c|c} \mathbf {A}| \varvec{b}^{\bot }&{} 0 \\ \hline \mathbf {0}&{} 1 \end{array}\right) \text { and }\mathbf {W}^{\!\scriptscriptstyle {\top }}\left( \begin{array}{c|c} \mathbf {B}| \varvec{a}^{\bot }&{} 0 \\ \hline \mathbf {0}&{} 1 \end{array}\right) $$for \(\mathbf {W}\leftarrow _{\textsc {r}}\mathsf {GL}_{k+2}\) a random invertible matrix. This “glues” the components of a ciphertext that are in \(\mathbb G_1\) to those that are in \(\mathbb G_2\).
-
We randomize the ciphertexts so as to contain \([\mathbf {A}\varvec{r}_i \cdot \gamma ]_1\) and \([\mathbf {B}\varvec{s}_j \cdot \sigma ]_2\), where \(\gamma , \sigma \leftarrow _{\textsc {r}}\mathbb {Z}_p\) are the same for all \(i \in [n]\), and \(j \in [m]\), but fresh for each ciphertext. The ciphertexts also contain \([\gamma \cdot \sigma ]_1\), for correctness.
Discussion on the Techniques. We note that the techniques used here share some similarities with Dual Pairing Vector Space constructions (e.g., [17, 30, 32, 33]). In particular, our produced ciphertexts and private keys are distributed as in their corresponding counterparts in [32]. The similarities end here though. These previous constructions all rely on the Dual System Encryption paradigm [39], where the security proof uses a hybrid argument over all secret keys, leaving the distribution of the public key untouched. Our approach, on the other hand, manages to avoid this inherent security loss by changing the distributions of both the secret and public keys. Our approach also differs from [12] and follow-up works [14, 21] in that they focus on the comparison predicate (see Sect. 5), a function that can be expressed via a quadratic function that is significantly simpler than those considered here. Indeed, for the case of comparisons predicates it is enough to consider vectors of the form: \([\mathbf {A}\varvec{r}_i + x_i \varvec{b}^{\bot }]_1, [\mathbf {B}\varvec{s}_j + y_j \varvec{a}^{\bot }]_2\), where \(x_i\) and \(y_j\) are either 0, or some random value (fixed at setup time, and identical for all ciphertexts and secret keys), or are just random garbage.
In the following theorem we show that the scheme satisfies correctness.
Theorem 3
(Correctness). For any \(k \in \mathbb {N}^*\) and any matrix distribution \(\mathcal {D}_k\), the functional encryption scheme \(\mathsf {FE}(k,\mathcal {D}_k)\) defined in Fig. 7 has perfect correctness.
Proof
of Theorem 3 . Correctness follows from the facts that for all \(i \in [n]\), \(j \in [m]\):
Therefore, the decryption gets
\(\square \)
Next, in the following theorem we prove that the scheme satisfies indistinguishability based security in a selective sense.
Theorem 4
(Security). For any \(k \in \mathbb {N}^*\) and any matrix distribution \(\mathcal {D}_k\), if the \(\mathcal {D}_k\)-MDDH and the 3-\(\mathsf {pddh}\) assumptions hold relative to \(\mathcal{G}\), then the functional encryption scheme \(\mathsf {FE}(k,\mathcal {D}_k)\) defined in Fig. 7 is selectively secure. Precisely, for any PPT adversary \(\mathcal {A}\), there exists PPT adversaries \(\mathcal {B}\) and \(\mathcal {B}'\) such that:
Games \({\mathrm {G}}_i\), \(i=0,\ldots ,5\) for the proof of selective security of \(\mathsf {FE}(k,\mathcal {D}_k)\) in Fig. 7. In each procedure, the components inside a solid (dotted, gray) frame are only present in the games marked by a solid (dotted, gray) frame.
We prove the security of \(\mathsf {FE}(k,\mathcal {D}_k)\) via a series of games that are compactly presented in Fig. 8. The complete details of the proof are given in the full version; here we give an intuitive description of each game transition:
-
Game \({\mathrm {G}}_0\) is the selective security experiment for scheme \(\mathsf {FE}\). For the sake of the proof, we look at the public key elements \(\{[\mathbf {A}\varvec{r}_i]_1, [\mathbf {B}\varvec{s}_j]_2\}_{i \in [2n], j\in [2m]}\) as a ciphertext of the \(\mathsf {FE}_{\mathsf {one}}\) scheme encrypting vectors \((\mathbf {0}, \mathbf {0})\in \mathbb {Z}_p^{2n} \times \mathbb {Z}_p^{2m}\).
-
Game \({\mathrm {G}}_1\): with the above observation in mind, in this game we change the distribution of the public key elements so as to be interpreted as an \(\mathsf {FE}_\mathsf {one}\) ciphertext encrypting the vectors
$$ (\widetilde{\varvec{x}}, \widetilde{\varvec{y}})= \left( \left( \begin{array}{c} \varvec{x}^{(\beta )} \\ \hline -\varvec{x}^{(0)} \end{array} \right) , \left( \begin{array}{c} \varvec{y}^{(\beta )} \\ \hline \varvec{y}^{(0)} \end{array} \right) \right) \in \mathbb {Z}_p^{2n} \times \mathbb {Z}_p^{2m} $$In the full version we show how to argue the indistinguishability of \({\mathrm {G}}_1\) from \({\mathrm {G}}_0\) based on the selective, single-ciphertext security of \(\mathsf {FE}_\mathsf {one}\) (that in turn reduces to \(\mathcal {D}_k\)-MDDH).
-
Game \({\mathrm {G}}_2\): in this game we change the distribution of the \(\varvec{c}_{i}\) components of the challenge ciphertext. We switch from using \(\{\gamma \mathbf {A}\varvec{r}_i + \widetilde{x}_i \cdot \gamma \varvec{b}^{\bot }\}_{i \in [2n]}\) to \(\{\gamma \mathbf {A}\varvec{r}_i + \widetilde{x}_i \cdot (\gamma + v) \varvec{b}^{\bot }\}_{i \in [2n]}\), for a random \(v \leftarrow _{\textsc {r}}\mathbb {Z}_p\). In the full version we argue the indistinguishability of this change under the \(3\text {-}\mathsf {pddh}\) assumption.
-
Game \({\mathrm {G}}_3\): by using a statistical argument we show that in this game the challenge ciphertexts can be rewritten as
$$ \varvec{c}_i := \begin{pmatrix} \gamma \mathbf {A}\varvec{r}_i + (\gamma + v) x^{(\beta )}_i \varvec{b}^{\bot }\\ 0 \end{pmatrix}^{\!\scriptscriptstyle {\top }}\mathbf {W}^{-1}; $$$$\varvec{c}_{n+i} := \begin{pmatrix} \gamma \mathbf {A}\varvec{r}_{n+i} - (\gamma + v) x^{(0)}_i \varvec{b}^{\bot }\\ x^{(0)}_i \end{pmatrix}^{\!\scriptscriptstyle {\top }}\mathbf {V}^{-1}; $$$$\widehat{\varvec{c}}_j := \mathbf {W}\begin{pmatrix} \mathbf {B}\varvec{s}_j + y^{(\beta )}_j \varvec{a}^{\bot }\\ 0 \end{pmatrix}; \widehat{\varvec{c}}_{m+j} := \mathbf {V}\begin{pmatrix} \mathbf {B}\varvec{s}_{m+j} + y^{(0)}_j \varvec{a}^{\bot }\\ y^{(0)}_j \end{pmatrix}.$$This step essentially shows that the change in game \({\mathrm {G}}_2\) made the ciphertexts less dependent on the bit \(\beta \).
-
Game \({\mathrm {G}}_4\): in this game we change again the distribution of the challenge ciphertext components \(\varvec{c}_i\) switching from using \(\{\gamma \mathbf {A}\varvec{r}_i + \widetilde{x}_i \cdot (\gamma + v) \varvec{b}^{\bot }\}_{i \in [2n]}\) to \(\{\gamma \mathbf {A}\varvec{r}_i + \widetilde{x}_i \cdot \gamma \varvec{b}^{\bot }\}_{i \in [2n]}\). This change is analogous to that introduced in game \({\mathrm {G}}_2\), and its indistinguishability follows from the \(3\text {-}\mathsf {pddh}\) assumption.
The crucial observation is that the public key in this game can be seen as an \(\mathsf {FE}_{\mathsf {one}}\) ciphertext encrypting vector \((\widetilde{\varvec{x}}, \widetilde{\varvec{y}})\), while the challenge ciphertext of game \({\mathrm {G}}_4\) can be seen as an encryption of vectors
$$ \left( \left( \begin{array}{c} \mathbf {0}\\ \hline \varvec{x}^{(0)} \end{array} \right) , \left( \begin{array}{c} \mathbf {0}\\ \hline \varvec{y}^{(0)} \end{array} \right) \right) \in \mathbb {Z}_p^{2n} \times \mathbb {Z}_p^{2m} $$using such public key. At a high level, the idea is that we moved to a game in which the dependence on the challenge messages \((\varvec{x}^{(\beta )}, \varvec{y}^{(\beta )})\) is only in the public key.
-
Game \({\mathrm {G}}_5\): in this game we change back the distribution of the public key elements so as to be interpreted as an \(\mathsf {FE}_\mathsf {one}\) ciphertext encrypting vectors \((\mathbf {0}, \mathbf {0})\). The indistinguishability of this game from game \({\mathrm {G}}_4\) can be argued based on the selective, single-ciphertext security of the \(\mathsf {FE}_\mathsf {one}\) scheme.
The proof is concluded by arguing that in this game the view of the adversary is independent of the bit \(\beta \).
4 Our Efficient Functional Encryption for Bilinear Maps in the GGM
In this section, we present a functional encryption scheme, \(\mathsf {FE}_{\mathsf{GGM}}\), that supports the bilinear map functionality, and is proven secure against adaptive adversaries in the generic group model. In addition to be proven adaptive secure, this scheme enjoys a simpler structure, and is more efficient, as it admits shorter ciphertexts that comprise \(2(n+m+1)\) group elements (as opposed to \(6n + 6m + 2\) in the SXDH instantiation of the scheme of Sect. 3.2). For ease of exposition, the scheme is presented for the case in which the functions act over vectors of the same dimension n. It is easy to see that the case in which \((\varvec{x}, \varvec{y}) \in \mathbb {Z}_p^{n} \times \mathbb {Z}_p^{m}\) with \(n>m\) can be captured by padding \(\varvec{y}\) with zero entries.Footnote 5
Technical Overview. We first provide a high-level view of the techniques used in this construction. The initial idea of the construction is to encrypt the two vectors \(\varvec{x}\) and \(\varvec{y}\) à la ElGamal in the two groups \(\mathbb G_1\) and \(\mathbb G_2\) respectively, i.e., the ciphertext includes \(\varvec{c} = [r \cdot \varvec{a}+ \varvec{x}]_1\) and \(\varvec{d}= [s \cdot \varvec{b} + \varvec{y}]_2\) where r, s are randomly chosen and the vectors \(([\varvec{a}]_1, [\varvec{b}]_2)\) are in the public key. At this point, we observe that, given \(\varvec{c}, \varvec{d}\) and a function \(\mathbf{F}\), one can use the bilinear map to compute \(U = [(r \cdot \varvec{a} + \varvec{x})^{\top } \mathbf{F}(s \cdot \varvec{b} + \varvec{y})]_T\). This basic idea is similar to that of the scheme of Sect. 3.2. However, here we develop a different technique to enable decryption.
The basic scheme presented above is extended as follows. First, we let the secret key for function \(\mathbf{F}\) be the element \([\varvec{a}^{\top } \mathbf{F}\varvec{b}]_1\). Now, if in the ciphertext we include the element \([rs]_2\), one can extract
Above the function’s result is still “blinded” by cross terms \(s (\varvec{x}^{\top } \mathbf{F}\varvec{b}) + r (\varvec{a}^{\top } \mathbf{F}\varvec{y})\). Our second idea, to solve this issue and enable full decryption, is to add to the ciphertext the ElGamal encryptions of the vectors \(s \cdot \varvec{x}\) and \(r \cdot \varvec{y}\). Namely, we add to the ciphertext the elements \(\varvec{\widehat{c}} = [t \cdot \varvec{a} + s \cdot \varvec{x}]_1\) and \(\varvec{\widehat{d}} = [z \cdot \varvec{b} + r \cdot \varvec{y}]_2\) for random t, z, and the element \([rs -t -z]_2\) (instead of \([rs]_2\)). With all this information, one can compute the value U in the same way as above, and then use the public key \(([\varvec{a}]_1, [\varvec{b}]_2)\) and the ciphertext components \(\varvec{\widehat{c}}, \varvec{\widehat{d}}\) to compute
By a simple calculation, the function’s result can be finally computed as
As a final note, in the full scheme secret keys are slightly different, we randomize them in order to achieve collusion resistance.
Below we present our second FE scheme in detail.
-
\(\mathsf{Setup}(1^{\lambda }, n)\) runs the bilinear group generator \(\mathsf{bgp}\leftarrow _{\textsc {r}}\mathcal{G}(1^{\lambda })\) to obtain parameters \(\mathsf{bgp}= (p, \mathbb G_1, \mathbb G_2, \mathbb G_T, g_1, g_2, e)\). Next, the algorithm samples a scalar \(w \leftarrow _{\textsc {r}}\mathbb {Z}_p\) and two vectors \(\varvec{a}, \varvec{b}\leftarrow _{\textsc {r}}\mathbb {Z}_{p}^{n}\) uniformly at random. The message space is \(\mathcal{M}\subseteq \mathbb {Z}_p^{n}\times \mathbb {Z}_p^{n}\) and the key space is the set of matrices \(\mathcal{K}\subseteq \mathbb {Z}_p^{n \times n}\). It returns the master secret key \(\mathsf {msk} := (w, \varvec{a}, \varvec{b})\), and the master public key \(\mathsf {mpk} := (\mathsf{bgp}, [\varvec{a}]_1, [\varvec{b}]_2, [w]_2)\).
-
\(\mathsf{KeyGen}(\mathsf {msk}, \mathbf{F})\) takes as input the master secret key \(\mathsf {msk}\) and a matrix \(\mathbf{F}\in \mathcal{K}\) and it returns a secret key \(\mathsf{sk}_{\mathbf{F}} := (S_1, S_2, \mathbf{F}) \in \mathbb G_1^{2} \times \mathcal{K}\) where \(S_1, S_2\) are computed as follows. It samples a random \(\gamma \leftarrow _{\textsc {r}}\mathbb {Z}_p\) and computes
$$ (S_1, S_2) := ( [\varvec{a}^{\top } \mathbf{F}\, \varvec{b}+ \gamma \cdot w ]_1, [\gamma ]_1). $$ -
\(\mathsf{Encrypt}(\mathsf {mpk}, (\varvec{x}, \varvec{y}))\) takes as input the master public key and a message consisting of two vectors \(\varvec{x}, \varvec{y}\in \mathcal{M}\), and returns a ciphertext \(\mathsf{Ct}:= (\varvec{c}, \varvec{\widehat{c}}, \varvec{d}, \varvec{\widehat{d}}, E, \widehat{E})\) computed as follows.
Choose \(r,s,t,z \in \mathbb {Z}_p\) uniformly at random and compute
$$\begin{aligned} \varvec{c} := [r \cdot \varvec{a}+ \varvec{x}]_1,&\quad&\varvec{\widehat{c}} := [t \cdot \varvec{a}+ s \cdot \varvec{x}]_1\\ \varvec{d} := [s \cdot \varvec{b}+ \varvec{y}]_2,&\quad&\varvec{\widehat{d}} := [z \cdot \varvec{b}+ r \cdot \varvec{y}]_2\\ E := [rs - z -t]_2&\widehat{E} := [w(rs - z -t)]_2 \end{aligned}$$ -
\(\mathsf{Decrypt}(\mathsf{sk}_{\mathbf{F}}, \mathsf{Ct}\)) parsing \(\mathsf{sk}_{\mathbf{F}} := (S_1, S_2, \mathbf{F})\) and \(\mathsf{Ct}:= (\varvec{c}, \varvec{\widehat{c}}, \varvec{d}, \varvec{\widehat{d}}, E, \widehat{E})\), it computes and outputs
$$V := \varvec{c}^{\top } \, \mathbf{F}\, \varvec{d} - {[\varvec{a}]_1}^{\top } \, \mathbf{F}\, \varvec{\widehat{d}} - \varvec{\widehat{c}}^{\top } \, \mathbf{F}\, [\varvec{b}]_2 - e(S_1 , E) + e(S_2, \widehat{E}) \in \mathbb G_{T}.$$
Correctness. To see the correctness of our scheme, let
and note that
Since \(V = A - B - e(S_1 , E) + e(S_2, \widehat{E})\) it is easy to see that \(V = [\varvec{x}^{\top } \, \mathbf{F}\, \varvec{y}]_{T}\).
Security of \(\mathsf {FE}_{\mathsf{GGM}}\) . In this section we state the security of the functional encryption scheme \(\mathsf {FE}_{\mathsf{GGM}}\) of Sect. 4 in the generic group model.
Theorem 5
The functional encryption scheme \(\mathsf {FE}_{\mathsf{GGM}}\) described in Sect. 4 satisfies security against chosen-plaintext attacks (i.e., indistinguishability-based security) in the generic bilinear group model. Precisely, for every adversary \(\mathcal{A}\) which makes at most Q key derivation oracle queries and \(\widetilde{Q}\) generic group oracle queries its advantage is
The full proof of security is deferred to the full version. Here we only provide an overview of the strategy.
At an intuitive level, the proof consists of two main steps. We first state and prove a master theorem that shows hardness in the generic bilinear group model for a broad family of interactive decisional problems, notably a family which includes the indistinguishability-based experiment for our functional encryption scheme. Slightly more in detail, our master theorem states that these problems are generically hard under a certain algebraic side condition on the distribution of the elements received by the adversary. These results and techniques are rather general and can be of independent interest.
Second, following the guidelines of our master theorem, the second step of the proof consists in showing that the scheme \(\mathsf {FE}_{\mathsf{GGM}}\) meets the algebraic side condition of our master theorem. This is the core part of the proof. Very intuitively, we look at the structure of the scheme’s group elements seen by the adversary – public key, ciphertext, secret keys for a bunch of functions – for which the matching of the side condition means that the only information extractable from them is the functions’ outputs. So, if the adversary issues only “legitimate” queries (i.e., queries for functions that produce the same results on the two challenge messages), it will not be able to understand which pair of vectors was encrypted.
5 Predicate Encryption for Bilinear Maps Evaluation
Here we show how to use our functional encryption schemes to build a Predicate Encryption (PE) scheme for the evaluation of bilinear maps over attributes (for lack of space, the definition of PE is recalled in Sect. 2.4). Specifically, we give a scheme for the predicate \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) where \(\mathcal {X}\subset \mathbb {Z}_p^{n} \times \mathbb {Z}_p^m\), \(\mathcal {Y}\subset \mathbb {Z}_p^{n\times m}\), and for all \((\varvec{x},\varvec{y}) \in \mathcal {X}\) and \(\mathbf {F}\in \mathcal {Y}\):
In Fig. 9, we present a generic construction of PE for \(\mathsf {P}\) from any functional encryption scheme \(\mathsf {FE}\) for the bilinear maps functionality \(F: \mathcal {K}\times \mathcal{M}' \rightarrow \mathcal {Y}'\), where \(\mathcal{M}' := \mathbb {Z}_p^{n} \times \mathbb {Z}_p^m\), \(\mathcal {K}:= \mathbb {Z}_p^{n\times m}\), \(\mathcal {Y}' := \mathbb G_T\) and for all \((\varvec{x},\varvec{y}) \in \mathcal{M}'\), \(\mathbf {F}\in \mathcal {K}\)
The PE scheme can be instantiated by using one of our FE constructions presented in Sects. 3 and 4. We compare our constructions with previous PE that support the evaluation of bilinear maps in Fig. 2.
Theorem 6
(Correctness). If \(\mathsf {FE}:=(\mathsf{Setup}_\mathsf {FE},{\mathsf {KeyGen}}_\mathsf {FE},\mathsf{Encrypt}_\mathsf {FE},\mathsf{Decrypt}_\mathsf {FE})\) is a perfectly correct functional encryption scheme for functionality F, then so is the predicate encryption scheme \(\mathsf {PE}\) defined in Fig. 9.
Proof
of Theorem 6 . By correctness of \(\mathsf {FE}\), we have for all \((\varvec{x},\varvec{y}) \in \mathcal {X}\), \(w \in \mathbb {Z}_p\), \(\mathbf {F}\in \mathcal {Y}\):
Thus, when \(\mathsf {P}((\varvec{x},\varvec{y}),\mathbf {F})=1\), decryption recovers the encapsulation key \([w]_T\).
Theorem 7
(Security). If \(\mathsf {FE}:=(\mathsf{Setup}_\mathsf {FE},{\mathsf {KeyGen}}_\mathsf {FE},\mathsf{Encrypt}_\mathsf {FE},\mathsf{Decrypt}_\mathsf {FE})\) is an adaptively (resp. selectively) secure encryption scheme for F, then so is the predicate encryption scheme \(\mathsf {PE}\) defined in Fig. 9. Namely, for any PPT adversary \(\mathcal {A}\), there exists a PPT adversary \(\mathcal {B}\) such that:
Similarly, in the selective case, for any PPT adversary \(\mathcal {A}\), there exists a PPT adversary \(\mathcal {B}\) such that:
Games \({\mathrm {G}}_i\), for \(i=0,1,2\) for the proof of adaptive security of \(\mathsf {PE}\) in Fig. 9. In each procedure, the components inside a solid (dotted) frame are only present in the games marked by a solid (dotted) frame.
Proof of Theorem 7, Adaptive Security. We prove the adaptive security of \(\mathsf {PE}\) via a series of games described in Fig. 10 and we use \(\mathsf {Adv}_i\) to denote the advantage of \(\mathcal {A}\) in game \({\mathrm {G}}_i\), that is \(\mathsf {Adv}_i := |1-2\Pr [{\mathrm {G}}_i \text { returns } 1]|\). \({\mathrm {G}}_0\) is defined as:
Where \(\mathbf {Exp}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{ind\text {-}pe\text {-}cpa}\text {-}\beta }(\lambda )\) is the experiment used in Definition 9 of fully attribute-hiding security for predicate encryption. In particular, we have that \(\mathsf {Adv}_0 = \mathbf {Adv}_{\mathsf {PE}, \mathcal{A}}^{\mathsf{ind\text {-}pe\text {-}cpa}}(\lambda )\). We explain in Remark 1 how to obtain the same results for selective security.
Lemma 6
( \({\mathrm {G}}_0\) to \({\mathrm {G}}_1\) ). There exists a PPT adversary \(\mathcal {B}_0\):
Proof of Lemma 6 . By definition of the security game, we know that if \(M_0 \ne M_1\), then it must be that for all queries \(\mathbf {F}\) to \(\mathsf {KeyGenO}(\cdot )\), \(\varvec{x}^{(\beta ){\!\scriptscriptstyle {\top }}} \mathbf {F}\varvec{y}^{(\beta )} = 0\) (i.e., the predicate over the challenge attributes is false). Therefore, using the adaptive security of the underlying FE scheme, we can switch: \(\mathsf{Encrypt}(\mathsf{mpk},(w\cdot \varvec{x}^{(\beta )},\varvec{y}^{(\beta )}))\), computed by \(\mathsf {EncO}\) when \(M_0\ne M_1\), to \(\mathsf{Encrypt}(\mathsf{mpk},(\mathbf {0},\mathbf {0}))\). \(\square \)
Lemma 7
( \({\mathrm {G}}_1\) to \({\mathrm {G}}_2\) ). There exists a PPT adversary \(\mathcal {B}_1\):
Proof of Lemma 7 . By definition of the security game, we know that for all queries \(\mathbf {F}\) to \(\mathsf {KeyGenO}(\cdot )\), \(\mathsf {P}\big ((\varvec{x}^{(0)},\varvec{y}^{(0)}),\mathbf {F}\big ) = \mathsf {P}\big ((\varvec{x}^{(1)},\varvec{y}^{(1)}),\mathbf {F}\big )\). Together with the fact that for all \((\varvec{x},\varvec{y}) \in \mathcal {X}\) and \(\mathbf {F}\in \mathcal {Y}\): \(\varvec{x}^{\!\scriptscriptstyle {\top }}\mathbf {F}\varvec{y}\in \{0,1\}\), we obtain that: \(\varvec{x}^{(0) {\!\scriptscriptstyle {\top }}} \mathbf {F}\varvec{y}^{(0)} = \varvec{x}^{(1) {\!\scriptscriptstyle {\top }}} \mathbf {F}\varvec{y}^{(1)}\). Therefore, using the adaptive security of the underlying FE scheme, we can switch: \(\mathsf{Encrypt}(\mathsf{mpk},(w\cdot \varvec{x}^{(\beta )},\varvec{y}^{(\beta )}))\), computed by \(\mathsf {EncO}\) when \(M_0=M_1\), to \(\mathsf{Encrypt}(\mathsf{mpk},(w\cdot \varvec{x}^{(0)},\varvec{y}^{(0)}))\). \(\square \)
Lemma 8
( \({\mathrm {G}}_2\) ). \( \mathsf {Adv}_2=0\).
Proof of Lemma 8 . We show that the \(\mathcal {A}\)’s view is independent of \(\beta \leftarrow _{\textsc {r}}\{0,1\}\) in this game. If \(M_0 \ne M_1\), the challenge ciphertext is of the form \((C_0,C_1)\) where \(C_0 := [w]_T + M_\beta \) for \(w \leftarrow _{\textsc {r}}\mathbb {Z}_p\), and \(C_1\) is independent of w and \(\beta \). Thus, the message \(M_\beta \) is completely hidden by the one-time pad \([w]_T\), and the ciphertext is independent of \(\beta \).
If \(M_0 = M_1\), the challenge ciphertext is of the form \((C_0,C_1)\) where \(C_0 := [w]_T + M_\beta \) for \(w \leftarrow _{\textsc {r}}\mathbb {Z}_p\), which is independent of \(\beta \) since \(M_0=M_1\); and \(C_1 := \mathsf{Encrypt}(\mathsf{mpk},(w\cdot \varvec{x}^{(0)},\varvec{y}^{(0)}))\), which is also independent of \(\beta \). \(\square \)
Theorem 7 follows readily from Lemmas 6, 7, and 8. \(\square \)
Remark 1
(Selective FE \(\Rightarrow \) selective PE). We can adapt straightforwardly the proof of Theorem 7, to the selective setting, simply by constructing PPT adversaries \(\mathcal {B}_0\) and \(\mathcal {B}_1\) against the selective security of the underlying FE, exactly as those in Lemmas 6 and 7, except that those adversaries first receive a challenge \((\varvec{x}^{(0)},\varvec{y}^{(0)}),(\varvec{x}^{(1)},\varvec{y}^{(1)})\) from the adversary \(\mathcal {A}\), playing against the selective security of the PE, upon which they sample \(w \leftarrow _{\textsc {r}}\mathbb {Z}_p\), and send \((w\cdot \varvec{x}^{(0)},\varvec{y}^{(0)}),(w\cdot \varvec{x}^{(1)},\varvec{y}^{(1)})\) as their selective challenge. Finally, we use the statistical argument from Lemma 8, which works exactly in the same way for the selective setting.
5.1 Applications of PE for Bilinear Maps Evaluation
In this section, we discuss two applications of our fully attribute-hiding PE scheme supporting bilinear maps evaluation.
PE for Constant Depth Boolean Formulas. As a first application, we can use the \(\mathsf {PE}\) scheme in Fig. 9 to handle boolean functions of constant degree d in n variables. This yields a solution where ciphertexts comprise \(O(n^{d/2})\) group elements, in contrast to \(O(n^{d})\) group elements in [28] (the asymptotic is taken for large n, constant d).
The idea is to encode a predicate for boolean formulas into a predicate for bilinear maps evaluation. This can be done as follows. Consider the following predicate \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\), with \(\mathcal {X}:= \mathbb {Z}_2^n\) and \(\mathcal {Y}:= \{T\in \mathbb {Z}_2[X_1,\ldots ,X_n], \deg (T) \le d\}\), such that for all \(\varvec{x}\in \mathcal {X}\), \(T \in \mathcal {X}\), \(\mathsf {P}(\varvec{x},T)=1\) iff \(T(\varvec{x}) = 1\). Below we describe how to encode \(\varvec{x}\in \mathcal {X}\) and \(T \in \mathcal {Y}\) into a vector \(\widetilde{\varvec{x}}\) and a matrix \(\widetilde{\mathbf {T}}\) such that \(\mathsf {P}(\varvec{x},T) = 1\) iff \(\widetilde{\varvec{x}}^{\!\scriptscriptstyle {\top }}\widetilde{\mathbf {T}} \widetilde{\varvec{x}} = 1\).
To see this, assume for simplicity that d is even, and let us consider the setting where \(n \ge \frac{d}{2}\). First, we map every \(\varvec{x}\in \mathcal {X}\) to \(\widetilde{\varvec{x}} := (M_1(\varvec{x}),\ldots ,M_{\widetilde{d}}(\varvec{x})) \in \mathbb {Z}_2^{\widetilde{d}}\), where \(\widetilde{d} := \sum _{i=0}^{\frac{d}{2}} {n \atopwithdelims ()i}\), and for all \(j \in \left[ {n \atopwithdelims ()\frac{d}{2}}\right] \), \(M_j\) is the j-th monomial of degree at most \(\frac{d}{2}\) on n variables (there are exactly \(\widetilde{d}\) such monomials, which we order arbitrarily). Second, we write every \(T \in \mathcal {Y}\) as \(\sum _{i,j \in [\widetilde{d}]} T_{i,j} M_i M_j\), where for all \(i,j \in [\widetilde{d}]\), \(T_{i,j} \in \mathbb {Z}_2\), and we map \(T \in \mathcal {Y}\) to \(\widetilde{\mathbf {T}} \in \mathbb {Z}_2^{\widetilde{d} \times \widetilde{d}}\) such that for all \(i,j \in [\widetilde{d}]\), \(\widetilde{T}_{i,j} := T_{i,j}\). This way, for all \(\varvec{x}\in \mathcal {X}\) and \(T \in \mathcal {Y}\), we have \(\mathsf {P}(\varvec{x},T) = 1\) iff \(\widetilde{\varvec{x}}^{\!\scriptscriptstyle {\top }}\widetilde{\mathbf {T}} \widetilde{\varvec{x}} = T(\varvec{x}) = 1\).
Therefore, using the PE which supports bilinear maps evaluation presented in Sect. 5, we obtain a PE for boolean formulas with ciphertexts of size \(O(\widetilde{d})\). Using a similar encoding to the PE from [28] that support linear maps evaluation yields a solution with ciphertexts of dimension \(O(\widehat{d})\) where \(\widehat{d} := \sum _{i=0}^d {n \atopwithdelims ()i}\). When considering asymptotic for large n, constant d, our ciphertext size is \(O(n^{d/2})\), against \(O(n^{d})\) for [28].
Finally, we note that boolean formulas can be arithmetized into a polynomial over \(\mathbb {Z}_2\), à la [38]. Namely, for boolean variables \(x,y \in \mathbb {Z}_2\), \(\mathsf {AND}(x,y)\) is encoded as \(x\cdot y\), \(\mathsf {OR}(x,y)\) is encoded as \(x+y-xy\), and \(\mathsf {NOT}(x) = 1-x\).
PE for Comparison. Let us consider the comparison predicate \(\mathsf {P}_{\le }: [N] \times [N] \rightarrow \{0,1\}\) that for all \(x,y \in [N]\) is defined by
We can reduce this predicate to a polynomial of degree two, as done (implicitly) in [12], as follows. First, any integer \(x \in [N]\) is canonically mapped to the lexicographically ordered pair \((x_1,x_2) \in [\sqrt{N}] \times [\sqrt{N}]\) (we assume \(\sqrt{N}\) is an integer for simplicity). Then \(x_1 \) is mapped to vectors \(\widetilde{\varvec{x}} := \begin{pmatrix} \mathbf {0}^{x_1} \\ \mathbf {1}^{\sqrt{N}-x_1} \end{pmatrix} \in \{0,1\}^{\sqrt{N}}\) where \(\mathbf {1}^\ell \), \(\mathbf {0}^\ell \) denote the all-one and all-zero vectors in \(\{0,1\}^{\ell }\), respectively; and \(\widehat{\varvec{x}} := \varvec{e}_{x_1} \in \{0,1\}^{\sqrt{N}}\), where for all \(i \in [\sqrt{N}]\), \(\varvec{e}_i\) denotes the i’th vector of the canonical basis of \(\mathbb {Z}_p^{\sqrt{N}}\). Finally, \(x_2 \in [\sqrt{N}]\) is mapped to \(\bar{\varvec{x}} := \begin{pmatrix} \mathbf {0}^{x_2 - 1} \\ \mathbf {1}^{\sqrt{N}-x_2 + 1}\end{pmatrix}\). For all \((x_1,x_2), (y_1,y_2) \in [\sqrt{N}] \times [\sqrt{N}]\):
where for any vector \(\varvec{z}\in \mathbb {Z}_p^{\sqrt{N}}\), and any \(i \in [\sqrt{N}]\), we denote by \(z_i \in \mathbb {Z}_p\) the i-th coordinate of \(\varvec{z}\).
This means that by using the above encoding, for an integer attribute \(x \in [N]\) one can use a PE for bilinear maps evaluation to encrypt the pair of vectors

This gives a PE for comparison with ciphertexts of \(O(\sqrt{N})\) group elements, as in [12, 21]. A more precise comparison is given in Table 3.
Notes
- 1.
Here by complex we intend, for instance, functions that are supposed to have some computational hiding properties. In particular, Boneh et al. [13] argue that, in applications where security relies on such properties, indistinguishability might become problematic.
- 2.
Indeed, we note that a functional encryption for linear polynomials can be used to support, say, quadratic polynomials, by simply encrypting all the degree-two monomials in advance. This however leads to an inefficient solution where the size of the ciphertexts is quadratic in the number of variables.
- 3.
Here we adopt the, by now standard, implicit representation \([x]_s = g^x \in \mathbb G_s\). This notion can be easily extended to vectors and matrices (see [18]).
- 4.
This means that in our scheme messages and functions coefficients are assumed to be sufficiently small integers.
- 5.
Furthermore, with a close look one can see that the last \(n-m\) components of the vectors \([\varvec{b}]_2\), \(\varvec{d}\) and \(\varvec{\widehat{d}}\) would become useless and thus can be discarded.
References
Abdalla, M., et al.: Searchable encryption revisited: consistency properties, relation to anonymous IBE, and extensions. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 205–222. Springer, Heidelberg (2005). doi:10.1007/11535218_13
Abdalla, M., Bourse, F., Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_33
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Better security for functional encryption for inner product evaluations. Cryptology ePrint Archive, Report 2016/011 (2016). http://eprint.iacr.org/2016/011
Abdalla, M., Raykova, M., Wee, H.: Multi-input inner-product functional encryption from pairings. IACR Cryptology ePrint Archive, 2016:425 (2016)
Agrawal, S., Freeman, D.M., Vaikuntanathan, V.: Functional encryption for inner product predicates from learning with errors. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 21–40. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_2
Agrawal, S., Libert, B., Stehlé, D.: Fully secure functional encryption for inner products, from standard assumptions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 333–362. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53015-3_12
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 152–181. Springer, Cham (2017). doi:10.1007/978-3-319-56620-7_6
Barthe, G., Fagerholm, E., Fiore, D., Mitchell, J.C., Scedrov, A., Schmidt, B.: Automated analysis of cryptographic assumptions in generic group models. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 95–112. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_6
Bishop, A., Jain, A., Kowalczyk, L.: Function-hiding inner product encryption. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 470–491. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_20
Boneh, D., Di Crescenzo, G., Ostrovsky, R., Persiano, G.: Public key encryption with keyword search. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 506–522. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24676-3_30
Boneh, D., Franklin, M.K.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_13
Boneh, D., Sahai, A., Waters, B.: Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 573–592. Springer, Heidelberg (2006). doi:10.1007/11761679_34
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_16
Boneh, D., Waters, B.: A fully collusion resistant broadcast, trace, and revoke system. In: Juels, A., Wright, R.N., Vimercati, S. (eds.) ACM CCS 2006, pp. 211–220. ACM Press, October/November 2006
Boneh, D., Waters, B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 535–554. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70936-7_29
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_20
Chen, J., Lim, H.W., Ling, S., Wang, H., Wee, H.: Shorter IBE and signatures via asymmetric pairings. In: Abdalla, M., Lange, T. (eds.) Pairing 2012. LNCS, vol. 7708, pp. 122–140. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36334-4_8
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_8
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press, October 2013
Garg, S., Kumarasubramanian, A., Sahai, A., Waters, B.: Building efficient fully collusion-resilient traitor tracing and revocation schemes. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 121–130. ACM Press, October 2010
Gentry, C.: Practical identity-based encryption without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 445–464. Springer, Heidelberg (2006). doi:10.1007/11761679_27
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 555–564. ACM Press, June 2013
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 545–554. ACM Press, June 2013
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_25
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., Vimercati, S. (eds.) ACM CCS 2006, pp. 89–98. ACM Press, October/November 2006. Available as Cryptology ePrint Archive Report 2006/309
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_9
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. J. Cryptol. 26(2), 191–224 (2013)
Lewko, A.B.: Tools for simulating features of composite order bilinear groups in the prime order setting. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 318–335. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_20
Lin, H.: Indistinguishability obfuscation from DDH on 5-linear maps and locality-5 PRGs. In: CRYPTO 2017 (to appear). Also available at Cryptology ePrint Archive, Report 2016/1096 (2016). http://eprint.iacr.org/2016/1096
Okamoto, T., Takashima, K.: Homomorphic encryption and signatures from vector decomposition. In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 57–74. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85538-5_4
Okamoto, T., Takashima, K.: Hierarchical predicate encryption for inner-products. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 214–231. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_13
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_11
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010). http://eprint.iacr.org/2010/556
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). doi:10.1007/11426639_27
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_5
Shamir, A.: IP=PSPACE. In: 31st FOCS, pp. 11–15. IEEE Computer Society Press, October 1990
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_36
Acknowledgements
The research of Dario Fiore is partially supported by the European Union’s Horizon 2020 Research and Innovation Programme under grant agreement 688722 (NEXTLEAP), the Spanish Ministry of Economy under project references TIN2015-70713-R (DEDETIS), RTC-2016-4930-7 (DataMantium), and under a Juan de la Cierva fellowship to Dario Fiore, and by the Madrid Regional Government under project N-Greens (ref. S2013/ICE-2731).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Baltico, C.E.Z., Catalano, D., Fiore, D., Gay, R. (2017). Practical Functional Encryption for Quadratic Functions with Applications to Predicate Encryption. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10401. Springer, Cham. https://doi.org/10.1007/978-3-319-63688-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-63688-7_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63687-0
Online ISBN: 978-3-319-63688-7
eBook Packages: Computer ScienceComputer Science (R0)





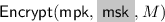 takes as input the master public key
takes as input the master public key  functional encryption. By opposition, when
functional encryption. By opposition, when 









