Model-Checking Linear-Time Properties of Parametrized Asynchronous Shared-Memory Pushdown Systems

Abstract

A parametrized verification problem asks if a parallel composition of a leader process with some number of copies of a contributor process can exhibit a behavior satisfying a given property. We focus on the case of pushdown processes communicating via shared memory. In a series of recent papers it has been shown that reachability in this model is Pspace-complete [Hague’11], [Esparza, Ganty, Majumdar’13], and that liveness is decidable in Nexptime [Durand-Gasselin, Esparza, Ganty, Majumdar’15]. We show that verification of general regular properties of traces of executions, satisfying some stuttering condition, is Nexptime-complete for this model. We also study two interesting subcases of this problem: we show that liveness is actually Pspace-complete, and that safety is already Nexptime-complete.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

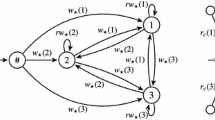
A parametrized verification problem asks if a given property holds for the parallel composition of a leader system with some arbitrary number of copies of a contributor system (see Fig. 1). This formulation appears already in a seminal paper of German and Sistla [19], see also the survey [3] for a recent overview of the literature. In this work, following [12, 15, 20, 21, 27], we consider parametric pushdown systems, where both the leader and contributors are pushdown automata, and communication is via shared variables without any locking primitives. Our primary motivation is the analysis of concurrent programs with procedure calls. While previous work on parametric pushdown systems focused mainly on reachability, or repeated reachability for the leader process, we show here that a large class of omega-regular properties is decidable for these systems.

Fig. 1.

A system consisting of one leader pushdown automaton and a number of copies of a contributor pushdown automaton.

In his pioneering work [21] Kahlon proposed parametrization as an abstraction step that avoids the undecidability barrier. A system composed of two copies of a pushdown automaton communicating via one register can simulate Turing machines [35], so no effective analysis of such systems is possible. Yet, if instead of two copies we ask if a system composed of an arbitrary number of copies of the pushdown automaton can write a specified value to a register, then the problem becomes decidable. Later Hague [20] showed that reachability is also decidable for a more general architecture proposed by German and Sistla. Namely he considered systems with a leader pushdown automaton and an arbitrary number of copies of a contributor pushdown automaton; cf. Fig. 1. Consecutively, Esparza et al. [15] have proved that the problem is Pspace-complete, thus surprisingly easy for such type of problem. La Torre et al. [27] showed that the reachability problem remains decidable if instead of pushdown automata one considers higher-order pushdown automata, or any other automata model with some weak decidability properties. Reachability was also shown to be decidable for parametric pushdown systems with dynamic thread creation [32].

Our motivating question is “what kind of linear-time properties are decidable for parametric pushdown systems?” Suppose that we want to check a universal reachability property: whether for every number of components, every run finally writes a specified value to the register. This problem translates into a safety query: does there exist some number of contributors, and some maximal run that does not write the specified value to the register? Maximality means here either an infinite run, or a finite run that cannot be prolonged. The maximality condition is clearly essential, as otherwise we could always take the empty run as a witness.

We show as our main result that verification of parametric pushdown systems is decidable for all regular properties subject to some stuttering condition linked to the fact that the number of contributors is not determined. We give precise complexities of the parametric verification problem for both the case when the property is given as a Büchi automaton, as well as when it is given by an LTL formula (Nexptime-complete). On the way we revisit the liveness problem studied in [12] and give a Pspace algorithm for it. This answers the question left open by [12], that provided a Pspace lower bound and a Nexptime upper bound for the liveness problem. It is somewhat surprising that for this kind of parametrized systems, checking liveness is not more difficult computationally than checking reachability, unlike for many other families of parametrized or, more generally, infinite-state systems (see e.g. Chap. 5 in [3] for a discussion and more references).

Another intermediate result of independent interest concerns universal reachability, which turns out to be coNexptime-complete. The lower bound shows that it is actually possible to force a fair amount of synchronization in the parametric model; we can ensure that the first $2^n$ values written into the shared register are read in the correct order and none of them is skipped. So the coNexptime-hardness result can be interpreted positively, as showing what can be implemented in this model.

Related Work. Parametrized verification of shared-memory, multi-threaded programs has been studied for finite-state threads e.g. in [2, 23] and for pushdown threads in [1, 5, 25, 26]. The decidability results in [1, 5, 25, 26] fall in the category of reachability analysis up to a bounded number of execution contexts, and in [1, 5], dynamic thread creation is allowed. The main difference with our setting is that synchronization primitives are allowed in those models, so decidability depends on restricting the set of executions. Our model does not restrict the executions, but has a weaker form of synchronization. In consequence our model rather over-approximates the set of executions while the approaches cited above under-approximate it.

In our model we have shared registers but no locks. Another option is to have locks and no registers. Analysis of pushdown systems with unrestricted locks is undecidable [22]. Interestingly, it becomes decidable for some locking disciplines like nested [22] or contextual locking [8]. This model remains decidable even when extended to dynamic pushdown networks [6]. Even reachability of regular sets of configurations is decidable in this model, provided it has a finitely many global locks together with nested locking [28, 30] or contextual locking [29]. Regular sets of configurations can compensate to some extent the lack of communication in the model, for example they can describe globally inconsistent configurations.

Besides the cited papers, there are numerous results on the German and Sistla model beyond the reachability property, but restricted to finite state processes. German and Sistla have already considered LTL properties of the leader or of the contributors. They have also studied the setting without a leader and observed that it is much easier to handle. Emerson and Kahlon have considered stuttering-invariant properties [13] of the whole system of finite state processes. Recently, Bouyer et al. [7] considered a probabilistic version without leader and only finite-state contributors. They consider the problem of almost-sure reachability, which asks if a given state is reached by some process with probability 1 under a stochastic scheduler. They exhibit the existence of positive or negative cut-offs, and show that the problem can be decided in Expspace, and is at least Pspace-hard.

Finally, we should mention that there is a rich literature concerning the verification of asynchronously-communicating parametrized programs, that is mostly related to the verification of distributed protocols and varies for approaches and models (see e.g. [9, 14, 19, 24] for some early work, and [3, 11, 31, 33] and references therein). Most of these papers are concerned with finite-state programs only, which are not the main focus of our results.

Outline of the Paper. Section 2 starts by introducing the problems considered in this paper, and states our main results. In Sect. 3, we present the formal definitions of parametrized pushdown systems. In Sect. 4 we study the liveness problem, and in Sect. 5 the safety problem. Finally, we show in Sect. 6 how these results may be used to verify more general $\omega$-regular properties. Throughout the paper we try to outline our arguments and give some intuitions for the proofs. The detailed proofs can be found in the in the full version of the paper [17].

2 Problem Statement and Overview of Results

The parametrized pushdown systems studied by [15, 20, 21] are described by two transition systems $\mathcal {D}$ and $\mathcal {C}$, traditionally called leader and contributor, which are both pushdown systems (cf. Fig. 1). Parametrization amounts to say that arbitrarily many contributor instances interact with one leader, and that contributors are anonymous. All participants communicate over lock-free, shared variables with finite domains. We distinguish read/write actions of the leader from those of contributors, for this we have two alphabets $\varSigma _D$ and $\varSigma _C$. Since contributors do not have identities we do not distinguish between actions of different contributors.

The question we ask in this paper is which kind of linear-time properties of $(\varSigma _D\cup \varSigma _C)$-labeled traces of parametrized pushdown systems can be model-checked. Unsurprisingly, it turns out that we cannot hope for model-checking arbitrary regular properties. In general, model-checking is undecidable because the ability to refer to actions of both leader and contributors allows to single out exactly one contributor instance. Since two communicating pushdown systems [35] can simulate a Turing machine, undecidability follows then immediately.

The solution to the above problem is to consider properties that are adapted to the parametrized setting. Technically we consider linear-time properties $\mathcal {P}$ where actions of contributors can be replicated: if $u_0 a_0 u_1 a_1 u_2 \cdots \in \mathcal {P}$ with $a_i\in \varSigma _C$, $u_i \in \varSigma _D^*$, and $f:\mathbb {N}\rightarrow \mathbb {N}^+$, then $u_0 a_0^{f(0)} u_1 a_1^{f(1)} u_2 \cdots \in \mathcal {P}$, too. We call such properties c-expanding.

A related, classical notion is stuttering. A property $\mathcal {P}$ is stutter-invariant if for every finite or infinite sequence $a_0 a_1 \cdots$ and every function $f:\mathbb {N}\rightarrow \mathbb {N}^+$, we have $a_0 a_1 \cdots \in \mathcal {P}$ iff $a_0^{f(0)} a_1^{f(1)} \cdots \in \mathcal {P}$. Observe that every stutter-invariant property is c-expanding. Stutter-invariance is a natural requirement in the verification of general concurrent systems, and moreover well studied, e.g. for LTL they correspond to the fragment LTL$\setminus X$ [16, 34]. Stutter-invariance is also common in parametrized verification [3], and for some synchronization primitives it allows to recover decidability in the finite-state case [13].

We will consider regular properties on both finite and infinite traces of parametrized systems, described either by LTL formulas or by Büchi automata with action labels from $\varSigma _C\cup \varSigma _D$.

Our main result is that model-checking c-expanding, $\omega$-regular properties¹ of parametrized pushdown systems is decidable, and Nexptime-complete.

Theorem 1

The following question is Nexptime-complete: given a parametrized pushdown system $\mathcal {S}$ and a c-expanding $\omega$-regular property $\mathcal {P}$ over $\mathcal {S}$ (described by a Büchi automaton or by an LTL formula), determine if $\mathcal {S}$ has some maximal trace in $\mathcal {P}$.

We list some particular instances of regular c-expanding $\omega$-properties, that are both interesting on their own, and essential for our decision procedure:

• 1. The reachability problem asks if the parametrized pushdown system has some trace containing a given leader action $\top$.

• 2. The liveness (repeated reachability) problem asks if the parametrized pushdown system has some trace with infinitely many occurrences of a given leader action $\top$.

• 3. The universal reachability problem asks if every maximal trace of the parametrized pushdown system contains a given leader action $\top$.

• 4. The complement of the previous question is the max-safety problem. It asks if the parametrized pushdown system has some maximal trace that does not contain a given leader action $\top$.

Example 1

Let us imagine the system from Fig. 1 that works as follows: first some contributors propose values, then the leader chooses some proposed value and announces this choice to contributors so that afterwards all the contributors should use only this value. For such a system one may be interested to verify if for every number of contributors every run satisfies:

• 1. The leader eventually decides on the value.

• 2. If the leader decides on the value then the contributors use only this value.

• 3. On runs where only one value is used infinitely often, some correctness property holds.

Following other works on the subject we will rather prefer existentially quantified questions, where we ask whether there is some number of contributors and some run satisfying a property. Solutions to the reachability problem from the literature can be used to verify the second property, as its negation is “there is some run where the leader decides on a value and then a contributor uses a different value”. The negation of the first property corresponds to max-safety: “there is some maximal run without the leader deciding on a value”. The third property is a more complicated liveness property that is neither reachability nor safety.   $\square$

Since max-safety and liveness problems are important steps towards our main result we also establish their exact complexities.

Theorem 2

The max-safety problem for parametrized pushdown systems is Nexptime-complete. It is NP-complete when contributors are finite-state systems.

Theorem 3

The liveness problem for parametrized pushdown systems is Pspace-complete.

The proof of Theorem 1 uses Theorems 2 and 3, and one more result, that is interesting on its own. Note that both the max-safety and liveness problems talk about one distinguished action of the leader, while c-expanding properties refer to actions of both leader and contributors. Perhaps a bit surprisingly, we show below that it suffices to consider only properties that refer to leader actions.

Theorem 4

For every parametrized pushdown system $\mathcal {S}$, there exists a parametrized pushdown system $\tilde{\mathcal {S}}$ such that for every c-expanding property $\mathcal {P}$ over traces of $\mathcal {S}$ there exists a property $\tilde{\mathcal {P}}$ over sequences of leader actions of $\tilde{\mathcal {S}}$ such that:

• 1. $\mathcal {S}$ has a finite (resp. infinite) maximal trace in $\mathcal {P}$ iff $\tilde{\mathcal {S}}$ has a finite (resp. infinite) maximal trace whose projection on leader actions is in $\tilde{\mathcal {P}}$;

• 2. every infinite run of $\tilde{\mathcal {S}}$ has infinitely many writes of the leader;

• 3. $\tilde{\mathcal {S}}$ has an infinite run iff $\mathcal {S}$ has one.

System $\tilde{\mathcal {S}}$ has size linear in the size of $\mathcal {S}$, and can be constructed in polynomial time. If $\mathcal {P}$ is a regular, respectively LTL property, then so is $\tilde{\mathcal {P}}$. An automaton or LTL formula of linear size for $\tilde{\mathcal {P}}$ is effectively computable from the one for $\mathcal {P}$.

3 Parametrized Pushdown Systems

In this section we recall the model of parametrized pushdown systems of [20] and its semantics. We start with some basic notations.

A multiset over a set E is a function $M: E \rightarrow \mathbb {N}$. We let $|M| = \sum _{x \in E} M(x)$. The support of M is the set $\{x \in E: M(x) > 0\}$. For $n \in \mathbb {N}$, we write nM, $M + M'$ and $M - M'$ for the multisets defined by $(nM)(x) = n \cdot M(x)$, $(M + M')(x) = M(x) + M'(x)$ and $(M - M')(x) = \max (0,M(x) - M'(x))$. We denote by [x] the multiset containing a single copy of x, and $[x_1, \ldots , x_n]$ the multiset $[x_1] + \ldots + [x_n]$. We write $M \le M'$ when $M(x) \le M'(x)$ for all x.

A transition system with actions over a finite alphabet $\varSigma$ is a tuple $\langle S,\delta ,s_{ init } \rangle$ where S is a (finite or infinite) set of states, $\delta \subseteq S \times \varSigma \times S$ is a set of transitions, and $s_{ init }\in S$ the initial state. We write $s \xrightarrow {u} s'$ (for $u \in \varSigma ^*$) when there exists a path from s to $s'$ labeled by u. A trace is a sequence of actions labeling a path starting in $s_{ init }$; so u is a trace if $s_{ init }\xrightarrow {u} s'$ for some $s'$.

A pushdown system is a tuple $\langle Q,\varSigma ,\varGamma ,\varDelta ,q_{ init },A_{ init } \rangle$ consisting of a finite set of states Q, a finite input alphabet $\varSigma$, a finite stack alphabet $\varGamma$, a set of transitions $\varDelta \subseteq (Q\times \varGamma ) \times (\varSigma \cup \{\varepsilon \}) \times (Q\times \varGamma ^*)$, an initial state $q_{ init }\in Q$, and an initial stack symbol $A_{ init }\in \varGamma$. The associated transition system has $Q \times \varGamma ^*$ as states, $q_{ init }A_{ init }$ as the initial state, and transitions $qA\alpha \xrightarrow {a} q'\alpha '\alpha$ for $(q,A,a,q',\alpha ') \in \varDelta$.

We proceed to the formal definition of parametrized pushdown systems. Given a leader process $\mathcal {D}$ and a contributor process $\mathcal {C}$, a system consists of one copy of $\mathcal {D}$ and arbitrarily many copies of $\mathcal {C}$ communicating via shared registers. For simplicity we assume that there is a single, finite-valued shared register (in the full version of the paper [17] we show how to reduce the case of several registers to that with one register). We write G for the finite set of register values, and use g, h to range over elements of G. The initial value of the register is $g_{ init }$. Since only processes of type $\mathcal {C}$ are parametrized we distinguish the read/write actions of $\mathcal {C}$ and $\mathcal {D}$, by using disjoint action sets: $\varSigma _C=\{\overline{r}(g),\overline{w}(g): g\in G\}$ and $\varSigma _D=\{r(g),w(g): g\in G\}$. Both processes $\mathcal {C}$ and $\mathcal {D}$ are (possibly infinite) transition systems with read/write actions:

$$\begin{aligned} \mathcal {C}=\langle S,\delta \subseteq S\times \varSigma _C\times S,s_{ init } \rangle \qquad \mathcal {D}=\langle T,\varDelta \subseteq T\times \varSigma _D\times T, t_{ init } \rangle \end{aligned}$$

(1)

In this paper we will consider the special case where $\mathcal {C}$ and $\mathcal {D}$ are pushdown transition systems:

$$\begin{aligned} \mathcal {A}_C=\langle P,\varSigma _C,\varGamma _C,\delta ,p_{ init },A_{ init }^C \rangle \qquad \mathcal {A}_D=\langle Q,\varSigma _D,\varGamma _D,\varDelta ,q_{ init },A_{ init }^D \rangle \end{aligned}$$

(2)

In this case the transition system $\mathcal {C}$ from (1) is the transition system associated with $\mathcal {A}_C$: its set of states is $S=P\times (\varGamma _C)^*$ and the transition relation $\delta$ is defined by the push and pop operations. Similarly, the transition system $\mathcal {D}$ is determined by $\mathcal {A}_D$. When stating general results on parametrized pushdown systems we will use the notations from Eq. (1); when we need to refer to precise states, or use some particular property of pushdown transition systems, we will employ the notations from Eq. (2).

So a parametrized pushdown system $\mathcal {S}$ consists of an arbitrary number of copies of $\mathcal {C}$, one copy of $\mathcal {D}$, and a shared register. A configuration $(M \in \mathbb {N}^S,t\in T,g\in G)$ of $\mathcal {S}$ consists of a multiset M counting the number of instances of $\mathcal {C}$ in a given state, the state t of $\mathcal {D}$ and the current register value g.

To define the transitions of the parametrized pushdown system we need to extend the transition relation $\delta$ of $\mathcal {C}$ to multisets: let $M\xrightarrow {a}M'$ if $s \xrightarrow {a} s'$ in $\delta$, $M(s) > 0$, and $M' = M - [s] + [s']$, for some $s,s' \in S$. Observe also that multiset transitions do not modify the size of the multiset. The transitions of the parametrized pushdown system are either transitions of $\mathcal {D}$ (the first two cases below) or transitions of $\mathcal {C}$ (the last two cases):

A run of $\mathcal {S}$ from a configuration (M, t, g) is a finite or an infinite sequence of transitions starting in (M, t, g). A run can start with any number n of contributors, but then the number of contributors is constant during the run. A run is initial if it starts in a configuration of the form $(n[s_{ init }],t_{ init },g_{ init })$, for some $n \in \mathbb {N}$. It is maximal if it is initial and cannot be extended to a longer run. In particular, every infinite initial run is maximal. A (maximal) trace of the parametrized pushdown system is a finite or an infinite sequence over $\varSigma _C\cup \varSigma _D$ labeling a (maximal) initial run.

4 Liveness

We show in this section that liveness for parametrized pushdown systems has the same complexity as reachability, namely Pspace-complete (Theorem 3). The lower bound comes from reachability [15], and our contribution is to improve the upper bound from Nexptime [12] to Pspace. We call a run of the parametrized pushdown system a Büchi run if it has infinitely many occurrences of the leader action $\top$. So the problem is to decide if a given parametrized pushdown system has a Büchi run.

Our proof has three steps. The first one relies on a result from [12], showing that it suffices to bound the stacks of contributors polynomially. This allows to search for ultimately periodic (lasso-shaped) runs of the parametrized pushdown system (Corollary 1), as in the case of a single pushdown system. The next step extends the technique introduced in [27] for the reachability problem, to Büchi runs: we reduce the search for Büchi runs to the existence of some run of the leader pushdown system, that is feasible in the global parametrized system (Lemma 2). The last step is the observation that we can replace the leader process by a finite-state system using downward closure (Lemma 3). Overall our procedure yields a Pspace algorithm for the liveness problem (Theorem 3).

Finite-State Contributors. As observed in [12], parametrization allows to replace pushdown contributors by finite-state contributors, preserving all behaviors of the leader. The reason is that any behavior of some contributor instance can be replicated arbitrarily (but finitely many times). To state the result of [12] we need the notion of effective stack-height for a pushdown system. Consider a possibly infinite run $\rho = q_1\alpha _1 \xrightarrow {a_1} q_2\alpha _2 \xrightarrow {a_2} \ldots$ of a pushdown system. We write $\alpha _i = \alpha '_i \alpha ''_i$, where $\alpha ''_i$ is the longest suffix of $\alpha _i$ that is also a proper suffix of $\alpha _j$ for all $j>i$. The effective stack-height of a configuration $q_i\alpha _i$ in $\rho$ is the length of $\alpha '_i$. (Notice that even though it is never popped, the first element of the longest common suffix of the $(\alpha _i)_{j\ge i}$ may be read, hence the use of proper suffixes).

Remark 1

It is folklore that every infinite run of a single pushdown system contains infinitely many configurations with effective stack-height one.

By $\mathcal {C}_N$ we denote the restriction of the contributor pushdown $\mathcal {A}_C$ to runs in which all configurations have effective stack-height at most N. More precisely, $\mathcal {C}_N$ is the finite-state system with set of states $\{p\alpha \in P\varGamma _C^*: |\alpha | \le N\}$, and transitions $p\alpha \xrightarrow {a} q\alpha '$ if $p\alpha \xrightarrow {a} q\alpha '\alpha ''$ in $\varDelta$ for some $\alpha ''$. Note that $\mathcal {C}_N$ is effectively computable in Pspace from $\mathcal {A}_C$ and N given in unary. One key idea in [12] is that when looking for Büchi runs of pushdown parametrized pushdown systems, $\mathcal {C}$ can be replaced by $\mathcal {C}_N$ for N polynomially bounded:

Theorem 5

(Theorem 4 in [12]). Let $N > 2|P|^2|\varGamma _C|$. The parametrized pushdown system $\mathcal {S}$ has some Büchi run iff the parametrized pushdown system $\mathcal {S}_N$ obtained from $\mathcal {S}$ by replacing $\mathcal {C}$ by $\mathcal {C}_N$, has some Büchi run.

The proof of the above theorem yields a similar result for finite runs. We state this in the next lemma, as we need to refer later to the form of configurations that are reachable in $\mathcal {S}_N$. The proof of the lemma relies on “distributing” the run of one contributor on the runs of two contributors, thereby decreasing the height of the stack. Recall that configurations of $\mathcal {S}$ are of the form $([s_1,\ldots ,s_n],t,g)$, where the n contributor instances have states $s_1,\dots ,s_n$, the leader has state t, and the shared register has value g.

Lemma 1

Let $N > 2|P|^2|\varGamma _C|+1$. A configuration $([p_1\alpha _1,\ldots ,p_n\alpha _n],t,g)$ of $\mathcal {S}_N$ is reachable iff there exists a reachable configuration of $\mathcal {S}$ of the form $([p_1\alpha _1\beta _1,\ldots ,p_n\alpha _n\beta _n],t,g)$, for some $\beta _i\in \varGamma _C^*$.

Notation. For the sake of clarity we write throughout the paper $\mathcal {C}_{ fin }$ instead of $\mathcal {C}_N$ with $N= 2|P|^2|\varGamma _C|+2$, and $\mathcal {S}_{ fin }$ for the parametrized pushdown system with contributor process $\mathcal {C}_{ fin }$ and leader process $\mathcal {D}$. We will use the notation $\langle P_{ fin },\varSigma _C,\delta ,p^{ fin }_{ init } \rangle$ for the finite-state system $\mathcal {C}_{ fin }$, and continue to write $\mathcal {A}_D=\langle Q,\varSigma _D,\varGamma _D,\varDelta ,q_{ init },A_{ init }^D \rangle$ for the pushdown system $\mathcal {D}$.

Theorem 5 and Remark 1 show that the existence of Büchi runs boils down to the existence of “ultimately periodic runs”:

Corollary 1

The parametrized pushdown system $\mathcal {S}$ has a Büchi run iff there is a run of $\mathcal {S}_{ fin }$ of the form

$$\begin{aligned} (n [p^{ fin }_{ init }],t_{ init }, g_{ init }) \xrightarrow {u} (M,t_1,g) \xrightarrow {v} (M,t_2, g) \xrightarrow {v} \ldots \end{aligned}$$

for some $n \in \mathbb {N}$, $g \in G$, $M \in (P_{ fin })^n$, $u,v\in (\varSigma _C\cup \varSigma _D)^*$, where:

• v ends by an action from $\varSigma _D$ and contains $\top$, and

• all configurations $t_i \in Q\varGamma _D^*$ of $\mathcal {D}$ have effective stack-height one, the same control state, and the same top stack symbol.

Capacities and Supported Loops. Our next goal is a Pspace algorithm for the existence of ultimately periodic runs of $\mathcal {S}_{ fin }$. Since the reachability problem is decidable in Pspace, we will focus on loops in $\mathcal {S}_{ fin }$ (i.e., runs of the form $(M,t,g) \mathop {\longrightarrow }\limits ^{+} (M,t',g)$ as in Corollary 1) and adapt the proof for the reachability problem proposed in [27].

In a nutshell, the idea of [27] is to split a parametrized pushdown system into a part that concerns the leader, and a part that concerns the contributors. What actually matters are the values that the contributors can write into the register because once these values are written they can be repeatedly written on demand, since we are in a parametrized setting. This information will be summarized by the notion of capacity. The leader, resp. any individual contributor, can work with an additional capacity that abstracts the details of runs of other contributors, by recording only the effect on the shared register. Of course, the capacity needs to be validated at some point, leading to the notion of “supported run”. The additional challenge is that this run should give a loop in the original system.

Following [27], $\mathcal {S}_{ fin }$ splits into a finite-state system $\mathcal {C}_{ fin }^\kappa$ representing the “capacity-aware” contributor, and a pushdown system $\mathcal {D}^\kappa$, representing the “capacity-aware” leader.

Formally, there is a new set of actions $\varSigma _\nu =\{\nu (g): g\in G\}$ denoting first contributor writes. In addition, each of $\mathcal {C}_{ fin }^\kappa$ and $\mathcal {D}^\kappa$ have a component K – the capacity – that stores the values that contributors have already written. The set of control states of $\mathcal {D}^\kappa$ is $\mathcal {P}(G)\times Q\times G$, and the initial state is $(\emptyset ,q_{ init },g_{ init })$. The input and the stack alphabets, $\varSigma _D$ and $\varGamma _D$, are inherited from $\mathcal {D}$. So a configuration of $\mathcal {D}^\kappa$ has the form $(K\subseteq G, \; t \in Q\varGamma _D^*, \; g\in G)$. The transitions of $\mathcal {D}^\kappa$ are:

The finite transition system $\mathcal {C}_{ fin }^\kappa$ is defined similarly, it just follows in addition the transitions of $\mathcal {D}^\kappa$ (first line below). The set of states of $\mathcal {C}_{ fin }^\kappa$ is $\mathcal {P}(G)\times P_{ fin }\times G$, input alphabet $\varSigma _C$, and initial state $(\emptyset ,p^{ fin }_{ init },g_{ init })$. The transitions of $\mathcal {C}_{ fin }^\kappa$ are:

$$\begin{aligned} (K,p,g)\xrightarrow {w(h)}&(K,p,h), \quad (K,p,g)\xrightarrow {r(h)} (K,p,h), \quad (K,p,g)\xrightarrow {\nu (h)} (K\cup \{h\},p,h) \\ (K,p,g)\xrightarrow {\overline{w}(h)}&(K,p',h) \quad \text {if } p\xrightarrow {\overline{w}(h)}p' \text { in } \delta \text { and } h\in K\\ (K,p,g)\xrightarrow {\overline{r}(h)}&(K,p',h) \quad \text {if } p\xrightarrow {\overline{r}(h)} p' \text { in } \delta \text { and } h\in K\cup \{g\}. \end{aligned}$$

Note that in both $\mathcal {D}^\kappa$ and $\mathcal {C}^\kappa$ some additional reads $r(h),\overline{r}(h)$ are possible when $h \in K$ – these are called capacity-reads.

Notation. We write $\varSigma _{D,\nu }$ for $\varSigma _D\cup \varSigma _\nu$. Similarly for $\varSigma _{C,\nu }$ and $\varSigma _{C,D,\nu }$. By $v|_\varSigma$ we will denote the subword of v obtained by erasing the symbols not in $\varSigma$. Note that the value of the register after executing a trace v, in both $\mathcal {C}_{ fin }^\kappa$ and $\mathcal {D}^\kappa$, is determined by the last action of v. We denote by $last (v)$ the register value of the last action of v (for v non-empty).

We now come back to examining when there exists an ultimately periodic run of $\mathcal {S}_{ fin }$. Clearly, a run (or loop) of $\mathcal {S}_{ fin }$ induces a run (or loop) of $\mathcal {D}^\kappa$, but the converse is not true. For the other direction we extend the notion of supported trace [27] to $\omega$ -support. Informally, a trace v of $\mathcal {D}^\kappa$ is called $\omega$ -supported when (1) for each first write $\nu (h)$ in v there is a trace of $\mathcal {C}_{ fin }^\kappa$ witnessing the fact that a contributor run can produce the required action $\overline{w}(h)$, and (2) all witness traces can be completed to loops in $\mathcal {C}_{ fin }^\kappa$.

Definition 1

Consider a word $v = v_1 \nu (h_1) \cdots v_m \nu (h_m) v_{m+1} \in \varSigma ^*_{D,\nu },$ where $v_1,\dots ,v_{m+1}\in \varSigma _D^*$, and $h_1,\dots ,h_m \in G$ are pairwise different register values. Let $p_1,\ldots ,p_m \in P_{ fin }$ be states of $\mathcal {C}_{ fin }$.

We say that v is $\omega$ -supported from $(p_1, \ldots , p_m)$ if for every $1\le i \le m$ there is some trace $u^i\in (\varSigma _{C,D,\nu })^*$ of $\mathcal {C}_{ fin }^\kappa$ of the form

$$\begin{aligned} u^i = u^i_1 \nu (h_1) \cdots u^i_i \nu (h_i) \; \varvec{\overline{w}(h_i)} \; u^i_{i+1} \cdots u^i_m\nu (h_{m})u^i_{m+1} \end{aligned}$$

such that: (i) $u^i|_{\varSigma _{D,\nu }} = v$, and (ii) $(\emptyset , p_i, g) \xrightarrow {u^i} (K,p_i,g)$ in $\mathcal {C}_{ fin }^\kappa$, where $g= last (v)$.

Note that $K=\{h_1,\ldots ,h_m\}$ in the above definition, and that $u^i_j|_{\varSigma _{D,\nu }} = v_j$ holds for all j. The next lemma states that the notions of capacity and of $\omega$-support suffice for checking the existence of Büchi runs. The intuition behind the proof of the lemma is that a finite number of contributor instances, starting in one of the states $p_i$, can simultaneously ensure that all capacity-reads are possible, and get back to state $p_i$.

Lemma 2

The parametrized pushdown system $\mathcal {S}$ has some Büchi run iff there is some reachable configuration $(M,q A \alpha ,g)$ of $\mathcal {S}_{ fin }$ and a word $v\in \varSigma ^*_{D,\nu }$ such that:

• 1. $\mathcal {D}^\kappa$ has a run of the form $(\emptyset , q A, g)\xrightarrow {v} (K, q A \alpha ', g)$, and $\top$ appears in v.

• 2. v is $\omega$-supported from some $(p_1, \ldots , p_m)$ such that $[p_1,\dots ,p_m]\le M$.

Observe that by Definition 1, we have $m\le |G|$ in Lemma 2.

Algorithm. Recall that a word u is a subword of v, written $u \sqsubseteq v$, if u is obtained from v by erasing some symbols. The downward closure of a language $L \subseteq \varSigma ^*$ is $L \!\downarrow \,= \{u \in \varSigma ^*: \exists v \in L.\, u \sqsubseteq v\}$. By a classical result in combinatorics (Higman’s lemma) we know that the downward closure of any language is regular, however not effective in general. For pushdown systems it is effective [10] and a finite-state automaton of exponential size can be computed on-the-fly in Pspace.

For our Pspace algorithm we first observe that the capacity-aware leader $\mathcal {D}^\kappa$ can be replaced by its downward closure, since adding some transitions of the leader does not affect the support of contributors:

Lemma 3

Let $v=v_1 \nu (h_1) \cdots v_m \nu (h_m) v_{m+1}$ be $\omega$-supported from $p_1, \ldots , p_m$, and let $v_j \sqsubseteq \overline{v}_j$ for every j. Assume that $\overline{v}=\overline{v}_1 \nu (h_1) \cdots \overline{v}_m \nu (h_m) \overline{v}_{m+1}$ satisfies $last (v)= last (\overline{v})$. Then $\overline{v}$ is also $\omega$-supported from $(p_1, \ldots , p_m)$.

The proof of Theorem 3 is based on Lemmas 2 and 3. The algorithm checks emptiness of the product of at most $|G|+1$ finite-state automata of exponential size – the automaton for the downward closure, and the automata for $\omega$-support. Together with a reachability check for the initial trace segment, we get a Pspace algorithm for liveness.

5 Max-Safety

Recall that universal reachability amounts to ask that some special action $\top$ of the leader occurs in every trace, no matter how many contributor instances are around. This is a typical question to ask when we are interested in something that is computed by a parametrized system. The max-safety problem is just the complement of universal reachability. A (maximal) safe run is a (maximal) run that does not contain $\top$.

We show in this section that the max-safety problem is NP-complete when contributors are finite-state systems, and Nexptime-complete when contributors are pushdown systems (the leader is in both cases a pushdown system). As for liveness, we can reduce the second case to the first one, thus obtaining the Nexptime upper bound. The lower bound is more challenging.

Set Semantics. As a first step we will introduce a set semantics of parametrized pushdown systems that is equivalent to the multiset semantics of Sect. 3 when only finite traces are considered. The idea is that since the number of contributors is arbitrary, one can always add some contributor instances that copy all the actions of a given contributor. So once a state of $\mathcal {C}$ is reached, we can assume that we have arbitrarily (but finitely) many copies of $\mathcal {C}$ in that state. In consequence, multisets can be replaced by sets. Very similar ideas have been already used in [15, 27]. Here we need to be a bit finer because we are interested in maximal runs.

Consider a parametrized pushdown system with the notations on page 7 (Eq. (1)):

$$\mathcal {C}=\langle S,\delta ,s_{ init } \rangle \qquad \mathcal {D}=\langle T,\varDelta , t_{ init } \rangle . $$

Instead of multisets $M \in \mathbb {N}^S$, we use sets $B \subseteq S$. As we have done for multisets, we lift the transitions from elements to sets of elements:

$$\begin{aligned} B \xrightarrow {a} B' \text { in } \delta&\quad \text { if } s \xrightarrow {a} s' \text { in } \delta , \text { and } B' \text { is either } B \cup \{s'\} \text { or } (B \cup \{s'\}) \setminus \{s\}\\&\quad \text { for some } s\in B. \end{aligned}$$

The intuition is that $B \xrightarrow {a} B \cup \{s'\}$ represents the case where some contributors in state s take the transition, and $B \xrightarrow {a} (B \cup \{s'\}) \setminus \{s\}$ corresponds to the case where all contributors in state s take the transition. The transitions in the set semantics are essentially the same as for the multiset case:

Remark 2

The set semantics is a variant of the accumulator semantics used in [27], in which only transitions of the form $B \xrightarrow {a} B \cup \{s'\}$ (but not $B \xrightarrow {a} (B \cup \{s'\})\setminus \{s\}$) were used. The accumulator semantics is nice because it is monotonic, and it suffices for reachability. But it is not precise enough when dealing with maximal runs.   $\square$

Recall that a support of a multiset is the set of elements that appear in it with non-zero multiplicity. We have modified the accumulator semantics so that runs preserve the support as stated in the next lemma.

Lemma 4

• 1. If $(M_0,t_0,g_0) \xrightarrow {a_1} \ldots \xrightarrow {a_n} (M_n,t_n,g_n)$ in the multiset semantics, and $B_j$ is the support of $M_j$, for every $j=0,\dots ,n$, then $(B_0,t_0,g_0) \xrightarrow {a_1} \ldots \xrightarrow {a_n} (B_n,t_n,g_n)$ in the set semantics.

• 2. If $(B_0,t_0,g_0) \xrightarrow {a_1} \ldots \xrightarrow {a_n} (B_n,t_n,g_n)$ in the set semantics, then there exist multisets $M_0, \ldots , M_n$ such that $M_j$ has support $B_j$, and for some $i_j >0$,

  $$(M_0,t_0,g_0) \xrightarrow {(a_1)^{i_1}} (M_1,t_1,g_1) \xrightarrow {(a_2)^{i_2}} \ldots \xrightarrow {(a_n)^{i_n}} (M_n,t_n,g_n)$$

  in the multiset semantics.

Corollary 2

Fix a parametrized pushdown system. In the multiset semantics the system has a finite maximal safe run ending in a configuration (M, t, g) iff in the set semantics the system has a finite maximal safe run ending in the configuration (B, t, g) with B being the support of M.

Finite-State Contributors. We start with the case where contributors are finite-state. An easy reduction from 3-SAT shows:

Lemma 5

The max-safety problem is NP-hard when contributor and leader are both finite-state systems.

For the upper bound of the max-safety problem with finite-state contributors we need to distinguish between finite and infinite maximal safe runs.

The case of infinite safe runs reduces to the liveness problem, using Theorem 4 (items 2 and 3): we can construct from a given parametrized pushdown system $\mathcal {S}$ a parametrized pushdown system $\mathcal {S}'$ such that $\mathcal {S}$ has an infinite safe run iff $\mathcal {S}'$ has a run with infinitely many leader writes, but not $\top$. To decide if $\mathcal {S}'$ admits such a run, we remove $\top$ and test for each possible value g of the register if there is a run with infinitely many writes $w(g)$. Since liveness is in NP for finite-state contributors [12] we obtain:

Lemma 6

For finite-state contributors and pushdown leader, it can be decided in NP whether a parametrized pushdown system has an infinite safe run.

It remains to describe an algorithm for the existence of a finite maximal safe run. By Corollary 2 we can use our set semantics for this. From now on we will also exploit the fact that $\mathcal {D}$ is a pushdown system. Recall that the states of $\mathcal {D}$ are of the form $q\alpha$ where q is the state of the pushdown automaton defining $\mathcal {D}$ and $\alpha$ represents the stack. The question is to decide if there is a deadlock configuration $(B,q\alpha ,g)$ in the parametrized pushdown system, such that $(B,q\alpha ,g)$ is reachable without using the $\top$ action. Note that we can determine whether $(B,q\alpha ,g)$ is a deadlock by looking only at B, q, g and the top symbol of $\alpha$. Our algorithm will consist in guessing B, q, g and some $A \in \varGamma _D$, and then checking reachability.

To check reachability in NP we first show that it is sufficient to look for traces where the number of changes of the first component of configurations (the set-component) is polynomially bounded:

Lemma 7

For every finite run $\rho$ of the parametrized pushdown system in the set semantics, there exists some run $\rho '$ with the same action labels, same end configuration and of the form $\rho '=\rho '_0 \cdots \rho '_k$ with $k \le 2|S|$, where in each $\rho '_j$, all states have the same set-component.

Proof

Take a run $\rho = (B_0, t_0, g_0) \xrightarrow {a_1} (B_1, t_1, g_1) \xrightarrow {a_2} \ldots \xrightarrow {a_n} (B_n,t_n,g_n)$ of the parametrized pushdown system. We claim that there exists a run $\rho ' = (B'_0, t_0, g_0) \xrightarrow {a_1} (B'_1, t_1, g_1) \xrightarrow {a_2} \ldots \xrightarrow {a_n} (B'_n,t_n,g_n)$ such that $B_0 = B'_0$, $B_n = B'_n$, and for all $s \in S$ and $0 \le i < n$, if $s \in B'_i$ and $s \notin B'_{i+1}$, then for all $j > i$, $s \notin B'_j$.

Indeed let us define $B'_i$ by induction on i: $B'_0 = B_0$, and for $i > 1$,

• if $B_{i+1} = B_i$, then $B'_{i+1} = B'_i$.

• if $B_{i+1} = B_i \cup \{s\}$, then $B'_{i+1} = B'_i \cup \{s\}$.

• if $B_{i+1} = (B_i \setminus \{s\}) \cup \{s'\}$ and $s \notin B_j$ for all $j > i$, then $B'_{i+1} = (B'_i \setminus \{s\}) \cup \{s'\}$. If $s \in B_j$ for some $j > i$, then $B'_{i+1} = B'_i \cup \{s'\}$.

Clearly, $\rho '$ is a run of the parametrized pushdown system. Moreover, for all i, $B_i \subseteq B'_i \subseteq \bigcup _{j = i}^n B_j$. So in particular, $B_n = B'_n$.

Now we take the run $\rho '$. Let $i_0 = 0$, and $i_1< \cdots < i_k$ be the indices such that $B'_i \ne B'_{i-1}$. Then $\rho '$ can be decomposed into $\rho ' = \rho '_0 \cdots \rho '_k$, where for all j, the set-component of all states in $\rho '_j$ is $B'_{i_j}$. Consider the sequence $B'_{i_0}, B'_{i_1}, \ldots , B'_{i_k}$. There are states $s_1, \ldots , s_k \in S$ such that for all $0 \le j < k$, $B'_{i_{j+1}} = B'_{i_j} \cup \{s_j\}$ or $B'_{i_{j+1}} = (B'_{i_j} \cup \{s\}) \setminus \{s_j\}$ for some s. Moreover, each $s\in S$ is added at most once, and removed at most once from some $B'_i$, which means that there are at most two distinct indices j such that $s = s_j$. Hence $k \le 2|S|$.    $\square$

The next lemma follows now from Lemma 7: we first guess a sequence of sets of states $B_0, B_1, \ldots , B_k = B$ of length $k \le 2|S|$, then construct a pushdown automaton of polynomial size according to the guess, and finally check reachability in polynomial time [4]:

Lemma 8

The following problem is in NP: given a parametrized pushdown system with finite-state contributors and a configuration (B, qA, g) in the set semantics, decide if there exists $\alpha$ such that $(B,qA\alpha ,g)$ is reachable from the initial configuration.

Proof

The set semantics of the parametrized pushdown system corresponds to a pushdown automaton $\mathcal {A}$ with set of control states $2^S\times Q\times G$, input alphabet $\varSigma _C\cup \varSigma _D$, and stack alphabet $\varGamma _D$. We first guess a sequence $\{s_{ init }\} = B_0, B_1, \ldots , B_k = B$ of sets of contributor states, where $k \le 2|S|$. Then we construct the restriction of $\mathcal {A}$ to runs where the first component of the state is equal to $B_0$, then $B_1$, up to $B_k$. The pushdown automaton thus obtained has polynomial size, and we can check in polynomial time whether it has some reachable configuration $(B,qA\alpha ,g)$ [4].    $\square$

Combining Lemmas 5, 6 and 8 we obtain the complexity result for finite-state contributors:

Theorem 6

The max-safety problem is NP-complete when contributors are finite-state systems.

Pushdown Contributors. We now return to the case where contributors are pushdown systems, and show first a lower bound, by a reduction from a tiling problem [18]:

Lemma 9

The max-safety problem is Nexptime-hard for parametrized pushdown systems.

Proof

We reduce the following tiling problem [18] to the max-safety problem:

Input: A finite set of tiles $\varSigma$, horizontal and vertical compatibility relations $H,V\subseteq \varSigma ^2$, and an initial row $x \in \varSigma ^n$.

Question: Is there a tiling of the $2^n \times 2^n$ square respecting the compatibility relations and containing the initial row in the left corner?

A tiling is a function $t: \{1,\ldots , 2^n\}^2 \rightarrow \varSigma$ such that $(t(i,j),t(i,j+1)) \in H$ and $(t(i,j),t(i+1,j)) \in V$ for all i, j, and $t(1,1)t(1,2) \cdots t(1,n) = x$.

The idea of the reduction is that the system will have a maximal run without $\top$ if and only if the leader can guess a tiling respecting the horizontal compatibility, and the contributors check that the vertical compatibility is respected as well.

The leader will write down the tiling from left to right and from top to bottom, starting with the initial row. The sequence of values taken by the register on a (good) run will have the form

$$\begin{aligned} A_{1,1}, \overline{A_{1,1}}, A_{1,2}, \overline{A_{1,2}}, \ldots , A_{1,2^n}, \overline{A_{1,2^n}},\ldots , A_{2^n, 2^n} \, \overline{A_{2^n, 2^n}}\; (\$ \overline{\$})^{2^n}\diamond . \end{aligned}$$

The $A_{i,j}$ are guessed and written by the leader, and the $\overline{A_{i,j}}$ are written by contributors. Letters $\overline{A_{i,j}}$ have two purposes: they ensure that at least one contributor has read the preceding letter, and prevent a contributor from reading the same letter twice. For technical reasons, this sequence is followed by a sequence $(\$ \overline{\$})^{2^n}\diamond$ of writes from the leader (with $\$,\diamond \notin \varSigma$), and we will consider that $(A,\$) \in V$ for all $A \in \varSigma$.

The leader uses her stack to count the number i of rows (using the lower part of the stack), and the number j of tiles on each row (using the upper part of the stack). So, she repeats the following, up to reaching the values $i = 2^n, j = 2^n$: (i) guess a tile A compatible with the one on its left (if $j \ne 1$), and write A on the register, (ii) wait for an acknowledgment $\overline{A}$ from one of the contributors, (iii) increment j, (iv) if $j >2^n$, increment i and set $j=1$.

Finally, she repeats $2^n$ times the actions $w(\$)$, $w(\overline{\$})$, then finishes by writing $w(\diamond )$ and going to some distinguished state $q_f$.

Each contributor is supposed to read the entire sequence of values written in the register. He alternates between reading values of the form A and $\overline{A}$, which ensures that no value is read more than one time. At the same time, he uses his stack to count the number of writes $w(A)$ ($A \in \varSigma \cup \{\$\}$) of the leader, up to $(2^{2n}+2^n)$, so that he can check that no value was missed. This operation will in fact be divided between counting up to $2^{2n}$, and counting up to $2^{n}$, as described below.

Every contributor decides non-deterministically to check vertical compatibility at some point. He chooses the current tile $A \not =\$$, and needs to check that the tile located below it (that is, occurring $2^n$ tiles later in the sequence of values written by the leader) is compatible with it. This is done as follows: after reading $A\not =\$$, the contributor writes $\overline{A}$ on the register (rather than waiting for another contributor to do so), and remembers the value. He interrupts his current counting, and starts counting anew on the top of the stack, up to $2^n$. Upon reaching $2^n$, he stores the value $A'$ of the register, for later check. Then he resumes the first counting while reading the remaining of the sequence, up to $2^{2n}$. At any moment, the contributor can read $\diamond$. If he reads $\diamond$ and either $(A,A') \notin V$ or the counting up to $2^n$ failed (i.e., his stack is not empty), then he writes $\#$ (with $\# \notin \varSigma \cup \overline{\varSigma }\cup \{\$,\diamond \}$) and stops; otherwise he simply stops. In state $q_f$, the leader may read any value $g \ne \diamond$, and she then does $\top$: $q_f \mathop {\longrightarrow }\limits ^{r(g)} \mathop {\longrightarrow }\limits ^{\top }$. From every other state $q \not = q_f$, the leader can do $\top$, too.

It can be verified [17] that there is a tiling of the $2^n \times 2^n$ square, if and only if, there is a maximal run without any occurrence of $\top$. For the left-to-right implication the leader should write a sequence of register values corresponding to the tiling, and every contributor can end up with the empty stack upon reading $\diamond$, so no $\top$ will be generated. For the right-to-left direction, observe that in the maximal run the leader should reach $q_f$. In this case the acknowledgment mechanism is set up in such a way that all the values written by the leader should be successfully checked by contributors.   $\square$

For the upper bound, similarly to the case of finite-state contributors we need to consider maximal finite and infinite runs separately. The case of infinite runs can be again reduced to liveness using Theorem 4, and turns out to be easier:

Lemma 10

It can be decided in Pspace whether a parametrized pushdown system has some infinite safe run.

For finite maximal runs, we show that we match the Nexptime lower bound. For this we reduce the problem to the case of finite-state contributors, using Lemma 1 that gives a polynomial bound for contributor stacks. Then we can apply Lemma 8 that states that the complexity is NP for finite-state contributors:

Lemma 11

It can be decided in Nexptime whether a parametrized pushdown system has some finite, maximal safe run.

The three lemmas together prove Theorem 2.

6 Regular C-expanding Properties

In this section, we outline the proof of our general result stated in Theorem 1. The proof is based on Theorem 4, that says that we can focus on properties that refer only to leader actions. The proof idea for Theorem 4 is that in the new parametrized pushdown system, the register becomes part of the leader’s state. This releases the register, that can be used now by contributors to communicate with the leader regarding the actions that they intend to perform, but the leader is in charge to execute them. Contributors in the new parametrized pushdown system write into the register the read/write action they want to execute; the leader executes the action and confirms this to the contributors by writing back into the register. The confirmation is read by contributors who at this point know that their action request has been read and executed. The simulation makes use of the fact that the property we want to check is c-expanding. The details of the construction, and the correctness proof, are a bit tedious since it is always possible that a value is overwritten before it gets read.

The proof of Theorem 1 is, once again, divided into two cases: one for finite and the other for infinite traces. For finite maximal traces we use the results about the max-safety problem, and for infinite traces we reduce the problem to liveness.

Lemma 12

The following question is Nexptime-complete: given a parametrized pushdown system $\mathcal {S}$ and a c-expanding $\omega$-regular property $\mathcal {P}$ over $\mathcal {S}$ (described by a Büchi automaton or by an LTL formula), determine if $\mathcal {S}$ has some maximal, finite trace in $\mathcal {P}$.

Proof Sketch. By Theorem 4 we can assume that we need to check a property $\mathcal {P}$ that refers only to actions of the leader. If $\mathcal {P}$ is given by an LTL formula, we start by constructing an equivalent finite automaton of exponential size. By taking the product of the leader $\mathcal {D}$ with this automaton representing $\mathcal {P}$, we can assume that $\mathcal {D}$ has a distinguished set of final (control) states such that a finite run of the parametrized pushdown system satisfies $\mathcal {P}$ iff $\mathcal {D}$ reaches a final state.

The result then follows using Lemma 1, together with Lemma 8. Recall that in order to decide if a finite run is maximal it is enough to look at the top of its last configuration. Lemma 1 then tells us that there exists a maximal finite run in the parametrized pushdown system $\mathcal {S}$ with $\mathcal {D}$ ending in a final state iff there exists such a run in the parametrized pushdown system $\mathcal {S}_{ fin }$, where contributors are finite-state; and by Lemma 8 the latter can be decided in NP in the size of $\mathcal {S}_{ fin }$, so overall in Nexptime. The matching Nexptime-hardness lower bound follows from the proof of Lemma 9, as the parametrized pushdown system constructed there has no infinite safe trace, and the max-safety problem restricted to finite traces is a special instance of our problem.   $\square$

As for the max-safety problem, the case of infinite runs turns out to be easier. It is also interesting to observe that the complexity now depends on whether the property is described by an automaton or by a formula.

Lemma 13

The following question is Pspace-complete: given a parametrized pushdown system $\mathcal {S}$ and a c-expanding $\omega$-regular property $\mathcal {P}$ over $\mathcal {S}$ described by a Büchi automaton, determine if $\mathcal {S}$ has some infinite trace in $\mathcal {P}$.

Proof Sketch. Applying again Theorem 4 and slightly modifying the parametrized pushdown system we can reduce the satisfaction of $\mathcal {P}$ to an instance of the liveness problem; observe also that liveness is a special case of our problem. With this reduction, Pspace-completeness follows from Theorem 3.    $\square$

Lemma 14

The following question is Exptime-complete: given a parametrized pushdown system $\mathcal {S}$ and a c-expanding $\omega$-regular property $\mathcal {P}$ over $\mathcal {S}$ described by an LTL formula, determine if $\mathcal {S}$ has some infinite trace in $\mathcal {P}$.

Proof Sketch. The lower bound comes from the situation where there are no contributors at all [4]. For the upper bound: from an LTL formula we first construct a Büchi automaton of exponential size. As in Lemma 13, the first step is to reduce the problem of deciding if the parametrized pushdown system has a trace in $\mathcal {P}$ to the liveness of some parametrized pushdown system $\mathcal {S}'$. In the obtained system $\mathcal {S}'$ the leader $\mathcal {D}'$ is of exponential size, and $\mathcal {C}'$ is of polynomial size. As a second step we adapt the procedure given in the proof of Theorem 3: we do not build the downward closure of the leader, and we enumerate all possible sequences $\nu (h_1), \ldots , \nu (h_m)$ and intermediate states, instead of guessing them. Then we follow the lines of the proof of Theorem 3, checking emptiness of pushdown systems of exponential size in Exptime.    $\square$

7 Conclusion

We have established the decidability and exact complexity for verifying linear-time properties of parametrized pushdown systems, a model introduced in [20] that can be seen as adapting a formulation from [19] to communicating pushdown processes as in [21]. For decidability we needed to require that properties are c-expanding, a lighter version of stuttering invariance. On the way to this result we have determined the exact complexity of deciding liveness properties, which turned out to be an easier problem than deciding the existence of maximal runs.

Technically, our upper bound results for liveness as well as for maximal runs require to build on both the techniques from [12] and [27]. As pointed out in [12] the techniques for deciding reachability are not immediately applicable to the liveness problem. For reachability we can assume that for every write there is a separate contributor responsible to produce it. This is a very useful simplification that does not apply to repeated reachability, since we require that the number of contributors is bounded over the complete infinite run. For the case of maximal runs we introduced a simplification of the original semantics that is sensitive to divergence. The lower bound result for this case shows that being able to detect termination increases the complexity of the problem.

The model considered in this paper can be extended with dynamic thread creation. Reachability is still decidable for this extension [32]. The decidability proof is based on upper closures and well-quasi orders, so it does not provide any interesting complexity upper bounds. It is actually open whether the verification of regular properties of parametric systems with dynamic thread creation is decidable.