Abstract
We present and evaluate a technique for computing path-sensitive interference conditions during abstract interpretation of concurrent programs. In lieu of fixed point computation, we use prime event structures to compactly represent causal dependence and interference between sequences of transformers. Our main contribution is an unfolding algorithm that uses a new notion of independence to avoid redundant transformer application, thread-local fixed points to reduce the size of the unfolding, and a novel cutoff criterion based on subsumption to guarantee termination of the analysis. Our experiments show that the abstract unfolding produces an order of magnitude fewer false alarms than a mature abstract interpreter, while being several orders of magnitude faster than solver-based tools that have the same precision.
Supported by ERC project 280053 (CPROVER) and a Google Fellowship.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
This paper is concerned with the problem of extending an abstract interpreter for sequential programs to analyze concurrent programs. A naïve solution to this problem is a global fixed point analysis involving all threads in the program. An alternative that seeks to exploit the scalability of local analyses is to analyze each thread in isolation and exchange invariants on global variables between threads [3, 18, 19]. Much research on abstract interpretation of concurrent programs, including this paper, aims to discover analyses that combine the scalability of the local fixed point computation with the precision of a global fixed point.
The abstract unfolding data structure and algorithm presented in this paper combines an abstract domain with the type algorithm used to analyze Petri nets. An unfolding is a tree-like structure that uses partial orders to compactly represent concurrent executions and uses conflict relations to represent interference between executions. There are several obstacles to combining unfoldings with abstract domains. First, unfolding construction requires interference information that is absent from abstract domains. Second, an unfolding compactly represents the traces of a system, while abstract domains approximate states and transitions. Finally, unfolding algorithms perform explicit-state analysis of deterministic systems while abstract domains are inherently symbolic and non-deterministic owing to abstraction.
The main idea of this paper is to construct an unfolding of an analyzer, rather than a program. An event is the application of a transformer in an analysis context, and concurrent executions are replaced by a partial order on transformer applications. We introduce independence for transformers and use this notion to construct an unfolding of a domain given a program and independence relation. The unfolding of a domain is typically large and we use thread-local fixed point computation to reduce its size without losing interference information.
Most pairs of transformers are not related by standard notions of independence. A counterintuitive observation in this paper is that by increasing the path-sensitivity of the analysis, we decrease interference, which reduces the number of interleavings to explore and improves scalability. From a static analysis perspective, our analyser uses the unfolding to represent a history abstraction (or trace partition) which is constructed using independence. From a dynamic analysis perspective, our approach is a form of partial-order reduction (POR) [23] that uses an abstract domain to collapse branches of the computation tree originating from thread-local control decisions.
Contribution. We make the following contributions towards reusing an abstract interpreter for sequential code for the analysis of a concurrent program.
-
1.
A new notion of transformer independence for unfolding with domains (Sect. 4).
-
2.
The unfolding of a domain, which provides a sound way to combine transformer application and partial-order reduction (Sect. 5.1).
-
3.
A method to construct the unfolding using thread-local analysis and pruning techniques (Sects. 6 and 6.1).
-
4.
An implementation and empirical evaluation demonstrating the trade-offs compared to an abstract interpreter and solver-based tools (Sect. 7).
The proofs of the formal results presented in this paper can be found in the extended version [24].
2 Motivating Example and Overview
Consider the program given in Fig. 1(a), which we wish to prove safe using an interval analysis. Thread 1 (resp. 2) increments i (resp. j) in a loop that can non-deterministically stop at any iteration. All variables are initialized to 0 and the program is safe, as the assert in thread 2 cannot be violated.
When we use a POR approach to prove safety of this program, the exploration algorithm exploits the fact that only the interference between statements that modify the variable g can lead to distinct final states. This interference is typically known as independence [10, 22]. The practical relevance of independence is that one can use it to define a safe fragment, given in Fig. 1(b), of the computation tree of the program which can be efficiently explored [1, 23]. At every iteration of each loop, the conditionals open one more branch in the tree. Thus, each branch contains a different write to the global variable, which is dependent with the writes of the other thread as the order of their application reaches different states. As a result, the exploration tree becomes intractable very fast. It is of course possible to bound the depth of the exploration at the expense of completeness of the analysis.
The thread-modular static analysis that is implemented in AstreeA [19] or Frama-c [26] incorrectly triggers an alarm for this program. These tools statically analyze each thread in isolation assuming that g equals 0. Both discover that thread 1 (resp. 2) can write [0, 100] (resp. [0, 150]) to g when it reads 0 from it. Since each thread can modify the variable read by the other, they repeat the analysis starting from the join of the new interval with the initial interval. In this iteration, they discover that thread 2 can write [0, 250] to g when it reads [0, 150] from it. The analysis now incorrectly determines that it needs to re-analyze thread 2, because thread 1 also wrote [0, 250] in the previous iteration and that is a larger interval than that read by thread 2. This is the reasoning behind the false alarm. The core problem here is that these methods are path-insensitive across thread context switches and that is insufficient to prove this assertion. The analysis is accounting for a thread context switch that can never happen (the one that flows [0, 250] to thread 2 before thread 2 increments g). More recent approaches [15, 20] can achieve a higher degree of flow-sensitivity but they either require manual annotations to guide the trace partitioning or are restricted to program locations outside of a loop body.
Our key contribution is an unfolding that is flow- and path-sensitive across interfering statements of the threads, and path-insensitive inside the non-interfering blocks of statements. Figure 1(c) shows the unfolding structure that our method explores for this program. The boxes in this structure are called events and they represent the action of firing a transformer after a history of firings. The arrows depict causality constraints between events, i.e., the happens-before relation. Dotted lines depict the immediate conflict relation, stating that two events cannot be simultaneously present in the same concurrent execution, known as configuration. This structure contains three maximal configurations (executions), which correspond to the three meaningful ways in which the statements reading or writing to variable g can interleave.
Conceptually, we can construct this unfolding using the following idea: start by picking an arbitrary interleaving. Initially we pick the empty one which reaches the initial state of the program. Now we run a sequential abstract interpreter on one thread, say thread 1, from that state and stop on every location that reads or writes a global variable. In this case, the analyzer would stop at the statement g += i with the invariant that \(\langle g \mapsto [0,0], i \mapsto [0,100]\rangle \). This invariant corresponds to the first event of the unfolding (top-left corner). The unfolding contains now a new execution, so we iterate again the same procedure by picking the execution consisting of the event we just discovered. We run the analyser on thread 2 from the invariant reached by that execution and stop on any global action. That gives rise to the event g+=j, and in the next step using the execution composed of the two events we have seen, we discover its causal successor a() (representing the assert statement). Note however that before visiting that event, we could have added event g+=j corresponding to the invariant of running an analyser starting from the initial state on thread 2. Furthermore, since both invariants are related to the same shared variable, these two events must not be present in the same execution. We enforce that with the conflict relation.
Our method mitigates the aforementioned branching explosion of the POR tree because it never unfolds the conflicting branches of one thread (loop iterations in our example). In comparison to thread-modular analysis, it remains precise about the context switches because it uses a history-preserving data structure.
Another novelty of our approach is the observation that certain events are equivalent in the sense that the state associated with one is subsumed by the second. In our example, one of these events, known as a cutoff event, is labelled by g+=i and denoted with a striped pattern. Specifically, the configuration \(\left\{ \texttt {g+=i}, \texttt {g+=j}\right\} \) reaches the same state as \(\left\{ \texttt {g+=j}, \texttt {g+=i}\right\} \). Thus, no causal successor of a cutoff event needs to be explored as any action that we can discover from the cutoff event can be found somewhere else in the structure.
Outline. The following diagram displays the various concepts and transformations presented in the paper:
Let M be the program under analysis, whose concrete semantics \(\mathcal {C}_M\) is abstracted by a domain \(\mathcal {D}_M\). The relations  and
and  are independence relations with different levels of granularity over the transformers of M, \(\mathcal {C}_{M}\), or \(\mathcal {D}_M\). We denote by
are independence relations with different levels of granularity over the transformers of M, \(\mathcal {C}_{M}\), or \(\mathcal {D}_M\). We denote by  the unfolding of \(\mathcal {D}'\) (either \(\mathcal {C}_{M}\) or \(\mathcal {D}_M\)) under independence relation
the unfolding of \(\mathcal {D}'\) (either \(\mathcal {C}_{M}\) or \(\mathcal {D}_M\)) under independence relation  (either
(either  or
or  ). This transformation is defined in Sect. 5.1. Whenever we unfold a domain using a weak independence relation (
). This transformation is defined in Sect. 5.1. Whenever we unfold a domain using a weak independence relation ( on \(\mathcal {C}_{M}\) and
on \(\mathcal {C}_{M}\) and  on \(\mathcal {D}_M\)), we can use cutoffs to prune the unfolding, represented by the dashed line between unfoldings. The resulting unfolding, defined in Sect. 6.1, is denoted by the letter \(\mathcal {P}\). The main contribution of our work is the compact unfolding,
on \(\mathcal {D}_M\)), we can use cutoffs to prune the unfolding, represented by the dashed line between unfoldings. The resulting unfolding, defined in Sect. 6.1, is denoted by the letter \(\mathcal {P}\). The main contribution of our work is the compact unfolding,  , an example of which was given in Fig. 1(c).
, an example of which was given in Fig. 1(c).
3 Preliminaries
There is no new material in this section, but we recommend the reader to review the definition of an analysis instance, which is not standard.
Concurrent Programs. We model the semantics of a concurrent, non-deterministic program by a labelled transition system \(M \mathrel {:=}\langle \varSigma , \rightarrow , A, s_0\rangle \), where \(\varSigma \) is the set of states, A is the set of program statements, \({\rightarrow } \subseteq \varSigma \times A \times \varSigma \) is the transition relation, and \(s_0\) is the initial state. The identifier of the thread containing a statement a is given by a function \(p :A \rightarrow \mathbb {N}\). If \(s \displaystyle \mathop {\rightarrow }^{a} s'\) is a transition, the statement a is enabled at s, and a can fire at s to produce \(s'\). We let \(\mathop { enabl } (s)\) denote the set of statements enabled at s. As statements may be non-deterministic, firing a may produce more than one such \(s'\). A sequence \(\sigma \mathrel {:=} a_1 \ldots a_n \in A^*\) is a run when there are states \(s_1, \ldots , s_n\) satisfying \(s_0 \displaystyle \mathop {\rightarrow }^{a_1} s_1 \ldots \displaystyle \mathop {\rightarrow }^{a_n} s_n\). For such \(\sigma \) we define \(\mathop { state } (\sigma )\mathrel {:=}s_n\). We let \(\mathop { runs } (M)\) denote the set of all runs of M, and \(\mathop { reach } (M) \mathrel {:=}\left\{ \mathop { state } (\sigma )\in \varSigma :\sigma \in \mathop { runs } (M)\right\} \) the set of all reachable states of M.
Analysis Instances. A lattice \(\langle D, \sqsubseteq _D, \sqcup _D, \sqcap _D\rangle \) is a poset with a binary, least upper bound operator \(\sqcup _D\) called join and a binary, greatest lower bound operator \(\sqcap _D\) called meet. A transformer \(f :D \rightarrow D\) is a monotone function on D. A domain \(\langle D, \sqsubseteq , F\rangle \) consists of a lattice and a set of transformers. We adopt standard assumptions in the literature that D has a least element \(\bot \), called bottom, and that transformers are bottom-strict, i.e. \(f(\bot ) = \bot \). To simplify presentation, we equip domains with sufficient structure to lift notions from transition systems to domains, and assume that domains represent control and data states.
Definition 1
An analysis instance \(\mathcal {D}\mathrel {:=}\langle D, \sqsubseteq , F, d_0\rangle \), consists of a domain \(\langle D, \sqsubseteq , F\rangle \) and an initial element \(d_0 \in D\).
A transformer f is enabled at an element d when \(f(d) \ne \bot \), and the result of firing f at d is f(d). The element generated by or reached by a sequence of transformers \(\sigma \mathrel {:=}f_1, \ldots , f_m\) is the application \(\mathop { state } (\sigma )\mathrel {:=}(f_m \circ \ldots \circ f_1) (d_0)\) of transformers in \(\sigma \) to \(d_0\). Let \(\mathop { reach } (\mathcal {D})\) be the set of reachable elements of \(\mathcal {D}\). The sequence \(\sigma \) is a run if \(\mathop { state } (\sigma )\ne \bot \) and \(\mathop { runs } (\mathcal {D})\) is the set of all runs of \(\mathcal {D}\).
The collecting semantics of a transition system M is the analysis instance \(\mathcal {C}_{M} \mathrel {:=}\langle \mathop {\mathscr {P}(\varSigma )}, \subseteq , F, \left\{ s_0\right\} \rangle \), where F contains a transformer \(f_a (S) \mathrel {:=}\left\{ s' \in \varSigma :s \in S \wedge s \displaystyle \mathop {\rightarrow }^{a} s'\right\} \) for every statement a of the program. The pointwise-lifting of a relation \(R \subseteq A \times A\) on statements to transformers in \(\mathcal {D}\) is \(R_\mathcal {D}= \left\{ \langle f_a, f_{a'}\rangle ~|~\langle a,a'\rangle \in R\right\} \). Let \(m_0 :A \rightarrow F\) be map from statements to transformers: \(m_0(a) \mathrel {:=}f_a\). An analysis instance  is an abstraction of \(\langle D, \sqsubseteq , F, d_0\rangle \) if there exists a concretization function \(\gamma : \bar{D} \rightarrow D\), which is monotone and satisfies that \(d_0 \sqsubseteq \gamma (\bar{d}_0) \), and that \(f \circ \gamma \sqsubseteq \gamma \circ \bar{f}\), where the order between functions is pointwise.
is an abstraction of \(\langle D, \sqsubseteq , F, d_0\rangle \) if there exists a concretization function \(\gamma : \bar{D} \rightarrow D\), which is monotone and satisfies that \(d_0 \sqsubseteq \gamma (\bar{d}_0) \), and that \(f \circ \gamma \sqsubseteq \gamma \circ \bar{f}\), where the order between functions is pointwise.
Labelled Prime Event Structures. Event structures are tree-like representations of system behaviour that use partial orders to represent concurrent interaction. Figure 3 depicts an event structure. The nodes are events and solid arrows, represent causal dependencies: events 4 and 7 must fire before 8 can fire. The dotted line represents conflicts: 4 and 7 are not in conflict and may occur in any order, but 4 and 9 are in conflict and cannot occur in the same execution.
A labelled prime event structure [21] (PES) is a tuple \(\mathcal {E}\mathrel {:=}\langle E, <, \mathrel {\#}, h\rangle \) with a set of events E, a causality relation \({<} \subseteq E \times E\), which is a strict partial order, a conflict relation \({\mathrel {\#}} \subseteq E \times E\) that is symmetric and irreflexive, and a labelling function \(h :E \rightarrow X\). The components of \(\mathcal {E}\) satisfy (1) the axiom of finite causes, that for all \(e \in E\), \(\left\{ e' \in E :e' < e\right\} \) is finite, and (2) the axiom of hereditary conflict, that for all \(e,e',e'' \in E\), if \(e \mathrel {\#}e'\) and \(e' < e''\), then \(e \mathrel {\#}e''\).
The history of an event \(\left\lceil e \right\rceil \mathrel {:=}\left\{ e' \in E :e' < e\right\} \) is the least set of events that must fire before e can fire. A configuration of \(\mathcal {E}\) is a finite set \(C \subseteq E\) that is (i) (causally closed) \(\left\lceil e \right\rceil \subseteq C\) for all \(e \in C\), and (ii) (conflict free) \(\lnot (e \mathrel {\#}e')\) for all \(e, e' \in C\). We let \(\mathop { conf } (\mathcal {E})\) denote the set of all configurations of \(\mathcal {E}\). For any \(e \in E\), the local configuration of e is defined as \([e] \mathrel {:=}\left\lceil e \right\rceil \cup \left\{ e\right\} \). In Fig. 3, the set \(\left\{ 1,2\right\} \) is a configuration, and in fact it is a local configuration, i.e., \([2] = \left\{ 1,2\right\} \). The set \(\left\{ 1,2,3\right\} \) is a \(\subseteq \)-maximal configuration. The local configuration of event 8 is \(\left\{ 4,7,8\right\} \).
Given a configuration C, we define the interleavings of C as the set
An interleaving corresponds to the sequence labelling any topological sorting (sequentialization) of the events in the configuration. We say that \(\mathcal {E}\) is finite iff E is finite. In Fig. 3, the interleavings of configuration \(\left\{ 1,2,3\right\} \) are \(wrr'\) and \(wr'r\).
Event structures are naturally (partially) ordered by a prefix relation \(\mathrel {\trianglelefteq }\). Given two PESs \(\mathcal {E}\mathrel {:=}\langle E, <, \mathrel {\#}, h\rangle \) and \(\mathcal {E}' \mathrel {:=}\langle E', <', \mathrel {\#}', h'\rangle \), we say that \(\mathcal {E}\) is a prefix of \(\mathcal {E}'\), written \(\mathcal {E}\mathrel {\trianglelefteq }\mathcal {E}'\), when \(E \subseteq E'\), < and \(\mathrel {\#}\) are the projections of \(<'\) and \(\mathrel {\#}'\) to E, and \(E \supseteq \left\{ e' \in E' :e' < e \wedge e \in E\right\} \). Moreover, the set of prefixes of a given PES \(\mathcal {E}\) equipped with \(\mathrel {\trianglelefteq }\) is a complete lattice.
4 Independence for Transformers
Partial-order reduction tools use a notion called independence to avoid exploring concurrent interleavings that lead to the same state. Our analyzer uses independence between transformers to compactly represent transformer applications that lead to the same result. The contribution of this section is a notion of independence for transformers (represented by the lowest horizontal arrows in Fig. 2) and a demonstration that abstraction may both create and violate independence relationships.
We recall a standard notion of independence for statements [10, 22]. Two statements \(a, a'\) of a program M commute at a state s iff
-
if \(a \in \mathop { enabl } (s)\) and \(s \displaystyle \mathop {\rightarrow }^{a} s'\), then \(a' \in \mathop { enabl } (s)\) iff \(a' \in \mathop { enabl } (s')\); and
-
if \(a, a' \in \mathop { enabl } (s)\), then there is a state \(s'\) such that \(s \displaystyle \mathop {\rightarrow }^{a.a'} s'\) and \(s \displaystyle \mathop {\rightarrow }^{a'.a} s'\).
Independence between statements is an underapproximation of commutativity. A relation  is an independence for M if it is symmetric, irreflexive, and satisfies that every
is an independence for M if it is symmetric, irreflexive, and satisfies that every  commute at every reachable state of M. In general, M has multiple independence relations; \(\emptyset \) is always one of them.
commute at every reachable state of M. In general, M has multiple independence relations; \(\emptyset \) is always one of them.
Suppose that independence for transformers is defined by replacing statements and transitions with transformers and transformer application, respectively. Example 1 illustrates that an independence relation on statements cannot be lifted to obtain transformers that are independent under such a notion.
Example 1
Consider the collecting semantics \(\mathcal {C}_{M}\) of a program M with two variables, x and y, two statements \(a \mathrel {:=}\texttt {assume(x==0)}\) and \(a' \mathrel {:=}\texttt {assume(y==0)}\), and initial element \(d_0 \mathrel {:=}\left\{ \langle x \mapsto 0, y \mapsto 1\rangle , \langle x \mapsto 1, y \mapsto 0\rangle \right\} \). Since a and \(a'\) read different variables, \(R \mathrel {:=}\left\{ \langle a,a'\rangle , \langle a',a\rangle \right\} \) is an independence relation on M. Now observe that \(\left\{ \langle f_a,f_{a'}\rangle , \langle f_{a'},f_a\rangle \right\} \) is not an independence relation on \(\mathcal {C}_{M}\), as \(f_a\) and \(f_{a'}\) disable each other. Note, however, that \(f_a(f_{a'}(d_0))\) and \(f_{a'}(f_{a}(d_0))\) are both \(\bot \).
Weak independence, defined below, allows transformers to be considered independent even if they disable each other.
Definition 2
Let \(\mathcal {D}\mathrel {:=}\langle D, \sqsubseteq , F, d_0\rangle \) be an analysis instance. A relation  is a weak independence on transformers if it is symmetric, irreflexive, and satisfies that
is a weak independence on transformers if it is symmetric, irreflexive, and satisfies that  implies \(f(f'(d)) = f'(f (d))\) for every \(d \in \mathop { reach } (\mathcal {D})\). Moreover,
implies \(f(f'(d)) = f'(f (d))\) for every \(d \in \mathop { reach } (\mathcal {D})\). Moreover,  is an independence if it is a weak independence and satisfies that if \(f(d) \ne \bot \), then \((f \circ f') (d) \ne \bot \) iff \(f'(d) \ne \bot \), for all \(d \in \mathop { reach } (\mathcal {D})\).
is an independence if it is a weak independence and satisfies that if \(f(d) \ne \bot \), then \((f \circ f') (d) \ne \bot \) iff \(f'(d) \ne \bot \), for all \(d \in \mathop { reach } (\mathcal {D})\).
Recall that \(R_\mathcal {D}\) is the lifting of a relation on statements to transformers. Observe that the relation R in Example 1, when lifted to transformers is a weak independence on \(\mathcal {C}_{M}\). The proposition below shows that independence relations on statements generate weak independence on transformers over \(\mathcal {C}_{M}\).
Proposition 1
(Lifted independence). If  is an independence relation on M, the lifted relation
is an independence relation on M, the lifted relation  is a weak independence on the collecting semantics \(\mathcal {C}_{M}\).
is a weak independence on the collecting semantics \(\mathcal {C}_{M}\).
Figure 2 graphically depicts the process of lifting an independence relation. Relation  (on the left of the figure) is an independence relation on M. Relation
(on the left of the figure) is an independence relation on M. Relation  is the lifting of
is the lifting of  to \(\mathcal {C}_{M}\), and by Proposition 1 it is a weak independence relation on \(\mathcal {C}_{M}\).
to \(\mathcal {C}_{M}\), and by Proposition 1 it is a weak independence relation on \(\mathcal {C}_{M}\).
We now show that independence and abstraction are distinct notions in that transformers that are independent in a concrete domain may not be independent in the abstract, and those that are not independent in the concrete may become independent in the abstract.
Consider an analysis instance \(\bar{\mathcal {D}} \mathrel {:=}\langle \bar{D}, \mathrel {\bar{\sqsubseteq }}, \bar{F}, \bar{d}_0\rangle \) that is an abstraction of \(\mathcal {D}\mathrel {:=}\langle D, \sqsubseteq , F, d_0\rangle \) and a weak independence  . The inherited relation
. The inherited relation  contains \(\langle \bar{f}, \bar{f'}\rangle \) iff \(\langle f, f'\rangle \) is in
contains \(\langle \bar{f}, \bar{f'}\rangle \) iff \(\langle f, f'\rangle \) is in  .
.
Example 2
(Abstraction breaks independence). Consider a system M with the initial state \(\langle x \mapsto 0,y \mapsto 0\rangle \), and two threads \(t_1: \texttt {x = 2}\), \(t_2: \texttt {y = 7}\). Let \(\mathcal {I}\) be the domain for interval analysis with elements \(\langle i_x, i_y\rangle \) being intervals for values of x and y. The initial state is \(\bar{d}_0 = \langle x \mapsto [0,0], y \mapsto [0,0]\rangle \). Abstract transformers for \(t_1\) and \(t_2\) are shown below. These transformers are deliberately imprecise to highlight that sound transformers are not the most precise ones.
The relation  is an independence on M, and when lifted,
is an independence on M, and when lifted,  is a weak independence on \(\mathcal {C}_{M}\) (in fact,
is a weak independence on \(\mathcal {C}_{M}\) (in fact,  is an independence). However, the relation
is an independence). However, the relation  is not a weak independence because \(f_1\) and \(f_2\) do not commute at \(d_0\), due to the imprecision introduced by abstraction. Consider the statements \(\texttt {assume(x != 9)}\) and \(\texttt {assume(x < 10)}\) applied to \(\langle x \mapsto [0,10]\rangle \) to see that even best transformers may not commute.
is not a weak independence because \(f_1\) and \(f_2\) do not commute at \(d_0\), due to the imprecision introduced by abstraction. Consider the statements \(\texttt {assume(x != 9)}\) and \(\texttt {assume(x < 10)}\) applied to \(\langle x \mapsto [0,10]\rangle \) to see that even best transformers may not commute.
On the other hand, even when certain transitions are not independent, their transformers may become independent in an abstract domain.
Example 3
(Abstraction creates independence). Consider two threads \(t_1: \texttt {x = 2}\) and \(t_2: \texttt {x = 3}\), with abstract transformers \(f_1(i_x) = [2,3]\) and \(f_2(i_x) = [2,3]\). The transitions \(t_1\) and \(t_2\) do not commute, but owing to imprecision, \(R =\left\{ (f_1, f_2),(f_2, f_1)\right\} \) is a weak independence on \(\mathcal {I}\).
5 Unfolding of an Abstract Domain with Independence
This section shows that unfoldings, which have primarily been used to analyze Petri nets, can be applied to abstract interpretation. This section defines the vertical arrows of Fig. 2.
An abstract unfolding is an event structure in which an event is recursively defined as the application of a transformer after a minimal set of interfering events; and a configuration represent equivalent sequences of transformer applications (events). Analogous to an invariant map in abstract interpreters and an abstract reachability tree in software model checkers, our abstract unfolding allows for constructing an over-approximation of the set of fireable transitions in a program.
5.1 The Unfolding of a Domain
Our construction generates a PES \(\mathcal {E}\mathrel {:=}\langle E, <, {\mathrel {\#}}, h\rangle \). Recall that a configuration is a set of events that is closed with respect to < and that is conflict-free. Events in \(\mathcal {E}\) have the form \(e = \langle f,C\rangle \), representing that the transformer f is applied after the transformers in configuration C are applied. The order in which transformers must be applied is given by <, while \(\mathrel {\#}\) encodes transformer applications that cannot belong to the same configuration.
The unfolding \(\mathcal {U}_{\mathcal {D},\mathrel {\bowtie }}\) of an analysis instance \(\mathcal {D}\mathrel {:=}\langle D, \sqsubseteq , F, d_0\rangle \) with respect to a relation \({\mathrel {\bowtie }} \subseteq F \times F\) is defined inductively below. Recall that a configuration C generates a set of interleavings \(\mathop { inter } (C)\), which define the state of the configuration,

If \(\mathrel {\bowtie }\) is a weak independence relation, all interleavings lead to the same state.
Definition 3
(Unfolding). The unfolding \(\mathcal {U}_{\mathcal {D},\mathrel {\bowtie }}\) of \(\mathcal {D}\) under the relation \(\mathrel {\bowtie }\) is the structure returned by the following procedure:
-
1.
Start with a PES \(\mathcal {E}\mathrel {:=}\langle E, <, {\mathrel {\#}}, h\rangle \) equal to \(\langle \emptyset , \emptyset , \emptyset , \emptyset \rangle \).
-
2.
Add a new event \(e \mathrel {:=}\langle f,C\rangle \) to E, where the configuration \(C \in \mathop { conf } (\mathcal {E})\) and transformer f satisfy that f is enabled at \(\mathop { state } (C)\), and \(\lnot (f \mathrel {\bowtie }h(e))\) holds for every <-maximal event e in C.
-
3.
Update <, \(\mathrel {\#}\), and h as follows:
-
for every \(e' \in C\), set \(e' < e\);
-
for every \(e' \in E \setminus C\), if \(e \ne e'\) and \(\lnot (f \mathrel {\bowtie }h(e'))\), then set \(e' \mathrel {\#}e\);
-
set \(h(e) \mathrel {:=}f\).
-
-
4.
Repeat steps 2 and 3 until no new event can be added to E; return \(\mathcal {E}\).
Definition 3 defines the events, the causality, and conflict relations of \(\mathcal {U}_{\mathcal {D},\mathrel {\bowtie }}\) by means of a saturation procedure. Step 1 creates an empty PES. Step 2 defines a new event from a transformer f that can be applied after configuration C. Step 3 defines e to be a causal successor of every dependent event in C, and defines e to be in conflict with dependent events not in C. Since conflicts are inherited in a PES, causal successors of e will also be in conflict with all \(e'\) satisfying \(e \mathrel {\#}e'\). Events from \(E {\setminus } C\), which are unrelated to f in \(\mathrel {\bowtie }\), will remain concurrent to e.
Proposition 2
The structure  generated by Definition 3 is a uniquely defined PES.
generated by Definition 3 is a uniquely defined PES.
If \(\mathrel {\bowtie }\) is a weak independence, every configuration of \(\mathcal {U}_{\mathcal {D},\mathrel {\bowtie }}\) represents sequences of transformer applications that produce the same element. If C is a configuration that is local, meaning it has a unique maximal event, or if C is generated by an independence, then \(\mathop { state } (C)\) will not be \(\bot \). Treating transformers as independent if they generate \(\bot \) enables greater reduction during analysis.
Theorem 1
(Well-formedness of  ). Let
). Let  be a weak independence on \(\mathcal {D}\), let C be a configuration of
be a weak independence on \(\mathcal {D}\), let C be a configuration of  and \(\sigma , \sigma '\) be interleavings of C. Then:
and \(\sigma , \sigma '\) be interleavings of C. Then:
-
1.
\(\mathop { state } (\sigma )= \mathop { state } (\sigma ')\);
-
2.
\(\mathop { state } (\sigma )\ne \bot \) when
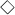 is additionally an independence relation;
is additionally an independence relation; -
3.
If C is a local configuration, then also \(\mathop { state } (\sigma )\ne \bot \).
Theorem 2 shows that the unfolding is adequate for analysis in the sense that every sequence of transformer applications leading to non-\(\bot \) elements that could be generated during standard analysis with a domain will be contained in the unfolding. We emphasize that these sequences are only symbolically represented.
Theorem 2
(Adequacy of  ). For every weak independence relation
). For every weak independence relation  on \(\mathcal {D}\), and sequence of transformers \(\sigma \in \mathop { runs } (\mathcal {D})\), there is a unique configuration C of
on \(\mathcal {D}\), and sequence of transformers \(\sigma \in \mathop { runs } (\mathcal {D})\), there is a unique configuration C of  such that \(\sigma \in \mathop { inter } (C)\).
such that \(\sigma \in \mathop { inter } (C)\).
We discuss the above theorems in the context of Fig. 2. We know that \(\mathop { runs } (M)\) is in bijective correspondence with \(\mathop { runs } (\mathcal {C}_{M})\). We said that  is a weak independence in \(\mathcal {C}_{M}\) (see Sect. 4). By Theorem 2, every run of M is represented by a unique configuration in
is a weak independence in \(\mathcal {C}_{M}\) (see Sect. 4). By Theorem 2, every run of M is represented by a unique configuration in  , and by Theorem 1 every configuration C of
, and by Theorem 1 every configuration C of  such that \(\mathop { state } (C) \ne \bot \) is such that \(\mathop { inter } (C) \subseteq \mathop { runs } (M)\).
such that \(\mathop { state } (C) \ne \bot \) is such that \(\mathop { inter } (C) \subseteq \mathop { runs } (M)\).
5.2 Abstract Unfoldings
The soundness theorems of abstract interpretation show when a fixed point computed in an abstract domain soundly approximates fixed points in a concrete domain. Our analysis constructs unfoldings instead of fixed points. The soundness of our analysis does not follow from fixed point soundness because the abstract unfolding we construct depends on the independence relation used. Though independence may not be preserved under lifting, as shown in Example 2, lifted relations can still be used to obtain sound results.
Example 4
In Example 2, the transformer composition \(f_1 \circ f_2\) produces \(\langle x \mapsto [2,4],y \mapsto [6,8]\rangle \), while \(f_2 \circ f_2\) produces \(\langle x \mapsto [2,4],y \mapsto [7,9]\rangle \). If \(f_1\) and \(f_2\) are considered independent, the state of the configuration \(\left\{ f_1, f_2\right\} \) is \(\mathop { state } (f_1,f_2)\sqcap \mathop { state } (f_2, f_1)\), which is the abstract element \(\langle x \mapsto [2,4], y \mapsto [7,7]\rangle \) and contains the final state \(\langle x \mapsto 2, y \mapsto 7\rangle \) reached in the concrete.
Thus, with sound abstractions, abstract transformers can be treated as (weakly) independent if their concrete counterparts were (weakly) independent, without compromising soundness of the analysis. The soundness theorem below asserts a correspondence between sequences of concrete transformer applications and the abstract unfolding. The concrete and abstract objects in Theorem 3 have different type: we are not relating a concrete unfolding with an abstract unfolding, but concrete transformer sequences with abstract configurations. Since \(\mathop { state } (C)\) is defined as a meet of transformer sequences, the proof of Theorem 3 relies on the independence relation and has a different structure from standard proofs of fixed point soundness from transformer soundness.
Theorem 3
(Soundness of the abstraction). Let \(\bar{\mathcal {D}}\) be a sound abstraction of the analysis instance \(\mathcal {D}\), let  be a weak independence on \(\mathcal {D}\), and
be a weak independence on \(\mathcal {D}\), and  be the lifted relation on \(\bar{\mathcal {D}}\). For every sequence \(\sigma \in \mathop { runs } (\mathcal {D})\) satisfying \(\mathop { state } (\sigma )\ne \bot \), there is a unique configuration C of
be the lifted relation on \(\bar{\mathcal {D}}\). For every sequence \(\sigma \in \mathop { runs } (\mathcal {D})\) satisfying \(\mathop { state } (\sigma )\ne \bot \), there is a unique configuration C of  such that \(m(\sigma ) \in \mathop { inter } (C)\).
such that \(m(\sigma ) \in \mathop { inter } (C)\).
Theorems 2 and 3 are fundamentally different. Theorem 2 shows that, given a domain and a weak independence relation, the associated unfolding represents all sequences of transformer applications that may be generated during the analysis of that domain. Theorem 3 relates a concrete domain with the unfolding of an abstract one. Given a concrete domain, a concrete weak independence, and an abstract domain, Theorem 3 shows that every sequence of concrete transformers has a corresponding configuration in the unfolding of the abstract domain.
Surprisingly enough, the abstract unfolding in Theorem 3 may not represent all sequences of applications of the abstract domain in isolation (because the lifted relation  is not necessarily a weak independence in \(\bar{\mathcal {D}}\)), but will represent (this is what the theorem asserts) all transformer applications of the concrete domain.
is not necessarily a weak independence in \(\bar{\mathcal {D}}\)), but will represent (this is what the theorem asserts) all transformer applications of the concrete domain.
In Fig. 2, let  be the lifted independence of
be the lifted independence of  . Theorem 3 asserts that for any \(\sigma \in \mathop { runs } (\mathcal {C}_{M})\) there is a configuration C of
. Theorem 3 asserts that for any \(\sigma \in \mathop { runs } (\mathcal {C}_{M})\) there is a configuration C of  such that \(m(\sigma ) \in \mathop { inter } (C)\).
such that \(m(\sigma ) \in \mathop { inter } (C)\).
6 Plugging Thread-Local Analysis
Unfoldings compactly represent concurrent executions using partial orders. However, they are a branching structure and one extension of the unfolding can multiply the number of branches, leading to a blow-up in the number of branches. Static analyses of sequential programs often avoid this explosion (at the expense of precision) by over-approximating (using join or widening) the abstract state at the CFG locations where two or more program paths converge. Adequately lifting this simple idea of merging at CFG locations from sequential to concurrent programs is a highly non-trivial problem [8].
In this section, we present a method that addresses this challenge and can mitigate the blow-up in the size of the unfolding caused by conflicts between events of the same thread. The key idea of our method is to merge abstract states generated by statements that work on local data of one thread, i.e., those whose impact over the memory/environment is invisible to other threads. Intuitively, the key insight is that we can merge certain configurations of the unfolding and still preserve its structural properties with respect to interference. The state of the resulting configuration will be a sound over-approximation of the states of the merged configurations at no loss of precision with respect to conflicts between events of different threads.
Our approach is to analyse M by constructing the unfolding of an abstract domain \(\mathcal {D}\mathrel {:=}\langle D, {\subseteq }, F, d_0\rangle \) and a weak independence relation  using a thread-local procedure that over-approximates the effect of transformers altering local variables.
using a thread-local procedure that over-approximates the effect of transformers altering local variables.
Assume that M has n threads. Let \(F_1, \ldots , F_n\) be the partitioning of the set of transformers F by the thread to which they belong. For a transformer \(f \in F_i\), we let \(p(f) \mathrel {:=}i\) denote the thread to which f belongs. We define, per thread, the (local) transformers which can be used to run the merging analysis. A transformer \(f \in F_i\) is local when, for all other threads \(j \ne i\) and all transformers \(f' \in F_j\) we have  . A transformer is global if it is not local. We denote by \(F_i^\text {loc}\) and \(F_i^\text {glo}\), respectively, the set of local and global transformers in \(F_i\). In Fig. 1(a), the global transformers would be those representing the actions to the variable g. The remaining statements correspond to local transformers.
. A transformer is global if it is not local. We denote by \(F_i^\text {loc}\) and \(F_i^\text {glo}\), respectively, the set of local and global transformers in \(F_i\). In Fig. 1(a), the global transformers would be those representing the actions to the variable g. The remaining statements correspond to local transformers.
We formalize the thread-local analysis using the function \(\mathtt {tla}{} :\mathbb {N}\times D \rightarrow D\), which plays the role of an off-the-shelf static analyzer for sequential thread code. A call to \(\mathop {\mathtt {tla}{}} (i, d)\) will run a static analyzer on thread i, restricted to \(F_i^\text {loc}\), starting from d, and return its result which we assume to be a sound fixed point. Formally, we assume that if \(\mathop {\mathtt {tla}{}} (i,d)\) returns \(d' \in D\), then for every sequence \(f_1 \ldots f_n \in (F_i^\text {loc})^*\) we have \((f_n \circ \ldots \circ f_1)(d) \sqsubseteq d'\). This condition requires any implementation of \(\mathop {\mathtt {tla}{}} (i,d)\) to return a sound approximation of the state that thread i could possibly reach after running only local transformers starting from d.

Algorithm 1 presents the overall approach proposed in this paper. Procedure unfold builds an abstract unfolding for \(\mathcal {D}\) under independence relation  . It non-deterministically selects a thread i and a configuration C and runs a sequential static analyzer on thread i starting on the state reached by C. If a global transformer \(f \in F_i^\text {glo}\) is eventually enabled, the algorithm will try to insert it into the unfolding. For that it first calls the function mkevent, which constructs a history for f from C according to Definition 3, i.e., by removing from C events independent with f until all maximal events are dependent. Function mkevent then calls mklabel to construct a suitable label for the new event. Labels are functions in \(D \rightarrow D\), we discuss them below. If the resulting event \(e \mathrel {:=}\langle \bar{f}, H\rangle \) is a cutoff, i.e., an equivalent event is already in the unfolding prefix, then it will be ignored. Otherwise, we add it to E. Finally, we update relations <, \(\mathrel {\#}\), and h using exactly the same procedure as in Step 3 of Definition 3. In particular, we set \(h(e) \mathrel {:=}\bar{f}\).
. It non-deterministically selects a thread i and a configuration C and runs a sequential static analyzer on thread i starting on the state reached by C. If a global transformer \(f \in F_i^\text {glo}\) is eventually enabled, the algorithm will try to insert it into the unfolding. For that it first calls the function mkevent, which constructs a history for f from C according to Definition 3, i.e., by removing from C events independent with f until all maximal events are dependent. Function mkevent then calls mklabel to construct a suitable label for the new event. Labels are functions in \(D \rightarrow D\), we discuss them below. If the resulting event \(e \mathrel {:=}\langle \bar{f}, H\rangle \) is a cutoff, i.e., an equivalent event is already in the unfolding prefix, then it will be ignored. Otherwise, we add it to E. Finally, we update relations <, \(\mathrel {\#}\), and h using exactly the same procedure as in Step 3 of Definition 3. In particular, we set \(h(e) \mathrel {:=}\bar{f}\).
Unlike the unfolding  of Definition 3, the events of the PES constructed by Algorithm 1 are not labelled by transformers in F, but by ad-hoc functions constructed by mklabel. An event in this PES represents the aggregated application of multiple local transformers, summarized by tla into a fixed point, followed by the application of a global transformer. Function mklabel constructs a collapsing transformer that represents such transformation of the program state. Given a global transformer f it returns a function \(\bar{f} \in D \rightarrow D\) that maps a state d to another state obtained by first running tla on f’s thread starting from d and then running f. While an efficient implementation of Algorithm 1 does not need to actually construct this transformer, we formalize it here because it is necessary to define how to compute the state of a configuration, \(\mathop { state } (C)\).
of Definition 3, the events of the PES constructed by Algorithm 1 are not labelled by transformers in F, but by ad-hoc functions constructed by mklabel. An event in this PES represents the aggregated application of multiple local transformers, summarized by tla into a fixed point, followed by the application of a global transformer. Function mklabel constructs a collapsing transformer that represents such transformation of the program state. Given a global transformer f it returns a function \(\bar{f} \in D \rightarrow D\) that maps a state d to another state obtained by first running tla on f’s thread starting from d and then running f. While an efficient implementation of Algorithm 1 does not need to actually construct this transformer, we formalize it here because it is necessary to define how to compute the state of a configuration, \(\mathop { state } (C)\).
We denote by  the PES constructed by a call to unfold(
the PES constructed by a call to unfold( ). When the tla performs a path-insensitive analysis, the structure
). When the tla performs a path-insensitive analysis, the structure  is (i) path-insensitive for runs that execute only local code, (ii) partially path-sensitive for runs that execute one or more global transformer, and (iii) flow-sensitive with respect to interference between threads. We refer to this analysis as a causally-sensitive analysis as it is precise with respect to the dynamic interference between threads.
is (i) path-insensitive for runs that execute only local code, (ii) partially path-sensitive for runs that execute one or more global transformer, and (iii) flow-sensitive with respect to interference between threads. We refer to this analysis as a causally-sensitive analysis as it is precise with respect to the dynamic interference between threads.
Algorithm 1 embeds multiple constructions explained in this paper. For instance, when \(\mathtt {tla}\) is implemented by the function \(g(d,i) \mathrel {:=}d\) and the check of cutoffs is disabled (iscutoff systematically returns false), the algorithm is equivalent to Definition 3. We now show that  is a safe abstraction of \(\mathcal {D}\) when tla performs a non-trivial operation.
is a safe abstraction of \(\mathcal {D}\) when tla performs a non-trivial operation.
Theorem 4
(Soundness of the abstraction). Let  be a weak independence on \(\mathcal {D}\) and
be a weak independence on \(\mathcal {D}\) and  the PES computed by a call to unfold
the PES computed by a call to unfold  with cutoff checking disabled. Then, for any execution \(\sigma \in \mathop { runs } (\mathcal {D})\) there is a unique configuration C in
with cutoff checking disabled. Then, for any execution \(\sigma \in \mathop { runs } (\mathcal {D})\) there is a unique configuration C in  such that \(\hat{\sigma } \in \mathop { inter } (C)\).
such that \(\hat{\sigma } \in \mathop { inter } (C)\).
6.1 Cutoff Events: Pruning the Unfolding
If we remove the conditional statement in line 6 of Algorithm 1, the algorithm would only terminate if every run of \(\mathcal {D}\) contains finitely many global transformers. This conditional check has two purposes: (1) preventing infinite executions from inserting infinitely many events into \(\mathcal {E}\); (2) pruning branches of the unfolding that start with equivalent events. The procedure iscutoff decides when an event is marked as a cutoff [17]. In such cases, no causal successor of the event will be explored. The implementation of iscutoff cannot prune “too often”, as we want the computed PES to be a complete representation of behaviours of \(\mathcal {D}\) (e.g., if a transformer is fireable, then some event in the PES will be labelled by it).
Formally, given \(\mathcal {D}\), a PES \(\mathcal {E}\) is \(\mathcal {D}\)-complete iff for every reachable element \(d \in \mathop { reach } (\mathcal {D})\) there is a configuration C of \(\mathcal {E}\) such that \(\mathop { state } (C) \sqsupseteq d\). The key idea behind cutoff events is that, if event e is marked as a cutoff, then for any configuration C that includes e it must be possible to find a configuration \(C'\) without cutoff events such that \(\mathop { state } (C) \sqsubseteq \mathop { state } (C')\). This can be achieved by defining iscutoff(\(e, \mathcal {E}\)) to be the predicate: \( \exists e' \in \mathcal {E}\text { such that } \mathop { state } ([e]) \sqsubseteq \mathop { state } ([e']) \text { and } |[e']| < |[e]|. \) When such \(e'\) exists, including the event e in \(\mathcal {E}\) is unnecessary because any configuration C such that \(e \in C\) can be replayed in \(\mathcal {E}\) by first executing \([e']\) and then (copies of) the events in \(C {\setminus } [e]\).
We now would like to prove that Algorithm 1 produces a \(\mathcal {D}\)-complete prefix when instantiated with the above definition of iscutoff. However, a subtle an unexpected interaction between the operators tla and iscutoff makes it possible to prove Theorem 5 only when tla respects independence. Formally, we require tla to satisfy the following property: for any \(d \in \mathop { reach } (\mathcal {D})\) and any two global transformers \(f \in F_i^\text {glo}\) and \(f' \in F_j^\text {glo}\), if  then
then
When tla does not respect independence, it may over-approximate the global state (e.g. via joins and widening) in a way that breaks the independence of otherwise independent global transformers. This triggers the cutoff predicate to incorrectly prune necessary events.
Theorem 5
Let  be a weak independence in \(\mathcal {D}\). Assume that \(\mathtt {tla}\) respects independence and that \(\mathtt {iscutoff}\) uses the procedure defined above. Then the PES
be a weak independence in \(\mathcal {D}\). Assume that \(\mathtt {tla}\) respects independence and that \(\mathtt {iscutoff}\) uses the procedure defined above. Then the PES  computed by Algorithm 1 is \(\mathcal {D}\)-complete.
computed by Algorithm 1 is \(\mathcal {D}\)-complete.
Note that Algorithm 1 terminates if the lattice order \(\sqsubseteq \) is a well partial order (every infinite sequence contains an increasing pair). This includes, for instance, all finite domains. Furthermore, it is also possible to accelerate the termination of Algorithm 1 using widenings in tla to force cutoffs. Finally, notice that while we defined iscutoff using McMillan’s size order [17], Theorem 5 also holds if iscutoff is defined using adequate orders [5], known to yield smaller prefixes. See [24] for additional details.
7 Experimental Evaluation
In this section we evaluate our approach based on abstract unfoldings. The goal of our experimental evaluation is to explore the following questions:
-
Are abstract unfoldings practical? (i.e., is our approach able to yield efficient algorithms that can be used to prove properties of concurrent programs that require precise interference reasoning?)
-
How does abstract unfoldings compare with competing approaches such as thread-modular analysis and symbolic partial order reduction?
Implementation. To address these questions, we have implemented a new program analyser based on abstract unfoldings baptized APoet, which implements an efficient variant of the exploration algorithm described in Algorithm 1. The exploration strategy is based on Poet [23], an explicit-state model checker that implements a super-optimal partial order reduction method using unfoldings.
As described in Algorithm 1, \(\textsc {APoet} \) is an analyser parameterized by a domain and a set of procedures: tla, iscutoff and mkevent. As a proof of concept, we have implemented an interval analysis and a basic parametric segmentation functor for arrays [4], which we instantiate with intervals and concrete integers values (to represent offsets). In this way, we are able to precisely handle arrays of threads and mutexes. \(\textsc {APoet} \) supports dynamic thread creation and uses \(\textsc {CIL} \) to inline functions calls. The analyser receives as input a concurrent C program that uses the POSIX thread library and parameters to control the widening level and the use of cutoffs. We implemented cutoffs according to the definition in Sect. 6.1 using an hash table that maps control locations to abstract values and the size of the local configuration of events.
\(\textsc {APoet} \) is parameterized by a domain functor of actions that is used to define independence and control the tla procedure. We have implemented an instance of the domain of actions for memory accesses and thread synchronisations. Transformers record the segments of the memory, intervals of addresses or sets of addresses, that have been read or written and synchronisation actions related to thread creation, join and mutex lock and unlock operations. This approach is used to compute a conditional independence relation as transformers can perform different actions depending on the state. The conditional independence relation is dynamically computed and is used in the procedure mkevent.
Finally, the tla procedure was implemented with a worklist fixpoint algorithm which uses the widening level given as input. In the interval analysis, we guarantee that tla respects independence using a predicate over the actions that identifies whether a transformer is local or global. We currently support two modes in \(\textsc {APoet} \): one that assumes programs are data-race free and considers any thread synchronisation (i.e., thread creation/join and mutex lock/unlock) a global transformer, and a second that considers any heap access or thread synchronisation a global transformer and can be used to detect data races.
Benchmark Selection. We used six benchmarks adapted from the SV-COMP’17 (corresponding to nine rows in Table 1) and four parametric programs (the remaining fifteen rows in Table 1) written by the authors: map-reduce DNA sequence analysis, producer-consumer, parallel sorting, and a thread pool. The majority of the SV-COMP benchmarks are not applicable for this evaluation since they are data deterministic (whereas our approach is primarily for data non-deterministic programs) or create unboundedly many threads, or use non-integer data types (e.g., structs, which are not currently supported by our prototype). Thus, we devised parametric benchmarks that expose data non-determinism and complex synchronization patterns, where the correctness of assertions depend on the synchronization history. We believe that all new benchmarks are as complex as the most complex ones of the SV-COMP (excluding device drivers).
Each program was annotated with assertions enforcing, among others, properties related to thread synchronisation (e.g., after spawning the worker threads, the master analyses results only after all workers finished), or invariants about data (e.g., each thread accesses a non-overlapping segment of the input array).
Tool Selection. We compare our approach against the two approaches most closely related to ours: abstract interpretation based on thread-modular methods (represented by the tool AstreeA) and partial-order reductions (PORs) handling data-nondeterminism (represented by two tools, Impara and cbmc 5.6). AstreeA implements thread-modular abstract interpretation for concurrent programs [19], Impara combines POR with interpolation-based reasoning to cope with data non-determinism [25], and cbmc uses a symbolic encoding based on partial orders [2]. We sought to compare against symbolic execution approaches for multithreaded programs, but we were either unable to obtain the tools from the authors or the tools were unable to parse the benchmarks.
Experimental Results. Table 1 presents the experimental results. When the program contained non-terminating executions (e.g., spinlocks), we used 5 loop unwindings for cbmc as well as cutoffs in APoet and a widening level of 15. For the family of \(\textsc {fmax}\) benchmarks, we were not able to run AstreeA on all instances, so we report approximated execution times and warnings based on the results provided by Antoine Miné on some of the instances. With respect to the size of the abstract unfolding, our experiments show that APoet is able to explore unfoldings up to 33 K events and it was able to terminate on all benchmarks with an average execution time of 81 seconds. In comparison with AstreeA, APoet is far more precise: we obtain only 12 warnings (of which 5 are false positives) with APoet compared to 43 (32 false positives) with AstreeA. We observe a similar trend when comparing APoet with the mthread plugin for Frama-c [26] and confirm that the main reason for the source of imprecision in AstreeA is imprecise reasoning of thread interference. In the case of APoet, we obtain warnings in benchmarks that are buggy (\(\textsc {lazy*}, \textsc {sigma*}\) and \(\textsc {tpoll*}\) family), as expected. Furthermore, APoet reports warnings in the \(\textsc {atgc}\) benchmarks caused by imprecise reasoning of arrays combined with widening and also in the \(\textsc {cond}\) benchmark as it contains non-relational assertions.
APoet is able to outperform Impara and cbmc on all benchmarks. We believe that these experiments demonstrate that effective symbolic reasoning with partial orders is challenging as cbmc only terminates on 46% of the benchmarks and Impara only on 17%.
8 Related Work
In this section, we compare our approach with closely related program analysis techniques for (i) concurrent programs with (ii) a bounded number of threads and that (iii) handle data non-determinism.
The thread-modular approach in the style of rely-guarantee reasoning has been extensively studied in the past [3, 9, 12, 15, 16, 18,19,20]. In [19], Miné proposes a flow-insensitive thread-modular analysis based on the interleaving semantics which forces the abstraction to cope with interleaving explosion. We address the interleaving explosion using the unfolding as an algorithmic approach to compute a flow and path-sensitive thread interference analysis. A recent approach [20] uses relational domains and trace partitioning to recover precision in thread modular analysis but requires manual annotations to guide the partitioning and does not scale with the number of global variables. The analysis in [7] is not as precise as our approach (confirmed by experiments with Duet on a simpler version of our benchmarks) as it employs an abstraction for unbounded parallelism. The work in [15] presents a thread modular analysis that uses a lightweight interference analysis to achieve an higher level of flow sensitivity similar to [7]. The interference analysis of [15] uses a constraint system to discard unfeasible pairs of read-write actions which is static and less precise than our approach based on independence. The approach is also flow-insensitive in the presence of loops with global read operations. Finally, the method in [12] focuses on manual thread-modular proofs, while our method is automatic.
The interprocedural analysis for recursive concurrent programs of [13] does not address the interleaving explosion. A related approach that uses unfoldings is the causality-based bitvector dataflow analysis proposed in [8]. There, unfoldings are used as a method to obtain dataflow information while in our approach they are the fundamental datastructure to drive the analysis. Thus we can apply thread-local fixpoint analysis while their unfolding suffers from path explosion due to local branching. Furthermore, we can build unfoldings for general domains even with invalid independence relations while their approach is restricted to the independence encoded in the syntax of a Petri net and bitvector domains.
Compared to dynamic analysis of concurrent programs [1, 6, 11, 14], our approach builds on top of a (super-)optimal partial-order reduction [23] and is able to overcome a high degree of path explosion unrelated to thread interference.
9 Conclusion
We introduced a new algorithm for static analysis of concurrent programs based on the combination of abstract interpretation and unfoldings. Our algorithm explores an abstract unfolding using a new notion of independence to avoid redundant transformer application in an optimal POR strategy, thread-local fixed points to reduce the size of the unfolding, and a novel cutoff criterion based on subsumption to guarantee termination of the analysis.
Our experiments show that APoet generates about 10x fewer false positives than a mature thread modular abstract interpreter and is able to terminate on a large set of benchmarks as opposed to solver-based tools that have the same precision. We observed that the major reasons for the success of APoet are: (1) the use of cutoffs to cope with and prune cyclic explorations caused by spinlocks and (2) tla mitigates path explosion in the threads. Our analyser is able to scale with the number of threads as long as the interference between threads does not increase. As future work, we plan to experimentally evaluate the application of local widenings to force cutoffs to increase the scalability of our approach.
References
Abdulla, P., Aronis, S., Jonsson, B., Sagonas, K.: Optimal dynamic partial order reduction. In: Principles of Programming Languages (POPL), pp. 373–384. ACM (2014)
Alglave, J., Kroening, D., Tautschnig, M.: Partial orders for efficient bounded model checking of concurrent software. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 141–157. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39799-8_9
Carre, J.-L., Hymans, C.: From single-thread to multithreaded: an efficient static analysis algorithm. arXiv:0910.5833[cs], October 2009
Cousot, P., Cousot, R., Logozzo, F.: A parametric segmentation functor for fully automatic and scalable array content analysis. In: Principles of Programming Languages (POPL), pp. 105–118. ACM (2011)
Esparza, J., Römer, S., Vogler, W.: An improvement of McMillan’s unfolding algorithm. Formal Methods Syst. Des. 20, 285–310 (2002)
Farzan, A., Holzer, A., Razavi, N., Veith, H.: Con2Colic testing. In: Foundations of Software Engineering (FSE), pp. 37–47. ACM (2013)
Farzan, A., Kincaid, Z.: Verification of parameterized concurrent programs by modular reasoning about data and control. In: Principles of Programming Languages (POPL), pp. 297–308. ACM (2012)
Farzan, A., Madhusudan, P.: Causal dataflow analysis for concurrent programs. In: Grumberg, O., Huth, M. (eds.) TACAS 2007. LNCS, vol. 4424, pp. 102–116. Springer, Heidelberg (2007). doi:10.1007/978-3-540-71209-1_10
Flanagan, C., Qadeer, S.: Thread-modular model checking. In: Ball, T., Rajamani, S.K. (eds.) SPIN 2003. LNCS, vol. 2648, pp. 213–224. Springer, Heidelberg (2003). doi:10.1007/3-540-44829-2_14
Godefroid, P. (ed.): Partial-Order Methods for the Verification of Concurrent Systems. LNCS, vol. 1032. Springer, Heidelberg (1996). doi:10.1007/3-540-60761-7
Günther, H., Laarman, A., Sokolova, A., Weissenbacher, G.: Dynamic reductions for model checking concurrent software. In: Bouajjani, A., Monniaux, D. (eds.) VMCAI 2017. LNCS, vol. 10145, pp. 246–265. Springer, Cham (2017). doi:10.1007/978-3-319-52234-0_14
Hoenicke, J., Majumdar, R., Podelski, A.: Thread modularity at many levels: a pearl in compositional verification. In: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, pp. 473–485. ACM, New York (2017)
Jeannet, B.: Relational interprocedural verification of concurrent programs. Softw. Syst. Model. 12(2), 285–306 (2012)
Kähkänen, K., Saarikivi, O., Heljanko, K.: Unfolding based automated testing of multithreaded programs. Autom. Softw. Eng. 22, 1–41 (2014)
Kusano, M., Wang, C.: Flow-sensitive composition of thread-modular abstract interpretation. In: Foundations of Software Engineering (FSE), pp. 799–809. ACM (2016)
Malkis, A., Podelski, A., Rybalchenko, A.: Precise thread-modular verification. In: Nielson, H.R., Filé, G. (eds.) SAS 2007. LNCS, vol. 4634, pp. 218–232. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74061-2_14
McMillan, K.L.: Using unfoldings to avoid the state explosion problem in the verification of asynchronous circuits. In: Bochmann, G., Probst, D.K. (eds.) CAV 1992. LNCS, vol. 663, pp. 164–177. Springer, Heidelberg (1993). doi:10.1007/3-540-56496-9_14
Miné, A.: Static analysis of run-time errors in embedded real-time parallel C programs. Log. Methods Comput. Sci. 8(1) (2012)
Miné, A.: Relational thread-modular static value analysis by abstract interpretation. In: McMillan, K.L., Rival, X. (eds.) VMCAI 2014. LNCS, vol. 8318, pp. 39–58. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54013-4_3
Monat, R., Miné, A.: Precise thread-modular abstract interpretation of concurrent programs using relational interference abstractions. In: Bouajjani, A., Monniaux, D. (eds.) VMCAI 2017. LNCS, vol. 10145, pp. 386–404. Springer, Cham (2017). doi:10.1007/978-3-319-52234-0_21
Nielsen, M., Plotkin, G., Winskel, G.: Petri nets, event structures and domains, part I. Theoret. Comput. Sci. 13(1), 85–108 (1981)
Peled, D.: All from one, one for all: on model checking using representatives. In: Courcoubetis, C. (ed.) CAV 1993. LNCS, vol. 697, pp. 409–423. Springer, Heidelberg (1993). doi:10.1007/3-540-56922-7_34
Rodréguez, C., Sousa, M., Sharma, S., Kroening, D.: Unfolding-based partial order reduction. In: Concurrency Theory (CONCUR). LIPIcs, vol. 42, pp. 456–469. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2015)
Sousa, M., Rodréguez, C., D’Silva, V., Kroening, D.: Abstract interpretation with unfoldings. CoRR abs/1705.00595 (2017)
Wachter, B., Kroening, D., Ouaknine, J.: Verifying multi-threaded software with impact. In: Formal Methods in Computer-Aided Design (FMCAD), pp. 210–217 (2013)
Yakobowski, B., Bonichon, R.: Frama-C’s Mthread plug-in. Report, Software Reliability Laboratory (2012)
Acknowledgments
The authors would like to thank Antoine Miné for the invaluable help with AstreeA and the anonymous reviewers for their helpful feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Sousa, M., Rodríguez, C., D’Silva, V., Kroening, D. (2017). Abstract Interpretation with Unfoldings. In: Majumdar, R., Kunčak, V. (eds) Computer Aided Verification. CAV 2017. Lecture Notes in Computer Science(), vol 10427. Springer, Cham. https://doi.org/10.1007/978-3-319-63390-9_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-63390-9_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63389-3
Online ISBN: 978-3-319-63390-9
eBook Packages: Computer ScienceComputer Science (R0)








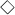 is additionally an independence relation;
is additionally an independence relation;