GPUDrano: Detecting Uncoalesced Accesses in GPU Programs

Abstract

Graphics Processing Units (GPUs) have become widespread and popular over the past decade. Fully utilizing the parallel compute and memory resources that GPUs present remains a significant challenge, however. In this paper, we describe GPUDrano: a scalable static analysis that detects uncoalesced global memory accesses in CUDA programs. Uncoalesced global memory accesses arise when a GPU program accesses DRAM in an ill-structured way, increasing latency and energy consumption. We formalize the GPUDrano static analysis and compare it empirically against a dynamic analysis to demonstrate that false positives are rare for most programs. We implement GPUDrano in LLVM and show that it can run on GPU programs of over a thousand lines of code. GPUDrano finds 133 of the 143 uncoalesced static memory accesses in the popular Rodinia GPU benchmark suite, demonstrating the precision of our implementation. Fixing these bugs leads to real performance improvements of up to 25%.

1 Introduction

Graphics Processing Units (GPUs) are well-established as an energy-efficient, data parallel accelerator for an increasingly important set of workloads including image processing, machine learning, and scientific simulations. However, extracting optimal performance and energy efficiency from a GPU is a painstaking process due to the many sharp corners of current GPU programming models. One particularly sharp corner arises when interacting with the memory hierarchy. We propose the GPUDrano system, the first scalable static analysis to identify an important class of memory hierarchy performance bugs for GPU programs. To show what GPUDrano does, we first explain a bit about the GPU memory hierarchy and the specific class of performance bugs, known as global memory coalescing bugs, that GPUDrano targets.

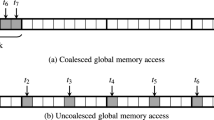
Load and store instructions that reference the GPU’s DRAM (known as global memory) must obey a certain structure to ensure that memory bandwidth is fully utilized. Accesses that do not exhibit this structure result in underutilization and can lead to significant performance problems. When a GPU program executes a load or store instruction, the memory address(es) referenced are mapped to aligned 128-byte cache blocks [18, Sect. 5.3.2], which is the physical granularity at which DRAM is accessed. GPUs bundle multiple threads together for single-instruction multiple-data (SIMD) execution, and we say that a SIMD load/store is coalesced if its accesses are contained within a single cache block, otherwise the access is uncoalesced. Uncoalesced accesses are difficult to spot, even for seasoned GPU developers, and in some cases rewriting can avoid such uncoalescing, as is the case for many of our benchmarks from an established benchmark suite.

Fig. 1.

Examples of coalesced and uncoalesced memory accesses.

Figure 1 shows simple examples of coalesced and uncoalesced memory accesses. Each thread in the program executes the code shown (we explain the GPU’s threading model in more detail in Sect. 2), and tid is a numeric thread id. Memory accesses that involve each thread accessing the same address (Example 1) or consecutive threads accessing consecutive addresses (Example 2) fall within a single cache line, and so are considered coalesced. Memory accesses that have consecutive threads accessing non-consecutive addresses, as in Example 3, result in significant slowdowns: Example 3 will run about 8x slower than the other examples.

Discovering uncoalesced accesses statically introduces many challenges. Expressions used for array indexing are often complex, and their coalesced or uncoalesced nature must be propagated through arithmetic operations, to each use. The size of the data types involved in a memory access affects coalescing. The number of threads that actually execute a particular access affects coalescing as well; e.g., Example 3 in Fig. 1 is coalesced if only a single active thread reaches this statement. In this paper, we define GPUDrano, a simple but effective abstraction for detecting uncoalesced accesses that uses intra-procedural dataflow analysis to identify uncoalesced memory accesses in GPU programs statically. We target GPU code written for Nvidia’s CUDA programming model. GPUDrano makes the following contributions:

• To the best of our knowledge, GPUDrano is the first scalable static analysis for uncoalesced global memory accesses in GPU programs.

• We provide a formal definition of both our analysis and the memory coalescing bugs we wish to detect.

• GPUDrano leverages well-established program analysis techniques to improve scalability and is able to analyze thousand-line CUDA programs in seconds, while incorporating relevant information such as accounting for the set of active threads to reduce the number of false positives.

• We demonstrate that GPUDrano works in practice by implementing it in LLVM and detecting over a hundred real uncoalesced accesses in the well-established Rodinia benchmark suite. We also validate GPUDrano against a dynamic analysis to show that GPUDrano has few or no false positives on most programs.

The remainder of this paper is organized as follows. Section 2 describes the CUDA programming model and a real memory coalescing bug from our benchmarks. Section 3 presents our formalization of CUDA programs, their executions, and uncoalesced accesses. Section 4 describes the GPUDrano static analysis. Section 5 describes the dynamic analysis we use to validate our GPUDrano implementation. Section 6 discusses our experimental results, and Sect. 7 related work. Finally, Sect. 8 concludes.

Fig. 2.

Kernel snippets from Gaussian Elimination program.

2 Illustrative Example

We use an example GPU program to briefly illustrate the GPU programming model and the problem of uncoalesced accesses. GPUs follow an SIMT (Single Instruction Multiple Thread) execution model, where multiple threads execute the same sequence of instructions, often called a kernel. Figure 2a shows one such kernel, Fan2, from Gaussian Elimination program in Rodinia benchmark suite [5]. The comments in the kernel can be ignored for now. The kernel performs row operations on matrix A (size $N\times N$) and vector B (size $N\times 1$) using the $t^{\mathrm {th}}$ column of a multiplier matrix M (size $N\times N$) and the $t^{\mathrm {th}}$ row of A and B. The kernel is a sequential procedure that takes in a thread id, $\mathsf {tid}$, to distinguish executions of different threads. The kernel is executed for threads with ids in range $[0, N-t-2]$. Each thread is assigned a distinct row and updates row $(\mathsf {tid}+ t + 1)$ of matrix A and vector B. Note that A, B and M reside in global memory and are shared across threads, while the remaining variables are private to each thread.

The GPU executes threads in bundles, or warps, where threads in each warp consist of consecutive ids and execute instructions in lock-step. The above kernel, for example, might be executed for warps $w_0$ with ids [0, 31], $w_1$ with ids [32, 63], and so on ...When a warp, say $w_0$, accesses A using index xy in A[xy] for some iteration of y, the elements $A[N(t+1) + y], A[N(t+2) + y], \dots , A[N(t+32) + y]$ are fetched simultaneously. The elements are at least N locations apart from each other, and thus, separate transactions are required to access each element, which takes significant time and energy. This is an uncoalesced access. Access to M[xt] is similarly uncoalesced. Now, Fig. 2b shows a fixed version of the kernel, where each thread is mapped to a column of the matrices A and M, instead of a row. The access to A[xy] by warp $w_0$ results in elements $A[Nx + t], A[Nx + t + 1], \dots , A[Nx + t + 31]$ to be accessed. These are consecutive elements, and thus, can be accessed in a single transaction. Access to M[xt] is similarly coalesced, and our experiments show a 25% reduction in run-time for the fixed kernel, when run for inputs with $N=1024$.

3 Formalization of Uncoalesced Accesses

This section describes the GPU programming model and uncoalesced accesses formally. A GPU program is a tuple $\langle T, V_L, V_G, K \rangle$, where T represents the set of all threads; $V_L$ and $V_G$ represent the sets of variables residing in local and global memories respectively; and K represents the kernel or the sequence of instructions executed by the threads. The kernel K is defined by the grammar in Fig. 3, and consists of assignments, conditionals and loops. The set $V_L$ further contains a special read-only variable, $\mathsf {tid}$, initialized with the thread id of the thread. The variable can appear in the right-hand-side of assignments and helps distinguish executions of different threads.

Fig. 3.

The grammar for kernel K.

We next present a simple operational semantics for GPU programs. We use a simplified execution model, where all threads in the program execute instructions in lock-step. While the standard GPU execution model is more flexible, this assumption simplifies the semantics without affecting the detection of memory coalescing bugs, and has been used in a previous formalization [4].

Excluded GPU Features. The GPU programming model represents threads in a two-level hierarchy, where a bunch of threads form a thread-block and the thread-blocks together form the set of all threads. Further, threads have access to a block-level memory space, shared memory, used to share data between threads within a block. Lastly, threads within a block can synchronize on a __syncthreads() barrier. These features do not directly affect uncoalesced accesses and have been excluded here for the ease of presentation.

3.1 Semantics

To describe the semantics, we define two entities: the state $\sigma$ and the active set of threads $\pi$. The state $\sigma$ maps variables to a type-consistent value $\nu$. It consists of a copy of local variables per thread and a copy of global variables, and thus, is a function $(V_L \times T) \cup V_G \rightarrow \mathcal {V}$. We further use $\bot$ to represent an undefined or error state. The active set of threads $\pi$ is a subset of T and defines a set of threads for which the execution is active. Now, the semantics for a statement S are given by the function $\llbracket S\rrbracket$, where $\llbracket S\rrbracket (\sigma , \pi ) = \sigma '$ represents the execution of statement S in state $\sigma$ for threads in set $\pi$ to generate a new state $\sigma '$.

Assignments. We first define the semantics for assignment statements when executed by a single thread t i.e. $\llbracket AS\rrbracket (\sigma , t) = \sigma '$. Let $l \in V_L$ and $g \in V_G$ represent a local and global variable, respectively. Let v represent a generic variable. Further, let the variables be either scalars or arrays. An assignment is of the form $[E := e]$, where E is the expression being updated, and consists of either a scalar variable v or an array variable indexed by a local v(l); and e is an expression whose value is assigned to E, and is built using scalar variables, array variables indexed by locals, constants, and arithmetic and boolean operations on them. Note that in an assignment at least one of E and e must be a local scalar variable l. We distinguish two types of assignments: global array read $[l' := g(l)]$, where the global array g indexed by l is read into $l'$, i.e. $\sigma '(l', t) = \sigma (g)(\sigma (l, t))$ and $\sigma '(v, t) = \sigma (v, t)$ for all $v \ne l$ ; and global array write $[g(l) := l']$, where g indexed by l is written with value of $l'$, i.e. $\sigma '(g)(\sigma (l, t)) = \sigma (l', t)$, $\sigma '(g)(\nu ) = \sigma (g)(\nu )$ for all $\nu \ne \sigma (l, t)$, and $\sigma '(v, t) = \sigma (v, t)$ for all $v \ne g$.

We now define the semantics when an assignment is executed by a set of threads $\pi$, i.e. $\llbracket AS \rrbracket (\sigma , \pi ) = \sigma '$. When the set $\pi$ is empty, the state remains unchanged i.e. $\llbracket AS\rrbracket (\sigma , \phi ) = \sigma$. When $\pi$ is non-empty i.e. $\pi = \{ t \} \cup \pi '$, the desired update is obtained by first executing $AS$ for thread $t$, and then the other threads in $\pi '$. Thus, $\llbracket AS\rrbracket (\sigma , \pi ) = \llbracket AS\rrbracket (\llbracket AS\rrbracket (\sigma , t ), \pi ')$. Note that, if different threads write to the same memory location, the execution is not deterministic and the updated state is set to the undefined state, i.e. $\llbracket AS\rrbracket (\sigma , t ) = \bot$.

Sequences. The execution of sequence of statements $( S _1; S _2)$ is described by first executing $S _1$, followed by $S _2$ i.e. $\llbracket S _1; S _2\rrbracket (\sigma , \pi ) = \llbracket S_2\rrbracket (\llbracket S_1\rrbracket (\sigma , \pi ), \pi )$.

Conditionals. Next consider $\llbracket \mathbf if \, l \,\mathbf then \, S _1 \,\mathbf else \, S _2\rrbracket (\sigma , \pi ) = \sigma '$, where $\langle test \rangle$ consists of a local boolean variable l. The semantics serializes the execution of statements $S _1$ and $S _2$. Let the set of threads for which the predicate $\sigma ( l , t )$ is $\mathsf {true}$ be $\pi _1$. The threads in $\pi _1$ first execute $S _1$ to get the state $\sigma _1$ i.e. $\llbracket S_1\rrbracket (\sigma , \pi _1) = \sigma _1$. Next, the remaining threads execute $S _2$ in state $\sigma _1$ to get the final updated state i.e. $\llbracket S_2\rrbracket (\sigma _1, \pi \setminus \pi _1) = \sigma '$. Note that, similar to assignments, if the same location is read or written by a thread executing the if branch and another thread executing the else branch with one of the accesses being writes, there is a potential conflict between the two accesses, and the final state $\sigma '$ is set to $\bot$.

Loops. We next describe the semantics for loops $\llbracket \mathbf while \, l \,\mathbf do \, S\rrbracket (\sigma , \pi ) = \sigma '$. We first consider semantics for terminating loops. The loop execution terminates when there are no threads active in the loop, and it is repeated until then. Formally, if there exist $\sigma _1, \pi _1, \sigma _2, \pi _2, \dots , \sigma _k, \pi _k$, such that $\sigma _i$ and $\pi _i$ represent the state and the active set of threads at the beginning of the ith iteration of the loop, i.e. $\sigma _1 = \sigma ,\, \pi _1 = \{ t \in \pi : \sigma (l, t) = \mathsf {true}\},\, \sigma _{i+1} = \llbracket S\rrbracket (\sigma _i, \pi _i)$, and $\pi _{i+1} = \{ t \in \pi _{i} : \sigma _{i+1}(l, t) = \mathsf {true}\}$, and the last active set is empty, $\pi _k = \phi$, then $\sigma ' = \sigma _k$. If the loop is non-terminating, $\sigma '$ is assigned the undefined state $\bot$.

Reachable Configurations. We now define the set $\mathcal {R}$ of configurations reachable during a kernel’s execution. A configuration is a tuple $(\sigma , \pi , S)$, where $\sigma$ is the current state, $\pi$ is the current active set of threads, and S is the next statement to be executed. We give a inductive definition for $\mathcal {R}$. The initial configuration $(\sigma _0, T, K)$ belongs to $\mathcal {R}$, where $\sigma _0$ is the initial state, T is the set of all threads and K is the kernel. In the recursive case, suppose $(\sigma , \pi , S)$ belongs to $\mathcal {R}$. When $S = S_1; S_2$, the configuration $(\sigma , \pi , S_1)$ belongs to $\mathcal {R}$, since $S_1$ is the next statement to be executed. Further, if the state after executing $S_1$, $\sigma ' = \llbracket S_1\rrbracket (\sigma , \pi )$, is not undefined i.e. $\sigma ' \ne \bot$, then $(\sigma ', \pi , S_2)$ also belongs to $\mathcal {R}$. Similarly, when S is a conditional $[\mathbf if \, l \,\mathbf then \, S _1 \,\mathbf else \, S _2]$, both if and else branches are reachable, and thus, $(\sigma , \pi _1, S_1)$ and $(\sigma , \pi _2, S_2)$ belong to $\mathcal {R}$, where $\pi _1 = \{ t \in \pi : \sigma (l, t) = \mathsf {true}\}$ and $\pi _2 = \pi \setminus \pi _1$. Lastly, when S is a loop $[ \mathbf while \, l \, \mathbf do \, S' ]$, the configuration $(\sigma , \pi ', S')$, where $\pi ' = \{ t \in \pi : \sigma (l, t) = \mathsf {true}\}$, is reachable. Further, if the state after executing $S'$ is not undefined, the configuration $(\llbracket S'\rrbracket (\sigma , \pi '), \pi ', S)$ is also reachable.

3.2 Uncoalesced Global Memory Accesses

To define uncoalesced global memory accesses, we first describe how the global memory is accessed by a GPU. Let the memory bandwidth for global memory be $\eta$ bytes i.e. the GPU can access $\eta$ contiguous bytes from the memory in one transaction. When a warp of threads with consecutive thread indices $W$ issues a read or write to the global memory, the addresses accessed by the active threads are coalesced together into as few transactions as possible. If the number of transactions is above a threshold $\tau$, there is an uncoalesced access.

We now define uncoalesced accesses formally. Consider the configuration $(\sigma , \pi , AS)$, where AS is a global array read $[l' := g(l)]$ or a global array write $[g(l) := l']$ and g is a global array with each element of size k bytes. Let $W$ be a warp of threads with consecutive thread indices. Let the addresses accessed by the warp, $\varGamma _{}(\sigma , \pi , AS, W)$, be defined as,

$$\begin{aligned} \varGamma _{}(\sigma , \pi , AS, W) = \bigcup _{ t \in W\cap \pi } \big [\sigma (l, t ).k, \sigma (l, t ).k + k - 1 \big ] \end{aligned}$$

Now, each contiguous set of $\eta$ bytes is accessed in one transaction. Thus, the number of transactions $N(\sigma , \pi , AS, W)$ required for the access equals the number of unique elements in the set $\big \{ \lfloor a/\eta \rfloor : a \in \varGamma _{}(\sigma , \pi , AS, W) \big \}$. If $N(\sigma , \pi , AS, W)$ is greater than threshold $\tau$ for some warp W, the configuration $(\sigma , \pi , AS)$ is an “uncoalesced"configuration. A global array access AS is uncoalesced, if an uncoalesced configuration involving the access is reachable.

For most current GPUs, the bandwidth $\eta = 128$ bytes, and warp size $|W| = 32$. We use the threshold $\tau = 1$, so that accesses that require more than one transaction are flagged as uncoalesced. Suppose the index variable l in a global array access is a linear function of $\mathsf {tid}$, i.e. $l \equiv c.\mathsf {tid}+ c_0$. The range of addresses accessed by a completely active warp W is $(31|kc| + k - 1)$ bytes and thus, the number of transactions N required is at least |kc| / 4. If $k \ge 4$ bytes and $|c| \ge 1$ (with one of the inequalities being strict), N is greater than 1, and hence, the access is uncoalesced. We refer to such uncoalescing, where the range of addresses accessed by a warp is large, as range-based uncoalescing.

Alternately, an uncoalesced access can occur due to alignment issues, where the range of accessed locations is small but mis-aligned with the cache block boundaries. Suppose $k = 4$ and $c = 1$, but $c_0 = 8$. The addresses accessed by a warp W with $\mathsf {tid}$s [0, 31] are [32, 159] and require two transactions, even though the range of locations is 127 bytes which is less than the bandwidth. We refer to such accesses as alignment-based uncoalesced accesses.

4 Static Analysis

This section presents a static compile-time analysis to identify uncoalesced accesses. We use abstract interpretation [8, 17] for the analysis, where-in we first define an abstraction of the state and the active set of threads. The abstraction captures features of the kernel execution essential to identify uncoalesced accesses. It tracks values, particularly access indices, as a function of $\mathsf {tid}$, and for the indices with potentially large linear or non-linear dependence on $\mathsf {tid}$, the analysis flags the corresponding global array access as uncoalesced. Further, if a segment of code is executed only by a single thread (which is often the case when some sequential work needs to be done), a single transaction is required for an access and it cannot be uncoalesced. Hence, our abstraction also tracks whether single or multiple threads are active during the execution of a statement.

After defining the abstraction, we associate abstract semantics with the statements in kernels, computable at compile-time, that preserve the abstraction. We then present our algorithm to execute kernels abstractly and identify global array accesses which can potentially be uncoalesced. Finally, we describe our implementation for the analysis.

Example. Before diving into the details of the analysis, let’s consider the example in Fig. 2a. Our abstraction tracks local variables as a function of $\mathsf {tid}$. All variables that are independent of $\mathsf {tid}$ are assigned value 0 in the abstraction. Thus, variables t and N are assigned the value 0 initially (shown in comments). Further, variables y and ty are constructed from $\mathsf {tid}$-independent variables, and hence, assigned 0. Next, all variables that are linear function of $\mathsf {tid}$ with coefficient 1 (i.e. of the form $\mathsf {tid}+ c$), are assigned value 1. The variable x is therefore assigned 1. Lastly, all variables that are either non-linear function of $\mathsf {tid}$ or linear function with possibly greater than one coefficient are assigned $\top$. Variable xt, for example, is assigned the expression $N(\mathsf {tid}+ t + 1) + t$, where the coefficient for $\mathsf {tid}$ is N. Since N can be greater than one, xt is assigned $\top$. Similarly, variable xy is assigned $\top$. Now, global array accesses where the index variable has value $\top$, are flagged as uncoalesced. Hence, accesses A[xy] and M[xt] are flagged as uncoalesced. Note that in the fixed kernel in Fig. 2b, none of the index variables are $\top$, and hence, none of the accesses are flagged as uncoalesced.

4.1 Abstraction

We now formally define our abstraction. Let $\alpha ($) be the abstraction function. The abstraction of state $\hat{\sigma }$ only tracks values of local scalar variables. We observe that indirect indexing through arrays is rare for coalesced accesses, and hence we consevatively flag all such accesses as uncoalesced. Further, we use a different abstraction for integer and boolean variables. We assign a single abstract value to each local variable, that tracks its dependency on $\mathsf {tid}$. For integer variables, we use the set $\widehat{\mathcal {V}}_{int} = \{ \bot , 0, 1, -1, \top \}$ to abstract values. The value $\bot$ represents undefined values, while $\top$ represents all values. The remaining values are defined here. Let l be a local variable.

$$ \alpha (\sigma )(l) = \left\{ \begin{array}{ll} 0, &{} \text {exists}\ c_0 \ \text {s.t. for all}\ t \in T,\, \sigma (l, t) = c_0 \\ 1, &{} \text {exists}\ c_0 \ \text {s.t. for all}\ t \in T,\, \sigma (l, t) = \mathsf {tid}(t) + c_0 \\ -1, &{} \text {exists}\ c_0 \ \text {s.t. for all}\ t \in T,\, \sigma (l, t) = -\mathsf {tid}(t) + c_0 \end{array} \right. $$

i.e. the abstract value 0 represents values constant across threads; 1 represents values that are a linear function of $\mathsf {tid}$ with coefficient 1; and, $-1$ represents values that are a linear function with coefficent $-1$. This abstraction is necessary to track dependency of access indices on $\mathsf {tid}$.

We use the set $\widehat{\mathcal {V}}_{bool} = \{ \bot , \mathsf {T}, \mathsf {T^-}, \mathsf {F}, \mathsf {F^-}, \mathsf {TF}, \mathsf {TT^-}, \mathsf {FF^-}, \top \}$ to abstract boolean variables. Again $\bot$ and $\top$ represent the undefined value and all values, respectively. The remaining values are defined here.

$$ \alpha (\sigma )(l) \equiv \left\{ \begin{array}{ll} \mathsf {T}, &{} \text {for all}\ t \in T,\, \sigma (l, t) = \mathsf {true}\\ \mathsf {T^-}, &{} \text {exists}\ t \in T\ \text {s.t.}\ \sigma (l, t) = \mathsf {false}\\ &{} \text {and for all}\ t' \in T \setminus t,\, \sigma (l, t') = \mathsf {true}\\ \mathsf {F}, &{} \text {for all}\ t \in T,\, \sigma (l, t) = \mathsf {false}\\ \mathsf {F^-}, &{} \text {exists}\ t \in T\ \text {s.t.}\ \sigma (l, t) = \mathsf {true}\\ &{} \text {and for all}\ t' \in T \setminus t,\, \sigma (l, t') = \mathsf {false}\end{array} \right. $$

i.e. the abstract value $\mathsf {T}$ represents values $\mathsf {true}$ for all threads; $\mathsf {T^-}$ represents values $\mathsf {true}$ for all but one thread; $\mathsf {F}$ represents values $\mathsf {false}$ for all threads; $\mathsf {F^-}$ represents values $\mathsf {false}$ for all but one thread. Further, we construct three additional boolean values: $\mathsf {TF}= \{\mathsf {T}, \mathsf {F}\}$ representing values $\mathsf {true}$ or $\mathsf {false}$ for all threads, $\mathsf {TT^-}= \{\mathsf {T}, \mathsf {T^-}\}$ representing values $\mathsf {false}$ for at most one thread, and $\mathsf {FF^-}= \{ \mathsf {F}, \mathsf {F^-}\}$ representing values $\mathsf {true}$ for at most one thread. We only use these compound values in our analysis, along with $\bot$ and $\top$. We use them to abstract branch predicates in kernels. This completes the abstraction for state. Note that $\hat{\sigma }$ is function $V_L \rightarrow \widehat{\mathcal {V}}_{int} \cup \widehat{\mathcal {V}}_{bool}$.

Now, the active set of threads $\pi$ can be seen as a predicate on the set of threads T. We observe that if at most one thread is active for a global array access, a single transaction is required to complete the access and hence, it is always coalesced. Thus, in our abstraction for $\pi$, we only track if it consists of at most one thread or an arbitrary number of threads. These can be abstracted by boolean values $\mathsf {FF^-}$ and $\top$ respectively, and thus, $\hat{\pi }\in \{ \mathsf {FF^-}, \top \}$.

Lastly, our abstraction for boolean and integer variables induces a natural complete lattice on sets $\widehat{\mathcal {V}}_{int}$ and $\widehat{\mathcal {V}}_{bool}$. These lattices can be easily extended to complete lattices for the abstract states and active sets of threads.

Justification. We designed our abstraction by studying the benchmark programs in Rodinia. We have already motivated the abstract values 0, 1 and $\top$ for integer variables in the example above. We found coefficient $-1$ for $\mathsf {tid}$ in a few array indices, which led to the abstract value $-1$. There were also instances where values 1 and $-1$ were added together to generate 0 or $\mathsf {tid}$-independent values. Next, the values $\mathsf {FF^-}$ and $\mathsf {TT^-}$ were motivated by the need to capture predicates in conditionals where one of the branches consisted of at most one active thread. Lastly, the value $\mathsf {TF}$ was necessary to distinguish conditionals with $\mathsf {tid}$-dependent and $\mathsf {tid}$-independent predicates.

4.2 Abstract Semantics

We briefly describe the abstract semantics $\widehat{\llbracket S\rrbracket }(\hat{\sigma }, \hat{\pi }) = \hat{\sigma }'$ for a statement S, which is the execution of S in an abstract state $\hat{\sigma }$ for abstract active set $\hat{\pi }$ to generate the abstract state $\hat{\sigma }'$. We first consider abstract computation of values of local expressions e (involving only local scalar variables) in state $\hat{\sigma }$, $\widehat{\llbracket e\rrbracket }(\hat{\sigma })$. Local scalar variable $l$ evaluates to its value in $\hat{\sigma }$, $\hat{\sigma }(l)$. Constants evaluate to the abstract value 0 ($\mathsf {TF}$ if boolean). Index $\mathsf {tid}$ evaluates to 1. Arithmetic operations on abstract values are defined just as regular arithmetic, except all values that do not have linear dependency on $\mathsf {tid}$ with coefficient 0, 1 or $-1$, are assigned $\top$. For example, $[1 + 1] = \top$ since the resultant value has a dependency of 2 on $\mathsf {tid}$. Boolean values are constructed from comparison between arithmetic values. Equalites $[\hat{\nu }_1 = \hat{\nu }_2]$ are assigned a boolean value $\mathsf {FF^-}$, and inequalities $[\hat{\nu }_1 \ne \hat{\nu }_2]$ a boolean value $\mathsf {TT^-}$, where one of $\nu _1$ and $\nu _2$ equals 1 or $-1$, and the other 0. Note that this is consistent with our abstraction. The equalities are of the form $[\mathsf {tid}= c]$, for some constant c, and are true for at most one thread. The inequalities are of the form $[\mathsf {tid}\ne c]$ and are true for all except one thread. For boolean operations, we observe that $\lnot \mathsf {TT^-}= \mathsf {FF^-}$, $[\mathsf {FF^-}\wedge b] = \mathsf {FF^-}$, and $[\mathsf {TT^-}\vee b] = \mathsf {TT^-}$, for all $b \in \{ \mathsf {TF}, \mathsf {FF^-}, \mathsf {TT^-}, \top \}$. Other comparison and boolean operations are defined similarly.

We next define the abstract semantics for different types of assignments AS in a state $\hat{\sigma }$, $\widehat{\llbracket AS\rrbracket }(\hat{\sigma }) = \hat{\sigma }'$. For local assignments $[ l := e ]$ where e is a local expression, l is updated with value of expression e, $\widehat{\llbracket e\rrbracket }(\hat{\sigma })$. For reads $[ l := g ]$, where g is a global scalar variable, all threads receive the same value, and the new value is $\mathsf {tid}$-independent. Hence, l is updated to 0 ($\mathsf {TF}$ if boolean). For array reads $[ l := v(l')]$, where $\hat{\sigma }(l') = 0$, all threads access the same element in the array v, and recieve the same value. Thus, the updated value is again 0 ($\mathsf {TF}$ if boolean). Lastly for array reads where $\hat{\sigma }(l') \ne 0$, the read could return values that are arbitrary function of $\mathsf {tid}$ (since we do not track the values for arrays), and hence, the updated value is $\top$.

Fig. 4.

Abstract semantics for compound statements.

We now define abstract semantics for the compound statements. We use rules in Fig. 4 to describe them formally. Note that, our abstract semantics for assignments are oblivious to the set of threads $\hat{\pi }$, and thus, the $[\textsc {Assign}]$ rule extends these semantics to an arbitrary set of threads. The $[\textsc {Seq}]$ rule similarly extends the semantics to sequence of statements. The $[\textsc {ITE}]$ rule describes the semantics for conditionals. The sets $\hat{\pi }_1$ and $\hat{\pi }_2$ represent the new active set of threads for the execution of $S_1$ and $S_2$. Note that $\hat{\pi }_1 = [\hat{\pi }\wedge \hat{\sigma }(l)]$, and gets a value $\mathsf {FF^-}$, only if either $\hat{\pi }$ or $\hat{\sigma }(l)$ is $\mathsf {FF^-}$. The new set of threads $\pi _1$ has at most one thread, only if either the incoming set $\pi$ or the predicate $\sigma (l, t)$ is true for at most one thread. Hence, $\hat{\pi }_1$ correctly abstracts the new set of the threads for which $S_1$ is executed. A similar argument follows for $\hat{\pi }_2$. Now, the concrete value for predicate $\sigma (l, t)$ is not known at compile time, and a thread could execute either of $S_1$ or $S_2$. Hence, our abstract semantics executes both, and merges the two resulting states to get the final state, i.e. $\varPhi ^{\hat{\sigma }(l)}_{\{S_1, S_2\}}(\hat{\sigma }_1, \hat{\sigma }_2)$.

The merge operation is a non-trivial operation and depends on the branch predicate $\hat{\sigma }(l)$. If $\hat{\sigma }(l)$ is $\mathsf {TF}$ or $\mathsf {tid}$-independent, all threads execute either the if branch or the else branch, and final value of a variable l is one of the values $\hat{\sigma }_1(l)$ and $\hat{\sigma }_2(l)$. In the merged state, our semantics assigns it a merged value $\hat{\sigma }_1(l) \sqcup \hat{\sigma }_2(l)$ or the join of the two values, a value that subsumes both these values. When $\hat{\sigma }(l)$ is $\mathsf {tid}$-dependent, however, this merged value does not suffice. Consider, for example, $y := (\mathsf {tid}< N)?\, 10 : 20$. While on both the branches, y is assigned a constant (abstract value 0), the final value is a non-linear function of $\mathsf {tid}$ (abstract value $\top$), even though the join of the two values is 0. Hence, in such cases, when the predicate is $\mathsf {tid}$-dependent and the variable l is assigned a value in $S_1$ or $S_2$, the merged value is set to $\top$.

The $[\textsc {While}]$ rule describes the abstract semantics for loops. Note that similar to conditionals, it is not known whether a thread executes S or not. Thus, the rule first transforms the original state $\hat{\sigma }$ into the merge of $\hat{\sigma }$ and the execution of S on $\hat{\sigma }$ and repeats this operation, until the fixed point is reached and the state does not change on repeating the operation. Note that our abstract semantics for different statements are monotonic. The merge operation $\varPhi$ is also monotonic. The abstract state can have only finite configurations, since each variable gets a finite abstract value. Thus, the fixpoint computation always terminates.

4.3 Detecting Uncoalesced Accesses

We first define the set of abstract configurations that are reachable during the abstract execution of the kernel. An abstract configuration is the tuple $(\hat{\sigma }, \hat{\pi }, S)$. The initial abstract configuration is $(\alpha (\sigma _0), \top , K)$, and is reachable. The other abstract reachable configurations can be defined by a similar recursive definition as that for reachable configurations.

Now, an abstract configuration $(\hat{\sigma }, \hat{\pi }, AS)$ is “uncoalesced", where AS is a global array read $[l' := g(l)]$ or global array write $[g(l) := l']$ and g is a global array with elements of size k, if both these conditions hold:

• $\hat{\pi }= \top$ i.e. the access is potentially executed by more than one thread.

• $(\hat{\sigma }(l) = \top ) \vee (\hat{\sigma }(l) \in \{ 1, -1 \} \wedge k > 4)$ i.e. l is a large linear or non-linear function of $\mathsf {tid}$, or it is a linear function of $\mathsf {tid}$ with unit coefficient and the size of elements of array g is greater than 4 bytes.

The analysis computes the set of abstract reachable configurations by executing the kernel using the abstract semantics, starting from the abstract initial configuration. It reports a global array access AS as uncoalesced, if an abstract uncoalesced configuration involving AS is reached during the abstract execution of the kernel.

Correctness. We show that for all global array accesses AS, if a range-based uncoalesced configuration involving a global array access AS is reachable, the analysis identifies it as uncoalesced. We first note that our abstract semantics preserve the abstraction. Hence, for any reachable configuration $(\sigma , \pi , AS)$, there exists an abstract reachable configuration $(\hat{\sigma }, \hat{\pi }, AS)$ that is an overapproximation of its abstraction i.e. $\alpha (\sigma ) \sqsubseteq \hat{\sigma }$ and $\alpha (\pi ) \sqsubseteq \hat{\pi }$. Now, for a range-based uncoalesced configuration to occur, the access needs to be executed by more than one thread, and thus $\alpha (\pi ) = \top$. Further, the access index l either has non-linear dependence on $\mathsf {tid}$, in which case $\alpha (\sigma )(l) = \top$, or as noted in Sect. 3.2, the index has linear dependence with one of $k > 4$ or $|c| > 1$, which again leads to an abstract uncoalesced configuration. Hence, GPUDrano identifies all range-based uncoalesced configurations as uncoalesced. There are no guarantees for alignment-based uncoalescing, however. This gives some evidence for the correctness of the analysis.

4.4 Implementation

We have implemented the analysis in the gpucc CUDA compiler [23], an open-source compiler based on LLVM. We implement the abstract semantics defined above. We work with an unstructured control flow graph representation of the kernel, where conditionals and loops are not exposed as separate units. So, we simplify the semantics at the cost of being more imprecise. We implement the abstract computation of local expressions and the abstract semantics for assignments exactly. We however differ in our implementation for the merge operation. Consider a conditional statement $[\mathbf {if}\, l \,\mathbf {then}\, S_1 \,\mathbf {else}\, S_2]$. Let the states after executing $S_1$ and $S_2$ be $\hat{\sigma }_1$ and $\hat{\sigma }_2$. The merge of states $\varPhi ^{\hat{\sigma }(l)}_{\{S_1, S_2 \}}(\hat{\sigma }_1, \hat{\sigma }_2)$ after the conditional is contigent on $\mathsf {tid}$-dependence of the value of l at the beginning of the conditional. This information requires path-sensitivity and is not available in the control flow graph at the merge point. Therefore, we conservatively assume l to be $\mathsf {tid}$-dependent. We use the SSA representation of control flow graph, where variables assigned different values along paths $S_1$ and $S_2$ are merged in special phi instructions after the conditional. We conservatively set the merged value to $\top$ for such variables. The values of remaining variables remain unchanged. This completes the implementation of merge operation. We define the set of active threads $\hat{\pi }'$ after the conditional as $\hat{\pi }_1 \sqcup \hat{\pi }_2$, or the join of incoming active sets from $S_1$ and $S_2$. The new active set $\hat{\pi }'$ equals the active set $\hat{\pi }$ before the conditional. If $\hat{\pi }= \top$, it must be split into $\hat{\pi }_1$ and $\hat{\pi }_2$ such that at least one of the values is $\top$ and hence, $\hat{\pi }' = \top$. Similarly, when $\hat{\pi }= \mathsf {FF^-}$, both $\hat{\pi }_1$ and $\hat{\pi }_2$ equal $\mathsf {FF^-}$, and hence, $\hat{\pi }' = \mathsf {FF^-}$.

Limitations. Our implementation does not do a precise analysis of function calls and pointers, which are both supported by CUDA. In the implementation, we assume that call-context of a kernel is always empty, and function calls inside a kernel can have arbitrary side-effects and return values. We support pointer dereferencing by tracking two abstract values for each pointer variable, one for the address stored in the pointer and the other for the value at the address. We do not implement any alias analyses, since we observe that array indices rarely have aliases. Our evaluation demonstrates that, despite these limitations, our static analysis is able to identify a large number of uncoalesced accesses in practice.

5 Dynamic Analysis

To gauge the accuracy of our GPUDrano static analysis, we have implemented a dynamic analysis for uncoalesced accesses. Being a dynamic analysis, it has full visibility into the memory addresses being accessed by each thread, as well as the set of active threads. Thus, the dynamic analysis can perfectly distinguish coalesced from uncoalesced accesses (for a given input). We use this to determine (1) whether the static analysis has missed any uncoalesced accesses and (2) how many of the statically-identified uncoalesced accesses are false positives.

The dynamic analysis is implemented as a pass in the gpucc CUDA compiler [23], which is based on LLVM. By operating on the LLVM intermediate representation (a type of high-level typed assembly), we can readily identify the instructions that access memory. So for every load and store in the program we insert instrumentation to perform the algorithm described below. A single IR instruction may be called multiple times in a program due to loops or recursion, so every store and load instruction is assigned a unique identifier (analogous to a program counter).

For every global memory access at runtime, we collect the address being accessed by each thread. Within each warp, the active thread with the lowest id is selected as the “computing thread” and it performs the bulk of the analysis. All active threads pass their addresses to the computing thread. The computing thread places all addresses into an array. This array will be at most of length n, where n is the warp size (if there are inactive threads, the size may be smaller). Next the computing thread determines all bytes that will be accessed by the warp, taking the size of the memory access into account. Note that, due to the SIMT programming model, the access size is the same for all threads in the warp since all threads execute the same instruction. Each byte accessed is divided by the size of the cache line using machine integer division. (for current generation Nvidia GPUs this number is 128 [18, Sect. 5.3.2]). Conceptually this assigns each address to a “bin” representing its corresponding cache line. For example, for a cache line of 128 bytes, $[0, 127] \mapsto 0$, $[128, 255] \mapsto 1$, etc. Finally, we count the number of unique bins, which is the total number of cache lines required. The computing thread prints the number of required cache lines, along with the assigned program counter, for post-processing.

A second, off-line step aggregates the information from each dynamic instance of an instruction by averaging. For example, if a load l executes twice, first touching 1 cache line and then touching 2 cache lines, the average for l will be 1.5 cache lines. If the average is 1.0 then l is coalesced, otherwise if the average is $>1.0$ l is uncoalesced. The specific value of the average is sometimes useful, to distinguish accesses that are mildly uncoalesced (with averages just over 1.0), as we explore more in Sect. 6.

6 Evaluation

This section describes the evaluation of GPUDrano on the Rodinia benchmarks (version 3.1) [5]. Rodinia consists of GPU programs from various scientific domains. We run our static and dynamic analyses to identify existing uncoalesced accesses in these programs. We have implemented our analyses in LLVM version 3.9.0, and compile with $\texttt {--cuda-gpu-arch=sm\_30}$. We use CUDA SDK version 7.5. We run our experiments on an Amazon EC2 instance with Amazon Linux 2016.03 (OS), an 8-core Intel Xeon E5-2670 CPU running at 2.60 GHz, and an Nvidia GRID K520 GPU (Kepler architecture).

Table 1. Results of GPUDrano’s static analysis (SA) and dynamic analysis (DA) on Rodinia benchmark programs. “-” indicates the DA hit the 2-h timeout.

Table 1 shows results of our experiments. It shows the benchmark name, the lines of GPU source code analyzed, the manually-validated real uncoalesced accesses, and the number of uncoalesced accesses found and running time for each analysis. The Rodinia suite consists of 22 programs. We exclude 4 (hybridsort, kmeans, leukocyte, mummergpu) as they could not be compiled due to lack of support for texture functions in LLVM. We synonymously use “bugs” for uncoalesced accesses, though sometimes they are fundamental to the program and cannot be avoided. We next address different questions related to the evaluation.

Do Uncoalesced Accesses Occur in Real Programs? We found 143 actual bugs in Rodinia benchmarks, with bugs in almost every program (Column “Real bugs” in Table 1). A few of the bugs involved random or irregular access to global arrays (bfs, particle filter). Such accesses are dynamic and data-dependent, and difficult to fix. Next, we found bugs where consecutive threads access rows of global matrices, instead of columns (gaussian). Such bugs could be fixed by assigning consecutive threads to consecutive columns or changing the layout of matrices, but this is possible only when consecutive columns can be accessed in parallel. Another common bug occurred when data was allocated as an array of structures instead of a structure of arrays (nn, streamcluster). A closely related bug was one where the array was divided into contiguous chunks and each chunk was assigned to a thread, instead of allocating elements in a round-robin fashion (myocyte, streamcluster). There were some bugs which involved reduction operations (for example, sum) on arrays (heartwall, huffmann). These bugs do not have a standard fix, and some of the above techniques could be applicable. A few bugs were caused by alignment issues where accesses by a warp did not align with cache-block boundaries, and hence, got spilled over to multiple blocks. These were caused, first, when the input matrix dimensions were not a multiple of the warp size which led consecutive rows to be mis-aligned (backprop, hotspot3D), or when the whole array was misaligned due to incorrect padding (b+tree). These could be fixed by proper padding.

Which Real Bugs Does Static Analysis Miss? While the static analysis catches a significant number of bugs (111 out of 143), it does miss some in practice. We found two primary reasons for this. 22 of the missed bugs depend on the second dimension of the $\mathsf {tid}$ vector, while we only considered the smallest dimension in our analysis. Uncoalesced accesses typically do not depend on higher dimensions unless the block dimensions are small or not a multiple of the warp size. We modified our analysis to track the second dimension and observed that all these bugs were caught by the static analysis, at the cost of 20 new false positives. Eight of the remaining missed bugs were alignment bugs which were caused by an unaligned offset added to $\mathsf {tid}$. The actual offsets are challenging to track via static analysis. Two missed bugs (particle filter) were due to an implementation issue with conditionals which we will address in the future.

What False Positives Does Static Analysis Report? For most programs, GPUDrano reports few or no false positives. The primary exceptions are CFD, dwt2D and heartwall, which account for the bulk of our false positives. A common case occurred when $\mathsf {tid}$ was divided by a constant, and multiplied back by the same constant to generate the access index (heartwall, huffman, srad_v1). Such an index should not lead to uncoalesced accesses. The static analysis, however, cannot assert that the two constants are equal, since we do not track exact values, and hence, sets the access index to $\top$, and reports any accesses involving the index as uncoalesced. Another type of false positive occurred when access indices were non-linear function of $\mathsf {tid}$, but consecutive indices differed by at most one, and led to coalesced accesses. Such indices were often either generated by indirect indexing (CFD, srad_v1) or by assigning values in conditionals (heartwall, hotspot, hotspot3D). In both cases, our static analysis conservatively assumed them to be uncoalesced. Lastly, a few false positives happened because the access index was computed via a function call (__mul24) which returned a coalesced index (huffmann), though we conservatively set the index to $\top$.

How Scalable is Static Analysis? As can be noted, the static analysis is quite fast, and finishes within seconds for most benchmarks. The largest benchmark, myocyte, is 3240 lines of GPU code, with the largest kernel containing 930 lines. The kernels in myocyte consist of many nested loops, and it appears the static analysis takes significant time computing fixed points for these loops.

How Does Static Analysis Compare with Dynamic Analysis? The dynamic analysis misses nearly half the bugs in our benchmarks. We found several benchmarks where different inputs varied the number of bugs reported (bfs, gaussian, lud). Similarly, the analysis finds bugs along a single execution path, so all bugs in unexecuted branches or uncalled kernels were not found. Due to compiler optimizations it can be difficult to map the results of dynamic analysis back to source code. In dwt2D, we were unable to do so due to multiple uses of C++ templates. Moreover, the dynamic analysis does not scale to long-running programs, as it incurs orders of magnitude of slowdown. While none of our benchmarks execute for more than 5 s natively, several did not finish with the dynamic analysis within our 2-h limit (CFD, heartwall, streamcluster).

7 Related Work

While the performance problems that uncoalesced accesses cause are well understood [18, Sect. 5.3.2], there are few static analysis tools for identifying them.

Several compilers for improving GPU performance [3, 7, 11, 20, 21, 24] incorporate some static analysis for uncoalesced global memory accesses, but these analyses are described informally and not evaluated for precision. Some of these systems also exhibit additional restrictions, such as CuMAPz’s [11] reliance on runtime traces, CUDA-lite’s [21] use of programmer annotations, or [3, 20] which are applicable only to programs with affine access patterns. Some systems for optimizing GPU memory performance, like Dymaxion [6], eschew static analysis for programmer input instead. GPUDrano’s precision could likely help improve the performance of the code generated by these prior systems and reduce programmer effort. [1] describes in a short paper the preliminary implementation of CUPL, a static analysis for uncoalesced global memory accesses. While CUPL shares similar goals as GPUDrano, no formalization or detailed experimental results are described.

GKLEE [15] is a symbolic execution engine for CUDA programs. It can detect uncoalesced accesses to global memory (along with data races), but due to the limitations of its underlying SMT solver it cannot scale to larger kernels or large numbers of threads. The PUG verifier for GPU kernels [14] has also been extended to detect uncoalesced memory accesses [10], but PUG is less scalable than GKLEE. In contrast, GPUDrano’s static analysis can abstract away the number of threads actually used by a kernel.

[9] uses dynamic analysis to identify uncoalesced global memory accesses, and then uses this information to drive code transformations that produce coalesced accesses. GPUDrano’s static analysis is complementary, and would eliminate [9]’s need to be able to run the program on representative inputs.

There are many programming models that can generate code for GPUs, including proposals to translate legacy OpenMP code [12, 13] or C code [2, 3, 22], and new programming models such as OpenACC [19] and C++ AMP [16]. An analysis such as GPUDrano’s could help improve performance in such systems, by identifying memory coalescing bottlenecks in the generated GPU code.

8 Conclusion

This paper presents GPUDrano, a scalable static analysis for uncoalesced global memory accesses in GPU programs. We formalize our analysis, and implement GPUDrano in LLVM. We apply GPUDrano to a range of GPU kernels from the Rodinia benchmark suite. We have evaluated GPUDrano’s accuracy by comparing it to a dynamic analysis that is fully precise for a given input, and found that the GPUDrano implementation is accurate in practice and reports few false positives for most programs. Fixing these issues can lead to performance improvements of up to 25% for the gaussian benchmark.

We would like to thank anonymous reviewers for their valuable feedback. This research was supported by NSF awards CCF-1138996 and XPS-1337174.