Abstract
This paper surveys the notions, conceptualisations and roles of mathematical competencies and their relatives in research, development and practice from an international perspective. After outlining the questions giving rise to this survey, the paper first takes a brief look at the genesis of competency-oriented ideas as a prelude to identifying and analysing recent trends. The relationships between different notions and terms concerning competencies and their relatives are discussed, and their roles in the 2015 PISA framework are presented. Two kinds of research, on and by means of mathematical competencies, are surveyed. The impact of competency-oriented notions and ideas on curriculum frameworks and documents in a number of countries is being charted, before challenges to the implementation of such notions in actual teaching practice are identified. Finally the paper takes stock of the international state-of-the-art of competencies and similar notions, with a focus on the need for further research.
This is a condensed and edited version of the comprehensive report of the Survey Team, Niss, Bruder, Planas, Turner, and Villa-Ochoa (2016).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Mathematical competencies
- Mathematical proficiency
- Mathematical practices
- Mathematical literacy
- Educational standards
- PISA
- Fundamental mathematical capabilities
Introduction: What Are the Issues?
Despite the title of this survey, focusing primarily on research, the authors also find it necessary to consider competencies, knowing and knowledge as they pertain to the development and practice of mathematics education. This is so because these notions are crucial to all aspects of mathematics teaching and learning. In fact, anyone involved in mathematics education in whichever capacity has to relate to the fundamental question:
What does it mean to master mathematics?
and to a number of related but not equivalent questions, such as: What does it mean to possess knowledge of mathematics? To know mathematics? To have insight in mathematics? To be able to do mathematics? To possess competence (or proficiency)? To be well versed in mathematical practices?
These questions reflect different facets of the title of the Survey Team. The former three of them focus on mathematical products (concepts, definitions, rules, theorems, formulae, methods, and historical facts), which have accumulated in the mind of “the knower”. The educational issue corresponding to these questions is: What does it take for a learner to become a knower of mathematics? The latter three questions focus on the enactment of mathematics, i.e. what is involved in carrying out characteristic mathematical processes. The corresponding educational issue is: What does it take for a learner to become a doer of mathematics?
“Knowing” and “being able to do” are two different things. Yet, it goes without saying that the relationships and balances between them are both intimate and delicate. Oftentimes, neither the initiating questions of this paper, nor the answers to them, are stated explicitly in official documents and other writings about mathematics education. So, it may seem natural to ask: why are these questions important at all? Well, they are important because the answers to them—whether explicit or implicit—determine at least three crucial components of mathematics education:
-
The purposes and goals of mathematics education (‘what do we wish to accomplish?’)
-
The criteria for and degree of success in mathematics teaching and learning (‘how can we know whether and how well we have accomplished what we want?’)
-
The structure and organisation of mathematics teaching (‘teachers’ and students’ respective activities as well as the framework and materials for teaching and learning’).
Markedly different answers to the initiating questions posed above give rise to marked differences in the realisation of these components. In fact, the diversity of mathematics education in different parts of the world can, in large part, be explained by the diversity of answers given to the main question: What does it mean to master mathematics?
Answers to the Main Question
Historical Excursion
Let us begin with a brief historical excursion. Classically, the main question was answered by specifying the mathematical content, including facts, that people should know about and the associated procedural skills that they should have. For example, the Danish national upper secondary curriculum in 1935 specified 38 content items and associated procedural skills in great detail, and also specified the structure and content of the written and oral final exams in considerable detail. However, such conceptions of what it means to master mathematics soon came under attack.
Thus the oft-quoted Spens Report (Board of Education, 1938), published in the UK requested that the subject should not ignore the “considerable truths in which Mathematics subserves important activities and adventures of civilised man. […] We believe that school Mathematics will be put on a sound footing only when teachers agree that it should be taught as art and music and Physical Science should be taught because it is one of the mail lines which the creative spirit of man has followed in its development” (pp. 176–177).
Here us another voice, that of George Pólya who, in the preface to the first (1945) edition of How to Solve It, wrote:
If [the teacher of mathematics] fills his allotted time with drilling his students in routine operations he kills their interest, hampers their intellectual development, and misuses his opportunity. But if he challenges the curiosity of his students by setting them problems proportionate to their knowledge and helps them to solve their problems with stimulating questions, he may give them a taste for, and some means of, independent thinking [Quoted from the 1957 (2nd) edition, p. v].
The first IEA study on mathematical achievement (1964–1967), the precursor of the TIMSS studies, listed five cognitive behavior levels as components of mathematical achievement including content knowledge. The last three of these were: “(a) translation of data into symbols or schema or vice versa; (b) comprehension: capacity to analyze problems, to follow reasoning; and (c) inventiveness: reasoning creatively in mathematics” (Husén, 1967).
Seymour Papert, the inventor of the educational computer language LOGO, wrote in 1972 (pp. 249–250):
Being a mathematician is no more definable as ‘knowing’ a set of mathematical facts than being a poet is definable as knowing a set of linguistic facts. […] being a mathematician, again like being a poet, or a composer, or an engineer, means doing rather than knowing or understanding. […] In becoming a mathematician does one learn something other and more general than the specific content of particular mathematical topics? Is there such a thing as a Mathematical Way of Thinking? Can this be learnt and taught? [Italics in the original]
These quotations point to other faces of mathematics than systematically organised subject matter, factual content knowledge and procedural skills, namely to significant mathematical processes. So, historically we are faced with rather different conceptualisations of what it means to master mathematics, such as:
-
focusing primarily on knowledge and understanding of content, e.g. definitions, concepts, theorems, and theoretical structures;
-
focusing primarily on skills pertaining to algorithmic procedures and techniques;
-
focusing primarily on the overall enactment of mathematics, i.e. working within and by means of mathematics in intra- and extra-mathematical contexts, especially problem solving;
-
focusing primarily on general mathematical thinking and on mathematics as part of human culture, like art and science.
None of these different foci can stand alone, and they are not contradictory. When people think they are, unfruitful controversies arise, cf. the maths wars in some countries. Rather, these foci represent different, albeit mutually dependent, emphases. There are, however, context-dependent balances to be struck amongst them.
Recent Trends
Next, we zoom in on some trends which since the 1980’s have put emphasis on the enactment of mathematics.
The National Council of Teachers of Mathematics (NCTM) in the USA took the lead in breaking significant new paths in this respect. Already NCTM’s An Agenda for Action: Recommendations for School Mathematics of the 1980s (1980), recommended, among other things, that “problem solving should be in the focus of school mathematics in the 1980s”, that “basic skills in mathematics be defined to encompass more than computational facility”, and that “the success of mathematics programs and student learning be evaluated by a wider range of measures than conventional testing” (p. 1).
The highly influential NCTM Curriculum and Evaluation Standards for School Mathematics, 1989, stated the following goals for all K-12 students: (1) that they learn to value mathematics; (2) that they become confident in their ability to do mathematics; (3) that they become mathematical problem solvers; (4) that they learn to communicate mathematically; and (5) that they learn to reason mathematically. (p. 5). From these goals four overarching standards for mathematics at all grade levels were derived: ‘Mathematics as problem solving’; ‘mathematics as communication’; ‘mathematics as reasoning’; and ‘mathematical connections’. The 1989 Standards gave rise to the Math Wars in the USA in the 1990s, because opponents held differing views of what it means and takes to come to grips with mathematics. This was one of the factors behind the publication of NCTM’s revised Principles and Standards for School Mathematics (2000), which preserved the overarching standards for all school levels, but added one more, ‘representations’, whereas attitudinal and dispositional aspects were omitted.
Similar conceptions were nurtured and implemented in Australia since the 1980s. Thus, the National Statement on Mathematics for Australian Schools (1990) gave emphasis both to mathematical products and processes, involving observing, representing and investigating patterns in social and physical phenomena and between mathematical objects, with a focus on mathematical thinking and mathematical modelling. The document Mathematics—a curriculum profile for Australian Schools (1994) focused on what it means to work mathematically: ‘investigating’; ‘conjecturing’; ‘using problem solving strategies’; ‘applying and verifying’; ‘using mathematical language’; and ‘working in context’.
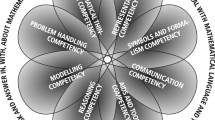
The Danish KOM Project (Niss & Jensen, 2002; Niss, 2003) developed the notion of mathematical competence and mathematical competencies, defined as follows:
“Possessing mathematical competence means to have knowledge about, to understand, to exercise, to apply and relate to and judge mathematics and mathematical activity in a multitude of contexts which actually do involve, or potentially might involve, mathematics”, whilst mathematical competencies are the main constituents in mathematical competence: “A mathematical competency is insight-based readiness to act purposefully in situations that pose a particular kind of mathematical challenge.” (p. 43). The project identified eight such competencies and depicted them by way of the so-called ‘competency flower’ (Fig. 1).
Roughly at the same time, but independently of the KOM Project, projects in the USA worked along similar lines. The National Research Council’s (NRC) Adding It Up: Helping Children Learn Mathematics (2001) and the RAND Mathematics Study Panel (2003) adopted the term mathematical proficiency, specifying five interwoven strands: ‘conceptual understanding’; ‘procedural fluency’; ‘strategic competence’; ‘adaptive reasoning’; and ‘productive disposition’ (p. 116). To the NRC team this notion captures what is believed “to be necessary to learn mathematics successfully” (our italics), whilst to the RAND panel it captures “what it means to be competent in mathematics” (our italics). The RAND Panel also introduced the notion of mathematical practices:
Because expertise in mathematics […] involves more than just possessing certain kinds of knowledge, we recommend […to] focus explicitly on mathematical know-how—what successful mathematicians and mathematics users do. We refer to the things that they do as mathematical practices. Being able to justify mathematical claims, use symbolic notation efficiently, and make mathematical generalizations are examples of mathematical practices (p. 29).
This notion was taken further by the Common Core State Standards Initiative (2012), in the US, which identified eight mathematical practices: “Make sense of problems and persevere in solving them. Reason abstractly and quantitatively. Construct viable arguments and critique the reasoning of others. Model with mathematics. Use appropriate tools strategically. Attend to precision. Look for and make use of structure. Look for and express regularity in repeated reasoning (pp. 1–2)”.
We have now seen that several different people, bodies and agencies have felt the need to insist that mastering mathematics goes beyond possessing mathematical content knowledge and procedural skills. It also involves the enactment of mathematics in a broad and comprehensive sense. There are significant similarities between the different conceptualisations of mathematical enactment, but there are characteristic differences as well, not only as far as terminology is concerned but also with regard to the scope of the notions, e.g. concerning the role of attitudinal, dispositional and volitional aspects.
Mathematical Competencies (and Their Relatives)
Obviously, widespread notions such as ‘mathematical literacy’, ‘numeracy’, ‘quantitative literacy’, ‘mathematical competence/competencies’ and—yes!—‘mathematics’ are related, yet not identical. How might we characterise relationships among them, for instance by way of a Venn diagram? Of course, there is no unique representation of these relationships. We perceive ‘mathematical competencies’ as encompassing ‘mathematical literacy’, which in turn encompasses ‘quantitative literacy’ (the US term) and ‘numeracy’ (the UK/Australia term). They are all intersected by the discipline ‘mathematics’ with its two facets ‘mathematical products’ and ‘mathematical processes’. Thus, ‘mathematics’ as a discipline is not a subset of ‘competencies’, ‘literacy’ or ‘numeracy’.
A related issue is what we should value and emphasise in mathematics teaching and learning, considering for example the following list of possible elements: ‘thinking mathematically’; ‘practical survival skills’; ‘number sense’; ‘doing mathematics’; ‘modelling, mathematising’; ‘what mathematicians do’; ‘mathematical communication—understanding, expressing’; ‘mathematical reasoning’; ‘mathematical algorithms and procedures’; ‘extracting/defining problems from work/life/world’; ‘inferences from data’; ‘definitions theorems, proofs’; ‘applying mathematics in context’; ‘cultural appreciation (nature, history and role of mathematics’.
These elements play rather different parts and are valued rather differently in different contexts. One such context is the notion of mathematical literacy as defined in PISA, here quoted from the 2015 framework:
Mathematical literacy is an individual’s capacity to formulate, employ, and interpret mathematics in a variety of contexts. It includes reasoning mathematically and using mathematical concepts, procedures, facts, and tools to describe, explain and predict phenomena. It assists individuals to recognize the role that mathematics plays in the world and to make well-founded judgments and decisions needed by constructive, engaged and reflective citizens (p. 5).
As appears, the key components in PISA are ‘formulate’, ‘employ’ and ‘interpret’, which are simply code for mathematical modelling. PISA mathematics does not make explicit use of the notion of mathematical competencies in the sense of the KOM Project, but of the derived notion of ‘fundamental mathematical capabilities’ that takes account of the realities of an international assessment in which elements have to be separable in order to be measurable. Figure 2 offers a diagrammatic summary of the PISA elements.
Aspects of Research Concerning Mathematical Competencies
There are two types of research on mathematical competencies. The first type has competencies as its main object of research. The second type employs competencies as an essential means of research for some other purpose. Both types comprise theoretical as well as empirical research. Since it is clearly not possible to do justice to the huge body of research in the field, we have confined ourselves to outlining a few selected topics.
As regards mathematical competencies as an object of research, much research—having theoretical perspectives as an integral part—investigates various notions of competence/competency and the specification of their components and facets. Are the notions of a purely cognitive nature or do they include dispositional and affective elements too? To what extent do the notions depend on culture, situations, mathematical levels or domains, and how are they related to universal or particular mathematical practices? There is also research trying to model the structure of the system of competencies.
Other research takes a predominantly empirical perspective on the entire system of competencies, e.g. in order to underpin the existence and significance of the construct, to identify the main dimensions of the competencies as well as stages of their development with individuals or groups, with the aim of fostering and supporting such development. Particular attention has been paid to the professional development of teachers, focusing on their coming to grips with the notion of competencies and supporting them in assessing them.
Still other research focuses on the individual competencies. It has been shown that competencies can be detected and identified empirically in people’s actual mathematical activities, albeit with some complications. One such complication is that mathematical competencies are neither developed nor possessed or enacted in isolation. So, in tests it is often difficult to measure particular facets of competencies exactly, for instance because problems often can be solved in rather different ways, invoking rather different sets of competencies. The solution of 1-step tasks cannot really show the difference between deep understanding of mathematics and rote learning of knowledge and procedures. Moreover, competencies are often defined to be overlapping (e.g. problem solving almost inevitably makes use of representations and of work with symbols and formalism). It is important to notice that lots of research has been conducted, also in the past, on individual competencies (e.g. problem solving, modelling, reasoning, representations) without ever referring to the term ‘competency’.
A growing body of theoretical and empirical research makes use of mathematical competencies as a means of research. For example to underpin new mathematics frameworks or curricula, to capture and understand what happens in actual mathematics teaching, or to create learning environments based on competencies. Competencies are also used to underpin test design, item formats and interpretation of item difficulty. Identifying and analysing misconceptions can also be supported by adopting a competency perspective. The same is true with regard to teachers’ beliefs and views of mathematics.
Competencies and National Mathematics Curricula
Competencies and their relatives play a variety of roles in different national curricula, even though several terms other than ‘competency’ are being used across countries. As it cannot be our ambition to provide geographical coverage of the world’s about 200 countries we have selected a sufficiently varied set of countries/regions to provide a fair representation of the spectrum of ideas and issues pertaining to these notions in a curriculum context.
In Spain, which is inspired by successive PISA frameworks, the 1989 NCTM Standards, the Common Core State Standards Initiative, and the Danish KOM Project, the role of mathematical competencies appears strong on paper but is weak in terms of actual implementation and practice. Spanish curricula use notions and terms in the intersection of the international sources and ad hoc combinations of them. Thus, Spain employs the term ‘sub-competencies’, e.g. reasoning mathematically, posing and solving problems, modelling, and communication in, with and about mathematics, for what is elsewhere called competencies. When developing related sub-competencies, the learner is supposed to acquire the ability to understand a chain of mathematical reasoning, (re)formulate a question as a mathematical problem, express oneself mathematically, and to deal with models set up by others.
Since the 1970s Portugal has placed problem solving and problem posing—initially viewed and referred to as skills across mathematical content areas—at the heart of mathematics education. Later, the national curricula have evolved to introduce and utilise the notion of mathematical competence and to state the development of mathematical competencies as educational goals for primary and secondary school. Like in Spain, teachers are struggling with competency-based mathematics teaching and with the diversity of terminology around it. Terms such as ‘basic content’, ‘basic skills’, ‘basic competencies’, ‘essential competencies’, and ‘capacities’ are used in Portuguese mathematics teacher education programmes. Recent curriculum developments show a tension between what is/should be considered ‘content’ and what ‘capacity’, along with debates on whether it is possible to reconcile the two notions, whilst avoiding merely seeing capacities as ways of dealing with specific content knowledge.
In Latin America, Brazil, Colombia, Costa Rica, Chile, Mexico and the Dominican Republic, among others, have experienced curriculum reforms inspired by PISA frameworks and competency-oriented ideas. A common thrust of these reforms has been to focus on learners’ recognition of the social role of school mathematics and of real world problem solving in everyday, social and societal life. Despite significant differences amongst countries, they all emphasise the functional use of mathematics. The purpose of education is defined in terms of ‘capabilities’ (Chile), ‘competencies’ (Mexico, Colombia and the Dominican Republic) and ‘abilities’ (Costa Rica). Relating mathematical thinking to specific mathematical topics and processes (problem solving, reasoning, communication and modelling) is commonplace. Chile, the Dominican Republic and Mexico include attitudes in their notions, while Colombia highlights contexts.
In the Australian curriculum of 2012, numeracy is included as one of the general capabilities: Students become numerate as they develop the knowledge and skills to use mathematics confidently across all learning areas at school and in their lives more broadly. Numeracy involves students in recognizing and understanding the role of mathematics in the world and having the dispositions and capacities to use mathematical knowledge and skills purposefully. The curriculum further contains three content strands: ‘number and algebra’; ‘measurement and geometry’; and ‘statistics and probability’, as well as four proficiency strands (close to the ones in “Adding It Up”): ‘understanding’; ‘fluency’; ‘problem solving, including modelling’, and ‘reasoning’.
In Korea, emphasis historically was placed on content, whilst doing mathematics was seen as part of learning that content. In 2011 there was a shift of focus so as to strengthen processes that can be seen as versions of mathematical competencies: Crucial capabilities for members of a complex, specialized, and pluralistic future are believed to be fostered by learning and practicing mathematical processes, including mathematical problem solving, communication and reasoning.
Several South-East Asian countries (Brunei Darussalam, Cambodia, Indonesia, Lao PDR, Malaysia, Philippines, Singapore, Thailand, Timor Leste, Vietnam) are introducing new regional assessment programmes and corresponding assessment frameworks. Definitions of mathematics include a clear focus on connecting conceptual and procedural knowledge to its use in daily life whilst emphasising broader goals of the mathematics curriculum, such as ‘mathematical thinking and reasoning’ and ‘problem solving’, referencing mathematical competencies in various ways. As particularly regards Singapore, doing is perceived as part of knowing, as depicted in the well-known regular pentagon having ‘mathematical problem solving’ as its core, placed in the interior of the pentagon, whereas the five edges—‘mathematical concepts’, ‘processes’, ‘skills’, ‘attitudes’ and ‘metacognition’—can be seen as facets of or prerequisites to problem solving.
The final stations on our excursion to national curricula are the German speaking countries in Europe. As a result of the so-called “PISA shock” in Germany in 2000, a multitude of concerted efforts were made to remedy the situation. A first outcome was the educational standards for mathematics agreed upon by all German Länder (states) in 2003, the core of which consists of six standards—‘reasoning’; ‘problem solving’; ‘modelling’; ‘using mathematical representations’; ‘dealing with symbolic, formal and technical aspects of mathematics’—that correspond closely to six of the eight Danish KOM Project competencies. These standards/competencies are placed in a three-dimensional structure, having five mathematical content areas (‘numbers’; ‘measure’; ‘space and shape’; ‘functional dependencies’; ‘data and randomness’) and three levels of mastery as in the early PISA frameworks (‘reproducing’; ‘making connections’; ‘generalising and reflecting’) as the other two dimensions. Austria, too, has adopted a rather complex three-dimensional model of processes (‘representing’; ‘building models’; ‘operating’; ‘interpreting’; ‘reasoning’), content areas (‘numbers and measures’; ‘variables’; ‘functional dependencies’; ‘geometric figures and solids’; ‘statistical representation and descriptors’), and finally three levels of mastery (‘activation of basic knowledge and skills’; ‘creating connections’; ‘activation of reflective knowledge’). Switzerland in 2007 adopted a national framework, inspired by the NCTM Standards, PISA, and the German educational standards, to harmonise compulsory school education across all cantons. The framework is based on eight fundamental aspects of mathematical action (‘knowing, realizing and describing’; ‘operating and computing’; ‘employing instruments and tools’; ‘representing and communicating’; ‘mathematising and modelling’; ‘reasoning and justifying’; ‘interpreting and reflecting on results’; ‘investigating and exploring’), combined with mathematical content in a matrix structure for each of the years 4, 8 and 11.
As can be seen, the three German speaking countries have embarked on similar developments, in which competencies/standards are placed in a three-dimensional cluster and also contain dispositional and volitional components. Efforts are being made to empirically measure facets of competencies of individuals and of larger groups of students, while attempting to stepwise reduce the number of activity dimensions so as to reduce overlaps.
This excursion has largely focused on curriculum frameworks and documents. But how strong is the match between goals and wishes expressed in these documents and the practices in mathematics classrooms? This takes us to our next section.
Challenges to Implementation
One major challenge to the implementation in classrooms of competency-oriented ideas, frameworks and curricula is that teachers are not always provided with the professional competencies and didactic-pedagogical resources needed to create classroom cultures in which systematic work to develop students’ mathematical competencies is the norm. Throughout the world there seems to be a lack of sufficiently helpful guidelines and support for pre-and in-service teachers.
This is not only an obstacle to the implementation of competencies in everyday classroom practice, but also to research and development committed to influence such practice. We need to better understand how research on mathematical competencies can be transformed into educational action and design of intervention, and vice versa: how can educational action and intervention become objects of research?
Building bridges between research and practice regarding mathematical competencies is notoriously difficult and has been approached in different places. Some approaches (e.g. in Germany) have focused on the design and implementation of professional development programmes for teachers, aiming at developing their theoretical understanding along with their teaching and assessment practice. Catalonia in Spain offers an example of the effective recognition of professional development as critically important for the implementation of competency-based mathematics teaching and learning. The aim is not only to acknowledge but also to work with practicing and future teachers. Thus the task of translating competency research into practice has been addressed in the development project ARC (Application of Resources to the Curriculum). The project was started in order to model, pilot and evaluate “mathematical activities within a competency framework”, assuming that this might help teachers meet “the challenge to assist all learners in the development of mathematical competencies by providing validated classroom experiences”. Projects involving collaboration of teachers and researchers have been conducted with specific schools, classrooms and activities, so as to make successful teaching public. The projects have brought up the complexity of changing culturally long established practices of mathematics teaching that have become routinised.
Findings from several cycles of these projects suggest further challenges to be taken into account. We have to work more to understand the operational dimensions of mathematical competencies, especially concerning what collaborative action research can contribute, and how. Here, researchers face the need to go beyond anecdotal research-and-development collaboration with particular schools, teachers, classrooms, and students.
Despite the success and relevance of context-bound local initiatives of professional development and research, it is not clear how the improvements obtained under such conditions can be sustained and scaled-up.
Perspectives and Concluding Remarks
We have attempted to present significant, yet necessarily selected, aspects of and challenges to what some call “the competency turn” in mathematics education, research and practice. This has given rise to a number of important observations and conclusions:
-
It remains crucial to come to grips with what it means and takes to master mathematics.
-
Focusing on the enactment of mathematics in a broad sense is seen as essential in more and more places.
-
Conceptualisation of this enactment needs further theoretical clarification and empirical investigations.
-
Understanding the relationships and balances between the enactment of mathematics and other components of mathematical insight and knowledge remains a challenge.
-
There is a need to clarify the role of attitudinal, volitional and dispositional factors in the conceptualisations and the reality of mathematical competencies.
-
Terminological issues continue to cause confusion. To what extent are things called by the same name—e.g. competencies—actually equivalent? And to what extent do things called by different names actually cover different notions? And to the extent they do, what exactly are the relationships between them?
-
The lack of a unified conceptual and theoretical framework for competencies, proficiency, processes, practices etc. tends to impede the possibilities of overcoming the challenges identified.
-
In summary, a plethora of research and development work will be facing us in the years to come. There is every reason to expect, therefore, that there will be substantial progress to report on in future ICMEs.
References
Australian Education Council. (1990). A national statement on mathematics for Australian school. http://files.eric.ed.gov/fulltext7ED428947.pdf. Accessed May 30, 2016.
Australian Education Council/Curriculum Corporation. (1994). A national statement on mathematics for Australian school. http://cataloguw.nla.gov.au/Record/80076. Accessed May 30, 2016.
Board of Education. (1938). Report of the consultative committee on secondary education with special reference to grammar schools and technical high schools (“The Spens Report”). London: HM Stationery Office.
Husén, T. (Ed.). (1967). International study of achievement in mathematics (vols. 1 & 2). Stockholm: Almqvist & Wiksell.
National Council of Teachers of Mathematics. (1980). An agenda for action: Recommendations for school mathematics of the 1980s. Reston: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston: National Council of Teachers of Mathematics.
National Research Council, & Mathematics Learning Study Committee. (2001). Adding it up: Helping children learn mathematics. National Academies Press.
Niss. M. (2003). The Danish KOM project and possible consequences for teacher education. In R. Strässer, G. Brandell, B. Grevholm, & O. Helenius (Eds.) (2003). Educating for the future. Proceedings of an International Symposium on Mathematics Teacher Education (pp. 178–192). Gothenburg: Royal Swedish Academy of Science.
Niss, M., Bruder, R., Planas, N., Turner, R., & Villa-Ochoa, J. A. (2016). Survey team on: Conceptualisations of the role of competencies, knowing and knowledge in mathematics education research. ZDM Mathematics Education, 48(5), 611–632.
Niss, M., & Jensen, T. H. (Eds.). (2002). Kompetencer og matematiklæring—Idéer og inspiration til udvikling af matematikundervisning i Danmark. Uddannelsesstyrelsens temahæfteserie nr. 18. Copenhagen: The Ministry of Education.
Papert, S. (1972). Teaching children to be mathematicians vs. teaching about mathematics. International Journal of Mathematical Education in Science and Technology, 3(3), 249–262.
Pólya, G. (1945). How to solve it?. Princeton: Princeton University Press.
RAND Mathematics Study Panel. (2003). Mathematical proficiency for all students. Toward a strategic research and development program in mathematics education. Santa Monica, CA: RAND.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access Except where otherwise noted, this chapter is licensed under a Creative Commons Attribution 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
Copyright information
© 2017 The Author(s)
About this paper
Cite this paper
Niss, M., Bruder, R., Planas, N., Turner, R., Villa-Ochoa, J.A. (2017). Conceptualisation of the Role of Competencies, Knowing and Knowledge in Mathematics Education Research. In: Kaiser, G. (eds) Proceedings of the 13th International Congress on Mathematical Education. ICME-13 Monographs. Springer, Cham. https://doi.org/10.1007/978-3-319-62597-3_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-62597-3_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-62596-6
Online ISBN: 978-3-319-62597-3
eBook Packages: EducationEducation (R0)